Comparisons of treatment optimization directly incorporating systematic patient setup uncertainty with a margin-based approach

Abstract

Purpose: To develop a probabilistic treatment planning (PTP) method which is robust to systematic patient setup errors and to compare PTP plans with plans generated using a planning target volume (PTV) margin optimized to give the same target coverage probability as the PTP plan.

Methods: Plans adhering to the RTOG-0126 protocol are developed for 28 prostate patients using PTP and margin-based planning. For PTP, an objective function that simultaneously considers multiple possible patient positions is developed. PTP plans are optimized using clinical target volume (CTV) structures and organ at risk (OAR) structures. The desired CTV coverage probability is 95%. Plans that cannot achieve a 95% CTV coverage probability are re-optimized with a desired CTV coverage probability reduced by 5% until the desired CTV coverage probability is achieved. Margin-based plans are created which achieve the same CTV coverage probability as the PTP plans by iterative adjustment of the CTV-to-PTV margin. Postoptimization, probabilistic dose-volume coverage metrics are used to compare the plans.

Results: For equivalent target coverage probability, PTP plans significantly reduce coverage probability for rectum objectives (−17% for D₃₅ < 65 Gy, p = 0.0010; −23% for D₂₅ < 70 Gy, p < 0.0001; and −27% for D₁₅ < 75 Gy, p < 0.0001). Physician assessment indicates PTP plans are entirely preferred 71% of the time while margin-based plans are entirely preferred 7% of the time.

Conclusions: For plans having the same target coverage probability, PTP has potential to reduce rectal doses while maintaining CTV coverage probability. In blind comparisons, physicians prefer PTP plans over optimized margin plans. (Work supported by NIH P01CA116602 and T32CA113277.)

INTRODUCTION

In planning fractionated external beam radiation therapy, treatment plans developed should be robust to random and systematic inter-fractional patient setup errors to ensure the target volume receives a tumoricidal dose and that organ at risk doses are kept below complication thresholds. The common approach to accommodate setup errors is to use a planning target volume (PTV) as a surrogate for the clinical target volume (CTV) during the planning process.^{1, 2} The intent of the PTV is to ensure that the CTV receives the prescription dose for an expected percentage of the setup errors. Geometrically, this is accomplished by expanding the CTV by a margin to create the PTV. Margin recipes have been developed which suggest the margin size as functions of the standard deviations (SDs) of random and systematic errors.^{3, 4, 5, 6} In principle, site and institution-specific SDs can be obtained by direct measurements of a suitable population of patients and margins directly computed. In practice, margins are based on clinical experience and are applied as uniform expansions of the CTV in three-dimensions, with possible adjustment depending on the site, and adjacent critical structures. In either case, due to the fact that the dose distribution imperfectly conforms to the PTV volume, the percentage of setup errors in which the CTV receives the prescribed dose level can differ from what is expected for a given PTV margin.^{7, 8} The CTV coverage is dictated by the treated volume, which is only indirectly a function of the PTV.

An alternative to margins is to use probabilistic treatment planning (PTP) or robust optimization methods, which ensure CTV coverage by optimizing the treatment plan dose distribution while incorporating the effects of the patient setup uncertainty.^{9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22} PTP methods do not require specification of PTVs or planning risk volumes (PRVs). Instead, given the probability distributions of setup errors, the plan optimization constructs a treated volume to meet the planning criteria without constricting the dose to predefined PTVs/PRVs. When the locational probability distributions of a CTV and organs at risk (OAR) volumes overlap, PTP optimization can directly optimize the trade-offs. PTP permits creation of nonuniform static dose distributions to meet the planning goals when the cumulative effect of patient setup errors are folded into the dose evaluation.

Potential benefits of PTP have been documented for methods designed to accommodate just the random component of the positioning uncertainty,^{16, 17, 20} and the combined effects of random and systematic positioning uncertainties.^{9, 13, 14, 15, 18, 21, 22} Considering only the random component, using a dose convolution approach, Balter et al.¹⁷ found that PTP reduces the treated volume by 6%–8% as compared to a margin-based approach for focal liver tumors. Using multiple offset replicas of the patient’s geometry to accommodate random errors, McShan et al.²⁰ confirmed that PTP reduced normal tissue doses and created plans which were more robust to positioning errors than margin-based plans. For prostate, Moore et al.¹⁶ used fluence convolution to mimic the random patient positioning variability in the accelerator coordinate system and found that PTP reduced the dose to local normal tissue by 48% and increased the probability of uncomplicated tumor control (P+) by 2.5% compared to margin-based methods.

Considering both random and systematic errors, using a stochastic optimization of P+ including the effects of setup uncertainties, Lof et al.⁹ demonstrated the potential for PTP to increase P+ compared to margin-based methods. For various treatment sites and using different effective uniform dose (EUD)-based PTP optimization approaches, Baum et al.,²² Birkner et al.,¹⁸ Yang et al.,²¹ and Witte et al.¹³ each found increased OAR sparing compared to margin-based methods. Yang confirmed improved OAR sparing even over methods that incorporate an ICRU 62 PRV.²¹ Gordon et al.^{14, 15} used probabilistic dose-volume histogram (PDVH)-based coverage criteria, evaluated via sampling setup error probability distribution functions, as an optimization goal, and found that, compared with standard margins, a ∼20% average reduction in volume receiving the treatment dose could be achieved while maintaining desired target coverage probabilities, or an increased target coverage probability could be achieved for same OAR dose.¹⁴ While the potential benefits of PTP using EUD or specialized coverage-based objective functions seem clear, except for Gordon et al.^{14, 15} who used 27/28 prostate patients and Witte et al. who used 19 prostate patients, these prior PTP studies are mainly demonstration studies, limited to at most three patients per treatment site. Furthermore, none of these studies is backed up with physician evaluation of the resultant treatment plans.

The purpose of this work is to explicitly incorporate dosimetric effects of random and systematic setup uncertainties into treatment plan optimization by performing a joint optimization over multiple probable patient setup positions. Due to its ability to consider relative locations of targets and risk structures during the optimization, it is hypothesized that this optimization method will produce plans with similar target coverage while reducing the dose received by treatment risk structures compared with margin-based plans. This is evaluated by comparing the PTP plans with margin-based plans. The primary differences from previous work include study of a large patient population, use of dose-volume objectives for optimization, and analysis with coverage probability, probabilistic dose-volume histograms, and physician assessment.

METHODS AND MATERIALS

This study compares margin-based and PTP-based treatment plans for a series of 28 prostate patients. For each patient, the process is split into three steps: (1) a PTP plan is created and the coverage probability is evaluated; (2) a margin-based plan is created with the same coverage probability (within tolerance) as the PTP plan; (3) metrics are compiled for each plan and used for plan comparison. This process is repeated until the entire patient population has been analyzed. The patient contouring and planning steps are described in detail in the sub-sections below.

Planning parameters

Imaging and contour data from 28 prostate patients treated under an approved institutional review board protocol are used in this study. The plan used for the patient treatment is discarded and new plans are generated for this virtual plan comparison study. Patient plans are generated with a research version of Pinnacle³ 8.1y (Philips Healthcare - Philips Radiation Oncology Systems, Fitchburg, WI) using a seven-beam setup with beam angles of 30°, 80°, 130°, 180°, 230°, 280°, and 330°, with the 180° beam corresponding with a posterior beam. The dose matrix resolution of 4 × 4 × 4 mm³ is used during the intensity modulation optimization. The CTV is defined as the prostate plus seminal vesicles. PTP directly uses the CTV during the optimization. For margin-based planning, the PTV is a uniform expansion of the CTV. Patient specific and population specific models are not considered in this study. In order to produce a fair comparison between plans, the size of the CTV-to-PTV margin is adjusted to match the CTV coverage achieved during the PTP planning (described below). The impact of using a variable margin instead of a fixed margin is discussed further in Sec. 4. The optimization objectives are based on the RTOG-0126 protocol (shown in Table TABLE I.). The PTP plans use custom objective functions (described below) while the margin-based plans use the standard objective functions available in Pinnacle. The patient setup errors are assumed to be normally distributed with a standard deviation in systematic uncertainty of 3 mm in each direction and the standard deviation in the random setup error of 3 mm. The use of normally distributed setup errors equal in each direction for this planning comparison study is justified in the discussion.

TABLE I.

Planning objectives according to RTOG-0126 with initial weights used in optimization.

Structure	Type	Dose (cGy)	Volume (%)	Weight
Target	Min DVH	7920	98	100
Target	Max DVH	8470	2	90
Rectum	Max DVH	6000	50	80
Rectum	Max DVH	6500	35	80
Rectum	Max DVH	7000	25	80
Rectum	Max DVH	7500	15	80
Rectum	Max dose	8470		80
Bladder	Max DVH	6500	50	80
Bladder	Max DVH	7000	35	80
Bladder	Max DVH	7500	25	80
Bladder	Max DVH	8000	15	80
Bladder	Max dose	8470		80
Left femur	Max DVH	3500	50	20
Left femur	Max dose	5000		20
Right femur	Max DVH	3500	50	20
Right femur	Max dose	5000		20

Probabilistic treatment planning

The main PTP optimization consists of two stages; creating an initial PTP plan followed by adjusting objective function weights to achieve acceptable coverage. To improve efficiency, the PTP optimization (Fig. 2) is wrapped in a loop (Fig. 1) which progressively increases the number of systematic errors sampled during the optimization. At the core of the PTP optimization is computation of the objective function and gradients used for updating the beam intensity profiles during the optimization. At initiation, objectives and weights are defined as shown in Table TABLE I.. An additional zero-weight target objective is added using a contour created by expanding the CTV contour by 1 cm. This objective ensures that active intensity values exist in locations where the target can be shifted to during the optimization. Since this objective has zero weight, it has no effect on the solution other than setting the initial intensities.

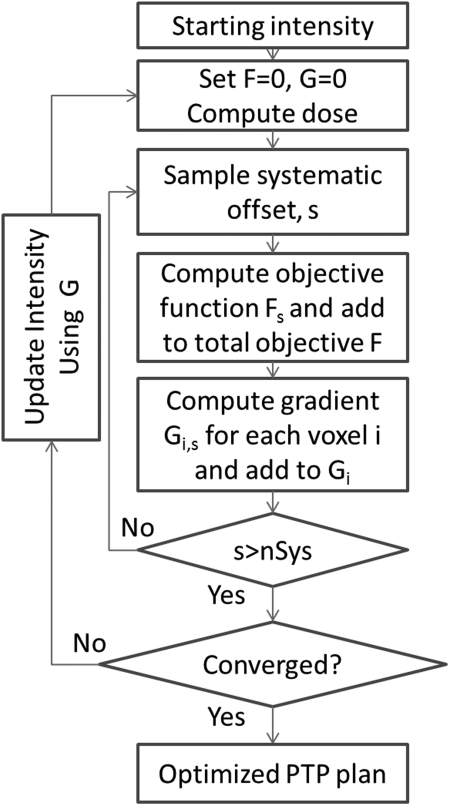
Figure 2.

PTP Process to generate an optimized plan accounting for systematic uncertainty. F is the total objective score, G is the total gradient matrix containing the first derivative of the objective function G_i for each voxel i. F_s is the objective function score for shift s.

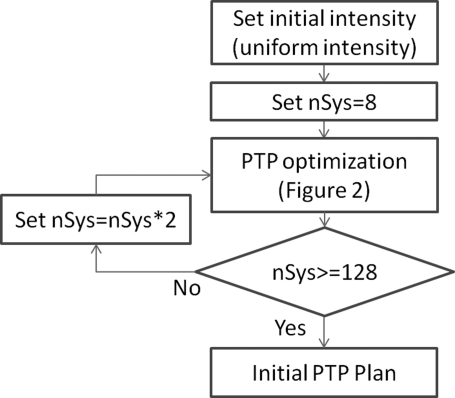
Figure 1.

Process for generating the initial PTP plan. nSys is the number of systematic shifts used during the PTP optimization process.

The general flow of creating an initial PTP plan is shown in Fig. 1. At initiation, the optimizer defines an initial uniform beam intensity which fully covers structures identified as target objectives for each beam. Systematic setup errors are simulated by shifting the dose distribution with respect to the patient anatomy and evaluating the objective function multiple times during the optimization. Initially, the number of systematic offsets nSys = 8. Optimization proceeds till convergence, then nSys is doubled and the inner optimization process restarts using the last intensity matrix as the initial intensity matrix. When nSys = 128, the initial PTP optimization is complete.

The inner loop of the PTP process is shown in Fig. 2. Note that initiating the process with the intensity matrix optimized in prior iterations, the process is jump-started permitting convergence with fewer iterations. Random setup uncertainties are incorporated into the optimization process in the dose computation step by convolving each beam’s incident fluence with a σ = 3 mm Gaussian in the dose calculation process. See Ref. 16 for details. Following dose computation, the planning objective function is evaluated for a sequence of nSys randomly sampled patient systematic errors. Assuming the dose distribution in the accelerator coordinate system is invariant to small patient shifts,²³ a systematic setup error corresponds with an offset of the dose distribution with respect to the patient’s anatomy. Offsets s are sampled from a Gaussian distribution with Σ = 3 mm. Each sampled systematic setup error s and associated objective function F_s (described below) evaluation therefore corresponds with a probable treatment course. The Pinnacle optimizer uses a Quasi-Newton gradient descent algorithm based upon a gradient matrix.²⁴ Every s generates an objective function gradient matrix, G_i,s, where the 3D matrix contains elements for each voxel i of the dose matrix. The cumulative objective function gradient for each voxel G_i is used to update the beam intensity matrix during the optimization, and the total objective function F is used to evaluate optimization convergence. The optimization terminates when the objective function F changes by less than 1 × 10⁻⁶ from the value in a preceding iteration or when 500 iterations have been completed.

Objective function

Dose-volume based objective functions are used in the simultaneous optimization over multiple sampled systematic errors. A standard maximum dose-volume objective function can be expressed as,

$$\begin{array}{c}\multicolumn{1}{c}{f^{\mathrm{MaxDVH}}=\frac{1}{N_{\mathit{roi}}}(p\sum _i^{N_{\mathit{roi}}}H(D_{V_{\mathit{Rx}}}-D_i)}\end{array}·H(D_i-D_{\mathit{Rx}})·{(D_i-D_{\mathit{Rx}})}^2),$$

where N_roi is the number of voxels in the region of interest (ROI) in which the dose-volume objective is being applied, p is the relative weight of the objective and is used when multiple objective functions are summed, D_Rx is the desired prescription dose, $D_{V_{\mathit{Rx}}}$ is the dose at the prescription volume such that $V\left(D_{V_{\mathit{Rx}}}\right)=V_{\mathit{Rx}}$, D_i is the dose in voxel i, and H is the Heaviside function. A minimum dose-volume objective, f^MinDVH, can be similarly defined. Details of dose-volume-based objective functions are described by Wu and Mohan.²⁵

In PTP optimization, the dose-volume objective function is evaluated for multiple potential treatment courses. Each treatment course is represented by a systematic shift s of the patient anatomy. For a given shift, s, the objective function is calculated by replacing D_i with the value from the shifted anatomy D_i+s and calculating $D_{V_{\mathit{Rx}}}$ for the shifted dose distribution $D_{V_{\mathit{Rx}},s}$ giving,

$$\begin{array}{c}\multicolumn{1}{c}{f_s^{\mathrm{MaxDVH}}=\frac{1}{N_{\mathit{roi}}}(p\sum _i^{N_{\mathit{roi}}}H(D_{V_{\mathit{Rx}},s}-D_{i+s})}\end{array}·H(D_{i+s}-D_{\mathit{Rx}})·{(D_{i+s}-D_{\mathit{Rx}})}^2).$$

The total objective function for a single ROI is obtained by summing over each systematic error sampled,

$$f=\sum _s^{n\mathrm{Sys}}{f}_s^{\mathrm{MaxDVH}}.$$

This results in each shifted anatomy contributing a component of the total objective function effectively creating a simultaneous optimization over all sampled shifts.

Note that in the equations above, a Heaviside function dependent on $D_{V_{\mathit{Rx},o},s}$ is used such as $H(D_{V_{\mathit{Rx},o},s}-D_{i+s})$. $D_{V_{\mathit{Rx},o},s}$ is dependent on the dose distribution underlying a specific shift and must be recomputed for each shift. Generally, $D_{V_{\mathit{Rx},o},s}$ will vary from shift to shift and thus changes the range of voxels the objective function operates on.

Weight-adjusted PTP plan

After initial optimization, the PTP plan is adjusted to ensure that the CTV D₉₈ dose-volume metric achieves a desired coverage probability (Refs. ^{14, 15}) Q_D, where the Q_D gives the probability of a treatment course meeting the specified dose-volume metric. To obtain a plan with the desired Q_D, the planning objective weights are adjusted using an iterative binary search. Only rectum and bladder weights are changed, and adjusted bladder weights are equal to adjusted rectum weights. Initially, the desired coverage probability (Q_D) is set to 95%. The iterative binary search investigates the weight range between 0 and 100, and halves the search range at each step until the desired weight is located. To avoid the trivial case of OARs with a weight of zero which effectively ignores the OARs entirely, the weight was required to be greater than zero. If the desired Q_D cannot be achieved with a nonzero OAR objective weight, Q_D is reduced by 5% and the search process re-initiated until an achievable value is reached. The iterative weight search process is stopped when the achieved coverage is within 0.5% of the desired coverage or the change in weight would be less than 1. The end result of this process is the final optimized PTP plan with a known Q_D.

Coverage optimized margin plan

To provide a fair comparison between margin-based planning and PTP, a margin-based plan is created which has the same Q_D as the final PTP plan. The method used to create a margin-based plan with a specific Q_D is similar to the iterative procedure described by Gordon et al.¹⁵ The objective function weights for the margin-based plan are given in Table TABLE I.. A uniform CTV-to-PTV margin M_T is used. To enforce OAR avoidance, each OAR structure is expanded by 1 cm to produce a PRV. Note, this 1 cm margin roughly corresponds with the value which would be recommended using the van Herk and Stroom margin formulas.^{4, 5, 6} The PRVs are not changed during the margin optimization process, but the CTV margin M_T is permitted to vary in the range of 0 cm to 1.0 cm. Any overlap in the structures is left to the optimizer to balance the objective scores. In all cases, postoptimization coverage is calculated on the original CTV structure, thus overlap is not considered. Similar to the process used to determine appropriate weights for the PTP plan, a binary search algorithm is used to cut the range of margin values in half at each step until the desired coverage probability is reached. The iterative process is stopped when the achieved coverage is within 0.5% of the desired coverage, or the change in margin would be less than 0.05 cm.

Comparison metrics

For both the final optimized PTP plan and the coverage optimized margin plan, coverage probabilities for all planning structures are computed along with PDVHs and dose-volume coverage maps (DVCMs) (Ref. ¹⁵) using the methods developed by Gordon et al.^{7, 14} A DVCM is a probability map which gives the probability of dose-volume values for a simulated set of setup errors. A DVCM is constructed by generating DVHs for many systematic shifts and computing the probability that the DVH curve lies above each dose-volume point. For this study, DVCMs are created assuming normally distributed 3 mm systematic and 3 mm random setup errors. Coverage values are read off at DVCM dose-volume pairs. To compare PTP and margin-based plans, coverage values are output for each optimization criteria dose-volume pair. A PDVH is a pseudo DVH created by interconnecting points at a given probability level on a DVCM. To assist in plan comparison, DVCMs are imported into MATLAB for display. Planning criteria for each structure are overlaid on the DVCMs to ease data interpretation. For a given patient, coverage values for two different planning scenarios can be compared by looking at the difference in the DVCMs. Dose-volume coverage difference maps (DVCDMs) are computed by subtracting one DVCM from another, e.g., the DVCM from the margin-based plan is subtracted from the DVCM from the PTP plan. DVCDM map values range from −1 to 1. Negative values indicate that the PTP plan has lower coverage for the dose-volume pair and positive values indicate that the PTP-based plan has a higher coverage for the dose-volume pair. To avoid dose interpolation errors, dose is recomputed on a 2 × 2 × 2 mm³ grid prior to coverage probability evaluations.

For comparing CTV PDVHs, 95 percentile values are used, which means that DVH values for 95% of the errors simulated will lie above the PDVH curve. For OARs, 5 percentile values are used so that 5% of the with-error simulated DVH values lie below the PDVH curve.

For each patient, DVHs and PDVHs for PTP and margin-based plans are also evaluated by two physicians to determine plan acceptability and preference. DVH and PDVH curves are generated and displayed for the target, bladder, rectum, left femur, and right femur structures. PDVHs are computed as above. For targets, DVHs were presented for nominal PTVs obtained by expanding the CTVs uniformly by 0.7 cm, except posteriorly where the expansion is 0.3 cm. Per physician preference, this PTV structure is used only in the assessment stage to generate a static DVH plot and was not used in any optimization. These nominal PTVs were used in preference to the actual PTVs used in optimizing margin-based plans, since they corresponded to current clinical practice at our institution, and therefore produced target DVHs that the physician could compare to familiar clinical examples. All curves for a given analysis type are presented on a single plot for each patient. Markers are placed on the graph to indicate the planning objectives used during optimization. To avoid bias, PTP and margin-based plans for each patient are randomized and labeled as A or B. Plots are presented to the physician to determine if a plan would be acceptable to treat and if both plans are acceptable, which plan would be the preferred plan to treat the patient.

RESULTS

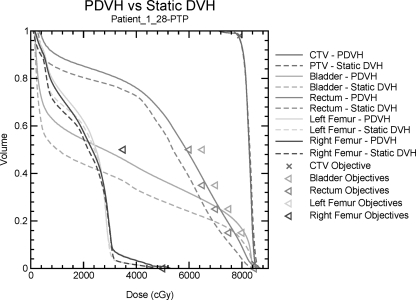
An example of a static DVH and a PDVH is shown in Fig. 3. Table TABLE II. lists the physician preference for each plan. Using static DVH plots for comparison, both physicians prefer the PTP plan for 23 patients while the margin plan is preferred for two patients. For three patients, one physician prefers the PTP plan, while the other prefers the margin plan. Using PDVH plots for comparison, both physicians prefer the PTP plan for 21 patients while the margin plan is preferred for four patients. For three patients, one physician prefers the PTP plan while the other prefers the margin plan. For 20 of the 28 patients, all physicians prefer the PTP plans using all assessment methods. The margin plan is preferred using all methods for only two patients.

Figure 3.

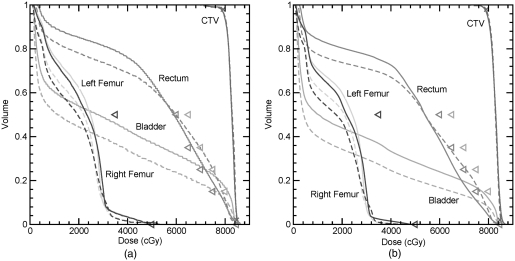
Static DVH and PDVH curves for the CTV, bladder, rectum, left femur, and right femur for the PTP generated for Patient 1. Solid lines represent PDVH curves and dashed lines represent static DVH. Objectives used during optimization are given as triangles.

TABLE II.

Physician assessment of PTP and margin-based plans. Preferred plan is indicated for each physician using probability dose-volume histograms or static dose-volume histograms.

Patient	PDVH		Static DVH
	Physician 1	Physician 2	Physician 1	Physician 2
1	PTP	PTP	PTP	PTP
2	PTP	PTP	PTP	PTP
3	PTP	PTP	PTP	PTP
4	PTP	PTP	PTP	PTP
5	PTP	PTP	PTP	PTP
6	PTP	PTP	PTP	PTP
7	PTP	PTP	PTP	PTP
8	PTP	PTP	PTP	PTP
9	PTP	PTP	PTP	PTP
10	Margin	Margin	Margin	Margin
11	PTP	PTP	PTP	PTP
12	Margin	Margin	Margin	PTP
13	PTP	PTP	PTP	PTP
14	PTP	PTP	PTP	PTP
15	PTP	PTP	PTP	PTP
16	Margin	PTP	PTP	PTP
17	PTP	PTP	PTP	PTP
18	PTP	PTP	PTP	PTP
19	PTP	PTP	PTP	PTP
20	Margin	PTP	PTP	PTP
21	PTP	PTP	PTP	Margin
22	PTP	PTP	PTP	PTP
23	PTP	PTP	PTP	PTP
24	PTP	PTP	PTP	PTP
25	PTP	PTP	PTP	PTP
26	Margin	Margin	Margin	Margin
28	Margin	PTP	PTP	Margin
30	Margin	Margin	PTP	PTP

For all patients, the margin required to meet the coverage in the PTP plan was recorded. The average margin required to match the PTP plan was 0.60 cm (min 0.46 cm, max 0.97 cm, SD 0.11 cm). The van Herk margin formula (VHMF) suggests a margin of 0.96 cm. This value only matched one sample using the optimized margin method, all others were lower. The specific plan which matched the VHMF produced 99.8% coverage probability to the CTV for the margin plan and 99.6% coverage for the PTP plan. The margin suggested by the VHMF being larger than the margin required using iterative margin expansion is consistent with the results shown by Gordon et al.⁷ In that work, it was shown that the volume receiving the prescription dose, termed the treated volume in ICRU nomenclature, is larger than the CTV-to-PTV margin, therefore yields greater coverage.

Coverage probability for OARs indicates the probability that a dose-volume objective will be exceeded. In an ideal plan, the OAR coverage probability for all points will be zero. In practice, this cannot be achieved, thus coverage below the planning objectives is allowed and the flexibility below plan objectives is used to reduce the score for other objectives. In a typical display, the OARs will have a lower coverage probability in the high dose regions, while the target structures will have a high coverage probability in the high dose regions.

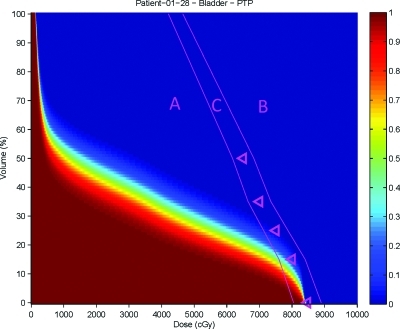
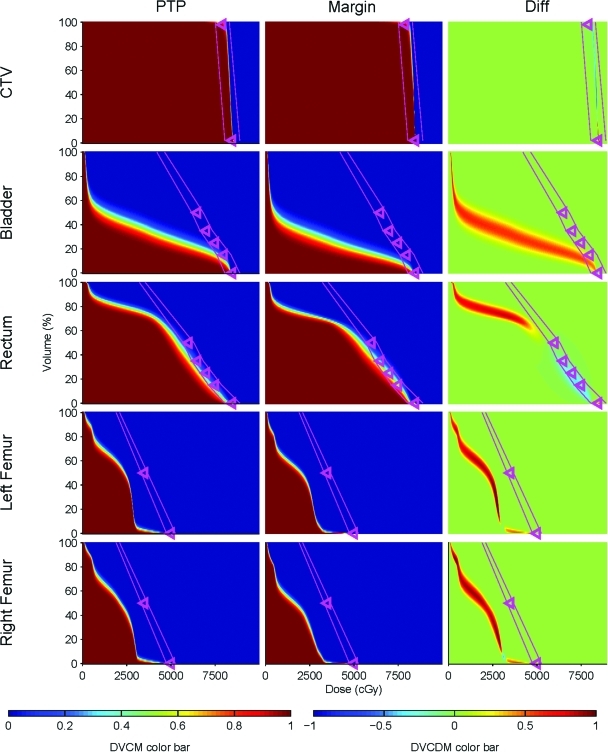
To understand the clinical meaning of the differences observed, it is useful to sub-divide OAR DVCMs into three regions as shown in Fig. 4. Region A is completely below the plan optimization objectives. Differences in region A can be considered to be unimportant as they are below the plan objectives. If doses in region A are deemed to be important for planning, an objective should be added to control dose in these areas, resulting in the point being moved to either region B or C. Region B is completely above the plan optimization objectives and is a clinically important region since this is where the optimizer failed to reduce the dose below the plan objectives. Region C is the intermediate region near the plan objectives, and is also clinically important since it demonstrates the objective function tradeoffs as the plan optimizer finds a solution.

Figure 4.

Regions of a DVCM. Region A is below the plan objectives, Region B is above the plan objectives, and Region C is the intermediate area near the plan objectives.

DVCMs and DVCDMs for the CTV, bladder, rectum and femur for Patient 1 are shown in Fig. 5. The trends in the data found for Patient 1 are typical of those for other patients. For the CTV, the DVCMs are similar, but not identical. Similarity is expected since the margin-based plan optimization is adjusted to provide the same coverage as the PTP plan. The CTV D₉₈ dose-volume objective has on average 90% coverage probability. Above D₉₈, dose coverage rapidly drops falling off towards the D₂ objective, with 45% at D₂. The rapid dose fall-off results from the upper and lower optimization DVH objectives which are set to achieve a uniform CTV dose. The DVCDM, which compares the PTP and margin-based DVCMs, shows a difference band with a width of ∼1 Gy. These minor differences are expected since, although the margin-based coverage was optimized to be equivalent, even if the margin and PTP-based coverage values are equivalent at D₉₈, coverage diverges at other dose values since the PTP and margin-based dose distributions differ. Although the primary convergence criterion requires coverage probability agreement within 0.5%, for some patients, target coverage differs by up to 8%. In the margin-based plans, target coverage can be very sensitive to slight changes in margin, thus it was not feasible to achieve exactly the same coverage as in the PTP plans. However, slight differences in target coverage were evaluated by physicians in their assessment of plans, and were judged not to be clinically significant.

Figure 5.

DVCMs and DVCDMs for the CTV, bladder, rectum, and femur for Patient 1. The DVCM indicates the probability that the dose-volume level is achieved in a given treatment course. Triangles on the DVCM indicate the dose-volume planning objectives used during plan optimization. The DVCDM compares the PTP and the margin-based plans. Values less than zero (blue regions) indicate lower doses by the PTP plan compared with the margin plan. Values greater than zero (red regions) indicate higher doses by the PTP plan. The pink lines differentiate the regions as shown in Fig. 4 .

Larger differences in DVCMs are observed for the OARs as shown in Fig. 5. The general trends seen for Patient 1 are evident for all patients: when an OAR dose is near the plan objectives, PTP reduces dose coverage in that region. This shows as blue in the DVCDM. However, PTP increases dose coverage at dose-volume regions well below the objective values. This shows as red in the DVCDM. From the methods used in this study, it cannot be determined if the increased OAR volumes receiving low doses are inherent to PTP or if adding dose-volume objectives for the lower volumes would push the dose to unspecified tissues. PTP shows higher coverage—the probability of the DVH curve exceeding the dose for a given volume—for all OARs in region A well below the planning objectives. For the bladder, neither method shows coverage in region B, while both methods show coverage in region C. PTP plans showed higher bladder coverage in region C for 9 out of 28 patients, while 5 patients showed higher coverage in the margin-based plans. For the rectum, none of the PTP plans showed coverage in region B while 7 out of 28 patients showed coverage in the margin-based plans. Margin-based plans showed higher rectal coverage in region C for 20 out of 28 patients while PTP plans show rectal coverage in region C for only one patient. For the femur, neither method shows coverage in region B. Femoral coverage is very low in both methods in region C. For the left femur a small dose tail extends out to the 5000cGy max dose objective in 21 out of 28 PTP plans, and 12 out of 28 for margin-based plans. For the right femur the tail reached the objective in 22 out of 28 PTP plans, and 12 out of 28 margin-based plans.

The average coverage probability for each structure is shown in Table TABLE III.. Target coverage probability is generally the same for each patient due to the design of the study. The average difference in coverage probability between PTP and margin plans is 0.7% ± 2.7%. The difference is not significant (p = 0.17) with a paired t-test.

TABLE III.

Coverage for PTP and Margin plans at planning objectives. Change represents coverage of PTP plan less coverage of margin plan. Significance is a result of a 2-sided paired t-test.

Structure	Volume (%)	Dose (cGy)	PTP	Margin	Change	P
BLADDER	50	6500	3	1	2	0.0005
BLADDER	35	7000	10	6	3	0.0156
BLADDER	25	7500	10	11	−1	0.7609
BLADDER	15	8000	5	11	−6	0.0146
BLADDER	0	8470	37	22	14	0.1084
CTV	98	7920	90	91	−1	0.2292
CTV	2	8470	45	32	12	0.2328
FEMUR_LT	50	3500	0	0	0	n/a
FEMUR_LT	0	5000	5	1	4	0.0078
FEMUR_RT	50	3500	0	0	0	n/a
FEMUR_RT	0	5000	6	0	6	0.0024
RECTUM	50	6000	1	6	−5	0.0962
RECTUM	35	6500	9	26	−17	0.0010
RECTUM	25	7000	18	41	−23	0.0000
RECTUM	15	7500	28	55	−27	0.0000
RECTUM	0	8470	19	10	9	0.1794

For organs at risk, the average coverage probability over all patients for PTP plans decreased 17% for the rectum D₃₅ < 65 Gy objective (p = 0.010) as compared to margin-based plans, decreased 23% for the rectum D₂₅ < 70 Gy objective (p < 0.0001) and decreased 27% for the rectum D₁₅ < 75 Gy objective (p < 0.0001). The bladder coverage changes are smaller, with PTP resulting in D₅₀ < 65 Gy increased by 2% (p = 0.0005), D₃₅ < 70 Gy increased by 3% (p = 0.156), D₁₅ < 80 Gy decreased by 6% (p = 0.0146), left femur 50 Gy max increased by 4% (p = 0.0078), and right femur increased by 6% (p = 0.0024) when compared to margin-based plans. Coverage for other objectives did not change significantly.

DISCUSSION

This study assumes random and systematic setup errors with standard deviations equal to 3 mm in each direction to simulate setup uncertainties. These numbers are typical of setup error values reported in the literature for (implanted marker-based) image alignment.^{4, 5, 13, 18, 26, 27} It is hypothesized that similar results will be obtained for image-based alignment procedures which have a larger setup error, however, this was not evaluated in the current study. In the case of larger uncertainties, PTP may show even more improvement when compared to the large margins calculated from population based formulas. On the other hand, as setup errors tend towards zero, no difference between PTP and PTV-based plans would be expected.

For the comparison purposes of this study, matching the setup-error to the clinical setup error is not required. While the general PTP method described in this paper allows non-normally distributed errors, unequal errors in each direction, and for tissue deformation, margin-based methods typically are not based on these assumptions. Standard margin formulas^{3, 4, 5, 6} assume normally distributed setup errors, and clinically, margins are typically chosen to be uniform in all directions around a structure, with occasional trimming to avoid nearby organs at risk. Use of normally distributed errors with the same standard deviation in each direction for PTP, while simplistic, realistically mimics the assumptions made in margin-based planning, but disregards the flexibility of PTP to address non-normal motion or tissue deformations. Thus, bias introduced by assuming uniform and normally distributed errors will be in favor of the margin-based approach. Nonetheless, the results demonstrate the advantages of PTP even when the assumptions of margin-based planning are followed. Future studies may include relaxing the requirement of isotropic distributions, however, these will require generation of margin-based plans from a similar distribution for comparison.

In the plan assessment stage, both static DVHs and PDVHs are used in this work. A comparison of static DVH and PDVH curves are displayed in Fig. 3. A static DVH represents a single patient setup. To ensure setup uncertainties are considered in planning, PTV DVHs are used to represent the DVH of the CTV.¹ For OARs, ideally PRVs are used to represent likely dose distributions to underlying structures. However, often PRVs are not used in planning, resulting in overly optimistic dose representation. A PDVH curve represents the DVH for a specified coverage probability. For the curves demonstrated in this work, the probability of CTV doses exceeding the PDVH is 95% and the probability of the dose to the critical structures being lower than the PDVH is 95%. Therefore, it is expected that in 95% of cases, the plan will perform better than the displayed curves.

Comparison of DVHs and PDVHs (e.g., Figs. 36) show that although margin-based plans seemingly meet or nearly meet the OAR optimization criteria when evaluated based on static DVHs, PDVH evaluation reveals a strong likelihood that the optimization criteria will be exceeded. Independent of the planning method, it would be prudent to provide physicians with the PDVH information for plan evaluation to allow incorporation of this information in the plan approval decision making process. Plans which have a significant probability of overdosing OARs should be rejected.

Figure 6.

(a) Probability dose-volume histogram for the 95% percentile DVH for the CTV and 5% DVH for the bladder, rectum, and femurs for PTP and margin-based plans. (b) Static dose-volume histograms for the CTV, bladder, rectum, left femur, and right femur for PTP and margin-based plans. Solid lines represent PDVH curves for the PTP plan and dashed lines represent the margin-based plan. Objectives used during optimization are given as triangles.

During the physician assessment of plans, only PDVHs and static DVHs are used. In a clinical situation, physicians would also evaluate the isodose lines for the targets and critical structures. The objective of this work is to compare PTP and margin-based planning subject to systematic uncertainty. While it is possible to produce isodose displays for each systematic offset, it is unreasonable for a physician to evaluate the isodose lines of a large number of systematic shifts. In the case of a high probability of a hot spot being located in the OARs, a longer tail will be noticed in the PDVH displays. Future research includes a method for displaying the isodose lines in a probabilistic manner.

To directly compare margin-based planning to PTP, patient specific coverage optimized margins were used in this study. In routine clinical practice, it is more common to use the same margin for each patient. An accepted method would be to use the van Herk margin formulation to determine the margin, which, for the setup errors assumed in this study would have yielded a margin of approximately 1 cm. In this work, all plans required a CTV-to-PTV margin of less than 1 cm to produce a similar target coverage probability as the PTP plans. Margin-based plans produced with a 1 cm margin would have resulted in both higher target coverage probability and an increase in dose to nearby local structures (an increased coverage probability for critical structures) compared to the optimized margins used in this study, similar to the findings of Gordon et al.¹⁵

Due to conflicting planning goals produced by PTV and PRV overlap structures and other considerations, PRV margins are often not used in conjunction with PTV-based planning. The 1 cm OAR-to-PRV margins used in this study therefore result in a level of OAR protection often not afforded by PTV-based planning. If the margin-based portion of this study would be repeated with zero OAR-to-PRV margins, OAR-to-PRV margins equal to the CTV-to-PTV margins, or any value less than 1 cm, the resultant optimized dose distributions would increase OAR doses, further exemplifying the advantages of PTP.

The work in this study required a great amount of computational resources. An average optimization including weight adjustment took nearly two days on a single 2.83 GHz processor. This is unrealistic in a clinical scenario. Fortunately, the methods proposed here can be easily parallelized. Computation of gradients and objective functions for different shifts are independent of each other. With a multiple processor machine or cluster, computation of shifts could be spread to multiple CPUs. Further enhancements and optimization of the code may also reduce the time required.

CONCLUSIONS

For the same CTV coverage probability, PTP results in a reduced rectal dose. DVCDMs show that dose is decreased in the neighborhood of the optimization constraints, while dose is increased in unconstrained areas. Physician assessment indicates that PTP plans are preferred by all physicians and assessment methods 71% of the time, while optimized margin-based plans are preferred by all physicians and assessment methods 7% of the time. Significant reductions in coverage of the rectal objectives were achieved (16%–27%) though small increases in coverage of the bladder and femurs were observed (2%–6%).