Principled sure independence screening for Cox models with ultra-high-dimensional covariates

Abstract

It is rather challenging for current variable selectors to handle situations where the number of covariates under consideration is ultra-high. Consider a motivating clinical trial of the drug bortezomib for the treatment of multiple myeloma, where overall survival and expression levels of 44760 probesets were measured for each of 80 patients with the goal of identifying genes that predict survival after treatment. This dataset defies analysis even with regularized regression. Some remedies have been proposed for the linear model and for generalized linear models, but there are few solutions in the survival setting and, to our knowledge, no theoretical support. Furthermore, existing strategies often involve tuning parameters that are difficult to interpret. In this paper we propose and theoretically justify a principled method for reducing dimensionality in the analysis of censored data by selecting only the important covariates. Our procedure involves a tuning parameter that has a simple interpretation as the desired false positive rate of this selection. We present simulation results and apply the proposed procedure to analyze the aforementioned myeloma study.

1. Introduction

An urgent need has emerged in the field of biomedicine for statistical procedures capable of analyzing and interpreting vast quantities of data. Selecting the best predictors of an outcome is a key step in this process, but traditional methods of variable selection, such as best subset selection or backward selection, have been found to be unstable and inaccurate when the dimension of the covariates is close to the number of observations. Furthermore, when there are more covariates than observations, as is often the case in genomic studies, these methods can fail completely.

To address these issues, recent work has focused on regularized regression procedures such as the lasso [1] and adaptive lasso [2], the elastic net [3], the smoothly clipped absolute deviation estimator [4], and the Dantzig selector [5]. These methods can handle the high-dimension-low-sample-size paradigm, have superior predictive accuracy, and under certain conditions can achieve the oracle property [4]: they are as accurate and efficient as an estimator that knows a priori which variables are truly important.

However, these procedures only work well with a moderate number of covariates. When the dimension of the covariates is ultra-high, both traditional and regularization methods have problems with speed, stability, and accuracy [6]. For example, many of the bounds on the accuracy of these methods involve factors of log pn, where pn is the dimension of the covariates [5, 7]. Thus the theoretical performance of these methods degrades as pn becomes very large, yet this ultra-high dimensionality characterizes many real-world biological datasets. Our work in this paper is motivated by one such dataset, in the area of multiple myeloma.

Multiple myeloma is the world’s second-most common hematological cancer and patients often present with bone lesions, immunological disorders, and renal failure. An effective treatment is still being sought, as only about 10% of patients survive 10 years after diagnosis. A deeper understanding of the molecular etiology of this disease would lead to novel therapeutic targets and more accurate risk classification systems. We studied overall survival for 80 multiple myeloma patients enrolled in a clinical trial of bortezomib [8]. With expression level measurements on 44760 probesets, this dataset defies analysis even with regularized regression.

Without tools to deal with this type of ultra-high dimensionality, many analysts employ an initial univariate screening step to reduce the number of covariates under consideration. The remaining covariates could then be fed to one of the more sophisticated regularization techniques in a second stage. But it was only recently that Fan and Lv [6] placed this ad-hoc practice on firm theoretical ground, showing that that screening could indeed improve the performance of regularization methods. They suggested fitting marginal regression models for each covariate, choosing a threshold, and retaining those covariates for which the magnitudes of the parameter estimates are above the threshold. When the data come from an ordinary linear model with normal errors, Fan and Lv [6] showed that this pre-screening procedure, which they termed sure independence screening (SIS), has desirable theoretical properties. Fan and Song [9] later gave theoretical justification for using SIS with generalized linear models.

But two important problems remain. First, one common type of outcome data seen in clinical settings, including in our myeloma dataset, is survival time, which is subject to censoring. Regularized regression methods for censored observations have been studied, as reviewed in Li [10], but these are subject to the same issues mentioned above when the dimension of the covariates is ultra-high. There is thus a need for a pre-screening procedure in this setting, but the results of Fan and Lv [6] and Fan and Song [9] cannot be applied because the issue of censoring is not addressed. Several ad-hoc solutions are available from Tibshirani [11] and Fan et al. [12], but none of these proposals has much theoretical support. The extension of the theoretical sure screening results to censored data is not immediate because it turns out that certain conditions on the relationship between the covariates and the censoring distribution are required for screening to have good theoretical properties, an issue which does not emerge with uncensored data.

The second problem is that existing screening procedures require choosing a threshold to dictate how many variables to retain, but there are no principled methods for making such a choice, making the resulting screened models difficult to evaluate. The threshold can be thought of as a regularization parameter, which in the regression setting is ordinarily chosen by optimizing out-of-sample prediction error using cross-validation or generalized cross-validation. However, this approach is unavailable for screening procedures because no prediction rule is ever generated.

In this paper we provide a screening method for censored survival data with ultra-high-dimensional covariates. We also propose a new, principled method for choosing the number of covariates to retain based on specifying the desired false positive rate. Finally, we give, to our knowledge, the first theoretical justifications of the sure independence screening procedure for censored data. Under the asymptotic framework where the number of covariates can grow with the sample size, we show that with probability going to 1, our procedure will select all of the important variables with a false positive rate close to the prespecified level.

Our paper is organized as follows. We briefly review sure independence screening for generalized linear models in Section 2. In Section 3 we discuss the implementation and the theoretical properties of our principled sure independence screening procedure, and present simulation results in Section 4. Section 5 describes our analysis of the myeloma dataset, and we conclude with a discussion in Section 6. All proofs are given in the Appendix.

2. Sure independence screening in generalized linear models

We first review the sure independence screening formulation of Fan and Song [9]. For subjects i = 1, …, n let Z_i = (Z_i1, …, Z_ipn) be the p_n- dimensional covariate vector. Assuming that observations Y_i come from an exponential family, we model E(Y_i | Z_i) as some function of a linear predictor ${\mathit{\alpha }}_0^T{\mathbf{Z}}_i$ with parameter vector α₀ = (α₀₁, …, α_0pn). When p_n is much larger than n we are unable to estimate α₀ with conventional procedures. To reduce p_n, sure independence screening proceeds by regressing Y_i on each Z_ij individually to calculate marginal maximum likelihood estimates β̂_j. The final screened model retains all covariates j : |β̂_j| ≥ γ_n for some prespecified constant cutoff γ_n.

Fan and Song [9] showed that under certain conditions, if γ_n follows an ideal rate, this procedure has two desirable properties, namely the sure screening property and the size control property. The former guarantees that the screened model will contain the true model with a probability approaching 1. The latter states that if log(p_n) = o(n^1–2κ) where κ < 1/2, the probability that the size of the screened model will be at most O{n^2κλ_max(Σ)} will also go to 1, where Σ = var(Z_i) and λ_max(Σ) is the largest eigenvalue of Σ.

These results, however, are restricted to non-censored generalized linear models. Furthermore, it is difficult to translate the ideal rate for γ_n into a method for selecting the cutoff in practice. Fan and Lv [6] suggest n/log(n) or n − 1 as the number of covariates to retain after screening, but without theoretical justification. To address these issues, we investigate here a reliable pre-screening procedure in a survival setting, where the outcomes are subject to right censoring, and propose a principled method for choosing γ_n based on controlling the false positive rate.

3. Principled Cox sure independence screening

3.1. Method

In the context of survival analysis, we assume that the underlying survival times T_i follow a Cox model [13] with the true hazard function

$$\lambda (x;{\mathbf{Z}}_i)={\lambda }_0(x)exp({\mathit{\alpha }}_0^T{\mathbf{Z}}_i),$$ (1)

where λ₀(x) is unspecified. Let C̃_i be potential censoring times, which are independent of T_i conditional on Z_i. Furthermore let τ > 0 be the finite study duration such that P{min(C̃_i, τ) < T_i} < 1, ensuring that enough events will be observed over [0, τ]. The effective censoring times are thus Ci = min(C̃_i, τ). We observe X_i = min(T_i, C_i), and δ_i = I(T_i ≤ C_i). Without loss of generality, we assume throughout that E(Z_ij) = 0 for all j.

To perform an initial screening procedure, we propose to fit marginal Cox regressions, possibly misspecified, for each Z_ij, namely ${\lambda }_0^{\ast }(x)exp(\beta Z_{ij})$. Let N_i(t) = I(X_i ≤ t, δ_i = 1) be independent counting processes for each subject i and Y_i(t) = I(X_i ≥ t) be the at-risk processes. For κ = 0, 1, …, define

$$\begin{array}{c}{S}_j^{(k)}(x)=n^{-1}\sum _{i=1}^n{Z}_{ij}^k{Y}_i(x)\lambda (x;{\mathbf{Z}}_i),s_j^{(k)}(x)=E\{S^{(k)}(x)\},\\ S_j^{(k)}(\beta ,x)=n^{-1}\sum _{i=1}^n{Z}_{ij}^k{Y}_i(x)exp(\beta Z_{ij}),s_j^{(k)}(\beta ,x)=E\{S^{(k)}(\beta ,x)\}.\end{array}$$

Then the maximum marginal partial likelihood estimator β̂_j solves the estimating equation

$$U_j(\beta )=\sum _{i=1}^n{\int }_0^{\tau }\left\{Z_{ij}-\frac{S_j^{(1)}(\beta ,x)}{S_j^{(0)}(\beta ,x)}\right\}{dN}_i(x)=0.$$ (2)

Finally, let β_0j be the solution to the limiting estimation equation

$$u_j(\beta )={\int }_0^{\tau }\left\{s_j^{(1)}(x)-\frac{s_j^{(1)}(\beta ,x)}{s_j^{(0)}(\beta ,x)}{s}_j^{(0)}(x)\right\}dx.$$ (3)

Define the information matrix to be I_j(β) = −∂U_j/∂β at β̂_j. We will denote the final screened model by 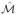= {j : I_j(β̂_j)^1/2|β̂_j| ≥ γ_n}. We would like a practical way of choosing γ_n such that we can achieve the sure screening property while controlling the false positive rate, or the proportion of unimportant covariates we incorrectly include in 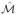. If the true model 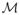= {j : α_0j ≠ 0} has size | 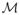| = s_n, then the expected false positive rate can be written as

$$\text{E}\left(\frac{|\widehat{\mathcal{M}}\cap {\mathcal{M}}^c|}{\mid {\mathcal{M}}^c\mid }\right)=\frac{1}{p_n-s_n}\sum _{j\in {\mathcal{M}}^c}\text{P}\left\{I_j{({\widehat{\beta }}_j)}^{1/2}\mid {\widehat{\beta }}_j\mid \ge {\gamma }_n\right\}.$$ (4)

We can show that I_j(β̂_j)^1/2 β̂_j has an asymptotically standard normal distribution, so we see that γ_n corresponds to controlling the expected false positive rate at 2{1 − Φ (γ_n)}, where Φ(·) is the standard normal cumulative distribution function.

However, we would like the false positive rate to decrease to 0 as p_n increases with n, though it can never exactly equal 0 or else γ_n = ∞. One sensible way to do this would be to first fix the number of false positives f that we are willing to tolerate, which would correspond to a false positive rate of f/(p_n−s_n). Because s_n is unknown, we can be conservative by letting γ_n = Φ⁻¹{1 − q_n/2)} where q_n = f/p_n, so that the expected false positive rate is 2{1 − Φ (γ_n)} = q_n ≤ f/(p_n − s_n). We can show that this procedure maintains the sure screening property, and more precise arguments will be given later (Theorems 4 and 5).

We term this method a principled Cox sure independence screening procedure (abbreviated PSIS), as the cutoff γ_n is selected to control the false positive rate. Specifically, PSIS is implemented as follows:

1. Fit a marginal Cox model for each of the covariates according to equation (2) to get parameter estimates β̂_j and variance estimates I_j(β̂_j)⁻¹.

2. Fix the false positive rate q_n = f/p_n and let γ_n = Φ⁻¹(1 − q_n/2).

3. Retain covariates j : I_j(β̂_j)^1/2|β̂_j| ≥ γ_n.

Our cutoff selection procedure is related to false discovery rate (FDR) methods [14, 15]. In particular, the FDR is defined as | 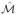∩ |/| |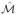, which is simply the product of the false positive rate in (4) and | |/| |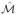, which is less than p_n/| 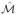|. Therefore, controlling the false positive rate at q_n = f/p_n is equivalent to controlling the FDR at f/| 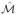|, conditional on | 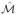|. Bunea et al. [16] have in fact shown that FDR methods can also have the sure screening property, though only in the linear regression case.

Our screening procedure resembles the “marginal ranking” methods for censored outcome data proposed by various authors [12, 11]. However, to our knowledge, none of these proposals has much theoretical support. A much more aggressive method of control has been proposed by Fan et al. [12]. We show below that our proposed procedure maintains the sure screening property, and will also control the false positive rate at close to the nominal level. Fan and Lv [6] also proposed an iterative sure independence screening procedure (ISIS) for linear models, which they showed can perform better than SIS. However, they were unable to offer theoretical support. In this paper we focus on first understanding non-iterative screening for the Cox model.

3.2. Theoretical properties

First, under certain assumptions, we find that we can distinguish α_0j, j ∈ 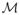from α_0j, j ∈ in the presence of censoring. It is this guarantee that makes the marginal screening approach possible.

Theorem 1

Under Assumptions 1–8 in the Appendix, β_0j = 0 if and only if α_0j = 0, for all j = 1, …, p_n.

Following Struthers and Kalbfleisch [17] and under Assumptions 1 and 2 in the Appendix, we know that the β̂_j are consistent for β_0j. It is therefore natural to ask how accurate these estimates are.

Theorem 2

Under Assumptions 1–8 in the Appendix,

$$p\left\{\sqrt{n}\mid {\widehat{\beta }}_j-{\beta }_{0j}\mid \ge 4K[1+{\mathrm{\Lambda }}_0(\tau )exp\{2K(A+L)\}](1+t)/H\right\}\le exp(-t^2/2)$$

for all j = 1, …, p_n, where K is the bound on the covariates Z_ij for all j, ${\mathrm{\Lambda }}_0(\tau )={\int }_0^{\tau }{\lambda }_0(s)ds$ is bounded by Assumption 4, A is the bound on the parameters α_0j for all j, L = || α₀ ||₁ and is bounded by Assumption 3, and H is defined in Assumption 5.

Theorem 2 is important as it suggests that |β̂_j−β_0j| is at most on the order of n^−1/2 with high probability. Hence in order to detect covariate j ∈ 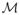, we need |β_0j| to be at least O(n^−1/2), which is indeed the case as shown by the following theorem.

Theorem 3

Under Assumptions 1–8 in the Appendix, there is a constant c₂ > 0 such that min_j∈ 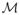|β_0j| ≥ c₂n^−κ, where κ < 1/2.

Because the |β_0j| are large enough to be detected with our marginal Cox regressions, and because they reflect the importance of the Z_ij in the true joint model, we can prove that our procedure maintains the sure screening property and controls the false positive rate at close to the nominal level.

Theorem 4 (Sure screening property)

Under Assumptions 1–8 in the Appendix, if we choose γ_n = Φ⁻¹ (1 − q_n/2), then for κ < 1/2 and log(p_n) = O(n^1/2−κ), there exists a constant c₃ > 0 such that

$$P(\mathcal{M}\subseteq \widehat{\mathcal{M}})\ge 1-s_{n}exp(-c_3{n}^{1-2\kappa }).$$

Theorem 5 (False positive control property)

Under Assumptions 1– 8 in the Appendix, if we choose γ_n = Φ⁻¹(1 − q_n/2), then there exists some c₄ > 0 such that

$$E\left(\frac{\mid \widehat{\mathcal{M}}\cap {\mathcal{M}}^c\mid }{\mid {\mathcal{M}}^c\mid }\right)\le q_n+c_4{n}^{-1/2},$$

where | 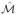∩ |/| | can be interpreted as the false positive rate.

It is often assumed that the true model is sparse and s_n is small [5], in which case Theorem 4 indicates that we will be able to retain all important covariates with high probability. The probability bound will converge to 1 if log(p_n) = O(n^1/2−κ), which is comparable to the rates allowed in Fan and Lv [6] and Fan and Song [9]. That p_n is allowed to incease exponentially justifies the use of sure independence screening in the Cox model when p_n is ultra-high-dimensional.

4. Simulations

To evaluate the finite-sample performance of our sure screening and false positive control properties, we performed PSIS on simulated datasets generated from Cox models and examined its average false positive and negative rates. We simulated 200 datasets, each consisting of p_n = 20000 covariates and n = 100 subjects. We generated the covariates from a multivariate normal distribution where the mean was 0 and the correlation between components Z_ij and Z_ik was ρ^|j−k| for ρ = 0.5, and 0.9. We next generated survival times from Cox models with baseline hazards of λ₀(x) = 1 and linear predictors ${\mathit{\alpha }}_0^T{\mathbf{Z}}_i$ for different parameter vectors α₀. We let the number of non-zero elements of α₀ be either s_n = 10 or 20 and set the first s_n components of α₀ to be either all equal to 0.35 or all equal to 0.7. Finally, we generated censoring times from a uniform and an exponential distribution, which gave bounded and unbounded censoring times respectively. Under each censoring mechanism, we considered censoring rates of approximately 20%, 50%, and 70%.

To explore how the variable selection performance of a few popular regularized regression techniques were affected by PSIS with different values of q_n, we followed PSIS by either lasso [18], adaptive lasso [19], or SCAD [20]. Since the initial parameter estimates required by adaptive lasso do not exist when p_n > n, we first applied ordinary lasso to reduce p_n and calculated the initial estimates using the remaining covariates. We implemented lasso and adaptive lasso using a coordinate descent algorithm [21] with the R package glmnet, and we implemented SCAD using the one-step estimator of Zou and Li [22] with the package SIS. We tuned each regularized regression with BIC to achieve selection consistency, and we denote these two-stage procedures by PSIS-L, PSIS-L-A, and PSIS-S, respectively.

Tables 1 and 2 report numerical results for our sure screening and false positive control properties when s_n = 20, α_0j = 0.35, and when censoring times were generated from an exponential distribution. The results when s_n = 10, α_0j = 0.7, or when the censoring times were uniformly distributed are similar and are omitted for the sake of space. We considered q_n = 10^r for r = −6, …,−2, and also ranging from 0.1 to 1 (corresponding to no screening) in increments of 0.1. The results support our principled cutoff procedure: the observed false positive rates closely match the nominal q_n when ρ = 0.5 for all censoring rates. When ρ = 0.9, the observed false positive rates can be higher than the nominal q_n for q_n ≤ 10⁻⁴, but since p_n = 20000 here, q_n = 10⁻⁴ corresponds to only 2 false positives. In other words, even when the nominal q_n underestimates the true false positive rate, the absolute number of false positives selected by PSIS is still fairly small.

Table 1.

Simulation results for Cox models with s_n = 20, α_0j = 0.35, and ρ = 0.5 under exponential censoring

% censoring	qn	| |	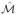PSIS		PSIS-L		PSIS-A		PSIS-S
			FN	FP	FN	FP	FN	FP	FN	FP
20	1e-6	0.86	0.96	3e-7	0.96	0.00	0.96	0.00	0.96	0.00
20	1e-5	2.45	0.89	1e-5	0.89	0.00	0.89	0.00	0.90	0.00
20	1e-4	7.29	0.74	1e-4	0.75	0.00	0.75	0.00	0.78	0.00
20	1e-3	30.74	0.52	1e-3	0.56	0.00	0.57	0.00	0.80	0.00
20	0.01	223.46	0.27	0.01	0.50	0.00	0.51	0.00	0.60	0.00
20	0.10	2066.62	0.07	0.10	0.45	0.00	0.46	0.00	0.64	0.00
20	0.20	4084.34	0.04	0.20	0.45	0.00	0.46	0.00	1.00	0.00
20	0.30	6085.28	0.03	0.30	0.45	0.00	0.46	0.00	1.00	0.00
20	0.40	8087.81	0.02	0.40	0.45	0.00	0.46	0.00	1.00	0.00
20	0.50	10076.05	0.01	0.50	0.45	0.00	0.46	0.00	1.00	0.00
20	0.60	12063.53	0.01	0.60	0.45	0.00	0.46	0.00	1.00	0.00
20	0.70	14049.73	0.01	0.70	0.45	0.00	0.46	0.00	1.00	0.00
20	0.80	16035.60	0.00	0.80	0.45	0.00	0.46	0.00	1.00	0.00
20	0.90	18018.92	0.00	0.90	0.45	0.00	0.46	0.00	1.00	0.00
20	1.00	19999.97	0.00	1.00	0.45	0.00	0.46	0.00	1.00	0.00
50	1e-6	0.46	0.98	8e-7	0.98	0.00	0.98	0.00	0.98	0.00
50	1e-5	1.48	0.93	9e-6	0.93	0.00	0.93	0.00	0.94	0.00
50	1e-4	5.53	0.82	1e-4	0.83	0.00	0.83	0.00	0.87	0.00
50	1e-3	27.48	0.64	1e-3	0.69	0.00	0.70	0.00	0.84	0.00
50	0.01	218.90	0.37	0.01	0.70	0.00	0.71	0.00	0.80	0.00
50	0.10	2055.34	0.11	0.10	0.84	0.00	0.84	0.00	0.82	0.00
50	0.20	4066.57	0.06	0.20	0.85	0.00	0.86	0.00	1.00	0.00
50	0.30	6072.90	0.04	0.30	0.86	0.00	0.87	0.00	1.00	0.00
50	0.40	8071.28	0.03	0.40	0.86	0.00	0.87	0.00	1.00	0.00
50	0.50	10061.46	0.02	0.50	0.87	0.00	0.87	0.00	1.00	0.00
50	0.60	12055.20	0.02	0.60	0.87	0.00	0.87	0.00	1.00	0.00
50	0.70	14048.17	0.01	0.70	0.87	0.00	0.87	0.00	1.00	0.00
50	0.80	16034.58	0.00	0.80	0.87	0.00	0.87	0.00	1.00	0.00
50	0.90	18018.47	0.00	0.90	0.87	0.00	0.87	0.00	1.00	0.00
50	1.00	19999.97	0.00	1.00	0.87	0.00	0.87	0.00	1.00	0.00
70	1e-6	0.04	1.00	1e-6	1.00	0.00	1.00	0.00	1.00	0.00
70	1e-5	0.33	0.99	7e-6	0.99	0.00	0.99	0.00	0.99	0.00
70	1e-4	2.33	0.96	8e-5	0.96	0.00	0.96	0.00	0.97	0.00
70	1e-3	20.34	0.86	9e-4	0.89	0.00	0.89	0.00	0.95	0.00
70	0.01	200.62	0.63	0.01	0.98	0.00	0.98	0.00	0.97	0.00
70	0.10	2036.15	0.28	0.10	0.99	0.00	0.99	0.00	1.00	0.00
70	0.20	4056.93	0.17	0.20	0.99	0.00	0.99	0.00	1.00	0.00
70	0.30	6073.71	0.11	0.30	0.99	0.00	0.99	0.00	1.00	0.00
70	0.40	8074.10	0.08	0.40	0.99	0.00	0.99	0.00	1.00	0.00
70	0.50	10069.87	0.06	0.50	0.99	0.00	0.99	0.00	1.00	0.00
70	0.60	12061.20	0.04	0.60	0.99	0.00	0.99	0.00	1.00	0.00
70	0.70	14053.00	0.03	0.70	0.99	0.00	0.99	0.00	1.00	0.00
70	0.80	16036.78	0.02	0.80	0.99	0.00	0.99	0.00	1.00	0.00
70	0.90	18018.22	0.01	0.90	0.99	0.00	0.99	0.00	1.00	0.00
70	1.00	19999.98	0.00	1.00	0.99	0.00	0.99	0.00	1.00	0.00

Table 2.

Simulation results for Cox models with s_n = 20, α_0j = 0.35, and = 0.9 under exponential censoring

% censoring	qn	| |	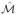PSIS		PSIS-L		PSIS-A		PSIS-S
			FN	FP	FN	FP	FN	FP	FN	FP
20	1e-6	20.57	0.03	6e-5	0.26	0.00	0.27	0.00	0.65	0.00
20	1e-5	22.00	0.01	1e-4	0.25	0.00	0.26	0.00	0.64	0.00
20	1e-4	25.39	0.00	3e-4	0.26	0.00	0.27	0.00	0.65	0.00
20	1e-3	46.84	0.00	1e-3	0.29	0.00	0.32	0.00	0.68	0.00
20	0.01	237.31	0.00	0.01	0.43	0.00	0.45	0.00	0.65	0.00
20	0.10	2069.38	0.00	0.10	0.39	0.00	0.41	0.00	0.69	0.00
20	0.20	4082.82	0.00	0.20	0.37	0.00	0.40	0.00	1.00	0.00
20	0.30	6085.60	0.00	0.30	0.38	0.00	0.40	0.00	1.00	0.00
20	0.40	8080.28	0.00	0.40	0.38	0.00	0.40	0.00	1.00	0.00
20	0.50	10072.06	0.00	0.50	0.38	0.00	0.40	0.00	1.00	0.00
20	0.60	12063.09	0.00	0.60	0.38	0.00	0.39	0.00	1.00	0.00
20	0.70	14052.35	0.00	0.70	0.38	0.00	0.40	0.00	1.00	0.00
20	0.80	16041.30	0.00	0.80	0.38	0.00	0.39	0.00	1.00	0.00
20	0.90	18017.65	0.00	0.90	0.38	0.00	0.39	0.00	1.00	0.00
20	1.00	19999.98	0.00	1.00	0.38	0.00	0.40	0.00	1.00	0.00
50	1e-6	19.38	0.07	4e-5	0.35	0.00	0.37	0.00	0.72	0.00
50	1e-5	21.08	0.03	8e-5	0.34	0.00	0.36	0.00	0.71	0.00
50	1e-4	24.35	0.01	2e-4	0.34	0.00	0.36	0.00	0.72	0.00
50	1e-3	44.27	0.00	1e-3	0.30	0.00	0.32	0.00	0.74	0.00
50	0.01	229.40	0.00	0.01	0.50	0.00	0.53	0.00	0.69	0.00
50	0.10	2059.74	0.00	0.10	0.51	0.00	0.54	0.00	0.78	0.00
50	0.20	4075.78	0.00	0.20	0.51	0.00	0.55	0.00	1.00	0.00
50	0.30	6082.62	0.00	0.30	0.51	0.00	0.55	0.00	1.00	0.00
50	0.40	8076.19	0.00	0.40	0.51	0.00	0.54	0.00	1.00	0.00
50	0.50	10069.25	0.00	0.50	0.51	0.00	0.54	0.00	1.00	0.00
50	0.60	12056.07	0.00	0.60	0.51	0.00	0.54	0.00	1.00	0.00
50	0.70	14049.39	0.00	0.70	0.51	0.00	0.55	0.00	1.00	0.00
50	0.80	16035.47	0.00	0.80	0.52	0.00	0.55	0.00	1.00	0.00
50	0.90	18016.56	0.00	0.90	0.52	0.00	0.55	0.00	1.00	0.00
50	1.00	19999.99	0.00	1.00	0.52	0.00	0.55	0.00	1.00	0.00
70	1e-6	17.07	0.17	2e-5	0.49	0.00	0.51	0.00	0.78	0.00
70	1e-5	19.29	0.09	6e-5	0.45	0.00	0.47	0.00	0.77	0.00
70	1e-4	22.88	0.04	2e-4	0.40	0.00	0.43	0.00	0.76	0.00
70	1e-3	42.52	0.01	1e-3	0.35	0.00	0.39	0.00	0.74	0.00
70	1e-2	225.35	0.00	0.01	0.63	0.00	0.66	0.00	0.78	0.00
70	0.10	2047.36	0.00	0.10	0.65	0.00	0.68	0.00	0.86	0.00
70	0.20	4061.41	0.00	0.20	0.65	0.00	0.68	0.00	1.00	0.00
70	0.30	6066.76	0.00	0.30	0.65	0.00	0.68	0.00	1.00	0.00
70	0.40	8069.35	0.00	0.40	0.65	0.00	0.68	0.00	1.00	0.00
70	0.50	10063.83	0.00	0.50	0.65	0.00	0.68	0.00	1.00	0.00
70	0.60	12052.45	0.00	0.60	0.65	0.00	0.68	0.00	1.00	0.00
70	0.70	14041.27	0.00	0.70	0.65	0.00	0.68	0.00	1.00	0.00
70	0.80	16029.24	0.00	0.80	0.65	0.00	0.68	0.00	1.00	0.00
70	0.90	18015.47	0.00	0.90	0.65	0.00	0.68	0.00	1.00	0.00
70	1.00	19999.99	0.00	1.00	0.65	0.00	0.68	0.00	1.00	0.00

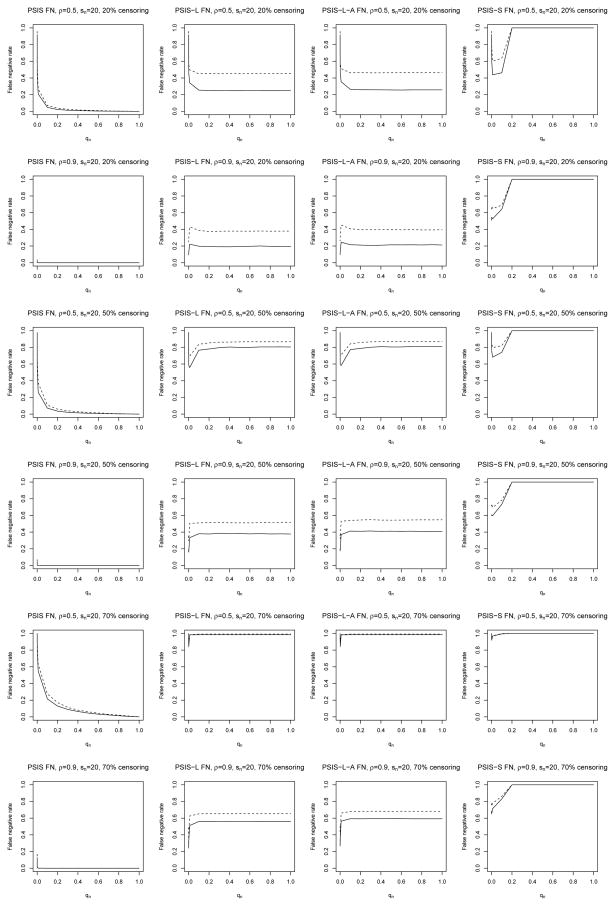
Figure 1 plots the average false negative rates for PSIS against q_n, which increase as q_n decreases but generally don’t rise dramatically until q_n ≈ 0.1. For a given q_n the false negative rates decrease with larger α_0j. The performance of PSIS actually improves when ρ = 0.9, perhaps because in our simulated data the correlation between the important covariates increases with ρ, making the marginal β̂_j estimates for those covariates more likely to be similar in magnitude. Higher censoring rates exhibit worse performance, as expected. These results suggest that q_n can be set fairly low and the false negative rate will not suffer much, as long as the amount of censoring is not too high.

Figure 1.

False negative rates for Cox models with α_0j = 0.35 (dashes) and α_0j = 0.7 (solid) under exponential censoring.

The average false negative rates for PSIS-L, PSIS-L-A, and PSIS-S are also plotted in Figure 1. The corresponding false positive rates are all very low and so are not plotted (see Tables 1 and 2). The PSIS-S results give false negative rates of 1 for large q_n because the SCAD algorithm fails when the number of covariates is too large, so we already see the usefulness of PSIS in facilitating computations. For all methods, higher values of α_0j exhibit lower false negative rates, and as before we see better performance when the covariates are more correlated.

Interestingly, with 50% censoring, when q_n is small the PSIS-L, PSISL- A, and PSIS-S false negative rates are noticeably lower than those after running lasso, lasso-adaptive lasso, or SCAD alone (i.e. q_n = 1). This supports the use of PSIS prior to running regularized regression. However, when the censoring rate is fairly low (20%) or fairly high (70%), this effect diminishes, to the point where PSIS actually degrades the performance of the regularized regressions when ρ = 0.5 at 20% censoring. This could be because with low censoring, there might already be sufficient data for the regularized regressions to select from the p_n = 20000 covariates, even in the absence of PSIS. At the other extreme, when there is 70% censoring, there might be so little data (with n = 100) that no regularized method, with or without PSIS, would perform well.

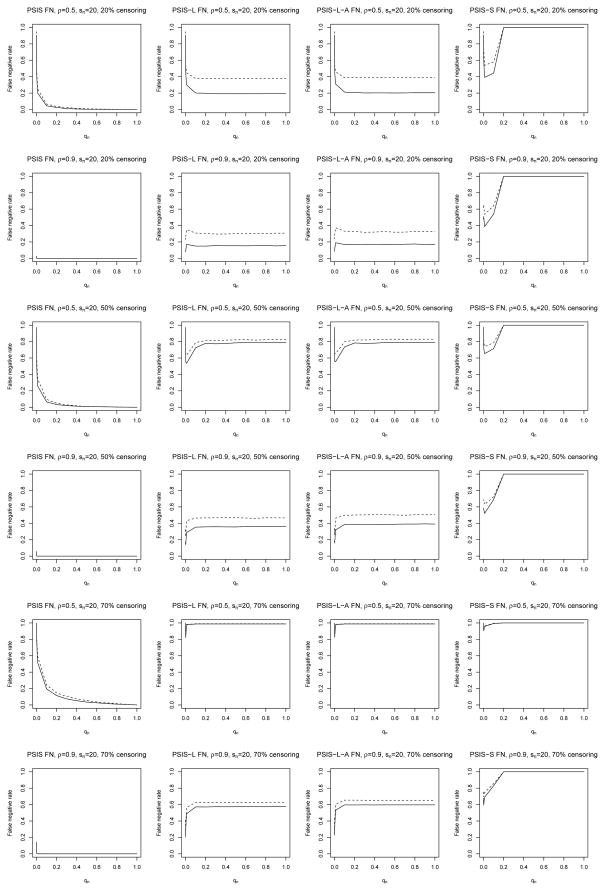
To assess the robustness of our procedure, we also generated 200 datasets from log-normal models. Each dataset had n = 100 and p_n = 20000, and covariates Z_i were generated using the same procedure as above, for ρ = 0.5 or 0.9. Survival times T_i were generated according to $log(T_i)={\mathit{\alpha }}_0^T{\mathbf{Z}}_i+{\epsilon }_i$, where ∈_i followed a standard normal distribution and α₀ had s_n = 10 or 20 nonzero elements all equal to either 0.35 or 0.7. Censoring times were generated using the same schemes and rates as before.

Tables 3 and 4 and Figure 2 show that PSIS can still perform very well when the Cox model is misspecified. Again, the numerical results when s_n = 10, α_0j = 0.7, or the censoring times were uniformly distributed are omitted from the tables to save space. These results follow the same trends as those of the correctly specified simulations discussed above. In particular, the principled cutoff procedure still shows good performance, and using PSIS when q_n is small can still lead to lower false negative rates than when q_n = 1.

Table 3.

Simulation results for log-normal models with s_n = 20, α_0j = 0.35, and ρ = 0.5 under exponential censoring

% censoring	qn	| |	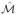PSIS		PSIS-L		PSIS-A		PSIS-S
			FN	FP	FN	FP	FN	FP	FN	FP
20	1e-6	1.07	0.95	5e-7	0.95	0.00	0.95	0.00	0.95	0.00
20	1e-5	2.92	0.86	1e-5	0.87	0.00	0.87	0.00	0.88	0.00
20	1e-4	7.83	0.71	1e-4	0.72	0.00	0.72	0.00	0.76	0.00
20	1e-3	31.64	0.50	1e-3	0.54	0.00	0.54	0.00	0.74	0.00
20	0.01	225.09	0.25	0.01	0.45	0.00	0.46	0.00	0.54	0.00
20	0.10	2072.03	0.07	0.10	0.38	0.00	0.39	0.00	0.58	0.00
20	0.20	4086.02	0.04	0.20	0.38	0.00	0.39	0.00	1.00	0.00
20	0.30	6091.88	0.02	0.30	0.38	0.00	0.39	0.00	1.00	0.00
20	0.40	8096.85	0.01	0.40	0.38	0.00	0.39	0.00	1.00	0.00
20	0.50	10084.36	0.01	0.50	0.38	0.00	0.39	0.00	1.00	0.00
20	0.60	12071.20	0.01	0.60	0.38	0.00	0.39	0.00	1.00	0.00
20	0.70	14053.60	0.00	0.70	0.38	0.00	0.39	0.00	1.00	0.00
20	0.80	16035.81	0.00	0.80	0.38	0.00	0.39	0.00	1.00	0.00
20	0.90	18014.10	0.00	0.90	0.38	0.00	0.39	0.00	1.00	0.00
20	1.00	19999.96	0.00	1.00	0.38	0.00	0.39	0.00	1.00	0.00
50	1e-6	0.58	0.97	2e-6	0.97	0.00	0.97	0.00	0.97	0.00
50	1e-5	1.68	0.92	8e-6	0.92	0.00	0.92	0.00	0.93	0.00
50	1e-4	5.74	0.80	9e-5	0.81	0.00	0.81	0.00	0.85	0.00
50	1e-3	28.12	0.61	1e-3	0.66	0.00	0.66	0.00	0.82	0.00
50	0.01	217.45	0.35	0.01	0.63	0.00	0.65	0.00	0.74	0.00
50	0.10	2053.91	0.10	0.10	0.79	0.00	0.80	0.00	0.79	0.00
50	0.20	4066.55	0.05	0.20	0.81	0.00	0.82	0.00	1.00	0.00
50	0.30	6071.31	0.03	0.30	0.81	0.00	0.82	0.00	1.00	0.00
50	0.40	8071.39	0.02	0.40	0.82	0.00	0.82	0.00	1.00	0.00
50	0.50	10067.45	0.01	0.50	0.82	0.00	0.83	0.00	1.00	0.00
50	0.60	12061.88	0.01	0.60	0.82	0.00	0.83	0.00	1.00	0.00
50	0.70	14045.89	0.00	0.70	0.82	0.00	0.83	0.00	1.00	0.00
50	0.80	16030.90	0.00	0.80	0.82	0.00	0.83	0.00	1.00	0.00
50	0.90	18017.08	0.00	0.90	0.82	0.00	0.83	0.00	1.00	0.00
50	1.00	19999.99	0.00	1.00	0.82	0.00	0.83	0.00	1.00	0.00
70	1e-6	0.07	1.00	8e-7	1.00	0.00	1.00	0.00	1.00	0.00
70	1e-5	0.45	0.98	7e-6	0.98	0.00	0.98	0.00	0.99	0.00
70	1e-4	2.62	0.95	8e-5	0.95	0.00	0.95	0.00	0.96	0.00
70	1e-3	20.59	0.83	9e-4	0.86	0.00	0.87	0.00	0.93	0.00
70	0.01	201.80	0.59	0.01	0.98	0.00	0.98	0.00	0.96	0.00
70	0.10	2032.38	0.24	0.10	0.99	0.00	0.99	0.00	1.00	0.00
70	0.20	4057.72	0.15	0.20	0.99	0.00	0.99	0.00	1.00	0.00
70	0.30	6071.12	0.10	0.30	0.99	0.00	0.99	0.00	1.00	0.00
70	0.40	8075.48	0.07	0.40	0.99	0.00	0.99	0.00	1.00	0.00
70	0.50	10069.12	0.05	0.50	0.99	0.00	0.99	0.00	1.00	0.00
70	0.60	12056.30	0.04	0.60	0.99	0.00	0.99	0.00	1.00	0.00
70	0.70	14044.67	0.03	0.70	0.99	0.00	0.99	0.00	1.00	0.00
70	0.80	16029.99	0.02	0.80	0.99	0.00	0.99	0.00	1.00	0.00
70	0.90	18015.69	0.01	0.90	0.99	0.00	0.99	0.00	1.00	0.00
70	1.00	19999.99	0.00	1.00	0.99	0.00	0.99	0.00	1.00	0.00

Table 4.

Simulation results for log-normal models with s_n = 20, α_0j = 0.35, and ρ = 0.9 under exponential censoring

% censoring	qn	| |	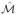PSIS		PSIS-L		PSIS-A		PSIS-S
			FN	FP	FN	FP	FN	FP	FN	FP
20	1e-6	20.63	0.03	6e-5	0.25	0.00	0.25	0.00	0.63	0.00
20	1e-5	21.98	0.01	1e-4	0.23	0.00	0.24	0.00	0.62	0.00
20	1e-4	24.94	0.00	2e-4	0.23	0.00	0.25	0.00	0.63	0.00
20	1e-3	45.60	0.00	1e-3	0.26	0.00	0.29	0.00	0.65	0.00
20	0.01	232.98	0.00	0.01	0.35	0.00	0.37	0.00	0.54	0.00
20	0.10	2064.58	0.00	0.10	0.31	0.00	0.33	0.00	0.64	0.00
20	0.20	4079.41	0.00	0.20	0.30	0.00	0.33	0.00	1.00	0.00
20	0.30	6089.45	0.00	0.30	0.30	0.00	0.32	0.00	1.00	0.00
20	0.40	8089.52	0.00	0.40	0.30	0.00	0.32	0.00	1.00	0.00
20	0.50	10075.52	0.00	0.50	0.30	0.00	0.33	0.00	1.00	0.00
20	0.60	12064.03	0.00	0.60	0.30	0.00	0.32	0.00	1.00	0.00
20	0.70	14048.61	0.00	0.70	0.30	0.00	0.32	0.00	1.00	0.00
20	0.80	16031.75	0.00	0.80	0.30	0.00	0.33	0.00	1.00	0.00
20	0.90	18014.60	0.00	0.90	0.31	0.00	0.33	0.00	1.00	0.00
20	1.00	19999.98	0.00	1.00	0.31	0.00	0.33	0.00	1.00	0.00
50	1e-6	19.65	0.06	4e-5	0.32	0.00	0.34	0.00	0.68	0.00
50	1e-5	21.14	0.02	8e-5	0.30	0.00	0.32	0.00	0.68	0.00
50	1e-4	24.32	0.01	2e-4	0.30	0.00	0.32	0.00	0.68	0.00
50	1e-3	44.18	0.00	1e-3	0.24	0.00	0.25	0.00	0.69	0.00
50	0.01	229.64	0.00	0.01	0.43	0.00	0.46	0.00	0.63	0.00
50	0.10	2056.83	0.00	0.10	0.46	0.00	0.50	0.00	0.72	0.00
50	0.20	4067.93	0.00	0.20	0.47	0.00	0.50	0.00	1.00	0.00
50	0.30	6075.55	0.00	0.30	0.47	0.00	0.50	0.00	1.00	0.00
50	0.40	8067.98	0.00	0.40	0.47	0.00	0.50	0.00	1.00	0.00
50	0.50	10065.84	0.00	0.50	0.47	0.00	0.51	0.00	1.00	0.00
50	0.60	12059.20	0.00	0.60	0.46	0.00	0.50	0.00	1.00	0.00
50	0.70	14048.42	0.00	0.70	0.46	0.00	0.50	0.00	1.00	0.00
50	0.80	16028.41	0.00	0.80	0.47	0.00	0.50	0.00	1.00	0.00
50	0.90	18014.56	0.00	0.90	0.47	0.00	0.50	0.00	1.00	0.00
50	1.00	19999.97	0.00	1.00	0.47	0.00	0.50	0.00	1.00	0.00
70	1e-6	17.46	0.14	2e-5	0.41	0.00	0.44	0.00	0.75	0.00
70	1e-5	19.54	0.07	5e-5	0.37	0.00	0.39	0.00	0.73	0.00
70	1e-4	22.92	0.03	2e-4	0.32	0.00	0.35	0.00	0.72	0.00
70	1e-3	43.28	0.01	1e-3	0.35	0.00	0.38	0.00	0.69	0.00
70	0.01	229.22	0.00	0.01	0.57	0.00	0.60	0.00	0.75	0.00
70	0.10	2062.75	0.00	0.10	0.63	0.00	0.65	0.00	0.86	0.00
70	0.20	4080.23	0.00	0.20	0.63	0.00	0.65	0.00	1.00	0.00
70	0.30	6083.23	0.00	0.30	0.62	0.00	0.65	0.00	1.00	0.00
70	0.40	8080.86	0.00	0.40	0.62	0.00	0.65	0.00	1.00	0.00
70	0.50	10073.59	0.00	0.50	0.62	0.00	0.65	0.00	1.00	0.00
70	0.60	12067.05	0.00	0.60	0.62	0.00	0.65	0.00	1.00	0.00
70	0.70	14053.72	0.00	0.70	0.62	0.00	0.65	0.00	1.00	0.00
70	0.80	16038.41	0.00	0.80	0.62	0.00	0.65	0.00	1.00	0.00
70	0.90	18019.44	0.00	0.90	0.62	0.00	0.65	0.00	1.00	0.00
70	1.00	19999.99	0.00	1.00	0.62	0.00	0.65	0.00	1.00	0.00

Figure 2.

False negative rates for log-normal models with s_n = 20, α_0j = 0.35 (dashes), and α_0j = 0.7 (solid) under exponential censoring.

5. Analysis of the myeloma study

Recent advances in understanding the biological mechanisms underlying multiple myeloma have offered new possibilities for therapy [23]. Time-to-event outcomes offer information about the progression of the disease, and in this vein several studies have examined the relationship between gene expression levels and survival [24]. In one such study conducted by Millennium Pharmaceuticals [8], mRNA expression levels were collected using Affymetrix U133A/B arrays from myeloma cells of 80 patients enrolled in a clinical trial of bortezomib (accession number GSE9782, trial 39). Median survival time was 684 days after randomization, and 50% of the observations were censored. We applied our methods to this data.

Expression values were measured for 44760 probesets, encompassing more than 22000 genes, and were log₂-transformed. We performed PSIS and chose q_n = 1/44760, for two reasons. First, our simulation results suggest that for large ρ, the true false positive rate can be larger than our nominal level, and genetic datasets are probably highly correlated. Second, gene expression levels are very likely related to the survival outcomes, but only weakly so. Many of our genes are probably not sufficiently important, in the sense of Assumption 7, so allowing even a small false positive rate would result in including a huge number of genes. For these reasons, we want to control the false positive rate to the extent possible, but on the other hand we cannot allow f = 0 or else γ_n = ∞. Thus we considered f = 1, which leads to our choice of q_n.

We could not directly evaluate the performance of PSIS without knowing which genes are “truly” important. Instead, we ran PSIS to get a screened model 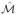and also randomly selected | 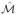| probesets. We then compared the prediction accuracies of PSIS-L, PSIS-L-A, and PSIS-S to those obtained by fitting lasso, lasso-adaptive lasso, and SCAD on the randomly selected probesets. Using random genes as negative controls is common in these type of experiments [25, 26, 12]. We also fit the regularized regression procedures on the full dataset, without any screening (i.e. q_n = 1).

For each of these methods, we randomly partitioned the data into a 60- patient training set and a 20-patient testing set. We then used the models fit in the training set to calculate scores for each subject in the testing set, and evaluated the predictive performance using the C-statistic [27]. We repeated this entire process 200 times. Better performances from the screened methods would provide evidence that PSIS is indeed finding predictively important genes.

Table 5 reports the average C-statistics and model sizes obtained by our different methods. We see that PSIS-L, PSIS-L-A, and PSIS-S perform much better than the corresponding regressions fit using randomly selected probesets. When we do not screen the data, SCAD fails, and lasso and lasso-adaptive lasso do not perform as well as the screened versions.

Table 5.

Predictive accuracies using myeloma data

	PSIS, qn = 0.0001		Random probesets		All probesets
Method	C-stat (SD)	Size (SD)	C-stat (SD)	Size (SD)	C-stat (SD)	Size (SD)
Lasso	0.60 (0.09)	11.43 (9.18)	0.15 (0.25)	3.33 (10.74)	0.33 (0.33)	20.91 (24.07)
Lasso-alasso	0.60 (0.09)	11.13 (8.97)	0.15 (0.25)	3.29 (10.60)	0.33 (0.33)	18.86 (21.74)
SCAD	0.60 (0.09)	7.13 (6.67)	0.33 (0.28)	2.48 (7.43)	—	—

Because of the selection consistency of the adaptive lasso [2, 19], we next applied PSIS-L-A with q_n = 1/44760 to all 80 patients. Table 6 gives the probesets we found to have nonzero parameter estimates, as well as their estimated coefficients. Indeed, our results include some genes previously found to be related to myeloma, e.g. IGHV3-23 [28] and PRKDC [29]. Finally, we evaluated the predictive performance of this model using an independent validation dataset (accession number GSE9782, trials 24, 25, and 40). The model in Table 6 achieved a C-statistic of 0.59, which matches the cross-validation estimate of Table 5. These results indicate that PSIS is an effective way to identify predictively important genes while controlling the false positive rate, and that implementing PSIS before regularized regression can lead to more computationally amenable, interpretable models with high predictive power.

Table 6.

Genes found using PSIS-L-A, q_n = 0.0001

Probeset	Gene	Description	Coefficient
219999_at	MAN2A2	mannosidase, alpha, class 2A, member 2	−0.27
207677_s_at	NCF4	neutrophil cytosolic factor 4, 40kDa	−0.14
216510_x_at	IGHV3-23	immunoglobulin heavy variable 3–23	−0.35
222610_s_at	S100PBP	S100P binding protein	0.15
203550_s_at	FAM189B	family with sequence similarity 189, member B	0.06
208694_at	PRKDC	protein kinase, DNA-activated, catalytic polypeptide	0.12
223277_at	C3orf75	chromosome 3 open reading frame 75	0.18
234980_at	TMEM56	transmembrane protein 56	−0.37
213893_x_at	PMS2L5	postmeiotic segregation increased 2-like 5	0.26
217518_at	MYOF	myoferlin	−0.13
202587_s_at	AK1	adenylate kinase 1	−0.11
232452_at	LOC148824	hypothetical LOC148824	0.42
209217_s_at	WDR45	WD repeat domain 45	−1.29
226692_at	SERF2	small EDRK-rich factor 2	−1.15
223114_at	COQ5	coenzyme Q5 homolog, methyltransferase	0.29

6. Discussion

This paper advances the field in three distinct ways. First, we have demonstrated that with censored outcomes, sure independence screening using marginal Cox regressions is a theoretically justified, effective way to reduce ultra-high-dimensional data to moderate sizes before applying more sophisticated variable selection procedures. In particular, we have described new, necessary condition on the dependence between the covariates and the censoring distribution. Second, we have provided a simple, principled method to select the number of variables to retain after screening and illustrated its effectiveness with simulated data. Our procedure could be easily extended to other screening methods. Finally, we have demonstrated through the motivating myeloma example that pre-screening may improve risk classification and identify predictive genes. There are a number of ways to broaden the scope of our method. So far we have dealt only with covariates that are constant in time, and we have not considered tied observations. Our method could also be extended to multivariate survival, competing risks, and other extensions of the Cox model.

While our simulations suggest that PSIS performs well even with correlated covariates, it would be interesting to explore other screening methods proposed specifically to deal with this situation. One approach is the ISIS method of Fan and Lv [6], which starts with an initial model of potentially important covariates, regresses the residuals from the working model on each of the remaining covariates to expand the working model, and iterates this process in order to capture any important covariates that would be missed in univariate screening. Residuals are unavailable with censored observations, but Fan et al. [12] generalized this iterative idea by working instead with log-likelihood ratios. Their formulation is easily applied to the log-partial likelihood of the Cox model, which they have implemented in the R package SIS. However, the theoretical properties of this procedure have not been investigated.

Finally, our theoretical analysis of sure independence screening touches on some philosophical questions about notions of variable importance. Biological phenomena often arise from the complex interactions of genes and other factors whose individual effects can be fairly weak but still non-zero. Thus merely having a non-zero contribution to the model is not a useful notion of importance, because then nearly every variable would be important. It may be more useful to conceive of importance as a finite sample property, in the sense that covariates whose signals are higher than the noise level of the estimator being used are to be considered important. In our method, for instance, the so-called important covariates satisfy Theorem 3, or else they could not be detected by marginal Cox regressions. Perhaps a good variable selection technique is one that, instead of selecting every variable with a non-zero contribution to the outcome, retains only those variables that, for a given n, meet the finite-sample definition of importance as defined in Theorem 3. The sure screening property of our method indicates that as n increases, we get closer to achieving this goal.

Appendix A. Assumptions

Let the true hazard function λ(x;Z_i) be given by (1), and denote the true survival functions of T_i and C_i as $S_T(x;{\mathbf{Z}}_i)=exp\{-exp({\alpha }_0^T{\mathbf{Z}}_i){\mathrm{\Lambda }}_0(x)\}$ and S_C(x;Z_i) = P(C_i > x|Z_i), where the cumulative baseline hazard function ${\mathrm{\Lambda }}_0(x)={\int }_0^x{\lambda }_0(s)ds$. To conserve space we will write these as S_T and S_C. For simplicity we will drop the subject-specific subscripts i, except in the proof of Theorem 2. We will also need the following assumptions. We use notation introduced in Section 3.1.

Assumption 1

There exists a neighborhood B of β_0j such that for each t < ∞,

$$\underset{x\in [0,t],\beta \in B}{sup}\mid S_j^{(0)}(\beta ,x)-s_j^{(0)}(\beta ,x)\mid \to 0$$

in probability as n → ∞, $s_j^{(0)}(\beta ,x)$ is bounded away from zero on B × [0, t], and $s_j^{(0)}(\beta ,x)$ and $s_j^{(1)}(\beta ,x)$ are bounded on B × [0, t].

Assumption 2

For each t < ∞ and j = 1, …, p_n, ${\int }_0^t{s}_j^{(2)}(x)dx<\infty$.

Assumption 3

The true parameter vector α₀ belongs to a compact set such that each component α_0j is bounded by a constant A > 0. Furthermore, || α₀ ||₁ is bounded by a constant L > 0.

Assumption 4

With τ (the study duration) as defined in Section 3.1, λ₀(τ) is bounded by a positive constant.

Assumption 5

There is some constant H > 0 such that n⁻¹|U_j(β̂_j) − U_j(β_0j)| ≥ H|β̂_j − β_0j | for all j = 1, …, p_n.

Assumptions 1 and 2 are standard in survival analysis. Assumption 3 controls the total effect size of the covariates, which intuitively should be bounded and independent of sample size. The bounded cumulative baseline hazard function required by Assumption 4 usually holds in practice. Finally, Assumption 5 is reasonable because by the mean value theorem, we know that n⁻¹|U_j(β̂_j)−U_j(β_0j)| = |n⁻¹I_j(β^*)||β̂_j −β_0j | for some β* between β̂_j and β_0j. It can be shown that I_j(β^*) converges to the absolute value of the limiting information −∂u_j(β)/∂β evaluated at the true β_0j [30], and it is reasonable to assume that this limiting information is bounded from below away from zero. Thus for n sufficiently large, we can take H = inf _β,j |∂u_j(β)/∂β| such that H ≠ 0.

Our PSIS method will have good theoretical properties if the covariates Z_i also satistify the following reasonable assumptions. Versions of these assumptions have been previously proposed [6, 9], but modifications are required when working with censored data.

Assumption 6

The Z_ij are independent of time and bounded by a constant K > 0, and E(Z_ij) = 0 for all j.

Assumption 7

If F_T (x;Z_i) is the cumulative distribution function of T_i given Z_i, then for constants c₁ > 0 and κ < 1/2, min_j∈ 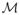|cov[Z_ij, E{F_T (C_i;Z_i) | Z_i}]| ≥ c₁n^−κ.

Assumption 8

The Z_ij, j ∈ are independent of the Z_ij, j ∈ 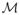and of C_i.

The validity of our proposed screening procedure hinges on whether the misspecified marginal Cox regressions can reflect the importance of the corresponding covariates in the joint model. In general it is difficult to directly link the true α_0j to the marginal β_0j because of the phenomenon of unfaithfulness [31], where the marginal correlation of Z_ij with the outcome can be zero even if α_0j is large, due to correlated covariates. Assumption 7 protects against unfaithfulness. Though the outcome is unobservable under censoring, F_T (C_i;Z_i) is the probability of observing a failure given Z_i and is a sensible surrogate. Assumption 8 is similar to the partial orthogonality assumption introduced in Fan and Song [9].

Appendix B. Proof of Theorem 1

We first relate β_0j to cov[Z_j, E{F_T (C; Z) | Z}]. Assumptions 7 and 8 will then relate the covariance to α_0j.

First, integration by parts gives that

$${\int }_0^{\tau }\text{E}\{Z_j{\lambda }_0(x)exp({\mathit{\alpha }}_0^T\mathbf{Z})S_T{S}_C\}dx=cov[Z_j,\text{E}\{F_T(C;\mathbf{Z})\mid \mathbf{Z}\}].$$

Next, we define the function

$$f(\beta )={\int }_0^{\tau }\frac{\text{E}\{Z_{j}exp(\beta Z_j)S_T{S}_C\}}{\text{E}\{exp(\beta Z_j)S_T{S}_C\}}\text{E}\{{\lambda }_0(x)exp({\mathit{\alpha }}_0^T\mathbf{Z})S_T{S}_C\}dx.$$

Then since β_0j is the solution to the estimating equation u_j(β) (3), we know that cov[Z_j, E{F_T (C;Z) | Z}] = f(β_0j). We can use the Cauchy- Schwarz inequality to show that ∂f(β)/∂β ≥ 0, with equality if and only

if P{Z_j exp(βZ_j/2)(S_T S_C)^1/2 = c exp(βZ_j/2)(S_T S_C )^1/2} = 1 for some constant c. Since this will not hold if Z_j is not constant, we see that f (β) is a monotone-increasing function in β.

Now suppose α_0j = 0 so that j ∈ . By Assumption 8, Z_j is independent of E{F_T (C; Z) | Z}, so that f (β_0j) = cov[Z_j, E{F_T (C; Z) | Z}] = 0. However, we also have that f(0) = 0, since E{Z_jS_T S_C} = E(Z_j)E(S_T S_C) = 0 by Assumption 6 and because Z_j and C are independent for j ∈ . Because f(β) is monotone we know that there is only one value of β such that f(β) = 0, so that β_0j = 0. Similarly, suppose that a_0j ≠ 0 so that j ∈ 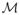. Then by Assumption 7, |f(β_0j)| = |cov[Z_j, E{F_T (C; Z) | Z}]| > c₁n^−κ. Therefore β_0j ≠ 0 by monotonicity, and we can conclude that α_0j = 0 if and only if β_0j = 0.

Appendix C. Proof of Theorem 2

We first bound |U_j(β̂_j)−U_j(β_0j)| by the supremum of an empirical process, where U_j(β) was defined in (2). We then use the concentration theorem of Massart [32] to derive a maximal inequality. We will conclude by using Assumption 5 to extend this inequality to |β̂_j − β_0j|.

First, let Ū_j(β) = n⁻¹U_j(β). Since we still have Ū_j(β̂_j) = 0, we can write |Ū_j(β̂_j) − Ū_j(β_0j)| = |Ū_j(β_0j)|. Because Ū_j(β_0j) is not a sum of independent terms, we cannot directly apply empirical process techniques. However, we know from Lin and Wei [33] that ${\overline{U}}_j({\beta }_{0j})=n^{-1}{\sum }_{i=1}^n{w}_i^{(j)}({\beta }_{0j})+o_p(1)$, where

$$w_i^{(j)}({\beta }_{0j})={\int }_0^{\tau }\left\{Z_{ij}-\frac{\text{E}\{Z_{ij}exp({\beta }_{0j}{Z}_{ij})S_T{S}_C\}}{\text{E}\{exp({\beta }_{0j}{Z}_{ij})S_T{S}_C\}}\right\}{dN}_i(x)-{\int }_0^{\tau }\frac{Y_i(x)exp({\beta }_{0j}{Z}_{ij})}{\text{E}\{exp({\beta }_{0j}{Z}_{ij})S_T{S}_C\}}\left\{Z_{ij}-\frac{\text{E}\{Z_{ij}exp({\beta }_{0j}{Z}_{ij})S_T{S}_C\}}{\text{E}\{exp({\beta }_{0j}{Z}_i)S_T{S}_C\}}\right\}E\{{dN}_i(x)\}.$$

and the $w_i^{(j)}({\beta }_{0j})$ are independent. Furthermore, it is easy to show that $\text{E}\{w_i^{(j)}({\beta }_{0j})\}=0$. If we let E_n denote the empirical measure, then we can $\mid {\overline{U}}_j({\widehat{\beta }}_j)-{\overline{U}}_j({\beta }_{0j})\mid \le {sup}_{\beta }\mid ({\text{E}}_n-\text{E})w_i^{(j)}(\beta )\mid +o_p(1)$. Thus |Ū_j(β̂_j) − Ū_j(β_0j)| is bounded by the sum of the supremum of an empirical process and a term that converges to zero in probability.

To derive a maximal inequality for this process, we first find a bound on $w_i^{(j)}(\beta )$ uniform over β and j = 1, …, p_n. Using Assumptions 3, 4, and 6, we can write that $\mid w_i^{(j)}(\beta )\mid \le 2K[1+{\mathrm{\Lambda }}_0(\tau )exp\{2K(A+L)\}]$ for j = 1, …, p_n. Next, we must find a bound on the expected value of our supremum. Let ε_i, i = 1, …, n be an independent, identically distributed sequence of random variables taking values ±1 with probability 1/2. In particular, they are independent of Z. Then $\text{E}\{{sup}_{\beta }\mid ({\text{E}}_n-\text{E})w_i^{(j)}(\beta )\mid \}\le 2\text{E}[{sup}_{\beta }\mid {\text{E}}_n\{{\epsilon }_i{w}_i^{(j)}(\beta )\}\mid ]$, by Lemma 2.3.1 of van der Vaart and Wellner [34]. But by the Cauchy-Schwarz inequality, independence of ε_i and Z_i, and the bound on | $w_i^{(j)}(\beta )$| derived above, we can show that the right side is bounded by $4K[1+{\mathrm{\Lambda }}_0(\tau )exp\{2K(A+L)\}]{\{var(n^{-1}{\sum }_{i=1}^n{\epsilon }_i)\}}^{1/2}$. Then from the concentration theorem of Massart [32], we know that

$$\text{P}\left[\underset{\beta }{sup}\mid ({\text{E}}_n-\text{E})w_i^{(j)}(\beta )\mid \ge n^{-1/2}4K[1+{\mathrm{\Lambda }}_0(\tau )exp\{2K(A+L)\}](1+t)\right]\le exp(-t^2/2).$$ (C.1)

Finally, we can relate this inequality back to |β̂_j − β_0j | with Assumption 5, though we must also deal with the o_p(1) term. Using a previously proven inequality, $\mid {\widehat{\beta }}_j-{\beta }_{0j}\mid \le H^{-1}{sup}_{\beta }\mid ({\text{E}}_n-\text{E})w_i^{(j)}(\beta )\mid +o_p(1)$, so we can write

$$\text{P}\left[\sqrt{n}\mid {\widehat{\beta }}_j-{\beta }_{0j}\mid \ge 4K[1+{\mathrm{\Lambda }}_0(\tau )exp\{2K(A+L)\}](1+t)/H\right]\le \text{P}\left[\underset{\beta }{sup}\mid ({\text{E}}_n-\text{E})w_i^{(j)}(\beta )\mid +o_p(1)\ge n^{-1/2}4K[1+{\mathrm{\Lambda }}_0(\tau )exp\{2K(A+L)\}](1+t)\right].$$ (C.2)

But for any ε > 0, P(A + B ≥ c) ≤ P(A ≥ c − ε) + P(B ≥ ε), where A and B are random variables and c is a constant. We conclude by combining this with (C.1) and (C.2) and taking ε arbitrarily close to 0.

Appendix D. Proof of Theorem 3

From Theorem 1, we know that β_0j ≠ 0 if j ∈ 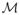. Then by Theorem 2.1 of Struthers and Kalbfleisch [17] and the mean value theorem, we know that $\mid u_j(0)\mid =\mid u_j({\beta }_{0j})-u_j(0)\mid =\mid u_j^{\prime }({\beta }^{\ast })\mid \mid {\beta }_{0j}\mid$ for some β* between β_0j and 0, where $u_j^{\prime }(\beta )={du}_j(\beta )/d\beta$. We will first bound $u_j^{\prime }(\beta )$ and then use Assumption 7 to conclude.

Integrating by parts, we can show that $\mid u_j^{\prime }(\beta )\mid \le 2K^2\mid \text{E}\{S_T(C;\mathbf{Z})\mid \mathbf{Z}\}\mid$. But E{S_T (C; Z) | Z} is bounded by 1, so

$$\mid {\beta }_{0j}\mid \ge 0.5K^{-2}\left|cov[Z_j,\text{E}\{F_T(C;\mathbf{Z})\mid \mathbf{Z}\}]-{\int }_0^{\tau }\frac{\text{E}(Z_j{S}_T{S}_C)}{\text{E}(S_T{S}_C)}\text{E}\{{\lambda }_0(x)exp({\mathit{\alpha }}_0^T\mathbf{Z})S_T{S}_C\}dx\right|.$$

Because S_T S_C is the probability of being at risk at time x, we can intuitively see, and also prove, that E(Z_jS_T S_C) = cov(Z_j, S_T S_C) and cov[Z_j, E{F_T (C; Z) | Z}] have opposite signs. This implied that j ∈ 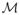, |β_0j| ≥ 0.5K⁻²|cov[Z_j, E{F_T (C; Z) | Z}]|, and Assumption 7 gives min_j∈ 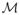|β_0j| ≥ c₂n^−κ for c₂ = 0.5K⁻²c₁.

Appendix E. Proof of Theorem 4

We first derive a probability bound for the standardized marginal regression parameters. We can then use this bound to find P( ⊆ ).

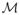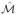Let 1+t = c₂Hn^1/2−κ/(8K[1+ Λ₀(τ ) exp{2K(A + L)}]), with c₂ and κ as defined in Theorem 3 and K, Λ₀(τ), A, and L as defined in Theorem 2. Then by Theorem 2 there exists a constant c₃ such that P(|β̂_j − β_0j| ≥ c₂n^−κ/2) ≤ exp(−c₃n^1−2κ).

If we now set our cutoff γ_n = Φ⁻¹(1 − q_n/2), then we can write the probability of retaining the important covariates as 1 − P{min_j∈ 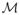I_j(β̂_j)^1/2|β̂_j| < γ_n} ≥ 1 − P{min_j∈ 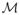|β̂_j| ≤ γ_n(Hn)^−1/2}. Using Theorem 3 we can show that c₂n^−κ − |β̂_j| ≤ |β_0j − β̂_j|, j ∈ M, so P{min_j∈ 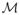|β̂_j| ≤ γ_n(Hn)^−1/2} ≤ P{max_j∈ 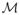|β̂_j − β_0j| ≥ c₂n^−κ − γ_n(Hn)^−1/2}. If we have γ_n ≤ c₂H^1/2n^1/2−κ/2, then the probability bound above gives P( 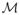⊆ 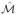) ≥ 1 − exp(−c₃n^1−2κ).

Finally, since q_n = f/p_n, the requirement on γ_n can be rewritten as p_n ≤ (f/2){1 − Φ(c₂H^1/2n^1/2−κ/2)}⁻¹. Using the fact that 1 − Φ(x) ≤ x⁻¹ exp(−x²/2), this inequality can be satisfied if $p_n\le f/2exp(c_2^{2}H{n}^{1-2\kappa }/8)$. Thus the sure screening property holds as long as log(p_n) = O(n^1-2κ).

Appendix F. Proof of Theorem 5

We first show that for j ∈ , U_j(β) evaluated at the true β_0j can be approximated by a sum of continuous-time martingales, just as it can in a correctly specified Cox regression. We can then appeal to an Edgeworth expansion by Gu [35] to conclude.

By Theorem 1 we know that β_0j = 0 for j ∈ . Thus we can rewrite

(2) as

$$\begin{array}{l}{U}_j({\beta }_{0j})=\sum _{i=1}^n{\int }_0^{\tau }\left\{Z_{ij}-\frac{n^{-1}{\sum }_l{Z}_{lj}{Y}_l(x)e^{{\mathit{\alpha }}_o^T{\mathbf{Z}}_l}}{n^{-1}{\sum }_l{Y}_l(x)e^{{\mathit{\alpha }}_o^T{\mathbf{Z}}_l}}\right\}{dN}_i(x)+\sum _{i=1}^n{\int }_0^{\tau }\left\{\frac{n^{-1}{\sum }_l{Z}_{lj}{Y}_l(x)e^{{\mathit{\alpha }}_o^T{\mathbf{Z}}_l}}{n^{-1}{\sum }_l{Y}_l(x)e^{{\mathit{\alpha }}_o^T{\mathbf{Z}}_l}}-\frac{n^{-1}{\sum }_l{Z}_{lj}{Y}_l(x)}{n^{-1}{\sum }_l{Y}_l(x)}\right\}{dN}_i(x)\\ =\sum _{i=1}^n{\int }_0^{\tau }\left\{Z_{ij}-\frac{n^{-1}{\sum }_l{Z}_{lj}{Y}_l(x)e^{{\mathit{\alpha }}_o^T{\mathbf{Z}}_l}}{n^{-1}{\sum }_l{Y}_l(x)e^{{\mathit{\alpha }}_o^T{\mathbf{Z}}_l}}\right\}{dM}_i(x)+n^{-1}\sum _{l=1}^n{\int }_0^{\tau }\left\{\frac{Z_{lj}{Y}_l(x)e^{{\mathit{\alpha }}_o^T{\mathbf{Z}}_l}}{n^{-1}{\sum }_l{Y}_l(x)e^{{\mathit{\alpha }}_o^T{\mathbf{Z}}_l}}-\frac{Z_{lj}{Y}_l(x)}{n^{-1}{\sum }_l{Y}_l(x)}\right\}\sum _i^n{dN}_i(x),\end{array}$$

where $M_i(x)=N_i(x)-{\int }^x{Y}_i(t){\lambda }_0(t)e^{{\mathit{\alpha }}_o^T{\mathbf{Z}}_i}dt$ is a continuous martingale in x.

Now let $S_m={\sum }_{l=1}^m{\xi }_l$, where

$${\xi }_l=\left\{\frac{Z_{lj}{Y}_l(x)e^{{\mathit{\alpha }}_o^T{\mathbf{Z}}_l}}{n^{-1}{\sum }_l{Y}_l(x)e^{{\mathit{\alpha }}_o^T{\mathbf{Z}}_l}}-\frac{Z_{lj}{Y}_l(x)}{n^{-1}{\sum }_l{Y}_l(x)}\right\}\sum _i^n{dN}_i(x).$$

Note that E(ξ_m | S_m−1) = E{E(ξ_m | S_m−1, Z_m) | S_m−1}, and

$$\text{E}({\xi }_m\mid S_{m-1},{\mathbf{Z}}_m)=Z_{mj}\text{E}\left[\left\{\frac{Y_m(x)e^{{\mathit{\alpha }}_o^T{\mathbf{Z}}_m}}{n^{-1}{\sum }_l{Y}_l(x)e^{{\mathit{\alpha }}_o^T{\mathbf{Z}}_l}}-\frac{Y_m(x)}{n^{-1}{\sum }_l{Y}_l(x)}\right\}\sum _i^n{dN}_i(x)|S_{m-1},{\mathbf{Z}}_m\right].$$

Given S_m−1, the conditional expectation on the right-hand side above is a random variable in Z_mk, k ∈ only, and by Assumption 8 is independent of Z_mj, j ∈ . Since E(Z_mj | S_m−1) = E(Z_lj) = 0 by Assumption 6, we find that E(ξ_m | S_m−1) = 0, implying that S_m is a discrete martingale in m. Then when m = n, by the inequality of Dharmadhikari et al. [36] we have that E(|n⁻¹S_n|^p) = Dn^−p/2 for p ≥ 2, where we can show that D does not depend on j.

We have shown that for j ∈ ,

$$U_j({\beta }_{0j})=\sum _{i=1}^n{\int }_0^{\tau }\left\{Z_{ij}-\frac{n^{-1}{\sum }_l{Z}_{lj}{Y}_l(x)e^{{\mathit{\alpha }}_o^T{\mathbf{Z}}_l}}{n^{-1}{\sum }_l{Y}_l(x)e^{{\mathit{\alpha }}_o^T{\mathbf{Z}}_l}}\right\}{dM}_i(x)+n^{-1}{S}_n,$$

where n⁻¹S_n satisfies the same conditions as R_{1, n} in (4.3) of Gu (1992). We can therefore extend the proof of Theorem 2.1 in Gu (1992) to show that

$$\underset{x}{sup}\left|\text{P}\{I_j{({\widehat{\beta }}_j)}^{1/2}\mid {\widehat{\beta }}_j\mid \ge x\}-\mathrm{\Phi }(x)\right|\le c_4{n}^{-1/2},$$

where c₄ does not depend on j. Then (4) implies

$$\text{E}\left(\frac{|\widehat{\mathcal{M}}\cap {\mathcal{M}}^c|}{\mid {\mathcal{M}}^c\mid }\right)\le \frac{1}{p_n-s_n}\sum _{j\in {\mathcal{M}}^c}[2\{1-\mathrm{\Phi }({\gamma }_n)\}+c_4{n}^{-1/2}].$$

The result follows if we choose γ_n = & Φ⁻¹(1 − q_n/2).