Abstract
The increase in insulin secretion caused by glucagon-like peptide-1 (GLP-1) and GLP-1 mimetics observed during an intravenous glucose test (IVGTT) has been reported in both normal and disease animal models, as well as in humans. In this study, a hierarchical population modeling approach is used, together with a previously reported model relating glucose to insulin appearance, to determine quantitative in vivo dose-response relationships between GLP-1 dose level and both first- and second-phase insulin release. Parameters of the insulin kinetic model were estimated from the complete set of glucose and insulin data collected in 219 anesthetized nonfasted NMR-imaged mice after intravenous injection of glucose (1 g/kg) alone or with GLP-1 (0.03–100 nmol/kg). The resulting dose-response curves indicate a difference in GLP-1 effect on the two release phases, as is also evident from the different ED50 parameter values (0.107 vs. 6.65 nmol/kg for phase 1 vs. phase 2 insulin release parameters). The first phase of insulin release is gradually augmented with increasing GLP-1 dose, reaching saturation at a dose of ∼1 nmol/kg, while the second-phase release changes more abruptly at GLP-1 doses between 3 and 10 nmol/kg and shows a more pronounced 100-fold increase between control and the high GLP-1 dose of 100 nmol/kg Moreover, separate disposition indices calculated for phase 1 and 2 insulin release, show a different pattern of increase with increasing GLP-1 dose.
Keywords: glucose tolerance, insulin secretion, insulin sensitivity, intravenous glucose test, population analysis
the enteroendocrine hormone glucagon-like peptide-1 (GLP-1) produced by the gastrointestinal tract enhances the glucose-dependent secretion of insulin from beta cells, promotes beta cell proliferation, and inhibits beta cell apoptosis (12, 16). Some evidence also suggests that GLP-1 inhibits glucagon secretion, slows gastric emptying, and promotes satiety (26). Because of these effects, GLP-1 has been explored as a novel therapy of diabetes. However, GLP-1 is rapidly degraded by the enzyme dipeptidyl peptidase-IV (DPP-4), which limits its therapeutic use. Consequently, GLP-1 analogs and GLP-1 receptor agonists, which are not prone to or are less sensitive to the effect of DPP-4, have been introduced for the treatment of type 2 diabetes mellitus (T2DM), as are DPP-4 inhibitors, which prevent the inactivation of endogenously released GLP-1 (6, 18).
Although the overall mechanism of the glucose-reducing effect of GLP-1 and GLP-1 mimetics is complex, the prominent glucose-dependent action of GLP-1 on the beta cell is its potentiating effect on insulin secretion (16). It is hypothesized that the GLP-1 agonist exenatide stimulates insulin response to exogenous glucose intake through its activation on both first- and second-phase insulin secretion (19). This effect can be especially evident, and thus accurately quantifiable, when GLP-1 is concomitantly given with intravenous glucose. The increase in insulin secretion caused by GLP-1 and GLP-1 mimetics observed during an intravenous glucose tolerance test (IVGTT) has been reported in both normal and disease animal models (2, 11, 15, 20), as well as in humans (12, 34), by evaluating insulin and C-peptide plasma concentrations. Other studies have examined the action of GLP-1 on first-phase insulin secretion rate in rodents and humans based on the area under the plasma concentration curve (AUC) of insulin during the first minutes after initiation of IVGTT, concluding that GLP-1 exerts a potent action on the first-phase insulin release (2, 29). First-phase insulin secretion in healthy volunteers was also explored in a study on the action of the GLP-1 analog liraglutide (1), which augmented both insulin release components proportionately with increased dose. Mager et al. (25), using the hyperglycemic clamp method in healthy volunteers and T2DM, reported a substantial increase in insulin release that was related to the plasma concentration of the GLP-1 agonist exendin-4 following a sigmoidal relationship.
The aforementioned studies, however, have been limited by the use of AUC-based methods to assess insulin release, by the small number of subjects evaluated, and by the limited GLP-1 doses tested. Thus, dose-response models that separately characterize the relationship between GLP-1 dose and first- and second-phase insulin response processes in a large number of subjects or animals over a range of GLP-1 doses are needed. In fact, a quantitative understanding of the reduction of the late beta-cell response, both due to the DPP-4-mediated vanishing effect of GLP-1 and to the lower levels of glucose, could be important in establishing the appropriate dosage regimen. Moreover, the attenuation of the insulin response may indicate stages of glucose impairment, as the diminished immediate insulin peak is observed, even in prediabetic individuals with impaired glucose tolerance (10). Furthermore, the restoration of both first- and second- phase insulin secretion demonstrates one of the most prominent antidiabetic features of GLP-1 and its mimetics.
The aim of our study was, therefore, to fully quantify the dose-dependent actions of GLP-1 on first- vs. second-phase insulin secretion, taking into account the mutual relation between insulin secretion and insulin resistance (4). To that end, we investigated the dose-response relationships between GLP-1 and both the first and second phases of insulin secretion following IVGTT in mice and examined whether exogenous GLP-1 affects the compensatory islet adaptation to insulin resistance. The investigation was performed by combining and modifying previously reported and validated mathematical models of plasma insulin dynamics (1) and of GLP-1 action on glucose disappearance (32). A hierarchical nonlinear modeling analysis is used that adopts a population framework and combines all the study data for the complete range of GLP-1 doses to construct in vivo dose-response relationships.
MATERIALS AND METHODS
Animals and experimental protocol.
A total of 219 NMR-imaged mice (Bomholdt Gaard, Ry, Denmark) weighing 20–25 g were included in the study, representing a subset of animals from a previous study (2). The experiments were approved by the Animal Ethics Committee of Lund University and Malmö, Sweden (certificate no. M98–07). The experiments were performed in the morning 4 h after removal of food from the cages. Details of the IVGTT were presented previously (27). Briefly, the mice were anesthetized and a basal blood sample was taken from the retrobulbar, intraorbital, capillary plexus in heparinized tubes, followed by a rapid intravenous injection of d-glucose (1 g/kg; British Drug House, Poole, UK) in a tail vein either alone or together with synthetic GLP-1 (Peninsula Laboratories Europe, Merseyside, UK) at various dose levels (nmol/kg): 0 (n = 120), 0.03 (n = 11), 0.1 (n = 8), 0.3 (n = 12), 1.0 (n = 8), 3.0 (n = 7), 10 (n = 23), 30 (n = 9), and 100 (n = 21). The volume load was 10 μl/g body wt. Additional samples were taken at 1, 5, 10, 20, 30, and 50 min after the intravenous administration. Serial blood sampling was performed from the retrobulbar plexus, which is less stressful than destructive sampling. Plasma samples were separated by centrifugation immediately and stored at −20°C until analysis.
Sample analysis.
Plasma glucose was determined with the glucose oxidase method with the use of 2,2′-azino-di-[3-ethyl-benzthiazoline sulfonate] as substrate (9). The intraassay coefficient of variation (CV) of the method is <2% at both low and high levels. The interassay CV is <3% at both low and high levels. Plasma insulin was determined radioimmunochemically using a guinea pig anti-rat insulin antibody with 125I-labeled human insulin as a tracer, and rat insulin as a standard (Linco Research, St. Charles, MO). An anti-IgG (goat anti-guinea pig) antibody (Linco) was used to separate free and bound radioactivity. The sensitivity of the assay was 12 pmol/l, the intraassay CV is <3%, and the interassay CV is <4% at both low and high levels.
Insulin kinetic models.
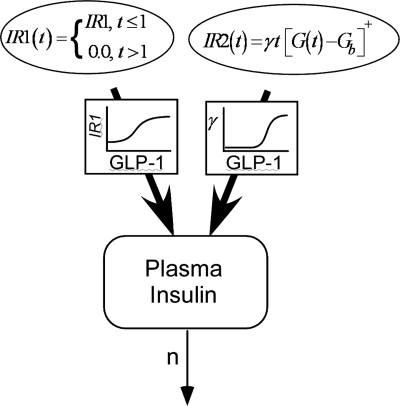
To describe plasma insulin kinetics, we adopted the model reported by Agerso and Vicini (1), which was derived from the insulin kinetic model introduced by Toffolo et al. (33). The model includes terms representing first- (IR1) and second-phase (IR2) insulin release and insulin turnover as follows:
| (1) |
where, I(t) plasma insulin concentration (pmol/l), Ib represents the reference insulin value (pmol/l) set at the 50 min measured value and n (min−1) is the rate constant for insulin degradation (i.e., the fractional insulin clearance). The first-phase insulin release rate IR1 (min−1·pmol−1·l−1) is assumed to be constant over the first minute following the glucose load and zero thereafter [see discussion for comparison to the model of Agerso and Vicini (1)]. The second-phase insulin release rate is assumed to begin after glucose injection and is modeled as follows:
| (2) |
where G(t) is measured plasma glucose concentration (mmol/l), Gb represents the reference glucose value (mmol/l) set at the 50 min measured value, t is time from glucose load (min), and γ is a constant relating plasma glucose to second-phase insulin release (pmol·min−2·mmol−1) that represents insulin response sensitivity to glucose. The notation [z]+ indicates the term is 0 when the argument z < 0. Also in Eq. 2, the measured values of glucose were used at each sample time (i.e., glucose treated as error free), and the values between sample times were obtained by linear interpolation.
Among the various relations considered between the parameters (IR1, γ) and the GLP-1 doses during the population modeling, the following sigmoidal models were selected on the basis of the fit of the insulin concentration data and model selection criteria (negative log likelihood and Akaike Information Criterion):
| (3) |
| (4) |
In the above equations, GLP1 is GLP-1 dose (nmol/kg), IR10 and IR1max (pmol·l−1·min−1) are the baseline (control), and the maximum GLP-1-induced values of IR1, ED50IR1 (nmol/kg), is the dose of GLP-1 that elicits 50% of the maximal responses, and HIR1 represents the sensitivity of the IR1 response to GLP-1. The units for the corresponding parameters of the γ relationship (γ0, γmax, ED50γ, Hγ) are given in Table 1. Such sigmoidal relationships are often used to model dose- and concentration-response relationships in pharmacokinetics and pharmacodynamics. Equations 1–4 represent the complete model for GLP-1 action on insulin kinetics. In Fig. 1, the diagram of the insulin kinetic model is shown.
Table 1.
Population parameter estimates for the plasma insulin kinetic model
| Parameter | Mean | Interindividual Variability, CV% |
|---|---|---|
| n, min−1 | 0.388 | 93.6% |
| Model Eq. 3—first phase (IR1) | 54.1% | |
| IR10, pmol·l−1·min−1 | 1690 | |
| IR1max (pmol·l−1·min−1 | 5570 | |
| ED50IR1, nmol/kg | 0.107 | |
| HIR1 | 1.06 | |
| Model Eq. 4—second phase, γ | 102% | |
| γ0, pmol·min−2·mmol−1 | 0.500 | |
| γmax, pmol·min−2·mmol−1 | 67.1 | |
| ED50γ, nmol/kg | 6.65 | |
| Hγ | 3.31 |
Fig. 1.
Model diagram illustrating the two insulin release phases and depicting the action of GLP-1 on the parameter of each release process.
Insulin sensitivity.
To investigate possible changes in the relationships between insulin release and insulin sensitivity during GLP-1 administration, we included in our analysis the minimal model of glucose disappearance applied to mice data (27). The model (equations not shown) has been widely used to assess the insulin sensitivity index SI [min−1/(pmol/l)] in mice in many different conditions (e.g., Refs. 2 and 32), and it has been validated against the gold standard glucose clamp (27). Insulin sensitivity and secretion are mutually related through a nonlinear inverse power function (a hyperbola in particular cases), which has been shown to hold in many different clinical and pathophysiological conditions (4). This relationship indicates that in the normal state, a reduction of insulin sensitivity is compensated by an increase of beta cell function, so that their product (the disposition index) remains constant (28). We thus explored the GLP-1 effect on this relationship by analyzing the changes in the disposition index. We introduce two indices describing the relationships between insulin sensitivity and first (IR1)- and second (IR2)-phase insulin release, after evaluating the linearity of the log-log function. Our data confirmed the nonlinear inverse relationship already observed in humans (22) and in mice (27) from parameters derived from the IVGTT.
Population analysis.
In hierarchical, nonlinear mixed effects modeling, data from all animals are analyzed simultaneously, thus allowing information from the separate experiments to collectively inform the model estimation (14, 31). This approach, therefore, is especially well suited to situations when only limited data are available from any one individual or animal, as is the case with the IVGTT mouse preparation. The population analysis yields estimates of the mean and interanimal variability for model parameters (e.g., IR1 and γ in the insulin kinetic model, SI in the glucose disappearance model), as well as for the parameters in the GLP-1 dose-response equations. The population modeling was accomplished via maximum likelihood estimation using the MLEM algorithm in the ADAPT 5 software for pharmacokinetic/pharmacodynamic system analysis (13). The parameters of the insulin kinetic model and glucose disappearance model were assumed to follow lognormal distributions, and the error associated with the measured insulin and glucose was each assumed to be normally distributed with standard deviations proportionally related to the measured variable (when an additive term was also included, it was found not to be significant).
RESULTS
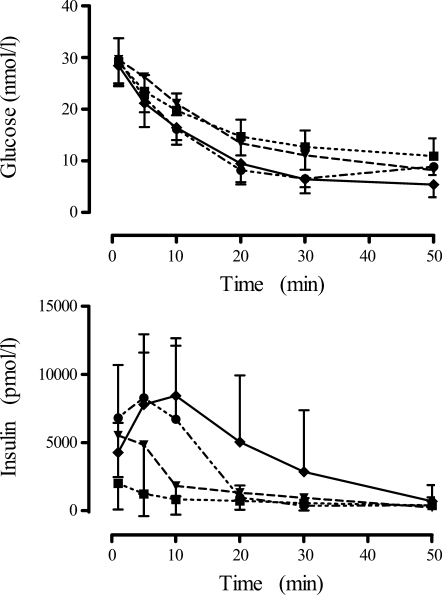
Figure 2 displays examples of IVGTT in mice. Medium (1.0 nmol/kg) to high (100 nmol/kg) doses of GLP-1 elicit an insulin response progressively higher than that of the regular IVGTT with no GLP-1, despite similar glucose patterns. Figure 2 (bottom) also indicates the dose dependence of the second-phase insulin, as indicated by the progressively elevated insulin concentrations observed at 10 through 30 min.
Fig. 2.
Measured plasma glucose concentrations (mmol/l) (top) and insulin concentrations (pmol/l) (bottom) for control mice (■, n = 120), as well as for the 1.0 nmol/kg (▾, n = 8), 30.0 nmol/kg (●, n = 9), and 100 nmol/kg (♦, n = 21) GLP-1-dosed animals. Values are expressed as means ± SD.
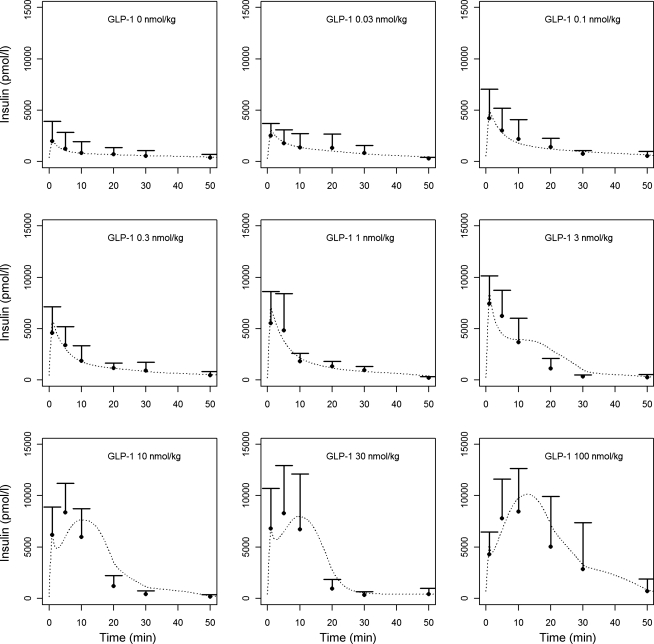
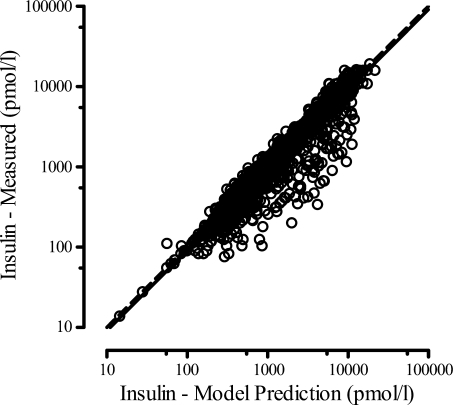
Table 1 lists the population model parameter estimates, including covariate parameters for the models of Eqs. 3 and 4, together with the interindividual variability. The fitted insulin concentration time profiles (first and second phase) are averaged and shown for each GLP-1 dose in Fig. 3, together with the measured plasma insulin concentrations. Through the composite graph of predicted vs. measured plasma insulin for all GLP-1 dose groups, Fig. 4 shows the performance of the model. Although some dispersion and model over prediction are noted, the coefficient of determination for the regression line is r2 = 0.81.
Fig. 3.
Insulin concentrations (means ± SD) measured in different GLP-1 dosing groups and average insulin profiles obtained from the insulin kinetic model (dashed lines).
Fig. 4.
Insulin data vs. model prediction from the insulin kinetic model. The linear regression (intercept set at zero) between measured insulin and model predictions (solid line) is 0.91 I(t) with R = 0.90. The line of identity is shown as a dashed line.
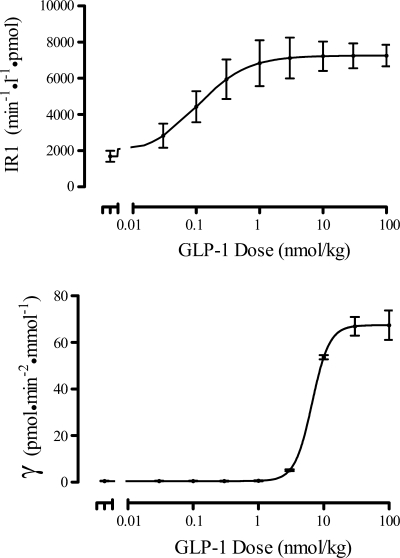
The relationships of the two phases of insulin release (IR1 and γ) with GLP-1 dose, obtained with the population analysis using the models of Eqs. 3 and 4, are shown in Fig. 5. These curves indicate a difference in GLP-1 effect on the two release phases, as is also evident from the different ED50 parameter values (0.107 vs. 6.65 nmol/kg; Table 1). The first phase of insulin release is gradually augmented with increasing GLP-1 dose, reaching a saturation at a dose of ∼1 nmol/kg, while the second-phase release changes more abruptly at GLP-1 doses between 3 and 10 nmol/kg. Moreover, the sensitivities of the two insulin releases phases to GLP-1 differ, as indicated by the more than three-fold difference in HIR1 and Hγ.
Fig. 5.
Population mean dose-response curves for first-phase insulin release (IR1 vs. GLP-1, top) and second-phase insulin release (γ vs. GLP-1, bottom). Mean (●) ± SE shown at each GLP-1 dose value.
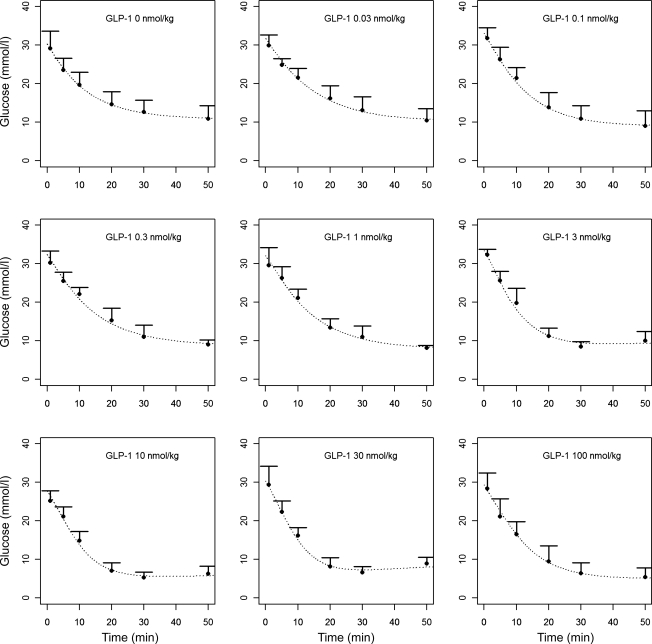
The results of the population analysis using the minimal model of glucose disappearance are presented in Table 2 (population means and interindividual variability). The population mean value of insulin sensitivity index SI from the minimal model was 0.0126 min−1/(pmol/l) with an interanimal standard deviation of 0.0087 min−1/(pmol/l). The mean of the individual estimates of SI was reduced from 0.0198 ± 0.0121 min−1/(pmol/l) in the control animals to 0.0116 ± 0.0058 min−1/(pmol/l) in all the GLP-1-dosed groups combined. There was no significant difference in the individual estimates of SI among those animals receiving GLP-1. The fitted glucose concentration time profiles are averaged and shown for each GLP-1 dose in Fig. 6, together with the measured plasma glucose concentrations.
Table 2.
Population parameter estimates for the minimal model of glucose kinetics
| Parameter | Mean | Interindividual Variability, CV% |
|---|---|---|
| SG, min−1 | 0.0655 | 28.9% |
| SI, min−1/(pmol/l) | 0.0126 | 69.6% |
| p2, min−1 | 0.0954 | 20.9% |
| V, liters | 0.00674 | 22.0% |
Fig. 6.
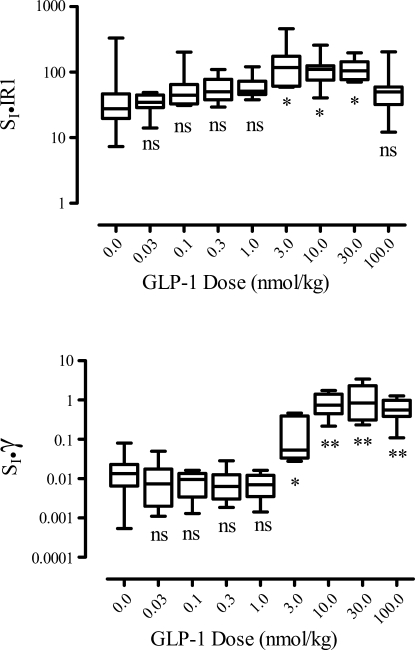
Disposition index associated with first-phase insulin release (top) (SI IR1) and second-phase (SI, γ) insulin release in lower panel for increasing GLP-1 doses. *P < 0.05; **P < 0.001. Box plots indicate median, interquartile range, as well as minimum and maximum values.
The resulting values of the disposition indices are plotted in Fig. 7 vs. GLP-1 dose. Although the disposition index associated with the first-phase insulin release SI·IR1 is different for the different dose groups (Kruskal-Wallis test), only the 3.0, 10.0, and 30.0 nmol/kg dose groups are different from control (P < 0.05, Dunn's multiple-comparison test), and the maximum change from control is 3.5-fold. In contrast, the second-phase disposition index SI·γ increases considerably for GLP-1 doses in the range of 3 to 10 nmol/kg, with an overall 40-fold increase from control to the 100 nmol/kg dose.
Fig. 7.
Glucose concentrations (means ± SD) measured in different GLP-1 dosing groups and average glucose profiles obtained from the glucose minimal model (dashed lines) (ns, not significant).
DISCUSSION
This report provides for the first time to the best of our knowledge a quantitative assessment of the action of GLP-1 on both the first and second phases of insulin secretion in rodents, by exploiting mathematical models of plasma insulin kinetics. Using a hierarchical population modeling approach, we established composite in vivo dose-response relationships between GLP-1 dose level and both first- and second-phase insulin release. These quantitative results support the finding that one of the most important antidiabetic aspects of GLP-1 and its analogs is their ability to increase both phases of insulin secretion in normal and diabetic subjects (25, 29, 30, 35).
Our modeling results indicate that GLP-1 markedly enhances the magnitude of insulin secretion in mice after IVGTT, through a dose-dependent action on both the first (IR1)- and second-phase (IR2) insulin release. Regarding the first-phase insulin release, the results indicate that GLP-1 stimulates insulin production in a sigmoidal fashion, increasing linearly between 0.03 and 0.3 nmol/kg GLP-1 and approaching an asymptote with larger GLP-1 dosage, possibly reflecting receptor saturation. GLP-1 was highly effective in stimulating first-phase insulin secretion, as indicated by the three-fold augmentation of glucose-stimulated insulin secretion produced at the highest GLP-1 dose relative to control. Concomitant administration of GLP-1 and glucose was also found to markedly potentiate second-phase insulin secretion, and the second-phase release rate term γ also followed a sigmoidal relation with GLP-1 dose. Second-phase release exhibited a more than 100-fold increase between control and the high GLP-1 dose of 100 nmol/kg (Table 1, Fig. 5). Qualitatively, a model-independent analysis of the data showed that GLP-1 significantly increased 1- and 5-min insulin concentrations, representing first-phase insulin secretion, at a lower dose than that required for potentiation of the whole 50-min AUC for insulin (2). This finding agrees with our quantitative modeling results in that the two insulin secretion processes show different potencies to GLP-1, as demonstrated by the difference in ED50IR1 and ED50γ.
A central finding of this study is that the beta-cell sensitivity to GLP-1-induced first-phase insulin secretion is higher than for GLP-1 induced second-phase insulin secretion, whereas the maximum magnitude of the GLP-1-induced second-phase response relative to control, exceeds that observed during the first phase. The two phases have different molecular actions in that the first phase is the immediate release of granules, which are readily releasable after increase of calcium concentrations in beta cells, while the second-phase insulin secretion is a consequence of release of slowly releasable granules within the beta cells (7, 21). While dose-response relationships of the two phases for various external secretagogues have not been studied before, our finding that the sensitivity to GLP-1 was higher for first-phase insulin secretion may indicate that this phase is more readily activated by the signals induced by GLP-1, mainly cAMP-derived signals (17). This conjecture requires further investigation via in vitro studies. Such a finding of higher sensitivity to GLP-1 in first-phase insulin secretion would reinforce the therapeutic value of GLP-1 in the treatment of type 2 diabetes, since several studies have demonstrated that reduction in first-phase insulin secretion is a very early phenomenon during development of type 2 diabetes and is evident in the prediabetic phase of impaired glucose tolerance (24, 36).
Regarding the combined effect of insulin secretion and insulin sensitivity on glucose disappearance (disposition index), we observed that the rise in the GLP-1-induced insulin release during the first insulin release phase was sufficient to raise the disposition index (3.0–30.0 nmol/kg dose range), albeit moderately, even though insulin sensitivity decreased from its control value in the GLP-1-dosed groups. The disposition index for the second phase, however, increased markedly for higher GLP-1 doses because the GLP-1-induced increase in insulin release in these higher-dose groups (see Fig. 7) easily offset the decrease in insulin sensitivity. This implies that higher doses of the incretins are necessary to elicit a substantial augmentation of increases responsible for glucose disposal.
In the model presented here, GLP-1 dose was used as a covariate and related directly to the insulin release terms. Lack of plasma measurements of GLP-1, as well as the limited number of plasma insulin measurements in each animal precluded any type of joint pharmacokinetic-pharmacodynamic analysis, which may have allowed estimates of plasma (or effect site) EC50s for the two insulin release phases. However, given the linearity of GLP-1 plasma kinetics and its short half-life, as shown both in man (23) and mice (3), GLP-1 dose itself can serve as a reasonable surrogate for GLP-1 plasma concentration (2). Because of the very short plasma GLP-1 half-life in mice (1–2 min), the plasma concentration-time profile is bolus-like relative to the duration of the experiment, with a concentration that is proportional to the dose administered, thus motivating the use of GLP-1 dose itself to characterize the insulin release terms. It should be emphasized that the drug effect at a particular time following drug administration will depend on the complete history of the drug concentration (and downstream cellular signaling events) up to the time that the effect is observed, not the drug concentration in the plasma (or the site of action) at the time the effect is measured. Thus, even though the second phase of plasma insulin secretion is not observed until well after the GLP-1 plasma concentration falls to a small fraction of its peak value, the early concentrations of the drug at the effect site also contribute to the later response. However, because of the confounding effects of GLP-1 pharmacokinetics, a more direct assessment GLP-1 action on the two insulin release phases is needed (e.g., via in vitro studies as noted above) to more clearly assess any difference in GLP-1 potency between the two insulin release phases.
While it is difficult to compare levels of GLP-1 after intravenous injection in mice vs. clinically obtained GLP-1 levels in humans, we note that a dose of 0.3 nmol/kg of GLP-1 results in a peak GLP-1 concentration of ∼100 pmol/l in rodents (3), which is equivalent to the peak level after administration of GLP-1 agonist in the clinic. In contrast, DPP-4 inhibition in the clinic results in peak levels of GLP-1 of ∼15–20 pmol/l, which is similar to what would be expected after administration of 0.03 nmol/kg.
The model of plasma insulin kinetics following IVGTT, reported by Agerso and Vicini (1), assumes a time-varying, first-phase insulin secretion rate profile and used a Gaussian time function to represent this process. Given the limited sampling design required for mouse studies (six samples in all and only two early samples at 1 and 5 min), the first-phase insulin secretion could only be represented as a constant secretion rate. Because of the sampling limitations, moreover, the first-phase release interval was fixed to 1 min after glucose injection. Reanalysis of the data with this duration set at 0.5 min or 1.5 min did not alter the model estimates or predictions (results not shown).
The population-modeling approach applied to analyze the IVGTT mouse data in this study combines the data from all animals from all dose groups to simultaneously estimate the mean and interanimal variability of the parameters of the insulin model. Moreover, any relationships between model parameters and GLP-1 dose can be explored as part of the analysis. This approach, therefore, allowed the limited data available from each single mouse experiment to be used to collectively inform the estimation of parameters of the insulin kinetic model under control and GLP-1 administration.
In conclusion, we have found following IVGTTs in mice that the two phases of insulin secretion respond differently to GLP-1. The first-phase insulin release is more sensitive to GLP-1 dose than is the second phase, while the magnitude of the second-phase insulin release to GLP-1, is considerably higher than that of the first-phase response. This overall increase in GLP-1-mediated insulin release compensated for a reduction in insulin sensitivity observed with GLP-1 dosing in our mouse model to produce an overall increase in disposition index at the higher GLP-1 doses used in the study.
GRANTS
This study was supported by the National Institutes of Health grant P41-EB001978 to D. Z. D'Argenio and the Swedish Research Council Grant 6834 (Region Skåne and Faculty of Medicine, Lund University) to B. Ahrén.
DISCLOSURES
Hui Min Chan and Ritesh Jain were supported by postdoctoral fellowships from Pfizer, Inc., during this work. The other authors have nothing to disclose relating to this study.
ACKNOWLEDGMENTS
We are grateful to Lena Kvist and Lilian Bengtsson for their help with the experiments and assay determination.
Present addresses for H. Min Chan and R. Jain: Ritesh Jain, Office of Clinical Pharmacology Review, United States Food and Drug Administration, Rockville, MD, 20857, USA; Hui Min Chan, Clinical Discovery, Bristol-Myers Squibb, Princeton, NJ, USA, 08543.
REFERENCES
- 1. Agerso H, Vicini P. Pharmacodynamics of NN2211, a novel long-acting GLP-1 derivative. Eur J Pharm Sci 19: 141–150, 2003 [DOI] [PubMed] [Google Scholar]
- 2. Ahrén B, Pacini G. Dose-related effects of GLP-1 on insulin secretion, insulin sensitivity, and glucose effectiveness in mice. Am J Physiol Endocrinol Metab 277: E996–E1004, 1999 [DOI] [PubMed] [Google Scholar]
- 3. Ahrén B, Holst JJ, Mårtensson H, Balkan B. Improved glucose tolerance and insulin secretion by inhibition of dipeptidyl peptidase IV in mice. Eur J Pharmacol 404: 239–245, 2000 [DOI] [PubMed] [Google Scholar]
- 4. Ahrén B, Pacini G. Importance of quantifying insulin secretion in relation to insulin sensitivity to accurately assess beta cell function in clinical studies. Eur J Endocrinol 150: 97–104, 2004 [DOI] [PubMed] [Google Scholar]
- 5. Ahrén B, Schmitz OO. GLP-1 receptor agonists and DPP-4 inhibitors in the treatment of type 2 diabetes. Horm Metab Res 36: 867–887, 2004 [DOI] [PubMed] [Google Scholar]
- 6. Ahrén B. Clinical results of treating type 2 diabetic patients with sitagliptin, vildagliptin and saxagliptin—diabetes control and potential adverse events. Best Pract Clin Endocrinol Metab 23: 487–498, 2009 [DOI] [PubMed] [Google Scholar]
- 7. Barg S, Eliasson L, Rorsman P. A subset of 50 secretory granules in close contact with L-type Ca2+ channels accounts for first phase insulin secretion in mouse beta-cells. Diabetes 51 Suppl 1: S74–S82, 2002 [DOI] [PubMed] [Google Scholar]
- 8. Brubaker PL, Drucker DJ. Minireview: glucagon-like peptides regulate cell proliferation and apoptosis in the pancreas, gut, and central nervous system. Endocrinology 145: 2653–2659, 2004 [DOI] [PubMed] [Google Scholar]
- 9. Bruss ML, Black AL. Enzymatic microdetermination of glycogen. Anal Biochem 84: 309–312, 1978 [DOI] [PubMed] [Google Scholar]
- 10. Caumo A, Luzi L. First phase insulin secretion: does it exist in real life? Consideration on shape and function. Am J Physiol Endocrinol Metab 287: E371–E385, 2004 [DOI] [PubMed] [Google Scholar]
- 11. Dachicourt N, Serradas P, Bailbe D, Kergoat M, Doare L, Portha B. Glucagon-like peptide-1 (7–36)-amide confers glucose sensitivity to previously glucose-incompetent β-cells in diabetic rats: in vivo and in vitro studies. J Endocrinol 155: 369–376, 1997 [DOI] [PubMed] [Google Scholar]
- 12. D'Alessio DA, Kahn SE, Leusner CR, Ensinck JW. Glucagon-like peptide 1 enhances glucose tolerance both by stimulation of insulin release and by increasing insulin-independent glucose disposal. J Clin Invest 93: 2263–2266, 1994 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.D'Argenio DZ, Schumitzky A, Wang X. ADAPT 5 User's Guide: Pharmacokinetic/Pharmacodynamic Systems Analysis Software. Los Angeles, CA: Biomedical Simulations Resource, 2009 [Google Scholar]
- 14.Davidian M, Giltinan DM. Nonlinear Models for Repeated Measurement Data. London: Chapman and Hill, 1995 [Google Scholar]
- 15. DeOre K, Greig NH, Holloway HW, Wang Y, Perfetti R, Egan JM. The effects of GLP-1 on insulin release in young and old rats in the fasting state and during an intravenous glucose tolerance test. J Gerontol A Biol Sci Med Sci 52: B245–B249, 1997 [DOI] [PubMed] [Google Scholar]
- 16. Doyle ME, Egan JM. Glucagon-like peptide-1. Recent Prog Horm Res 56: 377–399, 2001 [DOI] [PubMed] [Google Scholar]
- 17. Doyle ME, Egan JM. Mechanisms of action of glucagon-like peptide 1 in the pancreas. Pharmacol Ther 113: 546–593, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Drab SR. Incretin-based therapies for type 2 diabetes mellitus: current status and future prospects. Pharmacotherapy 30: 609–624, 2010 [DOI] [PubMed] [Google Scholar]
- 19. Fehse F, Trautmann M, Holst JJ, Halseth AE, Nanayakkara N, Nielsen LL, Fineman MS, Kim DD, Nauck MA. Exenatide augments first- and second-phase insulin secretion in response to intravenous glucose in subjects with type 2 diabetes. J Clin Endocrinol Metab 90: 5991–5997, 2005 [DOI] [PubMed] [Google Scholar]
- 20. Hendrick GK, Gjinovci A, Baxter LA, Mojsov S, Wollheim CB, Habener JF, Weir GC. Glucagon-like peptide-1-(7–37) suppresses hyperglycemia in rats. Metabolism 42: 1–6, 1993 [DOI] [PubMed] [Google Scholar]
- 21. Hou JC, Min L, Pessin JE. Insulin granule biogenesis, trafficking and exocytosis. Vitam Horm 80: 473–506, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Kahn SE, Prigeon RL, McCulloch DK, Boyko EJ, Bergmann RN, Schwartz MW, Neifing JL, Ward WK, Beard JC, Palmer JP. Quantification of the relationship between insulin sensitivity and beta-cell function in human subjects. Evidence for a hyperbolic function. Diabetes 42: 1663–1672, 1993 [DOI] [PubMed] [Google Scholar]
- 23. Kreymann B, Williams G, Ghatei MA, Bloom SR. Glucagon-like peptide-1 [7–36]: a physiological incretin in man. Lancet 2: 1300–1304, 1987 [DOI] [PubMed] [Google Scholar]
- 24. Leahy JL. Pathogenesis of type 2 diabetes mellitus. Arch Med Res 36: 197–209, 2005 [DOI] [PubMed] [Google Scholar]
- 25. Mager DE, Abernethy DR, Egan JM, Elahi D. Exendin-4 pharmacodynamics: insights from the hyperglycemic clamp technique. J Pharmacol Exp Ther 311: 830–835, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Nauck MA, Heimesaat MM, Behle K, Holst JJ, Nauck MS, Ritzel R, Hufner M, Schmiegel WH. Effects of glucagon-like peptide 1 on counterregulatory hormone responses, cognitive functions, and insulin secretion during hyperinsulinemic, stepped hypoglycemic clamp experiments in healthy volunteers. J Clin Endocrinol Metab 87: 1239–1246, 2002 [DOI] [PubMed] [Google Scholar]
- 27. Pacini G, Thomaseth K, Ahrén B. Contribution to glucose tolerance of insulin-independent vs. insulin-dependent mechanisms in mice. Am J Physiol Endocrinol Metab 281: E693–E703, 2001 [DOI] [PubMed] [Google Scholar]
- 28. Pacini G. The hyperbolic equilibrium between insulin sensitivity and secretion. Nutr Metab Cardiovasc Dis 16 Suppl 1: S22–S27, 2006 [DOI] [PubMed] [Google Scholar]
- 29. Quddusi S, Vahl TP, Hanson K, Prigeon RL, D'Alessio DA. Differential effects of acute and extended infusions of glucagon-like peptide-1 on first- and second-phase insulin secretion in diabetic and nondiabetic humans. Diabetes Care 26: 791–798, 2003 [DOI] [PubMed] [Google Scholar]
- 30. Rachman J, Gribble FM, Barrow BA, Levy JC, Buchanan KD, Turner RC. Normalization of insulin responses to glucose by overnight infusion of glucagon-like peptide 1 (7–36) amide in patients with NIDDM. Diabetes 45: 1524–1530, 1996 [DOI] [PubMed] [Google Scholar]
- 31. Sheiner LB. The population approach to pharmacokinetic data analysis: rationale, and standard data analysis methods. Drug Metab Rev 15: 153–171, 1984 [DOI] [PubMed] [Google Scholar]
- 32. Thomaseth K, Pavan A, Pacini G, Ahrén B. Glucagon-like peptide-1 accelerates the onset of insulin action on glucose disappearance in mice. Am J Physiol Endocrinol Metab 292: E1808–E1814, 2007 [DOI] [PubMed] [Google Scholar]
- 33. Toffolo G, Bergman RN, Finegood DT, Bowden CR, Cobelli C. Quantitative estimation of beta cell sensitivity to glucose in the intact organism: a minimal model of insulin kinetics in the dog. Diabetes 29: 979–990, 1980 [DOI] [PubMed] [Google Scholar]
- 34. Vahl TP, Paty BW, Fuller BD, Prigeon RL, D'Alessio DA. Effects of GLP-1-(7–36)NH2, GLP-1-(7–37), and GLP-1-(9–36)NH2 on intravenous glucose tolerance and glucose-induced insulin secretion in healthy humans. J Clin Endocrinol Metab 88: 1772–1779, 2003 [DOI] [PubMed] [Google Scholar]
- 35. Vilsbøll T, Brock B, Perrild H, Levin K, Lervang H.-H. T, Kolendorf K, Krarup T, Schmitz O, Zdravkovic M, Le-Thi T, Madsbad S. Liraglutide, a once-daily human GLP-1 analogue, improves pancreatic B-cell function and arginine-stimulated insulin secretion during hyperglycaemia in patients with Type 2 diabetes mellitus. Diabet Med 25: 152–156, 2008 [DOI] [PubMed] [Google Scholar]
- 36. Weiss R, Caprio S. Development of type 2 diabetes in children and adolescents. Minerva Med 97: 263–269, 2006 [PubMed] [Google Scholar]