Planar biaxial characterization of diseased human coronary and carotid arteries for computational modeling

Abstract

Computational models have the potential to provide precise estimates of stresses and strains associated with sites of coronary plaque rupture. However, lack of adequate mathematical description of diseased human vessel wall mechanical properties is hindering computational accuracy. The goal of this study is to characterize the behavior of diseased human coronary and carotid arteries using planar biaxial testing. Diseased coronary specimens exhibit relatively high stiffness (50–210 kPa) and low extensibility (1–10%) at maximum equibiaxial stress (250 kPa) compared to human carotid specimens and values commonly reported for porcine coronary arteries. A thick neointimal layer observed histologically appears to be associated with heightened stiffness and the direction of anisotropy of the specimens. Fung, Choi-Vito and modified Mooney-Rivlin constitutive equations fit the multiaxial data from multiple stress protocols well, and parameters from representative coronary specimens were utilized in a finite element model with fluid-solid interactions. Computed locations of maximal stress and strain are substantially altered, and magnitudes of maximum principal stress (48–65 kPa) and strain (6.5–8%) in the vessel wall are lower than previously predicted using parameters from uniaxial tests. Taken together, the results demonstrate the importance of utilizing disease-matched multiaxial constitutive relationships within patient-specific computational models to accurately predict stress and strain within diseased coronary arteries.

INTRODUCTION

Cardiovascular disease is the largest health risk for Americans, and coronary heart disease results in approximately eight-hundred thousand therapeutic interventions each year (Lloyd-Jones et al., 2010). Morbidity of coronary artery disease is believed to be related to the magnitudes of stress and strain within the vessels, thus quantification of these values is of great importance (Holzapfel et al., 2005; Lally et al., 2004). Deformations can be measured in vivo using imaging (with limited resolution); however, to estimate stress and strain distributions, computational modeling of the vessels and related cardiovascular interventions is needed (Holzapfel et al., 2005; Yang et al., 2009).

One promising approach for accurately predicting vessel stresses and strains is to utilize finite element analysis (FEA) with geometric models generated from patient-specific imaging data (Tang et al., 2009b; Yang et al., 2009). Our fluid-structure interaction (FSI) models indicate that sites of rupture in human atherosclerotic carotid plaques are associated with high structural stresses (Tang et al., 2009a). However, lack of adequate mathematical description of diseased vessel wall mechanical properties is hindering computational modeling accuracy (Holzapfel et al., 2005; Yang et al., 2009). Ideally, constitutive models would be based on multiaxial test data and include the nonlinear, anisotropic, and viscoelastic multiaxial behaviors of both healthy and diseased arterial tissues (Lally et al., 2004).

To estimate coronary artery mechanical properties, researchers have performed tests on porcine (Dixon et al., 2003; Lally et al., 2004; Lu et al., 2004; van den Broek et al., 2010; Wang et al., 2006), murine (Ning et al., 2010), and canine coronary arteries (Gow and Hadfield, 1979). Although interspecies physiological similarities exist between humans and certain animals, diseases such as hypertension, intimal hyperplasia, and plaques alter the mechanical properties of the artery necessitating the need for age- and disease-matched mechanical properties (Desk et al., 1989). For example, inflation tests indicate that aged human coronary and mammary arteries exhibit a three-fold lower elastic extensibility than young porcine arteries (van Andel et al., 2003). Ideally, patient-specific mechanical parameters could be determined non-invasively (Schulze-Bauer and Holzapfel, 2003); however, the nonlinear, anisotropic behavior of the tissue complicate parameter estimation from image and pressure data alone.

To date, very little mechanical data from diseased human coronary artery tissues have been obtained. Our previous uniaxial tests of intact of human coronary arterial strips indicate that the circumferential direction is approximately twice as stiff as the longitudinal direction; however, these tests did not differentiate between the layers and the extent of disease was not assessed (Yang et al., 2009). Holzapfel et al. (2005) performed uniaxial stretch tests on separate layers of nonstenotic human coronary arteries and determined material parameters of intima, media, and adventitia. Their results showed that the adventitia and intima are stiffer along the longitudinal axis, while the opposite is true for media.

Although the authors developed a detailed constitutive model to describe their data, the uniaxial testing modality does not capture the complex cross-coupling between different axes that is observed in biaxial testing of soft tissues (Billiar and Sacks, 2000). To obtain multiaxial stress-strain behavior, inflation tests have been utilized for human coronary arteries (van Andel et al., 2003); however, the nonuniform vessel geometry and heterogeneous properties due to intimal hyperplasia and distribution of plaques make it difficult both to obtain a uniform inflation and to measure local properties of the diseased but non-calcified vascular wall tissue. Planar equibiaxial testing has been used to characterize healthy vascular wall tissue from porcine coronary arteries (Lally et al., 2004), but varied biaxial protocols necessary for constitutive model development have not been applied to human (or animal) coronary tissue.

The goal of this study is to characterize the multiaxial behavior of diseased human coronary arteries using planar biaxial testing. Five stress-controlled protocols with varied longitudinal and circumferential stress ratios were applied, and the experimental data were fit to three different constitutive models to provide material parameters for computational modeling simulations. Data from diseased human carotid arteries were also obtained for comparison. The parameters from two representative coronary specimens were utilized in an FSI computational model to predict magnitudes and locations of maximum stress and strain in the vessel wall along with fluid velocity and wall shear stress. The impact of the thick neointimal layer observed in the diseased arteries on the multiaxial mechanics of the intact tissue is discussed.

MATERIALS AND METHODS

Materials

A total of four coronary arteries and three carotid arteries from 7 cadavers (age range: 44–81) were obtained from the National Disease Research Interchange, PA and from Washington University, St. Louis with proper consent. Coronary specimens-1 and 2 were from donor 1, an 81-year-old Caucasian female with history of diabetes, chronic obstructive pulmonary disease (COPD), breast cancer, hyperthyroidism, and stroke. Coronary-3 and 4 which showed obvious signs of plaque were from donor 2, a 61-year-old Black male with hypertension who died from subarachnoid hemorrhage. Coronary-5 and 6 were from donor 3, a 50-year-old Black male with end stage renal disease, cardiomegaly, hypertension, hyperlipidemia, and diabetes mellitus type 2. Coronary- 7 and 8 were from donor 4, an 81-year-old Caucasian male with history of hypertension, chronic heart failure, and COPD (cause of death). Carotid-1, 2, and 3 were from a young donor with no history of disease (no other history provided). Carotid-4 had small plaques and was from a 44-year-old Black male who suffered from acute myocardial infarction and moderate atherosclerosis of the coronary arteries. Carotid-5 was from a 74-year-old Black female who suffered from hypertension, hyperlipidemia, and bilateral frontal strokes. Tissues were preserved by freezing to −80°C within 24 hours of excision. A solution of 85% culture medium (RPMU 1640), 5% albumin solution (20%), and 10% dimethyl sulfoxide (DMSO) is utilized as a cryopreservation agent to prevent ice crystals from damaging the tissue.

Sample preparation

Before testing, the samples were defrosted with a four-step procedure as follows: after being kept in room temperature for 30 minutes, samples were put into a 37°C water bath until they were completely defrosted. The cryopreservation agent was removed in four 10-minute stages of soaking in PBS then washed with varying DMSO concentrations at room temperature (10, 5, 2.5, and 0%). The arteries were cut into segments, then cut along the longitudinal axis, and splayed to obtain square samples for biaxial testing (Figures 1A, B). Small segments were cut adjacent to each biaxial test sample for opening angle measurement and for histological analysis Thickness measurements were taken from different regions on the samples using a micrometer (Mitutoyo 7322S, ±50 μm). The sample thickness varied from region-to-region along the vessel; however, it was relatively uniform in the samples chosen for biaxial testing since calcified regions were avoided. Out of necessity, the mean thickness was utilized for stress calculations.

Figure 1.

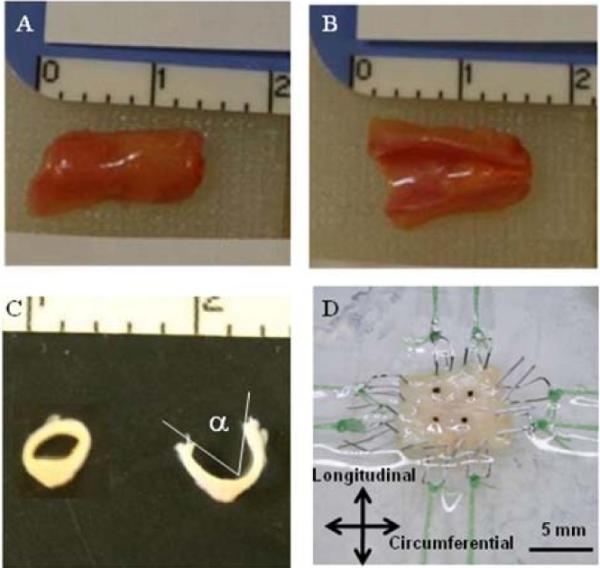
A coronary artery specimen before (A) and after (B) longitudinal cut, before (C inset) and after opening angle cut (C), and mounted on the biaxial testing machine via custom stainless steel hooks and tethers (D). Ruler scale is in centimeters in A, B, and C.

Opening angle

To determine opening angle, α, a measure of circumferential residual stress as defined by Fung (1991), vessel rings were placed in saline and cut radially. Dimensions were measured using ImageJ (NIH, Bethesda, MD) from digital pictures taken at equilibrium before and after the cut (Figure 1C).

Histology

All tissue samples were fixed in 10% neutral-buffered formalin and embedded in paraffin. Five micrometer sections were cut and adhered to Platinum Line slides (Mercedes Medical, Sarasota, FL). The sections were stained with hematoxylin and eosin (H&E; reagents from Sigma Aldrich, St. Louis, MO) and Movat's pentachrome (reagents from Sigma). Images were acquired on an upright microscope (Leica DMLB2) equipped with a digital camera (Leica DFC 480).

Biaxial mechanical characterization

A custom planar biaxial test device was used under stress control to obtain stress/strain measurements over a wide range of ratios of stress along the longitudinal and circumferential axes of splayed arterial specimens. Approximately 1 cm long sections of coronary artery samples, free from visible and tactile evidence of calcified plaque, were cut to yield roughly 1 cm² square specimens. Four graphite particles were attached to each specimen to measure deformation. The sample was mounted to the test device via tethered hooks, and the specimen was brought to a tare load of 0.05 N along each axis (Figure 1D). Due to the small size of the samples, four separate tethers could not be used, thus two tethers, each attached in the center of a dual hook, were utilized. Five biaxial protocols were applied when the samples were immersed in PBS. The applied maximum longitudinal:circumferential stress ratios were 1:1, 0.7:1, 0.5:1, 1:0.7, and 1:0.5 (Table 1).

Table 1.

Maximum engineering stress values for test protocols

	Coronary	Carotid
	Plong/Pcirc (kPa)	Plong/Pcirc (kPa)
Protocol-1	250/250	60/60
Protocol-2	250/170	60/45
Protocol-3	250/125	60/30
Protocol-4	170/250	45/60
Protocol-5	125/250	30/60

The forces along the axes were measured via two torque transducers (effective resolution ~0.002 N), and the deformation gradient, F, was measured by a CCD camera, detecting the positions of four graphite particles attached to the sample (effective resolution ~0.07 %). In this terminology, F₁₁ = λ_θ and F₂₂ = λ_z, where λ indicates stretch ratio (l/l₀) in a given axial direction and is related to axial engineering strain by λ_i = ε_i + 1. For modeling purposes, the Green's strain tensor, E, was calculated as:

$$\mathit{E}=0.5({\mathit{F}}^T\mathit{F}-I)$$ (1)

where bold variables indicate tensor quantities.

Engineering shear stresses were considered negligible due to the pulley apparatus utilized to apply equal force at each tether which allowed the sample to shear freely; however, we recognize that, due to changes in the directions of the edges upon loading, shear stresses do exist in the samples (as per Eqn. 2 below). Approximate alignment of the test axes with the circumferential and longitudinal directions (roughly the overall material axes) resulted in relatively low average shear deformations, yet due to heterogeneity of the samples, local shear strains were inconsistent from location to location and often non-negligible (e.g., for Carotid −5 the average shear strain was −0.1%, yet it ranged from −12% to 9.7% depending upon location within the sample). Because of the non-uniformity of the strain field, we chose to focus on the average strain in the longitudinal and circumferential directions over the entire sample, not on the local strains. Maximum stress values applied to both carotid and coronary samples were chosen to be as large as possible to encompass as much of the stress-stress plane as possible without ripping at the tethers or allowing the specimen to curl or buckle during unloading. The 1^st Piola-Kirchhoff (engineering) stress (P), 2^nd Piola-Kirchhoff (S), and Cauchy (σ) stress tensors are related as follows:

$$\mathit{P}=\raisebox{1ex}{$f$}\!\left/ \!\raisebox{-1ex}{$A_0$}\right.,\mathit{S}={\mathit{F}}^{-1}\mathit{P}\text{and}\sigma =\frac{1}{J}\mathit{FP}$$ (2)

where J is the determinant of F.

Stiffness and extensibility in both the circumferential and longitudinal directions were computed from the equibiaxial stress curves as material metrics. Unlike the case of an incompressible isotropic linear elastic material where the equibiaxial stiffness is equivalent to twice the (uniaxial) Young's modulus, there is no simple relationship between uniaxial and biaxial stiffness for non-linear materials thus they cannot be compared directly. Linear regression was used to calculate both high and low modulus in regions of the stress-strain plots which were most linear. For coronary samples low and high moduli were calculated in 15 ±5 kPa and 175 ±25 kPa stress ranges, respectively, while, the low and high stress ranges for carotid samples utilized were 7.5 ±2.5 kPa and 45 ±5 kPa. Extensibility was defined as the maximum engineering strain in the equibiaxial protocols. Strain anisotropy was defined as the ratio of strains along the axes, ε_z/ε_θ. at maximum equibiaxial loading.

Constitutive Modeling

For this study, three different constitutive models were used to fit the experimental data. Following Fung (1993), the tissue behavior is considered pseudoelastic at low strain rate, thus only the quasistatic loading curves are analyzed. Due to the nonlinear nature of the stress-strain response, a wealth of mathematical descriptions have been utilized including polynomial, logarithmic, and exponential forms formulated in terms of both Lagrangian and Eulerian coordinate frames. Exponential formulations in terms of Green's (Lagrangian) strains have the benefits of being invertible and fairly simple to interpret if a low number of parameters can be used to fit the data sufficiently. Thus, the first model utilized was a Fung-type model (Fung, 1991), well-known for artery wall properties e.g., (Pandit et al., 2005), with the strain energy density function given by:

$$\Psi =\frac{C}{2}(e^{\mathcal{Q}}-1),$$ (3)

where $\mathcal{Q}=c_Z{E}_{\mathit{ZZ}}^2+2c_{\theta z}{E}_{\theta \theta }{E}_{\mathit{ZZ}}+c_{\theta }{E}_{\theta \theta }^2$ and, C, c_z, c_θ, c_θz are constitutive parameters, and E_θθ and E_ZZ are the circumferential and longitudinal Green strain values, respectively.

The second model was the Choi-Vito model (Choi and Vito, 1990) which is similar to the Fung model but has the advantage of having the terms for the different directions in separate exponentials. In the Choi-Vito model, the strain energy density is given by:

$$\Psi =C(e^{{\mathcal{Q}}_1}+e^{{\mathcal{Q}}_2}+e^{{\mathcal{Q}}_3}-3)$$ (4)

where ${\mathcal{Q}}_1=c_z{E}_{\mathit{zz}}^2$, ${\mathcal{Q}}_2=c_{\theta }{E}_{\theta \theta }^2$, ${\mathcal{Q}}_3=2c_{\theta z}{E}_{\mathit{zz}}{E}_{\theta \theta }$ and C, c_z, c_θ and c_θz are the material parameters.

Both the Fung and Choi-Vito models have relatively straightforward interpretation of parameter values with respect to overall stiffness and anisotropy. The product of C*c_z and C*c_θ provide metrics for overall nonlinear stiffness in each direction, C*c_zθ indicates interaction between the axes, and c_z/c_θ provides a metric for anisotropy of stiffness.

Formulations based on polynomials and exponentials of strain invariants, such as Mooney-Rivlin models from rubber elasticity, are also common in the literature and have been implemented into many standard FE packages. Based on extensive uniaxial data from circumferential and longitudinal tissue strips, we previously fit the anisotropic behavior of human coronary arteries using a modified Mooney-Rivlin model (Yang et al., 2009):

$$\Psi =c_1(I_1-3)+D_1[\text{exp}\left(D_2(I_1-3)\right)-1]+\frac{K_1}{2K_2}[\text{exp}[K_2{(I_4-1)}^2-1]$$ (5)

where the tissue was assumed to be incompressible, thus $I_1=1={\lambda }_z^2+{\lambda }_{\theta }^2+{\left({\lambda }_z{\lambda }_{\theta }\right)}^{(-2)},I4=C_{ij}{\left(n_c\right)}_i{\left(n_c\right)}_j$, C = F^TF is the Cauchy–Green deformation tensor, n_c is the circumferential direction of the vessel, and c₁, D₁, D₂ and K₁ and K₂ are material constants. Based on previous work, D₂ was set to 2 without appreciably reducing the goodness of fit. We chose not to include shear terms in the models as the shear strains were not representative of the entire sample, and adding additional parameters for the shear terms lead to over-parameterization of the models.

Statistics

We used the standard nonlinear Levenberg-Marquardt algorithm to obtain material parameters given by each model with the following error function:

$${\gamma }^2=\sum _{i=1}^n{({\sigma }_{\theta {\theta }_i}-{\sigma }_{\theta {\theta }_i}^m)}^2+{({\sigma }_{{\mathit{zz}}_i}-{\sigma }_{{\mathit{zz}}_i}^m)}^2$$ (6)

where n is the number of data points, σ_θθ σ_zz are the stresses (2^nd P-K stress for the Fung and Choi-Vito models, and Cauchy stress for the Mooney-Rivlin model) along the circumferential and longitudinal axis, respectively. The superscript m indicates stress values predicted by the models. We minimized the objective function and obtained material parameters for each model using custom MATLAB code (Mathworks, Natick, MA).

Comparisons between coronary and carotid metrics (low and high modulus, extensibility, and anisotropy index) were made using two-tailed Student's t-test with unequal variances with p < 0.05 considered statistically significant (Graphpad Software, Inc). Grubb's test was utilized to remove outliers (Graphpad Software, Inc).

Computational Modeling and Simulation

An intravascular ultrasound (IVUS) imaging technique was used to obtain the 3D geometry of the coronary artery from a single patient (female; age: 50) with calcified, lipid-containing plaque as describe in a previous study of our group (Yang et al., 2009). For IVUS image acquisition, a 20-MHz, 2.9-F phased-array Eagle Eye Gold IVUS catheter (Volcano Corporation, Rancho Cordova, CA) was placed 2 cm beyond a stricture region in the middle segment of the right coronary artery and it was pulled back with a velocity of 0.5 mm/s to 2 cm proximal to the lesion for recording digitized cross-sectional IVUS images. As described in a previous work (Tang et al., 2005), the 3-D vessel geometry was reconstructed from the 44-slice series within a multicomponent FSI model to calculate flow and stress/strain distributions. The Navier–Stokes equations with arbitrary Lagrangian–Eulerian formulations were used as the governing equations. The FSI models were solved by a commercial finite-element package ADINA (ADINAR&D, Inc., Watertown, MA). ADINA uses unstructured finite-element methods for both fluid and solid models. The nonlinear anisotropic Mooney-Rivlin model is one available model in ADINA that we have utilized previously based on uniaxial data; here we utilized the model parameters obtained from biaxial data as described in the previous section. For the FSI simulations, the pressures were set to P_in=100 kPa and P_out=99 kPa; no cyclic bending or pre-stretch were applied in the present simulations.

RESULTS

General observations

Visual and tactile inspection revealed varied degrees of disease in each arterial sample. Specimens for mechanical testing were taken from areas without obvious calcific deposits. The arterial segments splayed open when cut longitudinally indicating substantial residual circumferential stress. Coronaries opened wider compared to carotids, 120° and 63°, respectively (p<0.05, Table 2). Once mounted in the biaxial device, the specimens required low force (~0.02–0.05 N) to flatten to a planar geometry indicating the presence of relatively low bending stresses. Since a tare load (0.05N) was applied obtain more reproducible data, the tissues were slightly prestretched (λ_init~ 1.05 –1.10) at the beginning of the test.

Table 2.

Stiffness and extensibility metrics calculated from the equibiaxial protocol. Note that equibiaxial stiffness is larger than Young's modulus derived from uniaxial loading.

	Dimensions			Longituinal Axis			Circumferential Axis			Anisotropy
	Do (mm)	T (mm)	α (°)	Low Modulus (Kpa)	High Modulus (Kpa)	Extensibility (%)	Low Modulus (Kpa)	High Modulus (Kpa)	Extensibility (%)	εz/εθ (−/−)
Coronary-1	3.90	0.55	107	11.4	110	5.01	4.98	48.9	7.72	0.65
Coronary-2	3.6	0.52	58.6*	31.8*	321*	0.82	8.86	73.1	6.98	0.12
Coronary-5	2.93	0.35	138	4.58	62.2	10.4	7.53	96.0	5.26	1.97
Coronary-6	3.03	0.45	116	7.68	120	5.11	45.6	141	4.22	1.21
Mean	3.37	0.47	120	7.87	97.3	5.33	16.7	89.9	6.04	0.88
SD	0.46	0.09	16.0	3.39	30.9	3.91	19.3	39.3	1.60	2.45
Carotid-1	7.99	1.03	54.8	0.79	4.09	32.02	1.26	6.89	20.4	1.57
Carotid-2	8.30	0.99	85.7	0.79	4.58	33.2	1.22	6.14	19.8	1.67
Carotid-3	8.22	1.00	44.4	1.04	4.89	27.99	1.01	4.86	25.0	1.12
Carotid-4	7.15	1.20	69.1	1.03	5.00	27.3	1.79	7.64	18.0	1.52
Carotid-5	8.85	1.4	43.6*	4.58*	24.1*	4.40*	1.27*	8.90*	16.2*	0.27*
Mean	8.13	1.15	63.5	0.91	4.64	30.1	1.32	6.38	20.8	1.47
SD	0.71	0.19	17.9	0.14	0.41	2.93	0.33	1.19	2.98	0.24

^*Data not included in the mean & SD as it is a statistical outlier from other specimens within its group (Grubb's test, p < 0.05)

With approximately half of the samples, it was not possible to recover tissue free of calcification. The samples were very difficult to test and ripped at the hooks before the full range of stress could be achieved thus preventing a proper test, and some were nearly inextensible in the longitudinal direction (data not shown for Coronary-3, 4, 7, and 8).

Coronary artery mechanical metrics

All non-calcified specimens exhibited “J-shaped” stress-stretch curves characteristic of soft tissues (see Figure 2 for equibiaxial loading protocol curves for all specimens). The coronary specimens had low equibiaxial moduli of 7.9 kPa and 16.7 kPa in the longitudinal and circumferential and directions, respectively. They exhibited high equibiaxial moduli of 97.3 kPa and 89.9 kPa in the longitudinal and circumferential directions, respectively. The circumferential stiffness values from Coronary-2 were statistical outliers (p < 0.05) and were excluded from further statistical analysis. Equibiaxial extensibility was relatively small in coronary specimens (5.3% and 6.0% in longitudinal and circumferential directions, respectively). In two specimens from one arterial sample, the extensibility was higher along the longitudinal axis, and in the other two specimens from another arterial sample it was higher along the circumferential axis resulting in different directions of anisotropy.

Figure 2.

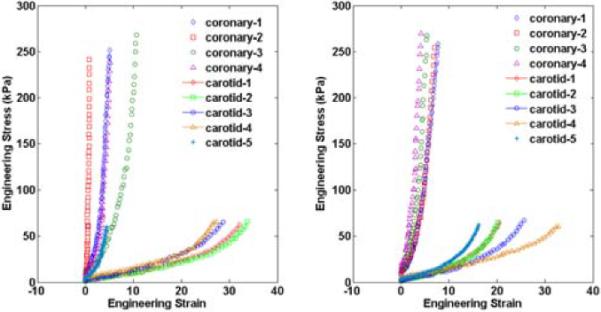
Experimental engineering (1^st P-K) stress-strain data at equibiaxial loading for each human coronary and carotid sample for the equibiaxial stress protocol in the longitudinal (A) and circumferential (B) directions. The coronary arteries are clearly stiffer and less extensible than the carotid arteries in both directions. The peak stresses applied are in the physiological range for each type of vessel.

Carotid artery mechanical metrics

The carotid specimens were significantly less stiff than the coronary specimens in both the low and high-modulus regions in the longitudinal direction (0.91 kPa and 4.64 kPa) and circumferential direction (1.32 kPa and 6.38 kPa) (p < 0.05 compared to coronary group, Table 2). Carotids also exhibited significantly greater extensibility than coronaries in both the longitudinal (25%) and circumferential (20%) directions (p < 0.05). Carotid-5 was a statistical outlier for most metrics and parameter (Grubb's test, p < 0.05), thus the mechanical data for Carotid-5 is not included in the descriptive statistics.

Axial cross-coupling

For all coronary specimens a strong coupling between the axes was observed as displayed in Figure 3. In some specimens, there was almost zero stretch or even shrinking in the longitudinal axis in the non-equibiaxial stretch protocols. The carotid specimens exhibited much less cross-coupling (less spread between protocols and lower c_zθ term). The anisotropy ratio was not significantly different between the coronary and carotid groups.

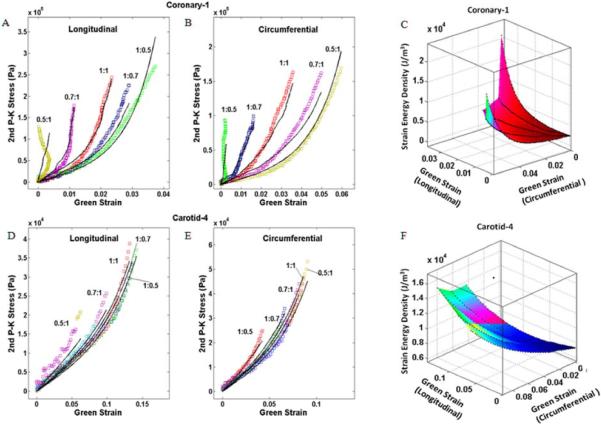
Figure 3.

Experimental data for a diseased coronary artery (Coronary-1) (A, B) and a carotid artery (Carotid-4) (D, E) with fit to Choi-Vito constitutive model. Strain energy density and the Green's strains along each axis for Coronary-1 (C) and Carotid-4 (F). Note the substantially larger spread in the curves typical for the coronary specimens indicating greater coupling between the axes than observed in the carotid specimens.

Constitutive model fit and parameter values

All of the constitutive models successfully fit the experimental data quantitatively (Table 3), with the Choi-Vito model providing the best qualitative fit to the data (Figure 3). The fits to the carotid data were generally better than for the coronary data. The descriptive statistics of the parameter values for each group are not given since the parameters (and their averages) are not individually meaningful; only as a set do the parameters completely describe the biaxial data.

Table 3.

Parameters for three constitutive models

FUNG
	C (kPa)	cz	cθ	czθ	cz / cθ	r2	rms
coronary-1	12.7	110	53.9	26.4	2.06	0.82	1740
coronary-2	7.10	460	152	118	3.02	0.90	2110
coronary-5	14.6	44.0	61.5	20.6	0.72	0.94	1390
coronary-6	5.40	209	149	64.0	1.41	0.74	2860
carotid-1	43.6	1.60	2.70	0.30	0.60	0.98	192
carotid-2	38.9	1.60	2.90	0.30	0.56	0.98	215
carotid-3	102	0.70	0.80	0.30	0.92	0.96	308
carotid-4	61.1	1.50	2.60	0.20	0.59	0.95	334
carotid-5*	6.30	34.9	19.7	7.50	1.77	0.91	318

CHOI-VITO
	C (kPa)	cz	cθ	cθz	cz / cθ	r2	rms
coronary-1	899	2180	817	1460	2.70	0.85	1450
coronary-2	536	9890	2120	5840	4.70	0.92	2010
coronary-5	2500	636	438	455	1.50	0.92	1700
coronary-6	1030	2720	1000	1700	2.70	0.83	2510
carotid-1	1275	60.0	135	45.0	0.40	0.99	95
carotid-2	1256	63.0	121	38.0	0.50	0.98	126
carotid-3	1690	48.0	82.0	33.0	0.60	0.98	146
carotid-4	1520	73.0	157	34.0	0.50	0.96	192
carotid-5*	416	712	336	473	2.10	0.83	330

MODIFIED MOONEY-RIVLIN
	c1(kPa)	D1 (kPa)	D2	k1 (kPa)	k2	c2 (kPa)	r2	rms
coronary-1	−2870	2030	2.00	−110	15.3	−1010	0.94	1920
coronary-2	−7360	4950	2.00	−375	11.2	−2065	0.97	1600
coronary-5	−1310	630	2.00	36.0	23.5	115	0.97	1790
coronary-6	−7840	4520	2.00	−41.2	67.4	−1080	0.92	2000
carotid-1	3.80	5.70	2.00	5.70	4.00	−9.6	0.98	198
carotid-2	7.50	5.10	2.00	1.70	9.00	−10.9	0.98	191
carotid-3	10.3	2.90	2.00	2.90	5.00	−4.60	0.98	185
carotid-4	17.2	7.50	2.0	4.90	9.00	−19.9	0.97	232
carotid-5*	−134	59.8	2.00	10.0	38.0	24.1	0.82	430

^*Carotid-5 is a statistical outlier from other carotid specimens for most parameters (Grubb's test, p < 0.05)

Computational FSI simulations

The largest maximum principal stresses were 61.5 and 48.5 kPa and largest maximum principal strains were 0.08 and 0.065 for the simulations using the parameters from Coronary-1 and Coronary-5, respectively. The largest magnitude maximum principal stress and strain were predicted to be near the luminal surface roughly in the area of thickest plaque as indicated with arrows in the stress and strain distribution plots (Figure 4). The flow velocity and the shear stress distribution (Figure 5) show highest values where the lumen is smallest. Carotid material parameters were not utilized in the coronary FSI model.

Figure 4.

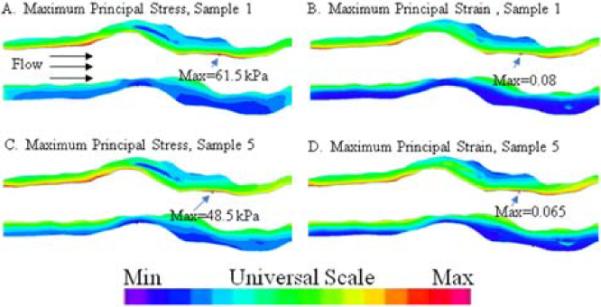
Maximum principal stress (A, C) and strain (B, D) distributions found with material parameters for Coronary-1 and 5. White area in between the pseudocolored walls represents the lumen. Universal scale applies to all plots, with maximum values indicated. Similar stress and strain distributions with approximately 20% lower values were predicted using the material parameters for Coronary-5 compared to Coronary-1.

Figure 5.

Flow velocity (A) and shear stress (B) in Coronary-1. Flow direction is left to right. Universal color scale in Figure 4 applies with respective maximum and minimum values of 39.2 cm/s and 0 cm/s for A, and 71.7 dyn/cm² and 0.6 dyn/cm² for B. The flow and shear stress distributions are similar to those predicted previously using parameters from uniaxial test data.

Histological analysis

A substantial neointimal layer was observed on each coronary sample. As shown in Figure 6, in samples from donor 1 (e.g., Coronary-1), the neointima appears to be thicker, more extensively remodeled with more pronounced collagen staining, and have a lower cell density than samples from donor 3 (e.g., Coronary-6). These characteristics indicate that the neointima may be older and more stable in Coronary-1 than in Coronary-6. The disease states of the patients from which the coronary and carotid arteries were obtained are substantially different, thus direct comparisons of their morphology are not instructive. However, it is important to note that the carotid samples had thicker walls than the coronary samples and, with the exception of Carotid-5, minimal neointima or plaque. Carotid-5 exhibited extensive neointimal formation similar to Coronary-1 (image not shown).

Figure 6.

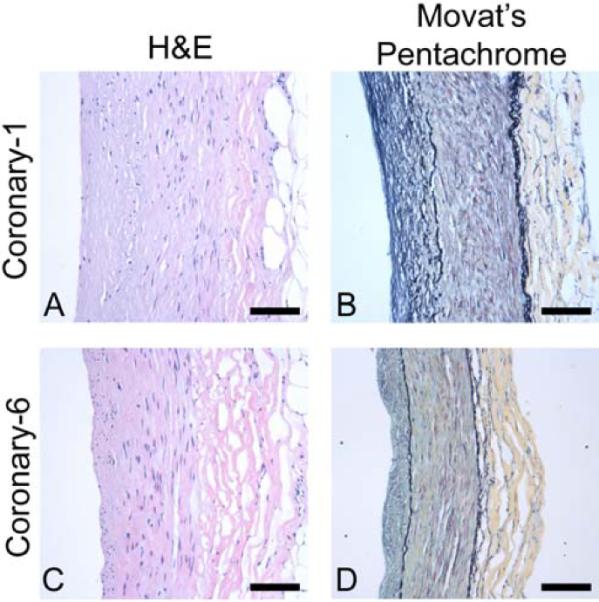
Histological sections for arterial segments adjacent to mechanical specimens Coronary-1 (A, B) and Coronary-6 (C, D) with lumen at left and adventitia at right. Hematoxylin and eosin staining (A, C) shows cellularity, and Movat's pentachrome (B, D) displays layered structure (black = elastin, yellow = collagen, red = muscle, blue = glycosaminoglycans, purple = nuclei). Note the relatively thick and remodeled neointima in B and the higher cellularity in the neointima in C. Also note the more pronounced collagen staining in the adventitia in B and in the media in D. Scale bar = 100 μm.

DISCUSSION AND CONCLUSION

This study provides the first complete set of planar biaxial data for human coronary arteries. Planar biaxial testing is a powerful method for obtaining data necessary for multiaxial constitutive modeling in that it provides independent control of stresses along perpendicular axes and information regarding in-plane coupling between axes. Our biaxial data clearly show the impact of coronary artery disease on the mechanical behavior of the intact wall, both in terms of axial stiffening and variability along an individual artery. The equibiaxial extensibility of the diseased coronary specimens is much lower and the stiffness higher than for human carotid arteries in this study and for healthy non-human coronary arteries previously reported (Lally et al., 2004). Implementation of specimen-specific material parameters into an FSI computational model demonstrates the impact of wall material properties on location and magnitude of maximal stress and strain, metrics which may be correlated with plaque rupture (Tang et al., 2009a). Mechanical variability between donors was substantial and correlated with morphological differences between specimens. Histological examination suggests an important role for the neointimal layer on the overall wall stiffness and the direction of anisotropy in agreement with previous findings (Holzapfel et al., 2005). Taken together, these results demonstrate the importance of utilizing multiaxial constitutive relationships within patient-specific computational models to accurately predict stress and strain within the vessel. The findings represent an important step in more accurate modeling of diseased vessels, but also indicate a need for the inclusion of layer-specific properties, in particular the neointima.

The importance of characterizing diseased human coronary tissue

Material properties obtained from mechanical characterization of animal models may not suitably represent diseased human coronary arteries. Porcine coronaries are much more elastic than human; data from these tissues may lead to underestimation of the stress values in human arteries (van Andel et al., 2003). Further, aged human coronary sinus tissues have been found to be significantly stiffer and more nonlinear than porcine arteries which suggests substantial structural differences between these tissues (Martin et al., 2010). Despite these dissimilarities, the majority of our knowledge of coronary artery mechanics is derived from mechanical testing of coronaries from young, healthy pigs due to their availability and similarity in size with human coronaries.

A constitutive model for coronary artery wall should be fully three-dimensional, capable of predicting tissue behavior over a broad range of deformations in arbitrary geometries, and suitable for implementation in finite element analysis software. The goal of this work was not to develop new constitutive equations, but to describe our complex biaxial data with existing models to allow more quantitative comparison between studies and to facilitate computational simulations. Kassab and colleagues (Lu et al., 2004; Pandit et al., 2005; Wang et al., 2006) have utilized combined inflation-stretch experiments to study the multiaxial properties of porcine coronary arteries including the relative influence of the media and adventitia. For intact, healthy porcine coronaries, they report much greater strain values than observed for the diseased coronary specimens in our study, even for the maximum stress values which were 1/3 of our maximum applied stress values (Pandit et al., 2005). To represent their multiaxial data, they implemented a Fung-type constitutive model (Eqn. 3). For the case of the intact wall, the combined indices C*c_z and C*c_θ are lower for the porcine data than for our diseased vessels indicating overall lower stiffness. Also C*c_zθ is lower in their study (5–10 kPa compared 300–800 kPa reported herein) indicating lesser coupling between the axes in porcine tissues. The stiffness anisotropy (c_z/c_θ) of the porcine samples (0.4–2.1) was similar in magnitude as found in our study and also varied in direction between specimens with ~30% the samples stiffer in the circumferential direction. Lally et al. (Lally et al., 2004) also found variable anisotropy in their planar equibiaxial study of porcine coronary arteries with 50% circumferentially stiffer. The authors report maximum strains under equibiaxial loading ranging from 5 to 25%, somewhat larger than the extensibility we observed for human diseased vessels. The maximum stresses applied (~1.5 MPa) were substantially larger than applied to our human samples.

Consistent with our data, the extensibility of aged human coronary arteries tested by inflation (van Andel et al., 2003) and uniaxial stretch (Holzapfel et al., 2005) is substantially lower than observed for young porcine coronaries. Although it cannot be concluded whether the difference in elasticity is due to age (and associated neointimal thickening) or interspecies morphological and compositional differences, the layer-specific mechanical properties of human coronary arteries obtained by Holzapfel et al. (2005) may shed light on this issue. Unlike healthy vessels where the intima plays a minor role in the intact wall mechanics, in these non-stenotic human vessels, the intima appears to play a relatively large role. The mechanical behavior of the (neo)intima is strikingly similar to the adventitia with high stiffness in the longitudinal direction. The media is the most compliant layer with its stiffest direction oriented circumferentially. Further, data from calcified regions of iliac arteries indicates these regions have uniaxial stiffness on the order of the stiffness of the adventitia in the high modulus region (Holzapfel et al., 2004). The thick neointima likely contributes to the high stiffness and low extensibility of the aged human specimens. The older and more stable appearing neointima in Coronary-1 may also lead to stiffer behavior in the longitudinal direction compared to the less remodeled-appearing neointima in Coronary-6 resulting in anisotropy in opposite directions in these samples. It is interesting to note that the mechanical metrics and model parameters of Carotid-5, with much thicker neointima than the other carotid samples, are much closer to those for coronary specimens consistent with longitudinal stiffening contributed by the neointimal layer.

The relatively low extensibility values in our study compared to inflation studies may be due, in part, to the biaxial tare load applied to obtain reproducible stress-strain curves. In situ axial prestretch values were not recorded before the vessels for our study were removed from the intact heart, thus the in vivo stretch state cannot be determined. Consistent with the value of axial prestretch reported by Holzapfel et al. (2005) for aged human nonstenotic arteries(~1.04), we posit that the ~1.05 to 1.1 equibiaxial stretch applied to the specimens at the tare load is close to the physiological prestretch level for our diseased coronary arteries. While substantially higher axial prestretch levels (~1.4) are generally reported for healthy porcine coronary arteries (Humphrey et al., 2009; van den Broek et al., 2010), axial prestretch has been reported to decrease up to 50% with experimental hypertension in animal models (Humphrey et al., 2009). Retraction when harvesting the vessels may also be reduced substantially due to the neointimal stiffness in aged arteries. Further, less than 10% strain in the circumferential direction is observed in the majority of locations along the length of similar diseased coronary arteries upon inflation to physiological pressure (16 kPa); strains > 20% are only found in isolated compliant regions (personal communication, Thuy Pham and Wei Sun, Ph.D., University of Connecticut).

Computational model incorporates complex geometry and nonuniform properties

Our group has previously employed 3D FEAs with fluid-solid interactions to determine the stress distributions in human coronary atherosclerotic plaques for a 3D geometry obtained for a single patient (Yang et al., 2009). Here we obtained FSI simulations for the same 3D geometry, modifying only the material parameters of the vessel wall with parameters obtained from biaxial testing of diseased coronary arteries. As expected, the fluid velocity and shear stress distributions obtained in this study are similar to those determined previously since the geometry of the vessel was identical. The maximum stress levels are lower than those predicted with uniaxial material properties, and the distribution of stresses is altered. Most importantly, in the previous study the largest principal stress (98.9 kPa) occurred in an area where the vessel wall was thin, whereas in the current study the largest principal stress occurs in the region of wall thickening containing a calcified plaque and lipid pools. The distribution of maximum principal strains corresponds with the distribution of stresses both in the current and previous studies; however, the magnitude of strain is much lower with the largest principal strain 6–8% with the biaxial data parameters compared to 33% with the uniaxial parameters. Clearly, the difference in equibiaxial extensibility of our samples (5–10% at 250 kPa) compared to uniaxial extensibility (>20% at 50 kPa) plays a large role in determining the predicted strains. As discussed above, the lower extensibility may be attributed to the biaxial nature of the loading, or it may be due to differences in the disease state of the vessels in the two studies.

The stress and strain values predicted using parameters from two very different specimens were relatively minor (within ~20%) despite the substantial difference in stiffness and direction of anisotropy. Specifically, equibiaxial stiffness values for Coronary-1 were two-fold higher than those for Coronary-5 in the circumferential direction, and roughly half the values in the longitudinal direction (Table 2). The insensitivity of the computational model predictions to the properties of a particular specimen (and donor) from which the model parameters are derived is encouraging. It would be far more manageable to obtain age- or disease-matched tissue properties than those from a specific patient. Recently, van de Broek et al. (2010) reported that generic model parameters obtained from a set of porcine coronary arteries were able to predict the mechanical behavior each individual artery using a single radius measurement at a physiologic pressure. While determining a set of generic parameters for the entire vessel wall is an appealing concept, and indeed the goal of the present study, the variability with disease along the human coronary arteries suggests that it may not be possible to obtain stress (or pressure-radius) predictions without knowing the properties of the vessel wall layers and patient-specific 3D geometry explicitly. There is a high degree of heterogeneity between our patients and between samples. Fresh diseased human tissues are extremely difficult to obtain, and once obtained, difficult to test. Further, diseased human coronaries are far from being homogeneous tubes. The present study represents an incremental step towards the biaxial characterization of diseased human coronary arteries. Our relatively small data set provides insight about the diverse plaque material properties and demonstrates the importance of quantifying plaque material properties. This study reveals the need for disease-specific and, at the same time, layer-specific artery characterization. Although the similar diseases are expected to cause similar alterations in the artery anatomy, differences in thickness ratios of individual layers among the patients may result in a difference in behavior of intact vessel. In the future we propose to test layer-specific properties, lipid pools, and calcified areas separately.

Patient-specific geometry would likely have a strong effect on the resulting stress and strain values in our simulations as well; for example, the non-uniform wall thickness would be different between Coronary-1 and Coronary-5 based on our histological analysis. Further, in our previous work, we demonstrated that bending and axial stretch each have a considerable effect on the magnitude of stress and strain in the vessel wall (Yang et al., 2009); these aspects should be incorporated with the biaxial mechanical parameters in future simulations. Finally, the residual stresses in the vessel and layer-specific properties would also likely alter the prediction of stress and strain distributions in the vessel; both the layer thickness and the residual stresses are known to change with diseases such as hypertension (Fung, 1991).

Conclusions

This study provides the first complete set of planar biaxial data for diseased human coronary arteries, and as such, it represents an important but, incremental step towards more accurate estimation of stress and strain states in coronary blood vessels. Our findings highlight the need to deconstruct the diseased vessels mechanically, paying close attention to quantification of the intermediate states including axial shrinkage when removed from the (pressurized) heart, opening angle when cut longitudinally, retraction or expansion when layers are separated, and the loading necessary to counteract bending stresses. The mechanical properties of each component (including neointima and plaque) should be characterized with planar biaxial testing or indentation as appropriate, the data fit to the most suitable constitutive model, and each component reassembled virtually within a patient-specific computational model. This approach has the potential for generating more reliable stress and strain metrics for determining the appropriate clinical intervention.