Detecting Local Ligand-Binding Site Similarity in Non-Homologous Proteins by Surface Patch Comparison

Abstract

Functional elucidation of proteins is one of the essential tasks in biology. Function of a protein, specifically, small ligand molecules that bind to a protein, can be predicted by finding similar local surface regions in binding sites of known proteins. Here, we developed an alignment free local surface comparison method for predicting a ligand molecule which binds to a query protein. The algorithm, named Patch-Surfer, represents a binding pocket as a combination of segmented surface patches, each of which is characterized by its geometrical shape, the electrostatic potential, the hydrophobicity, and the concaveness. Representing a pocket by a set of patches is effective to absorb difference of global pocket shape while capturing local similarity of pockets. The shape and the physicochemical properties of surface patches are represented using the 3D Zernike descriptor, which is a series expansion of mathematical 3D function. Two pockets are compared using a modified weighted bipartite matching algorithm, which matches similar patches from the two pockets. Patch-Surfer was benchmarked on three datasets, which consist in total of 390 proteins that bind to one of 21 ligands. Patch-Surfer showed superior performance to existing methods including a global pocket comparison method, Pocket-Surfer, which we have previously introduced. Particularly, as intended, the accuracy showed large improvement for flexible ligand molecules, which bind to pockets in different conformations.

Introduction

Elucidating function of uncharacterized proteins is one of the most important tasks in molecular biology. Bioinformatics is expected to play a significant role for this task given the fact that computational methods are quick in screening existing data^1–5. Function annotation for newly determined genes and genomes by sequence database searches⁶ has long become a routine in wet biology laboratories. Recently, the urgent need was raised for function elucidation for protein structures due to the increasing number of protein structures of unknown function that have been solved by structural genomics projects⁷. As of this writing, there are over 3200 structures of unknown function deposited in the Protein Data Bank (PDB)⁸. In the post structural genomics era, making use of protein structure data for functional studies both by high-throughput experimental methods and computational methods is of the highest priority^9–11.

Function of proteins has broad meaning and can be classified into different semantic classes. For example, the Gene Ontology¹² classifies vocabulary of functional terms into three major categories, biological process (BP), molecular function (MF), and cellular component (CC). In this work, we focus on predicting binding small ligand molecules for proteins. Ligand binding is an essential role of proteins in a cell and thus provides clues of protein function in all the GO categories. Binding ligand prediction also has a broader impact to applications such as computational drug discovery¹³ and protein design¹⁴.

A binding ligand for an uncharacterized protein can be predicted by evaluating the similarity of either the whole protein structure¹⁵ or the binding pocket to those of known proteins in the database. Pocket comparison methods have an advantage over global structure comparison-based methods because the former could detect similar pockets independent from homologous relationship of proteins. Indeed, there are numerous examples of proteins that are evolutionary unrelated yet bind the same ligand molecule¹⁶. There are several approaches proposed for pocket comparison in the past. In the Catalytic Site Atlas¹⁷, AFT¹⁸, and SURFACE¹⁹, a functional site is represented as a set of few residue positions and the root mean square deviation (RMSD) is computed as the measure of the similarity between a query and a site in the database. SiteBase²⁰ and MultiBind²¹ use geometric hashing for comparing conformation of pseudo-centers of residues in ligand binding sites. A method introduced by Hoffmann and his colleagues applies a convolution kernel method for comparing surface atom positions and charges at ligand binding sites²².

An alternative approach to the residue/atom-based representations is to describe protein surface of a binding pocket²³. A surface representation describes geometrical and physicochemical properties of a pocket on a continuous surface often discarding residue type information. Thus they are less dependent on available homologous structures from which the features are extracted. The eF-seek method represents a protein surface as a graph with nodes charactering local geometry and the electrostatic potential²⁴. A maximum sub-graph matching algorithm is used for seeking similar sites in two proteins. The Thornton group explored the use of spherical harmonics in representing and comparing protein pockets^25,26. The property-encoded shape distributions method by Das et al.²⁸ extended the D2 shape distribution method²⁷ so that surface properties can also be incorporated. In our previous work, we introduced a pose independent binding pocket comparison method, named Pocket-Surfer, which uses the pseudo-Zernike descriptors and the 3D Zernike descriptors (3DZD) to quantify the similarity of the global surface shape and the electrostatic potential of binding pockets²⁹. Pocket-Surfer allows real-time pocket database search and it was shown that it performed superior to existing methods^5,29.

These pocket comparison methods describe the property of binding pockets as a whole. However, studies have found that often binding pockets of the same ligand show variation in their shape and physicochemical properties^26,30. The variation in the geometrical and physicochemical properties is due to several different reasons. For example, some ligand molecules can take different conformations upon binding. Often, additional ligand molecules or water molecules bind at the same pocket, which results in change in the overall pocket shape and associated properties. However, even with such pockets that do not exhibit overall shape and physicochemical similarity, there are usually local regions that show consistent properties across different proteins. Based on this observation, we propose a new perspective on binding site comparisons, which evaluates the similarity of binding pockets by the combination of similarity of its local patch regions. The proposed method, named Patch-Surfer, segments the binding pockets to circular patches and compares them using a weighted bipartite matching algorithm. Two geometric properties, the surface shape and the visibility³¹, and two physicochemical prosperities, the hydrophobicity and the electrostatic potential, of the patches are encoded with the 3DZD, a mathematical series expansion of a three dimensional function³², which offers a compact and rotationally invariant representation of the patch properties.

We benchmarked Patch-Surfer on three binding pocket datasets. Pocket retrieval results on the first dataset compiled by Kahraman et al.³³ showed that Patch-Surfer performed overall better than Pocket-Surfer²⁹, our previously developed pocket comparison method that captures global similarity of pockets. Then the parameters trained on the Kahraman dataset were further tested on the extended Kahraman dataset to examine the transferability of the parameters. Subsequently, the result of the third dataset, the Huang dataset³⁴, was shown to validate that Patch-Surfer can perform well for different sets of ligand binding pockets. The method was further applied for ligand unbound and predicted pockets. Overall, Patch-Surfer showed better accuracy compared to Pocket-Surfer²⁹ and other pocket descriptors. As intended, the accuracy showed large improvement for flexible ligand molecules, which bind to pockets in different conformations. Further, Patch-Surfer allows a fast ligand pocket database screening owing to the compact representation of patches with the 3DZD. A search against a database of over 5000 representative pockets (the current size of PDB) takes approximately only 3 minutes 20 seconds.

Materials and Methods

Ligand binding pocket datasets

Three datasets of ligand binding pockets were used for benchmark. The datasets consist of the tertiary protein structures with a bound ligand molecule, which are solved by X-ray crystallography. Redundancy of entries was removed so that sequence similarity between any pairs of proteins in each dataset is kept under 30%. The first dataset, compiled by Kahraman et al.³³ consists of 100 pockets, each of which binds to one of the following nine ligands: adenosine monophosphate (AMP), adenosine-5'-triphosphate (ATP), flavin adenine dinucleotide (FAD), flavin mononucleotide (FMN), alpha- or beta-d-glucose (GLC), heme (HEM), nicotinamide adenine dinucleotide (NAD), phosphate (PO4), or 3-beta-hydroxy-5-androsten-17-one (AND) and estradiol (EST), which are two types of steroids (STR). Table 1A lists detailed information the binding pockets. This dataset has been also used in our previous work of Pocket-Surfer²⁹.

Table 1A.

The ligand pocket benchmark dataset from Kahraman et al.

Binding ligand molecule	Average Sizea) (Å)	Molecular mass (g/mol)	Average number of seedsb)	Number of PDB entries	PDB entries
AMP	8.8	347.22	23.7	9	12asA, 1amuA, 1c0aA, 1ct9A, 1jp4A, 1khtB, 1qb8A, 1tb7B, 8gpbA
ATP	9.5	507.18	29.5	14	1a0iA, 1a49A, 1aylA, 1b8aA, 1dv2A, 1dy3A, 1e2qA, 1e8xA, 1esqA, 1gn8B, 1kvkA, 1o9tA, 1rdqE, 1tidA
FAD	11	785.55	44.1	10	1cqxA, 1e8gB, 1eviB, 1h69A, 1hskA, 1jqiA, 1jr8B, 1k87A, 1poxA, 3grsA
FMN	9.7	456.34	27.7	6	1dnlA, 1f6vA, 1ja1A, 1mvlA, 1p4cA, 1p4mA
GLC	8.5	180.16	15.2	5	1bdgA, 1cq1A, 1k1wA, 1nf5C, 2gbpA
HEM	10.2	616.49	36.9	16	1d0cA, 1d7cA, 1dk0A, 1eqgA, 1ew0A, 1gweA, 1iqcA, 1nazE, 1np4B, 1po5A, 1pp9C, 1qhuA, 1qlaC, 1qpaB, 1soxA, 2cpoA
NAD	10.1	663.43	36.8	15	1ej2B, 1hexA, 1ib0A, 1jq5A, 1mewA, 1mi3A, 1o04A, 1og3A, 1qaxA, 1rlzA, 1s7gB, 1t2dA, 1toxA, 2a5fB, 2npxA
PO4	7.4	94.97	9.7	20	1a6q, 1b8oC, 1brwA, 1cqjB, 1d1qB, 1dakA, 1e9gA, 1ejdC, 1eucA, 1ew2A, 1fbtB, 1gypA, 1h6lA, 1ho5B, 1l5wA, 1l7mA, 1lbyA, 1lyvA, 1qf5A, 1tcoA
STR	9.2	278.8	22.2	5	1e3rB, 1fdsA, 1j99A, 1lhuA, 1qktA

^a)The pocket size is defined as the average distance from the center of the mass of the pocket to the pocket surface.

^b)The average number of seed points in the pockets.

The second dataset, the extended Kahraman dataset (Table 1B), is designed to test the transferability of the parameters trained with the original Kahraman dataset. The dataset consists of 144 proteins that bind to one of the following eight ligands, AMP, ATP, FAD, FMN, GLC, HEM, NAD, and PO4, as listed in the Table 1B. This dataset provides different structures to the same ligand molecules as the original Kahraman set. STR was removed from this dataset because STR contains two similar but different molecules as mentioned above. Proteins share the sequence identity of less than 30% to each other within this extended Kahraman dataset and also with any proteins in the original Kahraman dataset (Table 1A). In these protein structures, more than 30% of the ligand atoms are within 4.5 Å to the protein surface atoms. The structures of the nine ligands in the Kahraman and the extended Kahraman dataset are shown in Figure 1A.

Table 1B.

Extended Kahraman dataset.

Binding ligand molecule	Average Size (Å)	Average number of seed	Number of PDB entries	PDB entries
AMP	8.8	22.2	5	1NH8A, 1QGXA, 1Y1PA, 1Z84B, 2R85B
ATP	9.5	32	4	1MJHA, 1OBDA, 1WUAA, 2YW2A
FAD	11	43.5	29	1B5QA, 1C0PA, 1EL5A, 1F0XA, 1F20A, 1F8SA, 1FNDA, 1GPEA, 1JU2A, 1KRHA, 1PBEA, 1PN0B, 1Q1RA, 1RYIA, 1TT0C, 1U8VA, 1W1OA, 1W4XA, 1X0PB, 1YOAA, 1ZK7A, 2BA9A, 2J4DA, 2MBRA, 2OLNA, 2QCUA, 2VFRA, 2YR5A, 2YYJA
FMN	9.7	30.8	8	1D3GA, 1JUEA, 1USCA, 1VYRA, 2D37A, 2H8ZA, 2NR4A, 2PIAA
GLC	8.5	11	9	1JG9A, 1PWBC, 1QK2A, 1RMGA, 1UA4A, 1UOZA, 2J73B, 2V8LA, 3BC9A
HEM	10.2	38.8	26	1BU7A, 1EW6A, 1FS7A, 1FT5A, 1GEJA, 1IO7A, 1IRDA, 1IT2A, 1IW0A, 1J0OA, 1KR7A, 1SY7A, 1TU9A, 1U55A, 1W4WA, 1YRCA, 256BA, 2BKMA, 2IJ7A, 2J0PA, 2Q9FA, 2RCHA, 2W31A, 2W3FA, 3B6HA, 3CX5D
NAD	10.1	39.9	15	1C1DB, 1DXYA, 1GIQA, 1GY8D, 1KOLA, 1N2SA, 1OBBB, 1ORRA, 1PL8A, 1R66A, 1SG6A, 1U1IA, 2DVMB, 2H7MA, 2VHXE
PO4	7.4	8.43	48	1A9XA, 1AOPA, 1AQZA, 1DXEA, 1EX2A, 1JE0A, 1K27A, 1KV8A, 1LC0A, 1NV0A, 1OWLA, 1P0KA, 1P1JA, 1PIIA, 1Q11A, 1RKDA, 1RWHA, 1T46A, 1TG7A, 1THFD, 1TZYE, 1V2XA, 1WCHA, 1WOQA, 1XA1B, 1XW3A, 1Y6VA, 1YB0A, 1YN9A, 1YRRA, 1YSQA, 2FYQA, 2HEKA, 2HHCA, 2IMFA, 2JE2A, 2JFRA, 2O4UX, 2O4VA, 2V3QA, 2VBMA, 2VLBC, 2VM9A, 2W3ZA, 2YXTB, 2ZAUA, 3B7NA, 3E9DA

Figure 1.

Ligand structures in the benchmark datasets. A, nine ligand structures in the Kahraman and the extended Kahraman dataset. B, twelve ligand structures in the Huang dataset. See texts for the full spelling of the abbreviated molecular names.

The third dataset, the Huang dataset³⁴, is for examining pocket retrieval performance of Patch-Surfer on different ligand types as well as on ligand unbound pockets. Total of 146 proteins are selected which bind either one of the following 12 ligand molecules (Table 1C): adenosine (ADN), biotin (BTN), fructose 6-phosphate (F6P), fucose (FUC), galactose (GAL), guanine (GUN), mannose (MAN), O1-methyl mannose (MMA), 2-phenylimidazole (PIM), palmitic acid (PLM), retinol (RTL), and 2'-deoxyuridine 5-monophosphate (UMP). From the dataset of the same name used in our previous work²⁹, we exchanged several PDB entries so that proteins do not share 30% or more sequence identity within the same ligand binding proteins and also between proteins with different ligand type. When ligand unbound proteins (rightmost column in Table 1C) are used as queries, homologous proteins that share 30% or more sequence identity are removed from the dataset. The structures of the twelve ligands are shown in Figure 1B.

Table 1C.

The ligand pocket benchmark dataset from Huang et al.

Ligand moleculea)	Average Sizea) (Å)	Average number of seed	Number of PDB entries	PDB entriesb)	Unbound Structurec)
ADN	9.1	22.27	12	1bx4A, 1fmoE, 1mrgA, 1pg2A, 1vhwA, 2evaA, 2fqyA, 2pgfA, 2pkmA, 2zgwA, 3ce6A, 3fuuA	1ahcA
BTN	8.4	18.63	8	1bdoA, 1hxdA, 1stpA, 2b8gA, 2c4iA, 3d9lA, 3ew2A, 3g8cA	1swbA
F6P	8.7	19.8	10	1fbpA, 1lbyA, 1tipA, 1uxrA, 2cxsA, 2r66A, 3bxhA, 3h1yA, 3iv8A, 4pfkA	2fbpA
FUC (SAC)	6.7	8.63	8	1k12A,1ivdB , 1lslA, 2a2qL, 2bs6A, 2j1tA, 2nzyA, 3cigA	1nnaA
GAL (SAC)	7.8	13.88	32	1gcaA, 1iszA, 1jz7A, 1kwkA, 1muqA, 1nsxA, 1okoA, 1r47A, 1rdk1, 1rvtJ, 1s5dD, 1tlgA, 1v3mA, 1w8nA, 1xc6A, 1z45A, 1zizA, 2b3fA, 2e9mA, 2ehnB, 2eukA, 2galA, 2j5zA, 2rjoA, 2v72A, 2vjjA, 2vnoB, 2zgnB, 3a23A, 3c69A, 3dh4A, 5abpA	1gcgA
GUN	8.1	14.64	10	1a95C, 1d6aA, 1it7A, 1sqlA, 1xe7A, 2i9uA, 2o74A, 2oodA, 2pucA, 3bp1B	1ulaA
MAN (SAC)	6.3	9.33	15	1apuE, 1bvwA, 1g12A, 1jndA, 1js8A, 1kdgA, 1kza1, 1m3yA, 1nhcA, 1qmoA, lxxrB, 2duqA, 2e3bA, 3c6eC, 3d87D	3appA
MMA (SAC)	7.6	13	8	1kiuB, 1kwuA, 1lob A, 1msaA, 1s4pA, 2bv4A, 2g93A, 5cnaA	2ctvA
PIM	8.1	14	5	1e9xA, 1f4tA, 1s1fA, 1pdbA, 2d0tA	1phcA
PLM	9.0	28.3	24	1e7hA, 1eh5A, 1gxaA, 1hxs1, 1lv2A, 1m66A, 1mzmA, 1sz7A, 1u19A, 2debA, 2dt8A, 2e9lA, 2go3A, 2ifbA, 2jafA, 2nnjA, 2qztA, 2uwhA, 2w3yA, 2z73A, 3bfhA, 3bkrA, 3eglA, 3epyA	1ifbA
RTL	9.3	31.2	5	1fbmA, 1fmjA, 1gx8Am 1rbqA, 2rctA	1brqA
UMP	8.7	22.5	8	1bidA, 1f7nA, 1r2zA, 1sehA, 2bsyA, 2jarA, 2qchA, 3dl5A	3tmsA

^a)FUC, GAL, MAN, and MMA are also grouped as saccaride (SAC).

^b)Homologous structures to the unbound proteins are underlined, which are used to identify ligand binding pockets of ligand unbound proteins. They are removed from the dataset when unbound structures are used as query.

^c)The unbound structures are used only for results in Table 5.

Computing protein surface properties

The protein tertiary structure is represented by its surface shape. The surface of a protein is computed with the Adaptive Poisson-Boltzmann Solver (APBS) program³⁵, which defines the surface as the boundaries of solvent accessible and solvent excluded regions. Surface shape information is stored in a 3D grid where grid points (voxel) that overlap with the protein surface are specified. For example, a 300 residue long protein fits into a 3D grid of the size 129 × 129 × 129 with a grid interval of 0.5 Å.

In addition to the geometrical shape, the protein surface is characterized with three other properties: the electrostatic potential, the hydrophobicity, and the visibility. These properties are assigned to each surface voxel. The electrostatic potential is computed with the APBS program, which solves the Poisson-Boltzmann equation. For the hydrophobicity, we use the Kyte-Doolittle hydrophobicity scale³⁶. The Kyte-Doolittle hydrophobicity scale assigns a value between −4.5 (hydrophilic) and 4.5 (hydrophobic) to amino acid residues. To obtain the hydrophobicity of each voxel, first, each surface voxel is assigned with the hydrophobicity value of the closest amino acid residue, and then values are smoothed by averaging hydrophobicity values assigned to its neighboring surface voxels that are within two voxels apart. The surface visibility³¹ indicates concaveness or convexness of a voxel. We defined the visibility of a voxel as the ratio of voxels occupied by the protein among the all the voxels within 5Å to the target voxel. The visibility value ranges from 0 to 1.0 where 0 indicates the voxel is not close to a protein and 1 indicates that the voxel is completely buried in the protein. A large visibility value indicates that the voxel locates at a concave region of protein surface. As will be discussed later, the four properties of surface points are represented as the 3D Zernike descriptors.

Pocket extraction by ray casting

The surface of a pocket region in the protein is extracted. The pocket surface is extracted by casting rays from the center of the ligand binding pocket after the protein surface properties are computed. A pocket is defined as surface points that are encountered by rays cast from the ligand center position. If the position of a binding ligand is known, the center of mass of the ligand atoms is used to represent the center of the pocket location. In case the ligand binding position is not known, the ligand binding site prediction method, LIGSITE³⁴, is used to predict the center of the binding pocket.

Local surface patch extraction

A pocket region is represented by a group of surface patches. A surface patch, which will be referred later simply as a “patch”, is a connected single surface region within a specified distance (5Å to 8Å is tested) from a center point (voxel) called a “seed”. The steps in seed selection are as follows: First, surface atoms of the selected pocket are determined as heavy atoms of residues within 3.5Å to the pocket surface. Second, the first seed is selected from surface points that are closest to one of the surface atoms. Then the rest of seeds are determined by applying an iterative procedure of selecting a closest surface point for each of the surface atoms that is not closer than 3.0Å to seed positions that are already selected. These steps distribute patches evenly on the pocket surface. On average there are 22.7 seeds (thus 22.7 patches) for a pocket.

Surface patch representation using the 3D Zernike descriptor

The four surface properties, the geometrical shape, the electrostatic potential, the hydrophobicity, and the visibility, mapped on a patch at the seed point x are considered as 3D grid functions, i.e. f_shape(x), f_ele(x), f_hyd(x), and f_vis(x), respectively, which are represented by the 3D Zernike descriptor (3DZD). The 3DZD allows compact and rotationally invariant representation of 3D objects (i.e. a 3D function)^32,37. Below we provide a brief mathematical derivation of the 3DZD. For more detail, see two previous studies of the 3DZD^32,37. The 3DZD has also been successfully applied to various protein and ligand structure analyses^23,38,39, including rapid protein global shape analysis (http://kiharalab.org/3d-surfer)^40,41, quantitative comparison for protein surface physicochemical properties⁴², small ligand molecule comparison⁴³, protein-protein docking prediction⁴⁴, and the comparison of low-resolution electron density maps^45,46. In our previous works we have shown that the 3DZD can also capture geometrical shape of local protein surfaces^47,48.

A 3D function, f(x), which contains a surface property of a patch, is expanded into a series in terms of Zernike-Canterakis basis³² defined as follows:

$$Z_{nl}^m(r,\vartheta ,\phi )=R_{nl}\left(r\right)Y_l^m(\vartheta ,\phi )$$ (1)

where −l < m < l, 0 ≤ l ≤ n, and (n − l) even. $Y_l^m(\vartheta ,\phi )$, are the spherical harmonics and R_nl (r) are radial functions constructed in a way that $Z_{nl}^m(r,\vartheta ,\phi )$ can be converted to polynomials in the Cartesian coordinates, $Z_{nl}^m\left(\mathbf{x}\right)$. To obtain the 3DZD of f(x), first, 3D Zernike moments are computed, which are defined by the expansion in this orthonormal basis:

$${\Omega }_{nl}^m=\frac{3}{4\pi }{\int }_{\mid \mathrm{x}\mid \le 1}f\left(\mathbf{x}\right){\stackrel{‒}{Z}}_{nl}^m\left(\mathbf{x}\right)d\mathbf{x}$$ (2)

Then, the 3DZD, F_nl, is computed as norms of vectorsΩ_nl. The norm gives rotational invariance to the descriptor:

$$F_{nl}=\sqrt{\sum _{m=-l}^{m=l}{\left({\Omega }_{nl}^m\right)}^2}$$ (3)

The parameter n is called the order of 3DZD and it determines the resolution of the descriptor. n defines the range of l and a 3DZD is a series of invariants (Eqn. 3) for each pair of n and l, where n ranges from 0 to the specified order. We use order n = 15 (72 invariants) in the local surface patch comparison. Finally, the obtained 3DZD is normalized to a unit vector by dividing each moment by the norm of the whole descriptor. This normalization is found to reduce dependency of 3DZD on the number of voxels used to represent a protein⁴².

The 3DZD for the electrostatic potential, f_ele(x), and the hydrophobicity, f_hyd(x), are computed for voxels with a positive value and those with a negative value separately, and then concatenated to result in a vector of 72 × 2 = 144 invariants. This additional step is necessary to capture a spatial distribution of positive and negative values as we discussed in our previous work⁴². Thus, f_shape(x) and f_vis(x) are represented by a vector of 72 invariant values while vectors for f_ele(x) and f_hyd(x) have 144 invariants.

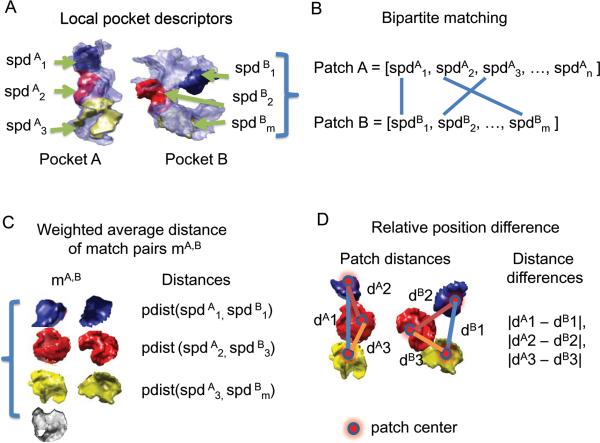
Using the 3DZDs, a surface patch at the i-th seed of a pocket P is described by the surface patch descriptor spd^p_i, which consists of the coordinate of the seed, s^P_i=(x^P_i, y^P_i, Z^P_i), and normalized local 3DZDs, lzd^P_i,,shape, lzd^P_i,,hyd, lzd^P_i,ele, and lzd^P_i,,vis, which are computed for the four features, shape, hydrophobicity, electrostatic potential, and visibility values that are mapped onto the surface points, f_shape(x), f_ele(x), f_hyd(x), and f_vis(x). A pocket P covered with n patches is represented as a set of the patches. Namely, Pocket(P) = [spd^p₁, spd^p₂, …, spd^p_n]. The pocket descriptor is illustrated in Figure 2A.

Figure 2.

Illustration of surface patch descriptors and the comparison method used in Patch-Surfer. A, pocket descriptors that are composed of surface patch descriptors (spds). B, the weighted bipartite matching algorithm. It matches pairs of surface patches from two pockets that have small distance defined by the score. C, a scoring term for a pair of pockets considers the average of pair-wise distance (Eq. 6) of matched patches. D, another scoring term compares mutual distance between patches in the two pockets (Eq. 7).

Procedure of pocket comparison

The similarity of two pockets is quantified as a score that considers the distance of matched pairs of patches from the two pockets, the relative distance between the patches within each pocket, and the size of the pockets (Fig. 2). A query pocket A and a pocket B in a database are compared in the following three steps: 1), computing the distance of local surface patch pairs from the two pockets; 2), finding the corresponding matching pairs of patches from pockets A to B; and 3), computing the overall distance score of the two pockets. Below we explain each step of the procedure.

• 1)
  Computing the distance of all the pairs of surface patch descriptors from two pockets. The i-th patch from the query pocket A and the j-th patch from a database pocket B, spd^A_i, and spd^B_j, is computed as:

  $$\mathit{pdist}({\mathbf{spd}}_i^A,{\mathbf{spd}}_j^B)=\sum _{t\in \{\mathit{shape},\mathit{hyd},\mathit{ele},\mathit{vis}\}}{w}_{j,t}^B\times L2({\mathit{lzd}}_{i,t}^A,{\mathit{lzb}}_{j,t}^B),$$ (4)

  where $w_{j,t}^B$ are the weighting factor for each property type t ∈ {shape, hyd, ele, vis}of the j-th patch of pocket B. $L2(lz{d}_{i,t}^A,lz{d}_{j,t}^B)$ is the L2 norm (the Euclidian distance) between two 3DZDs of the two patches of type t, $lz{d}_{i,t}^A$ and $lz{d}_{j,t}^B$. Thus, the patch distance is weighted sum of the distances between the 3DZDs of the four surface properties, shape, hydrophobicity, electrostatic potential, and visibility, which characterize the patches.
  The weighting factors in Eqn. 4 are for normalizing the difference of the value distribution of the four properties. The weighting factors consider the average (avg) and the standard deviation (std) of the Euclidian distance computed for 3DZDs of patches at the equivalent position in binding pockets of the same ligand type in the dataset. The weight for the feature t of the i-th patch in pocket P is defined as follows:

  $$w_{i,t}^P=\frac{\frac{1}{({\mathit{avg}}_{a\left(i\right),t}+2\ast {\mathit{std}}_{a\left(i\right),t})}}{\sum _{s\in \{\mathit{shape},\mathit{hyd},\mathit{ele},\mathit{vis}\}}\frac{1}{({\mathit{avg}}_{\mathrm{ALL},s}+2\ast {\mathit{std}}_{\mathrm{ALL},s})}}.$$ (5)

  a(i) is the ligand atom where the seed of the i-th patch is closest to. Thus, avg_a(i),t and std_a(i),t is the average and the standard deviation of the Euclidean distances of 3DZDs of type t that are computed for patches locating at the same ligand atom a(i) in the same ligand type. The average and the standard deviation are computed for pockets in the dataset, excluding the query pocket. Avg_ALL,s and std_ALL,s are computed from all the patches of all ligand types in the dataset. For ligand binding pockets that are not abundant in the dataset (STR in the Kahraman dataset), the overall average and the standard deviation values are used, which are computed for all the pairs of patches in all ligand binding pockets in the dataset. Thus, avg_{a(i), t} and std_{a(i), t} in the numerator in Eqn. 5 are replaced with avg_ALL,t and stdALL,t.
• 2)Finding matching patches from pockets A and B. Patches are matched so that the resulting matched patch pairs in the two pockets have the total minimum distance score. This problem is known as the weighted bipartite matching problem with only a difference being that our problem needs minimization of the score while the original problem seeks for maximization of a score. The weighted bipartite matching problem can be approximately solved by the auction algorithm^48,49. The distance score of each pair of patches is computed using Equation 4. We introduced a distance threshold value to the original auction algorithm so that only similar patches are selectively paired, leaving dissimilar ones out from the matching. The bipartite matching is illustrated in Figure 2B and the detail of the modified auction algorithm is provided as Supporting Material (Figure S1).
• 3)
  Computing the overall distance score of the two pockets. After surface patch matching is established, the overall score of the two pockets is computed using three terms, the weighted average distance score, a term for evaluating consistency of mutual position of matched patches, and the pocket size information. The average distance score of patches is defined as

  $$\mathit{avgZd}(A,B,{\mathbf{m}}^{A,B})=\left(\frac{n_A}{N}\right)\left(\frac{1}{N}\sum _{i\in {\mathbf{m}}^{A,B}}\mathit{pdist}({\mathbf{spd}}_{m_i^{A,B}}^A,{\mathbf{spd}}_{m_i^{A,B}}^B)\right),$$ (6)

  where n_A is the number of patches in a pocket A, N is the number of pairs of patches from pockets A and B, and pdist is the distance score of two patches as defined in Equation 5. m^A,B contains the list of matched patch pairs from pockets A and B (Figure 2C). $m_i^{A,B}$ is the i-th matched patch pairs. $\frac{n_A}{N}$ is a weighting factor for penalizing a match m^A,B when the number of matched pairs (N) is smaller than the number of patches in the query i.e. pocket A (n_A).

The second term considers the relative position of matched patches in pockets A and B (Figure 2D). Relative position difference (rpd) of a match m^A,B in pocket A and B is defined as

$$rpd(A,B,{\mathbf{m}}^{A,B})=\left(\frac{n_A}{N}\right)\left(\frac{2}{N(N-1)}\sum _{i=0}^{N-1}\sum _{j=i+1}^N\mid L2\left({\mathbf{s}}_{m_i^{A,B}}^A,{\mathbf{s}}_{m_j^{A,B}}^A\right)-L2\left({\mathbf{s}}_{m_i^{A,B}}^B,{\mathbf{s}}_{m_j^{A,B}}^B\right)\mid \right),$$ (7)

${\mathbf{s}}_{m_i^{A,B}}^A$ is the coordinate of the seed point of the $m_i^{A,B}$-th patch in pocket A. Thus, the score computes the average of the difference of the Euclidean distance between the i-th and the j-th patches in pocket A and B.

The two terms are linearly combined to yield the pocket match distance (pocketMd) with weights w₁ and 1-w₁, where 0 ≤ w₁ ≤ 1:

$$pocketMd(A,B,{\mathbf{m}}^{A,B})=w_1\times avgZd(A,B,{\mathbf{m}}^{A,B})+(1-w_1)\times rpd(A,B,{\mathbf{m}}^{A,B})$$ (8)

In addition, we also considered the difference of the pocket size because they have been found to be effective in the previous studies^29,33:

$$pocketSd(A,B)=\mid \frac{n_A-n_B}{n_B}\mid .$$ (9)

Thus, it is computing the difference of the number of patches in the two pockets. The three terms are combined with another weighting factor, w₂ (0 ≤ w₂ ≤ 1), as follows:

$$Totalscore(A,B)=w_2\times pocketMd(A,B,{\mathbf{m}}_{A,B})+(1-w_2)\times pocketSd(A,B)$$ (10)

The weight values of w₁ = 0.3 and w₂=0.2 are used in the study. These weights have been found to provide the best prediction rate on the Kahraman dataset using all the four surface properties and the pocket size score (Figure S2 A). The second column of Table 1 lists the average pocket size. In Figure S2 B, we also show the average prediction success rate without using the weighting factor $\frac{n_A}{N}$ in Equations 6 and 7. By comparing Figure S2 A & B, it is shown that the inclusion of the $\frac{n_A}{N}$ term increases the prediction success rates for majority of the weight combinations forw₁ and w₂. For example, for the weight combination w₁ = 0.3 and w₂ = 0.2 removing n_A/N deteriorates the average top-1 success rate from 0.522 to 0.450, and top-3 success rate from 0.824 to 0.814.

Ligand type prediction score

Pockets in the database are ranked in ascending order according to the distance to a query pocket using the scoring function (Eqn. 10). Based on the ranked pockets, we use the following Pocket_score to predict the type of binding ligand molecules for the query pocket as proposed in our previous work²⁹. Using the k closest pockets to the query, the score for a ligand type F for the query pocket P is defined as

$$Pocket\_score(P,F)=\sum _{i=1}^k\left({\delta }_{l\left(i\right),F}\text{log}\left(\frac{n}{i}\right)\right).\frac{\sum _{i=1}^k{\delta }_{l\left(i\right),F}}{\sum _{i=1}^n{\delta }_{l\left(i\right),F}},$$ (11)

where l(i) denotes the ligand type (e.g. AMP, FAD, etc.) of the i-th closest pocket to the query, n is the number of pockets in the database, and the function δ_l(i),F equals to 1 if i-th pocket is of type F, and is 0 otherwise. The first term is to consider k closest pockets to the query, with a higher score assigned to a pocket with a higher rank. The second term is to normalize the score by the number of pockets of the same type F included in the database. The ligand with the highest Pocket_score is predicted to bind to the query pocket.

Performance evaluation of binding ligand prediction

Prediction performance is evaluated by the fraction of successful predictions where the correct ligand for the query pocket is predicted within top 1 or top 3 pocket scores. These are called the Top-1 and Top-3 success rate. We also use the area under curve (AUC) of the receiver operating characteristic (ROC) curve. To obtain the ROC curve, the k closest pockets in the database to the query are retrieved. Then they are evaluated by computing false positive (x-axis) and true positive (y-axis) rate at different score cutoff values. The value of k is varied from 1 to N where N is the number of pockets in the dataset. The false positive rate is defined as the ratio of the number of retrieved pockets of different ligands to the query (i.e., false positives) relative to the total number of pockets of different ligands the dataset. The true positive rate is the ratio of the number of correctly retrieved pockets of the same ligand type relative to the total number of pockets of the same type in the dataset. The false positive rate equals true positive rate, on average, in random retrieval, which yields an AUC value of 0.5.

Results

Variance of properties of ligand binding pockets

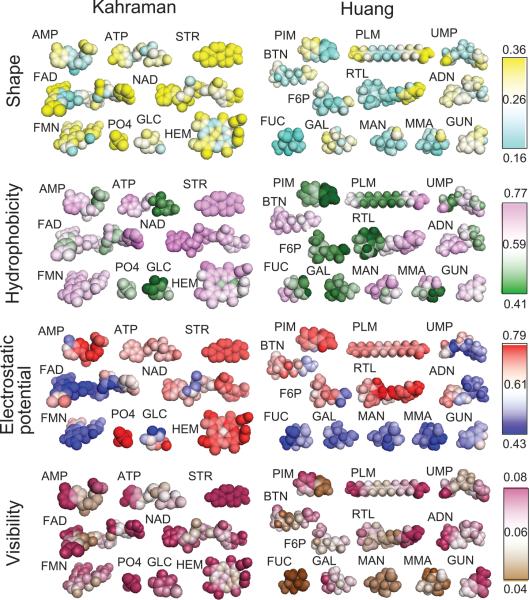
To begin with, we examined the variation of properties of pockets in the Kahraman dataset and the Huang dataset. Figure 3 shows the mapping of average Euclidian distances of 3DZDs of surface patches that are grouped and mapped according to the closest ligand atom. The maps are computed for the four properties, the shape, the hydrophobicity, the electrostatic potential, and the visibility. The figure shows different ligand binding pockets have different levels of conservation of the properties. Fucose (FUC) is relatively well conserved in all four properties, while retinol (RTL) binding pockets show a large variation in all the properties at the alcohol group at the end of the poly unsaturated side-chain (the right side of RTL in Figure 3). Also, the conserved regions can be different for the different properties. For example, phosphate binding region is the most conserved region in the ATP binding pockets in terms of the hydrophobicity (green) while the same region is not well conserved in terms of the other properties, especially for the electrostatics potential and the visibility. The observed diversity of the different properties at equivalent position in binding pockets has motivated us to segment pocket surface into local patches so that the comparison can accommodate the difference in the surface properties within the pockets.

Figure 3.

Average 3DZD distance of four properties used to characterize pockets. The average distance of 3DZDs of patches at equivalent position in pockets is computed and mapped to the closest ligand atoms. The distance is shown in color, from cold color (smaller distance) to warm color (larger distance). The first row shows distances of surface patch shape. Second row shows the hydrophobicity. The third row shows the electrostatic potential. The last row shows the visibility. The ranges of color codes shown in the bars are average distance plus/minus two times of the standard deviation. For STR, the average distance of all patch pairs in the pockets are mapped to all the atoms because there are not many structures available for meaningful statistics (three EST and two AND).

Retrieval Performance of Pocket-Surfer and Patch-Surfer

Next, we examine overall pocket retrieval performance of the Patch-Surfer and Pocket-Surfer using surface shape and size information on the Kahraman dataset and the Huang dataset. The resulting ROC curves are shown in Figure 4. The performance was compared with and without pocket size information for both methods. More concretely, Eqn. 8 was used for considering pocket shape while Eqns. 9 and 10 were used for encoding shape and the size information for Patch-Surfer. As the pocket size information, the average number of seeds in pockets was used (Table 1A for the Kahraman data set and Table 1C for the Huang dataset). The number of seeds correlates well with the molecular mass of the ligand molecules with the correlation coefficient of 0.994. For Pocket-Surfer, the average distance from the center of a pocket to the pocket surface is used following our previous work²⁹ (Tables 1A & 1C). As described in Materials & Methods, Patch-Surfer uses the weighting factors $w_{i,shape}^p$ (Eq. 5) to balance contribution of each patch at a different position in the overall score. For the results shown in Figure 4, we conducted a leave-one-out procedure, i.e. the query pocket is excluded when the average and standard deviation of the Euclidian distance of the 3DZDs were computed to obtain the weighting factor values.

Figure 4.

ROC curves of Pocket-Surfer and Patch-Surfer using the shape and the size information. A, the Kharaman dataset. B, the Huang dataset. The AUC values of the curves are shown in Table 2. The patch radius was set to 5Å. A random retrieval yields the AUC of 0.5.

It is shown that Patch-Surfer outperforms Pocket-Surfer with and without pocket size information (Figure 4 & Table 2). For the both datasets, Patch-Surfer using pocket size information performed the best followed by Patch-Surfer without pocket size. Table 2 summarizes the ROC AUC values of the two methods along with four similar pocket descriptors reported in previous work²⁹. Legendre moments, 2D Zernike moments, and 2D pseudo-Zernike moments are two dimensional shape descriptors, which encode two dimensional projections of pockets that describe the distance of the pocket wall from the pocket center. The results of spherical harmonic method are taken from the paper by Kahraman et al.³³ The four descriptors are global descriptors of pockets, which are the same as Pocket-Surfer. Among these descriptors, Patch-Surfer clearly outperforms the others. Note that Pocket-Surfer was previously^29,39 shown to outperform four other existing methods, eF-Seek²⁴, SitesBase⁵⁰, PROSURFER⁵¹, and XBsite2F⁵². And here we show that Patch-Surfer performs even better than Pocket-Surfer.

Table 2.

Average Area Under ROC Curve for different methods.

Methods	Kahraman dataset		Huang dataset
	Shape	Shape + Size	Shape	Shape + Size
Patch-Surfer	0.81	0.84	0.64	0.68
Pocket-Surfer (3DZD)a)	0.66	0.81	0.54	0.63
Legendrea)	0.53	0.77	-	-
Pseudo-Zernikea)	0.66	0.79	-	-
2D Zernikea)	0.66	0.78	-	-
Spherical harmonicsb)	0.64	0.77	-	-
Random	0.5	0.5	0.5	0.5

^a)The results are taken from our previous work (Rayan, Sael, Kihara, Proteins 2010).

^b)The results are taken from the paper by Kahraman et al. The results for the Huang dataset are not available because it was not used in their paper.

Patch-Surfer and Pocket-Surfer with/without size information showed better retrieval performance on the Kahraman dataset than the Huang dataset. One of the reasons for poorer performance on the Huang dataset is that they are composed of similar sized pockets for smaller ligand molecules. Pockets in the Kahraman dataset have an average of 22.5 seed points with standard deviation of 11.0 while the Huang dataset has an average of 18.0 seeds with the standard deviation of 7.1. Also, the Huang dataset includes pockets with ligand molecules with similar chemical structures, i.e. FUC, GAL, MAN, and MMA, which are all single ring sugar molecules and were not well distinguished between each other, as we will show later.

Parameter Optimization on the Kahraman Dataset

In the previous section, we demonstrated that Patch-Surfer performs the best among the related pocket descriptors (Table 2, Figure 4). Here, we examine prediction performance of Patch-Surfer with different patch sizes and different combinations of surface properties (Table 3). The binding ligand type prediction was made by considering the top eighteen (k=18 in Eq. 11) retrieved pockets. k=18 was found to provide the best average prediction rate (Figure S3). Eighteen is twice the number of ligand types included in the Kahraman dataset.

Table 3.

The success rate of binding ligand prediction on the Kahraman dataset using different parameters.

Score combination		Top-1 prediction success rate					Top-3 prediction success rate
Properties useda)		PRb) 5Å	PR 6Å	PR 7Å	PR 8Å	Avg.c)	PR 5Å	PR 6Å	PR 7Å	PR 8Å	Avg.c)
Without pocket size	S - - -	0.382	0.338	0.315	0.315	0.338	0.754	0.693	0.780	0.780	0.752
	S - -V	0.383	0.333	0.364	0.364	0.361	0.739	0.732	0.775	0.775	0.755
	S-EV	0.371	0.392	0.383	0.383	0.382	0.764	0.744	0.749	0.749	0.752
	SH-V	0.306	0.350	0.337	0.337	0.333	0.742	0.705	0.786	0.786	0.755
	SHEV	0.382	0.322	0.350	0.350	0.351	0.729	0.730	0.685	0.685	0.707
With pocket size	S - - -	0.483	0.478	0.461	0.461	0.471	0.840	0.851	0.888	0.888	0.867
	S - -V	0.470	0.462	0.444	0.444	0.455	0.843	0.848	0.866	0.866	0.856
	S-EV	0.480	0.486	0.436	0.436	0.460	0.848	0.848	0.843	0.843	0.846
	SH-V	0.432	0.460	0.442	0.442	0.444	0.837	0.866	0.803	0.803	0.827
	SHEV	0.455	0.463	0.486	0.486	0.473	0.870	0.829	0.848	0.848	0.849
Average		0.414	0.408	0.402	0.402	0.407	0.797	0.785	0.802	0.802	0.797

^a)Combination of the properties used for prediction are shown. The shape (S), the hydrophobicity (H), the electrostatic potential (E), and the visibility (V).

^b)The patch radius (PR) of the sphere used to define patch regions.

^c)Average over different patch sizes.

As consistent with Figure 4, adding the pocket size information improved the prediction rate for all the combinations of properties and the patch sizes tested. For example, when the pocket size information was not used, the average Top-3 success rate by using pocket shape information only (S - - -) was 0.752, which was improved to 0.867 when the pocket size information was combined. As for the patch size, four different radii, 5.0, 6.0, 7.0, and 8.0Å were tested. We observe a moderate trend that a smaller patch size performed better for Top-1 prediction success rate while larger patch sizes showed better performance for the Top-3 success rate on average. Adding more terms did not simply improve the success rate. Using all the four properties (SHEV) performed best on average with the pocket size in terms of the Top-1 success rate (0.473). On the other hand, using only the shape information (S - - -) showed the highest average Top-3 success rate with the pocket size information (0.867). Overall, we did not observe a single best combination of the properties that consistently performed better than the others. This observation is somewhat consistent with a previous work²⁶, which reports that combining the electrostatic potential to the size information did not make consistent improvement of pocket retrieval accuracy. This may be due to the diverse nature of property conservation of ligand binding pockets as we have seen in Figure 3.

In the following sections, we will provide results of using the patch radius of 5.0 Å, which showed the highest average prediction rate of 0.414 for the Top-1 prediction and the second best prediction rate (0.797) when the Top-3 predictions considered. As for the property combinations, we use the shape only (S - - -) and all four properties (SHEV). These two combinations had the two highest average Top-1 prediction rate over the four different patch radii, 0.471 and 0.473 respectively, when the pocket size information was used.

Prediction results of individual ligand types in the Kahraman Dataset

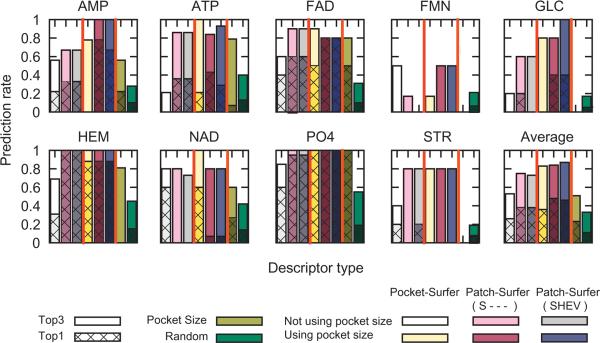
Figure 5 shows the breakdown of prediction accuracy for individual ligand types in the Kahraman dataset. The performance of Patch-Surfer are analyzed using the two property sets, the shape only (S - - -) and all four properties, i.e. the shape, the hydrophobicity, the electrostatic potential, and the visibility (SHEV) with and without pocket size information. For comparison, retrieval results for Pocket-Surfer are shown along with the results for Patch-Surfer using only the pocket size information and the result of random retrieval. In each panel in Figure 5, the first three bars from the left show the results without using the pocket size information, while the next three bars are the results using the pocket size information by Pocket-Surfer, Patch-Surfer (S - - -), and Patch-Surfer (SHEV), respectively.

Figure 5.

Prediction success rates for each ligand type in the Kahraman dataset. For each ligand type, the first three bars from the left show the results without using the pocket size information while the next three bars are results with the pocket size information. Three bars are the results of Pocket-Surfer, Patch-Surfer with shape information (S - - -), Patch-Surfer with shape, the hydrophobicity, the electrostatic potential, and the visibility (SHEV) information, from left to right. The bar in olive (the second one from right) shows the retrieval results using the pocket size information only. The rightmost bar is the results of a random retrieval. The cross-hatched bars show the Top-1 success rate and the solid bars show the Top-3 success rate.

By observing the average performance over different ligand types (Figure 5, bottom right panel), both Pocket-Surfer and Patch-Surfer showed a Top-3 success rate of over 0.80. Clearly, both Pocket-Surfer and Patch-Surfer performed better than size information alone or random retrieval. Patch-Surfer with the shape information only (S - - -) outperformed over the Pocket-Surfer for both with and without pocket size. Using the pocket size information improved the prediction rates for both Pocket-Surfer and Patch-Surfer by 0.08 to 0.20. The best Top-3 success rate, 0.87, was achieved by Patch-Surfer using all four properties (SHEV) and pocket size information.

When assessing the prediction success rate of individual ligand types, the prediction success rate differs from ligand to ligand. For example, the Top-3 success rate by Patch-Surfer using the four properties and the pocket size (purple bars) ranged from 0.50 for FMN to 1.00 for AMP, GLC, HEM, and PO4. When only the surface shape property was used without the pocket size information (the two leftmost bars in each panel), Patch-Surfer showed better Top-3 success rate than Pocket-Surfer in seven out of nine ligand cases (two exceptions are FMN for which Pocket-surfer showed better results and NAD for which had tied performance), indicating that patches used in Patch-Surfer effectively captured the local geometrical similarity of ligand binding pockets. The prediction accuracy of the PO4 binding pockets was perfect (1.0) even when only the pocket size was used due to its distinctively smaller pocket size (Table 1A).

Evaluation of the transferability of parameters

Next, we benchmark Patch-Surfer on the extended Kahraman dataset (Table 1B), which contains different sets of proteins that bind the same ligand molecules as the original Kahraman dataset. This dataset was used to examine how well the parameters determined with the original Kahraman dataset perform for unseen proteins. Figure 6 and Table 4 compares the prediction success rates of Patch-Surfer on the original Kahraman set (x-axis) and the extended Kahraman set (y-axis) using the combination of with/without pocket size information and shape only (S - - -) or all four properties (SHEV).

Figure 6.

Comparison of the prediction success rate by Patch-Surfer for the original and the extended Kahraman dataset. The Top-1 and Top-3 success rates of individual ligand types as well as the average success rate over all the ligands are compared. A, Only shape property was used (S - - -); B, the shape property was used in the combination with the pocket size infromation; C, the shape, the hydrophobicity, the electrostatic potential and the visibility properties (SHEV) were used; D, the four properties (SHEV) were used with the size information.

Table 4.

Summary of prediction on the original and the extended Kahraman datasets.

	Not using pocket size				Using pocket size
Descriptor	S---		SHEV		S---		SHEV
	Top1	Top3	Top1	Top3	Top1	Top3	Top1	Top3
Original Kahraman	0.38	0.75	0.38	0.73	0.48	0.84	0.46	0.87
Extended Kahraman	0.48	0.79	0.43	0.74	0.43	0.87	0.44	0.91

It is shown that the prediction performance for the two datasets is comparable. Moreover, results from the extended dataset were often better than those from the original dataset. Concretely, the Top-3 average success rate on the extended dataset was better than the original dataset for all the cases (Figs. 6A–6D, Table 4). Looking at the results for individual ligand types, several ligands have lower Top-1 success rate in the extended dataset when the pocket size information is used (Figs. 6B & 6D). However, on average the Top-1 success rate was also comparable between the original and the extended datasets. Without pocket size information, the Top-1 success rate was larger for the extended dataset (Figs. 6A & 6C). When the pocket size information is combined (Figs. 6B & 6D), the Top-1 success rate of the extended dataset was lower than that of the original dataset, but the difference was marginal (Table 4). We conclude that the weighting factor values trained on the original dataset can be applied to other proteins, which are not homologous to proteins in the original dataset.

Ligand Prediction on the Huang Dataset

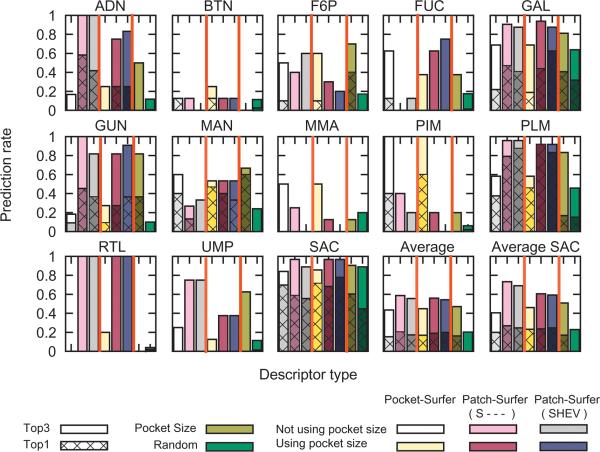
We further examine the prediction performance of Patch-Surfer and Patch-Surfer on the Huang dataset, which contains twelve different ligand types to those of the Kahraman dataset (Fig. 7). Again, Patch-Surfer shows overall higher Top-1 and Top-3 accuracy as compared with Pocket-Surfer (the “Average” panel at the bottom right). We find that ligand types that were better predicted with Patch-Surfer, ADN, PLM, RTL, and UMP, are relatively larger and more flexible, which are difficult for Pocket-Surfer (Fig. 3). In addition, GAL and GUN are two small ligands for which Patch-Surfer performed better than Pocket-Surfer.

Figure 7.

Binding ligand prediction on the Huang dataset. The Top-1 and Top-3 prediction success rate for each ligand types as well as the average values on the Huang dataset by Pocket-Surfer and Patch-Surfer are shown. The ligand group SAC (saccharides) composes of FUC, GAL, MAM, and MMA. “Average SAC” considers FUC, GAL, MAM, and MMA as a single ligand type. See Figure 5 for more captions.

Patch-Surfer did not show improved performance over Pocket-Surfer for some of small pockets whose shape is well conserved. For example, pockets of BTN are consistent in shape, and have no strongly conserved region of hydrophobicity, electrostatic potential and visibility. Also, FUC, MAN, MMA, each has a low prediction success rate by both methods due to their high mutual similarity. In fact, these ligands are known to interchangeably bind to the same protein pockets. For example, GAL and MMA bind to the same pocket in the lactoferrin crystal structures (PDB ID: 2dqvA and 2g93A). Similarly, MAN and MMA bind to the same location in lectin (1rinA and 1lobA). Also, a crystal structure of human EPHB2 receptor (1b4fA) binds MAN and FUC at the same pocket whereas a crystal structure of glutathione synthetase (1gltA) has FUC and GAL binding in the same location. Considering the similarity of these four ligands, we also examined the success rate by grouping these ligands into a single group, saccharides (SAC). The success rate for SAC was very high (panel named “SAC” in the bottom row) for both Patch-Surfer and Pocket-Surfer, which also made an improvement on the overall average prediction success rate (“Average SAC” panel).

Effect of the ligand flexibility to prediction accuracy

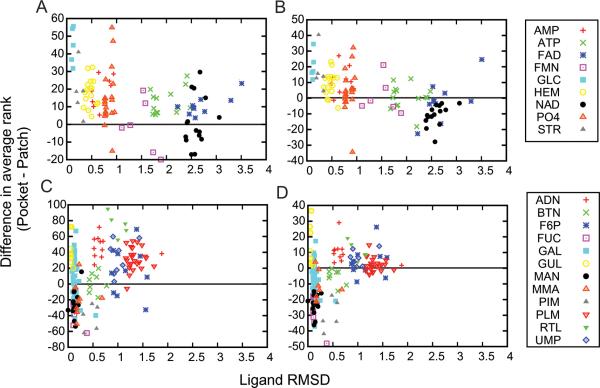
Since one of the motivations of developing Patch-Surfer is to better handle pockets for flexible ligand molecules, we examined how much the flexibility of ligands affect to the retrieval accuracy. In Figure 8 the difference in the rank of the top ranking correct binding site by Pocket-Surfer and Patch-Surfer for each query pocket (y-axis) is plotted relative to the RMSD of ligand pairs (x-axis). The y axis shows the rank of a binding pocket by Pocket-Surfer minus the rank by Patch-Surfer; thus, positive values indicate superior performance by Patch-Surfer. Overall, on both Kahraman and Huang datasets, Patch-Surfer retrieved binding sites of the same type as query at a lower rank than Pocket-Surfer except for some ligand types (e.g. NAD in the Kahraman dataset, Figs. 8A & B; MAN in the Huang dataset, Figs. 8C & D). The advantage of Patch-Surfer is more obvious when the pocket size information was not combined (Figs. 8A & 8C). On the Kahraman dataset, Patch-Surfer show large improvement in retrieving for flexible ligands, ATP and FAD, for which many pairs have an RMSD higher than 2 Å (Fig. 8 A). In the Huang dataset, Patch-Surfer showed improved retrieval ranks for two of the most flexible ligands, F6P and PLM, especially when the size information is not used (Fig. 8C).

Figure 8.

The ligand RMSD and the retrieval rank difference by Pocket-Surfer and Patch-Surfer. The x-axis shows the average RMSD between the ligand molecule of each query pocket to the other ligands of the same type in the dataset. The y-axis shows the difference in the retrieval rank of each ligand of the same type by Pocket-Surfer and by Patch-Surfer (rank by Pocket-Surfer – rank by Patch-Surfer). A, B, results on the Kahraman dataset using pocket shape information with and without using pocket size information, respectively. C and D are results on the Huang dataset. Retrieval was performed using pocket shape information C, without and D, with pocket size information.

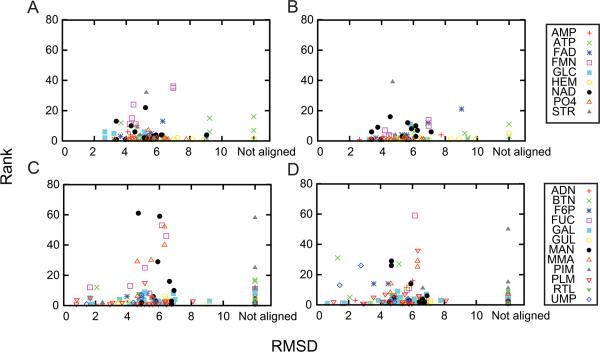
Effect of global structural similarity to the retrieval performance

Next, we examine how much the global structure similarity of a query protein to proteins in the database affect to the retrieval (Fig. 9). For both Kahraman (Figs. 9A & 9B) and the Huang dataset (Figs. 9C & 9D), no correlation was observed between the global RMSD (x-axis) of the protein structure and the rank of the retrieved pocket. Thus, Patch-Surfer is able to identify binding pockets of the same ligand type even if the global structure of the proteins is very different. This is advantageous in annotating function of proteins that do not have apparent sequence and structure similarity to proteins of known function.

Figure 9.

The RMSD of the global structure of proteins and the rank of the pockets retrieved by Patch-Surfer. For each query pocket, the best rank among the pockets of the same ligand type plotted (y-axis) relative to the global RMSD of the proteins (x-axis). The Combinatorial Extension (CE) program⁵³ was used to compute the RMSD. Points at the rightmost bar are proteins that CE could not structurally align to the query protein because their structures are overly different. Results for the Kahraman dataset is shown in A, using the shape information only; B, using the shape combine with the size information. Result for the Huang dataset is shown in C, using the shape only; and D, using the shape and the size information.

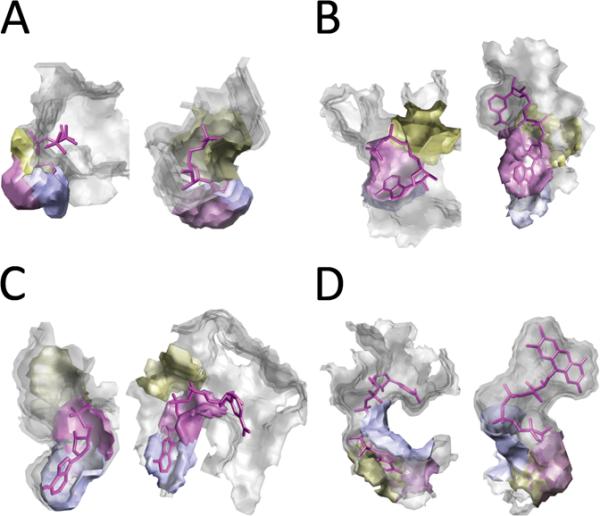
Examples of Pocket Matching

In this section we provide several examples that illustrate how similar patches in pockets are matched by Patch-Surfer. In these examples, all four surface properties were used to define the similarity of the patches. Figure 10 shows pairs of binding pockets of the same ligand type that have different overall pocket shape due to the flexibility of binding ligands. For these pockets, Patch-Surfer retrieved them at higher ranks than Pocket-Surfer by correctly identifying the corresponding surface patches. The first example is a pair of FAD binding proteins (Fig. 10A). In the crystal structure of flavohemoglogin (1cqx, left), the bound FAD is bound in a stretched form. On the other hand, rotatable bonds of the phosphate groups in the middle of FAD have different angles when bound to thiol oxidase (1jr8, right), which induces the change in conformation of FAD and thus causing the overall binding pocket shape to be very different from 1cqx. The apparent difference in the overall shape between the two pockets made it difficult for Pocket-Surfer to retrieve the correct pocket when queried by the other (1jr8 was retrieved for a query 1cqx that was ranked 21^st by Pocket-Surfer). In contrast, Patch-Surfer managed to retrieve 1jr8 as the fourth rank by identifying equivalent patches in the two pockets. In the figures pairs of identified corresponding patches in the two pockets are shown in the same color. The next example is NAD binding pockets (Fig. 10B). Similar to the previous example, NAD binds to the two pockets with very different conformation (the RMSD of the two NAD in 1mi3 and 1s7g is 3.49Å). A NAD binding protein, 1s7g, was ranked as 3^rd by Patch-Surfer and as the 9^th by Pocket-Surfer, when queried using 1mi3. Figures 10C–F show four more examples of the same ligand type binding pockets that are retrieved with a higher rank by Patch-Surfer than Pocket-Surfer. A protein with a F6P binding pocket, 3bxh, was ranked fourth by Patch-Surfer while ranked 26^th by Pocket-Surfer when queried using 2r66 (Fig. 10C). Likewise, the pair of RTL binding proteins, 1rbp was ranked 9^th and 38^th by Patch-Surfer and Pocket-Surfer respectively, when queried using 1gx8 (Fig. 10D). A UMP binding proteins, 2jar, was retrieved at the 3^rd rank and the 27^th (Fig. 10E) by Patch-Surfer and the Pocket-Surfer respectively, using 2qch as the query. A PLM binding proteins, 2w3y, was ranked 3^rd by Patch-Surfer while ranked 28^th by Pocket-Surfer when queried using 2nnj (Fig. 10F).

Figure 10.

Examples of pocket matching by Patch-Surfer. A query pocket is shown in left and a pocket retrieved from the dataset is shown on the right hand side. A, a pair of proteins that bind FAD, 1cqx (left) and 1jr8 (right). The RMSD of two FAD is3.79Å. B, a pair of NAD binding proteins, 1mi3 (left) and 1s7g (right). The RMSD of the ligand molecules is 3.49 Å. C, a pair of F6P binding proteins, 2r66 (left) and 3bxh (right). The RMSD of the ligands is 1.02 Å. D, a pair of RTL binding proteins, 1gx8 (left) and 1rbp (right) where the ligand RMSD is 0.90 Å. E, a pair of UMP binding proteins, 2qch (left) and 2jar (right) where the ligand RMSD is 1.45Å. F, a pair of PLM binding proteins, 2nnj (left) and 2w3y (right) where the ligand RMSD is 1.34 Å. Matching pairs of local patches for each of the pairs of proteins are shown. Color codes indicate corresponding matched patches from two proteins.

The previous examples shown in Figure 10 demonstrate that Patch-Surfer is more tolerant to the conformational differences in the binding pockets. However, the patch representation of pockets sometimes does not contribute to improvement of the binding ligand prediction accuracy, rather in the opposite way. The main cause of this is attributed to the shared chemical groups between ligand molecules, in which local binding surfaces are recognized as similar patches by Patch-Surfer. Figure 11 shows several of such examples. AMP, ATP, FAD, and NAD contain adenosine (Figs. 11A–D). Binding surfaces of the adenosine moiety of these molecules are identified as similar patches by Patch-Surfer, which often makes Patch-Surfer retrieve them at high ranks when queried by each other. Figure 11A is a pair of ATP binding (left, 1b8a) and AMP binding (right, 1kht) pockets. The obvious chemical similarity of binding pockets of these two molecules was identified by Patch-Surfer. When the original Kharaman dataset was searched from 1b8a, 1kht was ranked at the top, whereas Pocket-Surfer ranked it at 13^th. In the next example (Fig. 11B), an ATP binding pocket (left, 1dy3) was ranked at the 2^nd when queried using a NAD binding pocket (right, 1tox) by Patch-Surfer (Pocket-Surfer ranked it at 43^rd). Figure 11C is a pair of pockets that bind NAD (left, 1s7g) and FAD (1k87), which also have the adenine group. The retrieved rank of 1k87 queried from 1s7g was the 4^th by Patch-Surfer and the 17^th by Pocket-Surfer. The last panel (Fig. 11D) shows the binding pockets of FMN and FAD, both of which contain flavin. Pocket-Surfer recognized the difference of the overall shape of the two pockets, ranking 1ja1 (the FMN binding pocket) at the 47^th when queried from 1pox (FAD binding pocket). On the other hand, Patch-Surfer ranked 1ja1 higher at 12^th due to the recognition of the similarity in flavin binding patches of the two pockets.

Figure 11.

Examples of pairs of pockets for ligands with the same chemical group whose same moiety regions were matched by Patch-Surfer. A, 1b8a (ATP binding) in left and 1kht (AMP) in right. B, 1dy3 (ATP) in left and 1tox (NAD) in right. C, 1s7g (NAD) in left and 1k87 (FAD) in right. D, FMN binding protein 1kht (left) and FAD binding protein 1pox (right).

The recognition of binding regions of chemical groups does not always contribute to improvement in the prediction accuracy of binding ligands; however, it suggests that Patch-Surfer can be developed into a unique method for predicting chemical group binding sites rather than predicting the entire ligand molecules.

Binding Ligand Prediction for Ligand Unbound pockets

We have performed an additional experiment for Patch-Surfer on a set of ligand unbound pockets. The purpose of this experiment is to mimic the actual situation in which binding ligand prediction for a protein that does not have bound ligand. We use the Huang dataset (Table 1C) because this dataset originates from a list of ligand bound and unbound protein pairs³⁴. The RMSD value of ligand bound structure (underlined PDB IDs in the fourth column of Table 1C) and ligand-free proteins (the right most column of Table 1C) ranges from 0.11 to 0.87 Å with an average value of 0.38 Å. This value is similar to a recent thorough study⁵⁴, which reports the average RMSD of ligand-bound and -unbound form is 0.74 Å. For a query protein structure without bound ligand, a ligand binding pocket was determined in two ways. In the first method, the ligand binding pocket taken from the bound structures was superimposed to the unbound structure using the align program in PyMOL (version 1.3) The first method is aimed to examine how the difference of the bound and unbound pocket shape affects to the retrieval accuracy. The second method uses a ligand binding site prediction method, LIGSITE³⁴, to predict the binding site in the unbound protein structure. This is aimed to directly simulate blind prediction when there is no clue in regard to the location of binding sites in the query protein.

Table 5 summarizes the prediction results. The middle columns show the Top-1 and Top-3 prediction success rate using unbound pockets identified by superimposing ligand bound pockets. Compared to the average success rate of ligand bound pockets previously shown with graphs in Figure 7 (leftmost columns), interestingly, the success rates for the unbound pockets are comparable and in some cases success rates are even better than that of the bound pockets. These findings are consistent with the Pocket-Surfer results shown in our previous work²⁹ (Fig. 9 of the paper). As for the results provided by using the predicted ligand binding pockets (the right most columns), their Top-1 success rate are better, while the Top-3 results are worse than the bound pocket results. However, the deterioration of the Top-3 success rate for the predicted pockets is much less than what was observed for Pocket-Surfer (Table 8 in the paper²⁹), where the Top-3 success rate for predicted pockets went down to almost half the success rate of using bound pockets. Thus, the patch representation of pockets is more tolerant to the inaccuracies of predicted binding pockets.

Table 5.

Prediction success rates for ligand bound and unbound pockets of the Huang dataset.

Features Used	Bound proteins a)		Unbound proteins
			Bound ligand position b)		LIGSITEcsc prediction c)
	Top1	Top3	Top1	Top3	Top1	Top3
S - - -	0.203 (0.269)	0.588 (0.733)	0.250 (0.333)	0.667 (0.750)	0.417 (0.417)	0.417 (0.500)
S - - - - + size	0.190 (0.236)	0.559 (0.606)	0.250 (0.500)	0.667 (0.750)	0.273 (0.273)	0.545 (0.636)
SHEV	0.172 (0.277)	0.555 (0.691)	0.250 (0.417)	0.750 (0.833)	0.250 (0.250)	0.500 (0.500)
SHEV + size	0.169 (0.170)	0.543 (0.592)	0.250 (0.500)	0.750 (0.833)	0.250 (0.322)	0.417 (0.417)

The values shown in parentheses are the prediction success rate computed when FUC, GAL, MAN, and MMA are grouped as SAC (saccaride) (see Fig. 7).

^a)The average values of the results using ligand bound pockets, i.e. the data presented in Figure 7, are shown.

^b)Ligand binding regions were extracted by referring to the corresponding ligand bound pockets.

^c)3appA was not included since LIGSITEcsc did not make a binding site prediction near the MAN binding site.

Computation Time

The computation time of each step in Patch-Surfer and Pocket-Surfer is summarized in Table 6. The times were evaluated on a desktop computer with an Intel core i7 at 2.67 GHz and 11GB memory. It takes more time to prepare the pocket model of a query pocket for Patch-Surfer than for Pocket-Surfer because Patch-Surfer represents a query pocket with around 20–40 surface patches while the whole pocket is represented as a single object in Pocket-Surfer. Likewise, the database search by Patch-Surfer against the original Kahraman dataset with 100 pockets took longer than Pocket-Surfer because the former needs identification of similar patches in the query and database pockets using the modified bipartite matching algorithm. We also measured the search speed of a dataset with 200 pockets (by duplicating the original Kahraman dataset), which resulted in 0.046s and 7.52s for Pocket-Surfer and Patch-Surfer, respectively. A search speed for a larger pocket database can be computed by extrapolating these two search speeds. For example, a search against 5438 pockets taken from a list of non-redundant ligand binding protein structures in the Protein-Small-Molecule DataBase (PSMDB)⁵⁵ (http://compbio.cs.toronto.edu/psmdb/downloads/CPLX_25_0.85_7HA.list) takes 1.04s and 3min. 23.42s by Pocket-Surfer and Patch-Surfer, respectively. Thus, although Patch-Surfer takes more time than Pocket-Surfer Patch-Surfer is still practically fast enough for interactive search against a database with a realistic number of entries.

Table 6.

The computation time of Pocket-Surfer and Patch-Surfer.

	Process	Pocket-Surfer	Patch-Surfer
Preparation	Binding site prediction by LIGSITEcsc	3.12s	3.12s
	Computation of the descriptor	16s	1 min 52.96s a)
Database	Computing distance to each pocket b)	0.027s	3.78s a)
	Ligand prediction	0.02s	0.02s
Total		31.54s	2min 12.26s

^a)Only shape information is encoded.

^b)Measured on the original Kahraman dataset which contains 100 pockets.

Discussion

In this article, we reported a new binding ligand prediction method, Patch-Surfer, which represents pockets by a group of surface patches to capture local similarity of pockets. Comparison with the previously developed method, Pocket-Surfer, which captures global features of pockets, has highlighted the Patch-Surfer's superior characteristics of identifying pockets of the same ligand type, which do not necessarily have global similarity but similar local surfaces between each other. As shown in Figure 3, ligand binding pockets contain conserved regions as well as diverse regions among different protein structures. Patch-Surfer can identify the conserved regions of the pockets and therefore better detect similarities among pockets that bind to same ligand type. Interestingly, the patch representation is also tolerant to predicted binding pockets, which may not be very precise in location but contain correct local regions of ligand binding pockets. The use of the 3DZD, a rotational invariant and compact descriptor of 3D object, provided convenient means of representing local surface shape and properties that enabled fast comparison and searches of pockets.

On the other hand, the patch representation occasionally leads to wrong binding ligand predictions, typically by identifying surface patches that bind to the same chemical group in different ligand molecules. Such examples of adenine moiety that is in common to ATP, AMP, FAD, and NAD are shown in Figure 11. Although this is not desirable for binding ligand prediction, the ability of detecting local surface similarities can lead to the development of a novel method that can identify binding sites of chemical groups in protein surfaces. Such a binding chemical group prediction method could be advantageous in predicting the binding of novel ligand molecules that consist of known chemical groups. It will be also very useful in rational drug design⁵⁶. Another direction of future development is to apply the patch-based surface recognition method to the identification of other functional regions in protein surface such as protein-protein binding and RNA or DNA binding regions.

Unlike existing binding ligand prediction methods that mainly rely on global protein structure similarity¹⁵, Patch-Surfer and Pocket-Surfer identify similarity of local shape and physicochemical properties of binding pockets. Our methods will be effective for annotating structures which do not have global structural and sequence similarity to known proteins. A growing number of protein structures of unknown function in PDB, indeed, do not have apparent global similarity to annotated proteins.

In summary, we have developed a new binding ligand prediction method, Patch-Surfer, which represents a pocket by a set of surface patches described with the 3DZDs. There are three major advantages of Patch-Surfer: First, Patch-Surfer is capable of identifying local similarities in ligand binding surface regions. This is effective in identifying binding pockets of the same ligand type that are flexible and binds to pockets in different conformations. Second, due to the local pocket surface comparison, the method can predict binding ligands of proteins that do not share apparent global sequence and structure similarity to known proteins in the database. Third, the use of the 3DZD enables fast comparison of binding pockets. We are currently in the process of developing a comprehensive database of binding pockets for more practical use of Patch-Surfer in binding pocket annotation for proteins⁵⁷. Further application of a patch-based approach using the 3DZD will open new perspectives in classification and analysis of biomolecules for biological function annotation.