Learning transcriptional regulation on a genome scale: a theoretical analysis based on gene expression data

Abstract

The recent advent of high-throughput microarray data has enabled the global analysis of the transcriptome, driving the development and application of computational approaches to study transcriptional regulation on the genome scale, by reconstructing in silico the regulatory interactions of the gene network. Although there are many in-depth reviews of such ‘reverse-engineering’ methodologies, most have focused on the practical aspect of data mining, and few on the biological problem and the biological relevance of the methodology. Therefore, in this review, from a biological perspective, we used a set of yeast microarray data as a working example, to evaluate the fundamental assumptions implicit in associating transcription factor (TF)–target gene expression levels and estimating TFs’ activity, and further explore cooperative models. Finally we confirm that the detailed transcription mechanism is overly-complex for expression data alone to reveal, nevertheless, future network reconstruction studies could benefit from the incorporation of context-specific information, the modeling of multiple layers of regulation (e.g. micro-RNA), or the development of approaches for context-dependent analysis, to uncover the mechanisms of gene regulation.

INTRODUCTION

One of the grand challenges in systems biology is uncovering the complex gene regulatory network that renders the phenotype or disease state of a biological system in response to environmental cues. The complex interaction between genes and environment that govern the cellular response cannot be understood at the level of individual components of the network, but emerges through the intricate interplay between genes, proteins and metabolites. The complexity of gene regulation at the transcriptional level is one of the impetuses for the rise in systems-level research in biology. Although many transcription factors (TFs) and their cis-regulatory modules have been dissected experimentally, the mechanism of how these factors control a network of genes and their overall gene expressions remains elusive [1]. The recent advent of high-throughput microarray data enabled the global analysis of the transcriptome, driving the development and application of computational approaches to study transcriptional regulation on the genome scale, by reconstructing in silico the regulatory interactions of the gene network [1, 2].

A basic idea of inference or reconstruction of gene regulatory network is to identify pair-wise relationship between the genes, or more specifically, to determine whether a gene (or its product) directly controls the expression of another. By learning the dependencies contained within the expression profiles, researchers are attempting to reconstruct a circuit map that depicts the global regulatory network of genes. The development and application of the theory and tools for network inference, or so-called ‘reverse-engineering’ tasks, have been predominantly based on statistical learning techniques. There are several in-depth reviews in the literature that introduce and compare the different modeling schemes for statistical learning [3–5], including a primer on regression methods [6]. In Margolin et al. [7] they examine the theoretical underpinnings behind current reverse-engineering algorithms that are based on systems control theory (e.g. linear or non-linear regression model), probabilistic graphic learning and information theory.

However, previous reviews and literature in this area have generally been concerned about the practical aspect of data mining, and few have paid attention to the relevance of the methodology to the biological problem. The focus on the difficulties in network reconstruction has been from the computational perspective. A major discussion point has been the limited sample size available (in most cases less than 100 samples) for identifying pair-wise relationships between the genes (which could be hundreds of thousands pairs). This results in an under-determined system requiring methods for dimensionality reduction, i.e. clustering or module/pathway analysis [3, 8, 9]. Another challenge is the large search space of possible regulatory schemes, which requires either advanced optimization strategies or a priori information to reduce the computation time [4, 10, 11]. Nevertheless, in addition to previous improvements to the ‘predictive power’ or ‘computational efficiency’, it is important to understand how much biological information can be appropriately extracted from expression data to deduce the rules of transcriptional control.

From a biological perspective, instead of studying the physical network, many reverse-engineering methods are actually learning the ‘influence network’, which is an interwoven mixture of direct or indirect effects [7], thereby creating a considerable divide between the influence network that is constructed and the real biological regulatory mechanisms. This is due largely to the limitations of the data set itself, and the presence of multiple, unobserved levels of regulation leading to difficulties in the biological interpretations and undermining the biological significance of these ‘influence networks’ and their further applications.

In this review, we attempt to dissect the information content in the expression data from a biological perspective, and scrutinize the biological foundations of the computational models, and critically analyze the underlying assumptions of most in silico learning approaches applied to expression data that confound the interpretation of the results [7], which are:

1. Statistical dependencies exist between the TFs and their target genes with respect to both their expression levels.

2. Measurements of the relative amount of mRNA level in the microarray data are predictive of the activity of the regulatory molecules. This assumption can be further sub-divided into three sub-types, as follows:

1. Type-1 model assumes the expression level of a TF correlates with the activity of the TF. (e.g. [12, 13])

2. Type-2 model estimates the activity of a TF based on the behavior of its target genes. (e.g. [9, 14, 15])

3. Type-3 model assumes co-expression implies co-regulation by the same TF, and estimates the existence or activity of an uncharacterized cis-motif by clustering analysis. (e.g. [16])

In this review, using the yeast microarray data as an example, we combine information on the yeast transcriptional regulatory network and different data-sets and -types to examine each of these assumptions. Sections 2 and 3 address the first assumption by estimating the extent to which the expression of the TFs and target genes are correlated, and further analyze the biological factors that may contribute to this relationship. Section 4 compares the different types of models that apply the second assumption in learning the transcriptional regulatory network, and illustrates the advantages and limitations of each model. Finally section 5 examines the combinatorial regulation and discusses the challenges in learning cooperativity from expression data.

THE ASSOCIATION BETWEEN TF AND THEIR TARGETS

To illustrate the first assumption, we used yeast data to characterize the information in the expression data that are used to infer interactions at the transcriptional level. The yeast data set contains 255 conditions from environmental stress [17] and cell cycle [18] microarray experiments. These data sets have been widely applied in previous studies to develop novel reverse-engineering methods [16]. Actually the yeast environmental stress response data set [17] has been cited 2260 times thus far, and among 1000 of these citations that are related to computational studies, there are 256 articles that discuss network reconstruction (citation data are provide by googleScholar, http://scholar.google.com), which reflects the utility of the data set.

Many of the yeast TFs have been studied and their cis-regulatory modules on gene promoters across the genome have been identified and are now available in public databases such as YEASTRACT [19, 20], thus enabling the attainment of a putative transcriptional regulatory network based on known motifs on the gene promoters collated in YEASTRACT.

Since the fundamental assumption is that the expression level of a gene depends on its regulators, we calculate the correlation between the expression level of the TFs and that of their target genes, where the target genes of a TF in the regulatory network are identified by corresponding cis-motifs on their promoters. As shown in Table 1, the average absolute correlation coefficient of the expression data, taking the absolute value since both positive and negative correlation represents perceptible dependencies, is ~0.08 between the TFs and their target genes. This appears to be negligible, even smaller than the background with a correlation of ~0.19 between any gene pair, suggesting that it is difficult to directly identify TF–gene (a TF and its target gene) pairs based on the dependencies of their expression.

Table 1:

The average Spearman correlation between the expression level of the TFs and the expression level of their target genes, considering the conditions when the TFs are highly expressed (higher than their own mean level for all available conditions)

Characteristic	Avg. Corr (variance)
Background (all gene pairs)	0.19 (0.02)
Overall (TF–target gene)	0.08 (0.02)
1-to-1 (gene–its only known TF)	0.16 (0.02)
1-to-1 (gene–its only known TF) (TF highly expressed)	0.18 (0.02)

^‘1-to-1’ considers genes with only one known TF that can bind to their promoters.

Next, we place a ‘1-to-1’ constraint that considers only the TF–gene pairs in which the target gene has no other type of known effectors besides the TF paired to it. That is in contrast to an ‘n-to-1’ relationship in which many TFs regulate the expression of one gene. We identify 596 ‘1-to-1’ TF–gene pairs in the yeast network. This constraint assumes that the target genes of these 596 pairs are not regulated by multiple TFs. We found that the average correlation of the expression data of these pairs (0.16), albeit still lower than background noise (0.19), is about two times higher than the overall TF–gene pairs (Table 1). This suggests that the combinatorial regulation of multiple TFs on a target gene plays an important role in the transcriptional regulation, thereby complicating the TF–gene relationship and the use of correlation of their expression profiles for inferring regulatory networks. Moreover, the correlation between a TF–gene pair could be increased slightly when the samples containing lowly expressing TFs are removed. A rationale for doing this is that low expression level may suggest reduced control by the regulator [21].

Overall our results demonstrate a weak correlation in the expression exists between the TFs and their target genes, thus making it difficult to uncover transcriptional regulation due to the high background. The high background could possibly be due to both direct and indirect associations between the genes in the network. The result is consistent with previous observations [22] that only a very small proportion of TFs’ mRNAs are significantly correlated with the expression level of its target genes. Our results also indicate that combinatorial regulation contributes to the reduced correlation between the TFs and their target genes.

Besides the combinatorial effect, there are many complex features on the binding sites or DNA–TF interactions that could impair the association between TFs and their target genes [23]. A TF may not bind to all its targets with the same binding affinity, indeed many specifically interact with only a few targets depending on other genomic features, i.e. DNA modifications, or due to stochasticity of the binding events [24]. Differences in the sequence of and around the binding site will also affect the binding affinity [25]. Thus, to determine bindings that are functional remains a challenge [26–28]. Moreover, there are other levels of regulation that cannot be obtained from the expression data and transcriptional regulatory network. For example, the protein–DNA interactions may depend on other protein co-factors in order to become functional, and sometimes the binding itself requires adaptors [23, 29] . The mRNA level of the target genes may also be regulated at the post-transcriptional level, through the coordination of different rates of mRNA decay [30].

INCORPORATION OF INFORMATION FROM MULTIPLE SOURCES

It is increasingly evident that the network reconstruction by microarray data alone is imperfect, in part due to the limited sample size use to infer a very complex network, but more importantly because of the limitation of the information content of microarray, in which only the mRNA expression level is measured. Incorporating biological knowledge on different levels of regulation (mRNA decay, protein interactions and modifications) could improve the results. Many recent studies on reverse engineering have attempted to integrate these information but focus on the technical utility of multi-source information in providing priors to limit the search space, and enable further validation or promote more intrinsic learning models [12, 31–33]. Here we show from a biological perspective, in an intuitive but quantitative manner, an enhancement in the TF–gene correlation by incorporating multiple sources of information with the yeast expression data.

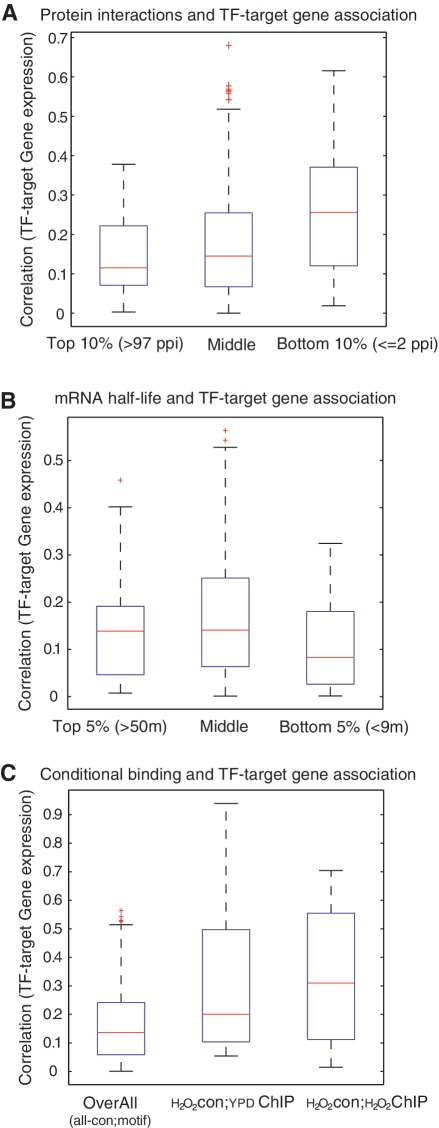
We consider the regulation of possible protein co-factors on the TFs, which have been suggested to impact the binding and activation of TFs. We impose an experimentally confirmed yeast protein–protein interaction (PPI) network on our transcription regulatory network. The physical interaction data are downloaded from SGD (http://www.yeastgenome.org/), and we compute for each TF the number of its potential interacting proteins—given that the PPI is static and context independent. We found that among all our 1-to-1 TF–target gene pairs (correlation of 0.16), those TFs with a low number of possible co-factors exhibits significantly better TF–gene correlation (P < 0.05, average correlation coefficient as high as 0.25), as shown in Figure 1A.

Figure 1:

Incorporation of information from multiple sources. (A) Box plots of the average correlation between the expression level of TFs and the expression of their target genes. A total of 596 1-to-1 TF–target gene pairs are considered. The data are categorized into three groups according to the number of interaction partners of each TF in the yeast PPI network. The group ‘Top 10%’ consists of TF–target pairs in which the TF has many interactions (more than 97 possible cofactors). The group ‘Bottom 10%’ consists of pairs where the TF has few protein interactions (no more than two cofactors). The others (80%) are in the ‘Middle’ group. The group ‘Bottom 10%’ exhibits significantly better average TF–gene correlation (P < 0.05). (B) Box plots of the average correlation between the expression level of TFs and the expression of the target genes. A total of 596 1-to-1 TF–target gene pairs are considered. The data are categorized into three groups according to the half-life of the mRNA of the target gene in each pair. Top 5% has the longest half-life, >97 min, and Bottom 5% has the shortest, <9 min. Genes in Bottom 5% group are less correlated with their TF regulators (P < 0.05). (C) Box plots of the average correlation between the expression level of TFs and the expression of the target genes. A total of 596 1-to-1 TF–target gene pairs are considered. CHIP-chip data are not available for every TF, so only 99 pairs have binding information and 20 of them are (condition-specific) conditional binding. The overall gene–TF (box on the left) describe the average correlation of all 596 pairs under all conditions. Under the H₂O₂ condition, the box in the middle (YDP-CHIP) uses the non-conditional binding (CHIP-chip results under normal condition, 99 pairs) to determine the average correlation of the gene–TF pairs that actually bind, and the box on the right uses conditional binding CHIP-chip data (20 pairs). The average TF–gene correlation increased significantly when conditional binding data were available (box on the right, P < 0.01 compared with the box on the left).

We also consider regulation at the mRNA level. The rate of mRNA decay for each gene [normal growth condition with yeast extract/peptone/dextrose (YPD) medium at 24°C] is obtained from the Global Yeast mRNA Decay data set [34]. Among our 596 1-to-1 TF–gene pairs, we assessed whether the mRNA decay of the target gene affects the TF–gene correlation. We observed no significant differences in the mRNA half-life among the gene categories grouped by different TF–gene correlations (Supplementary Figure S1). However the target genes that have very high mRNA degradation rates are less correlated with their TF regulators (P < 0.05), Figure 1B. Considering the usually longer time-scale of transcriptional regulation, the expression level of genes with very short mRNA half-life may be rapidly influenced by degradation, thus their amount of mRNA is decoupled from the expression level of the TFs.

These results show that the relationship between the expression of TFs and their target genes are affected by many factors, such as mRNA decay and protein co-factors. Nevertheless, there is no single factor that is sufficient to explain all the variation in TF–gene correlation for different genes under different circumstances (Supplementary Figures S1 and S2), since the regulatory mechanisms may depend on the dynamics of the regulatory network connections. In this sense, the static data sets (TF binding motif, mRNA decay in YPD media, static PPI) would not be able to capture the context information, and more detailed conditional or context-dependent knowledge is required to better reveal the TF–gene relationship.

Currently conditional-specific high-throughput data are rarely available due to the cost and technical difficulties in securing them. We searched the ChIP-Chip data and found a conditional ChIP-chip data set [35] containing 23 TFs under H₂O₂ (0.4 nM) treatment of yeast for which we also have microarray expression profiles. We therefore can define conditional TF–gene pairs using actual binding profiles (i.e. in the CHIP-chip data a significant P-value indicates TF binding on the gene promoters), rather than the sequence-level motif analysis that indicates only the possibility of TF binding instead of actual binding events. We compare the correlation coefficient of TF–gene pairs defined by cis-motifs, or by non-conditional CHIP-chip (under normal growth condition in YPD media), with that of gene pairs defined by conditional binding information (Figure 1C). The average correlation increased significantly (coefficient >0.3) when conditional binding data were available, confirming the importance of context-specific information.

Besides correlation analysis, we applied a different dependency measurement based on information theory by calculating the information-gain/reduction of entropy when incorporating biological knowledge to expression data. The measurement describes the increase of dependencies between TF and their target genes observed by acquiring more information. These conditional entropy calculations provided similar results as the correlation analysis, e.g. the increase of information-gain with few cofactors or with conditional information, and the decrease of information-gain with fast mRNA decay (Supplementary Table S1).

In this section we observed stronger correlation in the TF–target gene relationship with multi-source data, especially when context-specific information is incorporated into the analysis, which would benefit network modeling and reconstruction by effectively reducing the unobserved, different layers of regulation. There are other sources of information that can be incorporated. For example, Hansen et al. [36] considered the effect of nucleosome positioning on the gene expression and showed better prediction accuracy of gene regulators by integrating these genomic information. However it is unclear to what extent such information is useful in the reconstruction of regulatory networks—although nucleosomes affect a large region of the genome, they may not specifically control the binding of TFs [37]. More recently, the post-translational modifications of TFs, another level of regulation, has attracted much attention. Hansen et al. [38] collated a small experimentally curated Post Translational Modifier (PTM) database and tried to incorporate information on post-translational modifications. Nevertheless, when we included the PTM data, the correlation between the expression level of the post-translational modifiers and the target gene of the corresponding TFs did not significantly increase. Although the data set is too small to draw any conclusions, we believe, based on the current knowledge, that the modifiers were usually kinases that are regulated to other kinases or phosphotases at the protein level which leaves few clues to their expression levels. As researchers continue to incorporate different combinations of data-types for reverse engineering of gene networks, it is critical to deliberate whether or not, and to what extent, the data being integrated have specific biological information that is beneficial for identifying the relationship or regulatory model to be investigated.

ESTIMATION OF THE TFs’ ACTIVITY

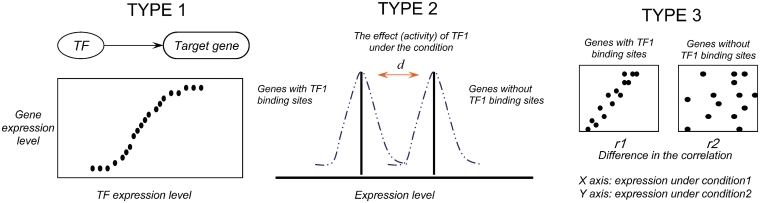
Besides the TF–target gene association, learning transcriptional regulation from expression data relies on a second assumption, that is, the mRNA measurements in the microarray data are predictive of the activity of the actual regulatory molecules. As in the aforementioned correlation analysis, one simply uses the expression level of a TF as the identifier for its activity, which we defined as Type-1 estimation (Figure 2). Since many TFs are largely reported as being regulated by post-transcriptional modifications, simply equating mRNA level and protein activity has been criticized [21]. Therefore, a different type of estimation has been suggested to represent the activity of a TF, which is based on the behavior of its target genes, which we call ‘Type-2’ estimation (Figure 2). Instead of the mRNA level, Type-2 model uses the expression level of the target genes to represent the TF activity.

Figure 2:

Schematic representations of different models to estimate activity of TFs. Type-1 models rely on the expression level of the TFs. Type-2 models compare the genes with the TF binding site (target genes) and genes without the binding site (background) and use the differences between expression of the target genes and the background genes to represent the activity of the TF. Type-3 models assume that target genes’ expression is better correlated if the TF is activated, and use the target gene correlation to represent the activation of the TF.

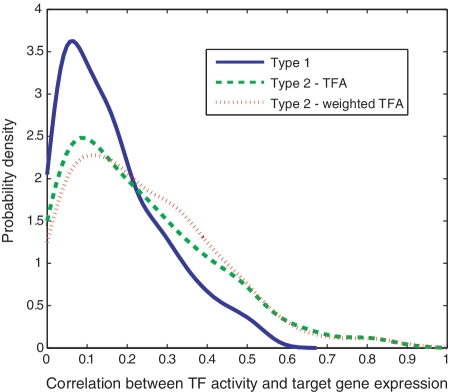
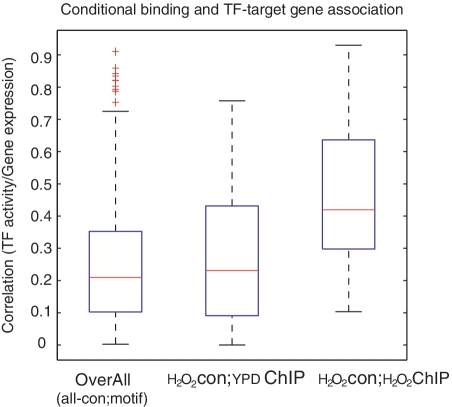
We apply the Type-2 estimation on the yeast expression data. We use the difference in expression between a TF's target genes and non-target genes as its activity level for a given condition. We then compare the 1-to-1 TF–gene correlations with the results obtained using the Type-1 estimation. All of the 1-to-1 pairs used in model assessment are excluded in the development of the Type-2 model, to ensure that the information used to estimate TF activity and the information for calculating the TF–gene correlations are mutually independent. As shown in Table 2 and Figure 3, there is a significant increase in the average correlation coefficient when using the Type-2 estimation (example of TF–gene pairs in Supplementary Figure S3). Genes with fewer TF binding sites on their promoters have less uncertainty of their regulatory mechanism; these genes thereby may contribute more to approximating the activity of its regulators. The TF activity inferred from target genes can then be weighted by ‘1/n’ where n is the total number of TFs that are able to control a particular gene. Such a weighted summation version of Type-2 model provides better correlation for some genes (Figure 3) although the average correlation does not increase significantly (correlation coefficient 0.24 as compared with 0.23 for the un-weighted Type 2). The weighting reduces the contribution of genes with many different cis-modules on their promoters; presumably they are subjected to combinatorial regulatory effects. Figure 4 shows that by applying the Type-2 estimation and incorporating context-specific information one could reach an average TF–gene correlation coefficient >0.4.

Table 2:

Comparison of different measurements of TF activity, consider those genes with only one known TF that can bind to their promoters

1-to-1 (gene–its only known TF) pairs	TF–gene expressiona	TFA: TF activity–gene expressionb	Weighted TFA–gene expressionc
Avg. Spearman correlation (variance)	0.16 (0.02)	0.23 (0.03)	0.24 (0.03)

^aTF–gene expression: The TF activity is represented by its expression level (Type 1). ^bTFA: The TF activity is represented by the difference between the mean expression value of its target genes and the mean expression value of the (other) unrelated genes. All 1-to-1 pairs used in model assessment are excluded in developing the Type-2 model. ^cWeighted TFA: Genes with fewer TF binding sites on their promoters contribute more to approximating the TF activity. TFA is then weighted by ‘1/n’ where n is the total number of TFs that are able to control a particular gene.

Figure 3:

Distributions of the correlation achieved by three different TF activity measures, only ‘1-to-1’ cases are considered. Although the average correlation does not improve much in the Type-2 model, there are more genes whose expression level is better correlated with their TFs. Type 1: The TF activity is represented by its expression level; Type 2-TFA: The TF activity is represented by the difference between the mean expression value of its target genes and the mean expression value of the (other) unrelated genes; all 1-to-1 pairs used in model assessment are excluded in the development of the Type-2 model. Type-2-weighted TFA: Genes with fewer TF binding sites on their promoters contribute more to approximating the TF activity, TFA is then weighted by ‘1/n’ where n is the total number of TFs that are able to control a particular gene. The probability density is calculated using the kernel smoothing density estimate function (ksdensity) in Matlab, with a Guassian kernel. A histogram describing the frequencies of gene expression in different categorical bins shows a less continuous but similar distribution.

Figure 4:

Box plots of the average correlation between activity of the TFs and the expression of the target genes. A total of 596 1-to-1 TF–target gene pairs are considered. The activity of TFs is estimated by Type-2 model, all 1-to-1 pairs used in model assessment are excluded in the development of the Type-2 model. CHIP-chip data are not available for every TF, so only 99 pairs have binding information and 20 of them are conditional-specific binding. The overall gene–TF (box on the left) describes the average correlation of all 596 pairs under all conditions. To estimate the activity of the TFs, target genes of each TF are determined by yeast transcriptional regulatory network, where the TF–gene interactions are based on motif/binding site. Under the H₂O₂ condition, the box in the middle (YDP-CHIP) uses the unconditional binding (CHIP-chip results under normal condition) to determine both the activity of TFs and the average correlation of the gene–TF pairs that actually bind, and the box on the right uses conditional binding CHIP-chip data. The average TF–gene correlation increased significantly when conditional binding data were available (box on the right, P < 0.05 compared with the box on the left).

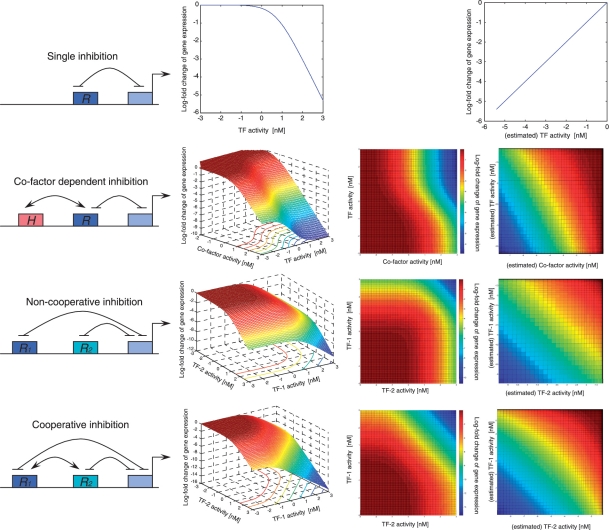
The Type-2 method provides better estimation of TF activity without assuming the mRNA level represents the TF activity, however the better estimation of TF activity by the Type-2 model does not benefit the network reconstruction. To demonstrate this, we simulate a kinetic model d[Gene]/dt = (1+[TF activity]/K)⁻¹ (with arbitrarily defined effective kinetic constant K) for the transcriptional regulation of a single TF on its target gene, shown in the first case of Figure 5 (and Supplementary Figure S5 for the other cases). If the mRNA level were to represent the TF activity, which is usually not the case in many real biological systems, the mechanism by which a gene is regulated by a single TF would be uncovered using the Type-1 model (in the single inhibition case, as shown in the responsive curve of the middle plot in Figure 5). The Type-2 model may have better estimation of the TF activity but it is difficult to identify the regulatory mechanisms even in the single TF cases (in the single inhibition case, as shown in the response-curve on the right in Figure 5). In our analysis of the assessment of the Type-2 model, the information used in the model and the information used in the assessment of the model do not overlap. However given that this method is used by the community, it is important to note the Type-2 model when applied to infer relationships other than 1-to-1 relationships could overlap. Even though the TF activity is estimated from the overall effect of its potential targets, while a TF–gene relationship is established by testing whether or not the change in the TF activity can explain the change in expression of a particular gene, care nonetheless must be taken in using the Type-2 model to ensure that the information used to estimate the TF activity and to infer the TF–gene relationship are mutually independent. In addition, the Type-2 estimation assumes the influence of a TF on all its targets is equal, which does not account for the variability in binding and the function of a TF on its various targets due to adapters and co-factors [39]. Another limitation is that the Type-2 and Type-1 estimations need a priori knowledge about the transcriptional regulatory network, and such information is less often available in other model organisms. Thus, the Type-3 estimation, which assumes co-expression genes are co-regulated by the same TF, has been widely implemented to predict cis-motifs or to estimate the activity of cis-motifs by co-expression analysis (Figure 2).

Figure 5:

Simulations of the combinatorial transcription regulation (more examples are in Supplementary Figure S5). The interactions between TFs and between TF and the initiation of the target gene transcription are modeled with kinetic equations [42]. Response curves are simulated and plotted. For regulation by a single transcription factor, the X-axis is the activity of the TF and the Y-axis is the expression level of the target gene. Both 3D plots and 2D color maps are provided for the combinatorial regulation of two TFs, where the X- and Y-axis represent the activity of the two TFs and the Z-axis/color represents the expression level of the target gene. Microarray data do not directly provide activities of TFs, so the rightmost plots for each regulatory scenario instead uses estimated activity (Type-2 model) of the TFs, showing what profiles that could be obtained from microarray analysis. Numerical simulation of the kinetic model is performed using the Runge Kutta method in Matlab and the plots are generated with a customized code in Matlab.

With the Type-3 model, one could use clustering analysis first to identify the co-expressed genes, followed by enrichment analysis on the promoters of genes within a same cluster, to identify functional cis elements. We applied bi-clustering analysis on the yeast data set, and compare the results with the known transcriptional regulatory network. The activation of many TFs could not be identified with this analysis (Supplementary Figure S4). One reason is that if a TF has only a few targets, such co-expression cluster would be too small to be recognizable from the background noise (e.g. with a 0.19 average correlation for any given gene pair) in the data. Thus, Type 3 is less effective in estimating the activity, but nonetheless it is the method of choice if one wants to discover functional cis-elements. However, the assumption that co-expression indicates co-regulation is imperfect. Since co-expression may occur in situations other than TF–gene associations [7], such as in a signaling cascade. Thus, one should be cognizant of the assumptions that lead to the results, and further experiments are required to validate the cis-elements uncovered in this manner.

TOWARDS A DETAILED MECHANISM OF TRANSCRIPTIONAL REGULATION

Most of the aforementioned analysis focus on the ‘1-to-1’ pairs whereby the genes are likely regulated by only one TF, nevertheless there are many more genes (>80%) with multiple promoter regions that bind different TFs, thereby complicating the regulatory mechanism through TF cooperation. Models of TF binding and gene transcription have been extensively studied experimentally on prokaryotes with small-scale quantitative measurements of numerous perturbations on a subset of the regulatory circuits [40]. A detailed thermodynamic binding and control model has been established [41] and successfully applied to many, highly specific regulatory models in Escherichia coli and Drosophila [13, 42], providing a quantitative framework for studying the combinatorial regulation of TFs. Researchers are now attempting to generalize the dynamic model to automate the procedure of learning the detailed mechanisms from high-throughput data. Questions have arisen on whether or not the information in large-scale expression data is adequate to support these detailed mechanistic models. Current knowledge of combinatorial regulation in real eukaryotic cell systems is very limited, thus making it difficult to assess predictions of combinatorial regulation. Rather, in our analysis we use simulation data to show scenarios of combinatorial control and to determine the extent of the mechanism that can be revealed by analyzing expression data alone. To address the combinatorial control of two TFs we explore the mechanistic cooperation schemes and acquire kinetic equations from previous studies of theoretical modeling (thermodynamic binding model) [41], then generate putative gene expression profiles. The simulations show different expression profiles depending on the cooperation mechanisms (Figure 5 and Supplementary Figure S5). These profiles demonstrate that the differences in the different cooperation schemes are so subtle that only a few specific perturbations/conditions would capture the distinctive features, as depicted by the narrow transition (regions with significant changes of colors representing target gene expression in the 2D response surface color-maps) in the response surface curves in Figure 5. We show in the right-most column of Figure 5 the profiles that could be obtained from microarray data using indirect measure of the TF activity, in which we apply the Type-2 model to estimate the TF activity based on gene expression profiles, assuming that there is enough number of perturbations to cover all possible combinations of the two TFs’ activity level. The results demonstrated that without independent measurements of the actual activity of the TFs, the subtle features in the different cooperation schemes are not sufficiently distinctive (Figure 5), which will be further exacerbated by the noise and limited array data measurements. Therefore, the ‘top-down’ approaches have serious limitations in their ability to learn these detailed mechanisms. Unlike the ‘bottom-up’ quantitative experiments performed for small systems, the high-throughput data involve many layers of interconnected regulations making it difficult to segregate the contributions of each TF on the expression of its target genes. As observed by Gitter et al. [43] in the systematic knock-out experiments [44], the overwhelming majority of its target genes would not be affected even if a TF is knocked out.

CONCLUSION AND PERSPECTIVE

The accumulation of high throughput expression data and current developments of data mining techniques enabled the global analysis of the transcriptome, and enhanced the system-wide studies on the transcriptional regulation on a genome scale. Although a growing body of literature within the community has presented and discussed the computational approaches on the inference of regulatory networks from expression data, these rarely highlight the limited information content in the expression data with respect to the biological factors, as discussed in this review. From a biological perspective, we evaluated the fundamental assumptions implicit in associating TF–target gene expression levels and estimating TFs’ activity, and further explored cooperative models. We confirm ‘quantitatively’ that the detailed transcription mechanism is overly-complex for expression data alone to reveal. A possible solution is to simplify the cooperation models to preclude over-fitting, e.g. apply logic functions [45]. Furthermore, a proper incorporation of multi-source biological knowledge, especially context-specific information, is beneficial for network reconstruction. One recent example is [46] which integrated a series of systematic measurements of the temporal binding profiles, and successfully reconstructed a complex dynamic circuit that coordinates a rapid stress response in yeast. Besides context-dependent information, a dynamic analysis of the microarray data could better identify regulators of a gene. For example, in the yeast data set, we separated the data into a ‘conditional set’ (containing microarray experiments under H₂O₂ treatment), and control set (all other microarray experiments), and calculated the differences in correlation for the 1-to-1 TF–target gene pairs in these two sets. A total of 99 pairs have conditional ChIP-chip data, 20 of which show conditional binding under H₂O₂ treatment. The average differences of correlation computed for the 99 pairs is 0.0 (variance 0.16), while the average differences of correlation for the 20 conditional binding pairs is 0.16 (variance 0.16). Despite the limited number of genes tested, the results suggest that context-dependent analysis (differences of correlation) of the microarray data is able to capture the conditional regulation of the genes. A similar idea was recently implemented in the Modulator Inference by Network Dynamics (MINDy) MINDy algorithm (http://wiki.c2b2.columbia.edu/workbench/index.php/MINDy), which uses gene expression data to determine a putative modulator gene that regulates the activity of a given set of TFs, by measuring changes in correlation (the algorithm uses mutual information) between TFs and their target genes.

Another important regulatory mechanism that controls gene expression, especially in mammalian systems, is the microRNA. Sequences analysis predicted >30% of human genes may be microRNA targets [47]. Micro RNAs bind to complementary sites in the 3'-UTR of target genes to control mRNA degradation, and we have shown that the RNA degradation rate could affect TF–gene association (Figure 1B). Therefore in future it is imperative to incorporate microRNA information, including microRNA expression and microRNA regulatory network, to improve the network reconstruction, e.g. integrating the effects of microRNAs on transcriptional processes into the learning model to better estimate the TF activity [48].

Overall we suggest a conscientious inspection of both the biological assumptions underlying the mathematical formulations of the models, and the information contents in the data in support of the statistical learning processes, which we believe is needed in order to achieve learning results with lasting biological significance. This would help accelerate fruitful capitalization and continuation of computation in promoting our understanding of the biological regulatory system.

SUPPLEMENTARY DATA

Supplementary data are available online at http://bib.oxfordjournals.org/.

Key Points.

• Weak correlation in gene expression exists between the TFs and their targets, thus making it difficult to uncover transcriptional regulation from gene expression data.

• The relationship between the expression of TFs and their target genes is affected by many factors, such as mRNA decay and protein co-factors. Combinatorial regulation also contributes to the reduced correlation between the TFs and their target genes. There is no single factor that is sufficient to explain all the variation in TF–target gene correlation for different genes under different circumstances.

• Measurements of the relative amount of mRNA level in the microarray data could be used to predict the activity of the TFs, under different assumptions. But one should be cognizant of the assumptions that lead to the results to be aware of the limitations in estimating TF activity from gene expression data.

• We confirm ‘quantitatively’ that the detailed transcription mechanism is overly-complex for expression data alone to reveal. A proper incorporation of multi-source biological knowledge, especially context-specific information, is beneficial for network reconstruction by effectively reducing the unobserved, different layers of regulation.

• Overall we suggest a conscientious inspection of both the biological assumptions underlying the mathematical formulations of the models, and the information contents in the data in support of the statistical learning processes, which we believe is needed in order to achieve learning results with lasting biological significance.

FUNDING

This research was supported in part by the NIH (R01GM079688-01 and R21RR024439), the NSF (CBET 0941055, CBET 1049127 and DBI 0701709) and the MSU Foundation.

Biographies

Ming Wu is a graduate student in the Department of Computer Science and Engineering at Michigan State University. He obtained his B.S. and M.S. in Biology from Tsinghua University. His research interests include genomic data mining, network reconstruction and dynamic modeling of gene network.

Christina Chan is a Professor of Chemical Engineering and Materials Science at Michigan State University, with secondary appointments in Biochemistry and Molecular Biology, and Computer Science and Engineering. A goal of her group is to elucidate the signaling pathways and networks altered in cancer and Alzheimer’s disease.