How Predictable are “Spontaneous Decisions” and “Hidden Intentions”? Comparing Classification Results Based on Previous Responses with Multivariate Pattern Analysis of fMRI BOLD Signals

Abstract

In two replication studies we examined response bias and dependencies in voluntary decisions. We trained a linear classifier to predict “spontaneous decisions” and in the second study “hidden intentions” from responses in preceding trials and achieved comparable prediction accuracies as reported for multivariate pattern classification based on voxel activities in frontopolar cortex. We discuss implications of our findings and suggest ways to improve classification analyses of fMRI BOLD signals that may help to reduce effects of response dependencies between trials.

The prospect of decoding brain activity to predict spontaneous or free decisions captivates not only the neuroscientific community (Haggard, 2008) but increasingly inspires researchers in other disciplines (Mobbs et al., 2007; Heisenberg, 2009).

The purpose of this paper is to draw attention to possible confounds and improved data analyses when decoding neural correlates to predict behavior. We focus on a specific task and set of results but we believe that the problem of sequential dependencies is pervasive and needs to be considered carefully when applying machine learning algorithms to predict behavior from brain imaging data.

In two replication studies we illustrate how individual response bias and response dependencies between trials may affect the prediction accuracy of classification analyses. Although our behavioral results are not sufficient to dismiss the original findings based on fMRI BOLD signals they highlight potential shortcomings and suggest alternative ways to analyze the data.

In recent studies Soon et al. (2008) and Bode et al. (2011) used a self-paced free or voluntary decision task to study unconscious determinants preceding “spontaneous” motor decisions. In both studies subjects spontaneously pressed a left or right response button with their corresponding index finger in a series of trials. Brain activity was measured by fMRI BOLD signals and the pattern of voxel activity before (and after) the decision was used to predict binary motor responses. Soon et al. (2008) applied a linear multivariate pattern classifier and searchlight technique to localize patterns of predictive voxel activities (Haxby et al., 2001) and achieved 60% prediction accuracy in a localized region of frontopolar cortex (FPC). Bode et al. (2011), using a high-resolution scan of the prefrontal cortex, reported 57% prediction accuracy for the same task. The authors conclude that patterns of voxel activities in FPC constitute the neural correlate of unconscious determinants preceding spontaneous decisions.

In both studies the activation patterns in FPC occurred up to 10–12 s before participants reported their conscious decisions. If validated this finding would dramatically extend the timeline of pre-SMA/SMA (Lau et al., 2004; Leuthold et al., 2004) as well as results on readiness potentials for voluntary acts (Libet et al., 1983; see however Trevena and Miller, 2010) with far-reaching implications (Mobbs et al., 2007; Heisenberg, 2009).

Soon et al. (2008) and Bode et al. (2011) made considerable attempts to control carry-over effects from one trial to the next and selected a subset of trials with balanced left and right responses to eliminate response bias. We argue that despite these precautions response dependencies in combination with response bias in the raw data may have introduced spurious correlations between patterns of voxel activities and decisions.

Naïve participants have difficulties to generate random sequences and sequential dependencies across trials are commonly observed in binary decisions (Lages and Treisman, 1998; Lages, 1999, 2002) as well as random response tasks (Bakan, 1960; Treisman and Faulkner, 1987). In some tasks, these dependencies are not just simple carry-over effects from one trial to the next but reflect stimulus and response dependencies (Lages and Treisman, 1998) as well as contextual information processing (Lages and Treisman, 2010; Treisman and Lages, 2010), often straddling across several trials and long inter-trial-intervals (Lages and Paul, 2006). These dependencies may indicate involvement of memory and possibly executive control (Luce, 1986), especially in self-ordered tasks where generation of a response requires monitoring previously executed responses (Christoff and Gabrieli, 2000).

In order to address the issue of sequential dependencies in connection with response bias we conducted two behavioral replication studies and performed several analyses on individual behavioral data, the results of which are summarized below.

Study 1: Spontaneous Motor Decisions

In this replication study we investigated response bias and response dependency of binary decisions in a spontaneous motor task. We closely replicated the study by Soon et al. (2008) in terms of stimuli, task, and instructions (Soon et al., 2008) but without monitoring fMRI brain activity since we are mainly interested in behavioral characteristics.

Methods

Subjects were instructed to relax while fixating on the center of a screen where a stream of random letters was presented in 500 ms intervals. At some point, when participants felt the urge to do so, they immediately pressed one of two buttons with their left or right index finger. Simultaneously, they were asked to remember the letter that appeared on the screen at the time when they believed their decision to press the button was made. Shortly afterward, the letters from three preceding trials and an asterisk were presented on screen randomly arranged in a two-by-two matrix. The participants were asked to select the remembered letter in order to report the approximate time point when their decision was formed. If the participant chose the asterisk it indicated that the remembered letter was not among the three preceding intervals and the voluntary decision occurred more than 1.5 s ago. Subjects were asked to avoid any form of preplanning for choice of movement or time of execution.

Participants

All participants (N = 20, age 17–25, 14 female) were students at Glasgow University. They were naïve as to the aim of the study, right-handed, and with normal or corrected-to-normal visual acuity. The study was conducted according to the Declaration of Helsinki ethics guidelines. Informed written consent was obtained from each participant before the study.

Results

Following Soon et al. (2008) we computed for each participant the frequency of a left or right response. If we assume that the spontaneous decision task produces independent responses then the process can be modeled by a binomial distribution where probability for a left and right response may vary from participant to participant.

$$P\left[t\left(x\right)=s|\theta \right]=\left({\mathrm{\hspace{0.17em}}}_s^n\right){\theta }^s{\left(1-\theta \right)}^{n-s}$$

The observed data t(x) is simply the sum of s left (right) responses, n is the total number of responses, and θ is a parameter that reflects the unknown probability of responding Left (Right) with þeta ∈ [0,1]. The hypothesis of a balanced response corresponds to a response rate of þeta = 0.5. Rather than trying to affirm this null hypothesis we can test whether the observed number of left (right) responses deviates significantly from the null hypothesis by computing the corresponding p-value (two-sided).

$$p_{\left(\text{two - sided}\right)}=\sum _{x_i=0}^{n-s}t\left(x_i\right)+\sum _{x_i=s}^{n}t\left(x_i\right)$$

We found that response frequencies of 4 out of 20 participants (2 out of 20 if adjusted for multiple tests according to Sidak–Dunn) significantly deviated from a binomial distribution with equal probabilities (p < 0.05, two-sided). Soon et al. (2008) excluded 24 out of 36 participants who exceeded a response criterion that is equivalent to a binomial test with p < 0.11 (two-sided). Bode et al. (2011) applied a similar response criterion but did not document selection of participants. They reported exclusion of a single participant from their sample of N = 12 due to relatively unbalanced decisions and long trial durations; responses from the remaining 11 subjects were included in their analyses. In the present study 8 out of 20 participants did not meet Soon et al.’s response criterion (for details see Table A1 in Appendix).

Selection of participants is a thorny issue. While the intention may have been to select participants who made truly spontaneous and therefore independent decisions they selected participants who generated approximately balanced responses. This assumption is fallible since subjects’ response probabilities are unlikely to be perfectly balanced and the null hypothesis of þeta = 0.5 can be difficult to affirm.

Excluding 2/3 of the subjects reduces generalizability of results and imposing the assumption of no response bias on the remaining subjects seems inappropriate because these participants can still have true response probabilities θ that are systematically different from 0.5.

To give an example of how a moderate response bias may affect prediction accuracy of a trained classifier, consider a participant who generates 12 left and 20 right responses in 32 trials. Although this satisfies the response criterion mentioned above, a classifier trained on this data is susceptible to response bias. If the classifier learns to match the individual response bias prediction accuracy may exceed the chance level of 50%. (If, for example, the classifier trivially predicts the more frequent response then this strategy leads to 62.5% rather than 50% correct predictions in our example.)

To alleviate the problem of response bias Soon et al. (2008) and Bode et al. (2011) not only selected among participants but also designated equal numbers of left (L) and right (R) responses from the experimental trials before entering the data into their classification analysis. It is unclear how they sampled trials but even if they selected trials randomly the voxel activities before each decision are drawn from an experiment with unbalanced L and R responses. As a consequence the problem does not dissipate with trial selection. After selecting an equal number of L and R responses from the original data set this subsample still has an unbalanced number of L and R responses in the preceding trials so that the distribution of all possible pairs of successive responses in trial t − 1 and trial t (LL, LR, RR, RL) is not uniform. Since there are more Right responses in the original data set we are more likely to sample more RR “stay” trials and less LR “switch” trials as well as more RL “switch” trials compared to LL “stay” trials. The exact transition probabilities for these events depend on the individual response pattern. Switching and staying between successive responses creates a confounding variable that may introduce spurious correlations between voxel activities from previous responses and the predicted responses. This confound may be picked up when training a linear support vector machine (SVM) classifier to predict current responses from voxel activities in previous trials.

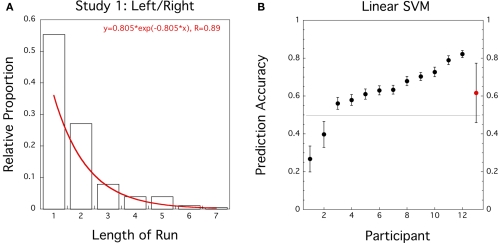
Similar to Soon et al. (2008) and Bode et al. (2011) we first computed the length and frequency of the same consecutive responses (L and R runs) for each participant and fitted the pooled and averaged data by an exponential function. However, here we fitted the pooled data with the (single-parameter) exponential probability distribution function

$$f\left(x\right)=\lambda e^{-\lambda x},\text{for}x\ge 0$$

(see Figure 1A). We found reasonable agreement with the exponential distribution (R = 0.89) as an approximation of the geometric distribution. The estimated parameter λ = −0.805 is equivalent to a response rate of þeta = 1 − e^−λ = 0.553, slightly elevated from þeta = 0.5.

Figure 1.

Study 1 (N = 12): Left/Right motor decision task. (A) Histogram for proportion of length of response runs pooled across participants. Superimposed in Red is the best fitting exponential distribution function. (B) Prediction accuracies of linear SVM trained on preceding and current responses for individual data sets (black circles, error bars = ± 1 SD bootstrapped) and group average (red circle, error bar = ± 1 SD).

Although the exponential distribution suggests an independent and memoryless process such a goodness-of-fit does not qualify as evidence for independence and stationarity in the individual data. Averaging or pooling of data across blocks and participants can hide systematic trends and patterns in individual data.

To avoid these sampling issues we applied the Wald–Wolfowitz or Runs test (MatLab, MathWorks Inc.) to each individual sequence of 32 responses. This basic non-parametric test is based on the number of runs above and below the median and does not rely on the assumption that binary responses have equal probabilities (Kvam and Vidakovic, 2007). Our results indicate that 3 out of the 12 selected participants in our replication study show statistically significant (p < 0.05) departures from stationarity (2 out of 12 adjusted for multiple tests). Similarly, approximating the binomial by a normal distribution with unknown parameters (Lilliefors, 1967), the Lilliefors test detected 4 out of 20 (4 out of the selected 12) statistically significant departures from normality in our replication study (3 out of 20 and 1 out of 12 adjusted for multiple tests). These violations of stationarity and normality point to response dependencies between trials in at least some of the participants (for details see Table A1 in Appendix).

Classification analysis

In analogy to Soon et al. (2008) and Bode et al. (2011) we also performed a multivariate pattern classification. To assess how much discriminative information is contained in the pattern of previous responses rather than voxel activities, we included up to two preceding responses to predict the following response within an individual data set. Thereto, we entered the largest balanced set of left/right response trials and the unbalanced responses from the preceding trials into the analysis and assigned every 9 out of 10 responses to a training data set. This set was used to train a linear SVM classifier (MatLab, MathWorks Inc.). The classifier estimated a decision boundary separating the two classes (Jäkel et al., 2007). The learned decision boundary was applied to classify the remaining sets and to establish a predictive accuracy. This was repeated 10 times, each time using a different sample of learning and test sets, resulting in a 10-fold cross validation. The whole procedure was bootstrapped a 100 times to obtain a mean prediction accuracy and a measure of variability for each individual data set (see Figure 1B; Table A1 in Appendix).

One participant (Subject 11) had to be excluded from the classification analysis because responses were too unbalanced to train the classifier. For most other participants the classifier performed better when it received only one rather than two preceding responses to predict the subsequent response and therefore we report only classification results based on a single preceding response.

If we select N = 12 participants according to the response criterion employed by Soon et al. (2008) prediction accuracy for a response based on its preceding response reaches 61.6% which is significantly higher than 50% (t(11) = 2.6, CI = [0.52–0.72], p = 0.013). If we include all participants except Subject 11 then average prediction accuracy based on the preceding response was reduced to 55.4%(t(18) = 1.3, CI = [0.47–0.64], p = 0.105).

Our classification analysis illustrates that a machine learning algorithm (linear SVM) can perform better than chance when predicting a response from its preceding response. The algorithm simply learns to discriminate between switch and stay trials. In our replication study this leads to prediction accuracies that match the performance of a multivariate pattern classifier based on voxel activities in FPC (Soon et al., 2008; Bode et al., 2011).

Discussion

Although our behavioral results show that response bias and response dependency in individual data give rise to the same prediction accuracy as a multivariate pattern classifier based on voxel activities derived from fMRI measurements, our behavioral results are not sufficient to dismiss the original findings.

In particular, the temporal emergence of prediction accuracy in voxel patterns as observed in Soon et al. (2008) and Bode et al. (2011) seems to contradict the occurrence of sequential or carry-over effects from one trial to the next because prediction accuracy from voxel activity in FPC starts at zero, increases within a time window of up to 10–12 s before the decision and returns to zero shortly after the decision.

It should be noted however that their results are based on non-significant changes of voxel activity in FPC averaged across trials and participants. We do not know how reliably the predictive pattern emerged in each of the participants and across trials. It is also noteworthy that the hemodynamic response function (HRF) in FPC, modeled by finite impulse response (FIR), peaked 3–7 s after the decision was made. Although the voxel activity above threshold did not discriminate between left and right responses, this activity in FPC must serve a purpose that is different from generating spontaneous decisions.

The FIR model for BOLD signals makes no assumption about the shape of the HRF. Soon et al. estimated 13 parameters at 2 s intervals and Bode et al. (2011) used 20 parameters at 1.5 s intervals for each of the approximately 5 by 5 by 5 = 125 voxels in a spherical cluster. The cluster moved around according to a modified searchlight technique to identify the most predictive region. Although a linear SVM with a fixed regularizer does not invite overfitting the unconstrained FIR model can assume unreasonable HRF shapes for individual voxels. If these voxels picked up residual activity related to the preceding trial, especially in trials where the ITI was sufficiently short, then this procedure carries the risk of overfitting. Activity in the left and right motor cortex, for example, showed prediction accuracies of up to 75% 4–6 s after a decision was reported (Soon et al., 2008).

It may be argued that at least some predictive accuracy should be maintained throughout ITIs if carry-over effects were present between trials. However, voxel activities were sampled at different ITIs due to the self-paced response task. It seems reasonable to assume that ITIs between “spontaneous” decisions are not uniformly distributed. Indeed the individual response times in our replication study were skewed toward shorter intervals, approximating a Poisson distribution that is typical for behavioral response times (Luce, 1986). When voxel activation is temporally aligned with a decision then this effectively creates a time window in which on average residual activation from a previous response is more likely to occur. As a consequence, and despite relatively long average trial durations, the FIR model parameters may pick up residual activation from the previous trial in a critical time window before the next decision (Rolls and Deco, 2011).

Although we would like to avoid a discussion of the difficult philosophical issues of “free will” and “consciousness,” the present task implies that participants monitor the timing of their own conscious decisions while generating “spontaneous” responses. The instruction to perform “spontaneous” decisions may be seen as a contradiction in terms because the executive goal that controls behavior in this task is to generate decisions without executive control (Jahanshahi et al., 2000; Frith, 2007). Participants may have simplified this task by maintaining (fluctuating) intentions to press the left or right button and by reporting a decision when they actually decided to press the button (Brass and Haggard, 2008; Krieghoff et al., 2009). This is not quite compatible with the instructions for the motor task but describes a very plausible response strategy nevertheless.

Study 2: Hidden Intentions

Interestingly, in an earlier study with N = 8 participants Haynes et al. (2007) investigated neural correlates of hidden intentions and reported an average decoding accuracy of 71% from voxel activities in anterior medial prefrontal cortex (MPFCa) and 61% in left lateral frontopolar cortex (LLFPC) before task execution.

We replicated this study in order to test whether response bias and dependency also match the prediction accuracies for delayed intentions. 12 participants (age 18–29, nine female) freely chose between addition and subtraction of two random numbers before performing the intended mental operation after a variable delay (see Haynes et al., 2007 for details). Again, we closely replicated the original study in terms of stimuli, task, and instructions but without monitoring fMRI BOLD signals.

Results

As in Study 1 we tested for response bias and 4 out of 12 participants significantly deviated from a binomial distribution with equal probabilities (p < 0.05, two-sided). Since Haynes et al. (2007) do not report response bias and selection of participants we included all participants in the subsequent analyses.

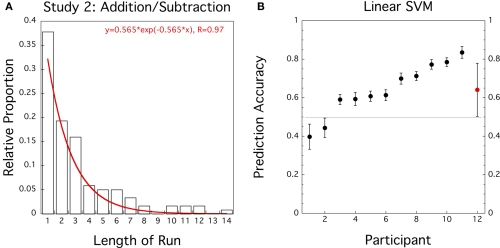
The exponential probability distribution with λ = −0.562 (equivalent to a response probability þeta = 0.430) fitted the pooled data of sequence lengths well (R = 0.97; see Figure 2A) but the Wald–Wolfowitz or Runs test on each individual sequence of 32 responses indicated that 5 out of 12 participants violated stationarity in the delayed addition/subtraction task (one participant when adjusted for multiple tests). Similarly, a Lilliefors test detected five significant violations of normality (three adjusted for multiple tests, see Table A2 in Appendix).

Figure 2.

Study 2 (N = 12): addition/subtraction in delayed intention task. (A) Histogram for proportion of length of response runs pooled across participants. Superimposed in Red is the best fitting exponential distribution function. (B) Prediction accuracies of linear SVM trained on preceding and current responses for individual data sets (black circles, error bars = ± 1 SD bootstrapped) and group average (red circle, error bar = ± 1 SD).

One participant (Subject 6) was excluded because responses were too unbalanced to train the linear SVM classifier. We then performed a classification analysis on selected trials with a balanced number of addition/subtraction responses using the preceding response as the only predictor. Averaged across N = 11 participants the prediction accuracy of the SVM classifier reached 64.1% which is significantly different from 50% (t(10) = 3.39, CI = [0.55–0.73], p = 0.0035). The classification results are summarized in Figure 2B and Table A2 in the Appendix.

Discussion

It has been suggested that the FPC is implicated in tasks requiring high-level executive control, especially in tasks that involve storing conscious intentions across a delay (Sakai and Passingham, 2003; Haynes et al., 2007), processing of internal states (Christoff and Gabrieli, 2000), modulation of episodic memory retrieval (LePage et al., 2000; Herron et al., 2004), prospective memory (Burgess et al., 2001), relational reasoning (Christoff et al., 2001; Kroger et al., 2002), the integration of cognitive processes (Ramnani and Owen, 2004), cognitive branching (Koechlin and Hyafil, 2007), as well as alternative action plans (Boorman et al., 2009). How much a participant can be consciously aware of these cognitive operations is open to discussion but they seem to relate to strategic planning and executive control rather than random generation of responses.

In an attempt to relate activity in the FPC to contextual changes in a decision task, Boorman et al. (2009) reported a study where subjects decided freely between a left and right option based on past outcomes but random reward magnitudes. In this study participants were informed that the reward magnitudes were randomly determined on each trial, so that it was not possible to track them across trials; however, participants were also told that reward probabilities depended on the recent outcome history and could therefore be tracked across trials, thus creating an effective context for directly comparing FPC activity on self-initiated (as opposed to externally cued) switch and stay trials. Increased effect size of relative unchosen probability/action peaked twice in FPC: shortly after the decision and a second time as late as 20 s after trial onset. Boorman et al. (2009) suggest that FPC tracks the relative advantage associated with the alternative course of action over trials and, as such, may play a role in switching behavior. Interestingly, in their analyses of BOLD signal changes the stay trials (LL, RR) differed significantly from the switch trials (LR, RL).

Following neuroscientific evidence (Boorman et al., 2009) and our behavioral results we recommend that multivariate pattern classification of voxel activities should be performed not only on trials with balanced responses but on balanced combinations of previous and current responses (e.g., LL, LR, RL, and RR trials) to reduce hidden effects of response dependencies. Similarly, it should be checked whether the parameters of an unconstrained FIR model describe a HRF that is anchored on the same baseline and shows no systematic differences between switch and stay trials. This will inform whether or not the FIR model parameters pick up residual activity related to previous responses, especially after shorter ITIs.

Conclusion

Applying machine learning in form of a multivariate pattern analysis (MVPA) of voxel activity in order to localize neural correlates of behavior brings about a range of issues and challenges that are beyond the scope of this paper (see for example Hanson and Halchenko, 2008; Kriegeskorte et al., 2009; Pereira et al., 2009; Anderson and Oates, 2010; Hanke et al., 2010).

In general, a selective analysis of voxel activity can be a powerful tool and perfectly justified when the results are statistically independent of the selection criterion under the null hypothesis. However, when applying machine learning in the form of MVPA the danger of “double dipping” (Kriegeskorte et al., 2009), that is the use of the same data for selection and selective analysis, increases with each stage of data processing (Pereira et al., 2009) and can result in inflated and invalid statistical inferences.

In a typical behavioral study, for example, it would be seen as questionable if the experimenter first rejected two-thirds of the participants according to an arbitrary response criterion, sampled trials to balance the number of responses from each category in each block, searched among a large number of multivariate predictors and reported the results of the classification analysis with the highest prediction accuracy.

In conclusion, it seems possible that the multivariate pattern classification in Soon et al. (2008) and Bode et al. (2011) was compromised by individual response bias in preceding responses and picked up neural correlates of the intention to switch or stay during a critical time window. The moderate prediction accuracies for multivariate classification analyses of fMRI BOLD signals and our behavioral results call for a more cautious interpretation of findings as well as improved classification analyses.

A fundamental question that may be put forward in the context of cognitive functioning is whether the highly interconnected FPC generates voluntary decisions independently of contextual information, like a homunculus or ghost in the machine. After all, the frontal cortex as part of the human cognitive system is highly integrated and geared toward strategic planning in a structured environment. In this sense it seems plausible that neural correlates of “hidden intentions” and “spontaneous decisions” merely reflect continuous processing of contextual information.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Appendix

Table A1.

Replication study 1: left/right key press in spontaneous motor decision task.

Subject	Resp. bias left/right	Bino. test p-value	No of Runs	Runs test p-value	Lilliefors p-value	SVM pred acc
[1]	21/11	0.1102	11	0.1194	0.0957	[0.5875]
2	16/16	1.0	17	1.0	0.1659	0.3973
3	13/19	0.3771	16	1.0	0.1116	0.2672
[4]	11/21	0.1102	15	1.0	0.0017**	[0.4970]
5	14/18	0.5966	26	0.0009***	0.4147	0.8218
6	15/17	0.8601	15	0.6009	0.0893	0.5607
[7]	22/10*	0.0501(*)	17	0.4906	>0.5	[0.4259]
8	20/12	0.2153	18	0.5647	>0.5	0.6295
[9]	10/22*	0.0501(*)	15	1.0	0.001***	[0.2845]
10	18/14	0.5966	21	0.1689	0.0936	0.6789
[11]	31/1***	0.0001***	3	1.0	>0.5	[NA]
12	19/13	0.3771	20	0.2516	0.4147	0.5790
13	20/12	0.2153	22	0.0280(*)	0.3476	0.7267
14	14/18	0.5966	21	0.1689	0.1659	0.6098
15	16/16	1.0	21	0.2056	0.1116	0.6330
[16]	4/28***	0.0001***	5	0.0739	0.0017***	[0.7513]
17	17/15	0.8601	22	0.0989	>0.5	0.7026
[18]	11/21	0.1102	16	0.9809	0.0893	[0.2985]
19	12/20	0.2153	7	0.00092***	0.001***	0.7891
[20]	11/21	0.1102	16	0.9809	0.0936	[0.2844]
Tot/Avg	4.25#	4 (2)	16.2	3 (2)	4 (4)	0.5539

Participant excluded according to Soon et al.’s (2008) response criterion (binomial test p < 0.11); ^#average deviation: Σ_i|x_i–n/2|/N for n = 32 and N = 20.

*p < 0.05, **p < 0.01, ***p < 0.001; (·) number of violations adjusted for multiple tests after Sidak–Dunn.

Table A2.

Replication study 2: addition/subtraction in hidden intention task.

Subject	Resp. bias add/sub	Bino. test p-value	No of Runs	Runs test p-value	Lilliefors p-value	SVM pred acc
1	11/21	0.1102	9	0.0184(*)	0.0112(**)	0.7725
2	14/18	0.5966	10	0.0215(*)	0.0271(*)	0.7124
3	11/21	0.1102	8	0.0057(**)	0.1153	0.6991
4	14/18	0.5966	9	0.0071(**)	0.001***	0.7847
5	21/11	0.1102	12	0.2405	0.001***	0.5932
6	2/30***	0.0001***	5	1.0	>0.5	N/A
7	17/15	0.8601	18	0.8438	0.3267	0.6074
8	20/12	0.2153	12	0.1799	0.0016**	0.5904
9	6/26***	0.0005***	4	0.0006***	0.4443	0.8351
10	18/14	0.5966	16	0.9285	0.2313	0.3972
11	9/23*	0.0201(*)	13	0.8488	0.4030	0.4434
12	9/23*	0.0201(*)	10	0.1273	>0.5	0.6131
Tot/Avg	5.33#	4 (2)	10.5	5 (1)	5 (3)	0.6408

*p < 0.05, **p < 0.01, ***p < 0.001; ^#average deviation: Σ_i|x_i–n/2|/N for n = 32 and N = 12. (·) Number of violations adjusted for multiple tests after Sidak–Dunn.