Monitoring late-onset toxicities in phase I trials using predicted risks

Abstract

Late-onset (LO) toxicities are a serious concern in many phase I trials. Since most dose-limiting toxicities occur soon after therapy begins, most dose-finding methods use a binary indicator of toxicity occurring within a short initial time period. If an agent causes LO toxicities, however, an undesirably large number of patients may be treated at toxic doses before any toxicities are observed. A method addressing this problem is the time-to-event continual reassessment method (TITE-CRM, Cheung and Chappell, 2000). We propose a Bayesian dose-finding method similar to the TITE-CRM in which doses are chosen using time-to-toxicity data. The new aspect of our method is a set of rules, based on predictive probabilities, that temporarily suspend accrual if the risk of toxicity at prospective doses for future patients is unacceptably high. If additional follow-up data reduce the predicted risk of toxicity to an acceptable level, then accrual is restarted, and this process may be repeated several times during the trial. A simulation study shows that the proposed method provides a greater degree of safety than the TITE-CRM, while still reliably choosing the preferred dose. This advantage increases with accrual rate, but the price of this additional safety is that the trial takes longer to complete on average.

1. INTRODUCTION

Phase I clinical trials focus on treatment-related adverse events so severe that they impose a practical limitation to the delivery of therapy. Such an event is called a dose-limiting toxicity (DLT) or simply “toxicity.” The primary scientific goal in a phase I trial is to determine the maximum tolerable dose (MTD), which is the highest dose with an acceptable risk of toxicity (cf. Storer, 1989; Babb and others, 1998). Because most DLTs occur soon after the start of therapy, most phase I methods are based on a binary variable indicating that a DLT has occurred within a time interval of fixed length, t^*, which we will call the assessment window.

The possibility of late-onset (LO) toxicities is an important concern in phase I trials. Basing dose finding on DLTs scored within a fixed window t^* is a practical compromise motivated by algorithms that choose doses sequentially for successive patients based on previous patients’ doses and outcomes. Conventional methods consider a patient to be fully evaluated if he/she experiences toxicity before t^* or is followed for this length of time without toxicity. A problem with such methods is that they may cause investigators to treat an undesirably large number of patients at toxic doses before LO toxicities are first observed. While a safer approach would be to use a very large t^* and wait for each patient's outcome before choosing the next patient's dose, in most settings this would produce an infeasibly long trial.

A method that deals with LO toxicities is the time-to-event continual reassessment method (TITE-CRM, Cheung and Chappell, 2000), which uses the time to toxicity, T, as the outcome, rather than a binary indicator. Denoting the cumulative distribution function (cdf) of T for dose d by F_T(t;d,θ) = Pr(T ≤ t|d,θ), where θ is the model parameter, the TITE-CRM relies on the fact that F_T(t;d,θ) = Pr(T ≤ t|d,θ,T ≤ t^*) Pr(T ≤ t^*|d,θ) for t ≤ t^*, approximates Pr(T ≤ t|d,θ,T ≤ t^*) by a weight function w(t,t^*) such as t / t^* or a sample-based estimator, and uses π_w(t,t^*,d) = w(t,t^*)Pr(T ≤ t^*|d,θ) as a weighted version of the usual probability in the CRM (O'Quigley and others, 1990). Indexing patients by i = 1, …, n and denoting the time to toxicity or right censoring for the ith patient by T_i^o, the resulting approximate likelihood is

(1.1)

where d_(i) is the dose for patient i. Using this approximation, the TITE-CRM applies the usual CRM criterion by choosing the dose with posterior mean E{π_w(T,t^*,d)|data} closest to a given target, π^*. Although the TITE-CRM does not increase the risk of LO toxicities when accrual is slow, if accrual is faster it has a higher risk of treating patients at unsafe doses. This is because, with faster accrual, new patients are more likely to be assigned to doses considered safe but later found to be unsafe if patients who have not been fully evaluated experience LO toxicities.

In this paper, we address the problem of LO toxicities by using predictive probabilities to quantify the risks that prospective doses for future patients will turn out to be excessively toxic. A fundamental difference between our method and existing methods is that we provide rules for suspending accrual if the predicted risk of toxicity (PRT) is unacceptably high. If additional follow-up data reduce the predicted risk at any prospective dose to an acceptable level, then accrual is restarted. We present a simulation study showing that, compared to the TITE-CRM, our proposed method provides an extra measure of safety when toxicities are likely to occur late in the assessment window, and this advantage increases with the patient accrual rate. The price of this improved safety is that, on average, the trial takes longer to complete.

The probability model is presented in Section 2. Priors and posteriors are developed in Section 3. Decision criteria and rules for trial conduct are presented in Section 4. In Section 5, we provide guidelines and an illustration of the method, and in Section 6, we present a computer simulation study, including comparison to the TITE-CRM. We conclude with a discussion in Section 7.

2. PROBABILITY MODEL

To describe the relationship between dose and time to toxicity, we use the sequential ordinal model of Albert and Chib (2001), which provides flexibility in modeling the hazard function while facilitating computation. We first fix a sequence of times 0 = t₀ < t₁ < ⋯ < t_{C −1} < t_C = ∞, where [t₀,t_{C − 1}] = [0,t^*] is the assessment window, and we define Y_i = j if patient i experiences toxicity in the jth interval, t_{j − 1} ≤ T_i < t_j, for j = 1, …, C. Thus, Y_i is a discretized ordinal representation of T_i, with Y_i = C if toxicity does not occur within the assessment window. Given the current time T_i^o to toxicity or right censoring, we denote the usual indicator δ_i = 1 if T_i^o < T_i and δ_i = 0 if T_i^o < T_i, and we also define Y_i^o = j if t_{j − 1} ≤ T_i^o < t_j so that Y_i^o is the current interval index for the ith patient. Denote the doses to be studied by d₁ < ⋯ < d_K. For j = 1, …, C − 1 and k = 1, …, K, denoting the standard normal cdf by Φ(·), we define the discrete-time hazard Φ(β_j,k) = Pr(Y₁ = j|Y₁ ≥ j,d_k) such that β_j,k is the effect of dose k on the hazard of toxicity in the jth interval. It can be shown that the probability of toxicity during the jth interval is Pr(Y₁ = j|d_k) = Φ(β_j,k) ∏_{h = 1}^{j − 1}{1 − Φ(β_h,k)}, and the probability of toxicity not occurring by Pr(Y₁ = j|d_k) =∏_{h = 1}^j{1 − Φ(β_h,k)} for j ≤ C − 1. Let k(i) be the index (level) of the dose administered to the ith patient. At any point in the trial, the discretized data from the current n patients take the form D_n = {(Y_i^o,k(i),δ_i), i = 1, …, n} and, denoting β = (β_1,1, …, β_{C − 1},K), the likelihood is

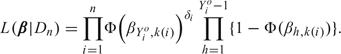(2.1)

Our procedure will be based on the conditional probabilities π(β,d_k,j) = Pr(Y ≤ C − 1|Y ≥ j,β,d_k) for j = 1, …, C − 1 and k = 1, …, K. This is motivated by the fact that π(β,d_k,Y_o) is the probability that a patient who has survived Y^o − 1 intervals without toxicity will experience toxicity by t^* = t_{C − 1} at dose d_k. Since Pr(Y ≥ 1) = 1, the unconditional probability of toxicity within the window [0,t^*] is π(β,d_k,1). We will abuse the notation slightly by writing this as π(β,d_k). It follows from the discrete-time hazard given above that π(β,d_kj)= 1 −∏_{h = 1}^{C = 1}{1 − Φ(β_h,k)}, and in particular π(β,d_k = 1 −∏_{h = 1}^{C = 1}{1 − Φ(β_h,k)}.

To facilitate computation of posterior quantities, following the general computational strategy of Albert and Chib (1993), we express the likelihood (2.1) using a latent variable formulation. For patient i, define the vector of latent variables Z_i = (Z_i,1,…,Z_i,Yi^o) if Y_i^o < C and Z_i = (Z_i,1,…,Z_{i,C − 1}) if Y_i^o = C, with Z_i,j∼N(β_j,k,1) if the ith patient received dose d_k. Denote the N(μ,σ²) density by φ(z;μ,σ²). Since Φ(μ) = ∫ _{− ∞}⁰φ(z;μ,1)dz, the likelihood (2.1) may be expressed equivalently in terms of the latent variables as

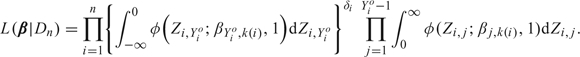(2.2)

Comparing the representation given in (2.2) to the original form given in (2.1) shows that one can think of Z_i,j as a continuous latent variable with mean equal to the patient's risk of toxicity during the jth interval given the dose administered. The general strategy is to reformulate (2.2) by including Z = (Z₁,…,Z_n) as arguments of the likelihood rather than integrating them out. The advantage of this “data-augmentation” technique, in terms of latent quantities, is that it provides full conditional distributions for the Gibbs sampling algorithm when computing the posterior. Without this device, computing posteriors would be very inefficient and time consuming. Thus, the augmented likelihood may be expressed as

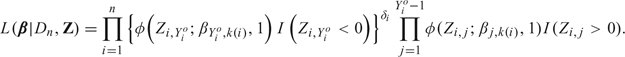(2.3)

Using this augmented likelihood, the latent variable vector Z is sampled repeatedly from its full conditional distribution as a step in the Albert–Chib Markov chain Monte Carlo (MCMC) framework.

3. PRIORS AND POSTERIORS

For each interval [t_{j − 1,}t_j),j = 2,…,C − 1, we assume a state-space model for the prior of β_j =(β_j,1, …, β_j,K), defined by the recursive relationship β_j,k|β_{j,k − 1}∼N(β_{j,k − 1},σ_β²) for k = 2,…,K, with β_j,1∼N(β_j,0,σ_β²) and β_j,0 fixed to ensure identifiability. Under this prior, E(β_j,k) = E{E(β_j,k|β_{j,k − 1})} = E(β_{j,k − 1}), which by recursion implies that E(β_j,k) = β_j,0 for all k = 1,…,K. However, var(β_j,k) = kσ_β² so that, with this prior, the uncertainty about the risk of toxicity increases with dose.

This model does not assume a parametric dose–toxicity function. Rather, β is used to characterize the probability of toxicity π(β,d_k,j) for j = 1,…,C − 1 and k = 1,…,K. Although the model can flexibly characterize the relationship between dose and toxicity, it does not guarantee that π(β,d_k,j) increases with d_k. Although a prior constraint on Φ(β_{j,k − 1}) < Φ(β_j,k) for all k and j would guarantee that the π(β,d_k,j) are monotone increasing in d_k, imposing such a constraint would lead to highly biased posterior estimates of the toxicity probabilities and would also lead to major computational difficulties. Thus, we take the alternative approach of applying the Bayesian isotonic regression method of Dunson and Neelon (2003). This method produces transformed versions of π(β,d_k,j) that are monotone increasing in d_k by taking weighted averages of subvectors of π(β,j) = (π(β,d₁,j), …, π(β,d_K,j)). In the present setting, this ensures that the probability of toxicity by t^* = t_{C − 1} is monotonically increasing in dose, while retaining the flexibility and tractability of the state-space model on β_k without introducing bias into posterior estimates for toxicity. We use the following 3-step algorithm to compute posteriors, applied each time a new patient is enrolled. These steps combine the Albert–Chib method for exploiting latent variables and the Dunson–Neelon method for enforcing monotonicity, in the context of our dose–toxicity model. Denote A₀ = ( − ∞,0],A₁ = (0,∞), and ${\stackrel{-}{A}}_{i,j}=A_{1-I(Y_i^o=j,{\delta }_i=1)}$. The following process is initialized using the prior mean of β; Steps 1 and 2 are iterated until convergence and then Step 3 is applied.

Step 1: Generation of the latent variables. Generate each Z_i,j independently from the full conditional which follows a truncated normal distribution $\phi (z;{\beta }_{j,k\left(i\right)},1\left)I\right(z\in {\stackrel{-}{A}}_{i,j})$.

Step 2: Generation of β. Denote

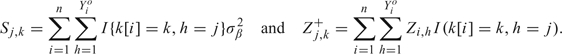Given Z and the current data, generate β from its full conditional distribution under which, for k = 1,…,K,β_j,k is normal with mean ${\stackrel{\sim }{\beta }}_{j,k}=\{{\sigma }_{\beta }^2{Z}_{j,k}^{+}+{\beta }_{j,k-1}+I(k<K){\beta }_{j,k+1}\}/\{1+I(k<K)+S_{j,k}{\sigma }_{\beta }^2\}$ and variance ${\stackrel{\sim }{\sigma }}_{\beta ,k}^2={\sigma }_{\beta }^2/\{1+I(k\hspace{0.17em}<\hspace{0.17em}K)+S_{j,k}{\sigma }_{\beta }^2\}$. This step exploits the fact that β has a closed-form full conditional distribution under the augmented likelihood, which is not the case using the original likelihood (2.1).

Step 3: Isotonic regression transformation. Apply the Dunson–Neelon algorithm to π(β,j) as follows. Denote the posterior variance–covariance matrix of π(β,j) by V_j and, for each pair of indices k₁,k₂∈{1,…,K} with k₁ ≤ k₂, denote the subvector π(β,j)_[k1:k2] =(π(β,d_k1,j), …, π(β,d_k2,j)). Let V_j,[k1:k2] be the submatrix of V_j of dimension (k₂ − k₁ + 1)×(k₂ − k₁ + 1) corresponding to π(β,j)_[k1:k2]. The vector obtained by the Dunson–Neelon Bayesian isotonic regression transformation is

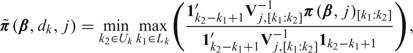where L_k = {s:s ≤ k},U_k = {s:s ≥ k}, and 1_k is the k-vector with all entries 1. This transformation ensures that 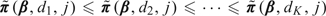for all j. Despite the apparent complexity of the above notation, this transformation is straightforward to apply in our setting and does not introduce any substantive computational difficulties. In summary, our approach is to first compute the posterior of π(β,j) without requiring monotonicity in dose (Steps 1 and 2) and then apply the Bayesian isotonic regression algorithm (Step 3) to obtain 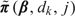, which increases in dose.

4. DECISION RULES

4.1. Specifying design parameters

Once a formal definition of what constitutes a DLT has been established, the physicians should be asked to choose t^* as the smallest value that includes possible LO toxicities based on their clinical judgment. For example, if one course of treatment lasts 6 weeks but there is substantial concern about DLTs occurring up to 12 weeks from the start of treatment, then t^* should be set equal to 12 weeks. Given this, they should then choose the corresponding target π^* for the posterior mean of Pr(T ≤ t^*|d,θ).

The decision rules for our method rely on 2 different types of Bayesian criteria, the posterior probabilities 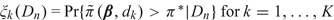, and predictive probabilities based on approximate values of the ξ_k‘s that involve both D_n and future outcomes. To characterize the level of risk associated with each dose, we partition the unit interval into 3 subintervals determined by the probability cutoffs $0<\underset{-}{\xi }<\stackrel{-}{\xi }\hspace{0.17em}<\hspace{0.17em}1$.

DEFINITION Given data D_n, the probability of toxicity at dose d_k is “negligible” if ${\xi }_k(D_n)<\underset{-}{\xi }$, “acceptable” if $\underset{-}{\xi }\le {\xi }_k(D_n)\le \stackrel{-}{\xi }$, and “excessive” if ${\xi }_k(D_n)\hspace{0.17em}>\hspace{0.17em}\stackrel{-}{\xi }$.

Reasonable values for these cutoffs are $0.05\le \underset{-}{\xi }\le 0.30$ and $0.70\le \stackrel{-}{\xi }\le 0.95$, with the particular values chosen to reflect how aggressively or conservatively the physicians wish the algorithm to behave. This decision should be guided by preliminary computer simulations, with $\underset{-}{\xi }$ and $\stackrel{-}{\xi }$ adjusted to obtain a design with desirable properties. In Section 6, below, we will illustrate how one may conduct such a sensitivity analysis in $(\underset{-}{\xi },\stackrel{-}{\xi })$.

4.2. Criteria for suspending accrual

Our goal is to construct a method that protects patient safety by controlling accrual without sacrificing the dose-finding method's reliability. To help motivate how we will address this problem, we first describe the following crude method. When a new patient arrives and a dose must be chosen, one may perform a deterministic look ahead (DLA) by assuming that, of the patients treated but not yet fully evaluated, either (i) all will have toxicity by t^* or (ii) none will have toxicity by t^*. If the next assigned dose is the same under both these extreme assumptions, then the next patient is accrued and treated at that dose. Otherwise, accrual is suspended (Thall and others, 1999). The problem with the DLA algorithm is that it does not account for the follow-up times of patients who have not been fully evaluated. For example, if t^* = 100 days and 2 patients have been followed without toxicity for 10 days and 90 days, respectively, the DLA algorithm treats them identically.

To address this problem, we define criteria for choosing doses and deciding whether to suspend accrual based on the “PRT”. Our approach may be considered as an extension of the DLA that utilizes predicted outcomes of patients treated but not yet fully evaluated, thus accounting for the times they have gone without toxicity. Let d_k denote the most recently assigned (current) dose. The basic idea is to use predictive probabilities of either negligible or excessive toxicity at the current dose to decide whether to treat the next cohort of patients at d_k, treat them at d_{k + 1}, or suspend accrual until subsequent follow-up data lead to a decision to either assign a dose or stop the trial.

Let p_k(a_k,b_k) be the beta(a_k,b_k) random variable defined to have the same mean and variance as 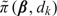under the current posterior. Specifically, 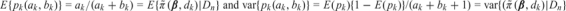. Thus, p_k(a_k,b_k) is a tractable approximation to . Let m_k be the number of patients treated at d_k who have not been fully evaluated, indexed by i₁,…,i_mk. For each r = 1,…,m_k, the available outcome data are δ_ir = 0 and the follow-up time T_ir^o without toxicity. We define the indicator W_ir = I(Y_ir ≤ C − 1) that patient i_r will eventually have toxicity within his/her assessment window. Thus, W_k = (W_i1,…,W_imk) is a vector of future observations, and S(W_k) = W_i1 + ⋯ + W_imk is the number of patients among the m_k not yet fully evaluated who will have toxicity by t^*. Let p_k(W_k,m_k,a_k,b_k) denote the probability following a beta(a_k + S(W_k),b_k + m_k − S(W_k)) distribution. This is an approximation of 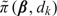that is obtained by updating a beta(a_k,b_k) prior with the future toxicity indicators for all patients treated at d_k. The PRT criteria are defined as follows:

(4.1)

and

(4.2)

where the sums in (4.1) and (4.2) are over the 2^m_k possible realizations of W_k. Thus, PN_k(D_n) and PE_k(D_n) are approximate predictive probabilities that d_k has negligible or excessive toxicity, respectively, and PA_k(D_n) = 1 − PN_k(D_n) − PE_k(D_n) is the predictive probability that d_k has acceptable toxicity. The PRT criteria will be used during the trial as a basis for deciding whether to suspend accrual or choose a dose for the next cohort. Computing the indicators in the sums in (4.1) and (4.2) is straightforward since they are determined by beta probabilities. Denoting the marginal posterior of β by f(β|D_n), since 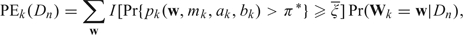, the predictive probabilities in the sums in (4.1) and (4.2) may be expressed as

(4.3)

which are computed as a by-product of the MCMC algorithm described earlier.

4.3. Rules for trial conduct

The following rules will be used to decide whether or not to suspend accrual and, if accrual is not suspended, determine an appropriate dose for the next cohort of patients. These rules will be applied after the last patient of the current cohort has been enrolled. If the rules indicate that accrual should not be suspended, the investigators should enroll the next cohort of patients and treat them at the dose indicated by the rules. If the rules indicate accrual should be suspended, the investigators should reapply these rules each time a new patient arrives at the clinic or a patient previously not allowed to enroll due to suspended accrual is reconsidered for enrollment. A patient previously not allowed to enroll may be reconsidered whenever the current trial data are updated, which occurs when a toxicity is observed or a currently enrolled patient advances from one interval to the next. From a practical perspective, the investigators may wish to define a maximum waiting time after which a patient would receive an alternative treatment. Reapplication of these rules may result in continued suspension or reopening of accrual. If accrual is reopened, then a new cohort of patients will be enrolled and the rules will be applied again after the last patient of this new cohort has entered the trial.

Index the current dose by k, let n_k be the total number of patients who have received that dose, and recall that m_k is the total number of patients out of the n_k who have not been fully evaluated. Now, define ${\stackrel{\sim }{\text{PN}}}_k(D_n)$ and ${\stackrel{\sim }{\text{PE}}}_k(D_n)$ such that

That is, ${\stackrel{\sim }{\text{PN}}}_k(D_n)=1$ if all n_k patients have been fully evaluated, and ${\stackrel{\sim }{\text{PN}}}_k(D_n)={\text{PN}}_k(D_n)$ otherwise. Similarly, ${\stackrel{\sim }{\text{PE}}}_k(D_n)=0$ if all n_k patients have been fully evaluated, and ${\stackrel{\sim }{\text{PE}}}_k(D_n)={\text{PE}}_k(D_n)$ otherwise. Recall that the current dose d_k has negligible toxicity if ${\xi }_k(D_n)<\underset{-}{\xi }$ , and it is excessively toxic if ${\xi }_k(D_n)\hspace{0.17em}>\hspace{0.17em}\stackrel{-}{\xi }$. The trial is conducted as follows:

• 1) The first cohort of patients are treated at a starting dose chosen by the physicians.

• 2) No untried dose may be skipped when escalating.

• 3) At any point in the trial, if ${\xi }_1(D_n)\hspace{0.17em}>\hspace{0.17em}\stackrel{-}{\xi }$, then stop the trial and conclude that none of the doses are acceptably safe.

• 4) If ${\xi }_k(D_n)>\stackrel{-}{\xi }$ and k > 1, then de-escalate to the highest dose k^′ < k such that ${\xi }_{k^{\prime }}(D_n)\le \stackrel{-}{\xi }$.

• 5) For lower probability cutoff ϵ, if $\underset{-}{\xi }\le {\xi }_k(D_n)\le \stackrel{-}{\xi }$ and

  • 5.1) ${\stackrel{\sim }{\text{PE}}}_k(D_n)\le ϵ$, then treat next cohort at d_k;
  • 5.2) ${\stackrel{\sim }{\text{PE}}}_k(D_n)\hspace{0.17em}>\hspace{0.17em}ϵ$, then suspend accrual.
• 6) If ${\xi }_k(D_n)\hspace{0.17em}<\hspace{0.17em}\underset{-}{\xi }$ and

  • 6.1) k = K or ${\xi }_{k+1}(D_n)\hspace{0.17em}>\hspace{0.17em}\stackrel{-}{\xi }$, then apply rules (5.1) or (5.2);
  • 6.2) $k\hspace{0.17em}<\hspace{0.17em}K,{\stackrel{\sim }{\text{PN}}}_k(D_n)\ge 1-ϵ$, and ${\stackrel{\sim }{\text{PE}}}_{k+1}(D_n)\le ϵ$, then treat next cohort at d_{k + 1};
  • 6.3) k < K, ${\stackrel{\sim }{\text{PN}}}_k(D_n)\ge 1-ϵ$, and ${\stackrel{\sim }{\text{PE}}}_{k+1}(D_n)\hspace{0.17em}>\hspace{0.17em}ϵ$, then suspend accrual;
  • 6.4) for k < K and ${\stackrel{\sim }{\text{PN}}}_k(D_n)\hspace{0.17em}<\hspace{0.17em}1-ϵ$, then suspend accrual.

• 7) At the end of the trial, among set of acceptable doses $\{j:{\xi }_j(D_{N_{\text{max}}})\le \stackrel{-}{\xi },j=1,\dots ,K\}$, select the dose minimizing .

Rules (5) and (6) utilize the PRT criteria when the risk of toxicity at the current dose based on the current data is either acceptable or negligible. These rules exploit the fact that predictive probabilities provide information about the risk of future toxicities that cannot be obtained from posterior probabilities alone. In a large sample evaluation of the method's asymptotic “dose-selection” properties, we relax rules (3) and (6.1) because these rules impose a constraint on the number of patients being exposed to unsafe doses, thus potentially preventing sample sizes at these doses from becoming arbitrarily large. Similar to our assumptions, published studies of the asymptotic properties of the CRM and the TITE-CRM do not include early stopping rules (Shen and O'Quigley, 1996; Cheung and Chappell, 2000), even though when used in a clinical trial setting early stopping is appropriate. Similarly, evaluations of the asymptotic properties of an algorithmic competitor to the CRM (the up-and-down design) also assume no early stopping rules (Gezmu and Flournoy, 2006), although, in practice, rules similar to (3) and (6.1) are typically used. Appendix A of the supplementary material available at Biostatistics online (http://www.biostatistics.oxfordjournals.org) provides consistency results and explains their practical relationship to the method's decision rules.

Computer programs for implementation of the method and running simulations, respectively, can be obtained at the MD Anderson software download site http://biostatistics.mdanderson.org/ SoftwareDownload/, under the name PRT.

5. GUIDELINES AND ILLUSTRATION

5.1. Guidelines

Because our method is complex, we provide the following guidelines. Initially, the model and design parameters must be established in collaboration with the physicians. These include the definition of toxicity, anticipated accrual rate, number of discrete-time intervals, C, length of the assessment window t^*, target toxicity probability π^*, maximum sample size N, and decision cutoffs $\underset{-}{\xi },\stackrel{-}{\xi }$, and ϵ. The choice of t^* and C should be guided by practical considerations including the particular disease, agent, and how often patients are evaluated. The target toxicity rate π^* should be chosen to correspond to the event T ≤ t^*. Because C = 1 reduces toxicity to a binary outcome while each interval requires K additional parameters, we recommend 4 ≤ C ≤ 10. Although π^* = 0.20 − − 0.30 are commonly used with the CRM or TITE-CRM, targets as high as 0.50 or as low as 0.10 may be appropriate. A rule of thumb is to set N = 6K, although resource limitations must also be considered. The design's sensitivity to ($ϵ,\underset{-}{\xi },\stackrel{-}{\xi }$) is discussed in Section 6. We found that $ϵ=0.05,0.20\le \underset{-}{\xi }\le 0.30$, and $0.90\le \stackrel{-}{\xi }\le 0.95$ gave reasonable designs with good operating characteristics.

At trial initiation, the first cohort of patients who enter the trial are enrolled immediately upon arriving to the clinic. Subsequently, after the last patient of any cohort has been enrolled, one should perform the computations in Steps 1–3 given in Section 3 and follow the rules for trial conduct in Section 4.3. If trial conduct rule (3) has not stopped the trial, there are two general cases.

Case 1. All currently enrolled patients have been fully evaluated, that is, have either experienced toxicity before t^* or been followed until time t^* without toxicity. Based on {ξ_k(D_n),k = 1,…,K}, if toxicity at the current dose is negligible, acceptable, or excessive, then “escalate, stay, or de-escalate,” respectively.

Case 2. Some currently enrolled patients have not been fully evaluated, that is, have been followed for less than time t^* and have not had toxicity. Based on {ξ_k(D_n),k = 1,…,K} and $\{{\stackrel{\sim }{\text{PN}}}_k(D_n),{\stackrel{\sim }{\text{PE}}}_k(D_n),{\stackrel{\sim }{\text{PE}}}_{k+1}(D_n),k=1,\dots ,K\}$ “escalate, stay, de-escalate, or suspend accrual.”

5.2. Illustration

We illustrate our method with a clinical trial of an experimental radio-sensitizing agent given in combination with radiation to patients with brain cancer or metastases to the brain due to other cancers. A known severe adverse side effect of this treatment is LO neurotoxicity, including cognitive problems, dementia and neuropathy. Typically, patients receiving a radio-sensitizing agent which has not been studied previously in humans will be followed for at least 3 months to assess these LO toxicities.

To illustrate implementation of our method, we consider a case exploring 6 dose levels where doses 1–4 are safe but severe LO neurotoxicity occurs with this agent at dose levels 5 and 6, first appearing roughly 5–6 weeks from the start of therapy. A reasonable approach for the agent and disease described above would be to design a trial with start at dose level 2, using 3 patients per cohort, a maximum sample size of 36 patients, toxicity window t^* = 90 days, ${\pi }^{*}=0.30,ϵ=0.05,\underset{-}{\xi }=0.30$, and $\stackrel{-}{\xi }=0.90$. Assuming that patients arrive in approximately 6-day intervals (4 per month), an example of how such a phase I trial would proceed is illustrated by the event chart in Figure 1, which shows results for the first 18 patients. The event chart is complemented by Table 1, which provides numerical values of the quantities ${\xi }_k,{\stackrel{\sim }{\text{PN}}}_k(D_n),{\stackrel{\sim }{\text{PE}}}_k(D_n)$, and ${\stackrel{\sim }{\text{PE}}}_{k+1}(D_n)$ used in the decision rules provided in Section 4.3. Each of the interim times at which a decision is made based on one or more of these quantities is denoted by a vertical arrow on the horizontal axis of Figure 1. The numerical values of these interim decision times also are given in Table 1 along with the corresponding decision criteria values and the decisions made. For example, on day 192 when the current dose is $k=3,{\stackrel{\sim }{\text{PN}}}_3(D_n)=0.999$ which is larger than (1 − ϵ) = 0.95, and ${\stackrel{\sim }{\text{PE}}}_4(D_n)$ is set equal to 0 since there is no data at dose level 4. Therefore, according to rule (6.2), we escalate and treat the next cohort at dose 4. In this illustration, the PRT method would have suspended accrual for a total of 210 days but resulted in only 3 toxicities in 36 patients. Figure 1 illustrates the general property of the algorithm that, early in the trial, it tends to suspend accrual for several weeks after each cohort is accrued, although patients still are enrolled at a reasonable rate. Once data at higher doses have been obtained, thereafter accrual tends to remain open. If desired, the method can be modified to suspend accrual for shorter amounts of time. For example, if we set ϵ = 0.20, accrual suspension can be shortened early in the trial, but at the cost of an increased average number of toxicities. If the method had been implemented with ϵ = 1 (i.e. disallowing any accrual suspension), we would have observed at least 6 toxicities but never suspended accrual, similar to what the TITE-CRM would have done. Alternatively, if ϵ = 0 (i.e. suspend accrual until all patients in a cohort have been fully evaluated for toxicity, as would be the case with a conventional CRM method), we would have suspended accrual for 1080 days and seen 3 toxicities. We believe that our approach provides a reasonable compromise between these two extremes, with an average savings of 1 toxicity for every 70 days of accrual suspension when compared to the design with no accrual suspension and a total of 870 fewer suspended days when compared to the conventional design.

Fig. 1.

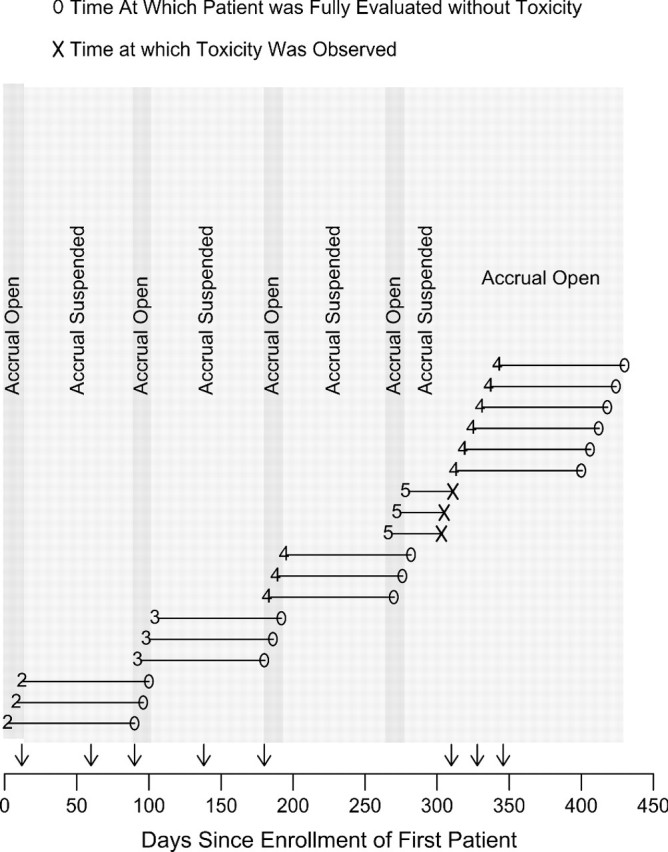
Illustration of the PRT method for a hypothetical phase I trial. We assume that patients arrive in 6-day intervals. The horizontal axis represents the days since first patient enrolled into the trial. Each horizontal line is the time course of a patient. Numerical values preceding each time course represent the dose administered to that patient. Open circles indicate times at which patients were fully evaluated without toxicity and x's indicate toxicity times. Darker gray denotes periods when accrual was open. Lighter gray denotes periods when accrual was suspended.

Table 1.

Each “time of interim decision” given here corresponds to a time denoted by “ ↓ ” on the horizontal (time) axis of Figure 1. For each time point, specific values of the quantities ξ_k, PN_k(D_n), PE_k(D_n), and PE_k+1(D_n) are given along with the rule in Section 4.3 triggered, and the decision to suspend accrual (SA), escalate to a higher dose (Esc), stay at the current dose (Stay), or de-escalate (D-Esc). Quantities not relevant to the decision made are denoted by NA

Current dose	Time of interim decision (days from 1st patient enrollment)
	18	67	90	138	192	312	324	342
	2	2	2	3	3	5	4	4
ξk	0.170	0.150	0.020	0.122	0.015	0.997	0.041	0.032
ξk+1	NA	NA	0.256	NA	0.260	NA	0.998	0.998
${\stackrel{\sim }{\text{PN}}}_k\left(D_n\right)$	0.620	0.66	0.988	0.740	0.999	NA	NA	NA
${\stackrel{\sim }{\text{PE}}}_k\left(D_n\right)$	NA	NA	NA	NA	NA	NA	0.001	0.001
${\stackrel{\sim }{\text{PE}}}_{k+1}\left(D_n\right)$	NA	NA	0.0	NA	0.0	NA	NA	NA
Rule triggered	6.4	6.4	6.2	6.4	6.2	4.0	6.1	6.1
Decision	SA	SA	Esc	SA	Esc	D-Esc	Stay	Stay

6. SIMULATIONS

6.1. Simulation design

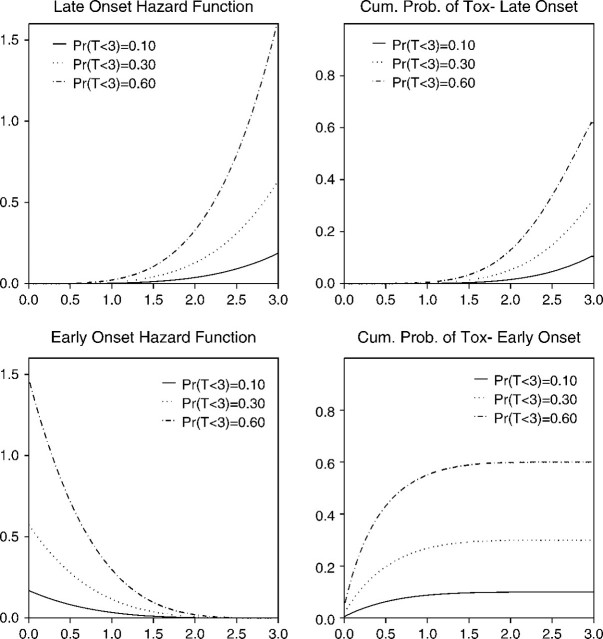
To assess the average behavior of the PRT method, we performed a simulation study under a wide variety of scenarios. We designed the study to address several key issues related to LO toxicities, including the shape of the hazard of toxicity within the window [0,t^*] and the accrual rate, as well as the usual considerations of how the true values of F_T(t^*|d_k) vary with d_k. Since addressing these issues requires a model sufficiently flexible to include a wide range of hazard functions, we simulated toxicity times from a piecewise exponential distribution, described in detail in Appendix B of the supplementary material available at Biostatistics online. In all scenarios studied, there were K = 6 doses, a maximum of N = 36 patients, the first patient was treated at the lowest dose level, and we assumed an accrual rate of 4 patients per month. Since patients are evaluated for toxicity on a weekly or biweekly basis in many oncology settings, for our simulations we chose biweekly assessments and assumed a t^* = 3-month assessment window, with target π^* = 0.30. Based on our preliminary simulations, we used $\underset{-}{\xi }=0.30,\stackrel{-}{\xi }=0.90$, and ϵ = 0.05. For the scenarios studied, Figure 2 illustrates the shapes of the hazard functions used in the simulations, in particular the distinction between late- and early-onset toxicities. Scenarios 1–5 have LO toxicities, while toxicities occur early in scenario 6. Since the state-space model is uniquely parameterized by β_0k and σ_β, for the prior we set β_0k = − 14 and σ_β = 28, which is a sufficiently large variance that the data dominate the method's decisions early in the trial.

Fig. 2.

Hazard functions and cumulative toxicity probabilities of the piecewise exponential distribution used in the simulations.

In additional preliminary simulations, we assessed the MCMC algorithm's convergence using standard diagnostics. Based on these results, we chose a burn-in of 1000 iterations with a chain of length 1000. Although the posterior sample size is constrained by the need to generate many replications in the simulations, one may use larger posterior sample sizes when used in a clinical trial setting. We simulated 1000 trials for each scenario. The computer program was written using Visual Fortran, and the simulations were carried out on an IBM compatible personal computer with dual 3.06-GHz math coprocessors and 1-GB memory. For each scenario, 1000 simulations were completed in approximately 1 h.

For the TITE-CRM, the model parameters are 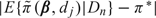, the probability of toxicity by time t^* at dose level k, where α has exponential prior with mean 1 and each ${\widehat{p}}_k$ is fixed with $0<{\widehat{p}}_1<{\widehat{p}}_2<\cdots <{\widehat{p}}_K<1$. The TITE-CRM is implemented with ${\pi }_w(T_i^o,t^{*},d_{\left(i\right)})=w(T_i^o,t^{*}){\widehat{p}}_{k\left(i\right)}^{\alpha }$, where {w(T_i^o,t^*),i = 1,…,n} are patient-specific weights calculated using the adaptive sample-based weighting scheme given in Display (3) of Cheung and Chappell (2000). For the simulations, we used $({\widehat{p}}_1,{\widehat{p}}_2,\dots ,{\widehat{p}}_6)=(0.05,0.10,0.20,0.30,0.5,0.70)$, with each successive dose chosen to minimize 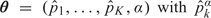. To ensure a fair comparison, we modified the TITE-CRM to stop early for excessive toxicity since our method does this. The additional rule is to terminate the trial if .

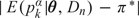6.2. Simulation results

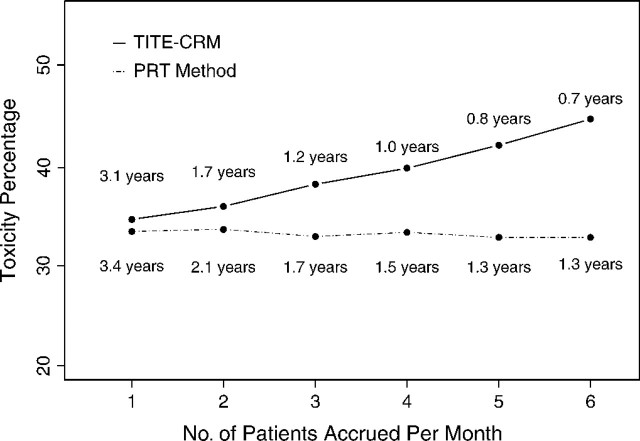
Table 2 summarizes the operating characteristics of the PRT method and TITE-CRM, including the selection probability, average number of patients treated, average number of toxicities at each dose, average total number of toxicities, and average overall trial duration. For all 6 scenarios, both methods had comparable correct selection probabilities. While both the average numbers of toxicities and the average numbers of patients treated at toxic doses were lower for the PRT method, the lengths of the trials using the PRT method were typically longer due to the accrual suspension rule. These simulations show that the PRT method has a trade-off between trial safety and trial duration. In addition, we varied the monthly accrual rate from 1 to 6 under scenario 1 (Figure 3) and showed that the percentage of toxicities allowed by the PRT method does not increase with accrual rate, while this is not the case for the TITE-CRM.

Table 2.

Operating characteristics of the PRT and TITE-CRM designs

	True Probability(T < 3 months|dk)
	d1	d2	d3	d4	d5	d6
Scenario 1 (late onset)	0.25	0.35	0.50	0.60	0.68	0.73	None	Total	Duration
PRT
% Selected	41	43	4	0	0	0	12	—	1.5
No. of patients	13.1	15.2	4.4	0.5	0.0	0.0		33.2	—
No. of toxicities	3.3	5.3	2.2	0.3	0.0	0.0		11.1	—
TITE-CRM
% Selected	46	42	8	0	0	0	4	—	1.0
No. of patients	10.6	11.0	7.8	4.0	1.4	0.6		35.5	—
No. of toxicities	2.6	3.8	3.9	2.4	1.0	0.5		14.1	—
Scenario 2 (late onset)	0.03	0.05	0.10	0.30	0.50	0.60
PRT
% Selected	0	1	26	64	9	0	0	—	1.8
No. of patients	3.5	4.8	9.8	12.5	4.6	0.8		36.0	—
No. of toxicities	0.1	0.3	1.0	3.7	2.2	0.5		7.8	—
TITE-CRM
% Selected	0	0	12	70	19	0	0	—	1.0
No. of patients	3.0	3.2	4.5	11.2	9.4	4.7		36.0	—
No. of toxicities	0.1	0.2	0.4	3.4	4.7	2.8		11.6	—
Scenario 3 (late onset)	0.50	0.60	0.68	0.73	0.76	0.78
PRT
% Selected	11	0	0	0	0	0	89	—	0.8
No. of patients	13.0	5.1	0.5	0.0	0.0	0.0		18.6	—
No. of toxicities	5.6	2.6	0.3	0.0	0.0	0.0		8.6	—
TITE-CRM
% Selected	18	0	0	0	0	0	82	—	0.7
No. of patients	15.1	5.6	3.7	1.8	0.7	0.3		27.2	—
No. of toxicities	5.7	3.1	2.2	1.2	0.5	0.2		12.8	—
Scenario 4 (late onset)	0.01	0.02	0.03	0.05	0.50	0.60
PRT
% Selected	0	0	0	67	32	1	0	—	1.8
No. of patients	3.1	3.5	4.5	13.1	9.4	2.4		36.0	—
No. of toxicities	0.0	0.1	0.1	0.6	4.7	1.5		7.0	—
TITE-CRM
% Selected	0	0	1	45	54	0	0	—	1.0
No. of patients	3.0	3.0	3.1	5.9	13.1	7.8		36.0	—
No. of toxicities	0.0	0.1	0.1	0.3	6.6	4.7		11.8	—
Scenario 5 (late onset)	0.05	0.06	0.08	0.11	0.19	0.34	None	Total	Duration
PRT
Selected	0	0	5	16	49	30	0	—	1.8
Patients	3.5	4.8	6.2	7.5	7.8	6.2		36.0	—
Toxicities	0.2	0.3	0.5	0.8	1.5	2.1		5.4	—
TITE-CRM
Selected	0	0	0	13	58	29	0	—	1.0
Patients	3.1	3.3	3.9	7.1	9.9	8.6		36.0	—
Toxicities	0.1	0.2	0.3	0.8	1.9	2.8		6.2	—
Scenario 6 (early onset)	0.250	0.350	0.500	0.600	0.680	0.730
PRT
% Selected	44	38	3	0	0	0	14	—	1.0
No. of patients	16.6	12.6	2.7	0.3	0.0			32.1	—
No. of toxicities	4.4	4.7	1.6	0.2	0.0			10.9	—
TITE-CRM
% Selected	40	41	6	1	0	0	12	—	0.9
No. of patients	17.0	11.4	3.8	0.6	0.0	0.0		32.8	—
No. of toxicities	4.2	4.0	1.9	0.3	0.0	0.0		10.5	—

Fig. 3.

Comparison of toxicities observed using the PRT method and TITE-CRM under scenario 1 with varying accrual rates. Each toxicity percentage is labeled by the mean trial duration in years.

Table 3 summarizes a sensitivity analysis in the parameters $\underset{-}{\xi }$ and $\stackrel{-}{\xi }$, under each of scenarios 1, 2, and 3. In this table, elasticity measures the total number of patients “spent” at doses with probability of toxicity more than 10% less than π^*. Based on these simulations, we see that setting $\underset{-}{\xi }=0.10$ results in relatively inelastic escalation while setting $\stackrel{-}{\xi }=0.85$ results in low correct selection probability and relatively high early stopping even when all doses are safe under scenario 1. These simulations suggest setting $\underset{-}{\xi }\in (0.20,0.30)$ and $\stackrel{-}{\xi }\in (0.90,0.95)$.

Table 3.

Sensitivity analyses of the PRT method to $\stackrel{-}{\xi }$ and ξ, under scenarios 1, 2, and 3 (S1, S2, S3). % Correct decision denotes the percentage of times the method selects a dose with true toxicity probability 0.25 ≤ Pr(T < 3) ≤ 0.35, within 0.05 of the target π^* = 0.30 under scenarios 1 and 2, and the early stopping probability under scenario 3. Elasticity denotes the number of patients assigned to doses with true toxicity probability ≤ 0.20

	ξ  = 0.10			ξ  = 0.20			ξ  = 0.30
	S1	S2	S3	S1	S2	S3	S1	S2	S3
$\stackrel{-}{\xi }=0.95$
% Correct decision	91.8	63.7	75.1	89.1	70.9	75.8	87.3	69.0	78.9
Total no. of toxicities	11.4	5.1	11.9	11.7	7.3	11.2	11.9	8.1	10.4
Elasticity	NA	25.4	NA	NA	19.2	NA	NA	16.6	NA
$\stackrel{-}{\xi }=0.90$
Correct decision	87.4	56.0	86.7	86.0	64.3	87.4	84.0	63.7	88.7
Total no. of toxicities	10.6	4.9	9.0	10.9	6.7	8.6	11.1	7.8	8.6
Elasticity	NA	27.0	NA	NA	21.0	NA	NA	18.5	NA
$\stackrel{-}{\xi }=0.85$
% Correct decision	82.2	52.6	91.6	81.8	60.3	94.2	81.8	59.0	89.6
Total no.  of toxicities	10.0	5.3	8.1	10.0	7.2	7.3	10.4	7.6	7.7
Elasticity	NA	26.2	NA	NA	19.8	NA	NA	19.0	NA

We also simulated various other scenarios which are presented in Appendix C of the supplementary material available at Biostatistics online. These simulations show the method is robust to nonconstant accrual rate, performs worse if instead of suspending accrual patients are assigned to lower doses, and performs worse if the isotonic regression transformation is not used.

6.3. Prior specification

Sensitivity to prior specification is an important concern. In most trials, the only prior information the principal investigator has available is that the probability of toxicity increases with dose, and it is reasonable to assume that the starting dose is relatively safe with low levels of toxicity. Apart from these considerations, physicians are generally most concerned that the method should reliably select the MTD or stop the trial early when all doses are too toxic. Before using the method, it is important to understand how changes in the hyperparameters β_0k and σ_β² can affect the performance of the method. Increasing β_0k results in higher E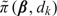 (for k = 1,…,K), the expected prior probabilities of toxicity at each dose, while higher values of σ_β² increase the uncertainty in the prior distributions of the 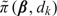‘s. Preliminary simulations (not provided) showed that setting σ_β² between 20 and 40 works well for our method.

Given these provisions, a first step is to calculate E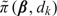. For our prior, these values were (0.03, 0.18, 0.33, 0.45, 0.53, 0.60) for doses 1 through 6, respectively. As with our parameter settings, we recommend that 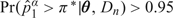be less than the target π^*. Model parameters may be calibrated by starting with an initial guess of the appropriate prior hyperparameters and then running a small number of simulations (50–100 repetitions) for scenarios in which the lowest dose is too toxic, or has toxicity close to the target, and also a case in which the target toxicity rate is achieved at a relatively high dose. These simulations allow one to assess the effect of the prior on the method's ability to stop appropriately when all doses are too toxic, not when the first dose is close to the target, and escalate appropriately without sticking too rigidly to doses that are not too toxic. In practice, it takes only a few iterations of this process to find a parameterization that works well. As a final step, a few parameter settings with reasonable operating characteristics should be presented to the principal investigators to allow them to choose a prior with which they are comfortable.

One also may carry out an analysis of the method's sensitivity to prior variability by extending the state-space model so that β_j,k|β_{j,k − 1}∼N(β_{j,k − 1},qσ_β²) for k = 2,…,K and 0 < q < 1. Since var(β_j,k) = ∑_{k = 1}^Kσ_β²q^{k − 1}, with this prior q may be used as a tuning parameter to adjust the rate at which the variability of the risk of toxicity increases with dose.

7. DISCUSSION

We have proposed a new method for controlling the risk of LO toxicities in a phase I clinical trial by using the PRT at prospective doses to decide whether to temporarily suspend accrual. Our main conclusions are that, if patient accrual is rapid and toxicities occur at the targeted rate in the toxicity evaluation window [0,t^*] but are likely to occur late in this interval, then, on average, (i) the PRT method gives a trial with fewer toxicities but a longer duration compared to the TITE-CRM, (ii) the percentage of toxicities allowed by the PRT method does not increase with accrual rate, while this is not the case for the TITE-CRM, and (iii) in some cases (scenarios 2 and 4 of our study), the TITE-CRM is much more likely than the PRT method to select a final dose having excessive toxicity probability. The additional safety provided by the PRT method compared to the TITE-CRM, in terms of percent reduction in number of toxicities and reduced probability of selecting a final dose that is excessively toxic, is greatest in the most dangerous cases, namely when the probability of toxicity increases sharply between dose levels, when toxicities occur late in the assessment interval, or when accrual is rapid. In the presence of LO toxicities, the lower toxicity rate of the PRT method is due to the fact that it treats fewer patients at excessively toxic doses, which may be attributed to the rules for delaying accrual based on predictive probabilities. In contrast, when toxicities occur early (scenario 5), the two methods perform nearly identically.

Our model and decision rules are complex. A less complex model or method, possibly under a frequentist approach, would be desirable, provided that it maintains the advantages of our method. Implementation of a frequentist version of our method, that is, with accrual suspension, stopping for excessive toxicity, and not escalating to excessively toxic doses, although theoretically possible, would pose certain challenges. One possible likelihood-based approach would employ a penalized time-to-event model to avoid singularities in estimation of model parameters, especially early in the trial before toxicities have been observed. Two possible models that might work in this context are a version of the TITE-CRM model in which the prior is treated as a penalty and a Cox model with Firth's penalty (Heinze and Schemper, 2001). For both models, dose finding could be based on maximum penalized likelihood estimation. In any case, estimation must be constrained to ensure that the probability of toxicity increases with dose. Moreover, the exact sampling distribution of the parameter estimates would be needed, possibly obtained using bootstrap methods, since asymptotic approximations would likely be inaccurate for use in decision making. A difficult challenge in developing such a method would be constructing reasonable frequentist rules for escalating, de-escalating, staying at the same dose, or suspending accrual.

There are some limitations to our method. For example, although in many trial settings toxicity is measured at discrete time points, there are other situations in which toxicity is evaluated continuously. Clearly, for such settings, using our method would be suboptimal due to loss of information. In this context, a model with nonconstant hazard such as a Weibull distribution may be better suited than our method. The main considerations in developing such a method would be model parameterization and prior calibration. Another limitation is that our method is not suited for choosing a best dose from a continuum since it was developed with the goal of selecting a best dose from a finite set of doses.

To address this problem, one could assume a model for the probability of toxicity as a smooth monotone function of dose and estimate dose using standard inverse dose–response methods. If LO toxicity is not a concern, a version of the TITE-CRM based on a logistic regression model, rather than the 1-parameter model given in (1.1), could be used for this purpose.

FUNDING

National Institutes of Health (CA-83932, CA-79466).