Fluid flows and forces in development: functions, features and biophysical principles

Abstract

Throughout morphogenesis, cells experience intracellular tensile and contractile forces on microscopic scales. Cells also experience extracellular forces, such as static forces mediated by the extracellular matrix and forces resulting from microscopic fluid flow. Although the biological ramifications of static forces have received much attention, little is known about the roles of fluid flows and forces during embryogenesis. Here, we focus on the microfluidic forces generated by cilia-driven fluid flow and heart-driven hemodynamics, as well as on the signaling pathways involved in flow sensing. We discuss recent studies that describe the functions and the biomechanical features of these fluid flows. These insights suggest that biological flow determines many aspects of cell behavior and identity through a specific set of physical stimuli and signaling pathways.

Introduction

Fluids (see Glossary, Box 1) provide the most fundamental way to transport chemical and biochemical elements in biology. Plants and animals contain a multitude of fluid-filled tubes that move products within the body. Even the most primitive single cells use fluids to facilitate feeding and intracellular transport, and to enhance chemical and biochemical reactions (Cartwright et al., 2009). The level of complexity of an organism usually increases with the complexity of the tubular networks within the body. In the embryo, formation of cavities and tubes is important because of the need to carry signaling molecules that organize the embryonic axes and sustain embryonic growth. As a matter of fact, biological flow and growth are so tightly intermingled that the separation of their function from each other constitutes an experimental challenge in itself.

Box 1. Glossary

Advection. Mechanism by which a substance is carried by fluid and transported at the fluid velocity.

Flow of finite inertia. Flow in which the momentum of fluid particles is non-negligible relative to viscous forces. When driving forces cease, motion continues at least transiently, such as in the cardiac pulse wave.

Fluid. A true fluid is, by definition, a material with no rigidity at all. When subjected to a shearing stress, no matter how small it is, a true fluid will flow and its shape will change continuously as long as the shearing stress is applied.

Newtonian fluids. Such fluids obey a linear relationship between shear stress and the rate of deformation. The constant proportionality corresponds to the viscosity, which, by definition in this case, does not vary with the shear rate. Water and gases are usually Newtonian fluids.

Non-Newtonian fluids. Fluids with a more-complex nonlinear relation between deformation rate and stress, depending on, for example, the flow rate (or shear stress) and generally its history. A weakly non-Newtonian fluid is blood; mucous can often be significantly non-Newtonian.

Peclet (Pe) number. In fluid mechanics, Pe quantifies the relative contribution of advection compared with diffusion. Pe=UL/D, with U and L being the characteristic velocity and length scales (as used in Re), and D the diffusion coefficient. Pe>>1 means that the advection dominates the particle transport. This number allows estimation of the potential for an advective mixing system, which increases with Pe (Stone et al., 2004).

Pulsatility. Blood flow is subject to periodic variations in velocity. Those velocities that are mainly due to the pumping activity of the heart, for example, cause the blood flow to oscillate between low and high rates.

Reynolds (Re) number. This dimensionless number characterizes the nature of a fluid flow and the relative contribution of inertia and viscous dissipation. In practice, flows with the same Reynolds number will display the same properties. For an object of typical length L moving at typical velocity U, in a fluid of dynamic viscosity μ and density ρ, the Reynolds number is Re=ULρ/μ. It also reads Re=UL/ν using the kinematic viscosity ν=μ/ρ. Driven flow involved in development that exhibits characteristic scales, L<100 μm and U<100 μm.s^–1, and taking the kinetic viscosity of water to be ν ≈ 10⁶ μm².s^–1 will lead to Re<10^–2. Generally, the fluid dynamics involved in most microscopic biological systems (Purcell, 1977) and in microfluidic devices (Stone et al., 2004) works at low Reynolds number.

Shear stress. A force that acts tangentially to a surface and causes deformations. When two rigid solids are moving on each other in opposite directions mediated by a force, a shear stress is generated.

Stokes flow (or creeping flow). A type of fluid flow in which viscous forces dominate the advective inertial forces. It occurs at a Reynolds number less than unity. Typically, these flows are slow, with small-length scale and high viscosities. Flow ceases immediately in absence of a driving force.

Biological flows are necessary for vertebrate organogenesis. Kidney morphogenesis (Serluca et al., 2002), inner ear and otolith formation (Colantonio et al., 2009), neuron migration (Sawamoto et al., 2006), cardiovascular development (Slough et al., 2008), hemotopoiesis (Pardanaud and Eichmann, 2009), and left-right (LR) symmetry breaking, which controls the asymmetric positioning of internal organs during development (Nonaka et al., 1998), are all mediated in one way or another by fluid-dependent mechanical stresses. Prominent biological flow-related diseases include ciliopathies (Hildebrandt et al., 2011) and cardiovascular diseases such as atherosclerosis (Hahn and Schwartz, 2009). Biological flows in various fluid-mechanical regimes also contribute to cell signaling. In the embryo, flow transports small signaling molecules and generates the frictional and tensile forces through recently discovered signaling pathways (Mammoto and Ingber, 2010). From chemical gradient formation to shear stress, the information carried by flows is complex and difficult to assess because flows usually operate within small time and space windows. Nonetheless, the physical properties of fluids are central to their function as they directly define the type of biological transport and the mechanical forces they produce. As such, consideration of biophysical principles in microfluidics offers opportunities for gaining insight into central features of vertebrate embryogenesis.

In recent years, key advances in the fields of developmental biology, imaging and biophysics have provided new opportunities for assessing the precise roles of flow during organogenesis and patterning. The goal of this review is to provide an overview of the developmental inputs of biological flows in different contexts, including the mechanisms by which flows are sensed by cells and their downstream effects, as well as the physical principles that dictate flow features and functions. We begin with the groundwork of flow mechanics. We then introduce the role of cilia-driven flows, which are viscosity-dominated flows, during LR patterning and inner ear development, and we discuss their role in establishing directional and mixing flows. We next discuss flows of finite inertia (see Glossary, Box 1), such as blood flow during cardiovascular development in vertebrates, emphasizing shear stress (see Glossary, Box 1) signaling in endothelial and hematopoietic cells. Throughout the review, we discuss the role of flow in diseases, as well as concepts in mechanobiology and imaging applied to understanding flow-dependent processes in the developing embryo.

Basic fluid mechanics: the governing equations

The fluid mechanical components of any biological system are unlike most chemical, biomolecular or structural components in that a specific, well-defined and often analytically tractable set of governing equations apply. Few, if any, modeling assumptions are required to craft these equations, and therefore there is a relatively high degree of confidence in what their solutions predict, although there are still certainly challenges in obtaining accurate solutions. What these equations represent are the basic laws of physics – conservation of mass, momentum and sometimes energy – applied to a generally small sample of fluid in a flow (Fig. 1A). They include the notions that a force, such as pressure or gravity, can accelerate fluid, that the viscosity of a fluid resists flow, and that fluid transports anything suspended and flowing within it (reviewed by Purcell, 1977). As a flow will generally be different at every point within it, these are differential equations; they are intricate and it is challenging even for experts to understand in detail the roles of different terms in all situations. However, their very existence offers a powerful research tool and, because they apply to flow anywhere, extensive techniques and tools have been developed for analyzing their results. The importance of flow in so many engineering systems has, in part, driven the development of these techniques, many of which can readily be applied in biological systems.

Fig. 1.

The equations that govern fluid flow. (A) The Navier–Stokes equations describe the motion of fluids and can be developed by considering the conservation laws (mass and momentum) applied to a general small fluid element (depicted here by a green square) subject to pressures (p, orange arrows) and shear stresses (τ, blue arrows), in this case those that have been generated by the movement of a cilium (red). What results is, in essence, a statement of Newton’s Law F=ma, but which includes the kinematic consideration necessary for it to apply to a moving and deforming fluid. A Newtonian fluid is one that has a linear relationship between the stress and the rate of strain (deformation) induced in the fluid. The viscosity μ is the proportionality constant. The Reynolds number (Re), which is a non-dimensional number that reflects the ratio of inertial forces and viscous forces in any flow, is the only parameter in these equations if the fluid is Newtonian, and is crucial for identifying the flow regime (i.e. whether it is dominated by viscous stresses or whether fluid inertia is also important). (B) Chart classifying the various types of flows encountered in vivo based on their average velocity and Re: between tissues (interstitial flows); in developing body plans (cilia-driven flows); and in vascular systems (vascular flows). The chart highlights the fact that biological flows generated in vivo vary in location and in velocity (see also Box 3, for more details on other in vivo flows). LR, left/right; CSF, cerebrospinal fluid.

In Newtonian fluids (see Glossary, Box 1), viscous resistance is linearly proportional to the rate of deformation of fluid elements, which provides a particularly simple description of the corresponding terms in the governing equations (Fig. 1A). This is essentially an exact description for water under physiological (and most engineering) conditions, and so it is not too surprising that it applies directly to many biological fluids. Large molecules and suspended cells, as in blood, can cause deviation from this Newtonian-linear behavior, but even in these cases the approximation has sufficient fidelity to describe many processes: small deviations from Newtonian behavior do not usually lead to fundamentally different flows. The flow equations for a Newtonian fluid are called the Navier–Stokes equations (Fig. 1A).

Extensive analysis has been accomplished for relative simple flow geometries and is reported in numerous fluid mechanics textbooks; in complex flows, when the geometry and conditions are such that analysis is no longer possible, software is widely available that can provide accurate numerical solutions. Studying simple geometries, especially those that can be solved exactly, has been invaluable for understanding how flow ‘works’; these exact solutions provide the basis for discussing flow more generally, as we do in this review. Complex geometries can be analyzed using computational fluid dynamics software, which is widely available, but a numerical flow solution is just one step in understanding its physical workings. In addition, care must be taken when using software because the implications of the approximations that go into the numerical solutions in the flow that is predicted cannot always be anticipated: it is easy to get the wrong answer if care is not taken. An easy way to anticipate the general character of a flow is by its Reynolds number (see Glossary, Box 1; Box 2), which indicates the relative importance of viscous versus inertia effects (Fig. 1B). We first consider some viscous-dominated flows.

Box 2. Flow types and Reynolds number

The Reynolds (Re) number characterizes the nature of a fluid flow and the relative contribution of inertia and viscous dissipation. Large Reynolds numbers, which correspond to larger geometries (L), higher velocities (U), higher densities (r) and smaller viscosities (μ), point to the importance of inertia. Human size is on the order of meters (L ≈ 1 m), we move at U ≈ 1 m/s in air (μ/ρ ≈ 10^–5 m²/s) or water (μ/ρ ≈ 10^–6 m²/s), and hence our flow experience is of high Reynolds numbers (Re=ρLU/μ>10⁵). High Reynolds number flows can be turbulent (Re>10⁴), which is a chaotic self-sustaining flow condition that is also governed by the Navier–Stokes equations. However, true turbulence is rare within biological systems. For example, the Reynolds numbers of an embryonic heart (U ≈ 5 × 10^–3m/second, L ≈ 50 μm and μ/ρ ≈ 5 × 10^–5 m²/second: thus, Re < 1) lead, at most, to unsteady laminar flows in which inertia plays a minor role.

Small Reynolds numbers tell us that viscous stresses dominate. Such viscous flows or ‘creeping’ flows are somewhat simpler than flows with finite inertia, but they are also often less intuitive because our personal experience is at high Reynolds numbers. If the driving force for such a flow (e.g. a cilium) suddenly ceases its action, then the induced flow also stops immediately owing to the viscous friction because there is insufficient inertia to maintain any appreciable motion. In the left-right organizer, flow speeds are U ≈ 10^–5 m/s, in L ≈ 50 μm region, leading to Re << 1. Although phenomenologically less intuitive, such viscosity-dominated flows are mathematically simpler because the nonlinear Navier–Stokes equations simplify to the linear Stokes equation. Functionally, this means that different solutions can be added together. Once the solution for a flow induced by the force on a point is found, such solutions are added together to solve the overall flow.

Flows dominated by viscous effects: cilia-driven flows

Cilia are organelles that protrude from nearly all vertebrate cells, and typically have lengths between 3 and 10 μm in growing tissues (Supatto and Vermot, 2011). In vertebrates, cilia are commonly thought to function as chemical and/or mechanical sensors. Importantly, the so-called motile cilia also move fluids, and, by doing so, they participate in controlling several key developmental processes, such as chemical gradient formation, biomineralization and tubulogenesis (Cartwright et al., 2009). Cilia-driven flows are generally slow (usually hundreds of microns per second, with a maximum near 2 mm per second (Mirzadeh et al., 2010) (Fig. 1B, see also Box 2). Motile cilia induce fluid motion primarily through stereotyped rotational (circular or helical) motion or by planar motion. On this scale, the slow flow renders inertia negligible relative to viscous effects (low Reynolds number, see Box 2). Thus, cilia flows are usually modeled by the simpler Stokes equation, which is linear (Fig. 1A). Alone, a cilium can generate a limited number of flow types; however, it is the combination of cilia, their beating pattern and their geometric environment that lead to more complex flows. Cilia-mediated flow speed will vary with distinct parameters, usually according to the beating frequency, the viscous resistance of the fluid and the number of cilia. In the following sections, we describe the hydrodynamics of such flows in the embryo.

Rotational flow and chaotic advection: theory and modeling

The ‘simplest’ flow a cilium will produce is rotational (or ‘circular’; Fig. 2A). If you consider a cilium spinning on an axis orthogonal to a cell membrane (Fig. 2B), the Stokes limit predicts that a time-averaged rotational flow will be generated around it (Fig. 2C). The flow produced is directly proportional to the force applied to the fluid by the cilium and, as a consequence, is symmetrical when averaged over one cycle. Away from the cilium and wall, the flow velocity will usually drop according to 1/r² (r being the distance from the cilium) (Cartwright et al., 2004; Vilfan and Julicher, 2006; Smith et al., 2007). Close to the cilium, proximity can cause the induced flow velocity and its concomitant advection (see Glossary, Box 1) to be faster than the Brownian wanderings that lead to diffusional transport. The thickness of this advection-dominated zone will increase with cilium amplitude and frequency. By the nature of Stokes flow (see Glossary, Box 1), when the cilium stops beating, the flow velocity stops in effect instantaneously. Importantly, if the cilium angle is not orthogonal to the cell membrane (Fig. 2B,C), additive effects, such as directional flow will be generated (see the following sections).

Fig. 2.

Types of cilia-driven flow. (A) Three types of cilia motion have been observed in vivo (black, from left to right): planar motion with asymmetric bending, helical rotation and circular rotation. The positions of the cilium at different time-points are depicted in different colors (blue, green and red). Gray arrows indicate the net flow in each case. (B) Cilia with an angle of tilt (θ) of 90° or 35° displaying circular motion. (C) Representation of the theoretical flow obtained with cilia displaying a circular motion with a tilt of 90° or a tilt of 35°. In the no tilt condition (θ=90°), a rotational flow (gray arrows) will be generated around the cilium and chaotic advections (blue arrows) will be seen close to the cilia. This orientation is good for mixing. When the cilium is tilted (θ=35°), the no-slip boundary condition results in fluid being propelled away from the boundary in the direction of cilia rotation (gray arrow). (D) Cilia flow in vivo follows the theoretical rules enunciated by modeling. Here, a tilted cilium (blue) shown in the left-right organizer of zebrafish generates a directional laminar flow (orange) several μm away from the tip, whereas chaotic advections (green) are recorded near the body of the cilium, as predicted by Stokes flow. Adapted, with permission, from Supatto et al. (Supatto et al., 2008).

Flow turbulence, which is so effective at mixing at higher Reynolds numbers, derives from the nonlinearities in the full flow equations and is therefore absent at the low Reynolds numbers of cilia flow. However, there is a functionally analogous mechanism that can promote mixing in Stokes flows called chaotic advection (Fig. 2C,D). One of the hallmarks of chaos is a strong dependence upon initial conditions – the well-known ‘butterfly effect’. For mixing, this has the important implication that where any fluid particle ends up after some time depends strongly upon where it started. Thus, particles, perhaps of one chemical species suspended in the fluid that start nearby each other (i.e. with nearly the same but still distinct initial conditions), can end up far apart, mixed with other fluid particles. This leads to a strong intermingling, which is tantamount to effective mixing.

Chaotic advection (Aref, 1984) around motile cilia can be predicted by simulations (Smith et al., 2007). The geometry and forcing of a flow – particularly its time-dependent character – are crucial factors in establishing whether there will be regions of chaotic advection in a flow. A cilium positioned orthogonally to the cell membrane will not be a good propeller of fluid but potentially yields a tremendous enhancement of mixing. Efficient fluid mixing by chaotic advection is used in microfluidics and has been observed directly for artificial motile cilia (Fahrni et al., 2009; Shields et al., 2010). Flows often have regions with only local regions of chaotic advection, and outside of these the sensitivity to initial conditions is diminished, leading to relatively deterministic flow and poor mixing.

Rotational flow and mixing in vivo: zebrafish otolithic biomineralization

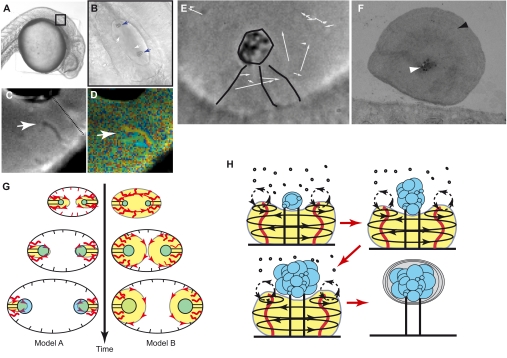
The function of cilia-driven mixing during embryogenesis has not been fully explored but is potentially an efficient mechanism for increasing molecular activity by advecting molecules into near proximity (Shields et al., 2010; Supatto and Vermot, 2011). Chaotic advection has been directly quantified in the left-right organizer of zebrafish near the beating cilium (Supatto et al., 2008) (Fig. 2D). Recent studies also suggest that active mixing near beating cilia could mediate the shaping of the otolith during zebrafish inner ear development (Wu et al., 2011). Otoliths are biomineralized composite crystals located on cilia bundles at the surface of epithelial cells (Fig. 3A-F). They provide cilia bundles with an inertia for response to acceleration, thereby enabling sensing of vibrations and gravity through hair cells (Fig. 3F). Otoliths form through a biomineralization process in which the aggregation of micrometer-sized mineral particles called spherules occurs on tether cilia. These tether cilia are located at the anterior and posterior poles of the inner ear, and develop into sensing hair cells (Tanimoto et al., 2011). Electron microscopy and time-lapse analyses show that otolith growth starts as a nucleus of spherules aggregating at the top of a tether cilium (Fig. 3F) (Pisam et al., 2002) and suggest that otoliths form through spherule self-aggregation (Clendenon et al., 2009). Spherules are secreted from the apical regions of the epithelial cells that line the inner ear cavity (Riley et al., 1997; Pisam et al., 2002) (Fig. 3B). At 40 hours post-fertilization, a mineralized ovoid otolith is visible (Pisam et al., 2002; Sollner et al., 2003) and spherule clusters are seen in the nucleus of the nascent otolith (Pisam et al., 2002) (Fig. 3F).

Fig. 3.

Cilia-driven flows in the zebrafish inner ear. (A,B) Side view of a zebrafish embryo at 26 hours post fertilization (hpf). The inner ear appears in the black box highlighted in A; B shows a zoomed-in view. The blue arrows point to the otolith and the white arrows to the spherules. (C) Two types of cilia are seen in the inner ear of zebrafish – the motile cilia that are located next to the otolith (white arrow) and the immotile, tether cilia located below the otolith (broken line). (D) Time-color display revealing the cilia motility next to the otolith. Here, moving elements are visible because a different color is applied to the frame at every time-point (arrow). (E) Side view of an immature otolith (black circle) with cilia marked in black and the flow field depicted by white arrows at 20 hpf. (F) Section of an otolith at 48 hpf seen by transmission electron microscopy, illustrating its mushroom-like shape and showing its globular internal structure (white arrowhead) and the concentric biomineralization at the periphery (black arrowhead). (G) Summary of the two proposed models for the flow field in the developing inner ear: the model put forward by Colantonio et al. (Colantonio et al. 2009) (Model A) suggests that local flow (yellow volume) is generated at the base of the otolith (green) by motile cilia (red; immotile cilia are shown as black horizontal lines) throughout its development, whereas Riley et al.’s model (Riley et al., 1997) (Model B) implies that the flow is ubiquitous at the beginning of the process and localizes progressively at the base of the otolith. (H) Schematic drawing illustrating the flow field generated during otolith growth: a rotational flow (yellow volume) occurs between 19 and 24 hpf around the growing otolith (blue), allowing transport near the otolith and mixing at the base of the otolith to limit aggregation and dictate its basal shape. Motile cilia are represented in red, and the immotile tether cilia as black vertical lines. The initial aggregation of the otolith depends on the formation of its nucleus (blue), which is made of spherules present in the inner ear cavity (small black circles). Radial mineralization then starts as flow vanishes (light gray ovals).

Early studies postulated a requirement for cilium-generated fluid flow in spherule movements and otolith assembly (Riley et al., 1997). Advanced imaging and genetic manipulation provided a test of this hypothesis, demonstrating that motile cilia at the poles of the developing inner ear generate fluid flows that guide otolith assembly and, further, that blocking cilia motility disrupts otolith assembly and positioning (Colantonio et al., 2009). The investigators proposed that motile cilia act locally to generate flow at the poles, which promotes spherule assembly on tether cilia (Colantonio et al., 2009). Flow modeling supports this and suggests that cilia-driven flow is required for proper otolith formation by transporting spherules towards the tether cilia (Wu et al., 2011). Modeling results suggest that the local Peclet number (Pe, see Glossary, Box 1) is sufficiently high for advection to overwhelm diffusion, which dominates outside the local area of cilia motility (Wu et al., 2011). This substantially increases the probability of spherules passing near the growing otolith, thus accelerating its formation (Colantonio et al., 2009) and altering its shape (Wu et al., 2011). Recent observations confirmed the requirement for cilia motility at the poles of the developing inner ear for proper otolith assembly (Yu et al., 2011). Although this study nicely confirms that beating cilia are necessary for otolith biogenesis, the authors suggest an alternative model to explain the role of cilia during this process. In this model, the authors propose that beating cilia are ubiquitously present in the inner ear at the beginning of spherule production and decrease over time to concentrate towards the pole as the otolith grows, thereby favoring particles trajectories that bring spherules near the tether cilia (Fig. 3H) (Yu et al., 2011). This somewhat varies from the model put forth by Colantonio and colleagues (Colantonio et al., 2009; Wu et al., 2011) in which motile cilia were almost only observed at the poles (see Fig. 3G for a more detailed description of the two models). Further investigations will be necessary to determine whether the differences between these models are due to subtle variations in the location of beating cilia between strains of zebrafish (e.g. Yu et al. analyzed transgenic lines overexpressing GFP within cilia, which could lead to artifacts in cilia motility) or to a strict staging issue. Nonetheless, these two models share numerous hydrodynamic features and both validate the role of beating cilia in otolith assembly, which provides fertile ground for studies of fluid flow contributions to embryogenesis.

Cilia inactivation by laser ablation demonstrates that flow indeed guides the shape of the otolith and decreases the number of spherules near the base of the tether cilia (Wu et al., 2011). Cilia can thus combine different functions through the generation of different flow regimens to control otolithic growth and morphogenesis, which depend on the flow field properties dictated by the ability of cilia to generate both transport and mixing (Wu et al., 2011).

Directional cilia-driven flows: theory and modeling

Motile cilia are the principal drivers of directed flow in the embryo, and this function often depends on their ability to generate quasi-steady, uni-directional flows. To do this, cilia must work in a manner that overcomes the inherent time reversibility of viscous flow: the mathematical character of the governing equations in the viscous flow limit indicate that changes in the sign of boundary conditions lead to an identical flow but in the opposite direction. For a beating cilium, the consequence is that a simple reciprocal motion, which might propel fluid at a finite Reynolds number, will produce no net flow in the Stokes limit. Some manner of asymmetry is required to break symmetry, leading to a net flow in a particular direction. So far, asymmetric cilia beating patterns are the most common theoretical and experimental explanation for allowing an asymmetry that permits directional flow. The most usual beating type is a planar motion with an asymmetric bending (Fig. 2A). This bending produces an asymmetry between what might be considered the forward and a recovery stroke of the beating. The mean induced-flow direction is perpendicular to the main axis of the cilium. Such a beating pattern has been observed in embryonic nervous epithelium in mice (Sanderson and Sleigh, 1981; Hirota et al., 2010) and possibly in tissues of other species, such as in the LR organizer (Schweickert et al., 2007) or the larval skin (Mitchell et al., 2009) in Xenopus. Interestingly, the beating frequency of cilia is rather similar between species and organs, and usually varies between 10 and 30 Hz (Supatto and Vermot, 2011). Mathematical models (Lukens et al., 2010) suggest that such a planar motion promotes mixing near the cilia.

Even an inflexible cilium can break symmetry if its forward and recovery strokes are not the same distance from its associated cell membrane. To a good approximation, fluids move at the speed of solids at points where they contact them. Thus, at the fixed cell surface, the fluid stops. This is the so-called no-slip boundary condition, and is essentially an exact model in most applications. Away from the cell, the velocity increases depending on the conditions driving it, but with viscous resistance due to the no-slip condition on the cell surface. There is in effect more resistance due to the cell wall the closer to it the cilium moves. Thus, symmetry can be broken if the cilium rotates about an axis that is tilted with an angle θ from a line perpendicular to the surface (Fig. 2B,C) (Cartwright et al., 2004; Vilfan and Julicher, 2006; Smith et al., 2007). Away from the cilium in this case, there is a net flow in the direction of motion of the cilium when it is furthest from the boundary. Cilium rotation with tilt is thought to be operating in the LR organizer of mice (Nonaka et al., 2005; Okada et al., 2005) and zebrafish (Supatto et al., 2008). Finally, the symmetry can be broken through helical rotation (Fig. 2A). This motion pattern is widespread in unicellular organisms (Jahn and Votta, 1972), but seems less common in vertebrates. This is a viscous flow analogue of a marine propeller, with the net flow parallel to the rotation axis of the cilium according to the sense of the helix and the direction of rotation. This type of motion might play a crucial role in zebrafish kidney development (Kramer-Zucker et al., 2005).

Cilia-driven directional flows in vivo: the left-right organizer

One of the most thoroughly described directional flows to date is that which organizes the left-right (LR) embryonic axis in most vertebrates. This cilia-mediated flow operates in the so-called LR organizer – a ciliated cavity present in most vertebrates – to control and maintain the establishment of the internal organ asymmetric polarity. Although the size and shape of the LR organizer are species dependent (Fig. 4, Table 1), cilia motility is seen in all but a few species, such as chicken and pigs (Gros et al., 2009). This flow triggers an asymmetric calcium response on the left side of the cavity (McGrath et al., 2003; Sharma et al., 2008), as well as a left-biased asymmetric expression of genes, such as the signaling molecules nodal (Collignon et al., 1996) and left-right determination factors 1 and 2 (lefty1 and lefty2) (Meno et al., 1998), and the transcription factor paired-like homeodomain transcription factor 2 (pitx2) in mouse (McGrath et al., 2003) and zebrafish (Essner et al., 2005; Kramer-Zucker et al., 2005) (Fig. 4A-D). Two functions have been postulated for the role of flow in this process: establishing a biochemical gradient towards the left side of the LR organizer and generating a flow direction-dependent physical stimulus.

Fig. 4.

Cilia-driven flows in the left-right organizer of mouse and zebrafish. (A-D) Schematic drawings summarizing the roles of cilia-driven flows in the mouse (A,B) and zebrafish (C,D) left-right organizers. Both left-right organizers are heavily ciliated but display different shapes when viewed dorsally (A,C) or transversally (B,D). While both flows are mainly directed from right to left (red arrows) with laminar flow features, a leftwards recirculatory flow (broken red arrows) is also generated. This backwards flow is more prominent in zebrafish, leading to an almost perfectly circular flow in the cavity (C,D). Both flows also lead to asymmetric calcium signaling on the left embryonic side (yellow) through the calcium channels PKD2 and PKDL1. In mouse, potentially, a chemical gradient of Fgf8 (blue) is generated, the concentration of which is higher on the left embryonic side (B). Furthermore, small nodal vesicular parcels (NVPs) are released in the flow, bypassing the chaotic flow present at the cell surface (represented in brown) to signal on the left embryonic side. In zebrafish, although asymmetric calcium signaling is well characterized, no gradient or NVPs have been identified so far. However, chaotic flow has been demonstrated in vivo (represented in brown).

Table 1.

Comparison of left-organizer features in some vertebrates

The ‘chemical gradient hypothesis’ is supported by several experiments in mice, including direct visualization using uncaged dyes (Okada et al., 2005) and direct bias of the LR axis using an artificial flow in the organizer (Nonaka et al., 2002). In mice, this chemical gradient is thought to have two shapes: a smooth gradient of fibroblast growth factor 8 (Fgf8), and possibly Nodal (Tabin and Vogan, 2003), that spans the entire organizer and that concentrates on the left embryonic side, and a steep gradient of sonic hedgehog (Shh) or retinoic acid, which travels through a small agglomerate of particles, called nodal vesicular parcels (NVPs; Fig. 4B), of dimensions 0.3 to 5 μm (Tanaka et al., 2005). Notably, however, the identity of the morphogens proposed to operate in the node is still debated (Tabin and Vogan, 2003). Here, again, the cilia flow in the process of LR determination raises the possibility of chaotic advection in at least parts of the system. The experiments suggest a model whereby mixing is avoided by bypassing the chaotic zone through local release within the flow. This bias is possible because it seems that NVPs are secreted through microvilli with lengths of just tenths of microns; this means that NVP release occurs away from the advective zone (Fig. 4B). Time-dependent flow modeling of the mouse organizer predicts that chaotic advection occurs in the vicinity of the beating cilia (Smith et al., 2007), which is supported by experimental evidence from zebrafish (Supatto et al., 2008). However, models also show that such release does not preclude the NVPs entering the region of chaotic advection. There is particle exchange predicted between chaotic and deterministic flow regions, and release away from the cell membrane also favors a rightward motion, which is generated at the roof of the organizer (Smith et al., 2011). Importantly, the two gradients could synergize, as Fgf8 increases the release of NVPs by the microvilli, creating a reinforcing mechanism. As Fgf8 and retinoic acid strongly interact genetically near the LR organizer (Vilhais-Neto et al., 2010), the feedback mechanism could also involve both molecular pathways.

NVPs are key players in initiating the asymmetric calcium response. Experiments show that, subsequent to their release, the NVPs, which comprise clusters of vesicles, are sheared and fragmented upon reaching the left side of the organizer. Speculation about the mechanisms that control this event include the interaction with immotile cilia located at the periphery of the organizer, as well as an active mechanism involving receptors located in the NVPs themselves (Hirokawa et al., 2006). Calculations infer that hydrodynamic forces themselves are insufficient to lead to fragmentation (Cartwright et al., 2007; Smith et al., 2011), suggesting the need for a biologically active process. It has been suggested that membrane channels, which remain to be identified, at the NVP surface could trigger this fragmentation (Hirokawa et al., 2006). Simulations also show that NVPs rarely reach the left side of the organizer because of a rightward flow, which is strongest at the roof (Smith et al., 2011). It is, thus, tempting to speculate that the cilia located at the periphery of the node act to promote contact with NVPs before they are advected back rightwards. Models should be able to predict whether NVP fragmentation reduces Pe number significantly for diffusion to overcome advection so that chemical signaling can occur more readily.

Despite the evidence for a chemical transport signaling mechanism, an alternative mechanism involving a mechanical stimulation by flow has been suggested (Tabin and Vogan, 2003) and might be important in this case or elsewhere in development. It has been observed that the calcium response depends on a calcium-permeable channel, polycystic kidney disease 2 (PKD2; TRPP2, also known as polycystin 2), a transmembrane encoding protein that is expressed within the cilia of LR organizers (McGrath et al., 2003; Kamura et al., 2011). PKD2 interacts with PKD1 (Hanaoka et al., 2000), and together they constitute the two polycystins involved in autosomal polycystic kidney disease (Delmas et al., 2004). They have also been associated with flow sensing in kidney cells through primary cilia (Nauli et al., 2003). It has thus been proposed that flow is sensed by cilia through PKD2, which in turn triggers calcium flux on the left side of the organizer. However, the ability of such a sensor to differentiate flow between left and right, as well as there being sufficient flow for ciliary deflection and thereby PKD2 activation, is still debated (Hirokawa et al., 2006; Cartwright et al., 2007). Indeed, considering the Reynolds number of the system, which is estimated at 10^–3 (Nonaka et al., 2005) (see Box 2, Fig. 1B), viscous forces dominate, suggesting that the shear stress magnitudes and flow speeds at the walls should be nearly symmetric, although the flow direction is asymmetric. For example, flow in the LR organizer of zebrafish rotates clockwise (Kramer-Zucker et al., 2005) so that cells on the left side of the organizer experience a flow that goes from posterior to anterior; this is the opposite on the right side (Supatto et al., 2008) (Fig. 4, Table 1). Even though computational tests suggest that cilia deflection is plausible at the node flow regime (Chen et al., 2011), for the model to be viable, it is necessary that cells discriminate flow direction to maintain asymmetry in the node. Yet, directional flow detection through cilia remains undemonstrated. Another area of debate is the possible function of the polycystic kidney disease 1 like 1 (PKD1L1)/PKD2 complex as a chemoreceptor in the LR organizer (Kamura et al., 2011), and there is now accumulating evidence to suggest that the closely related family members, the PKD1L3/PKD2L1 channels, act as pH sensors involved in sour taste detection (Huang et al., 2006; Inada et al., 2008).

Cilia-driven flows: challenges and perspectives

Overall, numerous questions remain on how morphogens and physical influences, such as cilia driven flows, interact during the process of LR specification in vertebrates. Among the hypotheses explaining the roles of flow during the process of LR determination, hydrodynamic forces alone fail to explain fully all processing that involves the NVPs and the mechanotransductive model that involves PKD. So far, the flow-induced gradients constitute the only mechanism consistent with all experimental observations, but its identity remains elusive. Mechanodetection, a chemical gradient, and an asymmetric gene response have to be connected via some theoretical and experimental framework. Extensive in vivo measurements are greatly needed in order to integrate these pieces together, including the development of precise flow measurement approaches and non-invasive labeling of the proposed morphogens (Fig. 5). Furthermore, addressing the connection with planar cell polarity and the mechanisms controlling cilia tilting will be crucial to understanding fully the establishment of flow over time (Borovina et al., 2010; Guirao et al., 2010; Hashimoto et al., 2010).

Fig. 5.

Approaches for addressing flow forces experimentally. (A,B) Blood cell tracking (A) and particle image velocimetry (PIV) (B) in the zebrafish dorsal aorta at 72 hpf. The use of the transgenic line Tg(flk:egfp, gata1:dsRed) allows blood vessels (green) and red blood cells (red) to be visualized. As shear stress depends on fluid velocity and tube diameter, the tracking of single blood cells (gray circles) allows indirect measurement of shear stress by extracting velocity over time (graph in A). When looking at a flowing particle, it is possible to consider its velocity as a whole. However, in the case of a fluid body (here, the embryonic dorsal aorta), this is more difficult because the different elements that make the fluid body can move independently of each other. In this case, motion involves a velocity field in the body rather than a single velocity. The field represents the aggregate of velocities of all elements of the body (i.e. all cells in the field; B, top panel) and is obtained using microparticle image velocimetry (μ-PIV) (B, bottom panel). Both approaches rely on a fast imaging rate (up to 1000 frames per second). (C) Flow mapping can also be achieved through local release of a particle controlled by laser-based ‘optical tweezing’ (or ‘trapping’), allowing the probing of flow velocity and direction very locally through particle tracking and μ-PIV. Optical tweezing can allow the immobilization of particles and the positioning of them anywhere in the flow field, permitting direct probing of the flow forces through tracking (left image) or μ-PIV (right image). Trap on indicates when laser trapping is on and immobilizes the particles, trap off when laser trapping is turned off and particles are released. Single or several particles can be trapped. This method allows us to seed flow and analyse flow fields in different areas.

Accumulating evidence shows that cilia are essential for symmetry breaking in a diverse set of vertebrates (Blum et al., 2009). Yet, addressing the LR organizer flow features remains a challenge even within vertebrates: comparing mouse nodal flow with flows observed in Xenopus and zebrafish reveals similarities of gross flow features but does not yet provide any obvious generalizations to other species (see Table 1). The influence of the environment on flow is not necessarily consistent with intuition, and quantitative modeling can assess the role of flow in the several LR organizers identified so far.

Both the biochemical and mechanosensing hypotheses have been challenged by hydrodynamic arguments: the chemical hypothesis was deemed viable only if diffusivity is such that the Peclet number meets the specific criteria (which experimentally corresponds to proteins of 15 to 50 kDa) (Okada et al., 2005). However, the subsequent discovery of NVPs showed that morphogens of smaller size, such as retinoic acid or SHH, could be predominately advected if incorporated in the NVP. More generally, the completion of a model including fluid forces needs to take into account an increasing number of physical parameters as the models become more complex. Similarly, otolith mineralization will necessitate the understanding of the mineralization properties as well as the fluid composition during this process. Engineered models, such as microfluidic channels and synthetic cilia, could be useful in that aspect as microfluidic flow can be precisely specified in such a device. Furthermore, important hydrodynamic features from ‘simpler’ ciliated structures, such as Chlamydomonas or Volvox model organisms, are also providing insights into fundamental in vivo principles that remain to be tested in more complex geometries when considering cilia synchronization (Goldstein et al., 2009; Polin et al., 2009) and the issue of large Peclet number (Short et al., 2006).

Flows with significant inertia: finite Reynolds number hemodynamics

Blood flow is usually of higher speed than cilia-driven flows (Fig. 1B), ranging, in the embryo, from microns per second to centimeters per second. This, and the size of the vessels through which the flow occurs, lead to sufficiently high Reynolds numbers (see Box 2, Fig. 1B), in some cases necessitating the inclusion of inertia effects in the flow equations, making them nonlinear and substantially more challenging to solve. Biophysically, blood flow dynamics (or hemodynamics) generate both steady and cyclical shear stresses, with the cyclical character being more pronounced near the heart but more dissipated deeper into the circulation tree. The viscous resistance against which the heart pumps requires a degree of pressure to overcome, which leads to a basal and an oscillatory tension (the so-called cyclical strain) to much of the circulatory system. Flow forces are important at multiple stages of vasculogenesis, hematopoiesis and cardiogenesis. We will introduce key hemodynamic concepts and discuss a few examples of the role of blood flow during development.

The theory of blood flow

Despite the same governing equations, flows in different configurations and under different conditions, even within a single embryo, can be extremely different. For example, the cilia-driven flow in the LR organizer ‘looks’ utterly different from the flow in a developing heart. The flow in the LR organizer is slow and circulatory, and relatively insensitive to the geometric details. If the cilia were to stop, the entire flow too would immediately stop owing to the dominance of viscous stresses. By contrast, the flow in the heart is faster, pulsatile (alternating fast and slow), much more sensitive to the geometric details of the heart and great vessels, and does not necessarily cease immediately in between myocardial contractions, owing to the inertia of the blood and the elasticity of the network. The same flow-governing equations apply to both cases, but the relative importance of the different physical mechanisms of inertia and viscosity, manifest as different terms in these equations, leads to these qualitatively different flows. Furthermore, blood flow can be weakly non-Newtonian (see Glossary, Box 1).

Flow in the developing vasculature

Although vessel identity and positioning are dependent on genetic hardwiring (Swift and Weinstein, 2009), accumulating evidence suggests that hemodynamics are crucial in the process and that the interconnection between the two is necessary for an optimal vascular network formation (Jones et al., 2006). It has been hypothesized that, for the vascular network to perfuse, for example, an organ, the network develops at least approximately in a manner dependent upon an optimization principle that requires vascular branching. Murray (Murray, 1926) proposed a simple optimality condition based on the assumption that the metabolic power is proportional to the vessel diameter, which seems to explain several observations regarding the vascular tree (Fung, 1997). This supports the notion that the vascular network is set to be in some sense optimal during its early formation, seemingly at the time of vessel remodeling and angiogenesis (Jones et al., 2006).

Although it seems obvious that developmental mechanisms evolved to ensure adequate and optimal perfusion depending on heart performance, the precise cellular and molecular mechanisms that establish this remain unclear (Jones et al., 2006). Direct endothelial cell adaptation to flow has been postulated to explain the plasticity of the developing vascular network (le Noble et al., 2005). However, flow is almost never steady in vivo (Fig. 5A,B). Indeed, owing to the cyclical activity of heart contraction, blood velocity varies over the time of a contraction cycle, which directly follows the status of myocardial contraction in the heart. Pulsatility (see Glossary, Box 1) is needed for essential functions in adults. For example, it drives lymphatic flow in the adult vascular system (Fung, 1997). In the embryo, pulsatile flow is seen in developing arteries and veins. In chicken embryos, the maximal acceleration rate of red blood cells is different between the arteries and veins owing to the viscous dissipation along the circulatory system (Buschmann et al., 2010) (see also Fig. 5A,B).

Microarray analysis shows that endothelial cells can discriminate between laminar and pulsatile flows by expressing and repressing different sets of genes (Garcia-Cardena et al., 2001; Dekker et al., 2002), and recent studies showed that genes potentially activated by flow have been involved in reinforcing artery versus vein identity in response to flow (Buschmann et al., 2010; Corti et al., 2011). It has thus been proposed that the different flow types observed in arteries and veins can set or reinforce arterial versus venous cell identity by activating different genes (le Noble et al., 2004). For example, the gap junction protein Gja5 has been shown to be flow responsive in the vascular endothelium in vivo and essential for arterial network development (Buschmann et al., 2010). Nevertheless, the mechanisms by which endothelial cells discriminate between pulsatile and laminar blood flow and how this impacts on the arterial/venous identity at the transcriptional level remains elusive and should stimulate exciting research in the next decade. Other genes are also flow responsive: the genes encoding the transcription factor Kruppel-like factor 2a (klf2a), the vasoconstrictive peptide endothelin 1 (edn1) and the promigratory chemokine receptors chemokine (C-X-C motif) receptor 4 (cxcr4) and Alk1 (acvrl1, activin A receptor type II like 1) are all responsive to shear stress in the zebrafish vascular system (Bussmann et al., 2011; Corti et al., 2011) (Fig. 6).

Fig. 6.

Roles of blood flow in the development of the zebrafish circulatory system. (A) The roles of blood flows have been explored in zebrafish in the hindbrain (b), in the gill-supporting branchial arches (c) and in the heart (d), and have uncovered multiple actions. Among the genes activated, klf2a is a key player that is flow activated in these three parts of the circulatory system. (B) In endothelial cells (blue) of the hindbrain, klf2a expression is followed by an increase in endothelial cell proliferation and a decrease in cell protrusion. (C) In the branchial arches, flow activates the expression of miR126 through the prior regulation of klf2a and potentiates VEGF signaling, which is required for angiogenesis. (D) Disturbed flow in the heart is also essential for locally activating the expression of klf2a and notch1b to control valvulogenesis. (E,F) Blood cell maturation during hematopoiesis is also dependent on blood flow occurring in the dorsal aorta (DA). Hematopoietic stem cells (HSCs) are generated in the dorsal aorta in the presence of flow and enter the circulation by intrasavating through the posterior cardinal vein (PCV): flow helps cells to become released in the vascular network during the early stages of a heartbeat and controls HSC maintenance by regulating klf2a expression and nitric oxide (NO) synthesis.

Gene expression and live imaging analyses have revealed the cellular mechanisms at work during zebrafish hindbrain vascular development (Bussmann et al., 2011; Fujita et al., 2011) (Fig. 6A). Here, flow downregulates the expression of cxcr4, a chemokine that mediates angiogenic sprouting (Fig. 6B). This leads to the reduction of cell sprouting. It establishes a mechanism that allows the cells that are not in contact with blood flow to maintain their sprouting activity towards the arterial circulation (Bussmann et al., 2011). Conversely, flow has been shown to positively regulate angiogenic sprouting in the aortic arches, where the gene klf2a is expressed in protruding endothelial cells in response to shear stress and promotes the angiogenic activity of the cell by promoting vascular endothelial growth factor (VEGF) signaling through miR126 (Nicoli et al., 2010) (Fig. 6C). In addition, the expression of ephrin B2 and neuropilin, two specific markers of arterial identity, has been shown to be flow dependent in chicken (le Noble et al., 2004), demonstrating that the influences of blood flow upon vascular development are widespread in vertebrates.

Alternative, all physical, explanations for patterning of the peripheral vascular network have progressively emerged, as it seems that effects of blood flow on vascular branching morphogenesis might not be fully encompassed in Murray’s law. Studies indicate that the forces exerted by interstitial pressure of the vessel could also contribute to vascular branching morphogenesis (Nguyen et al., 2006). Furthermore, the patterning of veins and arteries can be ‘self-organized’, owing to an optimization of force distributions at the tissue level, not only because of the flow forces generated in blood vessels (Nguyen et al., 2006; Al-Kilani et al., 2008).

Another interspecies conserved role of flow is seen in hematopoiesis. Hematopoietic stem cells (HSCs) are formed in close association with the endothelial cells that line blood vessels. Thus, hematopoiesis occurs in strict proximity with blood flow. For example, the onset of blood flow slightly precedes blood cells moving out from the hematopoietic sites and helps this process to occur in zebrafish (Iida et al., 2010). In embryonic stem cell cultures, fluid shear stress increases both the expression of genes marking HSC identity and the potential of stem cells to form colonies of hematopoietic cells (Adamo et al., 2009). In zebrafish and mice, an absence of blood flow affects HSC formation and the expression of hematopoietic-specific genes (Adamo et al., 2009; North et al., 2009). The signal involves the nitric oxide signaling pathway, which is shear inducible in endothelial cells and depends on the expression of klf2a in zebrafish (Wang et al., 2011) (Fig. 6E,F). There is reason to believe that flow impact on vascular patterning could also affect blood stem cells formation. It is known that HSCs emerge from the endothelium in vertebrates through an endothelial-to-hematopoietic transition (Bertrand et al., 2010; Boisset et al., 2010; Kissa and Herbomel, 2010) and that the absence of flow stops this transition (Lam et al., 2010). Live imaging and mutant analysis should reveal whether flow sensing is necessary for this cell fate switch to occur.

Disturbed flow in the developing heart

Another type of flow can be seen in the developing heart. While pulsatile and laminar flows are considered as ‘healthy’ flows, disturbed turbulent flows are usually associated with atherosclerotic disease in adults (Hahn and Schwartz, 2009) as well as congenital or idiopathic valvular heart diseases (Armstrong and Bischoff, 2004). In the embryo, similarly disturbed flows have been observed in the developing yolk sac of mouse (Jones et al., 2004), in the zebrafish heart (Liebling et al., 2006) and in the chicken heart (Yalcin et al., 2011). These flows can have regions of flow reversal. Developing valves are well positioned to be in contact with reversing flows, particularly the mitral valve, which is located between the atrium and the ventricle. If the valves are not fully developed, the valvulogenic area experiences a negative flow, owing to the concomitant atrial diastole and ventricular systole in zebrafish (Scherz et al., 2008; Vermot et al., 2009) (Fig. 6D). Similar observations have been made in chicken, and disturbed flows have been recorded in the same areas as klf2a expression sites that correspond to the site of valve formation (Groenendijk et al., 2004). In all these cases, the role of klf2a could be to control the cellular rearrangement through cytoskeletal remodeling, as it has been shown that it can inhibit c-Jun N-terminal kinase signaling and induce actin shear fiber formation (Boon et al., 2010). Disturbed flows could also be high in the convoluted trabeculae, where flow has been found to be crucial for their development in zebrafish (Peshkovsky et al., 2011).

Challenges and perspectives

Although they are clearly important, many of the details concerning the role of flow forces during cardiovascular development remain to be understood. The challenges of flow visualization and characterization have certainly hampered the field, and, to date, many basic issues regarding such as the roles of flow (and tension) during vessel tubulogenesis, maturation, regeneration and its role in biological product transport in the growing embryo are still not well understood. Yet, the factors guiding cardiovascular development in response to flow have started to be identified, and imaging methods have greatly advanced, suggesting that key details will come in the near future (Fig. 5). Furthermore, the contribution of other flows that are less well characterized (see Box 3) during development and regeneration should be addressed in the future. Finally, identifying the important mechanodetectors in each system, their location and the flow that induces a response still remain key issues in the field. The following section summarizes the principles of mechanodetection at work at the cellular level.

Box 3. Other in vivo flows

Besides blood- and cilia-driven flows, many flows are generated in living tissues. For example, in adult tissues, low flow amplitudes correspond to lymphatic flows [∼1000 μm/s (Dixon et al., 2006)], which are interstitial transmural flows emanating from endothelium fenestrations or from endothelium-free vascular lesions (≤1 μm/s) through the neighboring tissue (see Fig. 7) (Swartz and Fleury, 2007). Such flows are manly driven by pressure gradients resulting from hydrostatic and osmotic pressure differences between the blood and the interstitial space (Swartz and Fleury, 2007). In pathological cases, such as vascular damage or tumor invasion, interstitial flow can activate residing vascular smooth muscles cells and fibroblasts on its way. Here, shear values can reach up to 0.1-1 dynes/cm² (Shi and Tarbell, 2011) (Fig. 7). Mechanical loading of the bone is also accompanied by deformations that lead to fluid movement in the lacunar-canalicular network. Osteocytes residing in this mineralized bone matrix have the ability to sense this flow, which reaches velocities of ∼60 μm/s (Price et al., 2011) and exhibits shear stress values comparable with values encountered in our vascular system [8-30 dynes/cm² (Weinbaum et al., 1994)].

Detecting flows at the cellular scale

An obvious question related to biological flow concerns the mechanisms that cells use to detect physical forces. In this section, we summarize some pathways involved in mechanodetection thought to participate in flow sensing in embryos and in embryonic stem cell culture. As these forces greatly vary in strength, it is not surprising that different molecular mechanisms seem to sense forces of different strengths. Fig. 7 presents an overview of some complexes involved in mechanotransduction.

Fig. 7.

Potential flow mechanosensing complexes. (A,B) Fluid flow-mediated mechanical forces (black arrows) can be sensed and transduced by various means at the cellular level, here illustrated as an overview (A) and in detail (B). (1) At the plasma membrane, flow-sensitive membrane channels (yellow) detect fluid flow or membrane stretch and respond by gating, leading subsequently to the entry of ions through channels. (2) Flow-mediated membrane tension and variations in fluidity are sensed and regulated by dynamic membrane trafficking and flattening of existing endocytic structures, such as caveolae. (3) Protruding cilia contain mechanosensitive proteins such as polycystic kidney disease (PKD) 1 (PC1), which interacts with and gates its partner PKD2 (PC2) upon experiencing flow, leading to a calcium influx (yellow star indicates proteolytic cleavage of PKD1). The cellular response and the downstream signaling events are further amplified by endoplasmic reticulum-mediated calcium-induced calcium release. Potentially, cytoskeletal deformation and tension upon cilia bending could also serve as a mechanosensitive mechanism, but this has yet to be demonstrated. (4) Upon being exposed to fluid shear, the endothelial glycocalyx (red) experiences drag forces that are transmitted to the underlying cortical cytoskeleton as well as to distant integrin-dependent adhesions (not illustrated) via an integrated torque. (5) Flow-mediated flow forces are transduced to the cytoskeleton, which comprises actin (stress fibers and cortical actin), microtubules and intermediate filaments. Flow forces could also be transduced mechanically into intercellular adhesions (adherens junctions, tight junctions and desmosomes; shown in orange) and into integrin-mediated focal adhesions (gray shapes), the latter being mechanically bound to the surrounding extracellular matrix.

Low-speed flow sensing through primary cilia

Because they protrude into the flow, primary cilia are geometrically suited for mechanosensing (Fig. 7A). In the past decade, cilia mechanodetection has been associated with flow sensing during the development of the heart, during LR patterning and during kidney development. The active mechanosensory macromolecular complex consists of PKD1 and PKD2 in renal cells (Nauli et al., 2003), and possibly PKD1L1 and PKD2 in the LR organizer (Field et al., 2011). All are located within cilia (Nauli et al., 2003; Field et al., 2011; Kamura et al., 2011). PKD1 is thought to act as the mechanical sensor that senses luminal shear stress via its large extracellular domain (Nauli et al., 2003) (Fig. 7B, part 3). It regulates the gating of the calcium-permeable channel PKD2 upon flow sensing in vitro in renal epithelial cells through cytoplasmic association with its partner, via their coiled-coil domains (Nauli et al., 2003) (Fig. 7B, part 3). In the zebrafish organizer, it has been proposed that a first burst of calcium influx at the cilia level is then sufficient to activate the calcium-induced calcium release cascade through the opening of ryanodine receptors (Francescatto et al., 2010). The subsequent massive release of intracellular calcium activates numerous cellular responses, including the phosphorylation of the calmodulin-dependent protein kinase type 2 in the LR organizer and kidney cells (Francescatto et al., 2010; Rothschild et al., 2011) (Fig. 7B, part 3).

PKD1 and PKD2 have been shown to participate in flow-dependent calcium release in endothelial cells, kidney epithelial cells and in the LR organizer. Importantly, the PKD1-PKD2 complex seems specifically involved in fluid flow and not in mechanical load sensing in endothelial cell culture (Nauli et al., 2008; Poelmann et al., 2008; AbouAlaiwi et al., 2009). Primary cilia are, however, fragile structures that can break when subject to sufficiently strong flow-induced shear stress (Nauli et al., 2008). Consistently, 2 hours of laminar shear stress at 15 dynes/cm² is sufficient to disassemble most of the cilia observed under normal conditions in human umbilical vein endothelial cells (HUVECs) (Iomini et al., 2004). Therefore, it remains unclear whether cilia can detect high, physiologically relevant flows. Nevertheless, cilia can potentially detect low velocity flow. In an embryonic heart, such a low-velocity area could correspond to the trabeculae, where the cellular convolutions do not allow high-speed flow. In the chicken embryonic heart, monocilia were specifically detected on endocardial-endothelial cells in the deeper part of ventricular trabeculations (Van der Heiden et al., 2006). Similar observations were made in mouse embryonic heart, where absence of cilia (or cilia-related PKD2) through gene knockout leads to abnormal endocardial cushions and compact myocardium (Slough et al., 2008). Interestingly, a lack of primary cilia is involved in shear-induced epithelial-to-mesenchymal transition, a process that is activated during valvulogenesis in higher vertebrates (Egorova et al., 2011).

A possibly important aspect of cilia mechanosensing is the detection of changes in flow speed. For example, the calcium response triggered by flow in kidney cell cultures varies according to the flow regime and flow velocity in the system, suggesting that cilia can relay complex information about fluid forces to the cell (Rydholm et al., 2010). In endothelial cells, cilia can sense differential shear (Nauli et al., 2008), with increased shear (7.2 dynes/cm²) inducing PKD1 proteolytic cleavage and abrogating ciliary mechanosensory potential without cilia shedding (Fig. 7B, part 3). This mechanism ensures that embryonic endothelial cells sense a narrow flow velocity range. It is noteworthy that only 25% of endothelial cells are ciliated, leaving many wide areas non-ciliated in the chicken embryonic heart (Poelmann et al., 2008). Nevertheless, non-ciliated cells seem connected to neighboring ciliated cells through intercellular calcium exchange (Nauli et al., 2008).

Additional mechanisms for flow- and cilia-independent mechanosensing abilities have also been attributed to polycystins (Sharif-Naeini et al., 2009). In myocytes, PKD2 senses changes in membrane tension triggered by blood pressure and responds by interacting with its partner PKD1 and thereby relieving its cytoskeletal-dependant inhibition of an unknown cation channel. In this context, gating of mechanosensitive channels is therefore highly sensitive to membrane tension, which could potentially also apply to blood flow sensing (Fig. 7B, parts 1-3).

High-speed flow sensing

In the endothelium, fluid shear stresses can exceed cilia disassembly limits by several orders of magnitude (Iomini et al., 2004). With blood flow pulsatility frequencies (reaching 8 Hz in mice) requiring fast response times, mechanosensitive cells use other mechanisms for prolonged high-shear flows.

Glycocalyx

Among these mechanisms of flow sensing, the endothelial glycocalyx has received significant attention during the past decade. The glycocalyx is a 3D quasiperiodic (10-12 nm) fibrous meshwork, the thickness of which ranges from 150-400 nm in mice to 2-9 μm in humans, that covers the endothelial surface in a bush-like pattern (Fig. 7A,B, part 4). Composed of proteoglycans and glycoproteins, it is tightly linked, via integrins, to the underlying cortical cytoskeleton. Primarily viewed as a hydrodynamic exclusion layer that is able to control interactions of proteins derived from red blood cells with the endothelial surface, as well as leukocyte attachment, the glycocalyx is now also seen as a major transducer of mechanical forces to the underlying endothelial cytoskeleton (Tarbell and Pahakis, 2006). Paradoxically, theoretical modeling of the glycocalyx suggests that this layer attenuates fluid shear stress in a way that shields the endothelial membrane (Smith et al., 2003). Near-complete attenuation of fluid shear stress at the endothelial surface has indeed been measured using high-resolution near-wall fluorescent microparticle image velocimetry (μ-PIV) (Smith et al., 2003). Elastohydrodynamic models suggest that the stiffness of the core proteins of the glycocalyx transmits the fluid forces at its tips through a local torque that transduces into an integrated torque in the underlying cortical cytoskeleton (Weinbaum et al., 2003; Weinbaum et al., 2007) (Fig. 7B, part 4). Glycocalyx-mediated flow sensing will thus be converted into two major routes leading either to production of nitric oxide (NO) or to reorganization of the cytoskeleton through remodeling of both intercellular and extracellular matrix-linked junctions (Tarbell and Pahakis, 2006). The glycocalyx is present in the developing vascular network (Henry et al., 1995), but its role during embryogenesis remains to be explored.

Mechanosensitive membrane channels

Mechanosensitive membrane channels exist in every organism. They are gated directly by forces and either convert this mechanical signal into an electrical one (Fig. 7A,B, part 1) or control the release of secondary messengers that eventually gate ion channels, which do not themselves sense mechanical signals. What makes these mechanosensitive channels particularly important from a mechanosensing point of view is that they respond and gate rapidly with short latency (order of milliseconds). The major mechanical signal responsible for their activation is membrane stretching, as has been shown for TRPC1 (transient receptor potential cation channel, subfamily C, member 1) (Maroto et al., 2005), a member of the mechanosensitive non-selective cation channels (MscCa) (Lansman et al., 1987). TRP channels such as PKD1 are mechanosensitive channels thought to be indirect mechanosensors that modulate the activity of mechanosensitive channels (Sharif-Naeini et al., 2009). Another TRP channel (TRPV4) has been found to control endothelial cell reorientation to flow (Thodeti et al., 2009), suggesting that it constitutes a receptor for mechanical strain. Interestingly, TRPV4 interacts with PKD2, forming a mechano- and thermosensitive calcium-specific channel in the cilia of kidney cells (Kottgen et al., 2008). More recently, new members of this very wide family of membrane mechanosensitive channels have been identified in Drosophila [Piezo1 and Piexo2 (Coste et al., 2010)]. Shear stress has also been shown to trigger K⁺ entry by activating the inwardly rectifying K⁺ channel Kir2.1 (Hoger et al., 2002). K⁺ currents mediated by Kir2.1 and Kir2.2 also control dilation of arteries (Zaritsky et al., 2000), the flow dependence of which is regulated by the vascular kallikrein-kinin system (Bergaya et al., 2001).

Plasma membrane mechanodetectors

Cells have different ways of preserving plasma membrane integrity in order to counter the tensile changes triggered by membrane tension. Recent studies show that endothelial cells have the ability to compensate rapidly for membrane tension changes upon mechanical stress through fast flattening of membrane invaginations, named caveolae, which provide the cell with instantaneous membrane reservoirs available for generating rapid responses (Sinha et al., 2011) (Fig. 7A,B, part 2). Time will show whether a corresponding mechanism is operating in cells experiencing flow, but this seems likely as any mechanical load or pulsatile fluid flow can also impact on surface tension.

Adhesive mechanosensory receptors

An important component of the mechanoresponsive machinery of endothelial cells lies in its cytoskeleton, particularly in the molecules that anchor it to either neighboring cells or the surrounding matrix (Fig. 7A,B, part 5). Cytoskeletal-dependent cell reorientation in response to fluid shear has been observed to involve actin, microtubules and intermediate filaments (Galbraith et al., 1998). Although it significantly remodels when subject to fluid shear, there is little evidence that the cytoskeleton can directly sense the flow. The cytoskeleton is, however, tightly linked to membrane-adhesion receptors and is therefore capable of transmitting forces from apical regions of the endothelium to both basal and basolateral regions (Fig. 7B, part 5). A mechanosensory complex consisting of platelet/endothelial cell adhesion molecule 1 (PECAM1) (a force transducer that mediates cell-cell junctions), VE-cadherin (an adaptor) and VEGFR2 (vascular endothelial growth factor 2; Kdr; an activator of phosphoinositide 3-kinase, PI3K) has been shown to respond mechanically to flow by favoring Src-dependent, ligand-independent activation of VEGFR2 (Tzima et al., 2005). Flow-dependent mechanical activation of VEGFR2 has been demonstrated, although the precise mechanical input remains elusive (Shay-Salit et al., 2002; Jin et al., 2003). Downstream signaling activated by both PECAM1 and VEGFR2 includes PI3K-Akt activation that will eventually phosphorylate endothelial NO synthase, allowing NO release and thereby vessel relaxation (Fleming et al., 2005). The same pathway orchestrates conformational activation of integrins, famously known as bidirectional mechanosensors of matrix compliance (Tzima et al., 2005). Activation of integrins, as well as small GTPases (Rho, Rac and Cdc42) coordinates cytoskeletal reorganization as well as flow-dependent gene expression upon shear stress (Tzima, 2006). Yet, the contribution of flow-mediated activation of integrins is minimal as physiological flow forces are expected to be one-hundred to one-thousandth that of forces existing between matrix and integrins (Hahn and Schwartz, 2009). Cellular and nuclear mediators of integrin-mediated forces have recently been deciphered through the identification of two transcriptional regulators, the Yorkie-homologues YAP and TAZ. Matrix stiffness and cytoskeletal tension sensed by integrins are relayed by nuclear translocation of YAP/TAZ, allowing differentiation of mesenchymal stem cells as well as survival of endothelial cells (Dupont et al., 2011).

Additionally, numerous proteins functioning in cell adhesion have been implicated in tension sensing through structural changes within the adhesion complex (Hoffman et al., 2011). More recently, hemidesmosomes have been shown to mature into cell junctions upon tension in the Caenorhabditis elegans embryo (Zhang et al., 2011). Here, tension triggers phosphorylation of intermediate filaments through a protein complex located at the hemidesmosome. As a consequence of mechanotransduction, tension thus can lead to the formation of a tight junction, which reinforces cell-cell adhesion in response to stress.

Mechanisms involving adhesion and subsequent biomechanical relays could correspond to a generic process used by cells experiencing cyclical stress, such as pulsatile fluid flow, to strengthen their junction and adapt their behavior in response to cyclic tangential forces generated between cells.

Conclusions

Overall, it is clear that biological flows are key for embryonic development. Biological flows are highly diverse, both in terms of velocity and flow fields, as well as the cellular outcome they control. Flow controls cell behavior through numerous signaling pathways. Specific links between flow, gene expression and morphogenesis are now becoming better understood, although we are just starting to uncover the complexity of interactions between flow, cilia and cells. Continuous efforts in investigating cell dynamics and behavior in response to flow, as well as in developing methods to measure and change flow forces, will continue to illuminate the biological response to flow during development. Much progress is anticipated concerning conservation of mechanisms between species, with numerous surprises expected both in terms of fluid mechanics and mechanobiology. Importantly, the quantitative description of flow as governed by the Navier–Stokes equations and the phenomenology of solutions of these equations provides an essential tool for establishing these links. Many proposed flow-driven aspects have been challenged by physicists and have now been reconsidered. The theory of the LR organizer flow is a good example because it directly changed our view of the process involved. Quantitative analysis and modeling are thus crucial to address flow function in the embryo and adults, as well as in many other fields of biology.