Characteristics of the Freshwater Cyanobacterium Microcystis aeruginosa Grown in Iron-Limited Continuous Culture

Abstract

A continuous culturing system (chemostat) made of metal-free materials was successfully developed and used to maintain Fe-limited cultures of Microcystis aeruginosa PCC7806 at nanomolar iron (Fe) concentrations (20 to 50 nM total Fe). EDTA was used to maintain Fe in solution, with bioavailable Fe controlled by absorption of light by the ferric EDTA complex and resultant reduction of Fe(III) to Fe(II). A kinetic model describing Fe transformations and biological uptake was applied to determine the biologically available form of Fe (i.e., unchelated ferrous iron) that is produced by photoreductive dissociation of the ferric EDTA complex. Prediction by chemostat theory modified to account for the light-mediated formation of bioavailable Fe rather than total Fe was in good agreement with growth characteristics of M. aeruginosa under Fe limitation. The cellular Fe quota increased with increasing dilution rates in a manner consistent with the Droop theory. Short-term Fe uptake assays using cells maintained at steady state indicated that M. aeruginosa cells vary their maximum Fe uptake rate (ρ_max) depending on the degree of Fe stress. The rate of Fe uptake was lower for cells grown under conditions of lower Fe availability (i.e., lower dilution rate), suggesting that cells in the continuous cultures adjusted to Fe limitation by decreasing ρ_max while maintaining a constant affinity for Fe.

INTRODUCTION

Iron (Fe) is one of the most essential micronutrients for almost all living organisms because of its critical roles in various metabolic processes (10). Cyanobacteria in particular have a relatively high Fe requirement since Fe is needed for the processes of photosynthetic and respiratory electron transfer and, in some cases, nitrogen fixation (48). Therefore, growth of cyanobacteria is influenced strongly by Fe availability (60). In surface waters at circumneutral pH, concentrations of ferrous iron ([Fe(II)]) and ferric iron ([Fe(III)]) in biologically available unchelated inorganic forms are typically low due to rapid oxidation of Fe(II) (43) and strong complexation of Fe(III) (32, 33) by a range of naturally occurring ligands (16). When Fe is a growth-limiting nutrient, photochemically and biologically mediated reduction of Fe(III) to more-soluble Fe(II) may become a critical step in increasing Fe availability (15, 17, 44, 49).

Occurrence of the bloom-forming freshwater cyanobacterium Microcystis aeruginosa in lakes, reservoirs, and slowly flowing rivers poses serious social and ecological concerns, with excessive growth typically deteriorating water quality and jeopardizing human and ecological health (12). Evidence exists that growth of this organism can be limited by supply of the trace nutrient Fe (39). Additionally, Fe nutrition alters basal metabolic functions of the organism, including photosynthesis, respiration, and nutrient uptake (28, 31, 65), as well as potentially inducing the biosynthesis of secondary metabolites, such as the potent hepatotoxin (microcystin), possibly to prevent cellular damage from reactive oxygen species that are generated by oxidative stress (2). Recent laboratory investigations into the Fe uptake mechanisms of M. aeruginosa indicated that photoreductive dissociation of chelated Fe(III) significantly increased Fe availability for Fe-limited cells growing in EDTA-buffered culturing medium (15). In contrast to many cyanobacteria which can produce siderophores to facilitate Fe uptake (30, 38, 45, 61), excretion of siderophores to assist in acquiring Fe is not believed to be used by M. aeruginosa (18, 40). A siderophore-independent iron acquisition mechanism was also observed in Fe-limited cells of the siderophore-forming freshwater cyanobacterium Anabaena flos aquae (64).

Most previous investigations of the cellular phenotype expressed under nutrient limitation employed batch culture incubations. However, temporal changes to physicochemical properties of the medium, including pH, nutrient concentrations, and metabolic products (27), occur during incubation, such that the batch method suffers severe limitations with regard to accurately assessing the effect of growth conditions on cellular response. In addition, the response of cultured microorganisms varies throughout the growth cycle, which typically consists of a lag phase, an exponential growth phase, a stationary phase, and a death phase in batch cultures (52). In contrast, the growth of microorganisms in continuous culture is maintained at steady state throughout the incubation, with metabolic processes and resultant growth occurring at a constant rate in a relatively stable environment (26).

The growth response of phytoplankton has been widely investigated in chemostats operating under nutrient limitation by not only macronutrients, including nitrogen (7, 8, 21) and phosphorus (6, 14, 22), but also trace metals (particularly Fe) (9, 23, 35, 47, 55–59, 62, 64, 66). However, a mathematical theory of trace metal-limited continuous culture is lacking. In fact, the chemostat theory used for describing cellular growth has been developed and subsequently reviewed thoroughly by several authors (3, 19, 26, 27, 36, 41) and shown to be applicable to macronutrients studies where the concentration of limiting substrate is considered as the total concentration of the macronutrient. In contrast, chemostat behavior and theory under trace metal-limited conditions are significantly different from those under macronutrient-limited conditions, because the limiting substrate is buffered by excess organic ligands and also because some trace metals (including Fe and Cu) are photoreactive. Indeed, under Fe-limiting conditions, the traditional chemostat theory is no longer suitable for description of the growth and behavior of microorganisms since, under these conditions, Fe availability is a function of unchelated Fe concentration and not total Fe concentration, with the kinetics of both light-mediated reduction of Fe(III) species and the oxidation of Fe(II) species critical determinants of steady-state concentration of unchelated Fe. In this work, a modified chemostat theory for Fe-limited phytoplankton growth is developed and applied to the description of the behavior (including steady-state cell density, Fe cell quota, and Fe uptake kinetics) of M. aeruginosa strain PCC7806 grown continuously in modified Fraquil medium (Fraquil*), with Fe activity buffered by the organic ligand EDTA. The modified chemostat theory developed here and used to describe the results obtained in this study is presented in full in the supplemental material.

MATERIALS AND METHODS

Materials.

Double-deionized Milli-Q (MQ) water (18 MΩ · cm resistivity) was used in preparation of all reagents. All chemicals used were of high purity (at least analytical grade) and purchased from Sigma-Aldrich, unless otherwise stated. Stock solutions were stored in the dark at 4°C when not in use. All pH measurements were made using a pH meter (pH/ION 340i; WTW, Germany) calibrated on the free-hydrogen scale with pH 4.01 and pH 6.88 buffers. Adjustment of pH was performed using highly purified 30% (wt/vol) HCl (Fluka) and 10 M NaOH (Riedel-deHaën, Germany) solutions. All glassware and plasticware were soaked for 24 h in a hot 2% detergent solution and thoroughly rinsed with MQ. The materials were then allowed to stand for at least 24 h at room temperature in a 5% (vol/vol) HNO₃ solution, thoroughly rinsed with MQ, and dried prior to use.

Culturing method.

Cells of the toxic strain PCC7806 of M. aeruginosa were cultured in modified Fraquil medium (Fraquil*) in which the speciation of trace metals present could be precisely defined. The detailed preparation of Fraquil* is described elsewhere (3, 17). Briefly, the medium is buffered by a single metal chelator, EDTA, and contains 0.26 mM CaCl₂, 0.15 mM MgSO₄, 0.5 mM NaHCO₃, 0.1 mM NaNO₃, 0.01 mM K₂HPO₄, 1 mM HEPES, 160 nM CuSO₄, 50 nM CoCl₂, 600 nM MnCl₂, 1.2 μM ZnSO₄, 10 nM Na₂SeO₃, 10 nM Na₂MoO₄, 300 nM thiamine HCl, 2.1 nM biotin, and 0.41 nM cyanocobalamin. In this work, the EDTA concentration was maintained constant at 26 μM, while total Fe concentration varied from 10 nM to 10 μM. All salt, trace metal, and vitamin stock solutions were made up in MQ individually rather than as a mixture. Then, the stocks were mixed in ∼1 liter MQ, except for Fe and EDTA. The 1 mM stock of ferric chloride [Fe(III)Cl₃; Ajax Finechem, Australia] in 0.1 M HCl was mixed with a 26 mM solution of EDTA (Na₂EDTA; Sigma) prior to mixing with the other stock solutions in order to prevent precipitation of Fe(III). After mixing all nutrient stocks, the pH of the medium was adjusted to 8.0 ± 0.05 using concentrated NaOH. The medium was then sterilized using a 700-W microwave oven for 10 min in intervals of 3, 2, 3, and 2 min. After cooling to room temperature, the filter-sterilized vitamin solutions were added into the medium. Fraquil* with radiolabeled Fe was also prepared by an identical procedure except for use of radiolabeled 23 mM ⁵⁵Fe(III)Cl₃ (in 0.5 M HCl, 185 MBq; PerkinElmer, Australia) instead of nonradiolabeled 1.0 mM Fe(III)Cl₃.

All cultures of M. aeruginosa PCC7806 in Fraquil* were grown in a temperature- and light-controlled incubator (Thermoline Scientific, Australia) at 27°C under a 14-h/10-h light/dark cycle with light intensity of 157 μmol photons m⁻² s⁻¹ horizontally supplied by cool-white fluorescent tubes. In the original culture used for long-term batch cultivation, total Fe and EDTA concentrations of 100 nM and 26 μM, respectively, were used. Cells were regularly subcultured into fresh media when cultures reached stationary growth phase. Cell density in the culture was counted on a Neubauer hemacytometer (0.1-mm depth) under an optical microscope (Nikon, Japan). Cellular size was determined using a Mastersizer 2000 particle size analyzer (Malvern).

Chemostat apparatus.

A metal-free sterile chemostat system was developed for four different flow rates with three replicates (see Fig. S1 in supplemental material). The culture medium reservoirs consisted of two 2-liter polycarbonate bottles containing sterile Fraquil* with screw-top caps vented by a 0.22-μm-pore-size air filter. Sterile fresh medium was distributed at four different flow rates into the 12 cultures in 250-ml polycarbonate culturing vessels using a high-precision 24-channel peristaltic medium pump (Ismatec). Inline air filtered with a 0.22-μm-pore-size filter was supplied by a 4-channel aquarium-style diaphragm air pump (Aqua-one) to create the positive pressure required in the headspace of the culture vessels. The air gap created between the culture and waste vessels flushed out the excess culture over the elevated weir into a 10-liter polycarbonate waste vessel via an overflow vent. The volume of the culture in each vessel was therefore maintained constant at 200 ml. To avoid sedimentation of cells, the culturing vessels were continuously gently shaken using a Benchtop digital shaker (Thermoline Scientific, Australia) at a rotation rate of 135 ± 5 rpm. A sampling port was equipped with a sterile one-way sampling valve that allowed sampling of the culture without bacterial or metal contamination. The system was placed in the incubator to control temperature and light conditions. Prior to use, all chemostat apparatuses were sterilized by autoclaving. During this treatment, all materials were protected from bulk trace metal contamination from metal leaching inside the autoclave by placement in a plastic bag.

Cellular Fe quota and external Fe concentration.

In order to quantify steady-state cellular Fe quotas and extracellular Fe concentrations, the chemostat system was operated at an inflowing ⁵⁵Fe concentration of 20 nM with four dilution rates (0.09, 0.14, 0.17, and 0.25 day⁻¹). For this purpose, cells were previously grown batchwise in 50 nM nonradiolabeled Fe Fraquil* and harvested during late exponential growth phase by filtration. The filtered Microcystis cells were then resuspended in 200 ml of Fraquil* containing 20 nM radiolabeled ⁵⁵Fe for each dilution rate in triplicate at a cellular density of ∼2.5 × 10⁸ cells liter⁻¹. The continuous system was maintained by introducing fresh Fraquil* prepared with 20 nM radiolabeled ⁵⁵Fe. The amount of ⁵⁵Fe incorporated within cells was then monitored in triplicate every 2 days until the system approached steady state using the following procedure: (i) sampling 1 ml of the cultures, (ii) filtering through a 25-mm-diameter, 0.65-μm polyvinylidene difluoride (PVDF) membrane (Millipore), (iii) gently washing the filtered cells at 1 ml min⁻¹ with a solution containing 50 mM Na₂-EDTA (Sigma) and 100 mM Na₂-oxalate (Sigma) adjusted to pH 7 (here referred to as EDTA-oxalate solution) for 15 min in order to eliminate nonspecifically adsorbed Fe from the cell surface (54), (iv) subsequent rinsing with 2 mM sodium bicarbonate buffer (pH 8), and (v) placing the washed cells in glass scintillation vials with 5 ml of scintillation cocktail. When the chemostat system reached steady state, in addition to the cellular Fe quota, steady-state Fe concentrations were also determined by collecting the filtrates from the filtration step and setting aside for radioactivity measurement. The activity (counts per minute) of radioisotope ⁵⁵Fe in the washed cells and the filtrates was measured in a Packard TriCarb liquid scintillation counter and converted to moles of Fe by performing concurrent counts of 1 to 5 μl of ⁵⁵Fe-EDTA stock in 5 ml scintillation cocktail. Procedural blanks were measured by repeating the identical procedure but with cells absent.

Short-term ⁵⁵Fe and ¹⁴C uptake.

To prepare steady-state Fe-limited cells used for the short-term uptake experiments, the chemostat system was operated with 20 nM nonradiolabeled Fe at four different dilution rates (0.09, 0.14, 0.17, and 0.25 day⁻¹). A total of 200 ml of batch culture acclimated in Fraquil* containing 50 nM nonradiolabeled Fe was removed in late exponential growth phase (cellular density was ∼1.5 × 10⁹ cells liter⁻¹) and transferred to the continuous culture apparatus. The cell density of the cultures was then monitored regularly every 2 days for a period of ∼1 month. When steady-state conditions were achieved, cells were harvested onto PVDF membrane filters and rinsed with 5 ml of 2 mM NaHCO₃ for 5 min. The washed cells were then resuspended into Fe- and EDTA-free Fraquil* at cell densities of 5 × 10⁸ to 7 × 10⁸ cells liter⁻¹. Preequilibrated ⁵⁵Fe(III)EDTA stock solutions with different Fe/EDTA ratios were added into the cultures to obtain concentrations of 200 nM ⁵⁵Fe and 20 to 200 μM EDTA. Cells were incubated at 27°C for 1 to 12 h under light with an intensity of 157 μmol photons m⁻² s⁻¹. After the incubation, cells were again vacuum filtered onto PVDF membrane filters and then rinsed three times with 1 ml EDTA-oxalate solution and twice with 1 ml of 2 mM NaHCO₃ (total rinsing time was about 10 min). The filtered cells were then collected in scintillation vials. The radioactivity was measured by using the procedure described above for determination of cellular Fe quota. Processing steps in the experiment examining short-term ¹⁴C uptake by M. aeruginosa were identical to those described in the short-term ⁵⁵Fe uptake experiments, except that cells were incubated in Fraquil* ([Fe]_T = 20 nM and [EDTA]_T = 26 μM, where T indicates total concentration) containing 0.5 mM ¹⁴C prepared by replacing the nonradiolabeled NaHCO₃ stock with radiolabeled NaH¹⁴CO₃ (PerkinElmer, Australia).

Kinetic model for unchelated Fe(II) calculation.

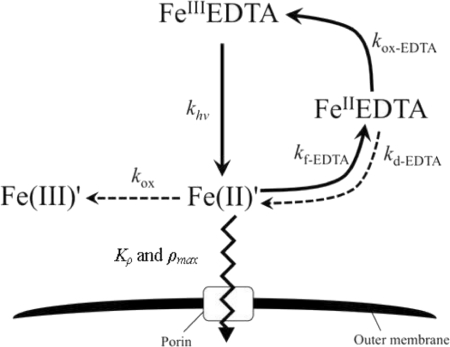
In the presence of light, photoproduced unchelated ferrous iron [i.e., Fe(II)′] rather than total Fe becomes the main substrate for uptake by M. aeruginosa in Fraquil*, as described in detail elsewhere (15). In a manner similar to that described in the previous work, the steady-state Fe(II)′ concentration ([Fe(II)′]_ss) was calculated using a kinetic model of Fe transformations that accounts for a variety of processes, including photoreductive dissociation of Fe(III)EDTA into Fe(II)′, complexation of photoproduced Fe(II)′ by EDTA, dissociation of Fe(II)EDTA, and oxidation of generated Fe(II)′ to Fe(III)′ by oxygen. The [Fe(II)′]_ss was calculated from the total Fe concentration (≈[Fe(III)EDTA]) and kinetic constants using the following expression:

$${\left[Fe\left(\text{II}\right)\prime \right]}_{\text{ss}}=\frac{k_{hv}\left[Fe\left(\text{III}\right)\text{EDTA}\right]+k_{d-\text{EDTA}}\left[Fe\left(\text{II}\right)\text{EDTA}\right]{}_{\text{ss}}}{k_{f-\text{EDTA}}\left[\text{EDTA}\right]+k_{ox}\left[{\text{O}}_2\right]}$$ (1)

where the unknown [Fe(II)EDTA]_ss represents the steady-state Fe(II)EDTA concentration and can be determined from knowledge of the rate of complexation of Fe(II)′ by EDTA and rates of dissociation and oxidation of Fe(II)EDTA, i.e.:

$${\left[Fe\left(\text{II}\right)\text{EDTA}\right]}_{\text{ss}}=\frac{k_{f-\text{EDTA}}\left[\text{EDTA}\right]{\left[Fe\left(\text{II}\right)\prime \right]}_{\text{ss}}}{k_{d-\text{EDTA}}+k_{ox-\text{EDTA}}\left[{\text{O}}_2\right]}$$ (2)

Rate constants reported by Fujii et al. (15) were assumed appropriate for use in equations 1 and 2 given that very similar experimental conditions were employed in both studies (Table 1 and Fig. 1). Assuming that dissolved oxygen is saturated (i.e., [O₂] of ∼0.25 mM at 25°C) and that [Fe(III)EDTA] is approximately equal to [Fe]_T and [EDTA] is approximately equal to [EDTA]_T when EDTA is in considerable excess of Fe, the two unknown parameters [Fe(II)′]_ss and [Fe(II)EDTA]_ss were calculated from equations 1 and 2 using an iterative trial and error method {i.e., by assuming an initial value of [Fe(II)′]_ss and calculating [Fe(II)EDTA]_ss from equation 2 and then substituting the calculated [Fe(II)EDTA]_ss value into equation 1 to obtain a new value of [Fe(II)′]_ss; repeating the process using the new estimate for [Fe(II)′]_ss and continuing until the calculated [Fe(II)′]_ss was equal to the assumed value of [Fe(II)′]_ss whereupon the solution had converged}. Under the conditions examined here, the calculated steady-state [Fe(II)′] was approximately proportional to [Fe]_T (≈[Fe(III)EDTA]) (see equation 1).

Table 1.

Kinetic model for Fe transformation and uptake in the presence of light by M. aeruginosa^a

Reaction	Rate constant/parameter	Value	Unit
Fe(III)EDTA + hυ → Fe(II)′ + EDTAox	khυ	6.4 × 10−6	s−1
Fe(II)′ + EDTA → Fe(II)EDTA	kf-EDTA	2.1 × 10−6	m−1 s−1
Fe(II)EDTA → Fe(II)′ + EDTA	kd-EDTA	1.2 × 10−3	s−1
Fe(II)′ + O2 → Fe(III)′ + O2−	kox	8.8	m−1 s−1
Fe(II)EDTA + O2 → Fe(III)EDTA + O2−	kox-EDTA	31	m−1 s−1
Fe(II)′ → uptake	ρmax or Kρb	ρFe = ρmax{Fe(II)ss/[Kρ + Fe(II)ss]}	mol cell−1 h−1 or M−1

^aAdapted with permission from reference 15. Copyright 2011 American Chemical Society.

^bFe uptake parameters (ρ_max and K_ρ) were determined as described in the text.

Fig 1.

Model for Fe uptake by M. aeruginosa in the presence of light. (Adapted with permission from reference 15. Copyright 2011 American Chemical Society.)

RESULTS AND DISCUSSION

Growth kinetics in batch culture.

As discussed in the supplemental material, if the values of four growth constants—maximum specific growth rate μ_max (day⁻¹), yield constant Y (cells mol⁻¹), and half-saturation constants K_ST and K_S′ (M) obtained when total and available concentrations (S_T and S′ [M], respectively) of the limiting substrate are considered substrate concentrations—are known, the behavior of a continuous culture at steady state under limitation of a buffered trace metal can be completely defined by equations 3 and 4:

$$\tilde{S}\prime =K_{S\prime }\left(\frac{D}{{\mu }_{\max }-D}\right)$$ (3)

$$\tilde{x}=Y\left(S_1-{\tilde{S}}_T\right)=Y\left[S_1-K_{S_T}\left(\frac{D}{{\mu }_{\max }-D}\right)\right]$$ (4)

where S̃ and S̃_T (M) are the total and available concentrations of substrate at steady state, respectively, S_I (M) is the concentration of substrate in the feed medium, x̃ (cells liter⁻¹) is the steady-state cell density, and D (day⁻¹) represents the dilution rate.

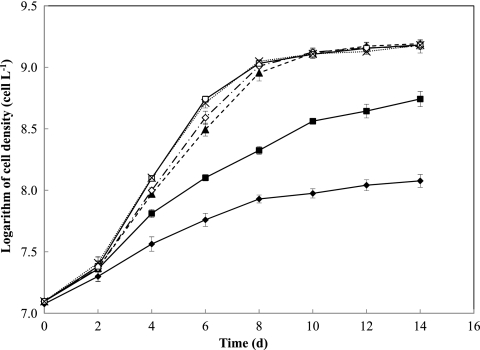
To predict the behavior of Fe-limited chemostat cultures of M. aeruginosa PCC7806, a preliminary study of the growth kinetics of this organism in batch cultures was conducted under incubation conditions identical to those used in the chemostat study with regard to the culture volume and vessels, growth medium, temperature, and light intensity. Only [Fe]_T was modified in order to investigate the growth kinetics under various degrees of Fe limitation. The parent culture in exponential growth phase was subcultured and grown in triplicate in Fraquil*, with [Fe]_T ranging from 0.01 to 10 μM. Application of the exponential-growth equation (see Equation S1 in the supplemental material) to the initial linear section of a semilog plot provided specific growth rates of M. aeruginosa PCC7806 in the batch culture ranging from 0.23 ± 0.012 to 0.82 ± 0.049 day⁻¹ (Fig. 2). [Fe]_T of >1 μM was found to be sufficient to support optimal growth of M. aeruginosa, while at [Fe]_T of ≤0.1 μM, the growth rate of M. aeruginosa declined due to the depletion of Fe available for uptake. These growth rates were consistent with previously reported values for the specific growth rates of M. aeruginosa PCC7806 in batch Fraquil* culture at somewhat higher [Fe]_T of 0.1 to 10 μM (17, 18).

Fig 2.

Growth curves in batch cultures of M. aeruginosa at different total Fe concentrations in Fraquil*. Total Fe concentrations were varied from 10 nM to 10 μM; all other medium components were constant. Symbols represent the means and error bars represent the standard deviations from duplicate incubations (filled diamonds, 10 nM [Fe]_T; filled squares, 20 nM [Fe]_T; filled triangles, 50 nM [Fe]_T; open diamonds, 100 nM [Fe]_T; open squares, 1 μM [Fe]_T; and crosses, 10 μM [Fe]_T).

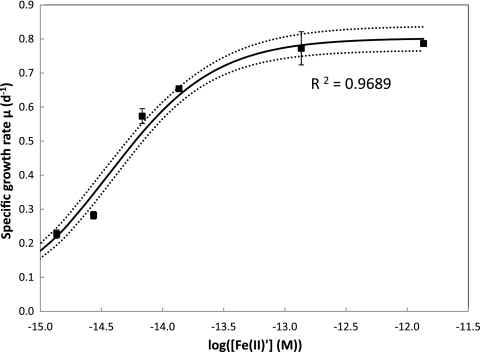
Maximum growth rate and half-saturation constants were estimated via nonlinear regression of the data using the Monod equation, i.e., μ = μ_max[S/(K_S + S)] (Fig. 3). The regression analysis was performed for cases where both total Fe and calculated steady-state Fe(II)′ were treated as the appropriate substrate concentration. Since the steady-state [Fe(II)′] is essentially proportional to the total [Fe] {≈[Fe(III)EDTA]}, in each case the theoretical specific growth rates as a function of Fe concentration fitted well the measured growth rates of M. aeruginosa, yielding the same value for the growth constant (μ_max = 0.80 ± 0.03 day⁻¹). In contrast, a much lower value of the half-saturation constant K_S′ of 3.6 ± 0.32 fM with respect to Fe(II)′ was deduced compared with a K_ST value of 26 ± 2.3 nM for total Fe. Although response of growth rate to Fe limitation is typically expressed in terms of total Fe, expression of K_S′ in terms of Fe(II)′ is more appropriate given that the bioavailable form of Fe in our system is unchelated Fe(II) as a result of the photoreductive dissociation of organically complexed Fe.

Fig 3.

Relationship between specific growth rate μ (day⁻¹) and log concentration of unchelated Fe(II)′ (where [Fe(II)′] is in molar [M] units) in batch culture studies of M. aeruginosa. Nonlinear regression analysis yielded a half-saturation constant for growth of K_S′ = 3.6 ± 0.32 fM [with respect to Fe(II)′] and a maximum specific growth rate μ_max of 0.80 ± 0.03 day⁻¹. Solid and dotted lines represent the regression line and 95% confidential interval, respectively. Symbols indicate data for experimentally determined growth rates under different degrees of Fe limitation.

In a batch culture where growth rate is controlled solely by the concentration of a single limiting nutrient, it would be reasonable to assume that the limiting substrate in the growth medium has been completely consumed upon reaching stationary growth phase. Hence, assuming that the concentration of limiting nutrient is approximately zero at this point, the yield constant Y of M. aeruginosa under Fe limitation ([Fe]_T of 0.01 to 0.1 μM) was determined to be 8.1 ± 0.21 × 10¹⁶ cells (mol Fe)⁻¹ by use of equation S4 in the supplemental material.

Performance of chemostat system under Fe limitation.

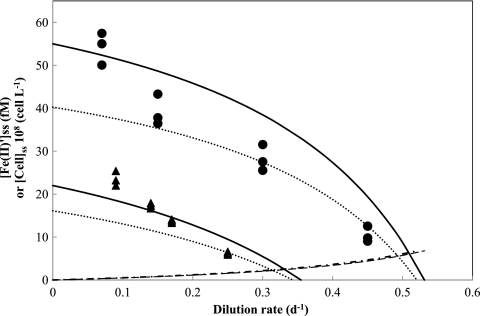
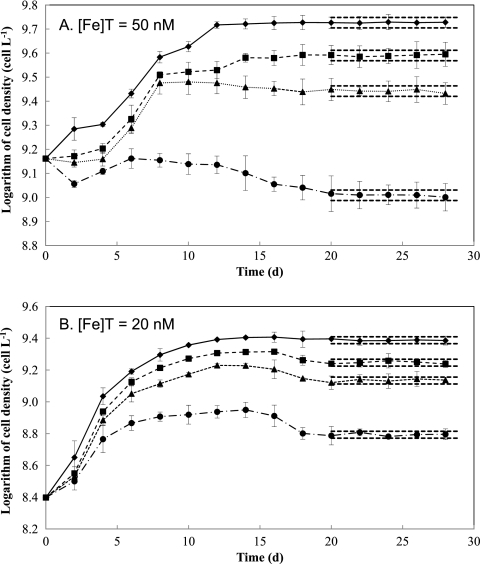
Total Fe concentrations of less than 50 nM in the Fraquil* growth medium were used in continuous cultures in this study to ensure that cultures were maintained under Fe-limited conditions. Using the growth parameters for M. aeruginosa PCC7806 obtained from the Fraquil* batch culture studies, expected values of both the steady-state concentrations of M. aeruginosa cells and unchelated photoreductively produced Fe(II)′ concentrations were calculated as a function of dilution rate, as illustrated in Fig. 4. Critical dilution rates were determined to be 0.34 day⁻¹ for an [Fe]_T of 20 nM and 0.52 day⁻¹ for an [Fe]_T of 50 nM. The continuous cultures were then maintained in Fraquil* at dilution rates less than the critical dilution rate (D_c) with 50 nM Fe (dilution rates of 0.07, 0.15, 0.30, and 0.45 day⁻¹) and 20 nM Fe (dilution rates of 0.09, 0.14, 0.17, and 0.25 day⁻¹) for a period of 4 weeks (Fig. 5).

Fig 4.

Predicted and measured steady-state cell density and substrate concentration in continuous cultures of M. aeruginosa as a function of dilution rate with different total Fe concentrations in the inflowing medium (50 nM and 20 nM). Symbols represent data for steady-state cell density in Fraquil* with total Fe of 50 nM (circles) and 20 nM (triangles). Dotted lines are the theoretical values of steady-state cell density calculated from equation 14 with growth parameters estimated from batch culture studies [μ_max = 0.80 ± 0.03 day⁻¹, K_S′ = 3.6 ± 0.32 fM with respect to Fe(II)′, K_ST = 26 ± 2.3 nM with respect to total Fe, and Y = 8.1 ± 0.21 × 10¹⁶ cells (mol Fe)⁻¹], while bold lines indicate the theoretical steady-state cell density estimated with parameters obtained from continuous culture studies (K_S′ = 3.4 ± 0.82 fM, K_ST = 25 ± 5.0 nM, and Y = 1.1 ± 0.2 × 10¹⁷ cell mol⁻¹), except for μ_max (0.80 ± 0.03 day⁻¹), which was obtained from the batch studies. Dashed and chained lines indicate predicted steady-state unchelated Fe(II)′ concentrations estimated using parameters from batch and continuous culture studies, respectively.

Fig 5.

Growth of M. aeruginosa in the continuous culture system at different dilution rates with total Fe concentrations in the inflowing Fraquil*. (A) [Fe]_T = 50 nM, with dilution rates of 0.07 day⁻¹ (diamonds), 0.15 day⁻¹ (squares), 0.30 day⁻¹ (triangles), and 0.45 day⁻¹ (circles). (B) [Fe]_T = 20 nM, with dilution rates of 0.09 day⁻¹ (diamonds), 0.14 day⁻¹ (squares), 0.17 day⁻¹ (triangles), and 0.25 day⁻¹ (circles). Symbols represent the means and error bars represent the standard deviations from triplicate incubations. Dashed lines represent the 95% confidence intervals at steady state.

In the system with an [Fe]_T of 50 nM (Fig. 5A), there was a 4-day lag before cells began to grow, suggesting that the cells took some time to adjust to the change in medium conditions. At lower dilution rates (0.07, 0.15, and 0.30 day⁻¹), cell density increased with time after day 4. In contrast, at the highest dilution rate (0.45 day⁻¹), the cell number declined significantly from day 4 to day 20, implying that the washout rate was initially higher than the net growth rate under these conditions. The continuous cultures appeared to be at steady state after ∼20 days, when the variation of the cell density with time was less than 5% of the average cell density. In the system with 20 nM radiolabeled ⁵⁵Fe, a lag of 2 days after inoculation was also observed, which was then followed by a stable increase of cells from day 2 to day 12, when each system achieved almost maximum cell yields. The cell concentrations then slightly decreased to reach steady-state growth at around day 20 (Fig. 5B). In both systems, as expected, the steady-state cell density declined with a decreasing degree of iron limitation (i.e., increasing dilution rate), which is consistent with data reported in other Fe-limited chemostat studies (55, 59).

When the chemostat system supplied with 20 nM ⁵⁵Fe reached steady state, cell density and the total concentration of Fe in each reactor was determined. The steady-state cell density (x̃) and steady-state total Fe (S̃_T) were subsequently used to recalculate the half saturation constant and the yield constant using the following equations derived from equations 3 and 4 (26):

$$K_{S_T}={\tilde{S}}_T\left(\frac{{\mu }_{\max }-D}{D}\right)$$ (5)

$$Y=\frac{\tilde{x}}{S_I-{\tilde{S}}_T}$$ (6)

This produced a value of Y = 1.1 ± 0.2 × 10¹⁷ cells (mol Fe)⁻¹, which is comparable to the value of 8.1 × 10¹⁶ cells (mol Fe)⁻¹ derived in the batch culture studies. Although we assumed that all Fe was completely consumed by cells at the stationary phase, a slight underestimation of Y from the batch cultures suggests that during these incubations, some portion of Fe present in the medium is transformed to a nonavailable form of Fe, possibly due to precipitation of Fe (as a ferric oxyhydroxide) or loss of Fe by adsorption to vessel surfaces. Similarly, equation 5 produced a value of K_ST of 25 ± 5.0 nM in the continuous culture studies, with equation S10 in the supplemental material providing a K_S′ value of 3.4 ± 0.82 fM. These values are also consistent with those determined in batch cultures.

The values for K_S′, K_ST, and Y obtained from the continuous culture studies and the estimated value of μ_max in the batch culture studies were used to recalculate the theoretical steady-state cell and Fe concentrations. For comparative purposes, measured steady-state cell densities at different dilution rates are plotted on the same graph as the theoretical data (Fig. 4). The theoretically calculated values are in reasonable agreement with the experimentally determined data, indicating that the cell density decreases in accordance with the increase in dilution rates, while increasing [Fe]_T from 20 to 50 nM leads to an increase in the cell number.

Finally, to verify the hydraulic performance of the chemostat system, the water level inside the culture vessels was monitored every 2 days, and the medium inflow rates were measured before and after the system had been operated continuously for 4 weeks. No significant change was observed in either parameter over this period. Thus, the chemostat system developed for the study of M. aeruginosa in this work is able to operate continuously for a period of at least 1 month without any evidence of contamination or other problems and, as such, cultures of this microorganism could be maintained at steady state over a range of Fe nutritional conditions.

Cellular Fe quota.

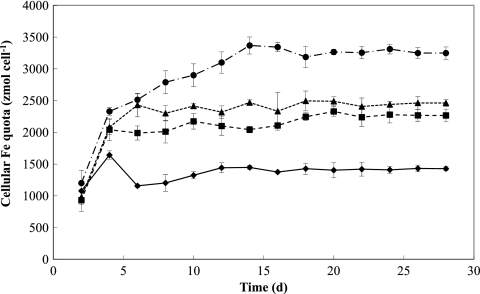
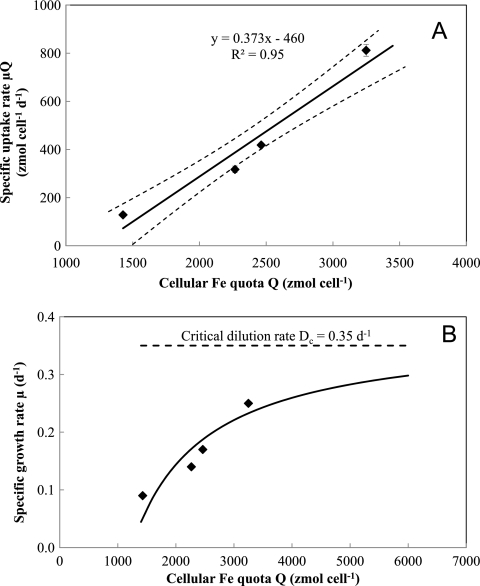
The amount of ⁵⁵Fe internalized by cells was measured every 2 days for a month in the cultures supplied with 20 nM Fe (Fig. 6). During the non-steady-state phase, relatively large fluctuations in cellular Fe quotas were observed at each dilution rate. After day 20, when the system approached steady-state growth, the cellular Fe quotas at each dilution rate became constant with time. Cellular Fe quotas (Q) under steady-state conditions increased as dilution rates (i.e., specific growth rates) increased, consistent with the Droop theory (13). According to this theory, specific growth rates are predicted to hyperbolically increase with increasing steady-state Fe quota (Fig. 7A) as follows:

$$\mu =\mu {\prime }_{\text{max}}\left(\frac{Q-Q_{\min }}{Q}\right)$$ (7)

or rearranging

$$\mu Q=\mu {\prime }_{\text{max}}Q-\mu {\prime }_{\text{max}}{Q}_{\min }$$ (8)

where μ′_max (day⁻¹) is the maximum (impossible) specific growth rate achieved at infinite cellular Fe quota, Q_min (zmol cell⁻¹) is the minimum subsistence quota, and μQ (zmol cell⁻¹ day⁻¹) represents the specific Fe uptake rate or the long-term uptake rate for growth ρ_μ (μQ). The cellular Fe quota parameter μ′_max in equations 7 and 8 (which relates to internal substrate concentration) is unrelated to the growth rate constant μ_max (0.80 day⁻¹) in equation S2 in the supplemental material (which relates to external substrate concentration).

Fig 6.

Time course of cellular Fe quotas for Fe-limited M. aeruginosa in the chemostat with an [Fe]_T of 20 nM as radiolabeled ⁵⁵Fe in the inflowing medium and dilution rates of 0.09 day⁻¹ (diamonds), 0.14 day⁻¹ (squares), 0.17 day⁻¹ (triangles), and 0.25 day⁻¹ (circles). Symbols represent the means and error bars represent the standard deviations from triplicate incubations.

Fig 7.

Relationship between the cellular Fe quota (Q) and the specific uptake rate of Fe (μQ) (A) or specific growth rate (μ) for Fe-limited M. aeruginosa (B) under steady-state conditions in continuous cultures. The system was operated at four different dilution rates (0.09, 0.14, 0.17, and 0.25 day⁻¹) and fed with Fraquil* containing 20 nM radiolabeled ⁵⁵Fe. In panel A, linear regression analysis (represented by the bold line) yielded the maximum, “impossible” growth rate μ′_max of 0.37 ± 0.04 day⁻¹ and minimum cellular quota Q_min of 1.2 ± 0.2 × 10³ zmol cell⁻¹. Symbols represent the means and error bars represent the standard deviations from triplicate incubations. In panel B, the solid line represents the theoretical curve calculated from the Droop equation using the obtained estimated values of μ′_max and Q_min. Symbols represent the mean from triplicate incubations.

Plotting μQ against Q produces a linear transformation of the Droop equation with a slope of μ′_max and an intercept of μ′Q_min, as shown in Fig. 7A for long-term Fe uptake by M. aeruginosa. This plot yields values of Q_min = 1.2 ± 0.24 amol cell⁻¹ and μ′_max of 0.37 ± 0.04 day⁻¹. Assuming that cell diameter of M. aeruginosa PCC7806 is about 4.0 μm, i.e., cell volume of ∼33.5 μm³, this results in Q_min of 3.58 × 10⁻⁵ mol Fe per liter-cell which was comparable to 2.1 ± 0.05 × 10⁻⁵ mol Fe per liter-cell of Thalassiosira weissflogii (4) or lower than those of other species reported previously, such as 4.8 × 10⁻⁵ to 33.3 × 10⁻⁵ mol Fe per liter-cell of Dunaliella tertiolecta (11), 6.9 × 10⁻⁵ to 15.9 × 10⁻⁵ mol Fe per liter-cell of Pavlova lutherii (13), and 9.3 × 10⁻⁵ to 18.6 × 10⁻⁵ mol Fe per liter-cell of T. weissflogii (24). The lower value of Fe quotas of M. aeruginosa observed in this study relative to those of other microorganisms in previous studies may partly be due to removal of extracellular iron during the washing step by EDTA-oxalate solution. As expected, the calculated μ′_max was comparable to the critical dilution rate (D_c) of 0.35 day⁻¹ for the system supplied with 20 nM Fe. The hyperbolic relationship between the cellular Fe quotas and the specific growth rates in this work (Fig. 7B) is consistent with other observations for cyanobacteria, such as Anabaena species and Microcystis species, under nitrogen or phosphorous limitation (1, 22, 42), and eukaryotic phytoplankta, such as green algae Chlamydomonas species and diatom Thalassiosira species, under Fe, Mn, vitamin B₁₂, or phosphorus limitation (20, 24, 50, 51).

Fe uptake kinetics.

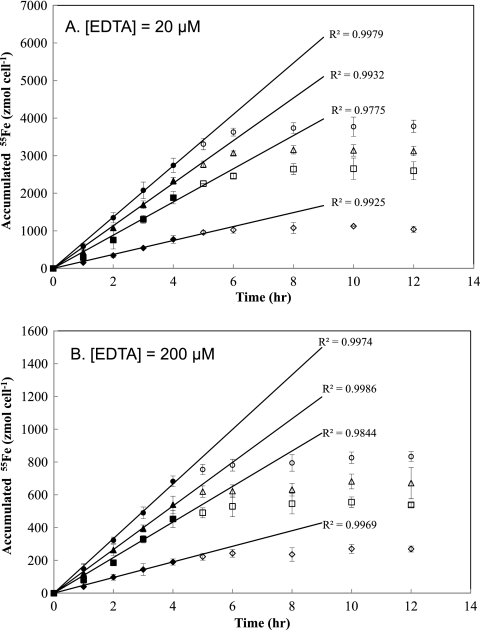
Short-term ⁵⁵Fe uptake assays were undertaken using cells collected from the chemostat supplied with 20 nM nonradiolabeled Fe. In this assay, four batch experiments were prepared by filtering cells from the steady-state chemostat cultures at each of the dilution rates examined and subsequently resuspending them in Fe- and ligand-free Fraquil*. The short-term uptake assay was then initiated by adding preequilibrated ⁵⁵Fe(III)EDTA to each batch experiment. Intracellular ⁵⁵Fe accumulated during incubation in the light was then measured every 1 to 2 h for 12 h. Incubations were conducted in the light based on previous findings that ⁵⁵Fe uptake rates by M. aeruginosa in EDTA-buffered Fraquil* are substantially higher under light irradiation than in the dark due to the higher concentration of bioavailable substrate resulting from photoreductive dissociation of the Fe(III)EDTA complex present in the medium (15). The Fe uptake rate of each steady-state culture of M. aeruginosa was investigated over a range of unchelated photoproduced Fe(II)′ concentrations by varying the EDTA concentrations from 20 to 200 μM, while ⁵⁵Fe concentration was maintained constant (200 nM). Intracellular ⁵⁵Fe accumulated in a linear manner with respect to time for at least 4 h, followed by rapid decline in uptake rate after 6 h, indicating that uptake became saturated in the later stages of the experiment (Fig. 8). An Fe mass balance in these experiments indicated that depletion of extracellular Fe available for uptake was unlikely to have occurred over the duration of the short-term assays.

Fig 8.

Time course of ⁵⁵Fe uptake during batch short-term Fe uptake assays using cells obtained at steady state from the chemostat cultures grown with an [Fe]_T value of 20 nM in the inflowing medium and dilution rates of 0.09 day⁻¹ (diamonds), 0.14 day⁻¹ (squares), 0.17 day⁻¹ (triangles), and 0.25 day⁻¹ (circles). In the short-term uptake assay, each culture was incubated in Fraquil* with either 20 μM EDTA (A) or 200 μM EDTA (B) and constant concentration of radiolabeled ⁵⁵Fe (200 nM). Symbols represent the means and error bars represent the standard deviations from triplicate experiments. The continuous lines were obtained by linear regression of data collected within 4 h (represented by closed symbols) for each culture.

Assuming that the short-term uptake rate for M. aeruginosa follows classical Michaelis-Menten kinetics, the Fe uptake rate can be described as follows:

$${\rho }_{\text{Fe}}={\rho }_{\max }\frac{{\left[Fe\left(\text{II}\right)\prime \right]}_{\text{ss}}}{K_{\rho }+{\left[Fe\left(\text{II}\right)\prime \right]}_{\text{ss}}}$$ (9)

where ρ_max (mol cell⁻¹ s⁻¹) is the maximum uptake rate and K_ρ (M) is the half-saturation constant for short-term Fe uptake. Steady-state concentrations of Fe(II)′ were calculated from equations 1 and 2 using a trial and error method (see Table S1 in the supplemental material). To determine the uptake parameters, an Eadie-Hofstee linear transformation was applied to the measured ⁵⁵Fe uptake rates in each culture as shown in Fig. 9. Linear regression analysis gave comparable half-saturation constants [K_ρ = 18 ± 2.2 fM, as Fe(II)′] but significantly different maximum uptake rates (ρ_max of 0.27 ± 0.030, 0.72 ± 0.060, 0.95 ± 0.080, and 1.0 ± 0.090 amol Fe cell⁻¹ h⁻¹) for the cultures grown at different dilution rates, suggesting that the cells in the continuous cultures adjusted to different degrees of Fe limitation by varying their maximum uptake rate ρ_max rather than the half-saturation constant K_ρ. This ability to regulate short-term uptake has previously been suggested in studies of algal growth under limitation by macronutrients such as N, P, and Si (20, 34, 53) as well as by Fe (24). In comparison to other studies, the maximum uptake rates ρ_max obtained in this study (assuming a cell volume of M. aeruginosa of ∼33.5 μm³) ranged from 0.8 × 10⁻⁵ to 2.9 × 10⁻⁵ mol Fe liter-cell⁻¹ h⁻¹ and were one order lower than those of Thalassiosira weissflogii reported in Anderson and Morel (4) (ρ_max = 1.1 × 10⁻⁴ to 2.1 × 10⁻⁴ mol Fe liter-cell⁻¹ h⁻¹), Harrison and Morel (24) (ρ_max = 2.4 ± 0.02 × 10⁻⁴ mol Fe liter-cell⁻¹ h⁻¹), and Morel (37) (ρ_max = 3.2 × 10⁻⁴ mol Fe liter-cell⁻¹ h⁻¹). This is likely because lower Fe availability in marine systems may lead to higher uptake capacity of marine microorganisms relative to those of freshwater microorganisms.

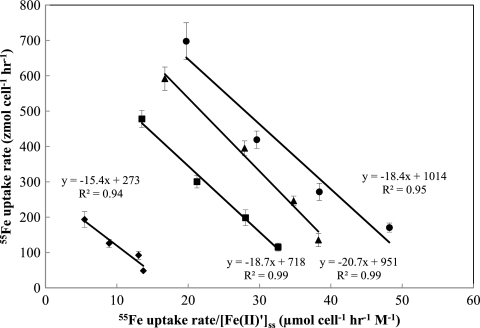
Fig 9.

Eadie-Hofstee plots demonstrating the linear relationship between the short-term ⁵⁵Fe uptake rate (ρ_Fe) and the ratio ρ_Fe/[Fe(II)′] (day⁻¹ M⁻¹) for cultures of M. aeruginosa. Linear regression analysis yielded comparable half-saturation constants for Fe uptake [K_ρ = 18 ± 1.9 fM, as Fe(II)′] but different maximum specific uptake rates (ρ_max of 270, 720, 950, and 1,010 zmol cell⁻¹ h⁻¹ for cultures grown at dilution rates of 0.09 day⁻¹ [diamonds], 0.14 day⁻¹ [squares], 0.17 day⁻¹ [triangles], and 0.25 day⁻¹ [circles], respectively). Lines for 95% confidential intervals were omitted for clarity.

Cellular response to Fe limitation in chemostat.

The half-saturation constant with respect to Fe uptake (K_ρ) was determined to be higher than that for the growth rate (K_S′) by ∼5-fold, suggesting that the decline in Fe uptake due to low Fe availability does not necessarily result in a decline in capacity for cellular growth. Rather, an optimal growth rate is maintained until Fe concentrations are imposed that are substantially lower than those at which a decline in Fe uptake begins to occur, after which growth rate starts to decrease. This is consistent with previous observations that cells of the marine cyanobacterium Synechococcus exhibit symptoms of Fe stress under low Fe availability (e.g., declining photosynthetic activity) well before growth rate is affected, implying that cellular division is accorded a higher priority than general metabolic functioning even in low-nutrient environments (25). Different preconditioning of cells in the Fe-limited chemostat resulted in altered responses of cells with regard to Fe uptake. The Fe uptake capacity increased as the degree of Fe limitation decreased from the most-starved condition to the least starved. A similar trend was also found in iron-limited chemostat cultures of green algae Chlamydomonas reinhardtii (55), Chlorococcum macrostigmatum, and Stichococcus bacillaris (59), where an increase in dilution rate (or decrease in degree of Fe limitation) led to an increase in plasma membrane ferric chelate reductase (FC-R) activity, hence, likely an increase in Fe(II) uptake capacity. However, this trend is the reverse of the expected relationship between cellular Fe quota and uptake rate, where cells with a higher degree of nutrient limitation generally exhibit higher uptake rates (21, 22, 42).

Provided that Fe uptake is mediated by concentration gradient-dependent passive diffusion through nonspecific transmembrane channels (porins) as suggested by Fujii et al. (15) for M. aeruginosa and by Jones and Niederweis (29) for Mycobacterium smegmatis, Fe uptake rate is likely proportional to cell surface area. A slight increase (by a factor of ∼1.5) in average cell volume (and hence cell surface area) was found in P-limited continuous cultures of Monochrysis lutheri, with an increase in dilution rate from 0.1 day⁻¹ to 1.0 day⁻¹ (6). A similar trend was found in N-limited continuous cultures of Chlorella pyrenoidosa (63). Thus, an increase in dilution rate may result in an increase in cell surface area and hence in the cell-normalized Fe uptake rate. However, there was no substantial change in the size of M. aeruginosa cells with increasing dilution rates in this work (mean diameters of 4.1 ± 0.07, 3.8 ± 0.01, 3.8 ± 0.05, and 3.8 ± 0.01 μm in cultures grown at dilution rates of 0.09, 0.14, 0.17, and 0.25 day⁻¹, respectively), consistent with the observed invariant K_ρ values among the four cultures. Therefore, change in cellular size could not account for the ∼5-fold relative increase in the ⁵⁵Fe uptake rate observed in the culture grown at the highest dilution rate versus that grown at the lowest dilution rate.

Another possible explanation is that the starved cells grown under extreme Fe stress require time to recover Fe uptake machinery before functioning optimally, while less-starved cells can immediately acquire Fe at optimal rates. As a result, within the recovery period, the less-starved cells would exhibit a higher Fe uptake rate (i.e., the Fe uptake trend observed in this work), but beyond this recovery period, more-starved cells would exhibit greater Fe uptake rates, corresponding to the expected trend suggested by others (37). However, the decrease in accumulated cellular Fe with an increasing dilution rate during both the linear Fe uptake period (0 to 4 h) and the nonlinear Fe uptake period (4 to 12 h) shown in Fig. 8 implies that such an explanation is unlikely.

Since the transport of Fe across the (cyto)plasmic membrane of cyanobacteria is generally mediated by ATP-binding cassette (ABC) transporters (5), a more plausible reason is that decline in either the efficiency of energy-dependent processes or of energy (i.e., ATP) production during photosynthesis causes decreasing Fe uptake under extreme Fe stress. For severely Fe-limited cells (those grown at lower dilution rates in this study), it is likely that the photosynthetic capacity and subsequent ATP production from the cyclic electron transport are minimal due to very low Fe availability, resulting in these cells being unable to drive high Fe uptake rates. This possibility is supported by results from short-term ¹⁴C uptake assays using the same steady-state cultures as those used for the short-term Fe uptake experiments. As shown in Fig. S2 in the supplemental material, the accumulation rate of radiolabeled carbonate in cells decreased with decreasing dilution rates during an incubation period of 12 h, similar to the trend observed in the short-term ⁵⁵Fe accumulation studies. Therefore, a shortage of resources necessary for Fe uptake, such as an internal transporter or ATP, may account for the short-term Fe uptake trend in this study. Additionally, a physiological trade-off may occur under Fe stress between the affinity for Fe at the cell surface (i.e., the number of surface uptake sites or Fe channels) and the maximum rate at which Fe can be assimilated (i.e., the number of internal transporters which assimilate Fe once it is encountered) (46). When grown under Fe stress for a long period, cells may acclimate by maintaining the number of surface uptake sites while decreasing the number of internal enzymes available for Fe uptake. In the presence of any pulse of Fe, cells with fewer internal transporters will likely exhibit lower Fe uptake rates than nonstressed cells. This physiological acclimation strategy has been used to explain the observed pattern of nitrate uptake by phytoplankton in the ocean (46).

In summary, we have shown that a continuous culturing system made of metal-free material provides a valuable tool to investigate the cellular responses of M. aeruginosa under Fe limitation. The system was successfully operated to produce steady-state cultures with different cell densities and different cellular properties. In particular, the cellular response to steady-state Fe limitation in the chemostat system followed the Droop equation, i.e., cellular Fe quotas decreased with increasing Fe availability. Under Fe stress, cells of steady-state cultures of M. aeruginosa regulated their short-term Fe uptake by varying their uptake capacity ρ_max but not their affinity for Fe (i.e., the half-saturation constant K_ρ). Fe uptake data from this study show that Fe-limited M. aeruginosa cells grown under severe Fe stress (i.e., lower dilution rates) are likely unable to synthesize sufficient resources (such as internal transporters and/or ATP) required for Fe uptake and therefore exhibit less Fe uptake ability than cells grown under conditions in which Fe is more available (i.e., at higher dilution rates).