Poisson Growth Mixture Modeling of Intensive Longitudinal Data: An Application to Smoking Cessation Behavior

Abstract

Intensive longitudinal data (ILD) have become increasingly common in the social and behavioral sciences; count variables, such as the number of daily smoked cigarettes, are frequently-used outcomes in many ILD studies. We demonstrate a generalized extension of growth mixture modeling (GMM) to Poisson-distributed ILD for identifying qualitatively distinct trajectories in the context of developmental heterogeneity in count data. Accounting for the Poisson outcome distribution is essential for correct model identification and estimation. In addition, setting up the model in a way that is conducive to ILD measures helps with data complexities – large data volume, missing observations, and differences in sampling frequency across individuals. We present technical details of model fitting, summarize an empirical example of patterns of smoking behavior change, and describe research questions the generalized GMM helps to address.

Technological advances, such as web-based assessments, hand-held computers (e.g. personal digital assistants, wrist watches, phones), and portable devices that automatically capture human behavior, physiology, and contextual surroundings (e.g. GPS, pedometers, cigarette and medication dispensers), yield detailed records at low cost with little intrusion in participants’ life. In the social sciences, this method of collecting data in real time and naturalistic settings is often called ecological momentary assessments (Schwartz & Stone, 1998; Smyth & Stone, 2003; Stone & Shiffman, 2002) or experience sampling (Larson & Csikszentmihalyi, 1983). In statistical terminology, such assessments are referred to as intensive longitudinal data (ILD; Collins, 2006; Walls & Schafer, 2006), which are characterized by “more than a handful of time points” (Walls & Schafer, 2006, p.xiii), usually exceeding 20 or more repeated assessments per person (Collins, 2006; Walls, Hoppner, & Goodwin, 2007). In addition, ILD collected in proximal time to the phenomena under investigation tend to have reduced recall and reactivity biases (Shiffman, Stone, & Hufford, 2008; Smyth & Stone, 2003; Stone et al., 1998). Importantly, they allow for a nuanced monitoring of time-sensitive developmental processes such as changes in smoking urges during a smoking cessation period, progression of post-operative pain intensity, or a pathway of emotional recovery after a traumatic event.

A number of statistical approaches have been applied to describe patterns of ILD-based developmental trajectories, while accounting for ILD challenges, such as inter-correlation between repeated assessments, data missingness, and differences in sampling frequency and timing of observations. Multilevel modeling (MLM; Armeli et al., 2003; Schwartz & Stone, 1998, 2007) has been the most widely used technique for describing time-dependent trajectories, which accounts for classical heterogeneity in developmental curves (Walls et al., 2007). Alternative techniques for modeling more complex time-dependent processes include time-series analysis (Nesselroade & Molenaar, 2004; Velicer & Fava, 2004) and a number of nonparametric models (Li, Root, & Shiffman, 2006; Walls et al., 2007). None of these approaches, however, account for large distinctions in trajectories; thus, modeling of unique developmental clusters falls outside the capacity of these methods.

In this paper, we introduce the generalized growth mixture modeling (generalized GMM) approach (Muthén, 2004, 2007; Muthén & Shedden, 1999) for modeling Poisson-distributed ILD. In social sciences, count data are very common. Some examples of ILD include daily alcohol or cigarette consumption, number of correct or incorrect responses during a learning process, frequency of health-related symptoms, rate of a particular coping strategy use, or frequency of experiencing certain feelings or emotions. In spite of high prevalence of count data, they are often not modeled appropriately. In previous applications of GMM to traditional repeated-measures data, some authors treated a count outcome as continuous (e.g. Beadnell, et al., 2005), dichotomized it in order to simplify a distribution to a binary case (e.g. Audrain-McGovern, et al., 2004), collapsed categories to reduce non-normality (e.g. Lansford, et al., 2010), or performed a logarithmic transformation (e.g. Jackson & Sher, 2005), which does not correct for the overrepresentation of low values (e.g. zeros and ones).

Thus, the goal of the current paper is two-fold. First, we strive to encourage researchers modeling count data with GMM to consider the nature of the outcome very carefully. Second, in response to increased popularity of ILD, we demonstrate how the model can be specified in a flexible way to account for ILD complexities.

GMM Research Questions and Applications

The purpose of the GMM method is to describe heterogeneity in development by identifying a number of qualitatively distinct trajectories. Conceptually, GMM can be used to address a number of unique and important research questions. First, the model can identify distinct trajectories of development as a parsimonious summary of inter-individual differences. Recognition of developmental groups (latent classes) is based on similarities in trajectories rather than predetermined person-level indicators, such as race or gender (common for describing heterogeneity in MLM). Second, the model allows linking each developmental class to a distal outcome for class validation purposes as well as examination of lingering developmental effects. Finally, covariates can be incorporated to build a profile of individuals following each developmental trend based on a combination of personal characteristics, which is essential for understanding early indicators of a particular developmental process.

Summarizing complex ILD-based developmental patterns may prove invaluable for epistemological and practical reasons. For example, learning about normative and pathological trajectories as well as related risk factors can help to identify individuals at risk and to prevent negative consequences or intervene to minimize them. In traditional longitudinal studies, GMM has been used to study the probability of criminal arrest in adulthood across classes of individuals exhibiting different progressions of antisocial behavior during adolescence (Schaeffer et al., 2006) and to study the risk of Alzheimer’s diagnosis for elders with various patterns of memory deterioration in pre-clinical years (Small & Backman, 2007). Another example involves identification of reading developmental profiles in primary school children and their association with reading difficulties in kindergarten (Boscardin, Muthén, Francis, & Baker, 2008). Two ILD studies applied the model to examine the mood patters and bulimic behaviors (a normally-distributed outcome; Crosby et al., 2009) and differential effects of the drug and behavioral therapy on the probability of drinking (Gueorguieva et al., 2010). In these applications, the model was specified in a traditional way, not accounting for differences in sampling schedules across individuals or missing data.

Implications for Count GMM

The central research question of GMM is the identification of distinct latent developmental classes. Statistically, this is accomplished by searching for the best solution that satisfies the conditional normality assumption, which posits that distributions of repeated measures within latent classes are normal. It has been demonstrated that GMM is very sensitive to violation of this assumption (Bauer, 2007; Bauer & Curran, 2003; Tofighi & Enders, 2008), such that, in cases when this assumption is violated even to a small degree, the number of extracted classes tends to be over-estimated, resulting in invalid findings, model misinterpretations, and possible non-intended practical implications. In case of a count outcome, if a Poisson distribution is not specified, false classes may emerge by artificially accounting for data non-normality.

In addition to improper class enumeration, misspecifying a model for count data may lead to problems with model interpretation. Examples of such difficulties include model predictions that fall outside the scale boundaries (e.g. taking negative values) or estimates that do not make practical sense (e.g. non-integer values).

The Current Study

To demonstrate how generalized GMM can be properly specified and carried out in the context of intensive longitudinal count data, we introduce its features, including the important stages of model fitting and selection. Next, we present an empirical demonstration of daily smoking data, carrying out analyses with the correct model specification. Technical materials are incorporated to describe data structure and syntax is provided to ease implementation of the model by other researchers. We conclude with remarks about the importance of generalized GMM for ILD Poisson-distributed outcomes and some software considerations.

Generalized GMM: a Model Overview

Generalized GMM is a statistical approach similar to but broader than Structural Equation Modeling (SEM), which can be used to answer a wide array of research questions related to growth processes. In this paper, the focus is on three major inquiries. First, we are interested in identifying and describing distinct developmental classes, measured by count ILD (e.g. describing profiles of smoking cessation behaviors). Second, as part of the class validation process, we are concerned with whether or not trajectories are predictive of a distal outcome (e.g. are people who take a particular behavioral approach to smoking cessation more successful in quitting than others?). Finally, we want to investigate whether baseline covariates (e.g. age, nicotine dependence) can be used to predict which behavioral pattern might be expected for individuals with certain characteristics.

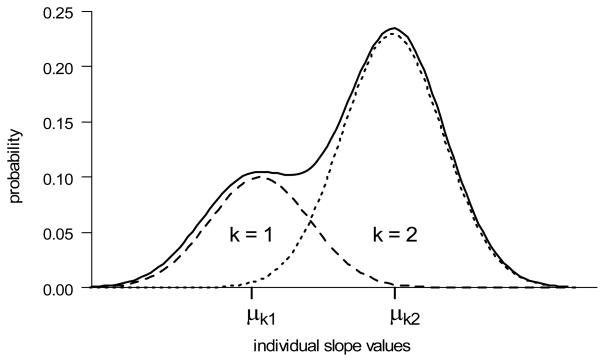
Theoretically, generalized GMM bridges out from finite mixture models (McLachlan & Peel, 2000), which relax the assumption of developmental homogeneity. This implies that intercept and slope growth parameters can have an underlying distributional mixture, which is constructed from several distinct distributions with their own parameters. Figure 1 presents a simulated example of a mixture of slopes from a model with two latent classes. When class membership is ignored, the combined single distribution of slopes appears bimodal. Practically speaking, detecting a mixture of distributions is not always straightforward, because the deviation from normality can be minor (Bauer & Curran, 2003, 2004; Nagin & Tremblay, 2005), and not all non-normal distributions consist of a mixture. A description of the model selection procedure is presented in the following section of this article.

Figure 1.

A Mixture of Slopes from Two Normal Distributions: Individual Distributions are Captured by Dashed Curves, the Mixture is Represented by a Solid Line.

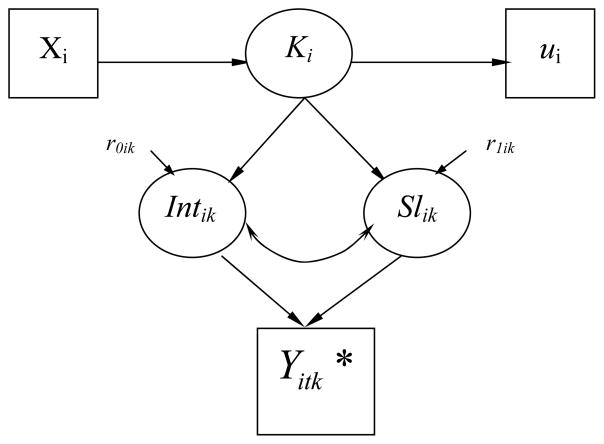
Figure 2 provides a conceptual overview of generalized GMM, where, in accordance with SEM conventions, observed variables are depicted in rectangles and latent variables in circles. In generalized GMM, developmental trajectories are specified at the class level K for each person i, measured at time t. Note that K_i is a person-level variable, as an entire personal trajectory is conceptualized to represent a particular latent behavioral class. It is possible to specify K_it on the observational level, but this is more commonly done in cross-sectional studies where individuals are nested within higher-level units, such as classrooms, neighborhoods, or hospitals. A developmental trajectory for each latent class K_i is described by individual random intercept Int_ik and slope Sl_ik parameters. Within-class individual variability in those parameters is captured by intercept and slope random effects r_0ik and r_1ik. Time-invariant baseline characteristics X_i differentiate between individuals falling within each developmental class. A distal outcome u_i is linked to each developmental trajectory to assess and compare the impact of each latent class.

Figure 2.

Conceptual Diagram for Generalized GMM for Poisson-Distributed ILD.

What distinguishes this model from a GMM for traditional longitudinal data is the ILD outcome Y_itk, measured on the count scale. The outcome can be expressed as a vector of responses {y_i1, y_i2, …, y_iTi} for each study participant i, measured at T_i different time points. Y_it takes on only positive integer values (i.e. 0, 1, …), such as the daily number of cigarettes smoked or the number of alcoholic drinks consumed. T_i is a continuous time indicator, specific to each person i. Due to differences in assessment schedules, t_it may differ across study participants, such that the second observation for two people can be measured at t_{2 (i=1)} = .3 and t_2(i=2) = 1.1 days, respectively. In addition, the number of observations (i.e., length of the response vector Y_it) can also vary across individuals due to differences in the total number of assessments.

In Poisson data, the outcome Y_itk is not modeled directly; this is signified with an asterisk (*) in the figure. Instead, the Poisson parameter representing a class-specific rate of behavior for a person i measured at time t is modeled. In contrast to the SEM convention, where data have a multivariate (i.e. wide) structure, we represent the repeated measures outcome Y_itk by a single rectangle, assuming a univariate (i.e. long) data structure, which is explained in detail in the model fitting section.

Generalized GMM: a Technical Model Summary

In count ILD, the outcome Y_itk has an underlying Poisson distribution, that isY_itk | K_i = k ~ Poisson (λ_itk), and the underlying mixture model is based on the mixture of Poisson probability functions of the form:

$$P(Y_{\mathit{itk}}=y_{\mathit{itk}}\mid K_i=k)=\frac{e^{-{\lambda }_{\mathit{itk}}}{\lambda }_{tk}^{y_{\mathit{itk}}}}{y_{\mathit{itk}}!}\mathit{for}{y}_{\mathit{itk}}=0,1,2,\dots .$$

The mean and variance parameter λ_itk defines the Poisson distribution. If the outcome were daily smoking count, the probability of observing a smoking rate of 5 cigarettes on a given day t would depend on the average observed rate λ for a particular day t for individuals in class K_i = k.

While the growth part of the model in Figure 2 can be defined in several ways, the MLM perspective (Goldstein, 2003; Hox, 2002; Raudenbush & Bryk, 2002; Singer & Willett, 2003) appears to best accommodate the demands of ILD. Such a model, with no baseline covariates, can be formulated in the following way:

$$ln({\lambda }_{\mathit{itk}})={\beta }_{00k}+{\beta }_{10k}\ast {\mathit{time}}_{ti}+r_{0ik}+r_{1ik}\ast {\mathit{time}}_{ti}.$$ (1)

In Equation 1, the natural logarithm of the Poisson parameter λ_itk is used as a link function to ensure that all model predictions fall within the positive continuum of the scale. Assuming a linear relationship after the logarithmic transformation, the rate of change is modeled as a simple linear function, conditional on latent class membership. The model can be extended to contain higher order polynomial terms to account for any remaining developmental non-linearity after the logarithmic transformation. The intercept β_00k and slope β_10k parameters are referred to as fixed effects that take on class specific values. They define the shape of developmental curves for each latent class. Within-class variability in growth parameters is captured by random intercept r_0ki and slope r_1ik effects that are also class specific; that is (r_0ik, r_1ik) ~ MVN(0,τ_k), where ${\tau }_k=\left[\begin{array}{ll}{\tau }_{00k}\hfill & {\tau }_{01k}\hfill \\ {\tau }_{10k}\hfill & {\tau }_{11k}\hfill \end{array}\right]$.

Inclusion of random effects in the growth model has been a topic of controversy. Some authors argue that allowing variability across average trajectories may lead to diffusion of classes (Nagin, 2005) and problems with model identification and convergence (Jung & Wickrama, 2008). Considering potential complications, random effects can be beneficial for describing latent classes, but need to be incorporated cautiously and, possibly, only for some model parameters and some latent classes (Asparouhov & Muthén, 2008). Generalized GMM is flexible enough to work on a class-by-class basis, freeing some model parameters and constraining others. Similarly, developmental shapes do not need to be identical across classes, such that a linear form may be sufficient for one class but quadratic or cubic functions are more descriptive for others.

In GMM, baseline covariates X_i serve an important role in describing profiles of individuals representing each latent group. Statistically, this relationship is characterized by multinomial logistic regression for unordered responses (Agresti, 2002):

$$ln\left[\frac{P(K_i=k\mid X_i)}{P(K_i=K\mid X_i)}\right]={\omega }_{0k}+{\omega }_{1k}\ast X_i\text{for}k=1,\dots ,K-1,$$ (2)

where K is the reference class. The log odds of being a member of a particular class k versus being in the reference class K are modeled as a function of person-level baseline covariates X_i.

Finally, in the case of a binary distal outcome (e.g. success vs. failure), the log odds of observing a positive outcome (u_i = 1) are estimated for each developmental class K by means of binary logistic regression:

$$ln\left[\frac{P(u_1=1\mid K_i=k_i,X_i)}{P(u_1=0\mid K_i=k_i,X_i)}\right]={\nu }_{0k}\text{for}k=1,\dots ,K.$$ (3)

The individual class membership k_i is estimated using the pseudo-class draw technique (Bandeen-Roche, Miglioretti, Zeger, & Rathouz, 1997; Wang, Brown, & Bandeen-Roche, 2005). For each pseudo-class draw, the model parameters in Equation 3 are estimated and, subsequently, averaged. Corresponding asymptotic variances of the estimates are computed (Schafer, 1997). It is possible to expand Equation 3 to accommodate baseline covariates X_i as possible predictors of u_i in addition to class membership information.

Finding the correct number of latent classes is of prime importance in fitting generalized GMM. According to recommendations from a number of simulation studies (Nylund, Asparouhov, & Muthén, 2007; Tofighi & Enders, 2008; Tolvanen, 2007) with four waves of longitudinal data, including conditions with small samples of 50 (Tolvanen, 2007) and 200 individuals (Nylund et al., 2007), BIC and ABIC were used in the empirical example presented in the following section to select a model with the smallest value on the information criteria. We also relied on classification tables (Boscardin et al., 2008; Wang & Bodner, 2007), graphical summaries (Boscardin et al., 2008), the magnitude and interpretability of model parameters, and the replicability of the best log likelihood (LL).

Generalized GMM for Poisson-distributed ILD: an Empirical Demonstration

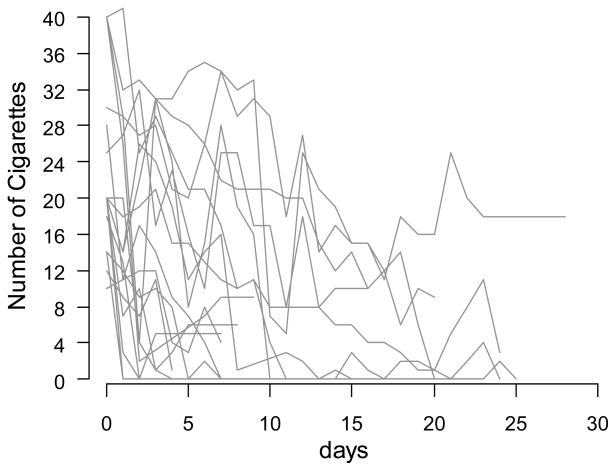
To illustrate the use of generalized GMM with Poisson-distributed ILD, we present an example of data collected as part of the smoking cessation trial for newly-diagnosed cancer patients awaiting cancer-related surgery. As part of the intervention, 74 individuals recorded their smoking behavior in real time, marking all smoked cigarettes on a personal digital assistant (PDA). After adding all daily smoked cigarettes for every patient, 896 daily amounts of smoking were reconstructed. On average, 12.1 days of total daily cigarette count were available per person (SD = 6.1, range: 2 to 29 days, median = 9.5). Figure 3 presents a random sample of smoking trajectories from 20 patients. The overall sample was comprised of an approximately equal number of men and women, with about a third diagnosed with smoking-related tumors (i.e., thoracic, head and neck, and bladder), an average daily baseline smoking rate of 18.8 cigarettes (SD = 9.2), and an average smoking history of 34.5 years (SD = 12.7). More details on sample and study design description are reported elsewhere (Ostroff et al., in preparation).

Figure 3.

Smoking Trajectories for a Random Sample of 20 Patients from the SRS Study.

Due to multiple smoking-related peri-operative complications as well as the smoke-free hospital policy, the study was designed to elicit a change in smoking behavior with the goal to achieve complete pre-hospitalization abstinence. All study participants were given a combination of the scheduled reduced smoking (SRS) intervention (Cinciripini et al., 1995), nicotine-replacement therapy, and counseling. SRS entailed a gradual tapering regimen, individualized for every patient based on the baseline smoking rate and time until surgery. Patients were free, however, to change the schedule by initiating an earlier quit attempt or postponing their quit date.

Due to hypothesized heterogeneity in pre-surgical smoking behavior, it was theorized that patterns in smoking behavior change would follow several qualitatively distinct latent classes. The analytical goal was to identify and describe classes of smoking behavior change; examine efficacy of each behavioral approach evaluated by verified smoking status at surgery admission; and describe profiles of individuals within each class based on a number of baseline covariates such as self-efficacy for quitting, number of smoking years, nicotine dependence, and time until surgery. In the following sections, we present a step-by-step description of fitting, selecting, and interpreting GMM for Poisson-distributed smoking data.

Model Fitting

In the social sciences, one of the most frequently used software packages for fitting growth mixture models is Mplus (Muthén & Muthén, 2007). While it may not be ideal for fitting generalized GMM for ILD for some reasons described later, it is flexible enough to accommodate ILD’s intensity, missingness, and between-person differences in measurement time. The “multilevel” and “mixture” add-ons to the “base” software package are required to fit the generalized GMM for Poisson ILD. The complete syntax with accompanying comments for fitting a single class and three-class generalized GMM is reported in Appendices 1 and 2. The current section only focuses on the data structure and several MODEL¹ statements that require explanation.

Appendix 1.

Mplus Syntax for the Final 1-Class MLM with a Distal Outcome

Syntax	Comments
DATA:
FILE is data.dat;	Specify the data file
VARIABLE:
NAMES ARE SubjID Day SmoRate …;	Variable names in the data file
MISSING = ALL (999);	Specify missing values
USEVARIABLE = SubjID Day SmoRate YRSsmo SEMean QuitSurg Fager;	Use variables for current analysis
CLUSTER = SubjID;	Clustering variable in MLM
CATEGORICAL = QuitSurg;	Categorical distal outcome
COUNT = SmoRate;	Poisson distributed count outcome
WITHIN = Day;	Level-1 time variable
BETWEEN = YRSsmo SEMean Fager;	Level-2 between-person covariates
ANALYSIS:
TYPE = TWOLEVEL RANDOM;	Type of analysis: MLM with random effects
ALGORITHM = INTEGRATION;	Numerical integration is used to obtain maximum likelihood
CHOLESKY = OFF;	Turning off Cholesky optimization method for numerical integration
STARTS = 20 5;	The number of EM random starts
MODEL:
%WITHIN%	Level-1 MLM
Sl | SmoRate ON Day;
%BETWEEN%	Level-2 MLM
phant0 BY SmoRate;	Intercept latent variable phant0 is measured by intercept parameter SmoRate
SmoRate@0;	Variance of intercept parameter SmoRate is constrained to zero
phant0 ON Fager;	Latent intercept is regressed on baseline covariate
phant1 BY Sl;	Slope latent variable phant1 is measured by slope parameter Sl
Sl@0	Variance of slope parameter Sl is constrained to zero
phant1 ON SEMean YRSsmo;	Latent slope is regressed on baseline covariate
phant0 WITH phant1@0;	Covariance of latent intercept and slope parameters is constrained to zero
QuitSurg ON phant0 phant1;	Distal outcome QuitSurg is regressed on intercept and slope latent parameters
OUTPUT:
SAMPSTAT	Request sample descriptive statistics
PATTERNS;	Request a summary of missing data patterns

Appendix 2.

Mplus Syntax for the Final 3-Class Generalized GMM

Syntax	Comments
DATA:
FILE is data.dat;
VARIABLE:
NAMES ARE SubjID Day SmoRate …;
MISSING = ALL (999);
USEVARIABLE = SubjID Day SmoRate QuitSurg SEMean cancer Fager SxTime;
CLASSES = cb (3);	Number of latent classes (3)
CLUSTER = SubjID;
COUNT = allSmo;
CATEGORICAL = QuitSurg;
WITHIN = SmoRate;
BETWEEN = cb QuitSurg SEMean cancer Fager SxTime;
ANALYSIS:
TYPE = TWOLEVEL RANDOM MIXTURE;	MLM mixture model with random effects
ALGORITHM = INTEGRATION;
CHOLESKY = OFF;
STARTS = 1500 10;
STITERATIONS = 20;	Maximum number of iterations in the initial EM stage
MODEL:
%WITHIN%	Level-1 MLM
%OVERALL%
Smo ON Day;	Model with fixed slopes
%cb#2% Smo ON Day;	Request separate estimation of model parameters for classes 2 and 3
%cb#3% Smo ON Day;
%BETWEEN%	Level-2 MLM
%OVERALL%
SmoRate;	Random intercept
CB on SEMean cancer Fager SxTime;	Predicting class membership from baseline covariates
%cb#2% SmoRate;	Request separate estimation of intercept variance for classes 2 and 3
%cb#3% SmoRate;
OUTPUT:
SAMPSTAT
TECH7	Request sample statistics for each latent class
SAVEDATA:	Saving data
FILE is 3CLmodel.dat;	Name of output data file
SAVE = cprob;	Save posterior class probabilities

Data Structure

When modeling the growth process for ILD, it is convenient to specify the model from the MLM perspective (Equation 1) with data following the long or univariate format (Table 1). With this data structure, the outcome vector y_it is stretched vertically, such that a single column contains all data values. The vector of responses is accompanied by a continuous time_ti indicator, specifying timing of each observation and differing across individuals, and a person indicator (i.e. SubjectID_i). This format of data structure accommodates extended time-series of records that differ in length and assessment times.

Table 1.

An Example of Long/Univariate Format of ILD Structure

Subject ID	Count Outcome (Yit)	Time (t)	Age (Xi)	Distal Outcome (ui)
01	20	0.2	62	0
01	18	1.6	62	0
01	17	2.3	62	0
01	12	4.0	62	0
02	40	0.0	55	0
02	36	1.9	55	0
02	36	2.2	55	0
02	25	7.4	55	0
…	…	…	…	…
74	15	1.8	54	1
74	3	4.3	54	1
74	0	6.8	54	1
74	0	7.1	54	1

Model Specification in MPlus

In MPlus, the MLM specification is done in the WITHIN part of the MODEL statement, where the amount of daily smoking SmoRate is regressed on the day indicator Day. The model is specified as follows: Sl | SmoRate ON Day;where both the intercept SmoRate and slope Sl parameters are random and estimated for each individual. In the process of model enumeration, consecutive model building requires an initial estimation of the model with a single class. Although such a model is a special case of generalized GMM, it requires special syntax statements to accommodate a distal outcome. With random intercept and slope parameter, a model with a distal outcome would address a question of whether there is a relationship between individuals’ initial level of smoking, magnitude of smoking decline, and later smoking status. With only one class, a distal outcome QuitSurg in the BETWEEN part of the model is regressed on random person-specific intercept and slope parameters, computed by the following formula:

$$\left[\begin{array}{l}{\mathit{Int}}_i\hfill \\ {Sl}_i\hfill \end{array}\right]=\left[\begin{array}{l}{\beta }_{00}+{\beta }_{01}\ast X_i+r_{0i}\hfill \\ {\beta }_{10}+{\beta }_{11}\ast X_i+r_{1i}\hfill \end{array}\right].$$ (4)

In MPlus, however, the distal outcome QuitSurg cannot be directly regressed on Int and Sl parameter estimates in a single-class model. Instead, two phantom (Grimm & Ram, 2009) latent variables phant0 and phant1 are created that absorb values of the parameters: phant0 BY SmoRate; phant1 BY Sl; Subsequently, variances of the original intercept and slope parameters are constrained to zero, while variances of newly created phantom parameters are freely estimated: SmoRate@0;Sl@0;. As a result, the distal outcome QuitSurg is regressed on two latent intercept and slope parameters: QuitSurg ON phant0 phant1;. For the multi-class generalized GMM, it is important to remember to indicate the number of latent classes in the VARIABLE statement:CLASSES = cb (3);and to assign the newly created class indicator cb to the list of variables measured on the between-person level:BETWEEN = cb …;.The rest of the syntax follows recommendations from the MPlus user guide (Muthén & Muthén, 2007).

Specification of GMM for traditional longitudinal data produces a number of graphical summaries that are necessary for model evaluation and interpretation (e.g. predicted and actual mean trajectories). They are unavailable for the univariate (i.e. long) data structure in GMM and need to be carried out outside of MPlus. In addition, prevalence of classes is not accurately estimated (i.e. prevalence is computed based on the number of repeated assessments rather than individuals), and posterior probabilities need to be saved in an external file through the SAVE DATA command for further computations. We used R (v. 2.9.2) for all additional graphical and statistical summaries.

Smoking Cessation ILD: Results

Model Selection Process

The model selection process in the context of ILD follows traditional steps of model selection, extensively described in the GMM literature (e.g. Jung & Wickrama, 2008; Li, Duncan, Duncan, & Acock, 2001; Muthén, 2004; Ram & Grimm, 2009; Wang & Bodner, 2007). They can be roughly divided into problem definition, model specification, estimation, selection, and interpretation (Ram & Grimm, 2009). We follow these steps below.

Problem definition and model specification

In our empirical example, we were interested in exploring heterogeneity of behavioral responses to a smoking cessation treatment. It is generally recommended to begin the analysis with a single-class MLM (with a Poisson link function for count data) to evaluate the model fit and practical usefulness. Parameters of the best-fitting model are summarized in the following prediction equation (with all estimates significant at the .01 level):

$$ln({\lambda }_{it})=2.839+.167\ast {\mathit{Fagerstrom}}_i-.323\ast {\mathit{days}}_{ti}-.01\ast {\mathit{NumberYRSmo}}_i\ast {\mathit{days}}_{ti}-.006\ast {\mathit{SelfEff}}_i\ast {\mathit{days}}_{ti}$$

with the covariance matrix for random effects $\tau =\left[\begin{array}{ll}{\tau }_{00}\hfill & {\tau }_{01}\hfill \\ {\tau }_{10}\hfill & {\tau }_{11}\hfill \end{array}\right]=\left[\begin{array}{ll}.116\hfill & .001\hfill \\ .001\hfill & .100\hfill \end{array}\right]$. In the above model, Fagerstrom is a measure of nicotine dependence (Fagerstrom, Heatherton, & Kozlowski, 1990; Heatherton, Kozlowski, Frecker, & Fagerstrom, 1991), SelfEff is an assessment of quitting confidence (Baer, Holt, & Lichtenstein, 1986), and NumberYRSmo is an indicator of the total smoking years.

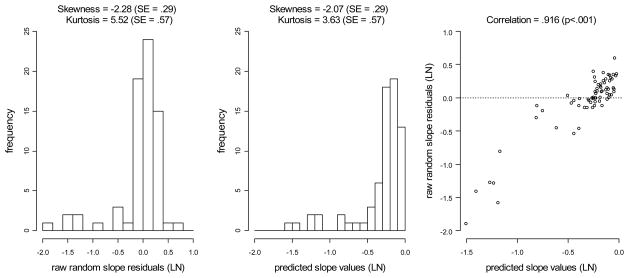
To investigate the fit of the MLM, individual estimates of intercept and slope parameters as well as their raw and empirical Bayes (EB) residuals were extracted. The distributions of raw and EB intercept residuals resembled a normal curve, thus satisfying the assumption of residual normality: r_0i ~ N(0, τ₀₀ ). Neither actual nor EB slope residuals, however, followed a normal pattern, which is evident from the graphical summary in Figure 4 as well as skewness and kurtosis statistics (p < .001), violating the normality assumption r_1i ~ N(0, τ₁₁). The distribution of predicted intercept parameters was normal, satisfying the assumption of normality β₀₀ ~ N(μ, σ²), but the distribution of slopes was highly skewed (p <.001), with a large proportion of slope values clustered between the values of zero and negative .5, and a left tail extending to negative 1.6 (middle graph in Figure 4), thus violating the assumption of normality β₁₁ ~ N(μ, σ²). A large positive association between the slope values and residuals was observed, with a Pearson product-moment correlation of .92 (p < .001), such that individuals with the steepest estimated slopes also had large residuals (last graph in Figure 4), indicating that average model parameters did not capture developmental patterns well for people with steep cessation slopes.

Figure 4.

Diagnostic Graphs for Slope Parameters from a Single-Class Multilevel Model.

Finally, the smoking presurgical outcome was predicted from individual-level intercept and slope parameters, computed from Equation 4. The smoking status remained unexplained (from logistic regression, p > .25), raising questions about the utility of MLM beyond explanation of some developmental inter-individual differences.

Model estimation and selection

Therefore, we pursued the generalized GMM analysis, hypothesizing that the distribution of slopes can be represented as two or more clusters of developmental trajectories. A comparison between models with several latent classes was carried out sequentially. Initially, unconditional models with intercept and slope residual variance parameters constrained to zero (τ_00k = 0 and τ_11k = 0 ) were fitted for Classes 1 through 5 (Table 2A). A continuous reduction in BIC and ABIC was observed, with additional classes significantly improving the overall model fit. To evaluate the practical usefulness of the model with five latent classes, we examined values of the slope parameters. Two classes had slopes of comparable magnitude: β₁₀₄ = −.118 (SE = .019) and β₁₀₅ = −.133 (SE = .012), with larger differences in intercepts: β₀₀₄ = 3.330 (SE = .12) and τ₀₀₅ = 2.642 (SE = .08). Relaxing the restriction on intercept variances (i.e. τ_00k ≠ 0) could account for inter-individual variability in baseline smoking rates without class over-extraction. Thus, the six-class model was not pursued due to little practical usefulness.

Table 2.

Model Fit Indices for Generalized GMM

Number of Latent Classes
	A. Fixed effects					B. Random Intercepts & Fixed Slopes			C. Two Covariates & Distal Outcome
	1	2	3	4	5	1	2	3	1a	2	3
BIC	9462.9	7022.7	5880.1	5494.6	5277.0	6002.4	5541.5	5135.7	5131.9	5384.1	5112.8
ABIC	9456.5	7006.8	5854.7	5459.6	5232.5	5992.9	5519.3	5100.8	5109.7	5349.2	5055.6
Number of parameters	2	5	8	11	14	3	7	11	7	11	18

^aNo covariates are included with a single latent class

Variability in intercept parameters was added to models with 1 through 4 classes. For the model with 4 latent classes, the best log likelihood (LL) was not replicable. Within-class slope variability was also tested for some classes (τ_11k ≠ 0), but resulted in model estimation problems and non-replicable LLs. Finally, baseline covariates were added as predictors of latent classes (Equation 2) for the full model with two and three latent classes, containing a distal outcome u_i (Equation 3). Quitting self-efficacy and time until surgery were identified as possible predictors (p < .1). According to the BIC and ABIC criteria, the three-class model fit the data better (Table 2C).

Based on a combination of statistical and conceptual indicators of model fit, a model with three classes, group specific random intercepts, fixed slopes, baseline covariates predicting a class membership, and a distal outcome was chosen. The model summary in combination with additional fit indicators is presented below.

Three-Class Generalized GMM Model Summary: Model Interpretation

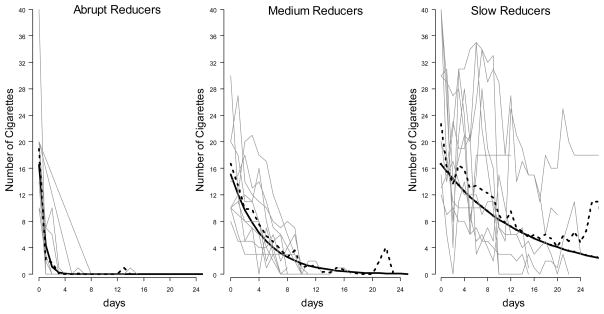
Parameters of the final growth mixture model with three behavioral classes are summarized in Table 3. Graphically, classes are represented in Figure 5. Based on the results, the baseline smoking rate was comparable across the classes with more interpersonal heterogeneity in Classes 2 and 3, as indicated by τ_00k and inspection of randomly sampled smoking trajectories from 10 patients within each latent class. Between-group qualitative differences are captured by slope parameters, with three latent classes exhibiting different reduction in smoking over time: abrupt, medium, and slow. The class of abrupt reducers exhibited an immediate drop in smoking with the largest slope parameter of τ₁₀₁ = −1.338, reducing smoking to nearly zero within the first 4 days. About 15% of the sample was identified as likely members of this behavioral class. The largest class (53%) was comprised of medium reducers, who were trimming down their smoking gradually (β₁₀₂ = −.220), consistent with the SRS intervention. Finally, a third of the sample followed a shallow decreasing smoking trajectory (β₁₀₃ = −.07), tapering down at a very slow and rather inconsistent rate.

Table 3.

Parameter Estimates of the Final Three Class Generalized GMM

Parameters	Parameter Estimate	Standard Error	p-value	Exp (Parameter)
Intercept-related parameters
β001	2.807	0.121	<.001	16.56
τ001	0.098	0.042	.020
β002	2.711	0.046	<.001	15.04
τ002	0.249	0.071	.001
β003	2.809	0.174	<.001	16.59
τ003	0.283	0.076	<.001
Slope parameters
β101	−1.338	0.286	<.001	.262
β102	−0.220	0.009	<.001	.803
β103	−0.070	0.015	<.001	.932
Probability of quitting at surgery
ν01	1.497	0.783		4.468
ν02	−0.059	0.334		.942
ν03	−0.968	0.492		.380
Baseline covariates as predictors of class membership (K = 2 is reference)
ω01	−2.137	1.764		0.118
ω11 * SelfEfficacy	0.043	0.021	.042	1.044
ω21 * SxDays	0.055	0.221	.802	1.057
ω03	−10.400	2.395		.0003
ω13 * SelfEfficacy	−0.040	0.028	.155	0.961
ω23 * SxDays	1.007	0.237	<.001	2.737

Figure 5.

Predicted (Solid) and Actual (Dotted) Average Developmental Trajectories for Three Latent Classes with 10 Randomly Sampled Actual Smoking Trajectories (in Gray) for Each Class

Predicted and actual mean smoking trajectories were compared. Actual trajectories were constructed based on daily smoking averages for individuals estimated to be members of a particular latent class. Dotted lines in Figure 5 represent actual mean smoking trajectories for each latent class. In all classes, there is a close match between actual and fitted trajectories, which indicates a good model fit. While predicted and average trajectories in abrupt and medium classes almost overlap, there is a slightly bigger discrepancy in the slow group, but it appears that the average captured the overall trend reasonably well.

It is important to note that class prevalence was computed outside the MPlus environment based on the saved posterior probabilities of class membership. In MPlus, the posterior summaries of class proportions are computed on the observational level, counting each repeated assessment rather than individuals, thus yielding inaccurate estimates of 11%, 43%, and 46% instead of 15%, 53%, and 32%, respectively. Of note, when the model is specified in a multivariate format for traditional longitudinal data, values of class prevalence from MPlus are accurate.

Individuals in each profile had observable differences in their presurgical smoking status. Specifically, the rate of cessation for abrupt reducers was estimated to be 81.7% (ν₀₁ = 1.497, SE = .783 on the logarithmic scale, see Table 3), 47.5% for medium reducers (ν₀₂ = −.059, SE = .334), and 28% for slow reducers (ν₀₃ = −.968, SE = .492). In terms of class profiles, abrupt reducers exhibited the highest level of baseline self-efficacy for quitting (bottom of Table 3). Abrupt and medium reducers had their surgery scheduled at a more proximal time to the beginning of the intervention, compared to the slow reducers.

Additional model fit indicators were examined for this three-class model. Posterior probabilities for class membership were cross-tabulated to assess the quality of class separation. As every person had a non-zero probability of being a member of each latent class, having a high probability for a single class is indicative of a clear class assignment. From Table 4, average posterior class probabilities are close to one, demonstrating a good model fit.

Table 4.

Classification Table of Posterior Probabilities and Actual Class Assignment for the Final Three-Class Generalized GMM

	Predicted classes
Assigned classes	1	2	3
1	.994	.006	0
2	0	.996	.004
3	0	.024	.976

Discussion

In the current paper we presented an innovative application of generalized GMM, appropriate for identifying underlying subgroups of individuals, characterized by similar patterns of intensively-measured behavior. In particular, we focused on modeling a phenomenon measured on a count scale over time, namely the number of daily smoked cigarettes. With advances in data collection techniques, researchers increasingly capture behavioral and psychological processes intensively. Growth models for ILD require flexibility in handling large data volumes as well as missingness in observations and unbalanced sampling. Additionally, multiple psychosocial phenomena measured on the count scale (e.g. number of cigarettes, number of alcoholic drinks, symptom frequency) need to be modeled according to the underlying Poisson distribution rather than with methods that rely on the assumption of normality. The proposed modeling approach brings together the following features: an intensively-measured process, an outcome best characterized by a Poisson distribution, and a latent class framework for organizing individuals according to similar developmental trajectories over time.

GMM has been previously used to discover unique developmental patterns in traditional longitudinal studies (e.g., Boscardin et al., 2008; Greenbaum, Del Boca, Darkes, Wang, & Goldman, 2005; Hunter, Muthén, Cook, & Leuchter, 2010; Schaeffer et al., 2006; Small & Backman, 2007) and can be successfully extended to model count-distributed ILD. By relaxing the assumption of normality in model parameters, this statistical approach allows the identification of qualitatively distinct trajectories, which may have important practical implications. Our empirical example demonstrated that patterns of smoking-behavior change may be indicative of smoking-cessation success. Other examples may include post-surgical patterns in physical symptoms as indicators of the quality of recovery, learning progressions as markers of mastery, or alcohol-use behaviors as predictors of alcohol dependence. As part of the generalized GMM, it is possible not only to distinguish developmental trajectories but also to identify a set of covariates that define individual profiles. Based on the set of covariates, it becomes plausible to identify at-risk individuals and intervene to minimize or prevent harmful consequences, while promoting the best allocation of resources.

From the methodological standpoint, modeling Poisson data appropriately is of great importance. Specifically, by using the Poisson link function, all predictions are made within the non-negative integer scale, allowing for a meaningful result interpretation (e.g., a prediction of −1.3 offenses on a criminal scale is ruled out). Further, with the Poisson-based model, a curvilinear development on the count scale can often be expressed linearly on the logarithmic scale, greatly simplifying the estimation process. Post transformation, non-linear relationships can still be accounted for with quadratic or cubic slope parameters on a class-by-class basis. Further, due to the nature of the Poisson distribution, λ_it represents the mean and variance parameter, which models higher variability for classes with larger mean trajectories. Our empirical example demonstrates an application of this property, where the variability in the “slow” class was accounted for by the high λ_it3 parameter and did not have to be modeled separately. This model feature is very important as, often, it is not computationally feasible to estimate unique variances across classes when a growth mixture model is applied to normally distributed data.

Finally, modeling count data properly assures that the assumption of conditional normality is not violated and, thus, latent classes are not artificially drawn to correct for a non-normally distributed outcome (Bauer, 2007; Bauer & Curran, 2003). As part of our empirical analysis, we attempted to ‘normalize’ daily cigarette counts and modeled the log-transformed outcome. Based on the model fit indices, a four-class solution was selected. An examination of growth parameters revealed that there were few substantive differences between the classes and the class of “abrupt” reducers (an important behavioral class) was not detected. Thus, a combination of our own research as well as work of others demonstrates that misspecifying a model can have important analytical and practical implications.

Although generalized GMM can be very flexible in accommodating time-varying covariates, complex developmental shapes, and random effects for growth parameters, one should be wary of a too-complex model. A good balance should be struck among model parsimony, practical and theoretical considerations, and statistical fit. Naturally, the overall sample size (on the individual rather than observational level), class prevalence, and class separation are of great importance when specifying the model (Wang & Bodner, 2007).

Software Considerations

To estimate the generalized GMM for Poisson-distributed ILD, we relied on the MPlus (Muthén & Muthén, 2007) commercial statistical package, which allows multi-level specification of the model to accommodate intensive data properties. It is worth noting some limitations of the software, however. These do not compromise the estimation process but require extra effort and care with model fitting and interpretation of results.

First, with the univariate (i.e., long) data structure, all graphics in the form of mean latent class trajectories, actual trajectories from individuals within each latent class, and mixtures of model parameters are disabled. Thus, all graphical summaries need to be carried out in a separate statistical package. Conveniently, the MPlus output files can be saved for further analysis.

Second, summaries of class prevalence statistics need to be carried out outside the MPlus environment. In spite of the specification of the class variable on the individual level, the posterior summaries of class proportions are still computed on the basis of individual observations, not persons. It is often appropriate for studies that use the long format of data structure, with individuals nested within institutions or geographic areas. However, for ILD nested within individuals, the MPlus software-produced class proportions are misleading.

As GMM develops into a widely researched and used method, other software alternatives become available. For example, an open-source software such as OpenMX (Boker et al., 2009), developed for use with R, can be currently used to carry out GMM analysis for traditional longitudinal data (Shiyko, Ram, & Grimm, in press). Further developments will soon allow for more advanced applications.

Conclusion

While multiple methodological concerns in regards to fitting generalized GMM to ILD in general and Poisson-distributed ILD in particular remain, this paper provides an overview of the model, demonstrates the model-fitting procedure, as well as interpretation of results. With increased collection of count ILD, the proposed model provides an opportunity to address complex research questions in regards to heterogeneity in developmental processes.