Study of Interaction Energies between PAMAM Dendrimer and non-Steroidal Anti-Inflammatory Drug Using a Distributed Computational Strategy and Experimental Analysis by ESI-MS/MS

Abstract

The structure of a dendrimer exhibits a large number of internal and superficial cavities, which can be exploited, to capture and deliver small organic molecules, enabling their use in drug delivery. Structure-based modeling and quantum mechanical studies can be used to accurately understand the interactions between functionalized dendrimers and molecules of pharmaceutical and industrial interest. In this study, we implemented a Metropolis Monte Carlo algorithm to calculate the interaction energy of dendrimer–drug complexes, which can be used for in silico prediction of dendrimer–drug affinity. Initially, a large-scale sampling of different dendrimer–drug conformations were generated using Euler angles. Then, each conformation was distributed on different nodes of a GRID computational system; where its interaction energy was calculate by semi-empirical quantum mechanical methods. These energy calculations were performed for four different non-steroidal anti-inflammatory drugs, each showing different affinities for PAMAM–G4 dendrimer. The affinities were also characterized experimentally by using Cooks’ kinetic method to calculate PAMAM–drug dissociation constants. The quantitative structure–activity relationship between the interaction energies and dissociation constants showed statistical correlations with r² > 0.9.

1. INTRODUCTION

Drug discovery and delivery are areas of continuous exploration and development of new platforms geared towards developing effective and specific treatments for the increasing number of illnesses for which molecular targets are currently unavailable.^1,2,3

The use of dendrimers as drug carriers is gaining ground as a nanotechnology application in medicine (nanomedicine) because of its potentially strong impact on the treatment of diseases.^2,3,4,5,6 Dendrimers are a type of nanomaterial with several attractive properties for biomedical applications.^7,8 The research on dendrimer–drug interactions is an increasingly active area of research in biomedical sciences and pharmaceutical industry.^9,10,11,12 Using dendrimers as carriers ¹³ to target drugs to specific sites may make it possible to reduce the dosage or increase the efficiency of these drugs. Additionally, dendrimers could allow, in extreme chemical conditions, the transport of otherwise insoluble or reactive molecules, and ensure their safe delivery to the targeted location.^5,6,14 The detailed understanding of dendrimer–drug interactions will help to establish the basis for developing novel dendrimer polymer chemistry applications in the field of biomedical sciences.^2,9,10,11

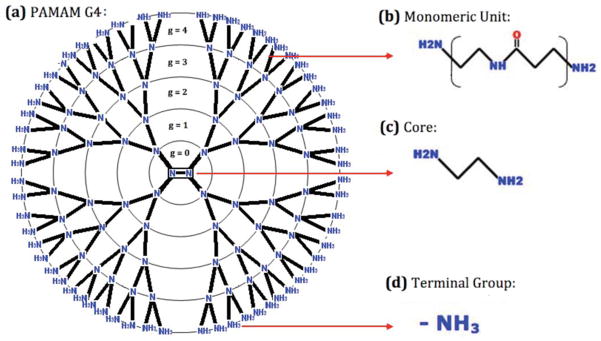
Dendrimers are well-shaped globular structures, hyperbranched and monodisperse.^15,17 These molecules can be synthesized in several steps, thus facilitating the design of versatile platforms¹⁸. Dendrimers are formed by a central core, followed by one or more monomeric units, which form the dendrimer’s branches and finally, terminal groups located on the ends of the branches.^16,17,18 The controlled addition of functional groups on the dendrimer’s surface allows for precise control of its properties, including its size, shape, density, polarity, flexibility, and solubility.^19,20 Polyamidoamine or PAMAM (Figure 1) is one of the most studied dendrimers, and has a wide range of applications in different fields.²² PAMAM dendrimers are frequently built around an ethylenediamine core to which amidoamine linkers are attached. The repeated addition of amidoamine groups form each PAMAM generation, where the PAMAM branching points involve tertiary amines.^15,16 Finally, the terminal branches are capped by amino groups. PAMAM dendrimers can interact with different types of drugs through specific interactions.¹² The structure of PAMAM displays a large number of internal and superficial cavities, which define flexible and adaptable microenvironments that are exploited to capture and deliver small organic molecules, giving PAMAM its desirable properties as a drug delivery system.^4,5,6 Therefore, understanding and controlling the dendrimer–payload interaction is the goal of dendrimer–drug in silico studies. The study of the physicochemical properties that govern the interaction between dendrimers and drugs represents a unique challenge because of the flexibility of dendrimers, the limited structural information currently available, and the lack of modeling and simulation tools necessary to build and optimize dendrimers. Thus, there is growing interest in creating and/or adapting computational chemistry tools to explore the intermolecular interactions within these systems (i.e., hydrogen bonding, electrostatic interactions, hydrophobic, and van der Waals forces)^21,23 and to evaluate specific structural properties that govern the affinity between dendrimers and molecules of scientific or industrial interest.^12,22 In contrast to proteins with well defined structures in which docking methods²⁴ are conventionally used, dendrimer flexibility is an obstacle for conventional simulation techniques and requires the implementation of novel simulation strategies that can explore possible modifications of the branched system and its interaction with putative payloads without resorting to the a priori knowledge of the target shape.

Figure 1.

(a) Schematic representation of a PAMAM dendrimer of generation 5. The structure contains tertiary amines as branching points, and the circles represent the boundaries between different generations “g.” (b) The monomeric unit that constitutes each generation. (c) PAMAM dendrimer has an ethylenediamine core and (d) charged amino-terminal groups.

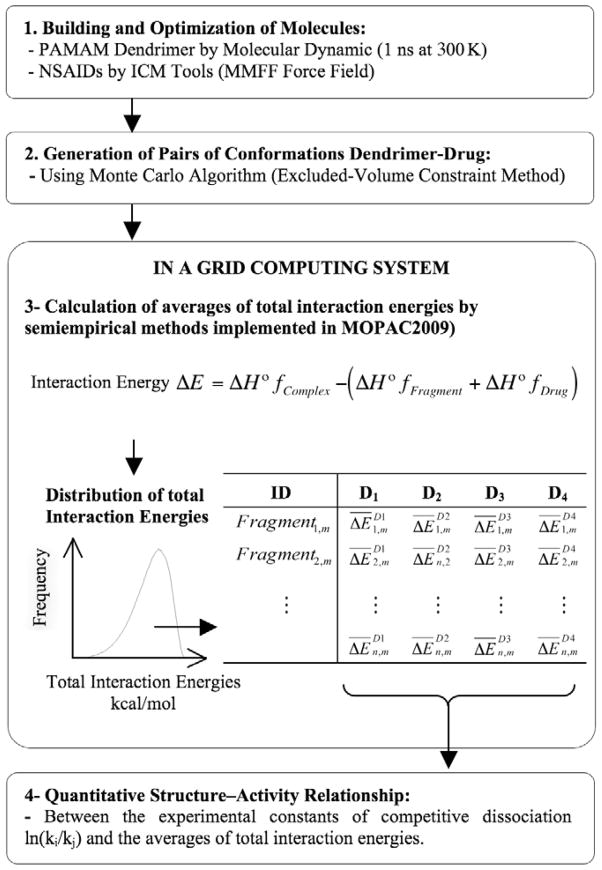
One of the main obstacles to understanding the nature of dendrimer–molecule interactions is the high computational cost of accurate conformational sampling and their respective interaction energy calculations. To overcome this obstacle, we have used advanced distributed computational methods (GRID computing) as the solution to performance hundreds of thousands of energy calculations in a reasonable amount of time with minimal loss in accuracy.^25,26 GRID computing has been consolidated as an important new field, distinguished from conventional distributed computing, due to its focus on large-scale resource sharing, innovative applications, and, in some cases, high-performance orientation to solving specific problems.²⁷

Here we present an efficient methodology for calculating the interaction energies between pairs of molecules (dendrimer–drug) along an exploratory path. The method offers a protocol based on the Metropolis Monte Carlo algorithm²⁸ to build large sets of PAMAM–drug conformational pairs with the aim of providing a good conformational sampling of the present interactions.^29,30,31 The process for calculating the energy of each pair is distributed in a specific node of a GRID computing system. Our distribution algorithm is based on a fast and efficient MPI program written using Single-Program Multiple-Data (SPMD) programming style³², which helps to drastically reduce the computational cost and runtime of the energy calculations.

The strategy for calculating the intermolecular interaction energy of dendrimer-drug systems consisted of the following steps: first, the geometry of the fragment of PAMAM dendrimer and the specific drug were optimized separately using the Parametric Method 6 (PM6) ³⁴. Then, the fragment-drug complex is formed with the conformations previously optimized. After that, the heat of formation (ΔH_f) is calculated for fragment, drug and complex using 1SCF and PM6-DH+^33,41. Finally, the intermolecular interaction energy (ΔE) was obtained by are described in the Equation 1:

$$\mathrm{\Delta }E=\mathrm{\Delta }{H}^{\text{o}}{f}_{\mathit{Complex}}-\left(\mathrm{\Delta }{H}^{\text{o}}{f}_{\mathit{Fragment}}+\mathrm{\Delta }{H}^{\text{o}}{f}_{\mathit{Drug}}\right)$$ (1)

The used of semi-empirical quantum mechanics methods SQMM through the last version of PM6-DH+ has allowed to study the intermolecular interactions with greater accuracy than molecular mechanical methods. Parameterization method 6 DH+ (PM6-DH+) was the SQMM selected for our energy evaluation because of its wide range of applicability, good accuracy for binding energy and good overall behavior. PM6-DH+ also includes empirical corrections for dispersion (D) and hydrogen-bond (H) interactions. ⁴¹ To overcome the high computational cost of SQMM, we used a GRID schema to spread these calculations in a distributed system.

Equally important to characterizing nanobiomaterials is the availability of accurate experimental measurements of their properties. The kinetic method proposed by Cooks and coworkers, Cooks’ kinetic method (CKM),³⁵ has been used to determine thermochemical properties based on rates of competitive dissociations of gaseous mass-selected ionic supramolecules as measured via mass spectrometry (MS) experiments. Because of the ease of use, broad applicability, high sensitivity to small thermochemical differences (typically as small as 0.1 kcal.mol⁻¹), and high precision, CKM has found a multitude of applications.^35–36 CKM was first described by Cooks and Kruger in 1977 for its use in determining the proton affinities of alkylamines.³⁶ Since then, it has been applied to both thermodynamic (e.g., proton or metal ion affinity and gas-phase basicity)^37,38 measurements and steric (chiral and isomeric discrimination) determinations.³⁹

In its simplest form, the method relies on the following major assumptions: a) negligible differences in the entropy requirements for the competitive channels; b) negligible reverse activation energies; and c) the absence of isomeric forms of the activated cluster ion. When these conditions are well satisfied, the ratio of fragment ion abundance for a proton-bound dimer Drug₁--- [PAMAM---nH]⁺ⁿ---Drug₂ (for example), as described in Equation (2), in which k₁ and k₂ are the rate constants for the competitive dissociations, is related to the binding affinity difference of the two bases, Δ(k_af), by Equation (3). T_eff is the effective temperature, a thermodynamic quantity⁴⁰ apparently related to the internal energy of the dissociating ions, and Δ (ΔS) is the reaction entropy difference between the two fragmentation channels.

$${\mathit{Drug}}_2---{\mathit{PAMAM}}^{+(n-1)}+{\mathit{Drug}}_1{H}^{+}\stackrel{k_1}{\leftarrow }{\mathit{Drug}}_1---{\mathit{PAMAM}}^{+n}---{\mathit{Drug}}_2\stackrel{k_2}{\to }{\mathit{Drug}}_1---{\mathit{PAMAM}}^{+(n-1)}+{\mathit{Drug}}_2{H}^{+}$$ (2)

$$\begin{gathered} ln\left(\frac{k_1}{k_2}\right)=ln\left(\frac{\left[{\mathit{Drug}}_1{H}^{+}\right]}{\left[{\mathit{Drug}}_2{H}^{+}\right]}\right) \\ \approx ln\left(\frac{{\left[{\mathit{Drug}}_2---\mathit{PAMAM}\right]}^{+(n-1)}}{{\left[{\mathit{Drug}}_1---\mathit{PAMAM}\right]}^{+(n-1)}}\right) \\ \approx \frac{k_{af}\left({\mathit{Drug}}_2---\mathit{PAMAM}\right)-k_{af}\left({\mathit{Drug}}_1---\mathit{PAMAM}\right)}{{RT}_{\mathit{eff}}}-\frac{\mathrm{\Delta }(\mathrm{\Delta }S)}{R} \end{gathered}$$ (3)

In this work we have evaluated and compared the average interaction energy and the binding constants obtained experimentally with the CKM for a series of dendrimer–non-steroidal anti-inflammatory drug (NSAIDs) complexes (PAMAM–naproxen, PAMAM–ketoprofen, PAMAM–ibuprofen, and PAMAM–diflunisal).

2. EXPERIMENTAL METHODS

Electrospray ionization mass spectrometry (ESI-MS) and ESI-MS/MS analyses were conducted in a high-resolution hybrid quadrupole (Q) and orthogonal time-of-flight (TOF) mass spectrometer (Q-TOF Micro, Waters-Micromass, UK) with a constant nebulizer temperature of 100 °C. The ESI source and the mass spectrometer were operated in the positive-ion mode, and the cone and extractor potentials were set to 10 and 4.5 V, respectively, with a scan range of m/z 150–3000. Samples were directly infused into the ESI source at flow rates of 5–10 mLmin⁻¹ by means of a microsyringe pump. Tandem ESI-MS/MS spectra were collected after 5 eV collision-induced dissociation (CID) of mass-selected ions with argon. Mass selection was performed by Q1 using a unitary m/z window, and collisions were performed in the rf-only quadrupole-collision cell, followed by mass analysis of product ions by the high-resolution orthogonal-reflectron TOF analyzer.

All sample mixtures were prepared for analysis in a 50:50 methanol/acetonitrile mixture (HPLC grade from Merck [Germany]). Final sample mixtures were composed of 5 μmol/L (μM) each of the analyte and reference molecules (1:1 stoichiometry), and 2.5 μM of PAMAM (G4 Sigma-Aldrich, USA). Diflunisal (Pfizer, USA), ibuprofen (Sanofi Aventis, Germany), ketoprofen (Medley, Brazil) and naproxen (Teuto, Brazil) were obtained from commercial sources.

3. THEORETICAL METHODS

3.1 Building and Simulation of Molecular Structure

To obtain multiple PAMAM–G4 conformations, 1 ns molecular dynamics simulation of PAMAM–G4 was performed in vacuum, and ten low-energy conformations were selected. The PAMAM–G4 was modeled using an adaptation of the CHARMM27 force field. The molecular dynamics simulation was done using NAMD program⁵¹. The repetitive units of dendrons were extracted from the conformational sampling to calculate interaction energies with the four NSAIDs.

The 10 PAMAM conformations were divided into several fragments to optimize the calculations and subsequent analysis of the interaction energies. The fragments comprise one or more monomer units and one or more amino terminal groups, as described in Table 1.

Table 1.

Characteristic Data of the PAMAM Dendrimer Fragment_n,m

fragment from a dendron of PAMAM-G4	molecular structure	number of monomers in the fragment	number of total amino groups	number of amino-terminal groups -NH+3	number of tertiary amines
Fragment1,m	C6H14O1N2	1	2	1	0
Fragment2,m	C11H27O2N5	2	5	2	1
Fragment3,m	C13H30O2N5	2	5	1	2
Fragment4,m	C17H39O3N7	3	7	2	2
Fragment5,m	C37H81O7N15	7	15	4	4
Fragment6,m	C55H117O10N21	10	21	4	7
Fragment7,m	C62H127O11N23	11	23	4	7
Fragment8,m	C89H189O17N33	17	33	8	10

3.2. Theoretical Calculations of Interaction Energies by Semiempirical Quantum Mechanic Methods

The schematic approach of our method, which integrates random sampling, energy calculations using semi-empirical quantum mechanical methods, and GRID computing, is presented in Scheme 1.

Scheme 1.

Workflow to generate and analyze the interaction energy averages for dendrimer–drug conformations. The averages for the same “n = 8” fragments, extracted from the “m = 10” different conformations of dendrimer PAMAM–G4 and four NSAIDs, which were denoted as D₁ = diflunisal, D₂ = ibuprofen, D₃ = ketoprofen, and D₄ = naproxen.

Our computational approach was implemented using a Message Passing Interfaces (MPI) program. This MPI code was written in SPMD style to optimize the performance of the calculations and minimize potential latency issues in a distributed environment.

The initial conformational search algorithm relies on the excluded-volume constraints method to generate configurations for the dendrimer–drug pair in a fast and efficient manner.³¹ The excluded-volume constraint method has been applied in a variety of situations to sample the molecular energy landscape of systems that present diverse complexity.^29,30 The procedure generates dendrimer–drug conformation pairs, where molecules are located in arrangements until their van der Waals (vdW) surfaces are barely touching,³¹ thus, avoiding interpenetrations. The sampling protocol was as follows: (A) Molecule 1 (monomer or a fragment_(g,m) of dendrimer) and molecule 2 (drug) are located at the geometric center of the pair and placed at the origin of the cartesian coordinates frame. (B) Then a set of random Euler angles (α, β, γ) are chosen to specify the orientation of molecule 2 in relation to molecule 1. (C) Molecule 2 is then translated along the vector (randomly chosen) until the vdW surfaces of each molecule touch each other (but do not interpenetrate). (D) After translation, the coordinates of these dendrimer(fragment)–drug conformations are sent to a GRID system, where single-point energies are calculated using a PM6-DH+ semi-empirical quantum chemistry method, as implemented in MOPAC2009^™ versión 11.038L (LINUX).³³

Steps A through D are repeated until a million different configurations and their corresponding total energies are generated. The interaction energy (ΔE) is calculated as the difference between the energy of the PAMAM–NSAIDs complex (fragment_n,m–drugs, where n and m indicate the fragment and conformation number) and the sum of the energy of their isolated parts (see Equation 1).

The Metropolis Monte Carlo sampling algorithm was used to weigh the appropriateness of the calculated interaction energy of each configuration. This interaction energy is accepted if it is less than or equal to the interaction energy of the previous configuration. If the interaction energy is higher, a random number between zero and one is generated, and the new configuration is accepted only if the exp(−ΔE_cc′/k_BT) is larger than or equal to the random value. In the exp(−ΔE_cc′/k_BT) formula, ΔE_cc′ is the interaction energy change from a conformation c to a new conformation c′; k_B is the Boltzmann constant and T is the absolute temperature in Kelvin (in this case 298 K).

Finally, the average of the interaction energies was extracted from the energy distribution of the million calculations performed for a specific dendrimer–drug complex, and it was used to establish structure–activity relationships. Note that this procedure allows for a direct averaging method with no recurrence or pre-evaluation stages like those present in other Monte Carlo methods and weighted approaches.

Albeit simple, the procedure proposed required a large number of samples, which resulted in larger computational requirements than is customary in quantitative structure–activity relationship (QSAR) strategies. Although single-point energy calculations for a specific conformation can be performed in a fraction of second, the aggregate computational cost of millions of interaction energies would quickly outrun the capacity of a single computer, requiring more than 6 months of computer time in a single server and rendering the approach of limited use in computer-aided design projects requiring fast return times. To address this problem, the procedure was implemented in a GRID scheme using the de-facto standard Globus^® Toolkit 4.⁴² Globus^® Toolkit mechanisms are in use at hundreds of sites and by dozens of major Grid projects worldwide.⁴³ The Globus^® Toolkit is a community-based, open-architecture, open-source set of services and software libraries that support Grids and Grid applications. The toolkit addresses issues of security, information discovery, resource management, data management, communication, fault detection, and portability. The Globus^® Toolkit includes Globus Resource Allocation Manager (GRAM),⁴⁴ Grid Information Service (GIS),⁴⁵ Grid Security Infrastructure (GSI),⁴⁶ and GridFTP (extension of the standard File Transfer Protocol [FTP] for use with G computing).⁴⁷ In this work, GRAM was used to implement the Monte Carlo remote-submission subtask and manage the execution of each subtask. GIS provides information services (i.e., the discovery of the properties and configurations of grid nodes) and offers security services such as authentication, encryption, and decryption for running the Monte Carlo applications on the grid.

The approach described was used to characterize the interactions between the eight fragments (n=8, see Table 1) extracted from 10 different PAMAM conformations (m=10) against the four drugs (D), D1 = diflunisal, D2 = ibuprofen, D3 = ketoprofen, and D4 = naproxen. Therefore, the interaction energies were calculated for 320 different complexes.

3.3. Theoretical Calculations of Interaction Energies by Molecular Mechanics (MM) Methods

In order to compare MM and QM methods we used the same conformational sampling procedure described previously to recalculate the energy interaction using a molecular mechanics force field⁴⁸. In particular, the single point energy for an ensemble of dendrimer-drug pairs were calculated using the Universal Force Field (UFF) ⁴⁹ and QEq charge implemented in the Gaussian 03⁵⁰.

3.4. Quantitative Structure–Activity Relationship

The experimental constants of competitive dissociation rates k₁, k₂ for each of the PAMAM–NSAIDs complexes were obtained via CKM and correlated with the interaction energy averages calculated theoretically by the implemented computational methodology.

4. RESULTS AND DISCUSSION

To analyze and relate the experimental affinity with the theoretical interaction energy calculations between the four NSAIDs and PAMAM–G4, We used the 10 lowest energy conformations of the PAMAM dendrimer extracted from a molecular dynamics simulation (at 300 K during 1 ns). Thus, eight different fragments representing a dendron of PAMAM (see Table 2) were extracted from each of these 10 conformations (80 fragments of different sizes). This conformational sampling allowed us to include the dendron’s degrees of freedom in the evaluation of the average of the total interaction energy of the PAMAM–drug complex.

Table 2.

Characteristic Data for the Four NSAID.

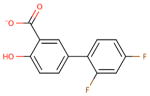
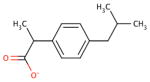
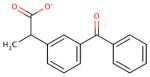
chemical Name	diflunisal D1	ibuprofen D2	ketoprofen D3	naproxen D4
molecular structure
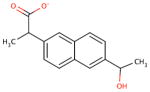
empirical formula	C13H8F2O3	C13H18O2	C16H14O3	C14H14O3
ln(ki/kj)	2,5	2,1	1,1	0

We generated PAMAM–drug pairs for each of the four drugs and each of the 80 PAMAM fragments, for a total of 320 pairs. Finally, by applying the Metropolis Monte Carlo algorithm, each pair was utilized to build one million new pairs. All the pairs generated (320 million pairs) were used to evaluate the average interaction energies using semi-empirical methods (PM6-DH+), which were distributed on a GRID computing system. From these 320 million values, we averaged over those with same fragment and drug to yield 32 average interaction energies, which were compared to experiment as shown in Table 3.

Table 3.

Average Values for Interaction Energies by Semiempirical Quantum Mechanic Methods and Molecular Mechanic Methods.

averages of interaction energies (kcal/mol)											energy difference kcal/mol
fragment from a dendron of PAMAM-G4	diflunisal D1 QM	diflunisal D1 MM	ibuprofen D2 QM	ibuprofen D2 MM	ketoprofen D3 QM	ketoprofen D3 MM	naproxen D4 QM	naproxen D4 MM	r2 QM	r2 MM	napo-diflu QM	napo-ibu QM	napo-keto QM
Fragment1,m	−65,1	−39,1	−66,0	−39,7	−66,6	−39,9	−67,3	−40,1	0,92	0,78	−2,2	−1,3	−0,7
Fragment2,m	−164,1	−69,1	−164,3	−72,3	−165,7	−74,6	−170,2	−74,9	0,91	0,77	−6,1	−5,9	−4,5
Fragment3,m	−91,4	−36,1	−92,8	−38,4	−96,0	−38,9	−109,2	−39,5	0,90	0,71	−17,8	−16,4	−13,2
Fragment4,m	−160,8	−64,4	−167,0	−66,5	−170,7	−67,1	−175,4	−67,8	0,92	0,77	−14,6	−8,4	−4,8
Fragment5,m	−186,6	−109,4	−190,8	−113,5	−208,5	−114,1	−211,7	−115,7	0,91	0,74	−25,2	−21,0	−3,2
Fragment6,m	−221,1	−90,7	−225,3	−98,9	−231,8	−99,8	−257,4	−103,6	0,92	0,75	−36,2	−32,1	−25,6
Fragment7,m	−185,8	−124,3	−188,5	−127,2	−189,4	−129,1	−192,0	−129,5	0,91	0,77	−6,2	−3,4	−2,6
Fragment8,m	−342,8	−153,9	−348,7	−170,2	−354,2	−171,2	−357,5	−180,6	0,91	0,77	−14,7	−8,8	−3,3
										Average	−15,4	−12,2	−7,2

For comparison, we also calculated the interaction energy using MM methods for the same set of fragments. As shown in Table 3, the average interaction energy calculated using the semi-empirical QM method showed a better correlation (r²=0.9) with experiment than that calculated using the MM method (r²=0.75). The lower accuracy of the MM results may be due to the fact that MM methods do not describe well aromatic systems such as NSAIDs. Therefore a semi-empirical method is the best option for performance a large sampling conformation to descriptions of NSAID–dendrimer interactions with the accuracy required for dendrimer design.

Using ESI-MS, positively charged supramolecules of PAMAM and all compounds investigated here (naproxen, ketoprofen, ibuprofen, and diflunisal), which were linked via weak O-H hydrogen bonds, were found to be efficiently transferred directly from their MeOH/MeCN solutions to the gas phase. Thus, fortunately, loosely hydrogen-bound polymeric supramolecular networks for PAMAM are conserved to a great extent during the ESI ion evaporation process.^52,53,54,55.

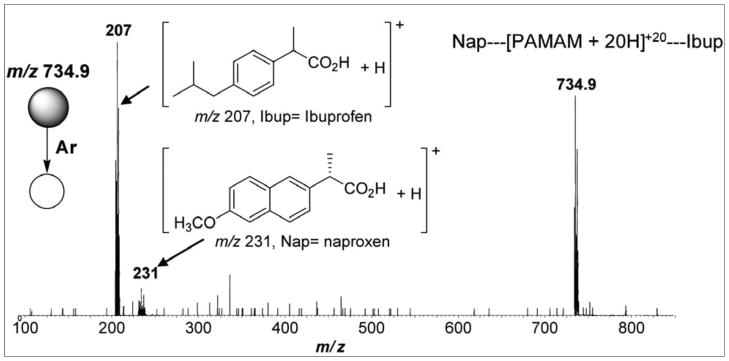
ESI-MS in the positive ion mode was a suitable technique to gently transfer to the gas phase, to determine supramolecular assemblies of PAMAM (M_w = 14242.22 Da) and NSAIDs, and to measure the relative strengths of their binding constants. Low-energy collision dissociation of mixed, loosely bound [Drug_XH]+ and Drug₁--- [PAMAM---nH]⁺ⁿ---Drug₂ supramolecules via tandem mass spectrometric experiments (ESI-MS/MS), with the application of Cooks’ kinetic method in its simplest form (entropy effects are negligible), provided relatively intrinsic magnitudes of the supramolecules’ weak, but very relevant, binding constant (Figure 2). The selected Drug₁--- [PAMAM---nH]⁺ⁿ ---Drug₂ supramolecules for ESI-MS/MS experiments were performed using [PAMAM + 20H]⁺²⁰ of m/z 713.1 and the respective supramolecular species formed between this ion and NSAIDs. The MS/MS spectra of the supramolecular species formed from PAMAM, naproxen, and ibuprofen is depicted in Figure 2. ESI-MS in the positive ion mode allowed us to perform an unprecedented series of experiments with gaseous supramolecules, including the formation, isolation, and gentle dissociation of gaseous Drug₁---[PAMAM + 20H]⁺²⁰---Drug₂ positively charged supramolecules now with mixed NSAIDs, and to compare the intrinsic strength of their binding constants. Figure 2 shows the tandem product-ion mass spectrum of one such supramolecules, Nap---[PAMAM + 20H]⁺²⁰---Ibup of m/z 734.9. Upon dissociation, the two NSAID ions competed for the central PAMAM, and the more loosely bound ion was preferentially expelled as the main ionic fragment. Since protonated ibuprofen of m/z 207 formed with higher abundance than naproxen of m/z (see Figure 2), we concluded that naproxen has a stronger bond to PAMAM.

Figure 2.

Tandem ESI-MS/MS product-ion mass spectrum for 5 eV CID of the mixed and 20 positively charged supramolecule naproxen--- [PAMAM + 20H]⁺²⁰---ibuprofen. Because the binding constant of naproxen at m/z 231 to PAMAM is stronger than ibuprofen, the protonated ibuprofen fragment ion at m/z 207 is formed to a greater extent.

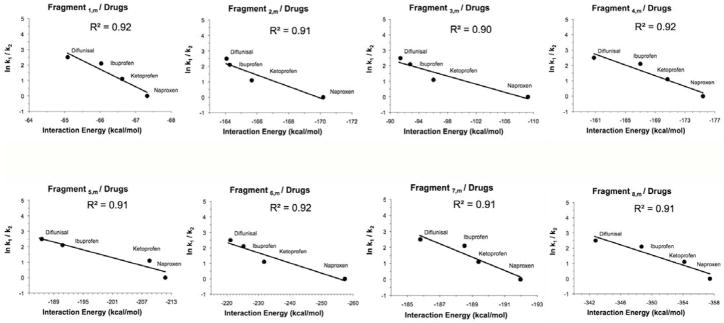
The calculated interaction energy averages were correlated with the experimental rate constants for competitive dissociation (see Figure 3). For the four compounds studied, the relative order of intrinsic binding strengths to PAMAM ion, [PAMAM---H]⁺²⁰, was found to be: naproxen (0 kcal.mol⁻¹1) > ketoprofen (1.1 kcal.mol⁻¹) > ibuprofen (2.1 kcal.mol⁻¹) > diflunisal (2.5 kcal.mol⁻¹).

Figure 3.

The correlation of the experimental constants of competitive dissociation rate ln(k_i/k_j) (naproxen = 0, ketoprofen = 1.1, ibuprofen = 2.1, and diflunisal = 2.5), derived from CKM studies, between a PAMAM dendrimer and four NSAIDs, versus the average of the total interaction energies calculated using the methodology implemented in this work. The r² value in all the graphs obtained was higher than 0.9, and the trend lines showed a correlation between the affinity degree of each drug by PAMAM and the theoretical values of the interaction energies calculated. Results showed the same relative affinity order observed experimentally for PAMAM–NSAIDs: naproxen > ketoprofen > ibuprofen > diflunisal.

The semi-empirical method used to evaluate the interaction energy had, as a principal benefit, a direct calculation without the necessity of implementing a force field for the fragment and the drug. Also PM6-DH+ allows estimate the dispersion energy and H-bond energy contribution. The dispersion energy shown a good correlation with our experimental values, while the H-bond contribution to the total energy is nearly the same for all the NAIDS (see supporting information). This dispersion energy correlation is particularly noticeable in the larger fragments due to the presence of larger hydrophobic cavities. The energy correlations agree more readily with the dispersion term than with the hydrogen bond contribution, which is near constant across the series. In fact, is observed that for the largest fragment the dispersion energy increase proportionally. This increase of the dispersion contribution is because these fragments contribute with larger hydrophobic cavities, which can increase the affinity of the drug.

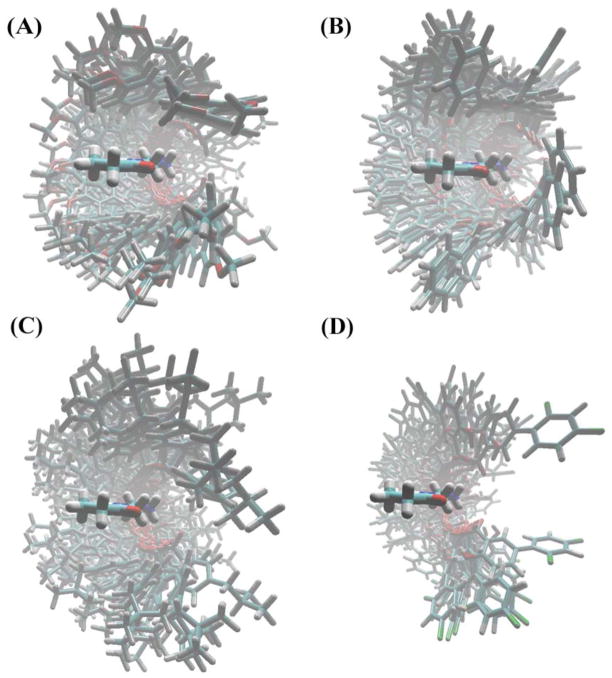
As was expected, the largest dispersion energy contribution was observed for naproxen, while the lowest was observed for diflunisal because it is the most rigid molecule of the drugs studied, as is shown in Figure 4. Then, the limited freedom of diflunisal’s torsional angle restrained the vdW contribution to the total interaction energy, decreasing the affinity of this molecule by PAMAM (see Figure 4).

Figure 4.

Spatial distribution for the 100 lowest energy conformations of (A) monomer–naproxen, (B) monomer–ketoprofen, (C) monomer–ibuprofen, and (D) monomer–naproxen complexes was used in the calculations of the radial pair distribution function. The four spatial distributions showed the following order of density: naproxen > ketoprofen > ibuprofen > diflunisal. Naproxen has a structure with more flexibility and torsional capacity than diflunisal, which has a rigid structure.

As a summary, the same relative order observed experimentally (naproxen > ketoprofen > ibuprofen > diflunisal) was reproduced theoretically through the implemented methodology. The total difference of the interaction energies between naproxen and diflunisal was −15.4 kcal/mol; naproxen and ibuprofen was −12.2 kcal/mol; and naproxen and ketoprofen was −7.2 kcal/mol (see Table 3). Drawing a straight line passing through the origin resulted in a correlation coefficient as high as 0.9 and a T_eff of 430 K, which showed an excellent theoretical–experimental agreement. This effective temperature was typical of loosely bound ionic species. For instance, weakly bound clusters or supramolecules such as H⁺, Cl⁺ and Br⁺ that bound to dimers of amines and pyridines⁵⁶ usually displayed T_eff below 700 K, whereas covalently bound species such as “electron-bound dimers” displayed considerably higher (greater than 1500 K) effective temperatures.⁵⁷

This excellent theoretical–experimental agreement allowed us to evaluate the structural properties (geometry, spatial distribution, densities, etc.) that modulate the affinity of PAMAM–NSAIDs complexes. These properties would be related to or governed by intermolecular interactions, specifically electrostatic interactions between amino terminal groups of the dendrimer surface and the carboxyl group of NSAIDs and the dispersion energy between the hydrophobic cavities of the dendrimer and aromatics ring of the NSAIDs. Considering that the number of terminal groups of PAMAM doubles with every generation, in increasing the number of functional groups, the dendrimer increases its capacity to encapsulate and interact with drugs. This capacity would permit the drugs to preserve the integrity and chemical pharmacological properties of the dendrimers.

4. CONCLUSIONS

Dendrimers present a uniform platform for the attachment or encapsulation of different drug types. Many small molecules of commercial interest with varied properties such as antimicrobial, anticancer, action and anti-inflammatory, have been successfully associated with dendrimers in recent years. The above-mentioned drugs, including NSAIDs such as naproxen, ketoprofen, ibuprofen, and diflunisal, have been widely studied with PAMAM dendrimers through electrostatic interactions. A common property of these drugs is that they are weakly acidic and have carboxyl groups in their structure. This has led to the rather simplistic evaluation that their interaction with anionic platforms (e.g. amino terminated PAMAMs at normal pH) is merely mediated by surface-charge interactions.

The work presented here proposes a direct method to evaluate the quantitative structure–affinity relationship in a dendrimer–drug system. Its methodology based on Monte Carlo sampling, semi-empirical methods, and GRID computing, should be an excellent tool to evaluate a priori the affinity of a drug in a specific dendrimer, thereby accelerating the design and development of new dendrimers. Additionally, this tool could be useful for de novo design of dendrimers or drugs with some specific affinity, among other applications, that could be extracted from the QSAR analysis.

The experimental affinity degree (naproxen> ketoprofen> ibuprofen> diflunisal) of each drug was reproduced theoretically through the methodology implemented in this work. Studies of the interaction energies between NSAIDs and fragments of the PAMAM dendrimer through semi-empirical quantum mechanical calculations (PM6-DH+) distributed in a GRID system show a good relationship with the experimental rate constants of competitive dissociation. Thus, and as expected, naproxen showed the major affinity to the different fragments from PAMAM–G4, and had the lowest values of total interaction energies. In this same way, diflunisal showed the weakest affinity from the four studied drugs and displayed the highest values of total interaction energies. The main difference in interaction energies between naproxen and diflunisal was approximately −15.4 kcal/mol.

The good correlation between the reported binding constants, and the total interaction energies allowed us to analyze the origin of the physicochemical properties that govern the dendrimer–drug affinity. The electrostatic interactions between the amino terminal group of the dendrimer surface and the carboxyl group of NSAIDs seem a principal component of this type of interaction. However, the most important contribution to the total energy is that of the dispersion term. Therefore, this work reveals, somewhat surprisingly, that the relative affinity of NSAIDs by PAMAM is controlled, largely, by the interaction of the drug with the hydrophobic cavities of the dendrimer, which are largely dominated by the dispersion energy terms. The flexibility of the drug has a high impact on the dendrimer–drug interaction, increasing the number of non-bonding contacts with the dendrimer for those drugs with highest freedom degree. Specifically, Diflunisal (weakest affinity) is a planar and rigid molecule, while Naproxen (major affinity) has 5 torsional angles. Ibuprofen has also many torsion angles, but has just one aromatic ring, therefore it is a flexible molecule but with a poor dispersion energy contribution. Potentially, this feature would indicate that the interaction degree of each drug could be enhanced due to nonbonding interactions between the aliphatic segments of the dendrimer monomer and drugs. Naproxen has a structure with more flexibility and torsional capacity than diflunisal, which has a rigid structure. It also adds the possibility of hydrogen bond formation between tertiary amines in the internal cavities of dendrimer and carboxylic segments of NSAIDs, also increasing hydrophobic contacts.