SAGITTAL PLANE KINEMATICS OF THE ADULT HYOID BONE

Abstract

The hyoid bone is a unique bone in the skeleton not articulated to any other bone. The hyoid muscles, which attach to the hyoid bone, may play a role in neck mechanics, but analysis of their function requires quantifying hyoid bone mechanics. The goal of this study was to obtain the detailed kinematics of the hyoid bone over a large range of flexion-extension motion using radiographs at 5 postures. The position of the hyoid bone in the sagittal plane was characterized with respect to head, jaw and vertebral movements. Sex differences in hyoid kinematics were also investigated. We hypothesized that (1) the position of the hyoid bone in the sagittal plane is linearly correlated with motion of the head, jaw and vertebrae, and (2) the hyoid position, size and kinematics are sex-specific. We found that the hyoid bone X, Y and angular position generally had strong linear correlations with the positions of the head, jaw and the cervical vertebrae C1–C4. Hyoid X and angular position was also correlated to C5. Sex differences were found in some regressions of the hyoid bone with respect to C1–C5. The angular and linear measurements of the hyoid bone showed sex differences in absolute values, which were not evident after normalization by posture or neck size. Incorporating these results to neck models would enable accurate modeling of the hyoid muscles. This may have implications for analyzing the mechanics of the cervical spine, including loads on neck structures and implants.

INTRODUCTION

The hyoid bone is the only bone in the skeleton not articulated to any other bone; it plays significant roles in speech (Shelton et al., 1960), chewing (Crompton et al., 1975), swallowing (Perlman et al., 1995), and airway patency (Janicka and Halczy-Kowalik, 2006). Many studies have assumed that the hyoid muscles (suprahyoid and infrahyoid muscles) do not take part in the movements of the head, and the ‘paravertebral flexor muscles’ should be the actual flexor muscles of the head and neck (Berzin, 1995; Last, 1955). However, several other studies have proposed that the hyoid muscle group has important functions in maintenance of head posture (Brodie, 1950; Thompson, 1941; Thompson and Brodie, 1942). This is supported by electromyographic (EMG) studies, where the suprahyoids and infrahyoids were activated during head flexion (Halbert, 1958; Siegmund et al., 2007; Vasavada, 1999). In addition to the activity during flexion, the infrahyoid muscles’ placement anterior to the vertebral column provides a large mechanical advantage, or moment arm. A biomechanical neck model which included the infrahyoid muscles (Oi et al., 2004) estimated that the infrahyoids could potentially account for one-quarter of the total moment developed by the flexors. For a better understanding of hyoid muscles’ function in head and neck movement, the hyoid bone and muscles should be incorporated into computational models of the head and neck system.

Modeling the hyoid muscles in neck musculoskeletal models requires knowledge of the hyoid bone kinematics. In previous neck models which included the infrahyoid muscles (Chancey et al., 2003; Oi et al., 2004), the hyoid bone (onto which the hyoid muscles attach) was assumed to maintain a fixed position relative to the head as it moved through the range of motion. It is not known if this is a reasonable assumption, or if hyoid bone kinematics is more closely related to another structure. Because hyoid bone kinematics will influence model predictions of hyoid muscle length, moment arm and moment, it is important to model the hyoid bone kinematics accurately. To our knowledge, the detailed kinematics of the hyoid bone during head flexion and extension is not available.

In previous research, the position of the hyoid bone has been examined at its neutral posture or self-balanced natural posture (Bibby and Preston, 1981; Rocabado, 1983; Tallgren and Solow, 1987; Valenzuela et al., 2005). Hyoid bone position was found to relate more closely to the curvature of the cervical spine (lordosis, straight or kyphosis) than to the craniocervical relationship (e.g., the angle between the head and C2) (Rocabado, 1983). The position of the hyoid bone in relation to the cervical column showed less variability than the hyoid position relative to the maxilla and the mandible (Tallgren and Solow, 1987). Furthermore, sex differences were found in hyoid bone shape and position (Kim et al., 2006; Marsan, 2008; SahIn Saglam and Uydas, 2006).

In the present study, the kinematics of the hyoid bone is examined over a wide range of flexion-extension motion. We hypothesized that (1) the position of the hyoid bone in the sagittal plane is linearly correlated with motion of the head, jaw (mandible) and vertebrae, and (2) the hyoid position, size and kinematics are sex-specific.

METHODS

Subjects

Sixteen females and sixteen males with a broad height distribution were recruited. Subjects with a history of neck pain, cervical spine disorder, thyroid disease or pregnancy were excluded. The study was approved by the Washington State University Institutional Review Board, and all subjects provided informed consent. Subject head and neck anthropometric data were measured as in a previous study in our lab (Vasavada et al., 2008) (Table 1).

Table 1.

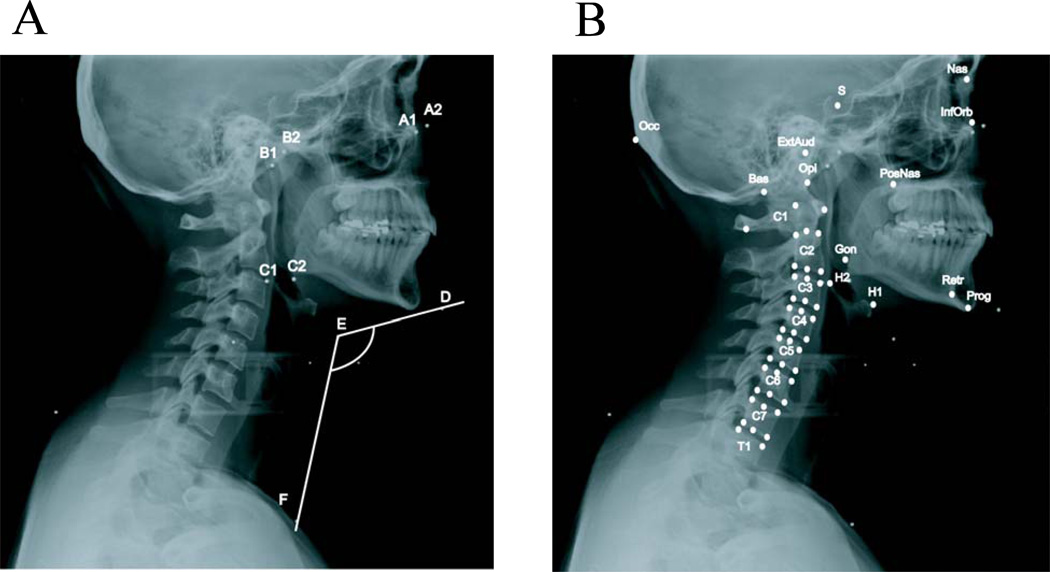
Anthropometric data for sixteen female and sixteen male subjects. Data shown are the average ± standard deviation, with the range in parenthesis. Neck length was defined as the vertical distance between the C7 spinous process and the tragus, measured using a wall-mounted stadiometer. Neck depth was measured using calipers at a level just above the thyroid cartilage. Hyoid size was defined as the distance between the most anterior and superior point on the hyoid bone (point H1 in Figure 2B) and the most posterior point on the hyoid greater horn (point H2 in Figure 2B).

	Female (n=16)	Male (n=16)
Age (years)	25.3 ± 7.1	22.7± 2.5
	(18–42)	(20–27)
Height (cm) **	162.0 ± 6.1	175.6 ± 9.9
	(151.7–175.5)	(148.7–190.4)
Weight (kg) **	63.1 ± 8.1	75.5 ± 14.3
	(47.4–78.7)	(52.2–96.4)
Neck Length (cm) *	11.0 ± 1.0	12.2 ± 1.6
	(8.8–12.6)	(9.3–14.3)
Neck Depth (cm) **	10.4 ± 0.4	12.2 ± 1.0
	(9.7–11.2)	(11.1–15.4)
Hyoid Size (cm) *	2.3 ± 0.4	2.7 ± 0.3
	(1.8–3.2)	(2.2–3.6)

There are significant sex differences for all measurements except age (sex differences noted by

^*0.01≤p<0.05,

^**p<0.01).

Radiography

Before the X-ray procedure, lead beads of 2 mm diameter (Y-Spots, Beekley Corporation, Bristol, CT) were placed on the skin above the right and left tragus, inferior border of both orbits, sternal notch, tip of chin, right and left angle of the jaw and intersection of chin and neck. Lateral radiographs of the cervical spine were obtained for each subject at five postures (Figure 1): upright neutral posture, maximum voluntary extension/flexion (subjects were instructed to curve their neck backward/forward as much as possible but still feel comfortable), and half maximum extension/flexion (the middle position between neutral posture and maximum extension/flexion). Subjects’ head angles were checked at each posture using a goniometer. During the x-ray acquisition, subjects were asked not to make other movements which could influence the position of the hyoid bone (e.g., clenching the teeth or swallowing).

Figure 1.

Lateral X-rays of a subject at five postures (from maximum voluntary extension to maximum flexion).

Size- and posture-related parameters were calculated by digitizing the lead beads and other bony landmarks on the hyoid, head, jaw and cervical vertebrae (Figure 2). One investigator performed all the digitizing, and the reliability was examined by digitizing images from one subject eight times, resulting in intraclass correlation coefficient (ICC) ranging from 0.988 to 0.995 over the five postures. To examine the effect of skin motion on the position of the metal beads, the distance between the lead beads on the skin and related bony landmarks was calculated for the beads used to calculate head and jaw position. The pairs of markers (lead beads and bony landmarks) examined were: orbit marker and infraorbitale; tragus marker and external auditory meatus; chin tip marker and prognathion; and angle of jaw and gonion. Averaged among subjects, the coefficients of variation (standard deviation divided by mean) of the distance between the skin marker and bony landmark over the 5 postures was 10% for the chin tip, 15% for the orbit, 22% for the tragus, and 41% for the angle of the jaw. These variations suggest the greatest amount of skin motion for the angle of the jaw marker.

Figure 2.

A. Lateral radiograph at the neutral posture, showing bony landmarks where lead beads were placed on the skin. A1/A2: left or right infraorbital socket; B1/B2: left or right tragus; C1/C2: left or right angle of jaw; D: tip of chin; E: intersection of chin and neck; F: sternal notch. B. Lateral radiograph with other landmarks digitized. Occ: external occipital protuberance; S: center of sella; Nas: the most anterior point of the frontonasal suture; ExtAud: external auditory meatus; Bas: basion; Opi: opisthion; InfOrb: infraorbitale; PosNas: posterior nasal spine; Gon: angle of the mandible (gonion); H1: the most anterior and superior point on hyoid bone; H2: the most posterior point on hyoid greater horn; Retr: most inferior and posterior point on the mandibular symphysis; Prog: the point on the madibular symphysis farthest from condylion (prognathion).

Data Analysis

All data were corrected for magnification and parallax. In each posture, coordinates of lead beads and bony landmarks were calculated in a coordinate system with its origin located at the center of the superior endplate of T1, to account for trunk motions among postures. The X-axis of the T1 coordinate system passed through the posterior-superior and anterior-superior corners of T1, pointing anterior; the Y-axis was perpendicular to the X-axis, passing through the origin, and pointing cephalad (Figure 3). Local coordinate systems were also defined for each vertebral body, which moved with the vertebrae through the 5 postures. The origins of the local coordinate system were located at the midpoint of the vertebral body (for C1, at the center of the anterior and posterior tubercles; for C2–C7, at the centroid of the four digitized corners); the X-axis passed through the midplane between the superior and inferior endplates of the vertebral body, pointing anterior; and the Y-axis was perpendicular to the X-axis, pointing cephalad (Figure 3).

Figure 3.

The definition of the T1 coordinate system (‘X’ and ‘Y’) and the definitions of the local vertebral body coordinate systems (‘x1’ and ‘y1’ through ‘x7’ and ‘y7’).

Size-related parameters such as hyoid bone size (Table 1) and distance between the hyoid bone to the head, jaw and cervical vertebrae (defined below) were averaged over the five postures. Posture-related parameters were calculated in the T1 coordinate system (Table 2 and Figure 3) to account for any trunk motion among postures.

Table 2.

Posture-related parameters used in regressions. For regressions, all variables were calculated in the T1 coordinate system.

Dependent Variables
X and Y positions of hyoid bone (‘X_Hyoid’ and ‘Y_Hyoid’)	Position of point H1, with respect to the origin of the T1 coordinate system
Angle of hyoid bone (‘Angle_Hyoid’)	Angle of the line connecting point H1 and H2 (Figure 2B) with respect to the X-axis of the T1 coordinate system
Independent Variables
X and Y positions of head (‘X_Orbit’ and ‘Y_Orbit’)	Position of orbit marker (average of left and right orbit beads), with respect to the origin of the T1 coordinate system
X and Y positions of jaw (‘X_ChinTip’ and ‘Y_ChinTip’)	Position of chin tip marker, with respect to the origin of the T1 coordinate system
X and Y positions of vertebrae (C1–C7) (e.g. ‘X_C1’ and ‘Y_C1’)	Position of vertebral center (origins of the local vertebral body coordinate systems), with respect to the origin of the T1 coordinate system (Figure 3A)
Angle of head (‘Angle_Head’)	Angle of the line connecting orbit and tragus, with respect to the X-axis of the T1 coordinate system
Angle of jaw (‘Angle_Jaw’)	Angle of the line connecting the angle of jaw and chin tip, with respect to the X-axis of the T1 coordinate system
Angle of vertebrae (C1–C7) (e.g., ‘Angle_C1’)	Angle of the line connecting the midpoint of the anterior and posterior vertebral body (X axis of the local vertebral body coordinate system), with respect to the X-axis of the T1 coordinate system
Head and neck angular posture (‘Angle_ChinNeck’)	Angle from the chin tip to the intersection of chin and neck to the sternum (‘∠DEF’ in Figure 2A)

The kinematics of the hyoid bone was investigated in several ways. First, the absolute distance between the hyoid bone and other bones in the neck was calculated as the distance between point H1 on the hyoid bone (figure 2B) and points on the head (orbit), jaw (tip of chin) and vertebral coordinate system origins (Table 2). If the distance between the hyoid and any other bone is consistent at different postures, this may indicate that the hyoid bone could be rigidly linked to that bone in a biomechanical model. For each subject, the average and standard deviation of the distance between the hyoid and other bones were calculated over the five postures. “Consistency” was quantified by the coefficient of variation (the ratio of the standard deviation to the average distance among all postures). Next, the bone with the most consistent distance to the hyoid bone was selected to examine if the X and Y coordinates of the hyoid bone in the selected local coordinate system were consistent over all the postures. Therefore, the trajectories of the hyoid bone (point H1 in Figure 2B) were plotted in the selected bone’s local coordinate system (with the local coordinate system moving as the bone moved among postures) to examine specifically the changes in X and Y directions over all the postures relative to the selected bony structures. A second order polynomial function was fitted to the trajectory (within the local coordinate system) for visualization purposes. For absolute distance and X- and Y-distances, the range (maximum – minimum) over all postures was also calculated for each subject.

If the X and Y positions of the hyoid bone relative to other bones are not consistent (defined as having a coefficient of variation larger than 10%), the kinematics of the hyoid bone may be better described by regression equations relating the motion of the hyoid bone to another individual bone’s motion or to a more global head-neck postural measure. First, the correlations between the position of the hyoid bone (X and Y coordinates and angle) and the position of the head, jaw, and all cervical vertebrae were calculated (Table 2). Linear, quadratic and cubic relations were examined for the regression equations. The angle of the hyoid bone (defined by a line connecting H1 and H2 in Figure 2B) was correlated to the angles of the X-axis of other bones. The X- and Y- positions of the hyoid bone were correlated to the X- and Y- positions of other bones, and also to the angular position of the other bones. The position of the hyoid bone was also regressed to a more global postural measure, the angle between the chin and neck (Angle_ChinNeck), defined by the beads placed on the tip of the chin, intersection of chin and neck, and the sternal notch (∠DEF in Figure 2A).

Sex differences were investigated in the absolute values of hyoid bone size and distance between the hyoid bone and other neck bones; to account for size effects, these values were also normalized (by neck length for Y (vertical) values or neck depth for X (horizontal) values). These sex differences were investigated by unpaired t-tests. For the regressions, sex differences were analyzed using analysis of covariance (ANCOVA), where the independent variables (e.g., posture-related factors) were used as covariates.

RESULTS

Hyoid Bone Kinematics

Over the range from flexion to extension, the hyoid bone had the most consistent distance to the midpoint of the C3 vertebral body; the average distance from the hyoid bone to C3 over all postures was 4.29 ± 0.45 cm (mean value and standard deviation among all the subjects). The maximum change in the distance between the hyoid bone and C3 among the different postures was 0.60 ± 0.18 cm (mean value and standard deviation among all the subjects). The distances from the hyoid bone to the landmarks on the head, jaw, T1 and other cervical vertebrae at all postures were less consistent. The coefficient of variation of the distance, averaged among all the subjects, was 5% for C3, whereas it ranged from 6% to 15% for the other cervical vertebrae and was 14% for T1, 12% for the chin tip, and 9% for the orbit.

Based on the consistency found for the absolute distance between the hyoid bone to C3, the trajectory of the hyoid bone was plotted in the C3 coordinate system (Figure 4A); the hyoid trajectory and the trajectory of the chin tip and C3 in the T1 coordinate system were also plotted for comparison (Figures 4B and 4C). In the T1 coordinate system, the hyoid bone moved anteriorly and inferiorly as the subject moved from extension to flexion (Figure 4B), and the hyoid bone trajectories of most subjects have similar shapes. In the C3 coordinate system, the hyoid bone generally had more motion in the inferior direction compared to anterior, and the shapes of the trajectories were not similar for all subjects (Figure 4A). Although the absolute distance from the hyoid bone to C3 changed only 0.60 ± 0.18 cm among postures, the maximum changes in X- and Y-directions over five postures were larger: 0.70 ± 0.22 cm and 1.70 ± 0.80 cm, respectively (mean value and standard deviation among all the subjects). Furthermore, the coefficient of variation for the Y coordinates in C3 coordinate system were usually greater than 100% for most of the subjects. Thus, the hyoid bone position in the X- and Y-dimensions is more variable than the absolute distance, indicating that the relationship cannot be described by constant X- and Y- values.

Figure 4.

A. Hyoid bone trajectories (for point H1 in Figure 2B) in the C3 coordinate system for five postures of each subject, fit with a second order polynomial function. B. Hyoid bone trajectories (H1 in Figure 2B) in the T1 coordinate system for five postures of each subject, fit with a second order polynomial function. C. Trajectories of chin tip, centroid of C3 vertebral body and hyoid bone (H1 in Figure 2B) in the T1 coordinate system for five postures of each subject, fit with a second order polynomial function.

The results supported the first hypothesis, that the position of the hyoid bone in the sagittal plane is linearly correlated to the position of the head, jaw and some cervical vertebrae. In general, the hyoid bone X, Y and angular position had strong linear correlations with the positions of the head, jaw and the cervical vertebrae C1–C4 (R² ranged from 0.61 to 0.91; Table 3). Hyoid X and angle, but not hyoid Y, had strong linear relationships to C5. None of the hyoid position parameters had a linear correlation with any of the vertebrae in the lower cervical spine (R² ranged from 0 to 0.32 for C6–C7). Good correlations were found for hyoid X- and Y-positions and angle, respectively, with the head (see Figure 5) and jaw. For C1–C4, there were good correlations between X-position and angle of the hyoid to the X-position and angle of the vertebrae (seen in Figure 6A and 6B for C3), but not between the Y-position of the hyoid and the Y-position of C1–C4 (R² from 0.004 to 0.22). Instead, there was a strong correlation between the Y-position of the hyoid and the X-position of the orbit, C1, C2 or C3 (Table 3; see also Figure 6C for C3). X- and Y-positions of the hyoid bone were found also to be related to the angular positions of jaw, head and C1–C4 (Table 3) and to the more global head and neck angular posture (Angle_ChinNeck). Increasing the order of the equation to a quadratic or cubic relationship did not significantly improve the R² values of the regressions. Therefore, only linear regression results are presented.

Table 3.

Results of regression analysis with significant correlations for the skull, jaw, C1–C4 and Chin-Neck Angle.

Related Bony Structure	X (degree or cm)	Y (degree or cm)	Regressions	R2
Head	Angle_Head	Angle_Hyoid	Y=0.68*X−8.51	0.82
	X_Orbit	X_Hyoid	Y=0.30*X+1.41	0.91
	Y_Orbit	Y_Hyoid	Y=0.60*X−1.65	0.70
	X_Orbit	Y_Hyoid	Y=−0.22*X+8.10	0.75
	Angle_Head	X_Hyoid	Y=−0.06*X+4.00	0.86
	Angle_Head	Y_Hyoid	Y=0.04*X+6.10	0.76
Jaw	Angle_Jaw	Angle_Hyoid	Y=0.66*X+9.58	0.82
	X_ChinTip	X_Hyoid	Y=0.53*X−1.40	0.89
	Y_ChinTip	X_Hyoid	Y=−0.38*X+5.59	0.76
	Y_ChinTip	Y_Hyoid	Y=0.34*X+4.43	0.89
	Angle_Jaw	X_Hyoid	Y=−0.06*X+2.46	0.86
	Angle_Jaw	Y_Hyoid	Y=0.04*X+7.29	0.78
C1	Angle_C1	Angle_Hyoid	Y=0.75*X−16.08	0.82
	X_C1	X_Hyoid	Y=0.74*X+4.60	0.82 **
	Y_C1	X_Hyoid	Y=1.03*X−7.98	0.69 *
	X_C1	Y_Hyoid	Y=−0.57*X+5.65	0.72 *
	Angle_C1	X_Hyoid	Y=−0.06*X+4.59	0.83
	Angle_C1	Y_Hyoid	Y=0.05*X+5.65	0.73
C2	Angle_C2	Angle_Hyoid	Y=0.87*X+1.26	0.80 *
	X_C2	X_Hyoid	Y=0.90*X+4.10	0.84 **
	X_C2	Y_Hyoid	Y=−0.67*X+6.08	0.71 *
	Angle_C2	X_Hyoid	Y=−0.07*X+3.18	0.84
	Angle_C2	Y_Hyoid	Y=0.06*X+6.78	0.69
C3	Angle_C3	Angle_Hyoid	Y=0.98*X+7.29	0.81 **
	X_C3	X_Hyoid	Y=1.32*X+4.24	0.82 **
	X_C3	Y_Hyoid	Y=−0.95*X+6.05	0.63 *
	Angle_C3	X_Hyoid	Y=−0.08*X+2.67	0.87
	Angle_C3	Y_Hyoid	Y=0.06*X+7.19	0.67
C4	Angle_C4	Angle_Hyoid	Y=1.27*X+8.22	0.77 **
	X_C4	X_Hyoid	Y=2.01*X+4.41	0.73 **
	Angle_C4	X_Hyoid	Y=−0.11*X+2.60	0.85
	Angle_C4	Y_Hyoid	Y=0.08*X+7.26	0.61
C5	Angle_C5	Angle_Hyoid	Y=1.69*X+6.63	0.63 **
	Angle_C5	X_Hyoid	Y=−0.15*X+2.79	0.76*
Head and Neck	Angle_ChinNeck	Angle_Hyoid	Y=0.68*X−59.85	0.64
	Angle_ChinNeck	X_Hyoid	Y=−0.06*X+8.29	0.65
	Angle_ChinNeck	Y_Hyoid	Y=0.05*X+2.25	0.71 **

There are significant sex differences for some regressions to upper cervical vertebrae (sex differences noted by

^*0.01≤p<0.05,

^**p<0.01)

Figure 5.

Regressions between hyoid bone and head (definitions in Table 2), which have no sex difference. A. Regression of angle of hyoid bone with respect to angle of head. B. Regression of X (anterior) position of hyoid bone with respect to X position of orbit. C. Regression of Y (superior) position of hyoid bone with respect to Y position of orbit.

Figure 6.

Regressions between hyoid bone and C3 (definitions in Table 2), which have a significant sex difference (p<0.05). A. Regression of angle of hyoid bone with respect to angle of C3. B. Regression of X (anterior) position of hyoid bone with respect to X position of C3. C. Regression of Y (superior) position of hyoid bone with respect to X position of C3.

Sex Differences

The results partially supported the second hypothesis: sex differences were found in some regression equations relating the hyoid position to C1–C5 (p<0.05), but not in the regressions relating the hyoid position to the head or jaw (Table 3; Figure 5 & 6).

The hyoid bone size was larger in males than in females (Table 1; p=0.01). In males, the distance from the hyoid bone to the centroid of the C3 vertebral body was larger compared to females (Male subjects: 4.62 ± 0.36cm; Female subjects: 4.00 ± 0.26cm; p<0.01). In the T1 coordinate system, the hyoid bones’ trajectories in males were significantly more cephalad than those in females (p<0.01; see Figure 4B). In the C3 local coordinate system, most females’ hyoids trajectories were concave and more posterior, but half of males’ trajectories were convex and more anterior (Figure 4A).

When the hyoid bone size was normalized by neck depth, the sex differences were no longer significant (p=0.8). The distance from the hyoid bone to the midpoint of the C3 vertebral body also had no sex difference after normalization by neck depth (p=0.7). Similarly, the hyoid trajectories of males in the T1 coordinate system were no longer more cephalad than those of females when normalized by neck length (p=0.9).

DISCUSSION

To our knowledge, the present study is the first study to report the kinematics of the hyoid bone over a large range of motion instead of at the natural or neutral posture only, which is difficult to standardize. However, the kinematics of the hyoid bone was only investigated in the sagittal plane; future studies should consider hyoid bone kinematics in the coronal and transverse planes.

In this study, the main focus was on the relationships between the hyoid bone and individual bony structures. Although other actions, such as speech, swallowing or movements of the jaw when opening the mouth, can affect the position of the hyoid bone, these actions were controlled during the radiographic study (subjects were asked to close their mouth and not speak or swallow during the X-ray procedure). During head and neck flexion and extension, the hyoid bone was found not to have a fixed X–Y position relative to any cervical vertebra, head or jaw. The position of the hyoid bone was linearly correlated to the head, jaw and cervical vertebrae, although slightly better regressions are found with respect to the head and jaw than to the upper cervical vertebrae (Table 3). This is illustrated by the similarity of the hyoid bone and jaw trajectories in the T1 coordinate system (e.g., compare the trajectory of the hyoid to those of the jaw or C3 in Figure 4C).

Posture and size may account for some of the sex differences in hyoid bone kinematics. In the literature (Marsan, 2008; SahIn Saglam and Uydas, 2006), the linear measurements of the hyoid bone to the head and cervical vertebrae showed statistically significant differences between sexes. In the present study, the sex differences found in the absolute values were not significant after normalization by neck depth or neck length. Some of the differences found between women and men in previous studies may also be related to head/neck posture. Sahin Saglam et al. (SahIn Saglam and Uydas, 2006) found that angular measurements of the hyoid bone with respect to the skull and mandible (three internal angles in the ‘Bas-H1-Retr’ triangle in Figure 2B) were significantly different between sexes, when the subjects held natural head postures. In the present study, those three internal angles were correlated with the head and neck angular posture (‘∠DEF’ in Figure 2A), and sex differences did not exist after applying ANCOVA, where the head and neck angular posture was used as the covariate. In our study, however, we found that there were sex differences in the regressions of the hyoid bone with respect to C1–C5.

The results of this study suggest that, rather than modeling the hyoid bone rigidly to the head as was done previously (Chancey et al., 2003; Oi et al., 2004), regression equations should be incorporated to model hyoid bone kinematics (and hyoid muscles accordingly). Linear regression equations were sufficient to describe hyoid kinematics; more complex quadratic or cubic equations do not appear to be necessary. Because the X- and Y-positions of the hyoid bone were found to have strong relationships to the angular positions of the head, jaw and C1–C4 (Table 3), the hyoid X-, Y- and angular positions may be modeled as a function of a single kinematic variable (e.g., head angle). This may be advantageous for modeling; for example, kinematics of the cervical vertebrae in the existing neck model from our lab (Vasavada et al., 1998) have also been defined as a linear function of the head angle.

Improved knowledge of hyoid bone kinematics will help guide diagnosis and treatment of neck disorders, not only those related to the hyoid bone and muscles, but of the entire cervical spine. Documenting hyoid kinematics of healthy subjects is essential before abnormal kinematics can be identified. Further, we believe it is important to include hyoid muscles in biomechanical neck models. For example, including hyoid muscles in a neck model may allow better prediction of the distribution of muscle forces or disc loads, which is important to evaluating the mechanics of implants or the causes of neck pain. To model the hyoid muscles accurately, it is critical to know how the hyoid bone moves, in order to calculate changes in the length, moment arm and force of the hyoid muscles over a range of motion. This information will allow a more complete analysis of the mechanics of the cervical spine for many clinical applications.