Cell Ingression and Apical Shape Oscillations during Dorsal Closure in Drosophila

Abstract

Programmed patterns of gene expression, cell-cell signaling, and cellular forces cause morphogenic movements during dorsal closure. We investigated the apical cell-shape changes that characterize amnioserosa cells during dorsal closure in Drosophila embryos with in vivo imaging of green-fluorescent-protein-labeled DE-cadherin. Time-lapsed, confocal images were assessed with a novel segmentation algorithm, Fourier analysis, and kinematic and dynamical modeling. We found two generic processes, reversible oscillations in apical cross-sectional area and cell ingression characterized by persistent loss of apical area. We quantified a time-dependent, spatially-averaged sum of intracellular and intercellular forces acting on each cell's apical belt of DE-cadherin. We observed that a substantial fraction of amnioserosa cells ingress near the leading edges of lateral epidermis, consistent with the view that ingression can be regulated by leading-edge cells. This is in addition to previously observed ingression processes associated with zipping and apoptosis. Although there is cell-to-cell variability in the maximum rate for decreasing apical area (0.3–9.5 μm²/min), the rate for completing ingression is remarkably constant (0.83 cells/min, r² > 0.99). We propose that this constant ingression rate contributes to the spatiotemporal regularity of mechanical stress exerted by the amnioserosa on each leading edge during closure.

Introduction

Embryogenesis involves a precisely orchestrated interplay among gene expression; posttranscriptional, translational, and posttranslational processes; molecular force production; cell-shape changes; and cell and tissue movements (1,2). Dorsal closure is an essential morphogenic movement that takes 2–3 h during mid-embryogenesis and results in the formation of a continuous protective epithelium that covers the irregular, prolate ellipsoid-shaped embryo. Before the onset of closure, the amnioserosa lies within an elliptically shaped, dorsal opening. The amnioserosa is a simple epithelium composed of ∼200 polygonally shaped cells. Actomyosin arrays and thin, circumferential belts of DE-cadherin collectively maintain the mechanical integrity of the tissue. These belts mediate intercellular adhesive forces and form an essentially two-dimensional network that lies just below the apical surface of the squamous-to-cuboidal amnioserosa cells. The peripheral-most row of amnioserosa cells is behaviorally distinct and persists until the end stages of closure (3). These cells are tucked underneath the leading edges of the lateral epidermis, which are transcriptionally distinct from the remainder of the lateral epidermis (4). As closure begins, opposing flanks of lateral epidermis form seams at the anterior and posterior ends of the elliptical opening and the opening becomes eye-shaped (the corners of the eye-shaped opening are called “canthi”). As closure progresses, zipping occurs at each canthus to extend the anterior and posterior seams. Concomitantly, the two flanks of lateral epidermis advance to replace the amnioserosa (Fig. 1 A). The geometry of the dorsal opening becomes well approximated as the intersection of two circular arcs (5–7) whose curvature remain nearly constant throughout closure (8,9). Forces produced by the amnioserosa and the leading edges of the lateral epidermis (with their supracellular, actomyosin-rich cables or purse-strings) drive closure, whereas forces from the bulk of the lateral epidermis oppose closure (8). The individual tissue stresses are larger by 2–3 orders of magnitude than the net stress that drives closure, and the two leading edges approach one another at an approximately constant rate from mid-to-late stages of closure.

Figure 1.

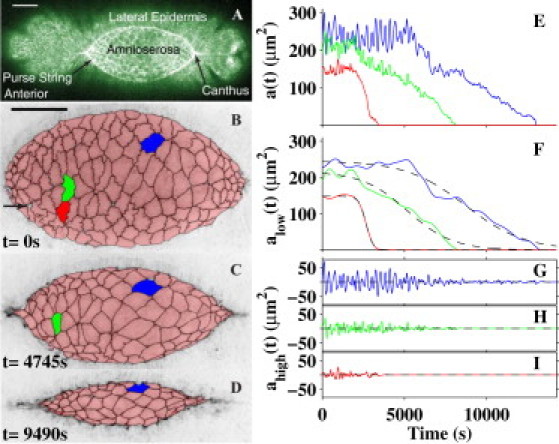
Cell oscillations and ingression. (A) Confocal image of the dorsal surface of a GFP moesin embryo, which prominently labels actin in the two purse-strings at the periphery of the dorsal opening. Key structures of the dorsal surface are labeled, where the scale bar is 50 μm. (B–D) Dorsal closure (embryo #3) as tracked by inverted-intensity confocal images of cell boundaries in a GFP DE-cadherin embryo, where the results of the segmentation are shown in pink with black boundaries. Results of the segmentation. The apical surfaces of the amnioserosa cells within the dorsal opening are prominent, surrounded by two less prominent flanks of lateral epidermis. The arrow in Panel B indicates a segmentation inaccuracy. The scale bar in panel B is 50 μm and applies to panels B–D. Anterior is to the left in all figures. (E) Plots of the apical cross-sectional area for the color-coded cells. (F–I) Each a_i(t) presented in panel E is separated into its low-frequency a_low,i(t) (F) and high-frequency a_high,i(t) (G –I) contributions. Panel F also presents the fitted ingression functions I_i(t) (dashed curves).

Ingression is a set of processes by which an amnioserosa cell internalizes below the remaining amnioserosa tissue. Two ingression processes have been described previously (5,10): First: during the mid-to-late stages of dorsal closure, ∼10% of the amnioserosa cells randomly ingress and undergo apoptosis, preferentially in the anterior two-thirds of the dorsal opening (10). Second, during zipping amnioserosa cells also ingress as they are internalized at each canthus. By the end of dorsal closure, all of the amnioserosa cells have ingressed and either have undergone or will soon undergo apoptosis.

Recently there has been interest regarding the role of force pulsations in the contraction of amnioserosa cells. Apical area pulsations have been correlated with fluctuating actomyosin concentrations found in both the apical medial network and in the cortical ring of actomyosin (11). Furthermore, as the cell began to contract there was a significant accumulation of apical medial myosin, eventually forming a continuous apical cap. The repeated assembly and disassembly of apical actomyosin networks have been observed to be regulated by the PAR complex (12). In addition, it has been suggested that a ratchet mechanism accounts for force production during dorsal closure before the onset of zipping (13). More specifically, the ratchet was attributed to an intercellular coupling between the leading edge and an amnioserosa cell and it was speculated that the cycle of a pulsation is restricted by tension maintained in a segment of the leading edge. The net result would be contraction of the cell and irreversible dorsal displacement of this segment of the leading edge. Furthermore, the onset of zipping was viewed to be an additional force process that complicates interpretation. In contrast, a subsequent investigation found that there are ∼4.2 mHz fluctuations in the apical areas of amnioserosa cells without any net tissue contraction (11). In addition, we observed previously that the net contraction of a leading-edge cell occurs near a canthus as part of the zipping process (14). We observed oscillations in the width of leading-edge cells when they are located along the leading edge far from a canthus, but no net contraction until this leading-edge cell is engaged in the zipping process. There also are oscillations in leading-edge cells that express variable amounts of myosin as seen in transgenic mosaic embryos (15). It is not clear that these experimental observations (11,14,15) are consistent with the proposed supracellular ratchet model (13).

Pulsed apical constrictions also occur at the onset of mesoderm invagination in ventral furrow cells, and were correlated with contractions of an actin-myosin network anchored at adherens junctions by Martin et al. (16). These investigators raised the possibility that the force-producing mechanism is based on a subcellular ratchet, although mechanistic details are vague. Furthermore, there are similarities between the oscillations observed during dorsal closure and those observed during mesoderm invagination (17). With regard to germband extension, force production also has been attributed in part to polarized medial actomyosin flows that are oriented by DE-cadherin and α-catenin (18). Actomyosin-based oscillations also have been observed in other biological systems at low-Reynolds number. For example, shape oscillations were observed in nonadhering fibroblast cells (19) and in purified preparations of actin and myosin that exhibit spontaneous oscillations (20,21).

Here we report the investigation of changes in apical cell shape by developing a method to segment confocal images of amnioserosa cells before and during closure. We analyzed the time dependence of changes in the shapes of subapical DE-cadherin belts with a kinematic model. We developed a dynamical model that quantifies the relative net force acting on each apical belt of DE-cadherin that drives changes in apical cell area. We investigated the variability and asymmetries in cell kinematics according to location within the dorsal opening. We attribute three invariant (time-independent, global) properties of dorsal closure to be a consequence of a constant rate of completing ingression.

Results

Our experimental approach was as follows (see Materials and Methods in the Supporting Material). To investigate changes in the cross-sectional areas of individual amnioserosa cells during closure, we imaged their apical belt of adherens junctions using GFP-labeled DE-cadherin. This collectively forms a surface in the image volume. We segmented confocal images of the amnioserosa during the early-to-late stages of closure to track apical areas in time (see Movie S1, Movie S2, Movie S3, and Movie S4 in the Supporting Material). The segmentation of three confocal images from one embryo is shown in Fig. 1, B–D. The segmented cell edges are shown in black and have been superimposed on inverse-intensity confocal images at three times. The segmented cell edges are largely indistinguishable from the fluorescent cell edges, but there were some inaccuracies (Fig. 1 B, arrow). Consequently, we developed methods to quantify cell-shape changes that were insensitive to these inaccuracies (see Section S1.2.3 in the Supporting Material). From this segmentation, we calculated the cross-sectional apical area of each cell, defined each cell's location by its centroid, and tracked these values in time. Three illustrative (red, green, and blue) cells completed ingression at ∼3400 s, 8100 s, and 13,000 s, respectively.

We assessed each area time series with methods based on Fourier transforms that are sensitive to oscillations and ingression processes (see Sections S1.3 and S2 in the Supporting Material). Fig. 1 E presents the apical cross-sectional area, a_i(t), for the three color-coded cells (i is an index that is unique to each cell). Each a_i(t) (Fig. 1 E) is characterized by oscillations (Fig. 1, G–I) around a background function (Fig. 1 F). For just under half of the amnioserosa cells that we investigated, this background is shoulder-shaped, as exhibited in Fig. 1 E (and see Quantifying Ingression for Amnioserosa Cells, below). To distinguish the oscillations from the background, the data traces in Fig. 1 E were processed in parallel: Fig. 1 F presents the lower-frequency contribution and Fig. 1, G–I, presents the higher-frequency contribution, where the cut-off frequency (1.1 mHz; see Section S2.2 in the Supporting Material) demarcates lower from higher frequencies. This filtering process is represented mathematically by the expression

$$a_i\left(t\right)=a_{low,i}\left(t\right)+a_{high,i}\left(t\right),$$ (1)

where a_low,i(t) is the lower-frequency contribution and a_high,i(t) is the higher-frequency contribution for the i^th cell. Each data trace in Fig. 1 F also is fitted with a dashed line, corresponding to a generic shoulder-shaped ingression function (see Quantifying Ingression for Amnioserosa Cells, below). Furthermore, the higher-frequency traces in Fig. 1, G–I, correspond to complex oscillations (see Dynamics of Oscillations and Ingression of Amnioserosa Cells, below).

Quantifying ingression for amnioserosa cells

A geometric signature for the ingression processes that internalize amnioserosa cells is based on the background function a_low,i(t) shown in Fig. 1 F. The signature includes the onset of a sudden decrease in cell area (experimentally observed in the plane of the adherens junctions), followed by an interval of persistent area loss until ingression is complete. To visualize the onset of an ingression process, consider the cells tracked in Fig. 1 E and analyzed in terms of a_low,i(t) in Fig. 1 F. It is clear that all three cells have an interval of persistent loss of apical area and then complete ingression. The red cell exhibits the clearest onset of an ingression process, preceded by the flattest plateau (nearly constant a_low,i(t) before ∼2000 s). This general description of the apical cross section of amnioserosa cells exhibiting oscillations about a shoulder characterizes the green and blue cells in Fig. 1 as well and applies to just under half of the 815 segmented cells.

We developed a kinematic model to account for changes in a_i(t) that exhibit the geometric signature for ingression, e.g., Fig. 1 F. Approximately four-fifths of the segmented cells (645 of the 815 cells from five embryos, enumerated in the legend to Table S1 in the Supporting Material) had area traces for sufficient durations to warrant this analysis (see Section S2 in the Supporting Material). The ingression function I_i(t) provides a kinematic description of an ingression process:

$$I_i\left(t\right)=\frac{{\alpha }_i}{2}\left[1-\tanh \left({\mathit{ϵ}}_{i}t-{\tau }_i\right)\right].$$ (2)

Here t is time (t = 0 corresponds to the initial confocal image) and area α_i determines the value of the plateau. Because the limits of tanh(ε_it − τ_i) are −1 at early times and +1 at later times, the right-hand side of Eq. 2 ranges from α_i to 0. The time of the inflection point is τ_i/ε_i and the rate of the transition at this time is α_iε_i/2. The fitting of I_i(t) to a_low,i(t) for the three cells produced the dashed lines of Fig. 1 F.

Although the ingression function I_i(t) can be applied to all 645 cells, its interpretation and the uncertainties in the parameters α_i, ε_i, and τ_i varied significantly. We found:

• 1.Approximately one-fourth (195) of the total cells produced reliable (see below) fitting parameters that allowed for more sophisticated analytical comparisons (hereafter referred to as “Category I cells”). Examples include the red and blue cells of Fig. 1, the cell in Fig. 2, the three cells from Fig. S5, Fig. S6, and Fig. S7, and the cell in Fig. S11 B in the Supporting Material. Typical values were: 50 μm² ≤ α_i ≤ 250 μm², 0.2 mHz ≤ ε_i ≤ 4.0 mHz, and 2 ≤ τ_i ≤ 8.
• 2.At the other extreme, approximately one-fourth (192) of the cells did not fit the generic description of oscillations about a shoulder and were more appropriately characterized as oscillations about a linear background (hereafter referred to as “Category III cells”). An example is the cell shown in Fig. S11 A.
• 3.Approximately one-third (258) of the cells exhibited oscillations, but their backgrounds were neither shoulder-shaped as for cells of Category I, nor linear as for cells of Category III. These Category II cells (e.g., green cell in Fig. 1) are more aptly described as exhibiting backgrounds that fall in between Categories I and III, with the numerical consequence that fitting these cells with I_i(t) resulted in unacceptably large uncertainties (up to 100%) in the parameters (see Section S2.3 in the Supporting Material).

Figure 2.

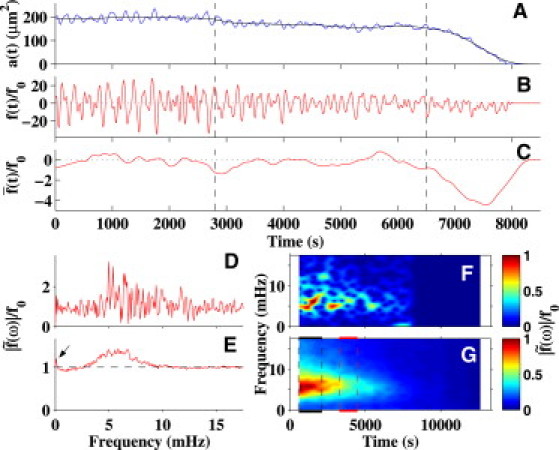
Analysis of the relative net force. (A) Plot of the area a_i(t) for a single amnioserosa cell (blue trace is data, black trace is low-pass, filtered data). (B) Calculated time dependence of f(t)/f₀ (negative indicates contraction). (C) The function $\overline{f}\left(t\right)/f_0$, where the overline indicates the data from panel B has been filtered to remove the high-frequency oscillations. (D) The function |f(ω)|/f₀, where the Fourier transform of the data in panel B was taken for the entire time series. (E) The average of Fourier transforms for all the segmented amnioserosa cells (embryo #2). (F) Spectrogram of the data from panel B. For this panel, the x axis reports time, the y axis reports frequency, and the normalized amplitude is reported in the false color-scale. (G) The analogous sum of the spectrograms for all the segmented cells. The two pairs of vertical dashed lines indicate when zipping commences (black indicates posterior, red indicates anterior); the ranges track the onset and full engagement of the zipping processes.

The sum of 195, 192, and 258, when added to the 170 cells that exhibited insufficient durations, totals 815 cells from five embryos. Cells from Categories I–III were used for parallel analyses that were independent of the ingression function as described in the following sections (see Section S1.2.3 in the Supporting Material).

The ingression function I_i(t) is a good approximation of the lower-frequency contribution a_low,i(t). Consider the difference between the filtered data traces (solid lines) and the fitted (dashed) lines in Fig. 1 F. Typically, this residual difference between a data trace and its fitted curve corresponded to values of 2–10% of the lower-frequency contribution a_low,i(t) (Eq. 1). Thus for Category I–III cells we can make the exact assignment, followed by the approximation

$$\begin{array}{c}{a}_{low,i}\left(t\right)=I_i\left(t\right)+residual,\\ \approx I_i\left(t\right).\end{array}$$ (3)

The fidelity of subsequent analyses of the area of the plateau and the rate of the transition at the inflection point strongly depends on the goodness of fit. A detailed description of the quantitative analysis of this lower-frequency residual and reliability is presented in Section S2 in the Supporting Material.

Dynamics of oscillations and ingression of amnioserosa cells

We developed an oscillations/ingression model to characterize the forces responsible for the observed kinematics. This dynamical model is based on a damped driven harmonic oscillator and specifies the forces that drive apical cell-shape changes in a viscoelastic tissue in the limit of low-Reynolds number (see Section S3 in the Supporting Material). It quantifies how a_i(t) depends on the net, active-contractile forces f_i(t), the passive-elastic restoring forces k_eff,i a_i(t), and the viscous drag b da_i/dt. The model starts with Newton's Second Law applied to a point on the apical belt of adherens junctions. Applying the condition of low-Reynolds number and then integrating around the belt results in Eq. 4, an equation that, in area, is well matched to the experimentally determined values for a_i(t), i.e., the original, unfiltered data:

$$b\frac{d}{dt}{a}_i\left(t\right)=-k_{eff,i}{a}_i\left(t\right)+f_i\left(t\right).$$ (4)

The value f_i(t) is a generalized force that spatially averages the intracellular and extracellular forces that act on the belt of adherens junctions to cause a change in apical cell area. Dividing by a constant f_0,i, the dimensionless result is

$$\frac{f_i\left(t\right)}{f_{0,i}}=\frac{b}{f_{0,i}}\left(\frac{d{a}_i\left(t\right)}{dt}+\frac{k_{eff,i}}{b}{a}_i\left(t\right)\right).$$ (5)

The dimensionless force f_i(t)/f_0,i required to cause changes in apical area in a single amnioserosa cell is shown in Fig. 2 B and is the result of applying Eq. 5 to the data a_i(t) shown in Fig. 2 A (Section S3 in the Supporting Material describes how da_i/dt, f_0,i/b, and k_eff,i/b were determined). Fig. 2 presents a good approximation of the magnitude and time-dependence of the active, contractile forces that drive cell-shape changes in apical area of this cell.

The oscillations/ingression model distinguished the forces that drive ingression from the forces that drive oscillations. More specifically, the time series of f_i(t)/f_0,i (Fig. 2 B) was filtered to remove higher-frequency (>1 mHz) oscillations, resulting in $\overline{f}\left(t\right)/f_0$ (Fig. 2 C). It is instructive to compare Fig. 2, A–C, in detail. Whereas initially there are relatively large amplitude and complex oscillations in the driving force (Fig. 2 B), the filtered value for ${\overline{a}}_i\left(t\right)$ shows little net decrease in area before ∼2800 s (Fig. 2 A, black trace). From ∼2800 to 6500 s (dashed lines in Fig. 2, A–C), ${\overline{a}}_i\left(t\right)$ decreases by a relatively small amount (Fig. 2 A, black trace). Thus, before ∼6500 s, the relatively large, oscillating forces do not promote steady loss of apical area. After ∼6500 s, inspection of Fig. 2, A and C indicate a distinguishing change, where a persistent decrease in ${\overline{a}}_i\left(t\right)$ (Fig. 2 A) correlates with an increase (until ∼7500 s) and then decrease in the magnitude of ${\overline{f}}_i\left(t\right)/f_{0,i}$ (Fig. 2 C). Note the similarity in the functional form of ${\overline{f}}_i\left(t\right)/f_{0,i}$ during ∼6500–8200 s in Fig. 2 C to that of either the derivative (slope) of ${\overline{a}}_i\left(t\right)$ or the derivative of I_i(t) (Fig. 2 A or Fig. 1 F, dashed curves, respectively), which highlights the consistency of the kinematic and dynamical models. The magnitude of the forces associated with the ingression process (Fig. 2 C, ∼6500–8200 s) are small relative to the maximum forces associated with the oscillations (Fig. 2 B, 0–6500 s; note different scales in Fig. 2, B and C). The key observation here is that the higher-frequency oscillating forces correlate with largely reversible changes in a_i(t), in contrast to the lower-frequency forces that correlate with a coherent (systematic) decrease in apical cross section (see Discussion).

We investigated distinctive frequency ranges for the oscillatory and ingression forces with Fourier analysis (see Section S1.3 in the Supporting Material). We calculated the Fourier transform (indicated by the overscore tilde, the two vertical bars indicate magnitude) $\left|{\tilde{f}}_i\left(\omega \right)\right|/f_{0,i}$ (Fig. 2 D) of the area trace shown in Fig. 2 A, using the expression

$$\frac{\left|{\tilde{f}}_i\left(\omega \right)\right|}{f_{0,i}}=\left[\frac{b}{f_{0,i}}{\left({\left(\frac{k_{eff,i}}{b}\right)}^2+{\omega }^2\right)}^{\frac{1}{2}}\right]\left|{\tilde{a}}_i\left(\omega \right)\right|.$$ (6)

The frequencies of the forces that drive the oscillations in this cell are most strongly peaked at ∼5–7 mHz. Fig. 2 E is the average of the Fourier transforms for all the segmented amnioserosa cells for this embryo and is analogous to Fig. 2 D in that the transform is for the entire time series. Generally, there were three common features in the Fourier analyses of the net, active-contractile forces: a background in $\left|\tilde{f}\left(\omega \right)\right|/f_0$ having a value of 1 (dashed line), a rise to larger amplitudes as the frequency approaches zero (arrow), and the emergence of a band of force oscillations from ∼2.4 to 9.0 mHz, e.g., Fig. 2 E. The first two features are attributable to the viscoelastic nature of the tissue and the forces driving the ingression process (Discussion and see Section S3 in the Supporting Material). Averaging over all the segmented cells for the five embryos, the band is centered at 5.7 ± 0.9 mHz. This is attributable to the higher-frequency oscillations and is consistent with previous observations of amnioserosa cell oscillations (11–13,22).

We then investigated how the oscillatory forces transition into ingression forces by analyzing the time course of their Fourier components. We calculated spectrograms to track changes in the Fourier transforms within a traveling window (1300 s) in time as a cell progressed into and completed ingression (see Section S3 in the Supporting Material). Fig. 2 F is the spectrogram of the time-dependent forcing function, where the frequencies are presented on the y axis, the amplitude information is contained in false colors, and the x axis is time. The distribution of frequencies changes as this amnioserosa cell progresses through ingression. Initially the amplitudes of the oscillations at ∼5 mHz are strongly peaked until ∼6500 s, followed by a shift to lower frequencies (light-blue island at ∼1 mHz in panel F) from ∼7000 to 8000 s, i.e., when ingression is occurring in earnest.

For each embryo, we see two notable features when we averaged the spectrograms of the cells (Fig. 2 G): First, the dominant mode centered at 5.7 mHz decays steadily; however, the variable amplitude features seen in the spectrograms of single cells (e.g., Fig. 2 F) have been averaged out. In particular, the blue island of Fig. 2 F corresponds to a faint but significant blue streak due to the staggered distribution of ingression, as shown in Fig. S10. Second, as time progresses we see a narrowing of the band of Fourier frequencies and a shift of the dominant mode to ∼5 mHz for this example embryo. Vertical dashed lines indicate zipping onset (see Fig. 2 legend).

We searched for correlations between the higher-frequency oscillations a_high,i(t) and the lower-frequency background a_low,i(t). For Category I cells, it was always the case that the onset of ingression is preceded by higher-frequency oscillations. Furthermore, comparing a_high,i(t) and a_low,i(t) in Fig. 1, F–I, and a_i(t) in Fig. 2 A indicates a second correlation between the amplitude of the oscillations and the area of a cell, detailed in Section S4 in the Supporting Material. Additional correlation analyses that failed to show significance are reviewed in Section S4 in the Supporting Material.

To summarize Quantifying Ingression for Amnioserosa Cells and Dynamics of Oscillations and Ingression of Amnioserosa Cells, these kinematic and dynamical models indicate that oscillations and ingression are distinguishable as follows. During the plateau, oscillations in apical areas are largely reversible and there is little if any net loss of apical area. The dominant process for decreasing apical area can be attributable to an ingression process. Furthermore, the Fourier analyses indicate the frequencies of oscillations lie at substantially higher frequencies than those that characterize ingression. In particular, there is a decrease in the amplitude of the higher-frequency oscillations as the duration of the plateau reaches its end. Concurrent with this transition is an increase in the amplitude of the lower frequencies associated with ingression.

Peripheral ingression process

We observed amnioserosa cell ingression along the periphery of the dorsal opening, a third process for ingression. More specifically, we investigated the location within the dorsal opening where each amnioserosa cell completed its ingression process by separating the dorsal opening into eight geometric regions as shown in Fig. 3 A and Fig. S12 (and see Section S1.4 in the Supporting Material). Each cell was classified (color-coded) by region, based on the location of its centroid in the first confocal image. Inspection of Fig. 3, A–C, indicates there is a notable loss of cells at the canthi as closure progresses, consistent with the ingression of amnioserosa cells as part of the zipping process. To quantify these observations, we assessed the proximity of a cell completing the ingression process to either purse-string (Fig. 3 D) and compared it to the proximity to either canthus (Fig. 3 E). Fig. 3 D is a histogram of the distance to the nearest purse-string (d_PS, see Section S1.4 in the Supporting Material) at the time a cell completes its ingression process. Cells from different embryos are distinguished by the color of the bars, where the solid black line represents the average over the five embryos. The y axis presents the normalized fraction of cells completing the ingression process for each embryo. The x axis is the distance to the nearest purse-string where each set of five bars (from five embryos) represents equally sized bins centered on a common value. This histogram shows a large clustering of cells that completed an ingression process within 10 μm of a purse-string. The cumulative distribution is shown as an inset, where the two dashed lines correspond to a distance of 10 μm and a fraction of 9/10. In other words, we found that, on average, >90% of the cells completed ingression when their centroids were within 10 μm of a purse-string. This region includes the periphery of the dorsal opening in general and was not limited to the two canthus regions. The remaining 10% of the cells completed the ingression process within the interior of the dorsal opening, consistent with previous observations (5,10).

Figure 3.

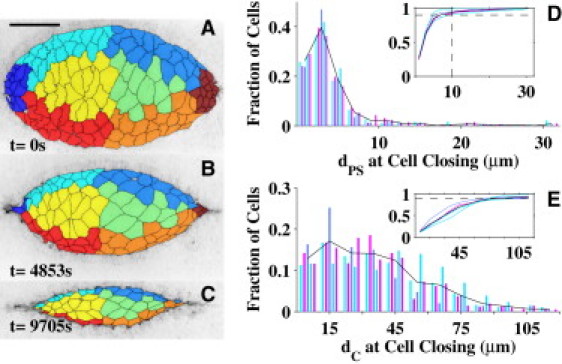
Location of amnioserosa cell ingression. (A–C) False-colored regionalization of embryo #3. The length bar is 50 μm. (D and E) Quantification of the location of each cell at the conclusion of its ingression process. (D) Histogram of the fraction of cells that completed ingression as a function of distance from the purse-string (d_PS at cell closing), where the rightmost set of bars corresponds to d_PS > 30 μm. (E) Reanalysis of those cells that are located within 10 μm of either purse-string; histogram of the distance from each of those cells to the nearest canthus (d_C at cell closing). (Insets) Integration of these results (horizontal dashed line indicates the 90% value).

We then reanalyzed those cells that completed their ingression processes within 10 μm of either purse-string (as identified in Fig. 3 D) and demonstrated that a substantial fraction of these cells completed ingression near a purse-string but far from either canthus. Fig. 3 E is a histogram of the distance to the nearest canthi d_C when ingression is completed. The cumulative distribution is shown in the inset, where the horizontal line corresponds to 90%. These results indicate that greater than half of these ingression sites were located at distances >30 μm from the nearest canthus (70% for distances >15 μm). These ingression sites would be adjacent to the peripheral-most amnioserosa cells, which persist until the end stages of closure (3). We have classified these cells as belonging to a third ingression process, although it is possible that all three ingression processes may share a common mechanism(s).

Asymmetric and invariant properties of dorsal closure

We also observed that cell kinematics within the interior regions of the dorsal opening were not spatially uniform. We developed quantitative methods to characterize these inhomogeneities (see Section S5 in the Supporting Material). Two asymmetries were observed for the interior regions: First, the average initial size of the amnioserosa cells in the posterior interior (green) region was ∼35% greater than that of the anterior (yellow). Second, relatively few cells completed ingression in the posterior and anterior interior regions at earlier stages of dorsal closure. In contrast, the canthus and peripheral regions were more symmetric. These results should be compared to those of the previous subsection, Peripheral ingression process, and summarized by Fig. 3. Jointly, these observations suggest the interior cells are gaining proximity to either leading edge as dorsal closure progresses and support the concept that the leading edge signals the ingression process in amnioserosa cells (see Discussion).

Cell dynamics also exhibited spatial inhomogeneities within the dorsal opening. To quantify any regional variability in the driving forces $\left|{\tilde{f}}_i\left(\omega \right)\right|/f_{0,i}$, we carried out a region-by-region Fourier analysis (see Section S5 in the Supporting Material). The function $\left|{\tilde{f}}_i\left(\omega \right)\right|/f_{0,i}$ was calculated for each cell and then averaged region by region, i.e., we added the Fourier transforms for cells in the same color category and then divided by the number of cells in that category at the initial time. We found that the average Fourier components of the driving force scale with the cell area (see Fig. S12).

We found two invariant quantities despite the inhomogeneous cell kinematics and cell dynamics reported above:

• First, we quantified when each cell completed ingression (measured in cells per min). The rate at which amnioserosa cells completed ingression during dorsal closure was remarkably constant for each embryo (see Table S1, columns G and H), where the average value was 0.83 ± 0.18 cells/min.

• Second, we considered the kinematics of the dorsal opening as a whole and identified a linear relationship as follows. As done previously, we idealized the dorsal opening as two intersecting arcs, i.e., the setting-sun model (8) (see Section S7 in the Supporting Material). The area of the dorsal opening is proportional to the product of the height h(t) (half of the maximum as calculated from leading edge to leading edge) and the width w(t) (half of the canthus-to-canthus distance). As derived in Section S7 in the Supporting Material, we found A(t) = (2.70 ± 0.05)h(t)w(t). The experimental value of 2.76 ± 0.09 (see column I in Table S1) compares favorably with the derived value 2.70 ± 0.05. Thus, although the setting-sun model is an idealization of the geometry of dorsal opening, it provides a reasonable account of the area of the dorsal opening from early-to-late stages of closure. Previously we have observed that dh/dt is essentially constant during the mid-to-late stages of closure, as are the curvatures of each purse-string (8,9).

Discussion

We observed time-dependent changes in the apical area of amnioserosa cells in tissue for five embryos, where confocal imaging commenced before or early in closure and continued to completion. We quantified the kinematics of the amnioserosa cells and developed a biophysical model to advance our understanding of the dynamics. We confirmed that apical areas exhibit complex oscillations (see Figs. 1 and 2, and see Movie S1, Movie S2, and Movie S4, and Fig. S5, Fig. S6, Fig. S7, Fig. S9, and Fig. S12) (11,13,22)). More importantly, we found that the higher-frequency oscillations are essentially reversible and the loss of area can be dominated by ingression. We attribute both types of area changes, which occur in the low-Reynolds number environment of amnioserosa tissue, to time-dependent imbalances in the net force acting on the adherens junctions. We also observed that a substantial fraction of the amnioserosa cells ingressed in the lateral-most regions of the dorsal opening, in addition to previously characterized ingression associated with zipping or with apoptosis in the bulk of the amnioserosa.

Cell ingression and oscillations

We found that the kinematics of the apical areas of amnioserosa cells can be well described by an ingression function I_i(t) (Eq. 2) in addition to higher-frequency oscillations. It is important to distinguish the mathematical, ingression function from the three biological ingression processes. This shoulder-shaped, ingression function describes the ingression processes of a large fraction of amnioserosa cells located throughout the dorsal opening and from the early through the late stages of closure. From cell-to-cell, we found a distribution of best-fit parameters (α_i, ε_i, τ_i) for the ingression function, where the maximum constriction rates varied from 0.2 to 13.6 μm²/min (see Section S2 in the Supporting Material). The cells with the largest constriction rates are consistent with ingression associated with apoptosis in the bulk of the amnioserosa. Ingression at either canthus or in a peripheral region is likely isovolumetric during dorsal closure. However, it is unclear whether an apoptotic cell is isovolumetric during ingression because they bleb as they are extruded into the interior of the embryo (10). All three ingression processes are thought to involve actomyosin-based forces mediating two-dimensional apical constriction of the cell, ultimately resulting in the internalization of a cell below the remaining tissue(s).

We distinguished oscillatory forces and ingression forces with a biophysical model based on a damped, driven harmonic oscillator (Eqs. 4–6, and see Section S3 in the Supporting Material). This model approximates, from experimental data (e.g., Fig. 2 A), relative net forces that represented a spatial average of the intracellular and intercellular net relative forces (Fig. 2 B) that drive cell area changes. A key feature of our oscillations/ingression model was that the lower-frequency, smaller-amplitude components of forces were more effective at driving cell-area changes than the higher-frequency, larger-amplitude components. This can be seen by rearranging Eq. 6:

$$\left|{\tilde{a}}_i\left(\omega \right)\right|=\left[\frac{1}{b\omega {\left(1+{\left(\frac{k_{eff,i}}{b\omega }\right)}^2\right)}^{\frac{1}{2}}}\right]\left|{\tilde{f}}_i\left(\omega \right)\right|.$$ (7)

The term in the square brackets is the transfer function that relates the Fourier components of a response in area to a Fourier component of force. The term of interest in the denominator is (k_eff,i/bω)². Fits of experimental data demonstrated that k_eff,i/b ranged from ∼0.01 to 0.1 mHz, thus for frequencies greater than 1 mHz (k_eff,i/bω)² was much less than 1. Therefore, $\left|{\tilde{a}}_i\left(\omega \right)\right|$ was well approximated by $\left|{\tilde{f}}_i\left(\omega \right)\right|/b\omega$.

Biology benefits from substantially more effective coupling between force production and area changes in the ingression process relative to that of the higher-frequency oscillations. The amplitude of the forces that drive higher-frequency oscillations (Fig. 2 B) in the millihertz range exceeded, by a factor of ∼5, the magnitudes of the forces that drive ingression (Fig. 2 C). Consider the following example based on Fig. 2 F, where the magnitude of the Fourier component $\left|{\tilde{f}}_i\left(0.5\text{mHz}\right)\right|$ = 0.9 and $\left|{\tilde{f}}_i\left(5\text{mHz}\right)\right|$ = 1.4. Due to the ω⁻¹ dependence of the transfer function, $\left|{\tilde{a}}_i\left(0.5\text{mHz}\right)\right|$ was approximately seven times that of $\left|{\tilde{a}}_i\left(5\text{mHz}\right)\right|$. This effect is a consequence of the ω⁻¹ term in Eq. 7. The physics underlying this ω⁻¹ dependence is directly attributable to the viscous drag term and thus is likely to be a general characteristic of tissue dynamics and a model independent result.

These results can be compared with previous observations of relatively high-frequency pulsations. A key consequence of our use of Fourier analysis to estimate $\left|{\tilde{f}}_i\left(\omega \right)\right|$ was the identification of a band of higher-frequency oscillations evident in Fig. 2 E. The band was centered at 5.7 mHz, extending from ∼2.4 to 9.0 mHz. A previous investigation characterized dorsal closure as progressing through early, slow, and fast phases, during which the amplitude of pulsations progressively decreased (11,23). Another investigation, focused on times before the engagement of the zipping process, found that amnioserosa cells pulsate, partially contract, and the amplitudes of the pulsations decreased as the cells reached minimal cross-sectional areas (13). In our experiments, some cells exhibited slow and fast phases of contraction (Figs. 1 and 2, and see Fig. S5, Fig. S6, Fig. S7, Fig. S9, and Fig. S11 B) and in other cases cells exhibited oscillations about a linearly decreasing background (Fig. S11 A). There was a distribution in the time of the onset of ingression that spanned the entirety of dorsal closure and a large distribution of initial apical cell areas (see Table S1). Thus our cell-by-cell analyses exhibited a diversity of individual cell behaviors, not all of which were represented in the previous research (analyses were based on 195, 645, or all of the 815 cells; see Section S1.2.3 in the Supporting Material).

Fourier analysis is sensitive to both the lower and higher frequency contributions, in contrast to methods used in other investigations focused on identifying oscillations based on cycle times, i.e., the duration from peak-to-peak in the apical area (or equivalently radius) traces (11,13). Cycle times capture an approximate period of the largest-amplitude, higher-frequency oscillation, but overlook both lower-amplitude and lower-frequency oscillations. The higher-frequency band (Fig. 2) that we observed lies between 2.4 and 9.0 mHz (periods of 110–500 s), corresponding favorably to the cycle times of 230 ± 76 s (13) and 180–250 s (11) that were previously reported. The frequency range of the ingression function is submillihertz, an order-of-magnitude lower than that of the band of higher-frequency oscillations and would be missed by the alternative cycle-time analyses used previously.

Our understanding of the mechanism(s) that generate force to drive cell area change is incomplete. Any consideration of such forces must address the contributions of both cell autonomous and cell nonautonomous forces, i.e., forces generated both within cells and by neighboring cells. Previously, pulsed oscillations in the millihertz range have been correlated with assembly/disassembly cycles of actin and myosin in the apical medial network (11,13,16,22) and have been proposed to be regulated by the PAR complex (12). Our observations are consistent with a role of actomyosin force production. It has been proposed that an increase in free calcium concentration contributes to cell-shape changes by severing actin filaments and activating myosin contractility (see, for example, Salbreux et al. (19) and Lee et al. (24), also reviewed in Bray (25)). Two unresolved questions include: 1), What intercellular feedback mechanism(s) accounts for oscillations in the first place? 2), What aspect of the molecular mechanism leads to the observed band of frequencies for these oscillations? Any oscillatory mechanism must include both feedback that overcomes the constraint of low-Reynolds number and an account of regulation. Alternative possibilities include feedback due to load-dependent detachment rates in actin-myosin networks (21,26), regulation of the actomyosin cytoskeleton by membrane channels (19,24), and/or domain growth and phase coherence (see Concluding Remarks).

A full two-dimensional treatment of the forces that alter cell shape requires subcellular knowledge of stresses and strains. The analyses reported here are well matched to available optical resolution and contrast mechanisms for tracking cell-shape in dorsal closure. Treating cell shape as an area allowed the dynamical modeling of closure based on a relative net force f_i(t) that was spatially averaged and time-dependent. A feature of our oscillations/ingression model is that any time dependence in elasticity or viscosity was accounted for in f_i(t), whereas spatial variability is treated in the spatial averaging process implicit in f_i(t) (see Section S3 in the Supporting Material). In addition, we have shown previously that treating b as constant is a very good approximation within the dynamic range of our observations (10). Because f_i(t) is a net force, time-dependent changes in f_i(t) are a consequence of changes in cell autonomous or nonautonomous forces. There are silent forces that change a cell shape without changing the area of the cell in addition to the forces f_i(t) reported here. We have estimated cell-shape changes and find that approximately half of them correspond to area changes (27). Nevertheless, f_i(t) accurately summarizes area changes due to the spatially averaged, net stresses acting along a cell's apical belt of adherens junctions.

Regional dynamics and regulation

We have observed that cell kinematics and dynamics depend on location within the dorsal opening, consistent with the leading edge playing a role in regulating amnioserosa cell shape. Our initial confocal images confirm that the largest cells were in two interior regions (Figs. 1 and 3, and see Fig. S12) and that apical cell areas typically decreased with proximity to either purse-string or the canthi where the purse-strings converge (Fig. 3) (13,22,23). In contrast, it has been reported that cells near the posterior canthus exhibited apical contraction earlier then those of the anterior canthus (23). It may be the case that the cells with smaller apical areas in the canthi and peripheral regions had already progressed into an ingression process before our imaging (potentially confounding the applicability of an ingression function I_i(t) to their behavior (see Section S2 in the Supporting Material)). Cells preferentially completed ingression near either purse-string in addition to having completed ingression near the canthi (Fig. 3, D and E). This correlation suggests the possibility that each leading edge was involved in the regulation of cell ingression, whether by chemical and/or mechanical signaling processes (9,13,19,23). In addition, we found an asymmetry between the anterior-interior and posterior-interior regions as measured by the completion of the ingression process, but did not observe a robust asymmetry between the two canthus regions (see Fig. S12).

The dorsal opening steadily progresses toward closure despite the variability in the details of cellular mechanics that we and others have described. Although cells can transition into a rapid loss of apical cross-sectional area, the amnioserosa stress is relatively homogeneous along each purse-string of the two leading edges (8–10,28,29). Several parameters that characterize the overall geometry of the dorsal opening were nearly invariant as closure progressed. This includes the area proportionality constant (see Table S1 and Section S7 in the Supporting Material) and, as reported previously, both the constant rate of dorsalward movement and the curvature of the two leading edges (8,9).

We propose that the emergence of these invariant parameters is attributable in part to the constant rate of ingression (0.83 cells/min). Although Fig. S12 B indicates that there is a regional dependence to the cellular rate of completing ingression, when these rates were summed over all of the regions it resulted in a constant rate for completing ingression from mid-to-late stages of dorsal closure (see Table S1). This implies a mechanism that relates the inhomogeneities in cellular dynamics to the homogeneity of tissue dynamics and includes the invariant ingression rate, where causality remains unclear. As a consequence, a temporal averaging of a spatial distribution of local cellular forces would produce nearly uniform spatial and temporal tissue stress. These observations are consistent with two previous observations: First, a cellular rate of ingression has been implicated in the upregulation of the stress of the amnioserosa in response to laser perturbation via a cellular apoptotic force (10). Second, anteroposterior asymmetry in the zipping rate constants correlated with the regional rate of apoptosis (9,10). When comparing the two interior (yellow and green) regions, for four out of five embryos investigated here, there was a distinctive asymmetry in the rate that cells completed the ingression process (see Fig. S12 B). The regulation of the cellular ingression rates throughout the amnioserosa is an open research question.

Concluding Remarks

A mechanistic understanding of apical-cell oscillations, the onset of cell ingression, and the variable rates of ingression during dorsal closure will require a more complete understanding of actomyosin complexes and their regulation. In particular, what mechanism(s) is responsible for the oscillations and the onset of ingression in amnioserosa cells? At the molecular level, actomyosin complexes almost certainly drive force production for both oscillations and ingression. Previously it was observed that the average fluorescent levels of myosin progressively increase (both in the apical medial network and along cell junctions) as dorsal closure enters a fast phase of loss of apical area (11) and that forces due to apical-medial networks become more important relative to the contractility of the adherens belt (29). The intracellular and intercellular mechanisms that produce such regulation are poorly understood.

Our working model views the systematic/coherent ingression process(es) to be qualitatively and quantitatively different from the process(es) of oscillations. Whereas the band that characterizes the higher-frequency lies in the millihertz range (∼2.4–9.0 mHz), the frequency content of the ingression process was dominated by an order-of-magnitude lower, submillihertz frequencies. The millihertz frequencies correspond to largely reversible oscillations in apical area, whereas the submillihertz frequencies correspond to a coherent loss of area. We hypothesize that the differences between oscillations and ingression are due to dynamical changes in subcellular domains of actomyosin, where a domain defines either a cortical and/or apical-medial region of coherently contracting cytoskeleton. We speculate that the largely reversible oscillations in apical area (during the plateau) are due to actomyosin assemblies that pulsate independently. In addition, we speculate the switching-on of an ingression process is attributable to domain growth, i.e., the merging of previously independent domains into a relatively large (but still subcellular) phase-locked domain whose dominant and coherent contraction supports the systematic loss of apical area. We also propose that the primary mechanism for systematic loss of apical area in amnioserosa cells during dorsal closure is associated with coherent ingression processes and the cell-to-cell variability in contraction rates is attributable to variability in the extent of domain growth. In particular, the rapidly ingressing cells correspond to relatively effective domain growth whereas the more slowly, linearly ingressing cells correspond to partial or delayed domain growth. We view the higher-frequency oscillations that precede ingression as reflecting the contractile activity of preliminary assemblies of the actomyosin machinery. With regard to regulation, previously it has been reported that Dpp (whose secretion is triggered by leading-edge cells via JNK signaling) can regulate cell shape changes in both the lateral epidermis and in the amnioserosa (22,30–32). Although this apparent regulation promotes the completion of ingression (Fig. 3, A–C), there is considerable cell-to-cell variability in the effect of proximity to the leading edge on both the rate of apical constriction and its completion (see Fig. S8). We propose that proximity to the leading edge is not the only contributing factor, i.e., there may be variability in the response of amnioserosa cells to the signal(s) that regulate the onset of ingression.

In summary, we have investigated dorsal closure in quantitative detail from cellular and tissue perspectives. We have described the kinematics of the majority of the cells in terms of oscillations and ingression, the latter of which was the dominant mechanism for loss of apical area in the amnioserosa. We observed a third ingression process for amnioserosa cells within the peripheral region of the dorsal opening. We have accounted for cell oscillations and ingression by applying a dynamical model based on an overdamped driven harmonic oscillator, which placed constraints on candidate dynamic mechanisms. Although our oscillations/ingression model preserved the frequency response of the tissue, the net force was based on a spatial average of the intracellular and intercellular forces. It would be advantageous to have more detailed knowledge of the force field to characterize stresses and strains at the subcellular level. This would enable a more complete description of the time-dependent molecular mechanisms for force production and their regulation, including the emergence of a band extending from ∼2.4 to 9.0 mHz and its biological significance.