Thermodynamic and Kinetic Analysis of an RNA Kissing Interaction and Its Resolution into an Extended Duplex

Abstract

Kissing hairpin interactions form when the loop residues of two hairpins have Watson-Crick complementarity. In a unimolecular context, kissing interactions are important for tertiary folding and pseudoknot formation, whereas in a bimolecular context, they provide a basis for molecular recognition. In some cases, kissing complexes can be a prelude to strand displacement reactions where the two hairpins resolve to form a stable extended intermolecular duplex. The kinetics and thermodynamics of kissing-complex formation and their subsequent strand-displacement reactions are poorly understood. Here, biophysical techniques including isothermal titration calorimetry, surface plasmon resonance, and single-molecule fluorescence have been employed to probe the factors that govern the stability of kissing complexes and their subsequent structural rearrangements. We show that the general understanding of RNA duplex formation can be extended to kissing complexes but that kissing complexes display an unusual level of stability relative to simple duplexes of the same sequence. These interactions form and break many times at room temperature before becoming committed to a slow, irreversible forward transition to the strand-displaced form. Furthermore, using smFRET we show that the primary difference between stable and labile kissing complexes is based almost completely on their off rates. Both stable and labile complexes form at the same rate within error, but less stable species dissociate rapidly, allowing us to understand how these complexes can help generate specificity along a folding pathway or during a gene regulation event.

Introduction

In recent years, reports of riboregulation have become commonplace, dramatically changing our view of the central dogma and the way in which gene regulation is controlled (1). Regulation may occur cotranscriptionally, as in the case of most metabolite sensing riboswitches (2), or posttranscriptionally, as in the case of the small bacterial regulatory RNAs (3) or eukaryotic microRNAs (4,5). Riboswitches are structures that allow small-molecule binding to an aptamer domain to control a unimolecular rearrangement, allowing the RNA to adopt either a termination or an antitermination structure, and hence, they affect the transcription of downstream genes (2,6). Posttranscriptional regulation typically requires two RNAs to recognize one another (an sRNA and its cognate mRNA target), sometimes on their own, but more commonly with the assistance of RNA-binding proteins (7,8). The resulting complex can then be recognized and acted upon by cellular machinery. Stability of these RNA-RNA complexes must be finely tuned. If the initial contact yields a species that is too stable, selectivity is lost, since release of the noncognate partner becomes slow. Conversely, if the initial complex interacts too weakly, its lifetime is too short to allow stable pairing interactions to form and the benefits of colocalization are lost. Thus, the initial contact must fall within a relatively narrow range of lifetimes to be beneficial.

In the case of bacterial and viral systems, loop-loop contacts (kissing interactions) are particularly prevalent in regulatory complexes. Kissing interactions occur when complementary sequences in apical loops of two hairpins can form Watson-Crick basepairing (9). The stability of these kissing complexes is primarily based on loop complementarity, but factors such as the orientation of the loops, internal loop structure, the loop-closing basepair, and the sequence of the stems adjacent to the loops are all known to contribute to the stability of these interactions (10–12). Numerous examples of rearrangements are known that depend upon the initial formation of loop-loop interactions. Complexes between CopA and CopT RNAs and between RNAI and RNAII were among the earliest members of this class of RNAs to be studied (10,13). Both systems control plasmid replication and copy number. In the biology of human immunodeficiency virus (HIV), the dimerization initiation sequences (DISs) form kissing complexes and ultimately resolve into an extended duplex that dimerizes the HIV genome for packaging into capsids (14–17). Despite the prevalence of these interactions, information on the thermodynamic and kinetic stabilities of these kissing hairpins is relatively scarce (18).

Multistep structural rearrangements involving transient metastable intermediates (i.e., kissing complexes that resolve into long-lived, thermodynamically stable duplexes) help to balance the needs for stability and selectivity in biological signaling networks (19). The paradigm for a kissing complex that resolves to an extended duplex is HIV DIS, but several other systems are also known. As illustrated in Fig. 1 A, the strand-displacement reaction can initiate through two possible mechanisms at modest temperatures: a), nucleation through the complementary hairpin loops, resulting in a kissing complex; or b), nucleation through 3′/5′ termini, resulting in formation of a zipper intermediate) (20,21). At elevated temperatures where small amounts of the unfolded state might be present, or in the presence of helicases that can actively unfold the RNAs, an unfolding and annealing pathway (Fig. 1 A, c) is also accessible.

Figure 1.

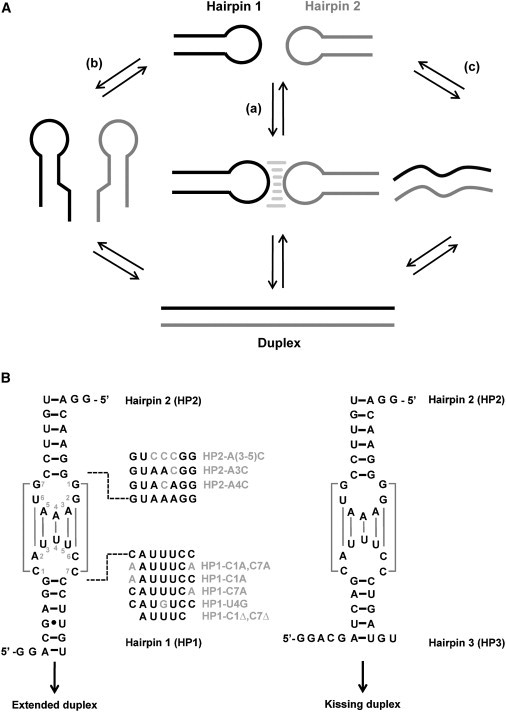
Structural rearrangements associated with KC formation and the model hairpins used. (A) Possible pathways for strand displacement reactions. Strand displacement can be nucleated by formation of a KC (a), by initiation at the termini (b), or through complete unfolding of the hairpins (c). (B) Schematic diagram of the hairpin constructs used in this study: hairpins capable of rearranging into ED complexes (left), and hairpin sequences incapable of further rearrangement (right).

In this study, we have used isothermal titration calorimetry (ITC), single-molecule Förster resonance energy transfer (smFRET), and other biophysical methods to study the kinetic and thermodynamic properties of a series of RNA hairpins that can form kissing complexes and the subsequent rearrangement to an extended duplex—a classical strand-displacement reaction such as might occur during a riboregulation event. For simplicity, in this study, all proteins have been removed from the system, although we recognize that in certain cases, reactions such as these would be facilitated by RNA chaperones such as Hfq or NCp7.

Our results show that the transition from the kissing interaction to an extended duplex has a large kinetic barrier and that in the absence of accessory components (such as the Hfq protein), dissociation is favored over strand displacement except at very high RNA concentrations. Our results imply that recognition between two RNAs is often under kinetic control at the level of the RNA-RNA intermediates, such as a kissing interaction. We further compared the thermodynamics of kissing complexes to those of simple RNA duplexes with identical sequences, showing comparable energetic trends despite the differences in structural context. Overall our work describes a potential thermodynamic and kinetic model for kissing-complex formation and associated structural changes.

Materials and Methods

Materials and methods that were used in this study can be found in the Supporting Material.

Results and Discussion

Design of RNA hairpins

In this study, kissing interactions have been probed between the complementary loops of short hairpins to measure the thermodynamics for these processes. Transformation of the kissing complex (KC) into an extended-duplex (ED) conformation was also measured to understand the energetic landscape faced by regulatory interactions that rely on this type of structural dynamics.

The hairpin constructs used in the study are shown in Fig. 1 B. The parent kissing hairpins HP1 and HP2 derive from the E. coli DsrA-rpoS bulge-loop interaction that occurs during cold shock (22). This interaction initiates a strand-displacement reaction in rpoS mRNA to activate translation in the presence of the chaperone protein Hfq. The kissing interaction between HP1 and HP2 has also been extensively studied previously during the development of the laser-assisted single-molecule refolding (LASR) technique (23). The parent hairpins are complementary in both their loop and stem regions, enabling them to form a KC and also to resolve into the ED state. HP3 derives from HP1, but lacks complementarity with HP2 within the stem region, arresting the reaction at the level of the KC. To assess the effects of loop size and sequence on the overall energetics, mutations were introduced as shown in Fig. 1 B.

Each of these hairpins was subjected to thermal melting analysis before biophysical analysis was initiated on these systems. The thermodynamic parameters for each hairpin are shown in Table S1 in the Supporting Material. In addition to the isolated hairpins, the bimolecular extended duplexes of HP1::HP2 and HP1::HP2-A(3-5)C were also assayed. The melting temperatures (T_M) of the hairpins were independent of sample concentration, showing that the observed transitions were unimolecular and thus represent the hairpins and not the dimeric forms of the molecules.

Thermodynamic analysis of kissing interactions by ITC

Thermodynamics of the kissing interactions were probed using ITC. ITC is a powerful method for measuring the thermodynamics of molecular interactions of biomolecules (24–27). Since calorimetry uses the heat of binding rather than hyperchromicity for detection, it is typically much more sensitive to kissing interactions than thermal melting studies. In addition, it allows one to probe temperature dependence of the reactions to look at their detailed thermal profiles. Since the formation of stably folded structures requires the compensation of the negative charges of backbone phosphates (whose electrostatic repulsion inhibits close packing), titrations were performed in the presence of either 1 M NaCl or 10 mM MgCl₂.

HP2 and HP3 can form up to seven basepairs within the kissing complex, of which four are AU pairs (Fig. 1 B, right). Native gel electrophoresis was used to confirm that these sequences folded into single stable hairpins without contaminating duplex structures after annealing (Fig. S1). Optical melting studies could not detect the kissing interactions because of the small change in hyperchromicity between the free and bound states (data not shown), but the interaction was clearly evident by ITC. A representative titration for the binding of HP2 to HP3 with formation of a KC is shown in Fig. 2 A. Thermodynamic parameters obtained for this interaction under various conditions are summarized in Table S2.

Figure 2.

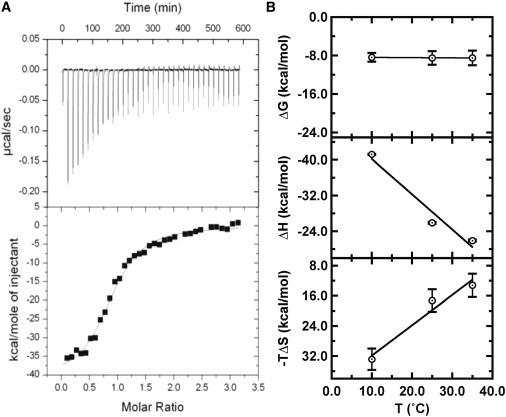
Representative ITC data. (A) (Upper) Thermograms showing formation of the HP2::HP3 kissing interaction. HP3 solution (60 μM) was titrated into 1.4 mL HP2 (3.5 μM) at 10°C in sodium-binding buffer. (Lower) Integrated data (solid squares) were fit to a single-site binding model (solid line), yielding: ΔH = −41.2 kcal mol⁻¹; −TΔS = 32.8 kcal mol⁻¹; K_A = 2.8 × 10⁶ M⁻¹; n =1.0. (B) Thermodynamic energies ΔG (upper), ΔH (middle), and −TΔS (lower) as a function of temperature.

Thermodynamics for the kissing interaction between HP2 and HP3 measured in 1 M NaCl are plotted as a function of temperature in Fig. 2 B, exemplifying the results. The heat of binding for the kissing interaction was measurable by ITC between 10°C and 35°C but unmeasurable at 45°C, indicating a melting transition between 40°C and 45°C. As shown in Fig. 2 B, ΔG of the kissing interaction was essentially unchanged over this range, but analysis of ΔH and TΔS shows significant enthalpy-entropy compensations, potentially originating from the reorganization of hairpin loops as a function of temperature. Significant ion-dependent effects were observed for these reactions as well, consistent with this interpretation. In 1 M NaCl, KC formation displayed a positive heat capacity change (ΔC_P) of 0.8 ± 0.2 kcal mol⁻¹ K⁻¹. ΔH was most favorable at low temperatures. On the other hand, in 10 mM MgCl₂ the trends were reversed, yielding a ΔC_P of −0.3 ± 0.2 kcal mol⁻¹ K⁻¹. The reaction was entropically opposed at all temperatures, but more so at lower temperatures. Furthermore, the overall free energy for KC formation was stabilized by ∼1.0 kcal/mol in 10 mM MgCl₂ relative to 1 M NaCl (Table S2). ITC experiments cannot determine whether the observed differences derive from changes in the ground state (conformation of the loop nucleotides) or product state (altered coaxial stacking in the KC), although based on the ion-dependent behavior, we believe loop confirmation may be the more likely of the two explanations.

To analyze sequence effects on the energetics of KCs, mutations were introduced within the loops. First, the central adenosine (A4) in HP2 was mutated to cytosine (HP2-A4C) together with its counterpart within HP3 to form HP3-U4G, changing the central A⋅U basepair of the kissing interaction into a G⋅C that would presumably form a slightly more stable KC. Thermodynamics were measured using ITC and are shown in Table S2. An extra stabilization of ∼2 kcal/mol in 1 M NaCl and ∼1 kcal/mol in 10 mM MgCl₂ was observed for this mutant relative to the parental species, presumably originating from the G⋅C basepair. Heat-capacity changes (ΔC_P) of −0.5 ± 0.1 and −0.7 ± 0.1 kcal mol⁻¹ K⁻¹ were measured in NaCl and MgCl₂, respectively, for this KC. In contrast to HP2::HP3, the entropy-enthalpy compensation here was counter ion-independent, implying that structure within the unimolecular loop is responsible for ion-dependent ΔC_P effects, similar to previous observations on duplex systems (28,29).

The observation that significant ΔC_Ps are associated with KC formation is interesting. Work from a number of laboratories has shown that changes in the internal structure of RNA and DNA in the single-stranded state contribute to the observed ΔC_P for duplex formation (30–32). Although modest differences as a function of ionic conditions were expected based on prior studies (33), the large magnitude of these changes was somewhat surprising. More negative ΔC_P values were consistently observed in 10 mM MgCl₂ solutions relative to 1 M NaCl, implying differences in salt stabilizations of reactant and product species. ΔC_P contributions toward the overall energies of these motifs are significant, and understanding the origin of these energies in nucleic acid folding is important if one wishes to accurately predict the stability of RNA structures. In fact, a recent study showed that incorporating experimentally determined ΔC_P values in conjunction with nearest-neighbor models helped overcome systematic deviations between predicted and experimentally determined thermodynamics in DNA duplexes (34). Similar data will eventually be required to accurately model thermodynamics for KCs.

Mutagenesis of the loops indicated that the stability of this kissing interaction is near the edge of the viable range for ITC analysis. Removal of two bases from the loop (HP3-C1Δ,C7Δ, 5 nt loop system) greatly destabilized the interaction with HP2. HP1-C1Δ,C7Δ::HP2 complex was neither stable on native gels at 4°C (Fig. S1) nor was it detectable by ITC, even at the lowest accessible temperatures (5°C) in 10 mM MgCl₂. The origin of this instability could be from diminished basepairing or from a reduction in the loop size, which has been shown to be important for KC stability (35). To distinguish between the two possibilities, the hairpin HP1-C1A,C7A was constructed, retaining the 7-nt loop of HP3 but with only 5 nt of complementarity. In the HIV DIS system, the unpaired purines (A) at the base of its 9-nt stem-loop-stem-loop structure were shown to be essential for dimerization and to attain significant association rates by influencing favorable loop structures for KC formation (12,15).

However, a stable KC of HP1-C1A,C7A::HP3 was not observed. Thus, the loss of the G⋅C basepairs at either end of this kissing interaction leads to significant destabilization. Apparently, this G⋅C basepair contributes significantly to the stability of this interaction in an otherwise AU-rich KC.

Thermodynamics of kissing complex versus duplex formation

We next compared the thermodynamics of the KCs to simple duplexes of the same sequences. This comparison allows us to determine whether the sequence and loop-size effects within the kissing interaction originated from the structural context of the hairpin loops or were inherent to sequences themselves. Thus, RNA2::RNA3 is equivalent to HP2::HP3, just removed from the constraint of the KC hairpins. Thermodynamic values measured in 1 M NaCl are provided in Table S3. Similar trends in stability were observed for duplexes and KCs of the identical sequence. Stable duplexes formed in the case of the wild-type sequence and the central GC mutant (A4C::U4G). The duplex with terminal GA mismatches (HP2::HP3-C1A,C7A) was detected at 5°C in ITC, but the shortened HP3 with 5′ and 3′ overhangs was not sufficiently stable to be observed. These results suggest that the inherent sequence- and loop-size effects observed in the ΔG of the KCs simply recapitulated stability issues of the underlying duplexes.

Given the matching trends that were observed in the energetics of KCs and duplexes, it is interesting to see how similar these kissing interactions are to simple duplexes of the same sequence. Can one simply use a nearest neighbor (NN) formalism (derived from simple duplexes) to predict the energies of the kissing complexes? To test this possibility, NN parameters (27,36,37) were used to calculate free energies for RNA duplexes mentioned above and then compared to the measured values for the relevant simple duplexes and kissing interactions (Table S4). As expected, NN rules predicted simple duplex stability quite well for these short RNAs with ΔΔG₂₉₈ < 1 kcal/mol. NN predictions fared less well with the kissing hairpins, where the kissing complexes were >2 kcal/mol more stable than predicted, likely due to additional stacking interactions from coaxial alignment of the helices, electrostatic interactions or possible metal binding events not accounted for in the NN model. Furthermore, for duplexes RNA2::RNA3-C1Δ,C7Δ and HP2::HP3-C1A,C7A free energies of ∼−2.6 and ∼−4 kcal/mol were predicted by NN methods. This was in good agreement with what was observed in duplex and kissing contexts where stable complexes were not detectable by ITC. Of even more interest, these data put forth the notion that at least for these sample systems, KC stability can be approximated using a slight offset predicted by the NN method for the identical RNA duplex. Thermodynamic analysis on a more extensive collection of sequences will be required to establish a suitable correction value to account for the offset.

Several interesting characteristics in energetics between KCs and duplexes were revealed by ITC, however (Table S2 and Table S3). Enthalpic and entropic components for duplex and KC formation vary significantly. In the context of a simple duplex, the energetics were more enthalpically favorable and more entropically opposed relative to that of the related KC. This is in part due to the expenditure of energy required by one hairpin, in reorganizing the internal structure of the loop, to interact with its complementary hairpin. In duplex formation, the reorganization energy is much smaller relative to KCs (28). On the other hand, the entropic penalty was greater in duplexes due to the higher loss in degrees of freedom from the random-coil state of single-stranded RNAs relative to the structured hairpins. These observations are similar to what was observed for another type of tertiary structure, the tetraloop-tetraloop receptor interactions (39) and thus may be part of a more general trend in the folding energetics of RNA tertiary structures.

Duplex formation was also accompanied by a sizeable ΔC_P, −0.4 kcal mol⁻¹ K⁻¹ for the parental sequence and a much larger −2.4 kcal mol⁻¹ K⁻¹ for the duplex with the central GC pair (RNA2-A4C::RNA3-U4G). The −0.4 kcal mol⁻¹ K⁻¹ value is typical of simple duplexes, which have an average of −42 cal mol⁻¹ K⁻¹ bp⁻¹ (40), whereas the larger sequence is more indicative of a species with a latent structure in the single-stranded state. The observed trends in ΔC_P are consistent between the KCs and duplexes. These data suggest that thermodynamic principles that govern duplex formations can readily be extrapolated to KCs.

Thermodynamic analysis of strand-displacement reactions

In the experiments described above, hairpins could only form KCs and could not proceed further, because the stems were noncomplementary. Next, the sequences were allowed to resolve into the ED conformation. Using ITC, HP1 was titrated into HP2 to determine the energetics of the strand-displacement reaction as a function of temperature in either 1 M NaCl or 10 mM MgCl₂ (Table S5). Thermodynamic parameters for these reactions are quite different from those associated with KC formation, indicating that the reaction proceeds rapidly to the ED state under these conditions. Similar to the case of KC formation, there is a significant ΔC_P associated with these transitions and the magnitude is highly dependent on the ionic strength of the solution. Using the approximation that ΔC_P is temperature-independent, values of −1.1 ± 0.1 and −1.8 ± 0.1 kcal mol⁻¹ K⁻¹ in 1 M NaCl and 10 mM MgCl₂, respectively, were observed for the rearrangement. The magnitude of ΔC_P observed for ED formation is slightly more negative than that seen for KC formation. The more negative heat-capacity change was once again associated with the MgCl₂ reaction conditions.

As described in Fig. 1 A, multiple pathways might allow ED formation from a pair of hairpins when the RNAs are self complementary. NMR and x-ray structures are available for both DIS KCs and ED formation produced by a number of groups (41–43) using 23-mer RNAs. The loop-loop contacts in the KC were retained during the transition to the ED (44) and the propensity for ED formation decreased with increasing RNA size and in the absence of Ncp7 (45,46), implying topological constrains faced during ED formation. If ED formation were solely dependent on an intermediate KC, mutations that reduce or abolish loop complementarity should prevent the reaction. To determine the effect of destabilizing the kissing interaction on strand displacement, all three adenosines in the loop of HP2 were substituted with cytosines (HP2-A(3-5)C). As expected, both native gel analysis and ITC at 5°C failed to show the formation of a stable kissing interaction, but strand displacement still proceeded rapidly to form the ED (Table S5). Since these RNAs cannot kiss to any appreciable extent, the data indicate that formation of a stable KC is not required for strand displacement in the context of this model system, and the fraying pathway described in Fig. 1 A (pathway c) may dominate in the absence of the KC. This result shows that the fraying pathway can also be accessible to a certain extent during this type of structural transition. Calorimetry showed relatively small changes in ΔG between KC and ED states at these temperatures. The enthalpic and entropic components of the ED state are, however, quite different from those of the KC, with much greater enthalpic stabilization in the case of the ED. The kinetic behaviors of the two species are also dramatically different, as described below.

This conclusion is similar to recent discussions on the mechanism of strand displacement for HIV DIS. There has been much discussion regarding the proposal that the KC proceeds through a two-step rearrangement wherein the first step involves pairing across the loop and the second step results in coaxial alignment of the three helical elements (20,47). Although this latter step may be critical to the stability of a KC, it likely inhibits the rapid expansion of the intermolecular basepairing at the expense of intramolecular interactions, as that pathway requires destacking of the helical elements at each step of the helix expansion.

Kinetic analysis of KC formation

To measure the kinetics of KC formation, surface plasmon resonance (SPR) and smFRET were used. For SPR, 5′-biotinylated hairpins were bound to streptavidin-coated sensor chips. The complementary hairpin was then introduced at varying concentrations to monitor the interaction in 10 mM MgCl₂. Sensorgram traces were fit to a Langmuir binding model to obtain association and dissociation kinetics. A representative SPR sensorgram for HP2::HP3 KC formation is shown in Fig. 3 A. Kinetic data obtained for HP2::HP3 and HP2-A4C::HP3-U4G KC formation are collected in Table S6. Both wild-type and HP2-A4C::HP3-U4G associate with moderate on-rates that slightly increase with temperature. On the other hand, off-rates for HP2::HP3 were faster at higher temperatures but changed minimally for HP2-A4C::HP3-U4G. Stability constants for KC formation were calculated using kinetic data obtained from SPR (Table S6) and are comparable to values measured by ITC (Table S2).

Figure 3.

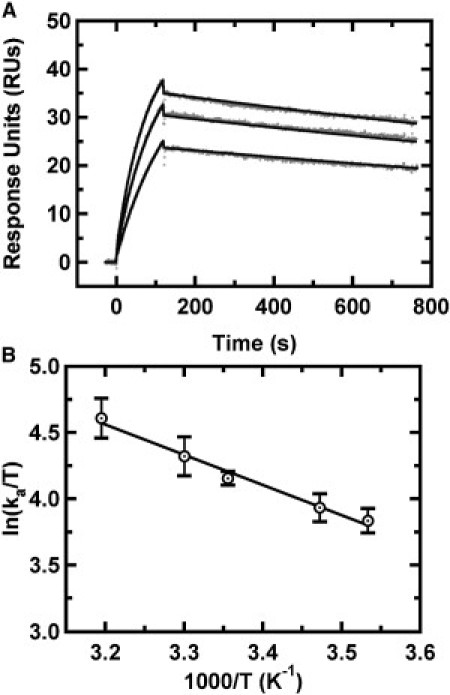
Kinetics of HP2::HP3 KC formation measured by SPR. (A) Representative sensorgrams as a function of HP3 concentration (400–800 nM), with surface-immobilized HP2 RNA monitored at 15°C. Association and dissociation data were fit into a Langmuir binding model. (B) Eyring plot of HP2::HP3 association rates studied between 10°C and 40°C.

Activation energetics for KC formation

As depicted in Fig. 1 A, kissing interactions might serve as key intermediates to structural transitions such as extended duplex formation. To understand the transition-state thermodynamics of KCs relative to ED formation, the temperature dependence of the rates for association and dissociation were probed. The measured rates were then subjected to Eyring analysis to provide activation parameters ΔH^‡, ΔS^‡, and ΔG^‡₂₉₈. A representative Eyring plot for HP2::HP3 KC is shown in Fig. 3 B with clean, linear Eyring behavior.

Activation parameters for HP2::HP3 and HP1-U4G::HP2:A4C complexes are collected in Table S6. Similar activation energies were observed for the association phase of both constructs. In contrast, activation parameters for dissociation varied significantly between the parent and G⋅C mutant. Both entropic and enthalpic components were more favorable for the dissociation of HP2::HP3 compared to HP2-U4G::HP3-A4C. These data suggest that the stabilities of these two complexes are dictated mainly by their dissociation transition states, whereas the energy landscapes for association are similar. From equilibrium measurements, it was observed that HP2-U4G::HP3-A4C formed a relatively stronger complex with a ΔΔG₂₉₈ of ∼1.1 kcal/mol, consistent with ITC data.

Kinetics of KC formation using smFRET

smFRET was also used to study the kinetics of these KCs and any potential intermediates formed en route toward strand-displaced products. The main difference between the two methodologies is that in SPR, the physical observable represents the average ensemble of the system, whereas in smFRET, changes at the molecular level can be measured. The basic overview of the smFRET setup is shown in Fig. 4 A. A Cy3-labled RNA hairpin was immobilized on a quartz slide via biotin-streptavidin interaction. FRET trajectories were recorded after addition of its Cy5-labeled binding partner at a concentration of 35 nM. A typical single-molecule time trajectory obtained for HP1::HP2 is shown in Fig. 4 B, where the fluorescence intensities of the donor and acceptor fluorophores change in an anticorrelated fashion (Fig. 4 B, upper). The resulting FRET trajectory (Fig. 4 B, lower) shows transitions between two distinct states at ∼0.0 and ∼0.5 FRET. Control experiments (Fig. 4 D) showed that the 0.5 FRET state corresponds to an intermediate state (KC) that occurs when HP1 and HP3 react together. As indicated in Fig. 4 D (upper two panels), when either HP2 only or HP2 and a noninteracting hairpin were present, a peak with FRET ratio ∼0.0 was observed. To identify FRET ratios for the intermediate states of the HP1 and HP2 reaction, the hairpins were preannealed or reacted in its hairpin context. When preannealed, the predominant state would be the ED (FRET = ∼1.0), since HP1 and HP2 have complementary stems. Although HP1 and HP2 resolve into an ED state under ITC conditions, this transition was extremely rare experimentally under the conditions required for smFRET analysis. Out of >600 molecules analyzed, only three ED-formation events were observed in the experimental time window. The majority of molecules showed FRET values at 0 or 0.5, which represents the dissociation and association of a KC. These data show that the KC can be long-lived (∼5 s on average (Fig. 4)) and can undergo many cycles of dissociation and association before progressing to the ED complex. The big difference in experimental parameters between these two experiments is the concentration of the individual RNAs. ITC is performed at high strand concentration so that the reaction generates sufficient heat to accurately measure the reaction, whereas the smFRET experiments are performed at very low dilutions to ensure spatial localization of individual molecules. Thus, the effect of local concentration can be seen as paramount in the expected outcome. Also, in ITC experiments, the use of higher concentrations of RNA may allow access to the fraying pathway that would facilitate ED formation. This may also represent one of the primary roles of accessory proteins in strand-displacement reactions in vivo, improving the likelihood of a forward progression which then can be kinetically trapped by the slow off-rate for the ED state.

Figure 4.

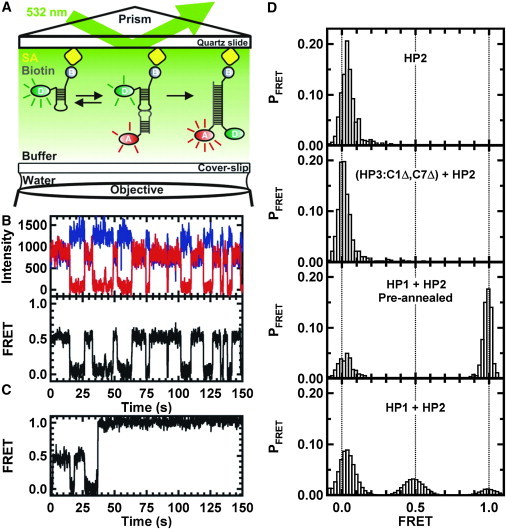
smFRET analysis of kissing kinetics. (A) Schematic representation of the total internal reflection setup. The donor RNA hairpin is immobilized by a biotin-streptavidin interaction on a biotin-BSA-coated quartz slide. A kissing interaction and an ED formation are shown in the presence of a 35-nM RNA hairpin with the acceptor fluorophore. (B) Typical single-molecule time trajectory. (Upper) Anticorrelated intensities of the donor (blue) and acceptor (red). (Lower) The corresponding FRET trajectory. Only the 0.0 and 0.5 FRET states are observed for the dissociated and kissing complexes. (C) Representative FRET trajectories showing several kissing interactions and their transition to the ED state. There are few molecules with a transition directly from KC to ED. (D) FRET histograms from single-molecule trajectories. (Upper) Donor-only RNA hairpin HP2 exhibits a single 0.0 FRET state. (Second from top) Preannealed noncomplementary hairpins (HP3-C1Δ,C7Δ + HP2) do not form the ED. (Third from top) Two preannealed complementary RNA hairpins (HP1 + HP2) show two distributions (0.0 and 1.0 FRET states) when preannealed before imaging. The distribution at 1.0 FRET state is due to ED formation. (Lower) Cumulative histogram built from >100 molecules. HP1 reacted with surface-immobilized HP2. This histogram shows three distributions at 0.0, 0.5, and 1.0 FRET states. The 0.0 FRET state is free HP2, the 0.5 FRET state represents the KC, and the 1.0 FRET state corresponds to the ED. ED molecules show no dynamic behavior and are trapped in that form under the experimental conditions.

Furthermore, the stem lengths of kissing hairpins were inversely proportional to the FRET value, indicating formation of the appropriate KC in these assays (Fig. S2). Molecules that successfully reached the ED were kinetically inert and showed no additional dynamic behavior before photobleaching. Presumably, they get trapped in this conformation due to a large activation barrier for escaping from this well, a pathway only accessible upon heating (23).

A dwell time distribution histogram was prepared for each FRET state and fit to an exponential decay to estimate the apparent rate constants for association (k_on = 3.4 ± 0.3 × 10⁶ M⁻¹ s⁻¹: calculated from the pseudo-first-order rate constant and the effective ligand concentration of 35 nM) and dissociation (k_off = 0.17 ± 0.02 s⁻¹) (Fig. S3) (48). From the rate constants, the free energy of KC formation was estimated as ΔG = −9.9 ± 0.2 kcal/mol (Table S6), which is in excellent agreement with the ensemble-averaged ITC and SPR data (Table S2). An estimate of ΔG° using the FRET distributions (Fig. 4 D, lower) yields the same result. The agreement between the single-molecule study and bulk measurement indicates that the immobilization approach does not affect the dynamic behavior of the kissing hairpins or their equilibrium.

Comparison of the kinetic data between SPR and smFRET shows significant differences, however. SPR rates were ∼100-fold slower for both k_on and k_off relative to smFRET values. Despite the difference in the rate constants, both methodologies produced identical ΔG values for the interactions. Similar observations were reported when smFRET and SPR was used to measure the kinetics of nucleotide binding to DNA polymerase (L. Romano and D. Rueda, unpublished results). Differences in surface passivation of smFRET slides and SPR sensor chips, and also issues related to mass transport into the boundary layer, may contribute to these kinetic effects. The origins of these anomalies are currently under investigation.

Kissing interactions of mutated hairpins using smFRET

smFRET was also used to measure the kinetics of kissing interactions of the mutated hairpins described above. KCs were detected for HP1-U4G::HP2-A4C, HP1-C7A::HP2, and HP1-C1A::HP2 (Table S6 and Fig. 5). As shown in Table S6, the association rate constant is invariant at ∼4 × 10⁶ M⁻¹ s⁻¹ for all hairpins. In contrast, the dissociation rate constants differ dramatically depending on the loop sequence. For HP1::HP2 and HP1-U4G::HP2:A4C, stable KCs were observed using ITC, SPR, and smFRET. Compared to the parent complex, the G⋅C mutant has one net extra hydrogen bond and slightly altered stacking potential, which decreased the k_off by approximately threefold and resulted in a 0.6 kcal/mol stabilization. Attesting to the power of smFRET, transient associations of HP1-C7A::HP2 and HP1-C1A::HP2 were detected, neither of which was observed by ITC or SPR. As shown in Fig. 5, KCs of HP1-C7A::HP2 and HP1-C1A::HP2 were short-lived (k_off = 6 ± 1 and 10 ± 1 s⁻¹, respectively) because of the mismatch within the KC. Both HP1-C7A::HP2 and HP1-C1A::HP2 KCs were destabilized by ∼2 kcal/mol as a result of this single base mismatch. When all three central basepairs of the KC were disrupted (HP2-A(3-5)C::HP2), or when the loop size was reduced from 7 nt to 5 nt (HP1-C1Δ,C7Δ::HP2), even transient formation of the KC was abolished. These results indicate that under these experimental conditions, one mismatch is sufficient to greatly destabilize the 7-basepair KC. These data also indicate that dissociation kinetics ultimately dictate the stability of the KC, similar to what was observed by activation parameters computed using SPR. These data support the notion that discrimination between cognate and near-cognate interactions occurs after transient sampling of the interaction, which either accommodates into a stabilized state or rapidly dissociates, allowing it to test many possible interaction partners and avoid getting trapped in nonproductive complexes.

Figure 5.

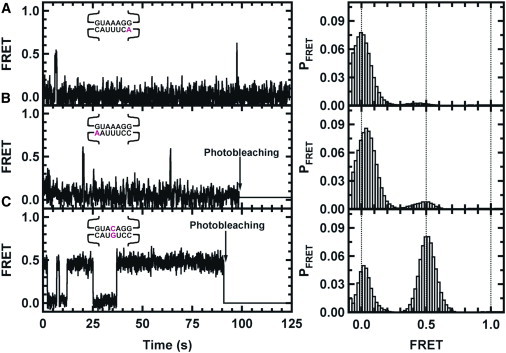
Representative single-molecule FRET trajectories (left) and histograms (right) from selected mutants HP1-C7A::HP2 (A), HP1-C1A::HP2 (B), and HP2-A4C::HP1-U4G (C), which allowed the formation of a GC basepair by replacing the AU basepair. Vertical arrows indicate the photobleaching point for each trace.

Energy landscapes for KCs and their rearrangement to ED structures

Using the thermodynamic (ΔG) and kinetic (ΔG^‡) data derived from the study of HP1::HP2 and HP2::HP3, a potential energy surface for the rearrangement from hairpins to extended duplexes can be proposed (Fig. 6). This surface combines the insights derived from each of the biophysical approaches described above, including ultraviolet (UV) melting, ITC, SPR, and smFRET. Random-coiled strands and free hairpins (Fig. 6, A and B, respectively) could be considered reactant states, whereas the KC and ED (Fig. 6, C and D, respectively) forms represented the low-energy products. These have been placed in coordinates of increasing intramolecular and intermolecular basepair interactions. Thermodynamics of transitions AD and AB were determined using UV melting analysis, whereas BC and BD were measured using ITC and SPR. Transition-state energetics for BC and CB was computed from SPR data. Energy wells have been drawn as symmetric Gaussian functions. That is a significant simplification, as the actual energy landscape is expected to be much more rugged than depicted here. Nonetheless, significant insight can derive from viewing the data in this way.

Figure 6.

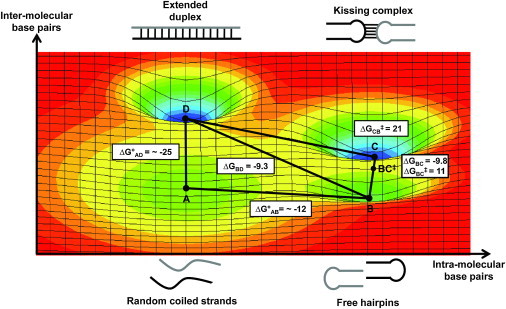
Putative potential energy surface for KC and ED formation. Thermodynamic (ΔG_IJ) and activation energies (ΔG^‡_IJ) for pathways associated with KC formation and their conversion to EDs. Thermodynamic data were obtained using ITC, UV melting, and smFRET, and activation parameters were derived from kinetic data obtained by SPR and smFRET. Reaction coordinates are defined by the number of intramolecular (X) and intermolecular (Y) basepairs present in the molecular ensemble of a particular state. Stabilization energies are plotted along the z axis. Four different states are shown: unfolded strands (A), free hairpins (B), the KC (C), and the ED (D). The energy of unfolded strands (A) was used as the reference state (ΔG_A = 0).

KCs and ED states lie in the lowest energy wells on this surface, whereas random-coiled strands and free hairpins occupy higher-energy regions. Data obtained from independent measurements when viewed as an ensemble correlate nicely within error in a thermodynamic cycle representing all possible transitions. KCs and EDs lie in comparable energy wells (Table S2) despite the differences in the two structural contexts from which they were measured. Free hairpins associate to form a KC that crosses an ∼11 kcal/mol energy barrier, whereas ∼21 kcal/mol energy is required for dissociation. These energetics yield a net stabilization of ∼10 kcal/mol, identical in ITC and smFRET observations. The smFRET data reveal that spontaneous rearrangement from KC to ED occurs with a probability of only ∼0.005 (out of 600 trajectories) within 2.5 min, suggesting a large activation barrier for this transition. Thus, one of the roles proteins should play in these rearrangements is to destabilize KCs. Using RNA-protein-binding energy to break the coaxial stacking of the KC will facilitate the rearrangement by providing a driving-force conversion to the kinetically inert ED state. Furthermore, the colocalization of such a complex could dramatically reduce the entropic cost during strand exchange. On-going experiments are looking at further defining the energetic landscape of these species and the role of protein cofactors in facilitating the refolding of RNAs such as these model hairpins to their ED conformation.

Conclusions

A detailed thermodynamic and kinetic analysis was performed using ITC, UV melting, SPR, and smFRET methodologies for RNA KCs and their progression into the ED. KCs followed energetic trends similar to RNA duplexes but with slightly higher stabilities. Significant ΔC_Ps were observed for KC, duplex, and ED formation, epitomizing the importance of these parameters in structural rearrangements. Kinetic and activation data obtained using smFRET and SPR on a variety of mutants show the kinetic profiles of stable and labile complexes. The association rate at a single molecular level was comparable for all kissing interactions, although only in the stable complexes were strands able to reside longer with their binding partners. The progression from a KC to an ED state was extremely rare in smFRET assays, exemplifying a larger energy barrier for such transitions. This shows that proteins such as Hfq and Ncp7 are required to facilitate these rearrangements in biological systems. Overall, this work puts forth a detailed perspective of the energetic profiles of kissing interactions and their progression to ED formation.