Abstract
Gold nanoparticles (GNPs) are non-toxic, can be functionalized with ligands, and preferentially accumulate in tumors. We have developed a 13.56 MHz radiofrequency-electromagnetic field (RF-EM) delivery system capable of generating high electric field strengths required for non-invasive, non-contact heating of GNPs.
The bulk heating and specific heating rates were measured as a function of NP size and concentration. It was found that heating is both size and concentration dependent, with 5 nm particles producing a 50.6±0.2°C temperature rise in 30 s for 25 μg/mL gold (125 W input). The specific heating rate was also size and concentration dependent, with 5 nm particles producing a specific heating rate of 356±78 kW/g gold at 16 μg/mL (125 W input).
Furthermore, we demonstrate that cancer cells incubated with GNPs are killed when exposed to 13.56 MHz RFEM fields. Compared to cells that were not incubated with GNPs, 3 out of 4 RF-treated groups showed a significant enhancement of cell death with GNPs (p<0.05). GNP-enhanced cell killing appears to require temperatures above 50°C for the experimental parameters used in this study. Transmission electron micrographs show extensive vacuolization with the combination of GNPs and RF treatment.
Keywords: Radiofrequency hyperthermia, gold nano-particles, cancer therapy, resonant circuits, nanotechnology
I. Introduction
Although radiofrequency and microwave electromagnetic (EM) fields have been used for tissue heating for many years [1-8], renewed attention has been given to the EM field approach following developments by John Kanzius, who invented a method combining a non-contact, capacitively-coupled electric field arrangement with electrically-conductive particles to heat tissue [9-13]. It is well known that systemic chemotherapy has serious, debilitating side effects, frequently without producing a substantial increase in survival [14, 15]. In accordance with Kanzius’ fundamental motivation to kill cancer without chemotherapy [16], a growing body of work based on his method has shown promise for cancer treatment [16-25].
In Kanzius’ method, radiofrequency (RF) current passes through a medium without physical contact between the medium and the transmitter-receiver pair [9-13], thus avoiding the need for contact electrodes. The non-contact approach is appealing for treating small animals and for whole body treatment of various systemic cancers, which would preclude the use of contact electrodes. Additionally, RF-EM fields can penetrate deeply within tissue, thus making the method promising for treating a wide range of cancers, potentially anywhere within the human body. The concept goes a step further from traditional RF-hyperthermia by incorporating metal ions or metal particles to enhance heating in localized regions as compared to surrounding regions where enhancers are not present. Initial studies demonstrated that low concentrations of conductive nanoparticles consisting of gold nanospheres [21] or carbon nanotubes [17] cause dramatically increased absorption of RF-EM energy which is then dissipated in the form of heat. It has also been demonstrated that metal ion solutions produce a similar effect [18]. Gold nanoparticles have been the primary catalyst for the technique, likely due to their biocompatibility [26] and potential for creating functionalized bioactive chemistries [27].
Mechanistic studies have primarily been performed in suspensions of gold nanoparticles in distilled and deionized water (ddH2O) and normal saline. Results obtained by Gannon et al. [22] indicate that RF-EM heating applied to solutions containing a suspension of 5 nm diameter gold nanoparticles experience significant heating in ddH2O. Using the RF therapy device provided by Kanzius-founded Therm Med LLC (Erie, PA), the heating of ddH2O solutions containing Au concentrations ranged from 1.1 μM up to 67 μM (0.217 μg/mL to 13.2 μg/mL), with concentration-dependent temperature increases in 1 mL solutions of up to 80°C (heating from 20°C to 100°C) using 800 W of 13.56 MHz RF exposure after 60 s of heating. Thus, the specific absorption rate (SAR) per gram of Au is calculated to be greater than 400 kW/g Au. For comparison, the highest SAR per gram of Fe obtained for ferromagnetic nanoparticles in alternating magnetic fields (AMF) is on the order of 1 kW/g Fe [28, 29]. To achieve therapeutic heating using ferromagnetic nanoparticles, concentrations on the order of 0.1-10 mg/cm3 (corresponding to a SAR range of 10-1000 W/g) of tissue are required based on a rule of thumb power deposition of 100 mW/cm3 [30], which may not be clinically-acceptable concentrations.
Kanzius’ method has been demonstrated both in vitro in cancer cells [17], [18], [20] and in vivo in mice [17], [18], [20-25]. Gannon et al. demonstrated cytotoxic effects of 5 nm gold nanoparticles absorbed within cancer cells, specifically Panc-1 and Hep3B cell lines incubated in 67 μM nanogold and treated at 800 W of RF-EM power [22]. Over 98% of the cells with nanoparticles were killed vs. less than 18% without nanoparticles after only 1 minute exposure, with no significant increase in bulk temperature observed with or without the nanoparticles.
To date, the majority of the work demonstrating cancer-therapy effects related to Kanzius’ method has been accomplished using the RF device provided by Kanzius (Therm Med LLC, Erie, PA), and the results published in [17, 18, 20-25, 31] and through popular media channels, including the CBS News program 60 Minutes [16, 32]. A primary objective of this work is to provide a framework for researchers to explore the method. We present and explore the RF-EM therapy method, from the circuit design and characterization, to the experimental application of the method for heating GNP suspensions, characterization of GNP heating, and exploration of the potential for cancer therapy in vitro.
II. Background
A. RF-EM circuit design considerations
The original design by Kanzius [10] utilizes a cascaded LC matching network to transmit 13.56 MHz electrical energy from a standard 50 Ohm source across an air gap to a receiving circuit that steps down the impedance to a 50 Ohm load. Since an air gap presents a large reactive load impedance, several LC sections are necessary to match to the load (3 sections for transmission matching and 3 for reception matching) while maintaining reasonable component values and dimensions; hence, this mode is referred to as a transmission-mode design. Tissue-like samples placed within the gap modify the load impedance, and consequently tuning of both the transmission and receiving circuits is necessary to minimize power reflected back into the generator and maximize power transmitted across the air gap. A modest amount of energy is absorbed from the applied electrical field by samples placed within the gap.
Our updated design presented here is based on the following key requirements:
a 50 Ohm real input to satisfy the source generator requirement of low reflected power;
an ease of tuning with various loads;
a high intensity electrical field strength sufficient to permit non-contact power delivery to the sample to create the intended heating requirement.
B. Resonant mode design
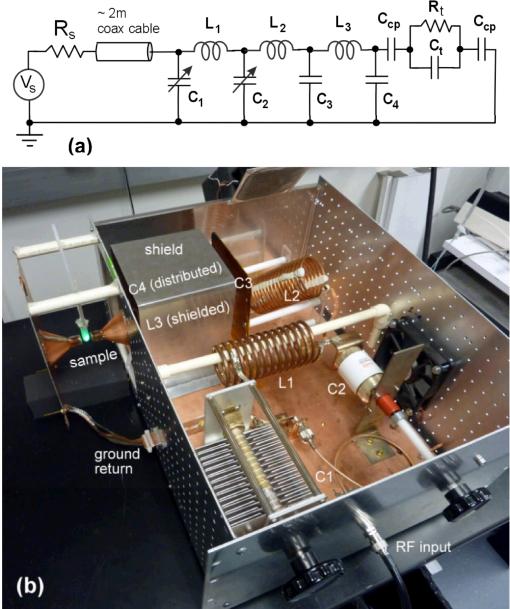
A practical resonant-mode schematic shown in Fig. 1 includes three LC stages to produce an easily adjusted circuit which provides a real 50 Ohm input through the use of multiple, non-identical s-plane poles. The voltage is increased at the output of each stage which culminates in a very large voltage available as the E-field source for non-contact heating. In Fig. 1, a high capacity voltage source (Vs) operating at 13.56 MHz (f0) with an output impedance (Rs) of 50 Ohms drives the passive circuit. All three inductors, L1, L2, and L3 are custom made from soft copper refrigerator tubing. L1 and L3 are wound using 6.35 mm diameter copper tubing and L2 is wound using 4.76 mm diameter copper tubing. The capacitors C1 and C2 are adjustable. C1 consists of a 500±20% pF fixed door knob capacitor (model HT57, High Energy Corp., Parkesburg, PA) in parallel with a 20-450 pF air-variable capacitor (model (CAV) 125-27, Surplus Sales of Nebraska, Omaha, NE). C2 is a 10-110 pF vacuum variable capacitor (model CVUN-100AC/20-BAJA, COMET Holding AG, Flamatt, Switzerland). The C3 component is a lumped equivalent capacitance created from a ground shield around the L3 inductor; the C4 capacitor is a parasitic component, and the two Ccp capacitances are the air coupling capacitances to the sample shown as a simple RC element. Refer to Table I for actual values and their derivations. Very important loss components for the three inductors as well as for the variable capacitor C2 are considered, but omitted in the figures for brevity. The loss resistances are all in series with their respective L or C component. The real part of the input power delivered to the RF-EM circuit will be divided unequally among these loss components and the Rt in the intended load, as will be shown in the following sections.
Fig. 1.
(a) “Resonant mode” RF-EM circuit with the major circuit components labeled and (b) corresponding physical circuit. In (a), the lossy resistances associated with the inductors and the C2 capacitor are omitted for brevity. Rt and Ct are the resistance and capacitance, respectively, of the sample placed in the gap. In (b), individual components are labeled. C3 is the parasitic capacitance formed between a sheet of copper clad and the grounded shield labeled to the left (and the ground plane). L3 is hidden from view inside the grounded shield, and C4 is the distributed parasitic capacitance between L3 and the shield (including the ground plane). The sample placed in the gap consists of a 2 mL Eppendorf tube containing a green neon lamp, which is illuminated in the RF-EM field. The circuit is tuned by adjusting C1 and C2 via the control knobs shown in order to minimize reflected power.
Table I.
Notation and selected nominal values in RF-EM Circuit at f0=13.56 MHz
| Symbol | Description | Values/Units | Derivation Method |
|---|---|---|---|
| Rs | generator source resistance | 50 Ω | manufacturer |
| C1 | parallel combination of air variable capacitor and fixed door knob capacitor | 1011 pF | measured |
| C2 | vacuum variable capacitor | 108.2 pF | measured |
| C3 | parasitic housing capacitance | 18.1 pF | measured |
| C4 | parasitic (radiation) capacitance | 3.65 pF | FEA |
| Ccp | air coupling capacitance | 0.251 pF | FEA |
| L1 | custom copper tubing inductor | 3.33 μH | measured |
| L2 | custom copper tubing inductor | 8.3 μH | measured |
| L3 | custom copper tubing inductor | 3.6 μH | measured |
| Rt | electrical “resistance” of tissue | 2333 Ω | est., peak heating |
| Ct | electrical “capacitance” of tissue | 6.5 pF | est., peak heating |
| RL1 | skin effect resistance, at f0 | 0.26 Ω | analytical est. |
| RL2 | skin effect resistance, at f0 | 0.92 Ω | analytical est. |
| RL3 | skin effect resistance, at f0 | 0.20 Ω | analytical est. |
| RC2 | dielectric effective series resistance | 0.005 Ω | manufacturer |
C. Power delivery to a sample in a non-contact RF-EM field
A theoretical model for the operation of the RF-EM circuit may be developed by examining the heating (or electrical power delivery and dissipation) in a small electrically conductive liquid sample suspended in an electric field without direct electrical contact to the field electrodes. A rigorous theoretical model incorporating the cylindrical geometry of the sample is presented in the Supplement. In effect, the heating of a sample involves determining the equivalent resistance and capacitance of the sample in addition to the coupling capacitances as shown in Fig. 2. Here, it is assumed that Ccp is the same on either side of a sample of saline, with dependent sample model components of resistance Rsal(σsal), where σsal is the saline conductivity, and capacitance Csal(T), where T is the temperature. The peak heating of the medium in this idealized example should occur with f = f0 at a conductivity of about 0.06 S m-1 [33]. An analysis with more accurate parameter values and effects such as the variation of medium capacitance with temperature is given in the Supplement.
Fig. 2.
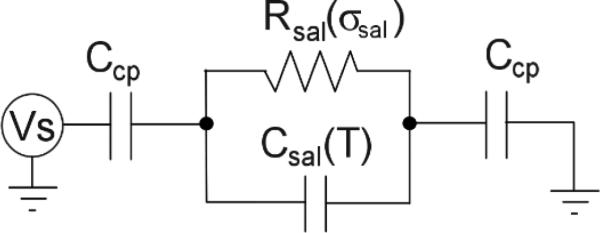
The electrical model of a sample of saline suspended in the E-field.
III. Methods
A. RF-EM circuit modeling, estimation, and measurement of component values
Several modeling approaches were utilized in the analysis of the circuit design. Based on the earlier references for this design [10] a circuit mesh equation analysis using MathCad (v14, Parametric Technology Corp., Needham, MA) was first performed, followed by a two-port model with a two variable solver routine to find the best values of C1 and C2 to use for tuning. Analysis was also performed with a SPICE circuit modeling package (ICAP4, IntuSoft, Carson, CA) to make additional verifications against lab and mesh model data.
The circuit tuning technique involves the measurement of the reflected power at the input node which can be accomplished with a vector network analyzer (VNA, model 4395A, Agilent Technologies, Inc., Santa Clara, CA). Correct circuit operation occurs when the reflected power is low and can be assessed with the voltage reflection coefficient at the input node, or the S11 metric, which is a function of frequency in terms of decibels as
| (4) |
where Zin(f) is the spectral input impedance of the circuit and Zgen is the output impedance of the source generator which is nominally 50 Ohms. An S11 of less than -26 dB is desirable, with less than 0.25% of the power being reflected.
The three custom inductors and the two adjustable capacitors were directly measured for use in the circuit modeling. The modeling of the effective series loss resistance for each of the three custom built inductors was found to be critically important to a reasonable estimation of circuit operation. The loss resistances have the undesirable effect of power consumption (especially L2), but otherwise provide easier circuit tuning since absolutely zero resistive loss would create very high Q elements resulting in difficult tuning adjustments as component values change with temperature and thermal expansion.
Since capacitances C4 and Ccp are very small, the direct measurement of these components is extremely challenging. To arrive at reasonable estimates of these values, a Finite Element Analysis (FEA) model (COMSOL Multiphysics, COMSOL, Inc., Burlington, MA) was assembled for their estimation using a charge integration (ΣQ) technique on the metal surface of the electrodes at unity voltage with the application of ΣQ = CV. Both C4 and Ccp were estimated by dividing the electrode surface into regions contributing to one or the other capacitance.
B. RF-EM power delivery to saline solutions
To refine estimates of critical circuit model component values, a comparison was made of the a) power required to heat a sample by a forward calculation using the circuit model and sample component values, and b) the power required in a finite element analysis (FEA) of heating the same sample.
A laboratory study was conducted to find the peak heating for a sample heated with the RF-EM system. A series of 0.5 mL samples were prepared in a serial dilution range of ten concentrations from standard 0.9% normal saline (0.154 M) to a dilution of 1/512 in concentration. Each of three samples at each dilution was heated for 30 s with 125 W of input power to the RF-EM system. A 0.5 mm fluoroptic temperature probe (Luxtron m3300, LumaSense Technologies, Inc., Santa Clara, CA) was placed in the heating tube before and immediately after E-field exposure.
The relationship between electrical conductivity and saline concentration at 13.56 MHz was established with our own laboratory measurements prompted by the appearance of nonlinear behavior in the saline concentration range from 0.01 M to 0.09 M [34]. Further elaboration on the conductivity tester and methods are provided in the Supplement.
C. RF-EM power delivery to gold nanoparticle solutions
Colloidal suspensions of citrate-coated GNPs were obtained from Ted Pella, Inc. (Redding, CA) in nominal diameters of 5 nm, 10 nm, 20 nm, and 50 nm in nominal concentrations of 0.01% Au (w/w). Diameters and concentrations were measured using a 1 mm path length UV-Vis absorption on a NanoDrop spectrophotometer (Thermo Fisher Scientific, Inc., Wilmington, DE) following the method detailed in [35]. In brief, using the stock solutions, the absorption at 450 nm was measured to determine the concentration based on extinction coefficients and equations provided in [35]. Due to the high variance in the optical estimation of the particle diameter, the nominal diameters provided by the manufacturer were used to estimate the concentration.
A series of 0.5 mL samples of GNP suspensions with varying concentration was placed in 2 mL Eppendorf tubes. The region of the tube containing the fluid sample was centered between two 17 mm diameter copper electrodes spaced apart by 17 mm, allowing approximately a 4 mm air gap on either side of the tube (Fig. S1 of Supplement). With a sample in place, the circuit was tuned using the VNA to minimize reflected power (S11) to better than -30 dB at 13.56 MHz. After tuning, the circuit was connected to a 1000 W capacity 13.56 MHz RF generator (model ACG-10B, ENI, Rochester, NY). Prior to RF-EM exposure, the initial temperature of each sample was measured using the fluoroptic temperature probe. The fluoroptic probe was removed, and each sample was exposed to 125 W of input power to the RF-EM system for 30 s. Following exposure, the peak temperature in the center of the sample was measured.
Heating efficiency was quantified as power per unit mass of Au, i.e. kW/g Au, which allows for the comparison of heating efficacy of various sizes and concentrations for a given RF delivery system. Throughout this work this quantity is referred to as the specific heating rate.
D. RF-EM treatment of cancer cells in vitro
Materials
GNPs were purchased from TedPella (Redding, CA). Met-1fvb2 mammary carcinoma cells [36] were obtained from the Alexander Borowsky Laboratory (Center for Comparative Medicine, UC Davis, Davis, CA). PC-3 cells were obtained from ATCC (Manassas, VA). TrypLE Express trypsin replacement, propidium iodide (PI), PBS, and Dulbecco's Modified Eagle's Medium (DMEM) high glucose media were purchased from Invitrogen (Carlsbad, CA). Phenol red-free powdered DMEM was purchased from Sigma-Aldrich (St. Louis, MO) and was made according to the manufacturer's directions. Fluorescence was measured using the Tecan (San Jose, CA) Infinite® M1000 microplate reader. Microscopy was performed using an Olympus (Center Valley, PA) IX71 inverted microscope.
Cell culture
Cells were grown to 85-95% (Met-1) or 70-75% (PC-3) confluency in 75 cm2 flasks in DMEM high glucose media (Met-1) or phenol red-free DMEM (PC-3) supplemented with 1% penstrep and 10% FBS.
Experimental treatments
Experimental sample sizes range from four to seven samples per RF-EM treatment protocol. Cells receiving gold treatments were incubated in media containing 3 μM, 10nm GNPs (1% volume) for 3 hours at 37°C in 5% CO2. No-gold control samples were incubated in media with 1% water. After incubation, media was removed, cells were detached using TrypLE Express, and were resuspended in phenol-red free media at approximately 2.5 × 106 cells/mL. A volume of 500 μL of cell suspension was pipetted into 2 mL centrifuge tubes. Cells were centrifuged at 300 × g, media was aspirated from cell pellet, and the pellet was resuspended in 30 μL phenol red-free DMEM prior to treatment. The resuspended pellets were treated with one of three RF-EM protocols, including 60 s or 30 s exposure at 100 W input power or no RF (control). After treatment, the volume of each sample was increased to 500 μL, and cells were incubated 3 hours post-treatment at 37°C in 5% CO2. Cell death was quantified by staining with 0.5 mg/mL propidium iodide (PI). Each sample was assayed in triplicate (100 μL/assay) in a 96-well microtiter plate. Fluorescence values were converted to number of cells by use of a standard curve obtained from serial dilutions of known concentrations of dead cells. Cells used for the standard curve were killed by heating at 58°C for 3 hours. Complete cell death was verified by microscopy after PI staining.
Transmission electron microscopy
Following RF exposure or control conditions, cells were fixed in 2.3% glutaraldehyde and 3.6% paraformaldehyde in phosphate-buffered saline (PBS) for 72 hours at 4°C. Cells were rinsed for 30 minutes in four changes of PBS, pH 7.4, followed by a 1 hour postfix in phosphate-buffered 1% OsO4. After washing with distilled water four times for 10 minutes, the tissue was en-bloc stained with 0.2% uranyl acetate overnight at 4°C. The cells were rinsed in three changes of distilled water, dehydrated in progressively higher concentrations of ethanol and embedded in Spurr's resin (Ted Pella, Redding, CA). Thin sections (80-100 nm) were cut on a LKB Nova ultramicrotome (LKB, Bromma, Sweden), mounted on 300 mesh copper grids, and stained with 2% uranyl acetate followed by 0.5% lead citrate. Transmission electron micrographs were taken at the UC Davis Materials Science Central Facility on a Philips CM12 electron microscope operating at 80kV (Philips, Eindhoven, Netherlands).
Acid-digestion of gold nanoparticles
Ten nanometer GNPs (Ted Pella, Redding, CA) were incubated overnight in PBS, pH 4.8, at 37°C. Transmission electron microscopy (TEM) was done after drop coating the GNPs on formvar-carbon coated copper grids (Ted Pella, Redding, CA).
Data analysis
One sided Student's t-tests assuming unequal variances were performed on the samples to test the null hypothesis represented by the controls. A 95% confidence interval was used to test significance.
IV. Results
A. Characteristics of the circuit
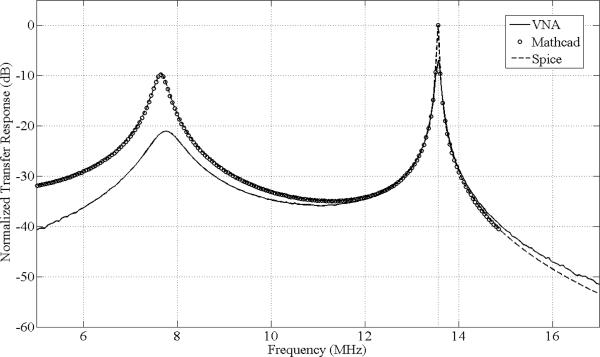
The circuit with its estimated component values given in Table I has been extensively modeled. For good power transfer at each node, the output and input impedances should be matched as complex conjugates; this circuit functions well in that regard. The circuit node terminus (cone at L3) produces an output impedance magnitude that is over 3100 Ohms and an output voltage peak above 8800V (for 125 W input). This high impedance and voltage make a direct sampling method challenging even with a very high impedance probe (we used a 40 MOhm sampling probe) which has resulted in a noticeable loading effect in the spectral plot in Fig. 3. A special E-field probe similar to an earlier design [37] has been constructed and tested to calibrate the high E-field generation, but even this carefully designed miniature probe has shown field loading effects. Alternative measurement methods are in development to enable easy and accurate monitoring of the field generated.
Fig. 3.
Normalized transfer response magnitude in decibles vs. frequency in MHz for VNA measured (solid), Mathcad model (dotted), and SPICE model (dashed). All results are normalized to the peak response at 13.56 MHz for the same input magnitude. The Mathcad and SPICE models are equivalent as indicated by the near exact agreement between their respective curves. Agreement between the model and experiment is reasonable considering many parasitic capacitances distributed throughout the circuit that were not modeled. The influence of parasitic capacitance due to the measurement is apparent near 13.56 MHz, where the measured response is approximately 6 dB below the prediction.
Table II shows the power budget analysis for the circuit operating with a 125 W input power from the generator, and a 0.5 mL sample load supported in a 2 mL Eppendorf tube containing a 1/32 dilution of 0.9% normal saline solution. Most importantly, we estimate the fraction of the total input power dissipated in this load to be ~3%.
Table II.
Predicted power distribution with 125W input and sample characteristic of Rt = 2333 Ω, Ct = 6.5 pF.
| Circuit Element | Real Power Dissipated (W) | Fraction of Total Power (%) |
|---|---|---|
| RL1 | 13.09 | 10.47 |
| RL2 | 105.67 | 84.53 |
| RL3 | 0.82 | 0.66 |
| RC2 | 1.59 | 1.27 |
| Rt (sample) | 3.83 | 3.06 |
| Total | 125.00 | 100.00 |
B. Power delivery to a serial dilution of 0.9% saline
In order to report results of saline heating in the RF-EM field, it is first necessary to report the concentration-dependent conductivity of saline at 13.56 MHz. Using a custom fluid impedance tester, a conductance value for 0.9% (0.154 M) saline was measured to be 1.44 S m-1 at 22°C (see Supplement).
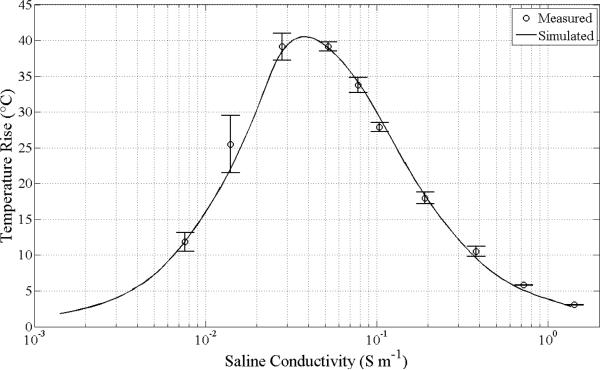
Measurements of saline heating in the RF-EM field as a function of concentration are summarized in Fig. 4. Across the tested dilutions starting with 0.9% saline, the peak heating is located at a concentration near 0.019% saline, which corresponds to an electrical conductivity of 0.040 S m-1 (close to the value of 0.06 S m-1 quoted in the literature [33] however this cited effort did not, for example, take into account the temperature dependence of the dielectric constant of water). Details of the thermal and electrical model used to generate the theoretical curve are presented in the Supplement. The agreement between theory and experiment is well within 10% in the vicinity of the peak. The absorbed power at a concentration producing the peak temperature rise is estimated to be 3.8 W for 125 W of input power, which corresponds to a sample E-field of 10.7 kV/m.
Fig. 4.
The comparison of the laboratory and model heating for a 0.5 mL saline sample dilution series and the resonant mode RF-EM non-contact heating system. Samples were exposed to 3.83W at the sample delivered from the 125 W input power to the RF system for 30 s. A correction for the non-linear relationship between saline concentration and conductivity has been made (see Supplement). The peak heating predicted by the model occurs at 0.040 S m-1.
C. Gold nanoparticle heating
The concentrations of the stock GNP solutions estimated using the method described above for 5, 10, 20, and 50 nm were found to be 59, 54, 59, and 75 μg/mL, respectively. Temperature increases measured in 0.5 mL samples of 5, 10, 20, and 50 nm GNP solutions following 30 s exposures in the RF-EM field using 125 W of transmitted power are summarized in Fig. 5. Heating is inversely dependent on particle size and directly dependent on concentration up to approximately 25, 40, 45, and 55 μg/mL for 5, 10, 20, and 50 nm GNPs, respectively. Beyond these concentrations, heating does not increase with further increases in concentration. At the highest concentrations, the heating rate ranged from 1.5-1.7 °C/s across all particle sizes.
Fig. 5.
Temperature rise of GNP suspensions in ddH2O following 30 s exposure to transmitted power of 125 W. Square, circle, diamond, and triangle data point labels denote 5, 10, 20, and 50 nm GNPs. Data point locations are based on fixed dilutions from stock solutions obtained commercially (Ted Pella, Inc., Redding, CA). Standard deviations for 3 trials are shown. The heating is inversely dependent on particle size and directly dependent on concentration up to approximately 25, 40, 45, and 55 μg/mL for 5, 10, 20, and 50 nm GNPs, respectively. Beyond these concentrations, heating appears to be unchanged with further increases in concentration.
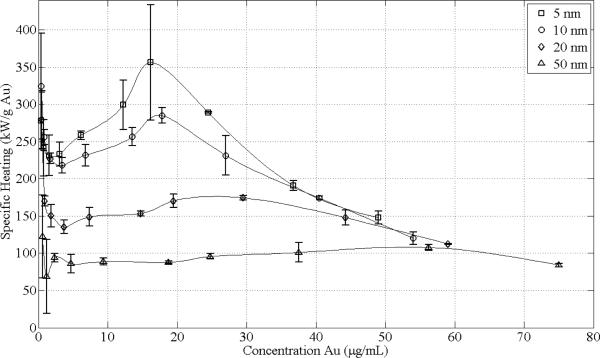
Additionally, specific heating rate estimates in units of kW/g Au are shown in Fig. 6 and were generated using the data in Fig. 5. The specific heating rate is inversely dependent on particle size. Exposure of particles with a diameter of 5 nm resulted in the greatest efficiency with a specific heating rate of 356±78 kW/g Au at a concentration of approximately 16 μg/mL. Beyond 50 μg/mL, the specific heating rates for all particle sizes appear to follow a common decreasing trend line. For concentrations below approximately 4 μg/mL, the heating of water begins to dominate, thus explaining the asymptotically increasing specific heating rate as zero Au concentration is approached (divide by zero condition).
Fig. 6.
Specific heating rate in kW/g Au characteristic of GNP suspensions in ddH2O following 30 s exposure to transmitted power of 125 W. Square, circle, diamond, and triangle data point labels denote 5, 10, 20, and 50 nm GNPs. Data point locations are based on fixed dilutions from stock solutions obtained commercially (Ted Pella, Inc., Redding, CA). Standard deviations for 3 trials are shown. The specific heating rate is inversely dependent on particle size, with 5 nm being the most efficient particle size for heating with a specific heating rate of 356±78 kW/g Au at a concentration of approximately 16 μg/mL. Beyond 50 μg/mL, the specific heating rates for all particle sizes appear to follow a common decreasing trend line. For concentrations below approximately 4 μg/mL, the specific heating rate of water begins to dominate the heating, thus explaining the asymptotically increasing specific heating rate as zero Au concentration is approached (divide by zero condition).
D. Cancer cell treatment
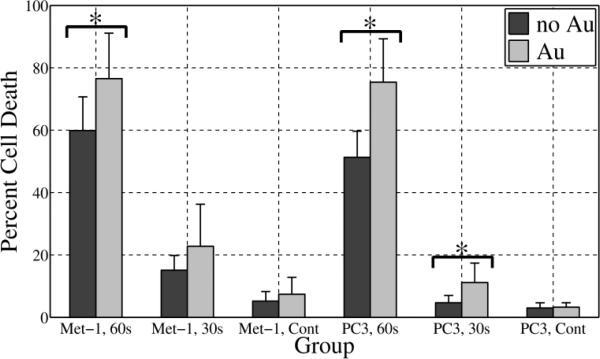
Preliminary in vitro results are summarized in Fig. 7. Percent cell death relative to the 100% kill control is presented for Met-1 and PC-3 cancer cell lines for three RF treatment protocols consisting of 60 s of RF at 100 W, 30 s of RF at 100 W, and no RF. Each treatment group consisted of cells not incubated with 10 nm GNPs and cells that were incubated with 10 nm GNPs so as to test if the presence of GNPs influences cell death. For the cells that were incubated with GNPs, the results shown include all of the cells regardless of GNP uptake.
Fig. 7.
In vitro cell killing relative to 100% cell death control for cells not incubated with GNPs (dark gray) and cells incubated with 10 nm GNPs (light gray). Results from two cancer cell lines, Met-1 and PC-3 are shown. For each cell line, the treatment groups included 60 s and 30 s RF exposure at 100 W. The corresponding no RF controls (Cont) are also shown. With better than 95% confidence (p<0.05), the combination of GNPs and RF exposure demonstrated statistically significant greater cell death compared to the no GNPs for groups labeled with an asterisk (*). In all cases with GNPs, the cells were incubated with 3 μM 10 nm GNPs.
Upon testing the influence of GNPs for the 3 treatment groups, a statistically significant (p<0.05) increase in cell death with the addition of 10 nm GNPs occurred for Met-1 cells treated with RF for 60 s (p=0.02, n=7) and for PC-3 cells incubated with 10 nm GNPs and treated with RF for both 60 (p=0.02, n=4) and 30 s (p=0.04, n=5). Met-1 cells treated for 30 s and incubated with GNPs did not show a significant increase in cell death (p=0.1, n=7). The no RF controls did not show a significant difference in death for either Met-1 cells (p=0.2, n=8) or PC-3 cells (p=0.3, n=5). For both cell lines, treatment with RF alone did produce a significant increase in cell death relative to the no Au, no RF controls (p<0.01).
The maximum temperatures were recorded for the RF-treated cells, and no statistical difference was found between the temperature rise with and without cells incubated with GNPs. Average maximum temperatures for the 30 s and 60 s treatments ranged from 53.5 to 55.7°C and 64.8 to 67.2°C, respectively. The starting temperatures averaged across all replicates (n=50) was 22.6±0.6°C.
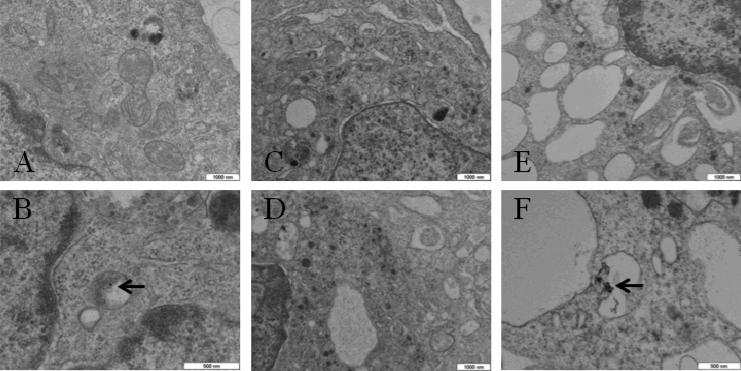
Representative TEM images of PC-3 cells shown in Fig. 8 illustrate a differential effect between RF-treated samples without GNPs (C and D) and with GNPs (E and F), where the latter exhibit extensive vacuolization. Cells incubated with GNPs but not RF-treated (A and B) exhibit similar morphology to cells treated with RF without GNPs (C and D).
Fig. 8.
Representative TEM images of PC-3 cells. (A, B) incubated with GNPs and not treated with RF; (C, D) not incubated with 10 nm GNPs and treated with RF (100W, 60s); (E, F) incubated with 10 nm GNPs and treated with RF (100W, 60s). Arrows point to locations of GNP clusters. Note extensive vacuolization in E and F. Scale bars are indicated.
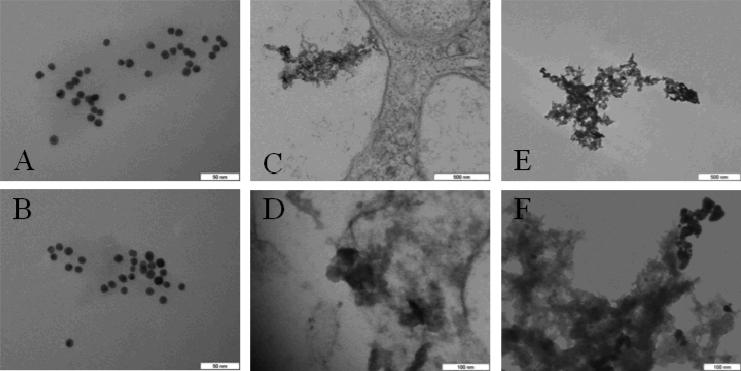
No apparent differences are observed in TEM images of bare 10 nm GNPs suspended in ddH2O (Fig. 9, A) versus samples heated to 86°C with 75 W RF for 4 min (Fig. 9, B). GNP aggregates observed in PC-3 cells following RF treatment at 100 W for 60 s (Fig. 9, C and D) show a similar morphology to GNP aggregates formed following overnight acid-digestion (Fig. 9, E and F).
Fig. 9.
Representative TEM images of (A) GNPs in ddH2O, (B) GNPs in ddH2O following 75 W RF for 4 min (heated to 86°C), (C, D) GNPs in PC-3 cells following 100 W RF for 60 s, and (E, F) GNPs following overnight incubation in PBS, pH 4.8, at 37°C. Comparing A and B, there is no observable effect of RF and high temperature on GNPs alone. The morphology of GNP degradation in lysosomes (C, D) is similar to acid-digestion (E, F). All GNPs are 10 nm, citrate-coated. Scale bars are indicated.
V. Discussion
A. The circuit
The electric circuit design proved to be challenging to build and tune due to its high Q nature. The “resonance mode” design is functionally equivalent to Kanzius’ original “transmission mode” design and easier to tune. Ease of tuning is an important design consideration as the load impedance may change due to physical movement of the load (e.g. breathing motion), and the high Q nature of the circuit is sensitive to small changes in the load impedance. Furthermore, automated tuning will require tuning 2 variable capacitors compared to 4 in the original design, which will assure more stable control of the RF exposure. One disadvantage of the “resonance mode” design is the elevated power dissipation in L2 from high reactive current, however considerable reduction in this inductor resistance is possible (e.g. with silvered coil surfaces). A small brushless fan is used to cool L2, which is effective up to approximately 200 W of input power in our design.
It was not possible to accurately measure C3 and C4 due to their high impedance and physically distributed nature. Although the tuning condition is met in simulation with reasonable measured and estimated component values, absolute confirmation is not easily possible. Nonetheless, the circuit model developed is a very functional representation of the physical circuit.
In the original design, Kanzius referred to the transmission and reception coils as end-fired antennas. It is not clear if there is a benefit to this design as the RF exposure takes place in the reactive near field region of the coils. More investigation is needed to determine if the electric field shape and time dependence is important for heating GNPs.
B. Gold nanoparticle heating
Using our system, the GNP suspensions produced a heating response in a manner consistent with the results using similar concentrations and particles sizes used in the system provided by Therm Med, LLC (Erie, PA) and published previously by Gannon et al. [22] and Moran et al. [31]. As Gannon noted boiling of GNP suspensions in ddH2O, we also achieved boiling of similar suspensions within 1 min at 125 W of input power. Similar to Moran et al., we demonstrated concentration-dependent and size-dependent heating characteristics of GNP suspensions. Using 125 W of input power and heating the solutions for 30 s (to avoid boiling), we measured a peak specific heating rate of 356±78 kW/g for 5 nm GNPs at a concentration of 16 μg/mL (16 ppm or 82 μM). Moran et al. reported a specific heating rate of 380 kW/g for GNPs at 1 ppm (size not specified but assumed to be 5 nm). The difficulty with quantifying specific heating rate at such a low concentration is the fact that ddH2O also absorbs RF, thus making it difficult to separate the contribution of GNPs to the overall heating. Based on measurements made by Gannon et al. on 5 nm GNPs, we calculated specific heating rate of ~420 kW/g at 67 μM Au; however, since our experimental system is different than that used by Gannon et al. and Moran et al., it is not possible to directly compare our results to theirs. More work is needed to standardize RF exposure levels between instruments as direct measurement of the electric field is not trivial. Nonetheless, the specific heating rate observed for GNPs in RF electric fields is considerable, especially given that the best magnetically-reactive nanoparticles have absorptions below 1 kW/g Fe when suspended in water.
Interestingly, for 5, 10, and 20 nm GNPs, a prominent peak in the specific heating rate was observed as a function of concentration, and the peak shifts to higher concentrations and a lower value as the particle size increases. At 50 nm, the peak is smoothed to the point where it is barely apparent. The reason for the peak in the specific heating rate for GNPs in suspension is not fully understood, though it follows a similar behavior to that of saline as a function of concentration. It is well known that a stable colloidal suspension of GNPs is possible due to charge on the surface of the particles due to the coating [38, 39], e.g. the anion citrate, and that this surface charge facilitates electrophoresis of GNPs [39].
C. Cancer cell treatment in vitro
The in vitro results presented demonstrate that the combination of cells incubated with GNPs and exposed to RF cause statistically significant increases in cell death for both Met-1 and PC-3 cancer cell lines. We did not observe significant differences in cell death as a function of GNP presence unless the samples were heated to above 50°C. This finding appears to be consistent with the results of Curley et al. [21] who show similar cell death percentages to ours for cells not incubated with GNPs yet exposed to RF, though the temperatures were not reported. It is not clear why high temperatures are a prerequisite for the GNP-induced cell death; however, this will be a focus of our future work. Concentrating the cells into a smaller fluid volume may have also played a role in minimizing the shunting of the RF current around the cells and more closely models tissue. Our in vitro tests were performed in 2 mL Eppendorf tubes using a pellet of ~1.25 × 106 cells resuspended in 30 uL of cell culture media; other groups used larger diameter Pyrex dishes with a monolayer of cells [21, 22].
TEM images of PC-3 cells indicate that the combination of GNPs and RF creates vacuoles within cells, possibly explaining the significantly higher cell death for RF-treated groups with GNPs. Vacuolization was not observed in RF-treated cells without GNPs present, similar to that observed by Gannon et al [22]. Additionally, degraded GNP aggregates were consistently observed in RF-treated cells (Fig. 8, C and D). It may be that as these cells die (via apoptosis or other mechanism), lysosomes break down and release their digestive enzymes and acidic contents into the cytoplasm, which may lead to degradation of the GNPs. The morphology of the aggregates observed in RF-treated PC-3 cells is very similar to aggregates observed in acid-digested GNPs.
The RF-field induced GNP heating in physiologic saline and culture media raises valid questions about the clinical application of the method in vitro and in vivo. The characterization of GNP heating in this work was performed in ddH2O, which is an ideal medium for maintaining a colloidal suspension of citrate-coated GNPs with minimal aggregation. In experiments not reported here, we obtained much lower heating of GNPs in saline and culture media solutions, possibly due to the well known effect of GNP aggregation in ionic solutions. TEM of the cells fixed 4 hours and 8 hours after incubation with GNPs indicates that cells accumulate and aggregate GNPs into organelles including lysosomes (data not shown). Consequently, it may be possible to improve the method by preventing aggregation of GNPs in carrier solutions and intracellularly. More work is needed to understand the mechanism of GNP heating in RF fields.
Selective killing of cancer cells in vivo requires targeting of GNPs directly to cancer cells by means of passive and/or active targeting. Fortunately, GNPs are readily functionalized and have been shown to target a wide range of cancers in vitro [40]. Additionally, GNPs have been shown to target specific organelles within cells such as the nucleus [41]. One study [42] evaluated in vivo tumor uptake of tumor necrosis factor (TNF) bound to GNPs with and without a protective layer of PEG-THIOL. Following intravenous injection in mice, they found significant accumulation of the PEG-THIOL-protected TNF-GNPs in MC-38 colon carcinoma tumors with little observable accumulation in the liver and spleen. In a more recent study [43], epidermal growth factor receptor targeted GNPs were used to target and detect tumors using surface-enhanced Raman scattering in vivo.
VI. Conclusion
A method for heating gold nanoparticles using radiofrequency electromagnetic radiation has been investigated. The electrical circuit was constructed according to a design similar to that detailed by John Kanzius [10], with improvements to reduce the number of components, and particularly, the number of variable components for easier tuning. The circuit demonstrated heating of saline solutions in good agreement with the model predictions. Such a model is useful for scaling the device up to larger treatment volumes. Heating of gold nanoparticle suspensions was demonstrated in ddH2O, and heating and specific heating rates similar to previously published values were obtained. Identification of gold nanoparticle concentrations to produce maximum specific heating rates was shown, which may be useful knowledge for cancer therapy. In vitro experiments yielded preliminary results confirming that radiofrequency electromagnetic radiation combined with gold nanoparticles has statistically significant cytotoxic effect on cancer cells. More work is needed to further elucidate the mechanisms of action.
Supplementary Material
Supplement
The analysis presented here describes the models we have constructed which allow the theoretical prediction and comparison with lab data of the temperatures in saline samples exposed to high intensity E-fields. An expression for bath temperature as a function of saline concentration is possible with consideration of the 0.5 mL bath geometry, physical material properties and their variation with temperature, and a reasonable thermal model for the Eppendorf tube in air. Simple models can be constructed [33] using the electrical equivalent circuit of Fig. S1. Using the model of Fig S1, the real power delivered to the saline medium as a function of saline conductivity, σsal , at a frequency f, shows the dissipation power peak at a saline conductance of
| (S1) |
where ε0 and εsal are the dielectric constants of free space and saline respectively. Historically, at 13.56 MHz the peak conductance has been estimated as 0.06 S/m. A modified model is now presented which compares well with laboratory data collected for saline bath heating in small plastic Eppendorf tubes with the EM heating system.
Fig. S1. Macroscopic modeling of the E-field exposed sample in a non- contact RF-EM system. A 0.5 mL sample is shown between two 1cm diameter electrodes; a fluoroptic sensor measures temperature post-heating.
A custom tester has been built, calibrated and implemented to measure saline bath conductance, σsal (S/m), as a function of concetration, csal (mol/L). This relation appears to be approximately linear as expressed by
| (S2) |
and produces less than 10% error with lab data in the range of 0.0002M to 0.154 M (largest error at bottom of range). With consideration for the cylindrical bath geometry of the Eppendorf tube, the effective saline bath electrical resistance as a function of saline conductivity, Rsal(σsal), and the saline bath electrical capacitance as function of temperature, Csal(T), can be easily estimated. The relationship between temperature and the relative dielectric constant of saline, εr_sal, can be approximated in the range between 0°C and 100°C with the expression for water from Ellison et al. [44] given by
| (S3) |
where T is in units of Celsius.
Following again the simple circuit of Fig. S1 the voltage Vsal(σsal,T) can be described as a function of the driving voltage Vs, the air coupling capacitance Cair, with Rsal(σsal) and Csal(T). This squared voltage magnitude, Psal, is related to the power dissipation in the saline bath as
| (S4) |
and is abbreviated as Psal below. This rate of heat production is translated into a temperature using simple heat transfer relationships. This is justified by examination of a simple lumped capacitance thermal model (LCTM) and the unitless Biot number (hL/k, where the tube convection coefficient is ~30 W m-2 K-1, L is the equivalent length, or approximately 0.001 m, k is the saline bath thermal conductivity, 0.6 W m-1 K-1). Since the Biot number is much less than 1 (the bath heat conduction is much greater than the external convective heat loss, Pconv), the LCTM is reasonable. To account for the convective heat loss from the Eppendorf tube, we used both lab measurements and FEA models to estimate a peak loss of 0.66 W at a peak dissipative power of 3.8 W.
The power balance can then be represented by a piecewise linear, LCTM as
| (S5) |
where ρ is the saline density, volsal is the saline volume, Cw is the specific heat for water, and ΔT(σsal) is the change in saline temperature over a time period Δt. Rearranging and scaling the result to the peak temperature rise condition, the complete expression for saline bath heating is
| (S6) |
where the factor in the bracket is the rate of temperature rise per second at the peak heating condition. This factor is 1.35° C s-1 for the peak heating case and a saline bath conductivity of 0.04 S m-1 (as shown in Fig. 4 of main text).
Acknowledgment
We wish to acknowledge financial support from NIH CA 103828, NIH 1R21EB009902, the American Cancer Society Institutional Research Grant #IRG-95-125-07, and the Dean, School of Medicine, UC Davis.
This work was supported in part by the National Institutes of Health under Grant CA 103828 and Grant R21EB009902, the American Cancer Society under Grant IRG-95-125-07, and the Dean, School of Medicine, UC Davis.
Biography
 Dustin E. Kruse received the B.A. degree in physics from the State University of New York College at Geneseo, Geneseo, NY, in 1996, and the M.E. degree in electrical engineering, and the Ph.D. degree in biomedical engineering, both from the University of Virginia, Charlottesville, VA, in 1999 and 2004, respectively. His graduate work focused on the development and application of high-frequency ultrasound to image blood flow in the microcirculation.
Dustin E. Kruse received the B.A. degree in physics from the State University of New York College at Geneseo, Geneseo, NY, in 1996, and the M.E. degree in electrical engineering, and the Ph.D. degree in biomedical engineering, both from the University of Virginia, Charlottesville, VA, in 1999 and 2004, respectively. His graduate work focused on the development and application of high-frequency ultrasound to image blood flow in the microcirculation.
He is currently an Assistant Research Professor in the Department of Biomedical Engineering, University of California, Davis. His research interests include ultrasound imaging, ultrasound tissue heating, contrast-assisted ultrasound imaging, and radiofrequency electromagnetic tissue heating.
Dr. Kruse is a member of Sigma Pi Sigma.
 Douglas N. Stephens (M'82) received the B.S. degree in physiology from the University of California, Davis, in 1976, and the B.S. and M.S. degrees in electrical and electronic engineering, and biomedical engineering in 1981 and 1983, respectively, from California State University, Sacramento, CA.
Douglas N. Stephens (M'82) received the B.S. degree in physiology from the University of California, Davis, in 1976, and the B.S. and M.S. degrees in electrical and electronic engineering, and biomedical engineering in 1981 and 1983, respectively, from California State University, Sacramento, CA.
In 1985, he joined the pioneering technical group at EndoSonics Corporation, where he was a key contributor in solid-state intravascular ultrasound (IVUS) technology, and was responsible for all catheter electronics and analog signal processing. He was also a Vice-President of strategic technology at EndoSonics and Jomed, where he was responsible for new designs of IVUS solid-state technology. He is currently in the Department of Biomedical Engineering, University of California, Davis. He is also engaged in the methods of ultrasound and electromagnetic-based targeted imaging and liposome-mediated drug delivery, and provides engineering design and management for a multisite research partnership developing novel intracardiac imaging catheters for use in electrophysiology procedures. He holds nine patents in the field of medical ultrasound. Mr. Stephens led the technical effort in the creation of the world's first commercial 3.5 F solid-state ultrasound imaging catheter and was awarded the first EndoSonics Fellowship Award in 1990.
 Heather A. Lindfors received the B.S. degree in biology from Appalachian State University, Boone, NC, in 1999, where she conducted undergraduate research in plant cytogenetics and animal behavior.
Heather A. Lindfors received the B.S. degree in biology from Appalachian State University, Boone, NC, in 1999, where she conducted undergraduate research in plant cytogenetics and animal behavior.
In 2000, she joined University of California, Davis, where she was the Laboratory Manager in the Department of Evolution and Ecology and involved in the research on molecular evolutionary genetics during 2000-2006, and is currently in the Department of Biomedical Engineering. In 2006, she also joined the Ferrara Laboratory as the Laboratory Manager/Research Associate. Her research interests include in vitro studies aimed at evaluating cell binding and internalization of various delivery vehicles, determination of drug formulation efficacy in different cell lines, complement binding and activation, peptide synthesis, and general method development.
 Elizabeth S. Ingham received the B.S. degree in biological sciences from the University of California UC Davis, in 2004, and the M.S. degree in molecular biology from California State University, Sacramento, CA, in 2008. Her Master's thesis was focused on the development of a cell-specific immunotoxin for selective ablation of melanopsin-containing retinal ganglion cells.
Elizabeth S. Ingham received the B.S. degree in biological sciences from the University of California UC Davis, in 2004, and the M.S. degree in molecular biology from California State University, Sacramento, CA, in 2008. Her Master's thesis was focused on the development of a cell-specific immunotoxin for selective ablation of melanopsin-containing retinal ganglion cells.
From 2005 to 2009, she was the Laboratory Manager at the Chronic Acceleration Research Unit, UC Davis, where she was engaged in the environmental influences of light and gravity on circadian physiology. In 2009, she joined the Department of Biomedical Engineering, UC Davis, where she is currently investigating the in vitro efficacy of various targeted drug delivery systems.
 Eric E. Paoli received the B.S. degree in biomedical engineering from the University of California, Davis, Davis, CA, in 2006. He is currently pursuing the Ph.D. degree in biomedical engineering at University of California, Davis. His research interests include designing targeted drug delivery vehicles, in combination with optical imaging and therapeutic ultrasound heating.
Eric E. Paoli received the B.S. degree in biomedical engineering from the University of California, Davis, Davis, CA, in 2006. He is currently pursuing the Ph.D. degree in biomedical engineering at University of California, Davis. His research interests include designing targeted drug delivery vehicles, in combination with optical imaging and therapeutic ultrasound heating.
 Katherine W. Ferrara (S'82-M'87-SM'99-F'10) received the B.S. and M.S. degrees in electrical engineering from the California State University, Sacramento, in 1982 and 1983, respectively, and the Ph.D. degree in electrical engineering and computer science from the University of California, Davis, in 1989.
Katherine W. Ferrara (S'82-M'87-SM'99-F'10) received the B.S. and M.S. degrees in electrical engineering from the California State University, Sacramento, in 1982 and 1983, respectively, and the Ph.D. degree in electrical engineering and computer science from the University of California, Davis, in 1989.
From 1983 to 1988, she was with Sound Imaging, Inc., Folsom, CA, and General Electric Medical Systems, Rancho Cordova, CA, where she was involved in the areas of magnetic resonance and ultrasound imaging. From 1989 to 1993, she was an Associate Professor in the Department of Electrical Engineering, California State University, Sacramento, CA. From 1993 to 1995, she was a Principal Member of the research staff at the Riverside Research Institute, New York, NY. From 1995 to 1999, she was an Associate Professor at the University of Virginia, Charlottesville, VA. She is currently a Professor in the Department of Biomedical Engineering, University of California, Davis, where she was the Founding Chair from 1999 to 2004.
Prof. Ferrara was a Regular Member of the Diagnostic Radiology Study Section during 2000-2004. She is also a Fellow of the Acoustical Society of America, and serves on the Editorial Board of Annual Reviews in Biomedical Engineering.
Contributor Information
Dustin E. Kruse, Department of Biomedical Engineering, University of California at Davis, Davis, CA 95616 USA (dekruse@ucdavis.edu)..
Douglas N. Stephens, Department of Biomedical Engineering, University of California at Davis, Davis, CA 95616 USA (dnstephens@ucdavis.edu)..
Heather A. Lindfors, Department of Biomedical Engineering, University of California at Davis, Davis, CA 95616 USA.
Elizabeth S. Ingham, Department of Biomedical Engineering, University of California at Davis, Davis, CA 95616 USA.
Eric E. Paoli, Department of Biomedical Engineering, University of California at Davis, Davis, CA 95616 USA.
Katherine W. Ferrara, Department of Biomedical Engineering, University of California at Davis, Davis, CA 95616 USA (kwferrara@ucdavis.edu)..
References
- 1.Gee W, Lee SW, Bong NK, Cain CA, Mittra R, Magin RL. Focused Array Hyperthermia Applicator - Theory and Experiment. IEEE Transactions on Biomedical Engineering. 1984;31(1):38–46. doi: 10.1109/TBME.1984.325368. [DOI] [PubMed] [Google Scholar]
- 2.Hauck ML, Larue SM, Petros WP, Poulson JM, Yu DH, Spasojevic I, Pruitt AF, Klein A, Case B, Thrall DE, Needham D, Dewhirst MW. Phase I trial of doxorubicin-containing low temperature sensitive liposomes in spontaneous canine tumors. Clinical Cancer Research. 2006 Jul 1;12(13):4004–4010. doi: 10.1158/1078-0432.CCR-06-0226. [DOI] [PubMed] [Google Scholar]
- 3.Knudsen M, Hartmann U. Optimal Temperature Control with Phased-Array Hyperthermia System. IEEE Transactions on Microwave Theory and Techniques. 1986 May;34(5):597–603. [Google Scholar]
- 4.Trembly BS, Wilson AH, Havard JM, Sabatakakis K, Strohbehn JW. Comparison of Power Deposition by in-Phase 433-Mhz and Phase-Modulated 915-Mhz Interstitial Antenna-Array Hyperthermia Systems. IEEE Transactions on Microwave Theory and Techniques. 1988 May;36(5):908–916. [Google Scholar]
- 5.Turner PF. Hyperthermia and Inhomogeneous Tissue Effects Using an Annular Phased-Array. IEEE Transactions on Microwave Theory and Techniques. 1984;32(8):874–882. [Google Scholar]
- 6.Turner PF. Regional Hyperthermia with an Annular Phased-Array. IEEE Transactions on Biomedical Engineering. 1984;31(1):106–114. doi: 10.1109/tbme.1984.325376. [DOI] [PubMed] [Google Scholar]
- 7.Wu LY, McGough RJ, Arabe OA, Samulski TV. An RF phased array applicator designed for hyperthermia breast cancer treatments. Physics in Medicine and Biology. 2006 Jan 7;51(1):1–20. doi: 10.1088/0031-9155/51/1/001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zhang Y, Joines WT, Jirtle RL, Samulski TV. Theoretical and Measured Electric-Field Distributions within an Annular Phased-Array - Consideration of Source Antennas. IEEE Transactions on Biomedical Engineering. 1993 Aug;40(8):780–787. doi: 10.1109/10.238462. [DOI] [PubMed] [Google Scholar]
- 9.Kanzius J. System and method for RF-induced hyperthermia. 2004 United States 10/969477.
- 10.Kanzius J. Enhanced systems and methods for RF-induced hyperthermia II. 2005 U.S. Patent, 11/215825.
- 11.Kanzius J. Enhanced systems and methods for RF-induced hyperthermia. 2005 United States 11/050422.
- 12.Kanzius J, Steinbrink WH, McDonald RJ, Keating MJ. RF-induced hyperthermia using biological cells and nanoparticles as RF enhancer carriers. 2005 United States 11/050,481.
- 13.Kanzius J, Steinbrink WH, McDonald RJ, Keating MJ. Systems and methods for combined RF-induced hyperthermia and radioimmunotherapy. 2005 United States 11/050,478.
- 14.Morgan G, Ward R, Barton M. The contribution of cytotoxic chemotherapy to 5-year survival in adult malignancies. Clinical Oncology (Royal College of Radiologists) 2004 Dec;16(8):549–560. doi: 10.1016/j.clon.2004.06.007. [DOI] [PubMed] [Google Scholar]
- 15.Polyzos NP, Pavlidis N, Paraskevaidis E, Ioannidis JP. Randomized evidence on chemotherapy and hormonal therapy regimens for advanced endometrial cancer: an overview of survival data. European Journal of Cancer. 2006 Feb;42(3):319–326. doi: 10.1016/j.ejca.2005.09.026. [DOI] [PubMed] [Google Scholar]
- 16.Stahl L. 60 Minutes. CBS Corp.; 2008. The Kanzius Machine. [Google Scholar]
- 17.Gannon CJ, Cherukuri P, Yakobson BI, Cognet L, Kanzius JS, Kittrell C, Weisman RB, Pasquali M, Schmidt HK, Smalley RE, Curley SA. Carbon nanotube-enhanced thermal destruction of cancer cells in a noninvasive radiofrequency field. Cancer. 2007 Dec 15;110(12):2654–65. doi: 10.1002/cncr.23155. [DOI] [PubMed] [Google Scholar]
- 18.Klune JR, Jeyabalan G, Chory ES, Kanzius J, Geller DA. P64: Pilot investigation of a new instrument for non-invasive radiofrequency ablation of cancer. Journal of Surgical Research. 2007;137(2):263–263. [Google Scholar]
- 19.Bansal R. A New Hope for Noninvasive Cancer Treatment? 2008 Dec;9(6):36–38. [Google Scholar]
- 20.Cardinal J, Klune JR, Chory E, Jeyabalan G, Kanzius JS, Nalesnik M, Geller DA. Noninvasive radiofrequency ablation of cancer targeted by gold nanoparticles. Surgery. 2008 Aug;144(2):125–132. doi: 10.1016/j.surg.2008.03.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Curley SA, Cherukuri P, Briggs K, Patra CR, Upton M, Dolson E, Mukherjee P. Noninvasive radiofrequency field-induced hyperthermic cytotoxicity in human cancer cells using cetuximab-targeted gold nanoparticles. J Exp Ther Oncol. 2008;7(4):313–26. [PubMed] [Google Scholar]
- 22.Gannon CJ, Patra CR, Bhattacharya R, Mukherjee P, Curley SA. Intracellular gold nanoparticles enhance non-invasive radiofrequency thermal destruction of human gastrointestinal cancer cells. J Nanobiotechnology. 2008;6:2. doi: 10.1186/1477-3155-6-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cherukuri P, Glazer ES, Curley SA. Targeted hyperthermia using metal nanoparticles. Advanced Drug Delivery Reviews. 2010;62(3):339–345. doi: 10.1016/j.addr.2009.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Glazer ES, Curley SA. Radiofrequency field-induced thermal cytotoxicity in cancer cells treated with fluorescent nanoparticles. Cancer. 2010;116(13):3285–3293. doi: 10.1002/cncr.25135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Glazer ES, Massey KL, Zhu C, Curley SA. Pancreatic carcinoma cells are susceptible to noninvasive radio frequency fields after treatment with targeted gold. Surgery. 2010;148(2):319–324. doi: 10.1016/j.surg.2010.04.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Connor EE, Mwamuka J, Gole A, Murphy CJ, Wyatt MD. Gold nanoparticles are taken up by human cells but do not cause acute cytotoxicity. Small. 2005;1(3):325–327. doi: 10.1002/smll.200400093. [DOI] [PubMed] [Google Scholar]
- 27.Bergen JM, Von Recum HA, Goodman TT, Massey AP, Pun SH. Gold nanoparticles as a versatile platform for optimizing physicochemical parameters for targeted drug delivery. Macromolecular Bioscience. 2006 Jul 14;6(7):506–516. doi: 10.1002/mabi.200600075. [DOI] [PubMed] [Google Scholar]
- 28.Hergt R, Hiergeist R, Zeisberger M, Glöckl G, Weitschies W, Ramirez LP, Hilger I, Kaiser WA. Enhancement of AC-losses of magnetic nanoparticles for heating applications. Journal of Magnetism and Magnetic Materials. 2004;280(2-3):358–368. [Google Scholar]
- 29.Mehdaoui B, Meffre A, Lacroix LM, Carrey J, Lachaize S, Gougeon M, Respaud M, Chaudret B. Large specific absorption rates in the magnetic hyperthermia properties of metallic iron nanocubes. Journal of Magnetism and Magnetic Materials. 2010;322(19):L49–L52. [Google Scholar]
- 30.Pankhurst QA, Connolly J, Jones SK, Dobson J. Applications of magnetic nanoparticles in biomedicine. J. Phys. D: Appl. Phys. 2003;36(13):R167–R181. [Google Scholar]
- 31.Moran CH, Wainerdi SM, Cherukuri TK, Kittrell C, Wiley BJ, Nicholas NW, Curley SA, Kanzius JS, Cherukuri P. Size-dependent joule heating of gold nanoparticles using capacitively coupled radiofrequency fields. Nano Research. 2009;2(5):400–405. [Google Scholar]
- 32.Stahl L. 60 Minutes. CBS Corp.; 2009. The Kanzius Machine. [Google Scholar]
- 33.Griffiths H, Ahmed A, Smith CW. Power Loss in Skin Cooling Pillows during RF Hyperthermia. British Journal of Radiology. 1984;57(675):254–256. doi: 10.1259/0007-1285-57-675-254. [DOI] [PubMed] [Google Scholar]
- 34.Gabriel S, Lau RW, Gabriel C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys Med Biol. 1996 Nov;41(11):2251–69. doi: 10.1088/0031-9155/41/11/002. [DOI] [PubMed] [Google Scholar]
- 35.Haiss W, Thanh NTK, Aveyard J, Fernig DG. Determination of size and concentration of gold nanoparticles from UV-Vis spectra. Analytical Chemistry. 2007 Jun;791(11):4215–4221. doi: 10.1021/ac0702084. [DOI] [PubMed] [Google Scholar]
- 36.Borowsky AD, Namba R, Young LJT, Hunter KW, Hodgson JG, Tepper CG, McGoldrick ET, Muller WJ, Cardiff R, Gregg JP. Syngeneic mouse mammary carcinoma cell lines: Two closely related cell lines with divergent metastatic behavior. Clinical & Experimental Metastasis. 2005 Jan;22(1):47–58. doi: 10.1007/s10585-005-2908-5. [DOI] [PubMed] [Google Scholar]
- 37.Kanda M, Driver LD. An Isotropic Electric-Field Probe with Tapered Resistive Dipoles for Broad-Band Use, 100 Khz to 18 Ghz. IEEE Transactions on Microwave Theory and Techniques. 1987 Feb;35(2):124–130. [Google Scholar]
- 38.Zhou JF, Ralston J, Sedev R, Beattie DA. Functionalized gold nanoparticles: Synthesis, structure and colloid stability. Journal of Colloid and Interface Science. 2009 Mar;33115(2):251–262. doi: 10.1016/j.jcis.2008.12.002. [DOI] [PubMed] [Google Scholar]
- 39.Schnabel U, Fischer CH, Kenndler E. Characterization of colloidal gold nanoparticles according to size by capillary zone electrophoresis. Journal of Microcolumn Separations. 9(7):529–534, 1997. [Google Scholar]
- 40.Ghosh P, Han G, De M, Kim CK, Rotello VM. Gold nanoparticles in delivery applications,” Advanced Drug Delivery Reviews. 2008 Aug;6017(11):1307–1315. doi: 10.1016/j.addr.2008.03.016. [DOI] [PubMed] [Google Scholar]
- 41.Kang B, Mackey MA, El-Sayed MA. Nuclear Targeting of Gold Nanoparticles in Cancer Cells Induces DNA Damage, Causing Cytokinesis Arrest and Apoptosis. Journal of the American Chemical Society. 132(5):1517–1519. doi: 10.1021/ja9102698. [DOI] [PubMed] [Google Scholar]
- 42.Paciotti GF, Myer L, Weinreich D, Goia D, Pavel N, McLaughlin RE, Tamarkin L. Colloidal Gold: A Novel Nanoparticle Vector for Tumor Directed Drug Delivery. Drug Delivery. 2004;11(3):169–183. doi: 10.1080/10717540490433895. 2011/01/04. [DOI] [PubMed] [Google Scholar]
- 43.Qian XM, Peng XH, Ansari DO, Yin-Goen Q, Chen GZ, Shin DM, Yang L, Young AN, Wang MD, Nie SM. In vivo tumor targeting and spectroscopic detection with surface-enhanced Raman nanoparticle tags. Nature Biotechnology. 2008 Jan;26(1):83–90. doi: 10.1038/nbt1377. [DOI] [PubMed] [Google Scholar]
- 44.Ellison WJ, Lamkaouchi K, Moreau JM. Water: A dielectric reference. Journal of Molecular Liquids. 1996 Apr;68(2-3):171–279. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplement
The analysis presented here describes the models we have constructed which allow the theoretical prediction and comparison with lab data of the temperatures in saline samples exposed to high intensity E-fields. An expression for bath temperature as a function of saline concentration is possible with consideration of the 0.5 mL bath geometry, physical material properties and their variation with temperature, and a reasonable thermal model for the Eppendorf tube in air. Simple models can be constructed [33] using the electrical equivalent circuit of Fig. S1. Using the model of Fig S1, the real power delivered to the saline medium as a function of saline conductivity, σsal , at a frequency f, shows the dissipation power peak at a saline conductance of
| (S1) |
where ε0 and εsal are the dielectric constants of free space and saline respectively. Historically, at 13.56 MHz the peak conductance has been estimated as 0.06 S/m. A modified model is now presented which compares well with laboratory data collected for saline bath heating in small plastic Eppendorf tubes with the EM heating system.
Fig. S1. Macroscopic modeling of the E-field exposed sample in a non- contact RF-EM system. A 0.5 mL sample is shown between two 1cm diameter electrodes; a fluoroptic sensor measures temperature post-heating.
A custom tester has been built, calibrated and implemented to measure saline bath conductance, σsal (S/m), as a function of concetration, csal (mol/L). This relation appears to be approximately linear as expressed by
| (S2) |
and produces less than 10% error with lab data in the range of 0.0002M to 0.154 M (largest error at bottom of range). With consideration for the cylindrical bath geometry of the Eppendorf tube, the effective saline bath electrical resistance as a function of saline conductivity, Rsal(σsal), and the saline bath electrical capacitance as function of temperature, Csal(T), can be easily estimated. The relationship between temperature and the relative dielectric constant of saline, εr_sal, can be approximated in the range between 0°C and 100°C with the expression for water from Ellison et al. [44] given by
| (S3) |
where T is in units of Celsius.
Following again the simple circuit of Fig. S1 the voltage Vsal(σsal,T) can be described as a function of the driving voltage Vs, the air coupling capacitance Cair, with Rsal(σsal) and Csal(T). This squared voltage magnitude, Psal, is related to the power dissipation in the saline bath as
| (S4) |
and is abbreviated as Psal below. This rate of heat production is translated into a temperature using simple heat transfer relationships. This is justified by examination of a simple lumped capacitance thermal model (LCTM) and the unitless Biot number (hL/k, where the tube convection coefficient is ~30 W m-2 K-1, L is the equivalent length, or approximately 0.001 m, k is the saline bath thermal conductivity, 0.6 W m-1 K-1). Since the Biot number is much less than 1 (the bath heat conduction is much greater than the external convective heat loss, Pconv), the LCTM is reasonable. To account for the convective heat loss from the Eppendorf tube, we used both lab measurements and FEA models to estimate a peak loss of 0.66 W at a peak dissipative power of 3.8 W.
The power balance can then be represented by a piecewise linear, LCTM as
| (S5) |
where ρ is the saline density, volsal is the saline volume, Cw is the specific heat for water, and ΔT(σsal) is the change in saline temperature over a time period Δt. Rearranging and scaling the result to the peak temperature rise condition, the complete expression for saline bath heating is
| (S6) |
where the factor in the bracket is the rate of temperature rise per second at the peak heating condition. This factor is 1.35° C s-1 for the peak heating case and a saline bath conductivity of 0.04 S m-1 (as shown in Fig. 4 of main text).