The Dynamics of HIV-1 Adaptation in Early Infection

Abstract

Human immunodeficiency virus type 1 (HIV-1) undergoes a severe population bottleneck during sexual transmission and yet adapts extremely rapidly to the earliest immune responses. The bottleneck has been inferred to typically consist of a single genome, and typically eight amino acid mutations in viral proteins spread to fixation by the end of the early chronic phase of infection in response to selection by CD8⁺ T cells. Stochastic simulation was used to examine the effects of the transmission bottleneck and of potential interference among spreading immune-escape mutations on the adaptive dynamics of the virus in early infection. If major viral population genetic parameters are assigned realistic values that permit rapid adaptive evolution, then a bottleneck of a single genome is not inconsistent with the observed pattern of adaptive fixations. One requirement is strong selection by CD8⁺ T cells that decreases over time. Such selection may reduce effective population sizes at linked loci through genetic hitchhiking. However, this effect is predicted to be minor in early infection because the transmission bottleneck reduces the effective population size to such an extent that the resulting strong selection and weak mutation cause beneficial mutations to fix sequentially and thus avoid interference.

THE interaction between selection and genetic drift over multiple loci may be complex. For a single locus, the product of the effective population size (N_e) and the selection coefficient (s), N_es, adequately measures the scaled intensity of selection. However, with more than one locus, selection at one locus may reduce N_e at linked loci. This has many ramifications, not least of which is that there is no species N_e, but that N_e varies across recombinational neighborhoods of the genome (see review by Comeron et al. 2008). On the other hand, with strong selection (N_es > 1) and weak mutation (N_eμ << 1), a new beneficial mutation that survives stochastic loss may spread to fixation before the emergence of the next beneficial mutation to survive stochastic loss (Gillespie 1984; Orr 2002). These conditions, therefore, reduce linkage interactions among loci.

N_e is the size of a model population that exhibits the same stochastic variation in allele frequencies as an actual population (see Charlesworth 2009 for a recent review). This is a useful quantity because it captures stochasticity due to numerous factors, including population bottlenecks and selection, allowing the model to focus on a limited set of loci and evolutionary forces of interest. Complexity is introduced by the fact that the intensity of selection is proportional to N_es, but that selection tends to reduce N_e. Selection does this in two ways: first, by generating, at least initially, additive genetic variance in fitness (without selection there is no variance in fitness), because this increases the variation in offspring number among parents (Robertson 1961; Nei and Murata 1966), and second, by reducing variation at genetically linked loci. This effect arises as a result of genetic drift because only in finite populations is there the necessary linkage disequilibrium between loci (Barton 2000). One manifestation of this linkage effect is known as hitchhiking because the frequency of an allele will increase if it is associated with a selected allele at a linked locus (Maynard Smith and Haigh 1974). This process is also known as a selective sweep (Berry et al. 1991) and is part of a more general class of processes, known as the Hill–Robertson effect (Hill and Robertson 1966; Felsenstein 1974), in which selection usually reduces N_e at linked loci (Comeron et al. 2008). It has been proposed that if adaptation is common, neutral variation may be more affected by selection at linked loci than by genetic drift, a scenario referred to as “genetic draft” (Gillespie 2000; Maynard Smith and Haigh 1974). At present, it is unclear whether neutral variation is strongly affected by linked selection in Drosophila (Andolfatto 2007; Sella et al. 2009) and in humans (Cai et al. 2009; Hernandez et al. 2011). A recent theoretical study suggests that genetic draft is an important determinant of genetic variation in human immunodeficiency virus type 1 (HIV-1) (Neher and Shraiman 2011).

The interaction between loci under selection and linked loci may also be viewed as clonal interference or negative linkage disequilibrium (Comeron et al. 2008). Clonal interference refers to the reduction in the rate of fixation of a beneficial mutation caused by beneficial mutations at other loci residing on different genomes, which are therefore in competition (Gerrish and Lenski 1998). This is equivalent to negative linkage disequilibrium between beneficial alleles because each allele is linked to a deleterious or neutral alternative allele at the other loci. Such interactions may be interpreted in terms of selection reducing N_e at linked loci (Keightley and Otto 2006) and clearly have important consequences for the efficiency of natural selection and the evolutionary maintenance of recombination (Felsenstein 1988; Kondrashov 1993; Keightley and Otto 2006).

The nature of the interaction between selection and drift in HIV-1 has been controversial. On one hand, a very large viral census population size within a patient of ∼10⁷–10⁸ infected host cells (Chun et al. 1997) and a high mutation rate of ∼10⁻⁵ per nucleotide per generation (Sanjuan et al. 2010) suggest that every possible point mutation occurs numerous times each viral generation (Coffin 1995). Together with evidence of strong selection by the immune system (Williamson 2003), this would suggest highly deterministic evolution (Coffin 1995; Overbaugh and Bangham 2001). On the other hand, the within-patient N_e during chronic infection has been routinely estimated to be only ∼10³, suggesting that stochastic genetic drift is a powerful force in HIV-1 evolution (Leigh Brown 1997; Nijhuis et al. 1998; Rodrigo et al. 1999; Drummond et al. 2002; Seo et al. 2002; Achaz et al. 2004; Shriner et al. 2004b). In addition, variation among patients in the rate and pattern of the evolution of HIV-1 resistance to antiviral drugs has been attributed to the effects of genetic drift (Leigh Brown and Richman 1997; Nijhuis et al. 1998; Frost et al. 2000).

Here, recent estimates of killing rates of infected cells by the immune system and patterns of fixation by viral mutants that escape immune recognition in the earliest stages of HIV-1 infection are used to investigate the dynamics of the virus’s adaptation to the earliest immune responses. The early stages of infection by HIV-1 are considered an opportune time to control viral replication (Haase 2010; McMichael et al. 2010). With the transmission of the virus from one host to another, and especially with sexual transmission, the viral population goes through a severe population bottleneck, drastically reducing genetic variation (Mcmichael et al. 2010). Furthermore, events in early infection determine the viral population size in clinically asymptomatic chronic infection, which is proportional to the rates of disease progression and viral transmission (Ho 1996; Mellors et al. 1996; Quinn et al. 2000; Fideli et al. 2001). Consequently, recent studies have attempted to characterize, in unprecedented molecular detail, the earliest immune responses to the virus and the virus’s adaptive responses to this selection (Asquith et al. 2006; Goonetilleke et al. 2009; Fischer et al. 2010).

Sexual transmission of HIV-1 is thought to typically involve a single viral genome (Keele et al. 2008; Abrahams et al. 2009; Salazar-Gonzalez et al. 2009; Fischer et al. 2010; Novitsky et al. 2011). This is followed by a rapid expansion of the virus population to a peak at 21–28 days postinfection (p.i.), known as peak viremia, and then an initially rapid decline in numbers, reaching a moderately stable level 1–2 orders of magnitude below the peak, known as the viral set point (De Loes et al. 1995; Ho 1996; Kinloch-McMichael et al. 2010). The earliest effective HIV-1-specific immune response detected is that of CD8⁺ T cells, first observed just prior to peak viremia (McMichael et al. 2010). Prior to this point there is no evidence of changes to amino acid frequencies in viral proteins due to immune selection. After this point, amino acid mutations that provide escape from immune detection (escape mutations) are observed to spread to fixation. Typically, eight such adaptive fixations occur throughout the early chronic phase of infection (McMichael et al. 2010), giving approximately one fixation every 22 days on average.

Although immune responses and viral adaptation to these in early HIV-1 infection have been described in some detail, the dynamics of both are poorly understood. In particular, a transmission bottleneck of a single genome seems difficult to reconcile with extremely rapid adaptation. In addition, the targeting by CD8⁺ T cells of several different epitopes simultaneously may interfere with the adaptive response at each epitope. The present study investigates how the transmission bottleneck and potential clonal interference affect the adaptive dynamics of HIV-1 in early infection. Stochastic simulations showed that, given realistic values for important population genetic parameters that permit rapid adaptive evolution, a transmission bottleneck of a single genome is not inconsistent with the observed rapid adaptation to the earliest immune responses. However, selection under these conditions is predicted to result in only minor reductions in N_e at linked loci because the transmission bottleneck reduces N_e to such an extent that beneficial mutations spread to fixation sequentially rather than simultaneously.

Methods

Model

CD8⁺ T cell epitopes:

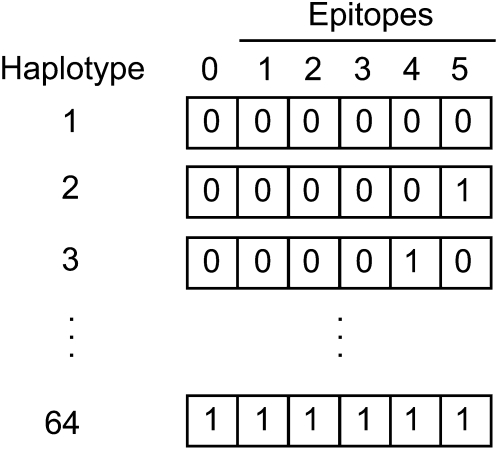
An epitope is defined as a portion of a molecule, usually a protein, that is bound by an immune receptor, in this case a CD8⁺ T cell receptor. A CD8⁺ T cell epitope was represented as a single “locus” at which a mutation conferred escape from a targeting CD8⁺ T cell response. A 0 allele at the locus indicated the wild-type epitope, which was subject to recognition by a CD8⁺ T cell response to the epitope, and therefore the possible death of its host cell. A 1 at the locus indicated an escape epitope allele, which carried a mutation that prevented the epitope from being recognized by the CD8⁺ T cells targeting the wild-type epitope. A haplotype consists of one or more loci and was represented as a binary sequence with each digit a locus. With L loci there are h = 2^L different haplotypes (Figure 1).

Figure 1 .

Haplotypes from five epitope loci (1–5) and one neutral locus (0). Each locus may have a wild-type allele (0) or a mutation (1). Six loci give 2⁶ = 64 possible haplotypes.

Fitness:

The difference in fitness between a wild-type epitope allele and an escape epitope allele at a single epitope locus in the presence of a CD8⁺ T cell response targeting the wild-type epitope resulted in selection for the escape epitope. Epitopes were not targeted by CD8⁺ T cell responses before peak viremia. Therefore, before peak viremia, the absolute fitness of the wild-type epitope, in terms of the proportion of infected cells surviving a CD8⁺ T cell response, is 1. For the escape epitope, the absolute fitness is 1 – φ, where φ is the cost of escape (Asquith et al. 2006) or equivalently, the proportion of infected cells dying before viral reproduction as a result of the mutation. These are also the relative fitnesses of the wild-type and escape epitopes. At and beyond peak viremia, epitopes were targeted by CD8⁺ T cell responses. For a targeted epitope, the absolute fitness of the wild-type epitope is 1 – c, where c is the proportion of infected cells killed by the CD8⁺ T cell response to the epitope (Asquith et al. 2006). And, the absolute fitness of the escape epitope is the same as for an untargeted escape epitope: 1 – φ. Therefore, the relative fitnesses of targeted wild-type epitopes and escape epitopes were defined as 1 and (1 – φ)/(1 – c), respectively. Epitope relative fitnesses are summarized in Table 1. The selective advantage of an escape epitope over the wild-type epitope being targeted by a CD8⁺ T cell response, or the selection coefficient, s, is calculated by equating 1 + s with the relative fitness of the escape epitope, giving s = (c – φ)/(1 – c). For example, if c = 0.45 day⁻¹ and φ = 0.005 day⁻¹, then s = 0.809.

Table 1 . Relative fitnesses of wild-type and escape epitopes before and after peak viremia.

Peak viremia	Wild-type epitope	Escape epitopea
Before	1	1 – φ
After	1	(1 – φ)/(1 – c)

^aφ is the cost of escape equivalent to the proportion of cells infected by virus carrying the escape mutation that die before viral reproduction, and c is the proportion of infected cells killed by a CD8⁺ T cell response targeting the epitope.

Epitope relative fitnesses were used to calculate the relative fitnesses of haplotypes. Before peak viremia (before epitopes are targeted), the relative fitness of haplotype i is $w_i={\left(1-\mathrm{\phi }\right)}^{l_i}$, where l_i is the number of escape epitopes in the haplotype. After peak viremia, when epitopes are targeted, the relative fitness of a haplotype is $w_i={\left(1+s\right)}^{l_i}$.

A weakening CD8⁺ T cell response was necessary to reproduce the observed pattern of escape epitope fixations in patients. A weakening response over time has been reported from a recent thorough analysis of the dynamics of CD8⁺ T cell responses (Liu et al. 2011). In the model this was accomplished by decreasing the rate of killing by CD8⁺ T cells, c, with the cumulative number of fixed escape epitopes. The decline in c was simulated using the logistic equation,

$$c_E=\frac{c_{\min }}{1+\left(c_{\min }/c_{\max }-1\right)e^{-bE}},$$ (1)

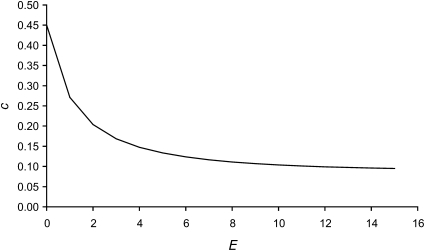
where c_min is the asymptotic minimum killing rate, c_max is the maximum killing rate, b is the intrinsic (maximum) rate of decrease of c, and E is the cumulative number of epitopes with fixed escape mutations. The value of c_E is plotted as a function of E in Figure 2. The value of c_E was used to calculate the fitness for all actively targeted epitopes. For example, before any escape epitopes had fixed (E = 0), the fitness of each epitope was calculated with c_E = c_max. Also note that with b = 0, c_E = c_max.

Figure 2 .

Logistic decline of the rate of killing by CD8⁺ T cells, c, as a function of the number of fixed escape epitopes, E. Parameter values are c_max = 0.45 day⁻¹, c_min = 0.09 day⁻¹, and b = 0.18.

The genetic basis of adaptation:

The evolution of a population was simulated stochastically in discrete generations with a Wright–Fisher model of reproduction. Recurrence equations were used to track changes in the frequencies of the h haplotypes due to selection, mutation, and recombination, in that order.

Selection:

If haplotype i has frequency x_i before selection, then its frequency after selection is

$$y_i=\frac{w_i}{\overline{w}}\hspace{0.17em}{x}_i\text{(}\overline{w}={\displaystyle \sum _{i=1}^h{w}_i{x}_i}\text{)}.$$ (2)

Mutation:

The frequency of haplotype i after mutation is the sum of the products of the frequency of each haplotype j before mutation and the probability of obtaining i after mutation of j,

$$z_i={\displaystyle \sum _{j=1}^h\left[y_j{{\mu }^{d_{ij}^1}}_f{\left(1-{\mu }_f\right)}^{I_{ij}^0}{{\mu }^{d_{ij}^0}}_b{\left(1-{\mu }_b\right)}^{I_{ij}^1}\right]},$$ (3)

where μ_f is the forward per-epitope mutation rate, μ_b is the backward mutation rate, $d_{ij}^1$ is the number of epitopes that are escape mutants (1) in haplotype i but not in j, $d_{ij}^0$ is the number of epitopes that are wild type (0) in i but not in j, $I_{ij}^1$ is the number of epitopes that are escape mutants in both i and j, and $I_{ij}^0$ is the number of epitopes that are wild type in both i and j.

Recombination:

The calculation of haplotype frequencies after recombination among three or more loci is not trivial (Crow and Kimura 1970). These were calculated following Bennett (1954). In this approach, sets of haplotypes and their compliments that may recombine to produce the haplotype of interest are identified. The following example is for six loci,

$$\begin{array}{c}{v}_i=z_i{\left(1-r\right)}^5+P\left(1\right)P\left(23456\right)r{\left(1-r\right)}^4+P\left(2\right)P\left(13456\right)r^2{\left(1-r\right)}^3\\ \hspace{1em}+P\left(3\right)P\left(12456\right)r^2{\left(1-r\right)}^3+P\left(4\right)P\left(12356\right)r^2{\left(1-r\right)}^3\\ \hspace{1em}+P\left(5\right)P\left(12346\right)r^2{\left(1-r\right)}^3+P\left(6\right)P\left(12345\right)r{\left(1-r\right)}^4\\ \hspace{1em}+P\left(12\right)P\left(3456\right)r{\left(1-r\right)}^4+P\left(13\right)P\left(2456\right)r^3{\left(1-r\right)}^2+\mathrm{...}\text{(15 terms)}\\ \hspace{1em}+P\left(123\right)P\left(456\right)r{\left(1-r\right)}^4+P\left(124\right)P\left(356\right)r^3{\left(1-r\right)}^2+\mathrm{...}\text{(10 terms)},\end{array},$$ (4)

where P(1) is the sum of the frequencies of haplotypes with the same allele at locus 1 as haplotype i, and so on, and r is the probability of a crossover between pairs of adjacent loci in the haplotype model (not adjacent on the genome) (Figure 1). The following general equation was used to calculate the frequency of haplotype i after recombination when the number of loci, L, is odd,

$$v_i=z_i{\left(1-r\right)}^{L-1}+{\displaystyle \sum _{j=1}^{L/2}{\displaystyle \sum _{k=1}^{{}_{L}C_j}{P}_{M_{jk}}{P}_{M_{jk}^{\text{c}}}{r}^{n_{M_{jk}}}}}{\left(1-r\right)}^{L-1-n_{M_{jk}}},$$ (5)

where j is the number of loci used to identify the kth set of haplotypes, $M_{jk}$, and $M_{jk}^{\text{c}}$ is the complement of $M_{jk}$. _LC_j, the binomial coefficient (the number of ways to sample j loci from a total of L), is the number of sets identified by j loci. $M_{jk}$ contains haplotypes with the kth set of j loci bearing the same alleles as haplotype i and either allele at the remaining L – j loci. The complement, $M_{jk}^{\text{c}}$, contains haplotypes with the kth set of L – j loci bearing the same alleles as haplotype i and either allele at the remaining j loci. $P_{M_{jk}}$ and $P_{M_{jk}^{\text{c}}}$ are the sums of the frequencies of the haplotypes in M_jk and $M_{jk}^{\text{c}}$, respectively. Finally, $n_{M_{jk}}$ is the number of crossovers between adjacent epitopes necessary to produce haplotype i from recombination between haplotypes in M_jk and $M_{jk}^{\text{c}}$. The number of crossovers is determined by counting the number of transitions between adjacent loci that are used to define the set and those that are not. Note that with odd L, the value of L/2 is truncated toward zero. L/2 is the highest number of loci necessary to define all sets of haplotypes and their complements. For even L, Equation 5 was modified as

$$\begin{array}{c}{v}_i=z_i{\left(1-r\right)}^{L-1}+{\displaystyle \sum _{j=1}^{L/2-1}{\displaystyle \sum _{k=1}^{{}_{L}C_j}{P}_{M_{jk}}{P}_{M_{jk}^c}{r}^{n_{M_{jk}}}}}{\left(1-r\right)}^{L-1-n_{M_{jk}}}\\ \hspace{1em}+{\displaystyle \sum _{k=1}^{{}_{L}C_{L/2}/2}{P}_{M_{L/2k}}{P}_{M_{L/2k}^c}}{r}^{n_{M_{L/2k}}}{\left(1-r\right)}^{L-1-n_{M_{L/2k}}}\end{array},$$ (6)

where the third term on the right accounts for the fact that, because sets are ordered, with even L only the first half of the _LC_L/2 sets based on L/2 loci are required to identify all sets of haplotypes and their complements.

Genetic drift:

The frequencies of haplotypes after selection, mutation, and recombination were calculated deterministically. Genetic drift due to a finite population size was incorporated by generating a random count for each haplotype in the next generation from a multinomial distribution with probabilities of possible mutually exclusive outcomes on any trial equal to the haplotype frequencies in the current generation (v₁,…,v_h), and a number of independent trials equal to the population size. This approach produces the same results as exact stochastic simulation, but is computationally much faster (Gillespie 1993).

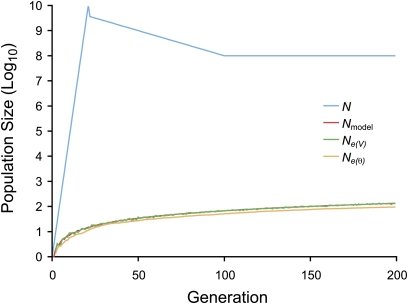
The population size in each generation used in the model, N_model, was the effective population size, N_e, of HIV-1 within a patient as determined from a typical profile of changes in the census population size in early infection. These changes in the census population size are as follows. The initial population size, at transmission, increases linearly on a log scale to peak viremia and then decreases linearly on a log scale to the set point value at the end of the acute phase of infection, where it remains throughout the early chronic phase of infection. From this profile, N_e in each generation was calculated as the harmonic mean of the census population sizes across the current and preceding generations, which gives an estimate of both the variance and inbreeding effective sizes for a population changing in size (Crow and Kimura 1970) (Figure 3). This estimate of N_e is insensitive to large changes in both the peak viremia and the set point, and depends mainly on the size of the population bottleneck at transmission. The model population size represents the effective size of an actual viral population within a patient in the absence of selection.

Figure 3 .

The within-patient viral census and effective population sizes. The initial population size (bottleneck) is one genome. The effective population size used in the model, N_model, is the harmonic mean of the census population size, N. The variance effective population size, N_e(V), estimated from simulations, overlaps N_model. The coalescent effective population size, N_e(θ), also estimated from simulations, underestimates N_model because the population is not at mutation-drift equilibrium. Both effective population sizes were estimated from 10,000 replicate simulations with an initial population size of one genome and no selection.

Model implementation:

To reduce computation time and computer memory requirements, mutation frequencies were tracked only for actively targeted epitopes and, optionally, a neutral locus (see below). Once a mutation fixed for an epitope (assumed at a frequency of 0.99), that epitope was no longer tracked and a new epitope was added to maintain a constant number of actively targeted epitopes. This reduced the number of haplotypes that had to be tracked compared to the situation in which all epitopes were tracked regardless of whether they were targeted. This approach meant that when an epitope with a fixed mutation was removed, the 2^L haplotypes consisted of 2^L/2 different pairs of identical haplotypes. Adding a new epitope involved adding a locus with a wild-type allele to one member of each pair of identical haplotypes and adding a locus with a mutation to the other member. The haplotype receiving the locus with a wild-type allele was assigned the total frequency of the two previously identical haplotypes; the other member of the pair, receiving the locus with a mutation in the new epitope, was assigned a frequency of 0. This reflects that the population was initialized with the wild-type allele at all epitope loci and that mutations are rare and are selected against in nontargeted epitopes (due to the fitness cost of an escape mutation).

Parameter values:

Values for the major parameters were chosen to give low, medium, and high rates of adaptive evolution (Table 2). The HIV-1 mutation rate per base pair per generation (including point mutations and deletions and insertions) has been reliably estimated as μ = 4.9 × 10⁻⁵ and 7.3 × 10⁻⁷ (Sanjuan et al. 2010). Assuming that 75% of nucleotide mutations in coding regions are nonsynonymous and that a CD8⁺ T cell epitope is 10 amino acids long, a whole-epitope forward mutation rate was calculated as μ_f = μ × 10 amino acids sites/epitope × 3 nucleotide sites/amino acid site × 0.75 amino acid changes/mutation. The backward mutation rate was calculated on the basis of the probability of an epitope with one mutation mutating to the particular amino acid that produces the wild-type epitope (assuming most mutations are point mutations): μ_b = μ_f × 1 amino acid site/10 amino acid sites × 1 amino acid/19 alternative amino acids.

Table 2 . Sets of values for the major parameters resulting in low, middle, and high rates of adaptive evolution.

Parameter	Low	Middle	High
No. of simultaneously targeted loci, L*	1	3	5
Mutation rate (/bp/generation), μ	7.3 × 10−7	6.0 × 10−6	4.9 × 10−5
Set point viral load (infected cells), N*	1 × 107	5 × 107	1 × 108
Viral generation length (days), g	2	1.5	1
Day of seroconversion (days p.i.), t*	28	25	21
Cell killing rate (day−1), c	0.15	0.30	0.45

The rate of killing of infected cells by a CD8⁺ T cell response directed at a single epitope has been estimated as c = 0.02–0.45 day⁻¹ (Asquith et al. 2006; Goonetilleke et al. 2009; Fischer et al. 2010), with higher values being attributed to estimation earlier in infection (McMichael et al. 2010) and sampling larger numbers of sequences (Fischer et al. 2010). The fitness cost of an escape mutation was φ = 0.005 day⁻¹ (Asquith et al. 2006). The number of epitopes targeted simultaneously has been estimated to range from zero to five, with a median of two (Goulder et al. 1997; Geels et al. 2003; Milicic et al. 2005).

The viral setpoint, estimated to be ∼10⁷–10⁸ infected cells (Chun et al. 1997), is 1–2 orders of magnitude below peak viremia (Kinloch-De Loes et al. 1995; Ho 1996; McMichael et al. 2010). Peak viremia occurs 21–28 days p.i. (McMichael et al. 2010). The reported adaptive dynamics are that typically three escape fixations occur by 50 days after peak viremia (McMichael et al. 2010). To maximize the opportunity for these dynamics to occur with a transmission bottleneck of one genome, for this purpose peak viremia was assumed to occur at 28 days and three fixations were expected by 78 days p.i.

The first 200 days of infection were simulated. These include acute infection, defined as the first 100 days, and early chronic infection, defined as the next 100 days (McMichael et al. 2010). The viral generation length has been estimated as 1–2 days (Perelson et al. 1996; Rodrigo et al. 1999; Markowitz et al. 2003; Murray et al. 2011). Populations were initialized with the haplotype carrying the wild-type allele at each locus.

For HIV-1, the rate of recombination between nonidentical genomes depends on the rate of co-infection of cells, which is high in splenocytes (Jung et al. 2002), but low in peripheral blood mononuclear cells (Josefsson et al. 2011). Because of this, the recombination rate may be as high as r = 10⁻³ per pair of adjacent nucleotide sites per generation or 1–2 orders of magnitude lower (Levy et al. 2004; Shriner et al. 2004a; Neher and Leitner 2010; Schlub et al. 2010; Batorsky et al. 2011). The rate of recombination between epitopes also depends on the number of nucleotides between epitopes. Therefore, recombination rates used ranged from 0.5, for free recombination, to 0.

The effect of selection on the effective population size

The effect of selection on N_e, in addition to the effect of genetic drift alone, may be studied by modeling a population and estimating N_e at a neutral locus linked to loci under selection (Santiago and Caballero 1998; Keightley and Otto 2006; Liu and Mittler 2008). To do so, a neutral locus was added and treated like any other locus except that it had no affect on fitness. The effective population size at the neutral locus may be estimated in various ways depending on which aspect of stochastic changes in allele frequencies is of interest.

Variance effective population size:

The variance effective population size, N_e(V), is the population size that gives the same sampling variance in allele frequency as the actual population, in this case the model population. The variance in the frequency of the mutant allele at the neutral locus in the next generation, p′, due to genetic drift in a Wright–Fisher population, is the binomial sampling variance, which depends on the frequency of the allele in the current generation, p, and N_e (Crow and Kimura 1970; Gillespie 2004):

$${\text{Var}}_N\{p\prime \}=\frac{p\left(1-p\right)}{N_{\text{e}}}.$$ (7)

This variance cannot be estimated directly for any generation in any one replicate simulation (because there is only one measure of p′), but may be estimated for a generation across replicates by assuming that p is the mean of p′ in each replicate and then calculating

$${\text{Var}}_N\{p\prime \}=\frac{{\displaystyle {\sum }_{i\hspace{0.17em}=\hspace{0.17em}1}^K{\left({p^{\prime }}_i-p_i\right)}^2}}{K-1},$$ (8)

where p_i′ and p_i are the allele frequencies in the ith of K replicates. This is justified because genetic drift does not change the mean of p between generations, making Equation 8 the variance of p′. Mutation does change the value of p between generations, but its impact was insignificant and may be ignored. Note that calculation of this variance includes only replicates in which the neutral locus is polymorphic (0 < P < 1), which is consistent with the fact that a monomorphic locus has a sampling variance of 0, for which the effective population size is undefined (Equation 7). This calculation of variance assumes a constant population size. Since the population size is increasing (Figure 3), the variance is underestimated because it is proportional to 1/N_e (Equation 7). Therefore, the variance was adjusted by multiplying by the ratio of the model population size in the next generation, N′, to the size in the current generation, N:

$${\text{Var}}_N\{p\prime \}=\frac{{\displaystyle {\sum }_{i=1}^K{\left({p^{\prime }}_i\hspace{0.17em}-\hspace{0.17em}{p}_i\right)}^2}}{K-1}\frac{N^{\prime }}{N}.$$ (9)

The effective population size was then estimated for each replicate within a generation with Equation 7 and averaged across replicates. In the absence of selection, this estimate of N_e(V) matched the model population size (Figure 3).

Coalescent effective population size:

The coalescent effective population size, N_e(θ), was estimated from the relationship between genetic diversity at a neutral locus and N_e: θ = 2N_eμ_T, for haploids, where μ_T is the total mutation rate (μ_f + μ_b) (Watterson 1975). This relationship holds at equilibrium between genetic drift and mutation and is therefore only approximate for a population changing rapidly in size (Charlesworth 2009). Genetic diversity at the neutral locus was estimated from its relationship with homozygosity: G ≈ 1/(1 + θ) (Gillespie 2004), where G = 1 – 2p(1 – p). This is valid only for θ ≤ 1 since for a biallelic locus the minimum value of G is 0.5, which gives a maximum value of θ = 1. Homozygosity and N_e(θ) were estimated for each simulation replicate in each generation and N_e(θ) was then averaged across replicates for each generation.

Estimating N_e from patient data

Viral N_e(θ) was estimated from the diversity of viral DNA sequences sampled from patients in the early stages of infection for comparison with model predictions. Only adults with sexually transmitted HIV-1 subtype B and not receiving antiviral treatment were considered. In the HIV Sequence Database (http://www.hiv.lanl.gov), three patients had five or more virus sequences sampled at three or more time points during early infection (≤ 200 days post seroconversion) from complete, or nearly complete, sequences from the major genes env and nef. Two of these patients had sequences sampled from the env gene (WEAU0575 and SUMA0874) and one from the nef gene (PIC1362). Data matching these criteria were not available for nonsexually transmitted virus. Sequences were aligned using ClustalW (Thompson et al. 1994). Sample times were given as days post seroconversion. As seroconversion coincides with peak viremia, these times were converted to days post infection by adding 21 days (to match the time of peak viremia used in simulations). θ was estimated as sequence diversity, π, the mean proportion of synonymous nucleotide sites that differ between a pair of sequences (Nei and Kumar 2000, Equation 12.56, p. 251) using the sequence analysis program MEGA4 (Tamura et al. 2007). The mutation rate used was the same one used in the compared simulations: μ = 4.9 × 10⁻⁵ per nucleotide. This is the appropriate neutral mutation rate since only synonymous sites were used.

Results

Adaptive dynamics

Simulations were used to determine the parameter values necessary to replicate the observed adaptive dynamics of typically three escape fixations by 78 days p.i. and a total of 8 fixations by 200 days p.i. (McMichael et al. 2010). Simulations were run with a transmission bottleneck of one genome, free recombination (r = 0.5) and a parameter value set for either a low, middle, or high rate of adaptation (Table 2). With the low-rate and mid-rate parameter value sets, the mean numbers of fixations were lower than those observed, whereas, with the high-rate value set, the numbers of fixations were higher than those observed (Table 3).

Table 3 . Mean numbers (1000 replicate simulations) of escape epitope fixations at 78 days (E₇₈) and 200 days (E₂₀₀) p.i. for parameter value sets generating low, middle, and high rates of adaptive evolution (see Table 2).

Parameter set	N200	E78	E200
Low	78	0	0.02
Middle	101	0.17	1.36
High	134	4.27	23.41

N₂₀₀ is the model population size at 200 days p.i.

To obtain the observed dynamics, the high-rate parameter value set was used with a rate of CD8⁺ T cell killing that declined logistically with the number of fixed escape epitopes. The observed dynamics could be achieved with an asymptotic minimum killing rate c_min < 0.1 and with appropriate values for the intrinsic rate of decline of the killing rate b (Table 4). Therefore, the observed adaptive dynamics could be reproduced with a transmission bottleneck of one genome, but only with a declining rate of CD8⁺ T cell killing. A high value for c_min (0.09) and an appropriate value for b (0.18) (Table 4) were used in subsequent simulations.

Table 4 . Mean numbers (1000 replicate simulations) of escape epitope fixations at 78 days (E₇₈) and 200 days (E₂₀₀) p.i. with a CD8⁺ T cell response declining logistically at rate b to asymptotic minimum killing rate c_min.

cmin	b	E78	E200
—	0	4.27	23.41
0.2	2.0	2.29	10.95
0.1	0.21	2.48	8.51
0.09	0.17	2.54	8.51
	0.18	2.51*	8.30*
	0.19	2.44	8.16
0.05	0.06	2.71	8.81
	0.07	2.58*	8.26*
	0.08	2.49	7.89
0.01	0.010	2.71	8.55
	0.011	2.68*	8.26*
	0.012	2.59*	7.98*
	0.015	2.49	7.37

Asterisks indicate matches to observed numbers of fixed escape epitopes at both time points rounded to the nearest whole number: E₇₈ = 3 and E₂₀₀ = 8. Parameter values in italics indicate those used in subsequent simulations.

The robustness of the simulation results to changes in values of the major parameters was investigated by using the set of parameter values giving a high rate of adaptation (Table 2) and changing the value of only one parameter at a time. Parameter values were constrained to within the range of realistic values, and therefore this analysis addresses the impact of the uncertainty in parameter values on the simulation results. This was done for all the major parameters, except the rate of recombination and the size of the transmission bottleneck, which were investigated separately (below). Table 5 shows that the mean numbers of escape epitope fixations at 78 days and 200 days p.i. are fairly robust to changes in the viral set point, the viral generation length, the number of days postinfection of seroconversion, and the cell killing rate. The numbers of fixations were sensitive to changes in the number of simultaneously targeted epitopes and the mutation rate. A high number of simultaneously targeted epitopes and a high mutation rate (Table 2) were used because these values give results consistent with a transmission bottleneck of one genome.

Table 5 . Robustness of the mean numbers (1000 replicate simulations) of escape epitope fixations at 78 d (E₇₈) and 200 d (E₂₀₀) p.i. to changes in values of the major parameters.

Parameter	Value	E78	E200
L*	1	0.73	2.77
	3	1.76	5.85
μ	7.3 × 10−7	0.07	0.60
	6.0 × 10−6	0.59	2.82
N*	1 × 107	2.42	8.17
	5 × 107	2.47	8.27
g	2	1.65	6.19
	1.5	1.94	7.13
t*	28	2.18	7.78
	25	2.28	8.01
c	0.15	0.95	6.03
	0.30	2.03	7.70

Parameters are defined in Table 2. The value of only one parameter is changed at a time, the values of all other parameters are from the high-rate set (Table 2) with a logistically declining cell killing rate (c_min = 0.09 and b = 0.18).

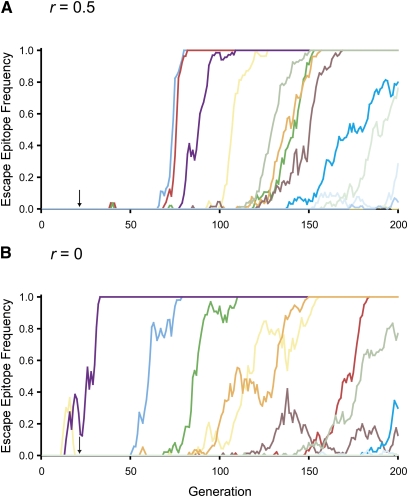
With a transmission bottleneck of one genome, reducing the rate of recombination, r, reduced the mean numbers of escape epitope fixations at 78 and 200 days p.i. (Table 6). However, even with no recombination, the effect is small, reducing the mean number of fixations from approximately three and eight to approximately two and seven. The reduction in the numbers of fixations may be explained equivalently in terms of the effect of selection on N_e or clonal interference. Plots of frequencies of escape epitopes over time show evidence of greater interference with no recombination than with free recombination: with no recombination, there are more frequent reversals in frequencies of escape epitopes (Figure 4). The impact of tighter linkage is greater with a transmission bottleneck of 10 genomes. With free recombination, there were approximately 5 and 12 fixations at 78 and 200 days p.i., respectively (Table 6). With no recombination these numbers decreased to approximately 3 and 9 fixations.

Table 6 . The effect of the transmission bottleneck, N₀, and recombination rate, r, on the mean numbers (1000 replicate simulations) of escape epitope fixations at 78 d (E₇₈) and 200 d (E₂₀₀) p.i.

N0	r	E78	E200
1	0.5	2.51*	8.30*
	0.1	2.40	8.14
	0.01	2.19	7.19
	0.001	2.13	6.65
	0	2.09	6.56
10	0.5	4.52	11.97
	0	3.26	9.11

Other parameter values are c_min = 0.09 and b = 0.18. Asterisks indicate matches to observed numbers of fixed escape epitopes at both time points rounded to the nearest whole number: E₇₈ = 3 and E₂₀₀ = 8.

Figure 4 .

Frequencies of escape mutants at epitope loci in single simulation replicates with a transmission bottleneck of one genome. Frequencies are shown for free recombination (A) and no recombination (B). Other simulation parameter values are: c_max = 0.45 day⁻¹, c_min = 0.09 day⁻¹, and b = 0.18. Arrows indicate the start of CD8⁺ T cell responses.

Effect of selection on N_e

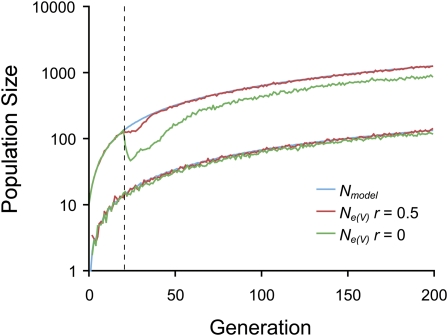
The effect of positive selection by CD8⁺ T cells on N_e was determined by estimating the variance effective population size, N_e(V), at a linked neutral locus. For HIV-1, the rate of recombination between nonidentical genomes depends on the rate of co-infection of cells, which may be as high as a mean of three integrated viral genomes (proviruses) per infected splenocyte (Jung et al. 2002), or only a single provirus per infected peripheral blood mononuclear cell (Josefsson et al. 2011). Therefore, between distantly separated epitopes there may be free to no recombination, depending on the rate of cell co-infection. With a transmission bottleneck of one genome and free recombination (r = 0.5) between the five loci under selection and the neutral locus, such recurrent positive selection reduced N_e(V) a negligible amount compared to the model population size: 131 vs. 133 at 199 generations p.i. (estimated using simple linear regression with the intercept constrained to 1; Figure 5). With no recombination, the reduction was greater, but still only 8%: 122 vs. 133 at 199 generation p.i. (Figure 5). Reducing the number of simultaneously targeted epitopes to one reduced N_e(V) by 5% relative to the model population size. Targeting five epitopes simultaneously, but reducing the mutation rate to the lower limit of the range of estimates (7.3 × 10⁻⁷ per nucleotide) also reduced the impact of selection on N_e(V), causing a reduction of only 4% relative to the model population size. With a transmission bottleneck of 10 genomes, the effect of selection was greater. With free recombination, selection reduced N_e(V) at the neutral locus from 1250 to 1241 at 199 generation p.i. (Figure 5). And, with no recombination, N_e(V) was reduced to 869, a reduction of 30%.

Figure 5 .

The effect of selection by CD8⁺ T cells and genetic linkage on the variance effective population size, N_e(V), at a neutral locus. The model population size, N_model, is shown for transmission bottlenecks of N₀ = 1 and 10. Corresponding values of N_e(V) are shown for free recombination, r = 0.5, and no recombination, r = 0. The vertical dashed line indicates the start of CD8⁺ T cell responses. The initial frequency of the mutant allele at the neutral locus was 0 for N₀ = 1 and 0.5 for N₀ = 10. Other parameter values were as in Figure 4.

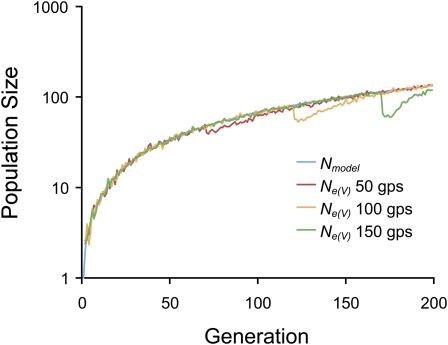
The effect of selection on N_e could be more pronounced when selection was not recurring, resulting in a single selective sweep, but was ephemeral. The effect depended on when selection started, with selection initiated later producing a greater decrease in N_e(V) (Figure 6). Selection was initiated at 50, 100, and 150 generations post-seroconversion (g.p.s.), with seroconversion occurring at 21 days (21 generations) p.i.. With a transmission bottleneck of one genome and no recombination, this corresponded to maximum decreases in N_e(V), relative to the model population size, of approximately 21, 36, and 49%, respectively. The increasing impact of selection with the time of selection initiation is apparently due to the increasing amount of variation at the neutral locus, providing greater opportunities for selective sweeps. Simulations were initialized with a single genome, and therefore the neutral locus was fixed for the wild-type allele; subsequent mutation increased variation until selection was imposed at a linked locus.

Figure 6 .

The effects of single selective sweeps on the variance effective population size, N_e(V). Selection was initiated at 50, 100, and 150 generations post-seroconversion (g.p.s.). The model population size, N_model, is shown for comparison. N_e(V) values were estimated as for Figure 5, but with no recombination.

N_e estimated from sequence data

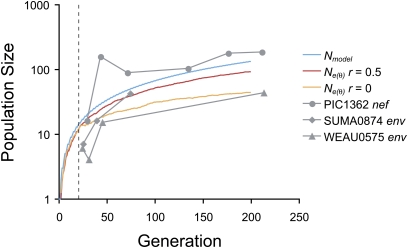
The coalescent effective population size, N_e(θ), was estimated from viral DNA sequences sampled from three patients (Figure 7). These values were compared to N_e(θ) estimated from simulations with recurrent selection on five epitopes simultaneously and with free recombination (r = 0.5) or no recombination. Estimates of N_e(θ) from simulations were below the model population size even with free recombination because these estimates assume equilibrium between mutation and genetic drift, but in acute infection the population is far from equilibrium. Estimates from env sequences from two patients were similar to the simulation estimates with free or no recombination, whereas the estimates from nef sequences from the third patient tended to be higher than the model population size (Figure 7). This may be explained if the transmission bottleneck was higher than a single genome for the third patient. Therefore, estimates from viral sequences generally matched the predicted values and are consistent with a transmission bottleneck of one genome in at least some patients.

Figure 7 .

Coalescent effective population sizes, N_e(θ), predicted from simulations and estimated from viral sequence data. The model population size, N_model, is shown for comparison. Values were predicted for free recombination (r = 0.5) and no recombination (r = 0). N_e(θ) was estimated for the viral genes env and nef from three patients. The vertical dashed line indicates the start of CD8⁺ T cell responses. Other parameter values are as in Figure 4.

Discussion

The extremely rapid adaptation of HIV-1 in early infection at first appears difficult to reconcile with the severe population bottleneck that occurs at transmission between hosts. Several analyses of sequence data using various methods have inferred that a single genome is typically transmitted between patients (Keele et al. 2008; Abrahams et al. 2009; Salazar-Gonzalez et al. 2009; Fischer et al. 2010; Novitsky et al. 2011). This study shows that the adaptive dynamics of early infection are consistent with a transmission bottleneck of one genome if the major population genetic parameters take realistic values that permit rapid adaptive evolution. These are a high number of simultaneously targeted epitopes (5), a high mutation rate (4.9 × 10⁻⁵/bp/generation), a high viral set point (10⁸ infected cells), a short generation time (1 day), early seroconversion (21 days p.i.), and an initially high rate of cell killing by CD8⁺ T cells (0.45 day⁻¹).

These results are most sensitive to changes in the number of simultaneously targeted epitopes and the mutation rate. The number of simultaneously targeted epitopes has been estimated from analyses of sequence data from all or most viral genes, which found escape mutations at zero to five epitopes spreading to fixation simultaneously (Goulder et al. 1997; Geels et al. 2003; Milicic et al. 2005). Since these analyses likely underestimate the number of targeted epitopes, use of the maximum number is justified (Asquith et al. 2006). Empirically reliable estimates of the HIV-1 mutation rate range from 7.3 × 10⁻⁷ to 4.9 × 10⁻⁵/nucleotide/generation, with a geometric mean of 2.4 × 10⁻⁵ (Sanjuan et al. 2010). Use of the highest rate, which is close to the mean, gives results that are consistent with a transmission bottleneck of a single genome. Using lower values for these parameters also reduced the effect of selection on N_e.

Reproduction of the observed pattern of adaptive fixations required that the rate of cell killing by CD8⁺ T cells decline with the number of escape mutations fixed. This allowed an initial rapid rate of three fixations in the 57 days following seroconversion (one fixation every 19 days) and a slower rate of an additional 5 fixations in the next 122 days (one fixation every 24 days). The rate of cell killing in the model declined from 0.45 day⁻¹ with no fixations to 0.17 day⁻¹ after three fixations, which is consistent with a range of 0.15–0.45 day⁻¹ estimated for early infection (Goonetilleke et al. 2009; Fischer et al. 2010). A clear reduction in the strength of CD8⁺ T cell responses from acute infection into chronic infection was recently reported from a thorough study of the dynamics of these responses (Liu et al. 2011). A population dynamic simulation study (Ganusov et al. 2011) suggests that a reduced rate of escape fixations in chronic infection may also be due to variation in the killing rate or cost of escape among epitopes, since early escapes will be due to stronger CD8⁺ T cell responses or to mutations that confer lower costs. This study also proposes that an increased breadth of CD8⁺ T cell responses will reduce the rate of fixation if responses are competitive and therefore reduce the effectiveness of each individual response. Another explanation for a declining rate of fixation is that some escape mutations reduce fitness below the wild-type level in the absence of a second, compensatory mutation. These double mutants would take longer to arise than single beneficial mutants. Fitness interactions of this type, more generally known as fitness epistasis, are common and strong in HIV-1 in the context of its adaptation to an alternative host-cell coreceptor (Da Silva et al. 2010) and have been reported for the evolution of escape mutants in response to CD8⁺ T cell selection (Yeh et al. 2006; Schneidewind et al. 2008).

Simultaneous selection on five epitope loci caused only a small (8%) decrease in the variance effective population size, N_e(V), at a tightly linked neutral locus (no recombination) when the transmission bottleneck was a single genome. Selection on single epitopes caused a greater decrease in N_e(V), but one that was ephemeral. This small effect explains the modest decrease in the numbers of fixations by 78 days and 200 days p.i. as the recombination rate decreased from 0.5 to 0 (linkage increased). This effect may also be understood in terms of clonal interference, with evidence of greater interference between spreading escape mutations in the absence of recombination compared with free recombination. In contrast, with a transmission bottleneck of 10 genomes, N_e(V) was reduced by 30% with no recombination, and there was a proportionally greater decrease in the number of fixations at 78 days and 200 days p.i. when recombination decreased from 0.5 to 0. The effect of the severity of the transmission bottleneck on the effect of selection on N_e(V) is explained by reduced clonal interference when selection is strong (N_es > 1) and mutation is weak (N_eµ << 1). Under these conditions a new beneficial mutation that survives stochastic loss is expected to spread to fixation before the appearance of the next beneficial mutation that survives stochastic loss (Gillespie 1984; Orr 2002). For the conditions of interest, s ≈ 0.81 and µ ≈ 10⁻³ mutations per epitope per generation. With a bottleneck of one genome, N_e ≈ 10², resulting in N_es ≈ 81 and N_eµ ≈ 0.1. Whereas, with a bottleneck of 10 genomes, N_e ≈ 10³, and N_es ≈ 810 and N_eµ ≈ 1. Therefore, clonal interference is not expected to be common when the transmission bottleneck is a single genome. A reduced effect of selection on N_e when the number of simultaneously targeted epitopes or the mutation rate were reduced supports this explanation.

When recurrent selection is strong and common relative to recombination, its effect on linked loci may be more pronounced than those of stochastic forces usually associated with the effects of a discrete population size, known as genetic drift (Maynard Smith and Haigh 1974; Gillespie 2000). Since the dynamics of stochastic changes in allele frequencies caused by linked selection are different from those caused by other stochastic forces, Gillespie (2000) suggested that the strong effects of linked selection be called genetic draft, even though, as he acknowledges, Wright (1955) included these effects in his original definition of genetic drift. A recent theoretical analysis of genetic draft argues that it is important in facultatively sexual organisms with large populations (Neher and Shraiman 2011). HIV-1 may be defined as facultatively sexual because recombination between nonidentical genomes depends on the co-infection of cells, which may be rare in peripheral blood (Josefsson et al. 2011), but not in other tissues, such as those of the spleen (Jung et al. 2002). Neher and Shraiman (2011) argue that with a low recombination rate and pervasive recurrent selection of moderate strength, as may be the case in chronic HIV-1 infection, the stochastic changes in allele frequencies in HIV-1 may be predominantly due to genetic draft. The present study suggests that this is not the case for early infection, where the effect of linked selection on N_e is minor compared to that caused by the severe transmission bottleneck.

Estimates of coalescent effective population sizes, N_e(θ), from viral DNA sequences sampled from three patients were generally consistent with model predictions for a population bottleneck of one genome. However, it is difficult to estimate N_e(θ) for several reasons. First, estimates of N_e(θ) have low precision because they are based on the relationship θ = 2N_eμ (for haploids), where, from the perspective of coalescent theory, N_e is the mean number of generations to coalescence for two alleles with standard deviation N_e (Rice 2004). Second, this relationship assumes equilibrium between mutation and genetic drift, which is clearly not the case in early infection. And third, estimates were made without knowledge of the linkage between the synonymous nucleotide sites analyzed, which are assumed to be neutral, and sites under selection. Nevertheless, assuming a transmission bottleneck of a single genome predicted values that overlapped the estimates from sequence data. However, because of the inherent difficulties of estimating N_e(θ), no conclusion can be drawn about the effect of selection on N_e on the basis of these data.

A severe transmission bottleneck of a single genome is consistent with the typical pattern of escape epitope fixations observed in early infection if values for the major population genetic parameters for HIV-1 are realistically set to allow rapid adaptive evolution. This involves strong selection by CD8⁺ T cells, but this selection is predicted to have only a small effect on N_e. Here, it is argued that the transmission bottleneck reduces the effective population size in early infection to such an extent that it prevents significant interference among escape mutations spreading to fixation. However, in chronic infection, when the effective population size is higher, although still several orders of magnitude below the census population size, and CD8⁺ T cell responses are weaker, genetic draft may become a more important force.