A Simple Method for Finding Explicit Analytic Transition Densities of Diffusion Processes with General Diploid Selection

Abstract

The transition density function of the Wright–Fisher diffusion describes the evolution of population-wide allele frequencies over time. This function has important practical applications in population genetics, but finding an explicit formula under a general diploid selection model has remained a difficult open problem. In this article, we develop a new computational method to tackle this classic problem. Specifically, our method explicitly finds the eigenvalues and eigenfunctions of the diffusion generator associated with the Wright–Fisher diffusion with recurrent mutation and arbitrary diploid selection, thus allowing one to obtain an accurate spectral representation of the transition density function. Simplicity is one of the appealing features of our approach. Although our derivation involves somewhat advanced mathematical concepts, the resulting algorithm is quite simple and efficient, only involving standard linear algebra. Furthermore, unlike previous approaches based on perturbation, which is applicable only when the population-scaled selection coefficient is small, our method is nonperturbative and is valid for a broad range of parameter values. As a by-product of our work, we obtain the rate of convergence to the stationary distribution under mutation–selection balance.

DIFFUSION processes, which are continuous-time Markov processes with almost surely continuous sample paths, have been successfully applied in various population genetic analyses in the past. Examples include finding the stationary distribution of allele frequencies and approximating fixation times and probabilities (see Karlin and Taylor 1981; Ewens 2004; Durrett 2008 for other applications of diffusion processes). This success is largely due to the fact that the diffusion approximation captures the key features of an evolutionary model while ignoring unimportant details, thereby arriving at a simpler process that facilitates computation. However, when a reasonably complex model of evolution is considered, one is faced with unwieldy equations even under the diffusion approximation. In particular, for Wright–Fisher diffusions with general diploid selection, finding an explicit analytic transition density function, which characterizes the evolution of population-wide allele frequencies over time, has remained a challenging open problem. The diffusion theory allows one to write down a partial differential equation (PDE) satisfied by the transition density, but solving the PDE analytically has proved to be difficult.

The transition density has several practical applications, including the following: Recently, there has been growing interest in analyzing samples taken from the same or related populations at different time points. For example, such data arise from experimental evolution of model organisms in the laboratory (e.g., bacteria, see Lenski 2011), from viral/phage populations (Shankarappa et al. 1999; Wichman et al. 1999), or from ancient DNA (Hummel et al. 2005); see also Bollback et al. (2008) and references therein. In particular, the recent sequencing of Neanderthal (Green et al. 2010) and Denisova (Reich et al. 2010) genomes should provide new opportunities for studying the evolution of allele frequencies over time, possibly under the influence of natural selection. In applying the diffusion process to study the evolution of the populations underlying such samples, it is important to find the transition density accurately. Bollback et al. (2008) analyzed samples from multiple time points by using a hidden Markov model in which the hidden states are the population-wide allele frequencies. To approximate the evolution of the allele frequencies, they applied finite difference methods to obtain approximate numerical solutions to the PDE satisfied by the transition density. Finite difference methods were also employed by Gutenkunst et al. (2009) to obtain numerical approximations of the transition density in Wright–Fisher diffusions with population substructure, which the authors applied to develop a useful tool for demographic inference. When employing such numerical methods, however, one needs to exercise caution in choosing appropriate discretization grid points. Which discretization is appropriate may depend strongly on the parameters (e.g., the selection coefficient) of the model, and it is difficult to predict a priori whether a particular discretization will produce accurate solutions. Also, in a numerical approach, note that the PDE needs to be solved afresh if the initial or the final frequency is changed. It would be useful to have a solution that is analytic in those variables.

Since the transition density of the Wright–Fisher diffusion with selection has practical applications, finding an explicit formula has significant merit and several researchers have considered the problem. As detailed later in the text, the so-called spectral representation of the transition density can be found if the eigenvalues and eigenfunctions of the diffusion generator are known. Indeed, this is the approach taken by Kimura (1955a, 1957), first for a diallelic model with genic selection (i.e., the case with the dominance parameter h = 1/2, as described shortly) and later for the case of complete dominant selection (i.e., with h = 1), assuming no recurrent mutation in both cases. More precisely, Kimura proposed perturbation expansions of the eigenvalues and eigenfunctions in powers of the population-scaled selection coefficient σ (defined more precisely later). Although this method is valid for σ < 1, the expansions fail to converge for σ substantially >1 [say, σ > 10, which is not so unusual for adaptive alleles (Eyre-Walker and Keightley 2007)]. Furthermore, the perturbation expansion scheme described in Kimura’s work is not entirely transparent.

For a neutral parent-independent mutation model, an explicit spectral representation of the transition density for the one-locus Wright–Fisher diffusion has been known for some time (Shimakura 1977; Griffiths 1979). Griffiths and Li (1983) and Tavaré (1984) showed that this spectral representation can be interpreted in terms of a stochastic process dual to the diffusion. The time dependency of the transition density is solely given through the probability distribution of this dual process (see Griffiths and Spanò 2010 for an overview). Barbour et al. (2000) extended this duality approach to include a general selection model, but the transition rates of the dual process depend on the moments of the stationary distribution, and under selection these moments are difficult to compute (Donnelly et al. 2001). Hence, while being of theoretical interest, their method does not readily lead to efficient computation of the transition density.

In this article, we develop a new, simple computational method with which to find analytic transition density functions of diallelic Wright–Fisher diffusions under recurrent mutation and arbitrary diploid selection. In contrast to the aforementioned mathematical work based on duality, our method explicitly finds the eigenvalues and eigenfunctions of the diffusion generator associated with the diffusion, thus leading to an explicit spectral representation of the transition density function. Specifically, the eigenfunctions are found as a series of orthogonal functions. Although somewhat advanced mathematical concepts are needed to derive the necessary system of equations, the resulting algorithm is quite simple to describe and easy to implement, involving only standard linear algebra. Furthermore, unlike previous approaches (Kimura 1955a, 1957) based on perturbation, which is applicable only when the population-scaled selection coefficient σ is small, our method is nonperturbative and is valid for a broad range of parameter values, including large values of σ and an arbitrary dominance parameter h. As an application of our work, we obtain the rate of convergence to the stationary distribution under mutation–selection balance.

The rest of this article is organized as follows. We begin with a brief review of the Wright–Fisher diffusion and describe the notion of spectral representation. Orthogonal polynomials, which we extensively employ in our work, are also introduced. Then, we illustrate the key ideas behind our method in the simple case of genic selection and no recurrent mutation. Afterward, we apply our method to the general case of arbitrary diploid selection and recurrent mutation and show how the results for the no-mutation case can be recovered as a special case. We then assess the performance of our method and end with discussions on possible applications and extensions.

Background

In this section, we review useful facts about diffusion processes. In particular, we highlight some key properties satisfied by backward generators of one-dimensional diffusions. We also introduce the relevant orthogonal polynomials that we utilize in our method.

Wright–Fisher diffusions

We consider a Wright–Fisher diffusion process with two alleles, denoted A₀ and A₁. The population-wide frequency of A₁ is denoted by x; hence, the frequency of A₀ is 1 − x. The genotype fitness scheme considered in this article is as follows:

• $\begin{array}{cccc}\hspace{1em}\hspace{1em}\hspace{0.5em}\hspace{0.17em}\text{Genotype}:& A_0/A_0& A_0/A_1& A_1/A_1\\ \text{Relative fitness}:& 1& 1+2\hspace{0.17em}h\hspace{0.17em}s& 1+2\hspace{0.17em}s\end{array}$

We refer to the case with the dominance parameter h = 1/2 as genic selection. The population-scaled selection coefficient is defined as σ = 2Ns, where N corresponds to the diploid population size, which is assumed to remain constant over time. The rate of mutation from A₀ to A₁ is given by α = 4Nu₀₁ and from A₁ to A₀ by β = 4Nu₁₀, where u₀₁ (respectively, u₁₀) denotes the per-generation probability of mutation from A₀ to A₁ (respectively, from A₁ to A₀).

Note that the genotype fitness scheme introduced above does not include the case in which the homozygotes have a relative fitness of 1 and the heterozygote has a relative fitness unequal to 1. However, by choosing s close to zero and h large, we can mimic such a scheme in our framework. More generally, it is straightforward to apply the technique developed in this article to a selection scheme in which the heterozygote has relative fitness 1 + s₁ and the homozygote A₁/A₁ has relative fitness 1 + s₂. However, to conform to the convention widely adopted in the literature, we use the above-mentioned parameterization of relative fitnesses.

Throughout, we use f to denote a twice continuously differentiable bounded function over [0,1]. The backward generator $\mathcal{L}$ of a one-dimensional diffusion process on [0,1] with diffusion coefficient ν²(x) and drift coefficient μ(x) acts on f as

$$\mathcal{L}f\left(x\right)=\frac{1}{2}{\nu }^2\left(x\right)\frac{{\partial }^2}{\partial x^2}\left\{f\hspace{0.17em}\left(x\right)\right\}+\mu \left(x\right)\frac{\partial }{\partial x}\left\{f \left(x\right)\right\}.$$

In the Wright–Fisher diffusion, ν²(x) = x(1 − x). The contribution to μ (x) from selection is

$$2\sigma x\hspace{0.17em}\left(1-x\right)\hspace{0.17em}\left[x+h\hspace{0.17em}\left(1-2\hspace{0.17em}x\right)\right],$$

while the contribution from recurrent mutation is

$$\frac{1}{2}\hspace{0.17em}\left[\alpha \hspace{0.17em}\left(1-x\right)-\beta \hspace{0.17em}x\right].$$

See Ewens (2004, Chap. 5.1) for a more detailed description.

Self-adjointness and the spectrum of a generator

Let L²([0,1],ρ) denote the space of real-valued functions on [0,1] that are square integrable with respect to some real positive density ρ(x). We refer to ρ as the weight function. Define the inner product 〈⋅,⋅〉_ρ as

$${\langle f,g\rangle }_{\rho }={\displaystyle {\int }_0^{1}f\left(x\right)g\left(x\right)\rho \left(x\right)\text{d}x,}$$ (1)

for f, g ∈ L²([0,1], ρ).

For a diffusion process with diffusion coefficient ν²(x) and drift coefficient μ(x), the scale density ξ(x) is defined as

$$\xi \left(x\right)=\text{exp}\left[-{\displaystyle {\int }_{x_0}^x\frac{2\hspace{0.17em}\mu \hspace{0.17em}\left(z\right)}{{\nu }^2\hspace{0.17em}\left(z\right)}}\hspace{0.17em}d\hspace{0.17em}z\right],$$ (2)

and the speed density π(x) is defined as

$$\pi \left(x\right)=\frac{\gamma }{{\nu }^2\hspace{0.17em}\left(x\right)\hspace{0.17em}\xi \hspace{0.17em}\left(x\right)},$$ (3)

where γ is some positive constant and x₀ is an arbitrary state in [0,1]. For the results derived in this article it is crucial to establish that $\mathcal{L}$ is self-adjoint with respect to π. To this end, let f, g ∈ L²([0,1], π) satisfy appropriate boundary conditions relevant to the boundary behavior of the corresponding diffusion. The diffusions considered in this article exhibit exit, regular reflecting, or entrance boundaries. If 0 is an exit boundary, then the appropriate boundary condition is Lim_x↓0 f(x) = 0. If 0 is either a regular reflecting or an entrance boundary, the appropriate boundary condition is ${\text{lim}}_{x\downarrow 0}\left(1/\xi \left(x\right)\right)\left(df\left(x\right)/dx\right)=0.$ Similar boundary conditions apply as x↑1. See Durrett (2008) or Ewens (2004) for more details. For the diffusions considered in this article, their corresponding boundary conditions and integration by parts imply

$${\langle \mathcal{L}\hspace{0.17em}f,g\rangle }_{\pi }={\langle f,\mathcal{L}\hspace{0.17em}g\rangle }_{\pi },$$

thus establishing that $\mathcal{L}$ is self-adjoint.

The key property (known as the spectral theorem) that we utilize in our work is the following: Suppose B and B′ are eigenfunctions of $\mathcal{L}$ that satisfy the requisite boundary conditions of the diffusion process. If their eigenvalues Λ and Λ′ are distinct, then the self-adjointness of $\mathcal{L}$ (i.e., ${\mathrm{\langle }B,\mathcal{L}\hspace{0.17em}{B}^{\prime }\mathrm{\rangle }}_{\pi }={\mathrm{\langle }\mathcal{L}\hspace{0.17em}B,B^{\prime }\mathrm{\rangle }}_{\pi }$) implies 〈B, B′〉_π = 0. Hence, eigenfunctions of $\mathcal{L}$ with distinct eigenvalues are orthogonal with respect to the weight function π(x).

That $\mathcal{L}$ is a self-adjoint negative semidefinite differential operator implies that its eigenvalues are all real and nonpositive. Furthermore, for many boundary conditions, including the ones considered in this article, solutions of $\mathcal{L}B\hspace{0.17em}\left(x\right)=-\Lambda \hspace{0.17em}B\hspace{0.17em}\left(x\right)$ satisfying the requisite boundary conditions exist for countably many distinct values of Λ. Thus, for the diffusion processes considered in this article, there is a unique sequence

$$0\le {\Lambda }_0<{\Lambda }_1<{\Lambda }_2<\cdots ,$$

with Λ_n → ∞ as n → ∞ (Karlin and Taylor 1981, Chap. 15.13). These eigenvalues ${\left\{-{\Lambda }_n\right\}}_{n=0}^{\mathrm{\infty }}$ are called the “spectrum” of $\mathcal{L}\mathrm{,}$ and it can be shown that their associated eigenfunctions ${\left\{B_n\hspace{0.17em}\left(x\right)\right\}}_{n=0}^{\mathrm{\infty }},$ which satisfy

$$\mathcal{L}\hspace{0.17em}{B}_n\hspace{0.17em}\left(x\right)=-{\Lambda }_n\hspace{0.17em}{B}_n\hspace{0.17em}\left(x\right),$$

form a basis of L²([0,1], π).

Spectral representation of the transition density

For any subset S ⊂ [0,1], the transition density function of a diffusion process is the function p: ℝ_≥0 × [0,1] × [0,1] → ℝ_≥0 such that

$$\mathrm{\mathbb{P}}\left[X_t\in S\mathsf{|}{X}_0=x\right]={\displaystyle {\int }_{S}p\left(t;x,y\right)dy.}$$

The transition density p(t; x, y) satisfies the Kolmogorov backward equation

$$\frac{\partial p\hspace{0.17em}\left(t;x,y\right)}{\partial t}=\mathcal{L}p\hspace{0.17em}\left(t;x,y\right)=\frac{1}{2}\hspace{0.17em}{\nu }^2\hspace{0.17em}\left(x\right)\hspace{0.17em}\frac{{\partial }^2}{\partial x^2}\hspace{0.17em}\left\{p\hspace{0.17em}\left(t;x,y\right)\right\}+\mu \hspace{0.17em}\left(x\right)\hspace{0.17em}\frac{\partial }{\partial x}\hspace{0.17em}\left\{p\hspace{0.17em}\left(t;x,y\right)\right\},$$

and the appropriate boundary conditions, see Karlin and Taylor (1981, Chap. 15.5). Here, the differential operator $\mathcal{L}$ is the backward generator of the diffusion and it acts on x.

Let {B_n(x)} be the eigenfunctions of $\mathcal{L}$ that satisfy the proper boundary conditions of the diffusion process. Further, let −Λ_n denote the eigenvalue of B_n(x). Then, ${\phi }_n\hspace{0.17em}\left(t,x\right)=e^{-{\Lambda }_n\hspace{0.17em}t}\hspace{0.17em}{B}_n\hspace{0.17em}\left(x\right)$ satisfies the partial differential equation

$$\frac{\partial {\phi }_n\hspace{0.17em}\left(t,x\right)}{\partial t}=\mathcal{L}\hspace{0.17em}{\phi }_n\hspace{0.17em}\left(t,x\right),$$ (4)

and the requisite boundary conditions. Furthermore, since $\mathcal{L}$ is a linear differential operator, a linear combination of $e^{-{\Lambda }_{n}t}{B}_n\left(x\right)$ is also a solution to (4). The spectral representation of p(t; x, y) is given by

$$p\hspace{0.17em}\left(t;x,y\right)=\stackrel{\mathrm{\infty }}{{\displaystyle \sum }_{n=0}}{c}_n\hspace{0.17em}\left(y\right)\hspace{0.17em}{e}^{-{\Lambda }_n\hspace{0.17em}t}\hspace{0.17em}{B}_n\hspace{0.17em}\left(x\right),$$

where the coefficients c_n(y) depend on y and are set to satisfy the initial condition. For p(0; x, y) = δ(x − y), the Dirac-delta distribution, we obtain

$$p\left(t;x,y\right)=\stackrel{\mathrm{\infty }}{{\displaystyle \sum }_{n=0}}{e}^{-{\Lambda }_n\hspace{0.17em}t}\hspace{0.17em}\pi \hspace{0.17em}\left(y\right)\frac{B_n\left(x\right)B_n\left(y\right)}{{\langle B_n,B_n\rangle }_{\pi }},$$ (5)

where π is the speed density defined in (3) and 〈⋅,⋅〉_π is the inner product defined in (1). See Karlin and Taylor (1981, Chap. 15.13) for further details and examples.

In summary, the transition density function of a diffusion process can be determined if the eigenvalues and the eigenfunctions of $\mathcal{L}$ are known. The orthogonal polynomials described in the following two subsections are such eigenfunctions for certain neutral Wright–Fisher diffusion processes, and we make extensive use of them in our work to solve the eigenvalue problem in the presence of selection.

In practice, we do not need to sum over infinitely many terms in (5). Since Λ_n → ∞ as n → ∞, the exponential term $e^{-{\Lambda }_n\hspace{0.17em}t}$ will be negligibly small for n sufficiently large. Hence, we can obtain accurate approximations of p(t; x, y) for t > 0 by summing over n from 0 to some reasonable finite cutoff. In Empirical transition densities and stationary distributions and Rate of convergence to the stationary distribution we provide explicit examples illustrating this property.

Jacobi polynomials

An excellent treatise on orthogonal polynomials can be found in Szegö (1939) and a concise collection of related formulas can be found in Abramowitz and Stegun (1965, Chap. 22). Here, we briefly review some key facts about a particular type of classical orthogonal polynomials.

For z ∈ [−1,1], the Jacobi polynomials $P_n^{\left(a,b\right)}\hspace{0.17em}\left(z\right)$ satisfy the differential equation

$$\left(1-z^2\right)\frac{d^{2}f \left(z\right)}{d{z}^2}+\left[b-a-\left(a+b+2\right)z\right]\frac{df\left(z\right)}{dz}+n\hspace{0.17em}\left(n+a+b+1\right)\hspace{0.17em}f\left(z\right)=0.$$ (6)

For fixed a, b > −1, $\left\{P_n^{\left(a,b\right)}\hspace{0.17em}\left(z\right)\right\}$ form an orthogonal system with respect to the weight function (1 − z)^a (1 + z)^b on the interval [−1,1]. Since the domain and the parameters of $P_n^{\left(a,b\right)}\hspace{0.17em}\left(z\right)$ are not suitable for our purpose, we define the following modified Jacobi polynomials, for x ∈ [0,1] and a, b > 0:

$$R_n^{\left(a,b\right)}\hspace{0.17em}\left(x\right)=P_n^{\left(b-1,a-1\right)}\hspace{0.17em}\left(2x-1\right).$$

Griffiths and Spanò (2010) use a slightly different, although related, convention.

For x ∈ [0,1], the modified Jacobi polynomials $R_n^{\left(a,b\right)}\hspace{0.17em}\left(x\right)$ satisfy the differential equation

$$x\hspace{0.17em}\left(1-x\right)\hspace{0.17em}\frac{d^2\hspace{0.17em}f\hspace{0.17em}\left(x\right)}{d{x}^2}+\left[a-\left(a+b\right)\hspace{0.17em}x\right]\hspace{0.17em}\frac{df\left(x\right)}{dx}+n\hspace{0.17em}\left(n+a+b-1\right)\hspace{0.17em}f \left(x\right)=0,$$ (7)

which follows immediately from (6). For fixed a, b > 0, $\left\{R_n^{\left(a,b\right)}\hspace{0.17em}\left(x\right)\right\}$ is an orthogonal system with respect to the weight function x^a−1(1 − x)^b−1 on [0,1]. More precisely,

$${\displaystyle {\int }_0^1{R}_n^{\left(a,b\right)}}\hspace{0.17em}\left(x\right)\hspace{0.17em}{R}_m^{\left(a,b\right)}\left(x\right)x^{a-1}{\left(1-x\right)}^{b-1}\hspace{0.17em}dx={\delta }_{n,m}{\Delta }_n\hspace{0.17em}\left(a,b\right),$$ (8)

where δ_n,m denotes the Kronecker delta and the coefficient Δ_n(a,b) is defined as

$${\Delta }_n\hspace{0.17em}\left(a,b\right)=\frac{\Gamma \left(n+a\right)\Gamma \left(n+b\right)}{\left(2\hspace{0.17em}n+a+b-1\right)\hspace{0.17em}\Gamma \hspace{0.17em}\left(n+a+b-1\right)\hspace{0.17em}\Gamma \hspace{0.17em}\left(n+1\right)}.$$ (9)

Furthermore, $\left\{R_n^{\left(a,b\right)}\hspace{0.17em}\left(x\right)\right\}$ form a complete basis of the Hilbert space L²([0,1], x^a−1(1 − x)^b−1).

For n ≥ 1, it can be shown that $R_n^{\left(a,b\right)}\hspace{0.17em}\left(x\right)$ satisfies the recurrence relation

$$\begin{array}{l}x\hspace{0.17em}{R}_n^{\left(a,b\right)}\hspace{0.17em}\left(x\right)=\frac{\left(n+a-1\right)\hspace{0.17em}\left(n+b-1\right)}{\left(2\hspace{0.17em}n+a+b-1\right)\hspace{0.17em}\left(2\hspace{0.17em}n+a+b-2\right)}\hspace{0.17em}{R}_{n-1}^{\left(a,b\right)}\hspace{0.17em}\left(x\right)\\ \hspace{1em}+\left[\frac{1}{2}-\frac{b^2-a^2-2\hspace{0.17em}\left(b-a\right)}{2\hspace{0.17em}\left(2\hspace{0.17em}n+a+b\right)\hspace{0.17em}\left(2\hspace{0.17em}n+a+b-2\right)}\right]\hspace{0.17em}{R}_n^{\left(a,b\right)}\hspace{0.17em}\left(x\right)\\ \hspace{1em}+\frac{\left(n+1\right)\hspace{0.17em}\left(n+a+b-1\right)}{\left(2\hspace{0.17em}n+a+b\right)\hspace{0.17em}\left(2\hspace{0.17em}n+a+b-1\right)}\hspace{0.17em}{R}_{n+1}^{\left(a,b\right)}\hspace{0.17em}\left(x\right),\end{array}$$ (10)

while, for n = 0,

$$x\hspace{0.17em}{R}_0^{\left(a,b\right)}\hspace{0.17em}\left(x\right)=\frac{a}{a+b}\hspace{0.17em}{R}_0^{\left(a,b\right)}\left(x\right)+\frac{1}{a+b}\hspace{0.17em}{R}_1^{\left(a,b\right)}\hspace{0.17em}\left(x\right).$$ (11)

Also, note that $R_0^{\left(a,b\right)}\hspace{0.17em}\left(x\right)\equiv 1$. The above recurrence relations plays an important role in our work.

Gegenbauer polynomials

The classical Gegenbauer polynomials are a special case of the classical Jacobi polynomials, namely $P_n^{\left(1,1\right)}\hspace{0.17em}\left(2x-1\right)$. In our work, we define G_n(x) as

$$G_n\hspace{0.17em}\left(x\right)=-x\hspace{0.17em}\left(1-x\right)\hspace{0.17em}{P}_n^{\left(1,1\right)}\hspace{0.17em}\left(2x-1\right)=-x\hspace{0.17em}\left(1-x\right)\hspace{0.17em}{R}_n^{\left(2,2\right)}\hspace{0.17em}\left(x\right)$$

and refer to them as modified Gegenbauer polynomials. The minus sign will prove convenient later. Using (7), it can be shown that G_n(x) satisfies the differential equation

$$x\hspace{0.17em}\left(1-x\right)\hspace{0.17em}\frac{d^{2}f\left(x\right)}{d{x}^2}+\left(n+2\right)\hspace{0.17em}\left(n+1\right)\hspace{0.17em}f\left(x\right)=0.$$ (12)

Further, {G_n(x)} form an orthogonal system of polynomials with respect to the weight function x⁻¹(1 − x)⁻¹:

$${\displaystyle {\int }_0^1{G}_n}\hspace{0.17em}\left(x\right)\hspace{0.17em}{G}_m\hspace{0.17em}\left(x\right)\hspace{0.17em}{x}^{-1}\hspace{0.17em}{\left(1-x\right)}^{-1}\hspace{0.17em}dx={\delta }_{n,m}\hspace{0.17em}\frac{n+1}{\left(n+2\right)\hspace{0.17em}\left(2n+3\right)}.$$

Using the completeness of the Jacobi polynomials, it can be shown that {G_n(x)} form a complete basis of L²([0,1], x⁻¹(1 − x)⁻¹).

For n ≥ 1, G_n(x) satisfies the recurrence relation

$$\begin{array}{l}x{G}_n\hspace{0.17em}\left(x\right)=\frac{n+1}{2\hspace{0.17em}\left(2n+3\right)}\hspace{0.17em}{G}_{n-1}\hspace{0.17em}\left(x\right)+\frac{1}{2}\hspace{0.17em}{G}_n\hspace{0.17em}\left(x\right)\\ \hspace{1em}+\frac{\left(n+1\right)\hspace{0.17em}\left(n+3\right)}{2\left(n+2\right)\left(2n+3\right)}\hspace{0.17em}{G}_{n+1}\hspace{0.17em}\left(x\right),\end{array}$$ (13)

while, for n = 0,

$$x\hspace{0.17em}{G}_0\hspace{0.17em}\left(x\right)=\frac{1}{2}\hspace{0.17em}{G}_0\hspace{0.17em}\left(x\right)+\frac{1}{4}\hspace{0.17em}{G}_1\hspace{0.17em}\left(x\right).$$

These relations follow from (10) and (11). Furthermore, we have G₀(x) ≡ −x(1−x).

Diffusions with Genic Selection and No Mutation

As described earlier, to obtain the spectral representation of p(t; x, y), we need to solve the eigenvalue problem for the diffusion generator. In this section, we illustrate the key ideas underlying our method by considering the simple case of no mutation and genic selection (h = 1/2), in which case the involved algebra simplifies significantly. Incidentally, the genic selection case has been considered by many other researchers in the past; for example, see Kimura (1955a, 1957), Etheridge and Griffiths (2009), and Griffiths (2003). The modified Gegenbauer polynomials introduced above will play an important role in this section. The case with both recurrent mutation and general diploid selection (i.e., h not necessarily equal to 1/2) is addressed in the next section.

Description of the main idea

Let ${\mathcal{L}}_0$ denote the diffusion part of the backward generator:

$${\mathcal{L}}_{0}f\left(x\right)=\frac{1}{2}\hspace{0.17em}x\hspace{0.17em}\left(1-x\right)\hspace{0.17em}\frac{{\partial }^2}{\partial x^2}\hspace{0.17em}\left\{f \left(x\right)\right\}.$$ (14)

As is well known (Kimura 1955a,b, 1957; Karlin and Taylor 1981), it follows from Equation 12 that the modified Gegenbauer polynomials G_n(x) are eigenfunctions of ${\mathcal{L}}_0$,

$${\mathcal{L}}_0{G}_n\hspace{0.17em}\left(x\right)=-{\lambda }_n\hspace{0.17em}{G}_n\hspace{0.17em}\left(x\right),$$

where

$${\lambda }_n=\left(\begin{array}{c}n+2\\ 2\end{array}\right).$$

With genic selection, the full backward generator is

$$\mathcal{L}\hspace{0.17em}f\hspace{0.17em}\left(x\right)=\frac{1}{2}\hspace{0.17em}x\hspace{0.17em}\left(1-x\right)\hspace{0.17em}\frac{{\partial }^2}{\partial x^2}\hspace{0.17em}\left\{f\left(x\right)\right\}+\sigma \hspace{0.17em}x\hspace{0.17em}\left(1-x\right)\hspace{0.17em}\frac{\partial }{\partial x}\hspace{0.17em}\left\{f\hspace{0.17em}\left(x\right)\right\}.$$ (15)

The speed density corresponding to this diffusion process is

$$\pi \hspace{0.17em}\left(x\right)=\frac{e^{2\hspace{0.17em}\sigma \hspace{0.17em}x}}{x\hspace{0.17em}\left(1-x\right)},$$ (16)

where we used x₀ = 0 and γ = 1 in (2) and (3), respectively.

Our goal is to find the eigenfunctions B_n(x) and the associated eigenvalues −Λ_n of the full generator $\mathcal{L}$:

$$\mathcal{L}{B}_n\hspace{0.17em}\left(x\right)=-{\Lambda }_n\hspace{0.17em}{B}_n\hspace{0.17em}\left(x\right).$$ (17)

As discussed in Background, $\mathcal{L}$ is self-adjoint with respect to the weight function π(x), which implies that its eigenfunctions B_n(x) and B_m(x), for n ≠ m, are orthogonal with respect to π(x); i.e.,

$${\displaystyle {\int }_0^1{B}_n}\hspace{0.17em}\left(x\right)\hspace{0.17em}{B}_m\hspace{0.17em}\left(x\right)\hspace{0.17em}\pi \hspace{0.17em}\left(x\right)\hspace{0.17em}dx\propto {\delta }_{n,m},$$

where π(x) is shown in (16). In addition to the eigenfunctions, there may exist other sets of functions that are orthogonal with respect to the same weight function π(y). For example, consider

$$H_n\hspace{0.17em}\left(x\right)=e^{-\sigma \hspace{0.17em}x}\hspace{0.17em}{G}_n\hspace{0.17em}\left(x\right).$$ (18)

We can verify that H_n(x) and H_m(x), for n ≠ m, are orthogonal with respect to the weight function π(x):

$$\begin{array}{c}{\displaystyle {\int }_0^1{H}_n}\hspace{0.17em}\left(x\right)\hspace{0.17em}{H}_m\hspace{0.17em}\left(x\right)\hspace{0.17em}\pi \hspace{0.17em}\left(x\right)\hspace{0.17em}\text{d}x={\displaystyle {\int }_0^1{G}_n}\hspace{0.17em}\left(x\right)\hspace{0.17em}{G}_n\hspace{0.17em}\left(x\right)\hspace{0.17em}{x}^{-1}\hspace{0.17em}{\left(1-x\right)}^{-1}\hspace{0.17em}dx\\ ={\delta }_{n,m}\hspace{0.17em}\frac{n+1}{\left(n+2\right)\hspace{0.17em}\left(2n+3\right)}.\end{array}$$

However, by directly applying $\mathcal{L}$ to H_n(x), one can check that H_n(x) are not eigenfunctions of $\mathcal{L}$. But, since both {H_n(x)} and {B_n(x)} are orthogonal with respect to the same weight function π(x), and {H_n(x)} form a basis of L²([0,1],π), we can represent B_n(x) as a linear combination of H_m(x),

$$B_n\hspace{0.17em}\left(x\right)=\stackrel{\mathrm{\infty }}{{\displaystyle \sum }_{m=0}}{u}_{n,m}\hspace{0.17em}{H}_m\hspace{0.17em}\left(x\right),$$ (19)

where u_n,m are constants to be determined. In the absence of mutation, states 0 and 1 are absorbing states (exit boundaries), so, as discussed in Background, B_n(x) must satisfy the boundary conditions lim_x↓0B_n(x) = lim_x↑1B_n(x) = 0. Indeed, our proposed eigenfunctions satisfy those conditions since H_m(0) = H_m(1) = 0 for all m ≥ 0.

Now, one can show

$$\begin{array}{c}\mathcal{L}{H}_n\hspace{0.17em}\left(x\right)=e^{-\sigma \hspace{0.17em}x}\hspace{0.17em}\left[{\mathcal{L}}_0\hspace{0.17em}{G}_n\hspace{0.17em}\left(x\right)-Q\hspace{0.17em}\left(x;\sigma \right)\hspace{0.17em}{G}_n\hspace{0.17em}\left(x\right)\right]\\ =-e^{-\sigma \hspace{0.17em}x}\hspace{0.17em}\left[{\lambda }_n\hspace{0.17em}{G}_n\hspace{0.17em}\left(x\right)+Q\hspace{0.17em}\left(x;\sigma \right)\hspace{0.17em}{G}_n\hspace{0.17em}\left(x\right)\right],\end{array}$$ (20)

where

$$Q\hspace{0.17em}\left(x;\sigma \right)=\frac{1}{2}{\sigma }^2\hspace{0.17em}x\hspace{0.17em}\left(1-x\right).$$ (21)

For small σ, Kimura (1955a) employed an equation similar to (20) to obtain perturbation expansions in powers of σ for the eigenvalues and the eigenfunctions of the forward diffusion generator. Here, we proceed along a different avenue. The key difference is that our approach is nonperturbative and that it is valid for all parameter values.

Using (20) together with (17) and (19), we obtain

$$\stackrel{\mathrm{\infty }}{{\displaystyle \sum }_{m=0}}{u}_{n,m}\hspace{0.17em}\left[{\lambda }_m+Q\hspace{0.17em}\left(x;\sigma \right)\right]\hspace{0.17em}{G}_m\hspace{0.17em}\left(x\right)={\Lambda }_n\hspace{0.17em}\stackrel{\mathrm{\infty }}{{\displaystyle \sum }_{m=0}}{u}_{n,m}\hspace{0.17em}{G}_m\hspace{0.17em}\left(x\right).$$ (22)

Now, for m ≥ 0, (13) can be used to show

$$Q\left(x;\sigma \right)G_m\left(x\right)=a_m^{\left(-2\right)}{G}_{m-2}\left(x\right)+a_m^{\left(0\right)}{G}_m\left(x\right)+a_m^{\left(+2\right)}{G}_{m+2}\left(x\right),$$

where

$$\begin{array}{l}{a}_m^{\left(-2\right)}=-{\sigma }^2\hspace{0.17em}\frac{1}{8}\hspace{0.17em}\frac{m\hspace{0.17em}\left(m+1\right)}{\left(2m+1\right)\hspace{0.17em}\left(2m+3\right)}\hspace{0.17em}{1}_{\{m\ge 2\}},\\ a_m^{\left(0\right)}=+{\sigma }^2\hspace{0.17em}\frac{1}{4}\hspace{0.17em}\frac{\left(m+1\right)\hspace{0.17em}\left(m+2\right)}{\left(2m+1\right)\hspace{0.17em}\left(2m+5\right)},\\ a_m^{\left(+2\right)}=-{\sigma }^2\hspace{0.17em}\frac{1}{8}\hspace{0.17em}\frac{\left(m+1\right)\hspace{0.17em}\left(m+4\right)}{\left(2m+3\right)\hspace{0.17em}\left(2m+5\right)}.\end{array}$$ (23)

In the first line of (23), 1_{Y} denotes an indicator function that is equal to 1 if statement Y is true or 0 otherwise. For a nonnegative integer k, multiplying (22) by G_k(x) and integrating over [0,1] with respect to the weight function x⁻¹(1 − x)⁻¹ yields

$${\lambda }_k\hspace{0.17em}{u}_{n,k}+a_{k+2}^{\left(-2\right)}\hspace{0.17em}{u}_{n,k+2}+a_k^{\left(0\right)}\hspace{0.17em}{u}_{n,k}+a_{k-2}^{\left(+2\right)}\hspace{0.17em}{u}_{n,k-2}={\Lambda }_n\hspace{0.17em}{u}_{n,k},$$ (24)

where we define $a_{-2}^{\left(+2\right)}=a_{-1}^{\left(+2\right)}=0.$ Note that (24) specifies a linear system of equations with u_n,0,u_n,1,u_n,2,…, as variables.

Algorithm 1 (genic selection)

The eigenvalues and eigenfunctions of the backward generator $\mathcal{L}$ (15) for the genic selection case can be obtained as follows. In matrix form, (24) can be written as

$$\begin{array}{l}\left(\begin{array}{cccccc}{\lambda }_0+a_0^{\left(0\right)}& 0& a_2^{\left(-2\right)}& 0& 0& \cdots \\ 0& {\lambda }_1+a_1^{\left(0\right)}& 0& a_3^{\left(-2\right)}& 0& \cdots \\ a_0^{\left(+2\right)}& 0& {\lambda }_2+a_2^{\left(0\right)}& 0& a_4^{\left(-2\right)}& \cdots \\ 0& a_1^{\left(+2\right)}& 0& {\lambda }_3+a_3^{\left(0\right)}& 0& \cdots \\ 0& 0& a_2^{\left(+2\right)}& 0& {\lambda }_4+a_4^{\left(0\right)}& \cdots \\ ⋮& ⋮& ⋮& ⋮& ⋮& \ddots \end{array}\right)\hspace{0.17em}\left(\begin{array}{c}{u}_{n,0}\\ u_{n,1}\\ u_{n,2}\\ u_{n,3}\\ u_{n,4}\\ ⋮\end{array}\right)\\ \hspace{1em}={\Lambda }_n\left(\begin{array}{c}{u}_{n,0}\\ u_{n,1}\\ u_{n,2}\\ u_{n,3}\\ u_{n,4}\\ ⋮\end{array}\right).\end{array}$$ (25)

Let M denote the infinite-dimensional matrix on the left hand side of (25). The key fact is that the eigenvalues Λ_n of M correspond to the eigenvalues of $\mathcal{L}$ (up to a sign), and the associated eigenvectors u_n = (u_n,0, u_n,1, u_n,2,…) of M determine the eigenfunctions of $\mathcal{L}$ via (19). Now, we consider a sequence of approximations by truncating (25). For a positive integer D, we let M^[D] be an D-by-D matrix obtained by taking the first D rows and the first D columns of M, and let ${\mathit{u}}_n^{\left(D\right)}=\left(u_{n,0}^{\left[D\right]},u_{n,1}^{\left[D\right]},\dots ,u_{n,D-1}^{\left[D\right]}\right)$. Then, we approximate (25) by

$$M^{\left[D\right]}\hspace{0.17em}{\mathit{u}}_n^{\left[D\right]}={\Lambda }_n^{\left[D\right]}\hspace{0.17em}{\mathit{u}}_n^{\left[D\right]}$$

and solve this finite-dimensional linear system to obtain eigenvalues ${\Lambda }_n^{\left[D\right]}$ and eigenvectors ${\mathbf{u}}_n^{\left[D\right]}.$ This linear algebra problem can be easily solved using standard software packages such as Matlab, Mathematica, or the freely available LAPACK library (http://www.netlib.org/lapack/). We show in Empirical Results that ${\Lambda }_n^{\left[D\right]}$ and $u_{n,m}^{\left[D\right]}$ converge very rapidly as the truncation level D increases.

The eigenvectors ${\mathbf{u}}_n^{\left[D\right]}$ come in two types: Either $u_{n,m}^{\left[D\right]}=0$ for all m even or $u_{n,m}^{\left[D\right]}=0$ for all m odd. In fact, the linear system $M^{\left[D\right]}\hspace{0.17em}{\mathbf{u}}_n^{\left[D\right]}={\Lambda }_n^{\left[D\right]}\hspace{0.17em}{\mathbf{u}}_n^{\left[D\right]}$ can be decomposed into two subsystems, one involving only the even rows and even columns of M^[D] acting on u_n,m for m odd, and the other involving only the odd rows and odd columns of M^[D] acting on u_n,m for m even. Hence, the eigenvalues and eigenvectors of M^[D], for D = 2D′, can be determined by solving two D′-dimensional linear systems.

In the case of genic selection with no recurrent mutation, the eigenfunctions B_n(x) of the backward generator $\mathcal{L}$ are also known as the oblate spheroidal functions in mathematical physics, and they have received considerable amounts of attention previously (e.g., see Stratton et al. 1941). Note that the algorithm presented in this section provides an efficient way to evaluate these functions, a problem that remained difficult in the past.

Due to the exponential weighting factors in the speed density (16) and in the basis functions (18) for the eigenfunction expansion, evaluation of the transition density for large selection coefficients involves combining quantities with substantially different orders of magnitude. Thus, to obtain accurate numerical values of the transition density under strong selection, the coefficients ${\mathbf{u}}_n^{\left[D\right]}$ must be determined with high precision.

Diffusions with General Diploid Selection and Recurrent Mutation

In this section, we generalize the method developed in the previous section by incorporating recurrent mutation and general diploid selection into the diffusion process. The same overall strategy described above applies here as well. The main computational differences are that general diploid selection leads to more involved algebra and that, to handle recurrent mutation, we need to deal with general Jacobi polynomials instead of the modified Gegenbauer polynomials.

Neutral diffusion with recurrent mutation

For a neutral diallelic model with recurrent mutation, the backward generator ${\mathcal{L}}_0$ is given by

$${\mathcal{L}}_0\hspace{0.17em}f\left(x\right)=\frac{1}{2}\hspace{0.17em}x\hspace{0.17em}\left(1-x\right)\hspace{0.17em}\frac{{\partial }^2}{\partial x^2}\hspace{0.17em}\left\{f\hspace{0.17em}\left(x\right)\right\}+\frac{1}{2}\hspace{0.17em}\left[\alpha \hspace{0.17em}\left(1-x\right)-\beta \hspace{0.17em}x\right]\hspace{0.17em}\frac{\partial }{\partial x}\hspace{0.17em}\left\{f\hspace{0.17em}\left(x\right)\right\}.$$ (26)

See Background for the definitions of α and β. By appropriately choosing the constants x₀ and γ in (2) and (3), the speed density corresponding to this diffusion can be defined as

$${\pi }_0\hspace{0.17em}\left(x\right)=x^{\alpha -1} {\left(1-x\right)}^{\beta -1},$$ (27)

which is the unnormalized Beta distribution. It can be shown (see Karlin and Taylor 1981, Chap. 15.13, or compare with Equation 7) that the Jacobi polynomials $R_n^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)$ are eigenfunctions of the backward generator ${\mathcal{L}}_0$ with eigenvalues $-{\lambda }_n^{\left(\alpha ,\beta \right)}$, where

$${\lambda }_n^{\left(\alpha ,\beta \right)}=\frac{1}{2}\hspace{0.17em}n\hspace{0.17em}\left(n+\alpha +\beta -1\right).$$ (28)

Furthermore, the Jacobi polynomials $R_n^{\left(\alpha ,\beta \right)}\left(x\right)$ form an orthogonal system with respect to the weight function π₀(x). Under recurrent mutation, the diffusion exhibits either regular or entrance boundaries (e.g., see Karlin and Taylor 1981, Chap. 15.6, Example 8). The respective conditions given in Background for x = 0 and x = 1 imply that the eigenfunctions ϕ(x) of ${\mathcal{L}}_0$ need to satisfy

$$\underset{x\downarrow 0}{\text{lim}}{x}^{\alpha }\hspace{0.17em}\frac{\partial }{\partial x}\hspace{0.17em}\left\{\phi \hspace{0.17em}\left(x\right)\right\}=0\hspace{1em}\text{and}\hspace{1em}\underset{x\uparrow 1}{\text{lim}}{\left(1-x\right)}^{\beta }\hspace{0.17em}\frac{\partial }{\partial x}\hspace{0.17em}\left\{\phi \hspace{0.17em}\left(x\right)\right\}=0,$$

and the modified Jacobi polynomials $R_n^{\text{(α,β)}}\text{(}x\text{)}$ obey these conditions.

Adding general diploid selection

The backward generator of the diffusion process with recurrent mutation and general diploid selection is

$$\mathcal{L}f\hspace{0.17em}\left(x\right)={\mathcal{L}}_{0}f\hspace{0.17em}\left(x\right)+2\hspace{0.17em}\sigma \hspace{0.17em}x\hspace{0.17em}\left(1-x\right)\hspace{0.17em}\left[x+h\hspace{0.17em}\left(1-2\hspace{0.17em}x\right)\right]\frac{\partial }{\partial x}\left\{f\hspace{0.17em}\left(x\right)\right\},$$ (29)

where ${\mathcal{L}}_{0}f\left(x\right)$ is the selectively neutral part shown in (26). With appropriate constants x₀ and γ in (2) and (3), the speed density for this diffusion can be defined as

$$\pi \hspace{0.17em}\left(x\right)=e^{\overline{\sigma }\hspace{0.17em}\left(x\right)}\hspace{0.17em}{\pi }_0\hspace{0.17em}\left(x\right),$$ (30)

where π₀(x) is given in (27) and $\overline{\sigma }\hspace{0.17em}\left(x\right)$ is the mean fitness function given by

$$\overline{\sigma }\hspace{0.17em}\left(x\right)=2\hspace{0.17em}h\hspace{0.17em}\sigma \cdot 2\hspace{0.17em}\left(1-x\right)\hspace{0.17em}x+2\hspace{0.17em}\sigma \cdot x^2=2\hspace{0.17em}\sigma \hspace{0.17em}x\hspace{0.17em}\left[x+2\hspace{0.17em}h\hspace{0.17em}\left(1-x\right)\right],$$ (31)

which simplifies to the linear function 2σx for h = 1/2. The discussion in Background implies that the full backward generator $\mathcal{L}$ is self-adjoint with respect to the weight function π(x), and that its eigenfunctions {B_n(x)} form an orthogonal system with respect to the same weight function. Now, if we define K_n(x) as

$$K_n\hspace{0.17em}\left(x\right)=e^{-\overline{\sigma }\hspace{0.17em}\left(x\right)/2}\hspace{0.17em}{R}_n^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right),$$ (32)

then (8) implies that {K_n(x)} is a complete system of orthogonal functions with respect to the weight function π(x). However, by applying the generator $\mathcal{L}$ to K_n(x), one can show that K_n(x) is not an eigenfunction of $\mathcal{L}$. Rather, we obtain

$$\begin{array}{c}\mathcal{L}\hspace{0.17em}{K}_n\hspace{0.17em}\left(x\right)=e^{-\overline{\sigma }\hspace{0.17em}\left(x\right)/2}\hspace{0.17em}\left\{{\mathcal{L}}_0\hspace{0.17em}{R}_n^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)-Q\hspace{0.17em}\left(x;\alpha ,\beta ,\sigma ,h\right)\hspace{0.17em}{R}_n^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)\right\}\\ \hspace{1em}\hspace{0.5em}\hspace{0.17em}=-e^{-\overline{\sigma }\hspace{0.17em}\left(x\right)/2}\hspace{0.17em}\left[{\lambda }_n^{\left(\alpha ,\beta \right)}\hspace{0.17em}{R}_n^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)+Q\hspace{0.17em}\left(x;\alpha ,\beta ,\sigma ,h\right)\hspace{0.17em}{R}_n^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)\right],\end{array}$$

where Q(x;α,β,σ,h) is the following degree-4 polynomial in x:

$$\begin{array}{l}Q\hspace{0.17em}\left(x;\alpha ,\beta ,\sigma ,h\right)=\sigma \hspace{0.17em}\left\{h\hspace{0.17em}\alpha +\left[1+\alpha -\left(2+3\hspace{0.17em}\alpha +\beta \right)\hspace{0.17em}h\right]\hspace{0.17em}x-\left(1+\alpha +\beta \right)\hspace{0.17em}\left(1-2\hspace{0.17em}h\right)\hspace{0.17em}{x}^2\right\}\\ \hspace{1em}+2\hspace{0.17em}{\sigma }^2\hspace{0.17em}x\hspace{0.17em}\left(1-x\right)\hspace{0.17em}{\left(h+x-2\hspace{0.17em}hx\right)}^2.\end{array}$$ (33)

For no recurrent mutation (α = β = 0) we get (1 − x)xσ[1 − 2h + 2(h + x −2hx)²σ], and for h = 1/2 (genic selection), (33) reduces to a degree-2 polynomial: $\frac{1}{2}\hspace{0.17em}\left\{\sigma \hspace{0.17em}\left[-\beta \hspace{0.17em}x+\alpha \hspace{0.17em}\left(1-x\right)\right]+{\sigma }^2\hspace{0.17em}x\hspace{0.17em}\left(1-x\right)\right\}.$ In the case of just drift and genic selection, we obtain $\frac{1}{2}\hspace{0.17em}{\sigma }^2\hspace{0.17em}x\hspace{0.17em}\left(1-x\right)$ as in (21).

Again, {B_n(x)} and {K_n(x)} are orthogonal with respect to the same weight function π(x), and {K_n(x)} form a basis of L²([0,1],π), where π is defined in (30). Hence, we pose a representation for the eigenfunctions of the form

$$B_n\hspace{0.17em}\left(x\right)=\stackrel{\mathrm{\infty }}{{\displaystyle \sum }_{m=0}}{w}_{n,m}\hspace{0.17em}{K}_m\hspace{0.17em}\left(x\right)=\stackrel{\mathrm{\infty }}{{\displaystyle \sum }_{m=0}}{w}_{n,m}\hspace{0.17em}{e}^{-\overline{\sigma }\hspace{0.17em}\left(x\right)/2}\hspace{0.17em}{R}_m^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right),$$ (34)

where w_n,m are constants to be determined. It can be checked that $K_m\hspace{0.17em}\left(x\right)=e^{-\overline{\sigma }\hspace{0.17em}\left(x\right)/2}\hspace{0.17em}{R}_m^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)$, for all m ≥ 0, satisfies the proper regular reflecting or entrance boundary conditions, and hence so does B_n(x).

Now, $\mathcal{L}{B}_n\left(x\right)\hspace{0.17em}=\hspace{0.17em}\mathrm{-}{\mathrm{\Lambda }}_n{B}_n\left(x\right)$ implies the following algebraic equation:

$$\stackrel{\mathrm{\infty }}{{\displaystyle \sum }_{m=0}}{w}_{n,m}\hspace{0.17em}\left[{\lambda }_m^{\left(\alpha ,\beta \right)}+Q\hspace{0.17em}\left(x;\alpha ,\beta ,\sigma ,h\right)\right]\hspace{0.17em}{R}_m^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)={\Lambda }_n\hspace{0.17em}\stackrel{\mathrm{\infty }}{{\displaystyle \sum }_{m=0}}{w}_{n,m}\hspace{0.17em}{R}_m^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right).$$ (35)

Using (10), we can represent $Q\hspace{0.17em}\left(x;\alpha ,\beta ,\sigma ,h\right)\hspace{0.17em}{R}_n^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)$ as a finite linear combination of $R_j^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)$:

$$\begin{array}{l}Q\hspace{0.17em}\left(x;\alpha ,\beta ,\sigma ,h\right)\hspace{0.17em}{R}_m^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)=b_m^{\left(-4\right)}\hspace{0.17em}{R}_{m-4}^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)+b_m^{\left(-3\right)}\hspace{0.17em}{R}_{m-3}^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)\\ \hspace{1em}+\cdots +b_m^{\left(+3\right)}\hspace{0.17em}{R}_{m+3}^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)+b_m^{\left(+4\right)}\hspace{0.17em}{R}_{m+4}^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right),\end{array}$$ (36)

where the coefficients $b_m^{\left(i\right)}$ are constants that depend on m, α, β, σ, and h.

For a nonnegative integer k, multiplying (35) by $R_k^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)$ and integrating over [0,1] with respect to the weight function π₀(x) yields

$${\lambda }_k^{(\alpha ,\beta )}\hspace{0.17em}{w}_{n,k}+b_{k+4}^{\left(-4\right)}\hspace{0.17em}{w}_{n,k+4}+b_{k+3}^{\left(-3\right)}\hspace{0.17em}{w}_{n,k+3}+\cdots +b_{k-3}^{(+3)}\hspace{0.17em}{w}_{n,k-3}+b_{k-4}^{\left(+4\right)}\hspace{0.17em}{w}_{n,k-4}={\Lambda }_n\hspace{0.17em}{w}_{n,k},$$ (37)

where we define $b_j^{\left(i\right)}=0$ if j < 0.

Algorithm 2 (recurrent mutation and general diploid selection)

We can now describe our algorithm for finding the eigenvalues and eigenfunctions of the backward generator $\mathcal{L}$ defined in (29) for the case with recurrent mutation and general diploid selection. From (37), we arrive at a linear system M w_n = Λ_n w_n, where w_n = (w_n,0,w_n,1,w_n,2,…) is an infinite-dimensional vector of variables and M is an infinite-dimensional matrix given by

$$M=\left(\begin{array}{cccccccc}{\lambda }_0^{(\alpha ,\beta )}+b_0^{(0)}& b_1^{(-1)}& b_2^{(-2)}& b_3^{(-3)}& b_4^{(-4)}& 0& 0& \cdots \\ b_0^{(+1)}& {\lambda }_1^{(\alpha ,\beta )}+b_1^{(0)}& b_2^{(-1)}& b_3^{(-2)}& b_4^{(-3)}& b_5^{(-4)}& 0& \cdots \\ b_0^{(+2)}& b_1^{(+1)}& {\lambda }_2^{(\alpha ,\beta )}+b_2^{(0)}& b_3^{(-1)}& b_4^{(-2)}& b_5^{(-3)}& b_6^{(-4)}& \cdots \\ b_0^{(+3)}& b_1^{(+2)}& b_2^{(+1)}& {\lambda }_3^{(\alpha ,\beta )}+b_3^{(0)}& b_4^{(-1)}& b_5^{(-2)}& b_6^{(-3)}& \cdots \\ b_0^{(+4)}& b_1^{(+3)}& b_2^{(+2)}& b_3^{(+1)}& {\lambda }_4^{(\alpha ,\beta )}+b_4^{(0)}& b_5^{(-1)}& b_6^{(-2)}& \cdots \\ 0& b_1^{(+4)}& b_2^{(+3)}& b_3^{(+2)}& b_4^{(+1)}& {\lambda }_5^{(\alpha ,\beta )}+b_5^{(0)}& b_6^{(-1)}& \cdots \\ 0& 0& b_2^{(+4)}& b_3^{(+3)}& b_4^{(+2)}& b_5^{(1)}& {\lambda }_6^{(\alpha ,\beta )}+b_6^{(0)}& \cdots \\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \ddots \end{array}\right)$$

Closed-form formulas for $b_m^{\left(i\right)}$ can be found easily using symbolic computation software such as Mathematica. In the Appendix, we provide a dynamic programming algorithm for computing $b_m^{\left(i\right)}$ which is useful for implementation in an imperative programming language such as C/C++. If h = 1/2, $b_m^{\left(-4\right)}=b_m^{\left(-3\right)}=b_m^{\left(+3\right)}=b_m^{\left(+4\right)}=0$ for all m ≥ 0, and therefore only the innermost five diagonals of M will be nonzero. As in Algorithm 1, we approximate Mw_n = Λ_n w_n by a finite-dimensional truncated linear system

$$M^{\left[D\right]}\hspace{0.17em}{\mathbf{w}}_n^{\left[D\right]}={\Lambda }_n^{\left[D\right]}\hspace{0.17em}{\mathbf{w}}_n^{\left[D\right]},$$

where ${\mathbf{w}}_n^{\left(D\right)}=\left(w_{n,0}^{\left[D\right]},w_{n,1}^{\left[D\right]},\dots ,w_{n,D-1}^{\left[D\right]}\right)$ and M^[D] is the submatrix of M consisting of its first D rows and D columns. This finite-dimensional linear system can be easily solved to obtain the eigenvalues ${\Lambda }_n^{\left[D\right]}$ and the eigenvectors ${\mathbf{w}}_n^{\left[D\right]}$ of M^[D]. We show in Empirical Results that ${\Lambda }_n^{\left[D\right]}$ and $w_{n,m}^{\left[D\right]}$ converge very rapidly as the truncation level D increases.

Note that the same cautionary remark mentioned at the end of Algorithm 1 also applies here.

Special case: No recurrent mutation

Let ${\mathcal{L}}_0$ denote the diffusion generator defined in (14), which can be obtained from (26) by setting α = β = 0. Since $R_0^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)\equiv 1$, it satisfies ${\mathcal{L}}_{0}B\hspace{0.17em}=\hspace{0.17em}\mathrm{-}\mathit{\lambda }B$ with λ = 0. However, for α = β = 0, the boundaries are exit boundaries, and therefore $R_0^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)$ does not satisfy the requisite boundary conditions. Furthermore, $R_1^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)=\beta x-\alpha \hspace{0.17em}\left(1-x\right)\to 0$ as α, β → 0, so it is not of interest. In contrast, for n ≥ 0, $R_{n+2}^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)$ converges to G_n(x) as α, β → 0, and, as established in Background, G_n(x) satisfies ${\mathcal{L}}_{0}B\hspace{0.17em}=\hspace{0.17em}\mathrm{-}\mathit{\lambda }B$ with $\lambda ={\lambda }_{n+2}^{\left(0,0\right)}$ and satisfies the requisite boundary conditions for α = β = 0. In summary, as α, β → 0, the first two modified Jacobi polynomials become irrelevant, while the rest converge to the appropriate eigenfunctions of ${\mathcal{L}}_0$. These facts have been noticed before (e.g., see Griffiths and Spanò 2010), and they allow us to embed the model with no recurrent mutation conveniently into the model with recurrent mutation as described below.

If α = β = 0, let Λ_n and w_n = (w_n,0,w_n,1,…), respectively, denote the eigenvalues and eigenvectors of M′, the submatrix of M obtained by omitting the first two rows and the first two columns. Defining $K_m\hspace{0.17em}\left(x\right):=e^{\overline{\sigma }}\hspace{0.17em}\left(x\right)/2\hspace{0.17em}{G}_m\hspace{0.17em}\left(x\right)$ (instead of Equation 32) yields the eigenvalues Λ_n and the eigenfunctions B_n(x) for the backward diffusion generator with a general diploid selection model but no recurrent mutation. Indeed, under genic selection (h = 1/2) and α = β = 0, one can show that $b_{m+2}^{\left(-4\right)}=b_{m+2}^{\left(-3\right)}=b_{m+2}^{\left(-1\right)}=b_{m+2}^{\left(+1\right)}=b_{m+2}^{\left(+3\right)}=b_{m+2}^{\left(+4\right)}=0$, while $b_{m+2}^{\left(-2\right)}=a_m^{\left(-2\right)}$, $b_{m+2}^{\left(0\right)}=a_m^{\left(0\right)}$, and $b_{m+2}^{\left(+2\right)}=a_m^{\left(+2\right)}$, where $a_j^{\left(i\right)}$ are defined in (23). The cases α > 0, β = 0 and α = 0, β > 0 can be treated along similar lines.

Empirical Results

In this section we study the convergence behavior of the eigenvalues and eigenvectors of the submatrix M^[D] as its dimension D increases. Further, we show how the spectral representation of the transition density can be employed to characterize the convergence rate of the diffusion to stationarity, i.e., mutation–selection equilibrium.

Convergence of the eigenvalues and eigenfunctions

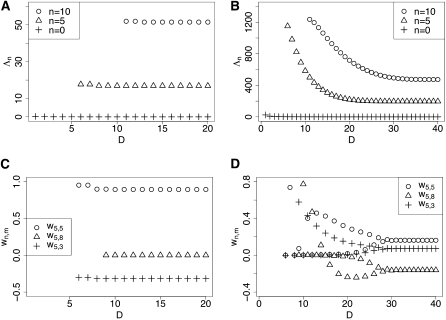
As the dimension D of the submatrix M^[D] increases, we generally observe rapid convergence of the eigenvalues ${\Lambda }_n^{\left[D\right]}$ and the entries $w_{n,m}^{\left[D\right]}$ of the eigenvectors, for fixed n,m < D. For example, the convergence behavior of ${\Lambda }_0^{\left[D\right]},{\Lambda }_5^{\left[D\right]},{\Lambda }_{10}^{\left[D\right]}$ is shown in Figure 1, A and B, for σ = 10 and σ = 100, respectively, with mutation parameters α = 0.01, β = 0.01 and the dominance parameter h = 1/2. Figure 1, A and B, illustrates that, for both σ = 10 and σ = 100, ${\Lambda }_0^{\left[D\right]}$ converges rapidly to 0 as D increases, consistent with our expectation (see below). The figures illustrate that in general ${\Lambda }_n^{\left[D\right]}$ converges rapidly for a wide range of σ values, but that the convergence rate slows down as σ increases. For α and β in biologically relevant ranges (say, 10⁻³ to 10⁻¹), we generally observe that changing the mutational parameters does not affect the convergence behavior significantly. Also, the dominance parameter h has little influence on the convergence rate provided that 0 ≤ h ≤ 1.

Figure 1 .

Convergence of the eigenvalues ${\Lambda }_n^{\left[D\right]}$ and coefficients $w_{n,m}^{\left[D\right]}$ with increasing truncation level D. The mutation rates are set to α = β = 0.01 and the dominance parameter h = 0.5. (A) ${\Lambda }_0^{\left[D\right]},{\Lambda }_5^{\left[D\right]},{\Lambda }_{10}^{\left[D\right]}$ for σ = 10. (B) ${\Lambda }_0^{\left[D\right]},{\Lambda }_5^{\left[D\right]},{\Lambda }_{10}^{\left[D\right]}$ for σ = 100. (C) $w_{5,3}^{\left[D\right]},w_{5,5}^{\left[D\right]},w_{5,8}^{\left[D\right]}$ for σ = 10. (D) $w_{5,3}^{\left[D\right]},w_{5,5}^{\left[D\right]},w_{5,8}^{\left[D\right]}$ for σ = 100.

The typical convergence behavior of the eigenvector entries $w_{n,m}^{\left[D\right]}$ is illustrated in Figure 1, C and D, for σ = 10 and σ = 100, respectively. As Figure 1C shows, the rate of convergence is very fast for small σ. For large σ, as in Figure 1D, $w_{n,m}^{\left[D\right]}$ may fluctuate for small values of D, but they stabilize rapidly as D increases. In general, we observe that the convergence of ${\Lambda }_n^{\left[D\right]}$ and that of $w_{n,m}^{\left[D\right]}$ are roughly synchronized; i.e., for a fixed n, Λ_n and $w_{n,m}^{\left[D\right]}$ stabilize near similar values of D.

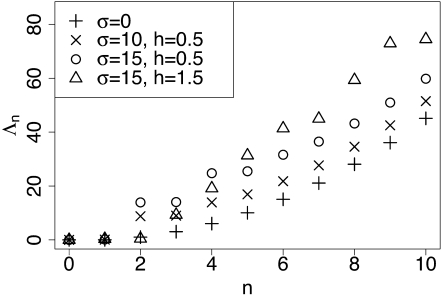
Figure 2 shows the dependence of ${\Lambda }_n^{\left[D\right]}$ on σ, h, and n. Observe that ${\Lambda }_n^{\left[D\right]}$ increases rapidly as n increases, which implies that using a finite number of terms in the spectral representation of the transition density should yield an accurate approximation of the true transition density. Increasing σ or choosing h significantly different from 0.5 (the genic selection case) shifts the entire spectrum upward, but in all cases we observe that ${\Lambda }_n^{\left[D\right]}$ increases rapidly with n.

Figure 2 .

Magnitude of the eigenvalues {−Λ_n} of the diffusion generator $\mathcal{L}$ for α = 0.01, β = 0.01, and various values of the selection coefficient σ and the dominance parameter h. The truncation level D was set to 400. Note that Λ_n gets larger with increasing n, a general trend that holds for other parameter settings. Also, Λ_n increases when selection gets stronger. For σ = 0, note that ${\Lambda }_n={\lambda }_n^{\left(\alpha ,\beta \right)}$, defined in (28).

Empirical transition densities and stationary distributions

For given mutation and selection parameters, the eigenvalues −Λ_n and the eigenfunctions B_n(x) found by our method can be used to obtain the transition density via the spectral representation (5), for arbitrary t > 0 and x, y ∈ [0,1]. This representation includes the stationary density, which admits a more explicit analytic form. To this end, note that a diffusion generator $\mathcal{L}$ maps constant functions to zero. In the case with recurrent mutation, we have either regular reflecting or entrance boundaries, and constant functions actually satisfy the requisite boundary conditions. Hence, constant functions are valid eigenfunctions of $\mathcal{L}$ with eigenvalue zero. That is, Λ₀ = 0 and B₀(x) = C, where C is some constant, for all x ∈ [0,1]. Thus, the density of the stationary measure is given by

$$\begin{array}{c}\underset{t\to \mathrm{\infty }}{\text{lim}}p\hspace{0.17em}\left(t;x,y\right)=\pi \hspace{0.17em}\left(y\right)\hspace{0.17em}\frac{B_0\hspace{0.17em}\left(x\right)\hspace{0.17em}{B}_0\hspace{0.17em}\left(y\right)}{{\langle B_0,B_0\rangle }_{\pi }}=\pi \hspace{0.17em}\left(y\right)\hspace{0.17em}\frac{C^2}{{\langle C,C\rangle }_{\pi }}\\ =\frac{\pi \hspace{0.17em}\left(y\right)}{{{\displaystyle \int }}_0^1\pi \hspace{0.17em}\left(z\right)\hspace{0.17em}\text{d}\hspace{0.17em}z},\end{array}$$

where $\pi \hspace{0.17em}\left(y\right)=e^{\overline{\sigma }\hspace{0.17em}\left(y\right)}\hspace{0.17em}{\pi }_0\hspace{0.17em}\left(y\right)$ is the speed density defined in (30). The integral in the denominator (which corresponds to a normalization constant for the stationary density) can be solved efficiently using our approach: Since B₀ is a constant function, we can express the integral as

$${\displaystyle {\int }_0^1\pi }\hspace{0.17em}\left(z\right)\hspace{0.17em}\text{d}\hspace{0.17em}z=\frac{{\mathrm{\langle }{B}_0,B_0\mathrm{\rangle }}_{\pi }}{B_0\hspace{0.17em}\left(1\right)\hspace{0.17em}{B}_0\hspace{0.17em}\left(1\right)}.$$

Then, using the representation

$$B_0\hspace{0.17em}\left(x\right)=\stackrel{\mathrm{\infty }}{{\displaystyle \sum }_{m=0}}{w}_{0,m}\hspace{0.17em}{e}^{-\overline{\sigma }\hspace{0.17em}\left(x\right)/2}\hspace{0.17em}{R}_m^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right),$$

and the facts $\overline{\sigma }\hspace{0.17em}\left(1\right)=2\hspace{0.17em}\sigma$ [cf., (31)] and $R_n^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(1\right)=\Gamma \hspace{0.17em}\left(n+\beta \right)/[\Gamma \hspace{0.17em}\left(n+1\right)\hspace{0.17em}\Gamma \hspace{0.17em}\left(\beta \right)]$, we obtain

$$\begin{array}{c}{\displaystyle {\int }_0^1\pi }\hspace{0.17em}\left(z\right)\hspace{0.17em}\text{d}\hspace{0.17em}z=\frac{{{\displaystyle \sum }}_{m=0}^{\mathrm{\infty }}{\left(w_{0,m}\right)}^2\hspace{0.17em}{\langle R_m^{\left(\alpha ,\beta \right)},R_m^{\left(\alpha ,\beta \right)}\rangle }_{{\pi }_0}}{e^{-\overline{\sigma }\hspace{0.17em}\left(1\right)}\hspace{0.17em}{\left[{{\displaystyle \sum }}_{k=0}^{\mathrm{\infty }}{w}_{0,k}\hspace{0.17em}{R}_k^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(1\right)\right]}^2}\\ =\frac{{{\displaystyle \sum }}_{m=0}^{\mathrm{\infty }}{\left(w_{0,m}\right)}^2\hspace{0.17em}{\Delta }_m\hspace{0.17em}\left(\alpha ,\beta \right)}{e^{-2\sigma }\hspace{0.17em}{\left[{{\displaystyle \sum }}_{k=0}^{\mathrm{\infty }}{w}_{0,k}\hspace{0.17em}\frac{\Gamma \hspace{0.17em}\left(k+\beta \right)}{\Gamma \left(k+1\right)\hspace{0.17em}\Gamma \left(\beta \right)}\right]}^2},\end{array}$$ (38)

where Δ_m(α,β) is the combinatorial coefficient defined in (9). Thus, the integral can be evaluated purely algebraically. For a fixed n, w_n,m → 0 as m → ∞, so we can obtain an accurate approximation of (38) by truncating the infinite sums and by computing w_0,m using the method described in this article. In special cases, the integral ${\displaystyle {\int }_0^1\pi }\hspace{0.17em}\left(z\right)\hspace{0.17em}\text{d}\hspace{0.17em}z$ can be evaluated numerically using other methods (e.g., see Wakeley and Sargsyan 2009), but, for general σ and h, standard numerical integration techniques do not seem to provide accurate answers.

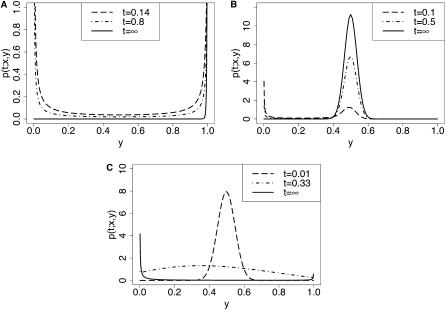
Figure 3 shows some examples of the time evolution of the transition density function, with the t = ∞ case corresponding to the stationary distribution. Specifically, three different types of selection schemes are illustrated:

Figure 3 .

The transition density p(t;x,y) as a function of y. Various times, selection parameters, and initial frequencies were considered. The mutation rates were set to α = β = 0.01 in all examples. The t = ∞ case corresponds to the stationary distribution. A truncation level of D = 1000 was used in the computation, and Equations 5 and 34 were approximated by summing over 0 ≤ n ≤ 300 and 0 ≤ m ≤ 500. (A) Strong positive selection: σ = 100, h = 0.5, x = 0.0005. (B) Balancing selection: σ = 0.01, h = 10000, x = 0.0005. (C) Weakly deleterious selection: σ = −1, h = 0.5, x = 0.5.

1. Illustrated in Figure 3A are the densities for strong positive selection (σ = 100, h = 0.5), when starting with a small initial frequency of x = 0.0005. As expected, for small t there is still some probability mass near 0, but already a substantial amount has moved to 1. At stationarity, the mass is concentrated at the boundaries, with the concentration near 1 being far more pronounced than that near 0.

2. Figure 3B shows the dynamics of balancing selection (σ = 0.01, h = 10000), starting from initial frequency x = 0.0005. As time evolves, the mass gets shifted from the boundary at 0 to an intermediate frequency of y = 0.5, where a large fraction of probability mass resides at stationarity.

3. In Figure 3C, the allele A₁ exhibits weakly deleterious selection (σ = −1, h = 0.5), with the initial frequency being x = 0.5. Initially most of the probability mass is concentrated around frequency y = 0.5. As the density evolves with time, it spreads out over the interval, and the peak of the density moves to lower frequencies. At stationarity, most of the mass is concentrated around the boundary at 0.

Rate of convergence to the stationary distribution

The spectral representation also allows us to obtain the rate of convergence to the stationary density. The difference d(t; x, y) between the transition density and the stationary density is given by

$$d\hspace{0.17em}\left(t;x,y\right):=p\hspace{0.17em}\left(t;x,y\right)-\frac{\pi \hspace{0.17em}\left(y\right)}{{{\displaystyle \int }}_0^1\pi \hspace{0.17em}\left(z\right)\hspace{0.17em}\text{d}\hspace{0.17em}z}=\stackrel{\mathrm{\infty }}{{\displaystyle \sum }_{n=1}}{e}^{-{\Lambda }_n\hspace{0.17em}t}\hspace{0.17em}\pi \hspace{0.17em}\left(y\right)\hspace{0.17em}\frac{B_n\hspace{0.17em}\left(x\right)\hspace{0.17em}{B}_n\hspace{0.17em}\left(y\right)}{{\langle B_n,B_n\rangle }_{\pi }}.$$

Define ${\Vert f\Vert }_{1/\pi }=\sqrt{{\langle f,f\rangle }_{1/\pi }}$. Then, by orthogonality of the eigenfunctions, we obtain

$$\begin{array}{c}{\Vert d\left(t;x,\cdot \right)\Vert }_{1/\pi }^2=\stackrel{\mathrm{\infty }}{{\displaystyle \sum }_{n=1}}{e}^{-2\hspace{0.17em}{\Lambda }_n\hspace{0.17em}t}\frac{{\left[B_n\hspace{0.17em}\left(x\right)\right]}^2}{{\langle B_n,B_n\rangle }_{\pi }}\\ =\stackrel{\mathrm{\infty }}{{\displaystyle \sum }_{n=1}}{e}^{-2\hspace{0.17em}{\Lambda }_n\hspace{0.17em}t}\frac{e^{-\overline{\sigma }\hspace{0.17em}\left(x\right)}\hspace{0.17em}{\left[{{\displaystyle \sum }}_{k=0}^{\mathrm{\infty }}{w}_{n,k}\hspace{0.17em}{R}_k^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)\right]}^2}{{{\displaystyle \sum }}_{m=0}^{\mathrm{\infty }}{\left(w_{n,m}\right)}^2\hspace{0.17em}{\Delta }_m\hspace{0.17em}\left(\alpha ,\beta \right)},\end{array}$$ (39)

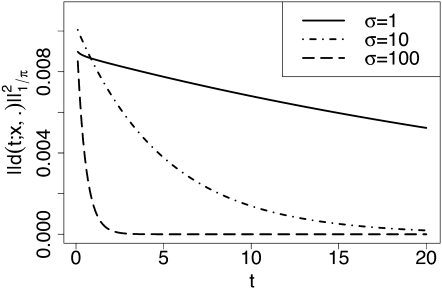
which can be approximated by truncating the infinite sums. Figure 4 shows the dependence of $\parallel d(t;x,\cdot ){\parallel }_{1/\pi }^2$ on time t, for α = 0.01, β = 0.01, h = 0.5, σ∈{1,10,100}, and initial frequency x = 0.0005. As expected, the distance to the stationary distribution decreases over time, and the rate of convergence is faster for larger σ. We note that the spectral representation can also be readily employed to study convergence rates measured by other metrics such as the total variation distance or relative entropy.

Figure 4 .

Convergence of the transition density to stationarity as time evolves, for initial frequency x = 0.0005. Deviation from the stationary density is measured by $\parallel d(t;x,\cdot ){\parallel }_{1/\pi }^2$, defined in (39). The mutation and selection parameters were set to α = 0.01, β = 0.01, h = 0.5, and σ ∈{1,10,100}. A truncation level of D = 1000 was used in the computation, and (39) was approximated by summing over 0 ≤ n ≤ 300 and 0 ≤ k, m ≤ 500.

Discussion

In this article, we developed a simple method for finding the eigenvalues and eigenfunctions of the diffusion generator associated with the Wright–Fisher diffusion with recurrent mutation and general diploid selection. As described in Background, these eigenvalues and eigenfunctions can be used to construct a spectral representation (5) of the transition density. Since the eigenvalues −Λ_n tend to −∞ as n → ∞, and the contribution of the nth eigenfunction to the transition density is proportional to $e^{-{\Lambda }_n\hspace{0.17em}t}$, we can truncate the series (5) at some appropriate level and obtain a highly accurate approximation of the transition density. The mathematical derivation of our work invokes the theory of self-adjoint operators and orthogonal functions, but the resulting algorithm involves only standard linear algebra, which is straightforward to implement. For a given set of parameters, computing the first 500 eigenvalues and eigenfunctions using our method takes only a few seconds in Mathematica.

An accurate transition density enables one to estimate the parameters of Wright–Fisher diffusions, perhaps most interestingly the selection parameters. As mentioned in the Introduction, Bollback et al. (2008) suggested a hidden Markov model framework for estimating the selection coefficient σ by analyzing samples taken from multiple time points. The analytic transition density obtained from our method can be incorporated into that framework and thereby ameliorate potential numerical problems that may arise from trying to solve the Kolmogorov equation using discretization. Furthermore, our approach can be applied to devise an algebraic method for computing the sampling probability at stationarity under a general selection model.

There are several interesting extensions of our work to explore. It is known (Shimakura 1977; Griffiths 1979; Griffiths and Spanò 2010) that multivariate Jacobi polynomials, orthogonal with respect to the Dirichlet distribution, are eigenfunctions of multiallelic diffusions under parent-independent mutation models. We believe that the technique developed in this article can be extended to find the spectral representation of the transition density of a multiallelic diffusion with parent-independent mutation and general diploid selection.

For a neutral diallelic Wright–Fisher model with subdivided population structure, Lukić et al. (2011) recently obtained numerical approximations of the transition density by using a certain class of orthogonal polynomials. We remark that the orthogonal polynomials used in that approach are not eigenfunctions of the diffusion generator. Further, the system of ordinary differential equations (ODEs) satisfied by the coefficients of the basis functions does not admit a simple solution, so Lukić et al. (2011) employed a finite difference method with which to solve the ODEs numerically. Note that their method does not provide a proper spectral representation of the transition density, since it does not find the eigenvalues and eigenfunctions of the diffusion generator. It might be possible to extend the technique developed in this article to obtain a spectral representation of the transition density in the case with subdivided population structure and general diploid selection.

In this article, we considered only one-locus Wright–Fisher diffusions. It is generally acknowledged that inference of evolutionary parameters, especially regarding selection, can be improved significantly by taking into account additional data at closely linked loci. Hence, it would be desirable to extend the approach described here to handle the dynamics of multilocus diffusions. However, our current technique relies on the fact that the eigenfunctions are known for the diffusion generator under neutrality. Therefore, to be able to apply our approach to multilocus diffusions with recombination and selection, one would have to know the eigenfunctions in the neutral case. To our knowledge, no such eigenfunctions are known.

Since diffusion processes also arise in other disciplines (e.g., physics and mathematical finance), several approaches have been proposed to obtain efficient approximations of the transition densities for diffusions more general than the Wright–Fisher diffusion (see Srensen 2004; Aït-Sahalia 2008, for example). It would be interesting to investigate whether one could borrow techniques from those fields to the population genetics applications mentioned above.

Finally, we note that Mano (2009) recently employed the representation of the transition density given by Kimura (1955a) and the moment duality used in Barbour et al. (2000) to investigate the dynamics of the number of lineages in the ancestral selection graph dual to the Wright–Fisher diffusion. The representation of the transition density found in this article can be employed to include recurrent mutation into that framework.

Appendix

Here, we describe the computation of the coefficients $b_m^{\left(i\right)}$ in Equation (36). Recall that the polynomial Q(x; α,β,σ,h) defined in (33) is of degree 4. Represent this polynomial as

$$Q\hspace{0.17em}\left(x;\alpha ,\beta ,\sigma ,h\right)=\stackrel{4}{{\displaystyle \sum }_{l=0}}{q}_l{x}^l,$$ (40)

where q_l are coefficients that depend on α, β, σ, and h. As shown in (10) and (11), $x\hspace{0.17em}{R}_m^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)$ satisfies a three-term recurrence relation of the form

$$\begin{array}{l}x\hspace{0.17em}{R}_m^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)=g\hspace{0.17em}\left(m,m-1\right)\hspace{0.17em}{R}_{m-1}^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)+g\hspace{0.17em}\left(m,m\right)\hspace{0.17em}{R}_m^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)\\ \hspace{1em}+g\hspace{0.17em}\left(m,m+1\right)\hspace{0.17em}{R}_{m+1}^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right),\end{array}$$

where g(m, m−1), g(m, m), g(m, m+1) are coefficients that depend on m and α, β. Note that (11) implies g(0, −1) = 0. Using the recurrence relation inductively gives

$$x^l{R}_m^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)=\stackrel{m+l}{{\displaystyle \sum }_{k=m-l}}h\hspace{0.17em}\left(m,l,k\right)\hspace{0.17em}{R}_k^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right),$$ (41)

where

$$h\hspace{0.17em}\left(m,l,k\right):=\{\begin{array}{l}{\delta }_{m,k},\hspace{1em}\\ \hspace{1em}\text{if}l=0,\\ {\mathsf{1}}_{\left\{\right|m-1-k|\le l-1\}}\hspace{0.17em}g\hspace{0.17em}\left(m,m-1\right)\hspace{0.17em}h\hspace{0.17em}\left(m-1,l-1,k\right)\\ \hspace{1em}+{\mathsf{1}}_{\left\{\right|m-k|\le l-1\}}\hspace{0.17em}g\hspace{0.17em}\left(m,m\right)\hspace{0.17em}h\hspace{0.17em}\left(m,l-1,k\right)\\ \hspace{1em}+{\mathsf{1}}_{\left\{\right|m+1-k|\le l-1\}}\hspace{0.17em}g\hspace{0.17em}\left(m,m+1\right)\hspace{0.17em}h\hspace{0.17em}\left(m+1,l-1,k\right),\hspace{1em}\\ \hspace{1em}\text{if}l>0.\end{array}$$ (42)

Now, (40) and (41) imply

$$\begin{array}{c}Q\hspace{0.17em}\left(x;\alpha ,\beta ,\sigma ,h\right)\hspace{0.17em}{R}_m^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)=\stackrel{4}{{\displaystyle \sum }_{l=0}}{q}_l\hspace{0.17em}\stackrel{m+l}{{\displaystyle \sum }_{k=m-l}}h\hspace{0.17em}\left(m,l,k\right)\hspace{0.17em}{R}_k^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right)\\ ={\displaystyle \sum }_{k=m-4}^{m+4}\left[\stackrel{4}{{\displaystyle \sum }_{l=\left|k-m\right|}}{q}_l\hspace{0.17em}h\hspace{0.17em}\left(m,l,k\right)\right]\hspace{0.17em}{R}_k^{\left(\alpha ,\beta \right)}\hspace{0.17em}\left(x\right).\end{array}$$

Thus, the coefficients $b_m^{\left(i\right)}$ in (36) are given by

$$b_m^{\left(i\right)}=\stackrel{4}{{\displaystyle \sum }_{l=\left|i\right|}}{q}_l\hspace{0.17em}h\hspace{0.17em}\left(m,l,k\right),$$

where h(m, l, k) can be computed efficiently using the dynamic programming in (42).