Role of mutual inhibition in binocular rivalry

Abstract

Binocular rivalry is a phenomenon that occurs when a different image is presented to each eye. The observer generally perceives just one image at a time, with perceptual switches occurring every few seconds. A natural assumption is that this perceptual mutual exclusivity is achieved via mutual inhibition between populations of neurons that encode for either percept. Theoretical models that incorporate mutual inhibition have been largely successful at capturing experimental features of rivalry, including Levelt's propositions, which characterize perceptual dominance durations as a function of image contrasts. However, basic mutual inhibition models do not fully comply with Levelt's fourth proposition, which states that percepts alternate faster as the stimulus contrasts to both eyes are increased simultaneously. This theory-experiment discrepancy has been taken as evidence against the role of mutual inhibition for binocular rivalry. Here, we show how various biophysically plausible modifications to mutual inhibition models can resolve this problem.

perceptual rivalry is a cognitive phenomenon where two or more perceptual interpretations of a given stimulus alternate. In binocular rivalry, which is a well-studied example of this phenomenon, two sufficiently different images are presented to each of the eyes (Clifford 2009; Alais and Blake 2005). The observer perceives one image at a time, and perceptual switches occur stochastically on the order of seconds. Mutual inhibition between neurons that represent different percepts has been long proposed as a cortical mechanism for rivalry (Blake 1989), and many theoretical models incorporating mutual inhibition have been developed (Matsuoka 1984; Lehky 1988; Arrington 1993; Lumer 1998; Kalarickal and Marshall 2000; Laing and Chow, 2002; Lago-Fernandez and Deco, 2002; Stollenwerk and Bode, 2003; Wilson 2003; Noest et al. 2007). In these models, the activity of a neural population encodes each percept. The populations inhibit each other with habituation processes taking the form of spike-frequency adaptation or synaptic depression. Switches in neural activity are facilitated by the habituation mechanisms, noise, or a combination of the two. An experimental hallmark for testing models of binocular rivalry is Levelt's four propositions (Levelt 1968), which characterize how the average perceptual dominance durations of the two percepts are affected by the strengths (contrasts) of the two stimuli.

Levelt's first three propositions (L1–L3), which characterize the effect of keeping the strength of one eye's stimulus constant while changing the other, are as follows: L1) increasing the contrast to one eye increases the predominance (fraction of time dominant) of that stimulus; L2) increasing the contrast to one eye does not affect the dominance duration of that stimulus; and L3) increasing the contrast to one eye increases the rivalry alternation rate. These first three propositions imply that an increase in contrast in one eye decreases the dominance time of the other eye, and in the literature L2 has often been used to represent this meaning. Levelt only considered the case where the fixed-contrast stimulus was held at high contrast. Subsequent research (Brascamp et al. 2006; Klink et al. 2008; Moreno-Bote et al. 2010) has found that when the fixed-contrast stimulus is held at low contrast, the reverse of L2 is true, i.e., L1 is accomplished primarily by an increase in dominance duration of the stronger, varying stimulus. Therefore, the revised L2 reads (Brascamp et al. 2006; Klink et al. 2008; Moreno-Bote et al. 2010): increasing contrast to one eye mainly affects the dominance durations of the stronger stimulus. Levelt's fourth proposition (L4), which is most pertinent to our current study, characterizes the effect of changing both strengths simultaneously and states: L4) increasing the contrasts to both eyes increases the rivalry alternation rate. Equivalently, simultaneously increasing the stimulus strengths decreases the average dominance duration of the percepts. Critically, the relationship between equal stimulus strengths and dominance duration (or alternation rate) is proposed to be strictly monotonic.

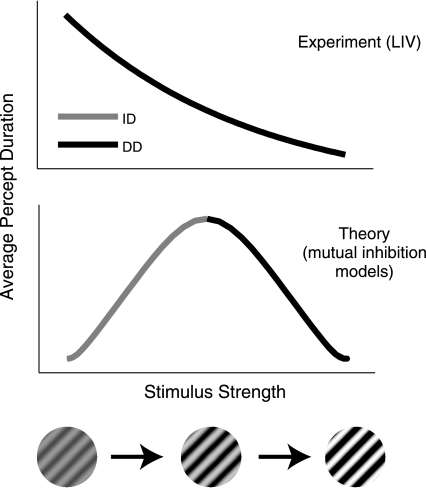
One appeal of mutual inhibition models is their ability to successfully replicate all of Levelt's propositions (Laing and Chow 2002; Wilson 2007) and even capture the revised L2/L3 (Moreno-Bote et al. 2010). It was once incorrectly believed that mutual inhibition is unable to capture L2 (Fox and Rasche 1969). Although mutual inhibition models give L4, a recent study from Shpiro et al. (2007) showed that this compliance is only true for a limited range of stimulus strengths. Specifically, Shpiro et al. (2007) analyzed four similar mutual inhibition models [the Wilson (2003) model and three variations of the Laing and Chow (2002) rate model] and found that in all four models increasing input strength simultaneously to both neural populations yielded an increase in percept duration followed by a decrease in percept duration for higher input strengths. That is, for a range of low input strengths, the four mutual inhibition models disobeyed L4, while for a range of higher input strengths the models obeyed L4 (Fig. 1). Although Shpiro et al. (2007) considered only four mutual inhibition models, further analytical work from Curtu et al. (2008) made a convincing case regarding the generality of the result. This observation has challenged the applicability of mutual inhibition to explain perceptual rivalry.

Fig. 1.

Top: schematic of Levelt's fourth proposition (L4). Bottom: 1 example of the percept duration dependence on stimulus strength as predicted by mutual inhibition models of binocular rivalry. Specifically, the models predict that increasing stimulus strength first yields increasing-duration (ID) followed by decreasing-duration (DD), while L4 proposes only DD behavior down to arbitrarily small stimulus strengths. Changes in model parameters can alter the shape of the curve at bottom, but the mathematical equations of mutual inhibition models seem to guarantee the existence of both ID and DD behavior.

This theory-experiment discrepancy is important because mutual inhibition models are otherwise successful in describing a wide variety of phenomena related to ambiguous stimuli. Notably, this class of models still obeys L1 and the revised L2/L3 even within the stimulus strength regime that fails to replicate L4 (see Fig. 4C). Additionally, in the presence of noise, mutual inhibition models replicate the distribution of dominance durations seen in experiments (Laing and Chow 2002; Shpiro et al. 2009), as well as features of stochastic resonance (Kim et al. 2006). These models have been successfully extended to account for “rivalry memory” phenomena (Wilson 2007; Noest et al. 2007). They can account for normalization and disambiguation (winner-take-all) behavior (Moldakarimov et al. 2005). They can give the recently discovered “maximal alternation rate at equi-dominance” result from Moreno-Bote et al. (2010). Finally, there is mounting independent experimental evidence for mutual inhibition, adaptation, and noise as mechanisms involved in rivalry (van Ee 2011; Alais et al. 2010; Kang and Blake 2010; van Ee 2009; Kim et al. 2006; Lankheet 2006; Brascamp et al. 2006; Suzuki and Grabowecky 2002; Klink et al. 2010).

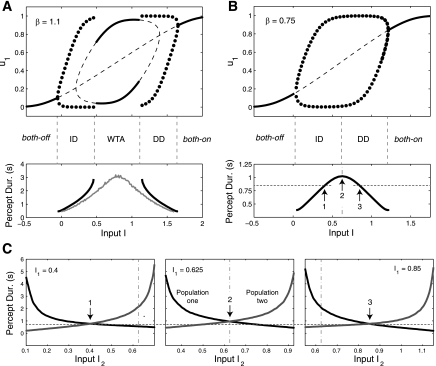
Fig. 4.

A and B: bifurcation diagram for the LC-SFA model studied in Shpiro et al. (2007) and Curtu et al. (2008) [sigmoid gain function (Eq. 10), adaptation (γ = 0.5), and no depression or recurrent excitation]. Solid lines represent stable fixed points and dotted lines represent unstable fixed points. Solid circles correspond to rivalry and show the maximum and minimum value of u₁ for a limit cycle (oscillations) of Eqs. 1–2. A: case where β = 1.1. A winner-take-all (WTA) regime exists for intermediate input. Gray curve shows average periods when noise is added to the net input (σ = 0.03; see Eq. 12). B: case where β = 0.75, with no WTA regime. C: plots showing L1–L3 for the model in B and with σ = 0.03. I₁ is fixed at 0.4, 0.625, and 0.85 and I₂ is varied. Black and gray curves show average dominance durations for population 1 and 2, respectively. Vertical line is set at 0.625 as a reference for the value that separates the ID and DD regimes in B. Arrows 1, 2, and 3 show different points where I₁ = I₂ (refer to B). Arrows 1 to 2 show ID, and arrows 2 to 3 show DD (the horizontal dotted line is for reference). Changes in percept duration for L4 (B) are very modest compared with changes for L1–L3 (C). These model predictions are in strong agreement with experimental observations (see text), with only the modest disagreement of L4, which our study shows can easily be fixed.

One possible explanation for the discrepancy between mutual inhibition models and L4 is that L4 itself may not always be true. Experimental data on L4 are limited, and it is unclear whether the proposition holds down to arbitrarily small contrasts. Many psychophysics studies on rivalry use stimuli with contrasts well above detection threshold (e.g., Hollins 1980). It is therefore conceivable that mutual inhibition models in fact make the correct prediction, and more experiments would be needed to verify this. However, data from van Ee (2009) and indirect evidence from Liu et al. (1992) suggest that L4 is valid down to contrast detection level (see discussion). Furthermore, the purely monotonic decrease in percept duration has been argued to follow naturally from a normative Bayesian framework for rivalry (Hohwy et al. 2008).

The inability of mutual inhibition models to fully comply with L4 has motivated alternative cortical models not based on mutual inhibition, most notably the models from Moreno-Bote et al. (2007) and Ashwin and Lavric (2010); both models successfully replicate L4 for all possible stimulus strength values. Other neural mechanisms for rivalry have also been proposed, although the issue of L4 has not been fully explored in these models (Borisyuk et al. 2009). Nevertheless, mutual inhibition models remain an attractive candidate for describing perceptual rivalry. Here, we show how biophysically plausible mechanisms can be easily incorporated into all mutual inhibition models such that they fully comply with L4, resolving the theory-experiment discrepancy.

GENERAL MUTUAL INHIBITION MODEL

The basic principle of mutual inhibition models is that each percept is represented by one of two populations of neurons under the influence of habituation processes like spike frequency adaptation and synaptic depression (Fig. 2). While this can be modeled with a neural circuit of a large number of biophysical Hodgkin-Huxley neurons (Laing and Chow 2002), the essential elements of the dynamics are captured in reduced population rate models where the collective activity of each population is represented by a single rate or activity variable. We therefore focus on a population rate model, although our observations generalize to a network of biophysical neurons. We also include recurrent excitation in the model, which has been mostly excluded in recent studies (Curtu et al. 2008; Wilson 2003, 2007; Shpiro et al. 2007, 2009). As we will show, the inclusion of recurrent excitation can be important for maintaining L4.

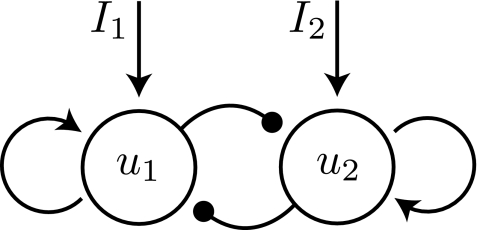
Fig. 2.

Two populations encode for each of the two rivalry percepts. The architecture contains mutual inhibition connections and recurrent excitation. I₁ and I₂ represent synaptic inputs to each population and are related to the strengths of the external stimuli.

Mutual inhibition models are often associated with the view that rivalry occurs as the result of interocular competition in early stages of the visual pathway (Blake 1989). That is, each population in the model contains monocular neurons from lateral geniculate nuclei or layer IV of V1, and local competition and habituation serve as the sole mechanisms of rivalry. However, electrophysiological evidence shows strong correlations between percepts and neural activity primarily in extrastriate visual cortex (Leopold and Logothetis 1999) while imaging has shown correlations in lateral geniculate nuclei (Haynes et al. 2005; Wunderlich et al. 2005) and V1 (Lee et al. 2007; Polonsky et al. 2000; Tong and Engel 2001). The emerging consensus is that rivalry does not occur at a single “site” but is instead a distributed process across early stage monocular channels and extrastriate sensory cortex, as well as frontal and parietal brain regions [see Sterzer et al. (2009) for a review]. Hence, the choice of mutual inhibition architecture between two populations does not imply that these populations consist of only early stage monocular neurons. The populations may contain neurons from several cortical areas. The idea is that the simplified mutually inhibiting two-population model is a sufficient and parsimonious description of rivalry dynamics. We note, for example, that the hierarchical Wilson (2003) model contains a monocular and binocular stage to account for “flicker and switch” stimuli (Logothetis et al. 1996), but mathematically reduces to a two-population mutual inhibition model for standard rivalry stimuli (as in the version of the model studied in Shpiro et al. 2007). We therefore assume that strong mutual inhibition may in fact arise from multiple cortical and subcortical areas.

We consider neural activities (u) of the two populations in the neural circuit to obey

$$\begin{array}{c}{\tau }_u{\dot{u}}_1=-u_1+f\left(\alpha u_1{d}_1-\beta u_2{d}_2-\gamma a_1+I_1\right)\\ {\tau }_u{\dot{u}}_2=-u_2+f\left(\alpha u_2{d}_2-\beta u_1{d}_1-\gamma a_2+I_2\right)\end{array}$$ (1)

and the adaptation and depression variables (a and d, respectively) to obey

$$\begin{array}{c}{\tau }_a{\dot{a}}_1=-a_1+u_1\\ {\tau }_a{\dot{a}}_2=-a_2+u_2\end{array}$$ (2)

$$\begin{array}{c}{\tau }_d{\dot{d}}_1=1-d_1-\delta d_1{u}_1\\ {\tau }_d{\dot{d}}_2=1-d_2-\delta d_2{u}_2\end{array}$$ (3)

where f(x) is the gain or firing rate function that takes the net input, x, to the population and translates it into an activity value. The spike frequency adaptation variables a represent hyperpolarizing potassium currents (McCormick and Williamson 1989; Sanchez-Vives et al. 2000). The synaptic depression variables d are modeled after Tsodyks and Markram (1997), Abbott et al. (1997), and Carpenter and Grossberg (1981). Specifically, d represents the percent strength of synaptic connections, which may reflect, for example, the availability of vesicle pools (Schneggenburger et al. 2002). The mutual inhibition strength is β, the adaptation strength is γ, the depression strength is δ, and the recurrent excitation strength is α. External inputs to each population are I₁ and I₂. The external inputs I₁ and I₂ explicitly represent synaptic input to the neural populations. The inputs can take on both positive and negative values but their values only have meaning with respect to the threshold of the gain function, which we choose to be zero for convenience. Thus negative values correspond to subthreshold inputs. Although the range of the inputs is unimportant for our purposes here, it can be scaled and shifted to match biophysical units if desired. In theoretical rivalry studies, it is often assumed that the strengths of the external stimuli (e.g., image contrasts from 0 to 100%) are linearly related to the scalar values I₁ and I₂. We will examine the implications of this assumption in later sections. We generally focus on the case where I₁ = I₂ = I (as per L4). We set the time constant of the activity variables τ_u to be 10 ms. The habituation time constants, τ_a and τ_d, must be significantly larger than τ_u for the system to mathematically give rise to rivalry-like behavior (Curtu et al. 2008); this is a reasonable assumption since habituation times are generally much longer than spike generation and synaptic decay times. The physiological values for τ_a and τ_d can span a wide range of scales (McCormick and Williamson 1989; Huguenard and McCormick 1992; Abbott et al. 1997; Varela et al. 1999). For simplicity, we set τ_a = τ_d = 1 s since results do not depend strongly on these time constants. We can also consider models where the synaptic depression for recurrent excitation is not the same as that for the mutual inhibition.

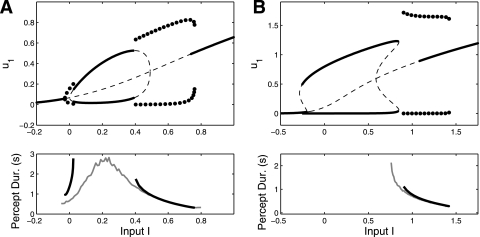
The mutual inhibition model (Eqs. 1–3) generally exhibits three basic behaviors (Moldakarimov et al. 2005; Shpiro et al. 2007; Curtu et al. 2008): 1) Simultaneous activity occurs when u₁ = u₂ is the only attractor of the system. Typically, this occurs when the net input to both populations is very low, resulting in both-off behavior (u₁ = u₂ ≈ 0), or when the net inputs are very high, resulting in both-on behavior. 2) Winner-take-all (WTA) behavior occurs when the system has two attractors: u₁ at high activity and u₂ ≈ 0, or the opposite. We term these on-off and off-on states, respectively. The system evolves to one of these two attractors and stays there indefinitely. 3) Oscillations occur when the system alternates between on-off and off-on states, corresponding to a limit cycle of the system and thus rivalry. Examples of oscillatory waveforms (u₁ and u₂ as functions of time) are shown in Fig. 3. The mechanisms for oscillations are discussed in Mechanisms for Oscillations. The period of oscillations can either increase or decrease as a function of (increasing) I, and these cases are denoted increasing-duration (ID) behavior and decreasing-duration (DD) behavior, respectively, after Shpiro et al. (2007). [More exotic behaviors may also occur but they are not generic (Curtu 2010).]

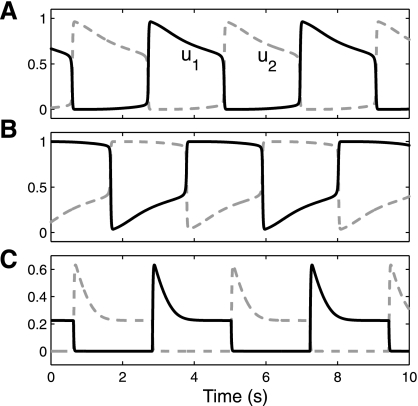
Fig. 3.

Three examples of u₁(t) and u₂(t) when the model is in an oscillation (rivalry) regime. Waveforms can assume different shapes depending on parameters. A and B: Laing and Chow-Spike Frequency Adaptation LC-SFA model (see Fig. 4) with I = 0.4 (A) and I = 1.2 (B). C: waveform for model parameters as in Fig. 6c, without noise, and with I = 0.5; such model parameters are similar to those used in Wilson (2007). Both B and C are in parameter regimes that comply with L4, while A is not in such a regime, even though the shapes of both A and C appear to share important similarities.

The type of behavior that the system exhibits depends on the external input values I₁ and I₂. A primary result from Shpiro et al. (2007) and Curtu et al. (2008) is reproduced in Fig. 4, A and B, where fixed points and limit cycles (oscillations) are plotted as a function of I₁ = I₂ = I. Figure 4 shows that as input I is increased, the system behavior transitions from both-off, to ID oscillations, to WTA, to DD oscillations, and finally to both-on. The WTA regime for intermediate input values seen in Fig. 4A is not always present. It can generally be destroyed by adding input noise (gray curve), decreasing β (Fig. 4B), or increasing adaptation strength γ. Figure 4, A and B, shows only two sets of parameter choices of Eqs. 1–3. However, these two bifurcation diagrams are remarkably general across other parameter choices. Specifically, the existence of a DD oscillation regime for high I values is almost always accompanied by an ID oscillation regime at low I values. Recall that it is the DD regime at high inputs that complies with L4.

Figure 4C shows that the inability for the mutual inhibition model to fully comply with L4 need not imply an inability to fully comply with L1–L3 [despite previous claims from Shpiro et al. (2007) and Ashwin and Lavric (2010)]. Figure 4C shows the dominance durations of population activity when one input is held fixed. As shown in Fig. 4C, left, inputs can be entirely restricted to ID regime values (here, I < 0.625), yet L1–L3 still hold. Also, the model predicts that the change in dominance durations for changes in I₁ = I₂ = I are relatively modest (within the range of ∼0.5–1 s) when compared with the changes seen with asymmetric inputs (spanning ∼1–5 s). This prediction agrees with psychophysics observations (Moreno-Bote et al. 2010). The same qualitative dynamics appear in a noise-driven model without any habituation mechanism.

The ID regime occurs between the both-off and DD oscillation regime. This implies that for two inactive populations, a smooth increase in I means that the model must pass through ID oscillations before reaching DD oscillations. If we assume that blank stimuli do not evoke significant responses in the neural populations, then blank presentations would correspond to the both-off regime. Consequently, starting from blank stimuli, a smooth increase in image contrast can yield DD behavior (L4) only after passing through an ID regime first, contradicting the proposition. The existence of the ID regime in mutual inhibition models is something we henceforth refer to as the “L4 problem.” We note that the L4 problem also exists for the noise-driven model.

Mechanism for Oscillations

Various versions of Eqs. 1–3 have been studied, yielding many insights on how the dynamical behavior depends on system parameters (Shpiro et al. 2007; Curtu et al. 2008; Wilson 2007). In this section, we present a simple version of the model with only adaptation (γ > 0, δ = 0) and a Heaviside gain function:

$$f\left(x\right)=\{\begin{array}{cc}0& \text{if}\hspace{0.17em}x<0\\ 1& \text{if}\hspace{0.17em}x\ge 0\end{array}$$ (4)

This simple example will provide intuition for how the mutual inhibition model gives rise to different dynamical behaviors and how these behaviors depend on input I. It will show the crucial mechanisms for both ID and DD oscillations and it will help motivate solutions to the L4 problem in general models.

A simple way to study the dynamics of Eqs. 1–2 is to assume that τ_a ≫ τ_u, which is implicit in our choice of τ_a = 1 s and τ_u = 10 ms. Mathematically, this reduces the dimensionality of Eqs. 1–2, such that we can essentially assume that u_i = 1 if that population's net input is above the x = 0 threshold and u_i = 0 if its net input is below threshold. Therefore, following the dynamics of the system simply becomes a matter of following the net input αu_i − βu_j − γa_i + I to each population. When the net input crosses threshold a sudden shift in population activity will occur, potentially giving rise to oscillations. To make these ideas more explicit, assume that u₁ = 1 and u₂ = 0. This WTA configuration (one active, other suppressed) is stable for intermediate input values. For I > γ − α, in the absence of any exogenous perturbation, the active population will never turn off because the net input will always be above threshold even for maximal adaptation a₁ = 1. Conversely for I < β, the inactive population can never cross threshold and thus remains suppressed. Therefore, if γ − α < β then WTA behavior ensues within this input interval. If I is very large, then both populations will be above threshold and will stay above threshold even after a₁ and a₂ have saturated, i.e., when I > γ − α + β. For very low I, both populations will stay below threshold even when a₁ = a₂ = 0, i.e., when I < 0.

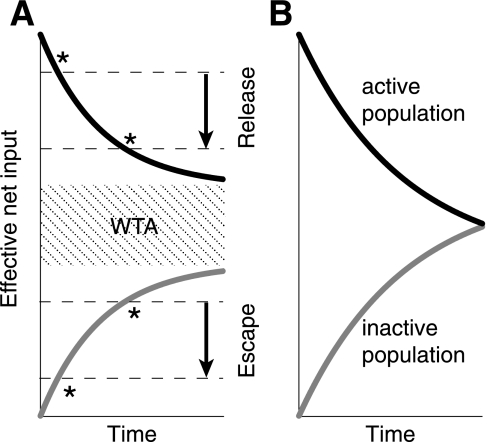
For I > β, which is outside of the WTA regime, the inactive population, u₂, can cross threshold at time T when I = β + γa₂(T), whereupon u₂ immediately switches on, inhibits u₁, and causes u₁ to switch off. This switch in activity has been termed escape, since the inactive population escapes from the suppression of the active population (Shpiro et al. 2007). Note that escape switches occur because the inactive population recovers from its adaptation sufficiently to switch back on, allowing it to suppress the other population, which is relatively weak from its own buildup of adaptation. Conversely, below the WTA regime for I < γ − α, the active population can drop below threshold at I = γa₁(t = T) − α, whereupon u₁ immediately switches off, releasing u₂ from suppression. As such, this type of switch has been termed release (Shpiro et al. 2007).

Oscillations occur when escape or release switches persist indefinitely. Shpiro et al. (2007) and Curtu et al. (2008) show that the dominance durations of escape oscillations decrease with increasing I, while the dominance durations of release oscillations increase with increasing I. This is easily seen in our simple example, which is illustrated in Fig. 5. In the escape regime, increasing I moves the inactive population closer to threshold, thus facilitating faster switches. In the release regime, increasing I moves the active population further from threshold, facilitating slower switches. To summarize, escape oscillations only occur for large external input (I > β) and give rise to DD behavior, while release oscillations only occur for low external input (I < γ − α) and give rise to ID behavior. This simple picture of two populations racing to a threshold holds in general for arbitrary gain functions (Curtu et al. 2008), and as seen in Fig. 5 implies that the DD oscillation regime must, in general, coexist with an ID oscillation regime.

Fig. 5.

Dynamics of the mutual inhibition model can largely be characterized by tracking the net inputs to each population. Here we show a case where f(x) is a Heaviside function and only adaptation is considered (δ = 0). We set u₁ = 1 and u₂ = 0. Net input to population one is therefore α − γa₁ (t) + I. Net input to the inactive population is −β − γa₂(t) + I. A switch in activity occurs when either population crosses the firing rate threshold at zero. Alternatively, a switch in activity occurs when the “effective net input” [α −γa₁(t), black curve, active population, and −β − γa₂(t), grey curve, inactive population] crosses −I. Input I can therefore be thought of as setting the “effective threshold” of the firing rate function. Increasing I (black arrows) therefore decreases the effective threshold (dotted lines). Switches in activity occur when either curve crosses the −I threshold (events marked by *). A: when I is low, switches occur when the active population crosses threshold (release), and increases in I lead to longer time durations before a switch occurs (ID behavior). For intermediate I, neither population will cross threshold and WTA ensues. For larger I, switches occur when the inactive population crosses threshold, and increases in I lead to shorter durations before a switch occurs (DD behavior). B: parameters can be set such that WTA can never occur for any value of I.

SOLUTIONS TO THE L4 PROBLEM

The dynamics of Eqs. 1–3 show that for mutual inhibition models to be entirely consistent with L4, the ID region must be removed. If L4 is experimentally invalid for some small range of very low contrast values, then minimizing the ID regime in the mutual inhibition model would suffice as a solution. We show how the ID region can be reduced or eliminated by manipulating the parameters of Eqs. 1–3 or by preprocessing the inputs. We elaborate these solutions in the following sections, giving biophysically plausible implementations for each.

Control of ID Region Through the Gain Function

Although the work from Shpiro et al. (2007) and Curtu et al. (2008) suggest the generality of the L4 problem in mutual inhibition models, two forms of Eqs. 1–3 have been studied (Taylor et al. 2002; Wilson 2007) that prohibit release, yet allow escape. Here, we show that both of these solutions, which rely on sharp thresholds in f(x), are not robust to noise but do suggest parameter choices that significantly minimize the ID regime.

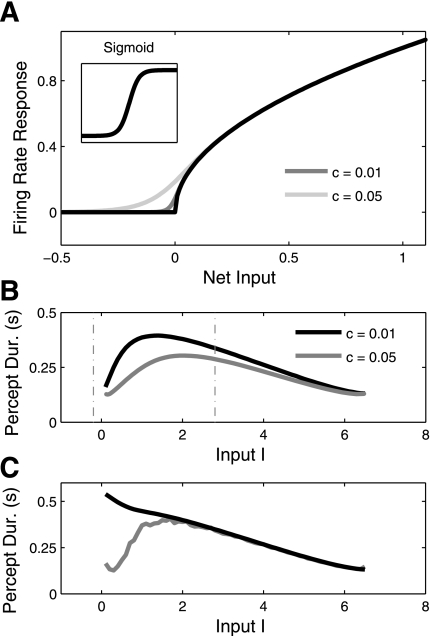
In Mechanisms for Oscillations, we included adaptation but omitted synaptic depression. As shown in Taylor et al. (2002) and Kilpatrick and Bressloff (2010), the Heaviside model with depression but no adaptation yields only DD oscillations, which solves the L4 problem. This occurs because synaptic depression only weakens the inhibition on the suppressed pool. Hence, when the inhibition is sufficiently weakened by the depression, escape can occur. Given that there is no habituating process acting on the active pool, there is no mechanism for release, and therefore no ID oscillation regime. However, Shpiro et al. (2007) studied a synaptic depression model with a sigmoid gain function (Eq. 10) and found that it included both ID and DD regimes. The exclusion of release switches in the Heaviside-depression model is thus dependent on the sharp, discontinuous threshold in the gain function. When this threshold is smoothed as would occur with noise, release oscillations become possible because as the synaptic depression weakens, inhibition from the suppressed population to the active one, which is always zero in the Heaviside case, increases and effectively weakens the active population. However, synaptic depression still favors escape switches over release switches and makes the DD regime larger because it primarily acts on the net input of the suppressed pool. This explains why the DD regimes are larger in simulations of a model with synaptic depression in Shpiro et al. (2007) (also see our Fig. 8A). This regime-size asymmetry can be controlled by the shape of the sigmoid function.

Fig. 8.

A: dynamical behavior for a model with f(x) = ${\sqrt{\left[x\right]}}_{*}$ with c = 0.05 and depression only. β = 2, ∂ = 2. Gray curve shows the case with input noise (σ = 0.02). B: Recurrent excitation is added. α = 1.75, β = 2.5, and δ = 1.5 (σ = 0.07; gray curve).

Alternatively, the adaptation-only model with weak recurrent excitation and a linear threshold gain function [f(x ≥ 0) = x; f(x < 0) = 0] can also preclude release switches (Wilson 2007). This gain function is continuous but not smooth at the x = 0 threshold. The active population weakens due to accumulating adaptation, but it can never push the population below threshold. This is because as adaptation a_i increases, u_i decreases until it reaches a steady state at u_i = a_i, i.e., u_i = I/(1 + γ − α). This value is always above zero for I > 0 (and for small α), making the escape condition the only possible mechanism for oscillation. Note that for I = 0, the only attractor is both-off, implying that the system transitions directly from both-off to escape oscillations. Compare this to the Heaviside-adaptation example, where a_i approached the fixed value u_i = 1; thus the net input α − γa_i + I could fall below threshold. Although the linear threshold gain function with adaptation yields only escape oscillations, the dominance duration, T, turns out to be constant for changes in I (see appendix). This can be changed if the x > 0 portion of f(x) is concave [i.e., f″ (x) < 0; Fig. 6A, black curve]. Such a choice of f(x) yields only DD oscillations (Fig. 6C, black curve), solving the L4 problem. However, this solution to the L4 problem by prohibiting release is not robust to noise. If we smooth out the sharp threshold then we regain the ID regime, as shown in Fig. 6, A and B. The ID regime reemerges because the inhibition for the active population is no longer precisely zero allowing a mechanism for release to become possible. Notice from Fig. 6B, however, that the DD regime is larger than the ID regime when we choose a smooth gain function that approximates a sharp threshold at x = 0.

Fig. 6.

A: 3 gain functions are considered: f(x) = ${\sqrt{\left[x\right]}}_{+}$ (see Eq. 8) with a sharp threshold at x = 0, f(x) = ${\sqrt{\left[x\right]}}_{*}$ (see Eq. 11) with c = 0.01 (less smoothing), and f(x) = ${\sqrt{\left[x\right]}}_{*}$ with c = 0.05 (more smoothing). Compare the shape of the square root function with the sigmoid (inset), which was used for Fig. 4, A and B. B: period-input curves for f(x) = ${\sqrt{\left[x\right]}}_{*}$ and adaptation only. C: period-input curves for f(x) = ${\sqrt{\left[x\right]}}_{+}$ without input noise (black curve) and with input noise (gray curve, σ = 0.05).

Thus the lack of ID regimes in Taylor et al. (2002) and Wilson (2007) is dependent on sharp thresholds in the gain functions. This is to be expected since Curtu et al. (2008) proved the coexistence of ID and DD regimes for models with adaptation only and smooth gain functions. This implies that the solutions are not robust to noise, because sharp cusps in input-output functions are “smoothed out” when input noise is added. For example, a white noise input to a Heaviside function results in an input-output relationship that can be approximated by a sigmoid. Additionally, the firing rate response curves of integrate-and-fire neurons have been shown to undergo similar “smoothing” in the presence of noise (Brunel and Latham 2003). Noise is considered an essential and inevitable feature of rivalry due to the stochasticity in dominance durations. Therefore, it may be appropriate to only consider smooth gain functions in our analysis. However, in both Taylor et al. (2002) and Wilson (2007), the ID regime can be made small by choosing smooth functions that closely approximate the sharp threshold function. In fact, the ID regime can be made arbitrarily small based on the degree of smoothing.

Control of ID Region Through Recurrent Excitation

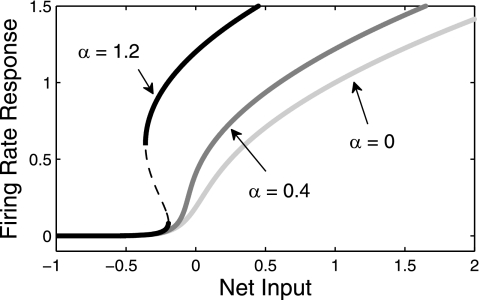
Strong recurrent excitation can preclude release oscillations even with smooth gain functions. Recurrent excitation steepens the population's firing rate response curve if it is weak (Fig. 7, gray curve); while strong recurrent excitation produces a hysteresis effect in the population's firing rate response (Fig. 7, black curve), where the population jumps to the active state at some input but drops back down to the inactive state at a lower level of input. Thus strong recurrent excitation yields a bistable regime in the population's response, which can destroy ID oscillations. Recurrent excitation may also destroy the DD regime but not with sufficient synaptic depression. In Mechanisms for Oscillations, the analysis showed that the distance from the beginning of the DD regime and the beginning of the both-on regime is given by γ − α. Likewise, the distance from both-off to the end of the ID regime is also γ − α. This implies that if α > γ, then neither escape nor release oscillations exist as a result of adaptation. We generally see the same effect for other gain functions: if recurrent excitation strength overpowers adaptation strength, then this generally destroys both adaptation-mediated ID and DD oscillations.

Fig. 7.

Effect of recurrent excitation on a population's firing rate response. Here, f(x) = ${\sqrt{\left[x\right]}}_{*}$ with c = 0.05.

Once depression is added to the model, the dynamics become more complicated. We showed that release oscillations are possible for models with smooth gain functions and depression only but that the ID regime is relatively small (Fig. 8A). Release oscillations can occur if the recovery of inhibition to the active population can cause the active population to drop below threshold. However, strong recurrent excitation of the active population can cause a persistent activity effect, overpowering the effects of the inhibition and ensuring that the active population remains above threshold. The persistent activity effect, however, does not necessarily prevent the inactive population from crossing threshold at higher I values. Simulations clearly show that escape oscillations at high I values remain possible across a variety of smooth gain functions (see Fig. 8B for one example). Therefore, strong recurrent excitation is one way to solve the L4 problem without resorting to a new mechanism. This solution is robust and holds for arbitrary gain functions.

A potential issue of recurrent excitation is that it can lead to rhythmogenesis in a single population (Shpiro et al. 2007). Strong adaptation could cause the population to alternate indefinitely between on and off states. However, this only occurs when the range of the adaptation spans the input range where the population is bistable. Also note that rhythmogenesis would be impossible if synaptic depression was the primary habituation mechanism since it only works to weaken the inhibition to the suppressed pool.

Figure 8B shows that a relatively large WTA regime persists before DD oscillations for increasing I. Input noise will induce oscillations in this regime by destabilizing each of the states. However, strong noise reintroduces ID behavior for low I, while weak noise does not produce robust oscillations in the center of the WTA regime. Hence, a smooth increase in I from I = 0 may not match experiments where rivalry occurs for even very low contrasts. This forces us to more closely examine how contrast is related to I, and we expand on this in the following sections. The model in Fig. 8B also shares important similarities with a L4-compliant nonmutual inhibition model proposed by Moreno-Bote et al. (2007), and this is discussed in Energy Well Models. Figure 8B also shows a region where both-on and oscillation behaviors overlap. In this region, the system evolves to the both-on fixed point when the initial d₁ and d₂ values are both near their asymptotic steady states. Sufficient asymmetry in the d₁ and d₂ initial values yields oscillations.

Control of Inputs

Here, we show how control of the inputs to the mutual inhibition circuit can lead to robust solutions to the L4 problem. It is not known how the strength of the external stimulus (e.g., contrast, which we denote by C) should be translated to the neural input I. For simplicity, rivalry models often assume a linear relationship between C and I. Although this assumption is not fully validated, it is nevertheless useful because it qualitatively captures any bijective map between contrast and neural input. That is, for any I = g(C), where g is an increasing one-to-one and onto function of C, the bifurcation diagram with C as the bifurcation parameter would be qualitatively unchanged. It would simply compress or stretch the different behavior regimes. Although we do not know how stimulus strength translates to input I precisely, the input must be bounded. For oriented gratings, the stimulus strength is bounded between 0 and 100% contrast, which places bounds on the value of neural input I. The lower 0% contrast (blank stimulus) bound could either translate to an I value that falls within the both-off regime or within one of the oscillation regimes. However, a constraint that must be satisfied is that there be no perception for blank stimuli. Although, the straightforward assumption is to assume that blank stimuli correspond to both-off, as we will discuss in more detail below, there can be other possibilities.

Restriction of input.

A simple way to solve the L4 problem is to assume that the biophysical I values lie only within the DD oscillation regime. For example, we can assume that for the model in Fig. 6B, I values are restricted to Iϵ [2, 6]. This implicitly assumes that C = 0 corresponds to I = 2 and the circuit will be active and undergoing rivalry in the absence of a stimulus. Neural activity in the absence of a stimulus is not necessarily problematic since spontaneous activity is prevalent throughout the brain, and sensory neurons exhibit background firing rates even when no stimuli are being presented (Sanseverino et al. 1973; Ringach 2009). Associating blank stimuli with an I value within the model's oscillation regime, however, predicts that spontaneous activity would exhibit neural firing that rivals (i.e., modulates) over a time scale of seconds. This would be in contrast to the both-off state, which would correspond to low spontaneous background activity with no temporal structure. The both-off regime corresponds to a u₁ = u₂ steady state that is low but nonzero given that a smooth (e.g., sigmoidal) gain function never goes completely to zero. For example, in Fig. 4, A and B, at the upper end of the both-off regime, we have spontaneous activity represented by u₁ = u₂ ≈ 0.1, which is ∼10% of the maximal firing rate given by the gain function of that model. In either case, we must assume that this spontaneous activity would be below a perceptual threshold so that the observer does not hallucinate one of the percepts during a blank presentation.

It is unclear which input regime, both-off or oscillations, best represents the spontaneous activity in the absence of a stimulus that is observed in cortex. Spontaneous activity is often regarded as a noisy background firing rate (Tolhurst et al. 1983), although there is evidence that spontaneous activity has coherent spatio-temporal structure (Ringach 2009), with modulations occurring over multiple time scales (Kohn and Smith 2005). In either case, it is important for rivalry models to be explicit on how they behave in the absence of stimuli if they are to replicate findings from psychophysics experiments that incorporate blank presentations [e.g., as in the on/off sequences that probe the phenomena known as “rivalry memory” (Pearson and Brascamp 2008)]. In the discussion, we argue that it is more difficult to reconcile findings from these experiments in a mutual inhibition framework if 0% contrast is taken to fall in an oscillation regime. Current rivalry memory models (Wilson 2007; Noest et al. 2007) indeed presume both-off behavior for blank stimuli (see discussion).

Mathematically, however, the restriction of input solution implies that if a nonmutual inhibition model solves the L4 problem but also assumes rivalrous activity in the absence of a stimulus [e.g., as in the models from Moreno-Bote et al. (2007) and Ashwin and Lavric (2010)], then this cannot be taken as evidence for that model over the mutual inhibition model, at least with regard to its ability to replicate L4. [We will analyze the models from Moreno-Bote et al. (2007) in Energy Well Models].

Preprocessing of input.

If we assume that the spontaneous activity is not modulated during blank presentations, then we require that both rivalry populations are inactive (where inactive implies nonrivalrous spontaneous firing rate) for subdetection contrasts. Here, we propose a solution that constrains the model to predict both-off activity for contrasts below detection threshold, and DD oscillations for contrasts above detection threshold. In Restriction of input we suggest that if we only require DD oscillations for some bounded range of inputs, then this can be accomplished trivially in mutual inhibition models. If we require a sharp transition from both-off to DD oscillations, then this cannot be accomplished trivially since mutual inhibition models generally pass through the ID regime first. Note, however, that such transitions are not uncommon in dynamical systems. As an example, the Hodgkin-Huxley model exhibits purely DD oscillations as input is increased. The stable fixed point at low inputs (resting membrane potential) undergoes a subcritical Hopf bifurcation (action potential threshold), yielding a monotonic decreasing-period dependence for repetitive action potentials. The Hodgkin-Huxley equations per se, however, are not likely candidates for rivalry because they lack an inherent symmetry between two percepts (e.g., as in Eq. 1 where equations for the two populations are identical but with opposite indexes). This symmetry makes finding the both-off to DD oscillation transition nontrivial.

A way to accomplish this transition is to preprocess the inputs I. One such preprocessing function could be

$$I=g\left(C\right)=\{\begin{array}{cc}0& \text{if}\hspace{0.17em}C<{\theta }_C\\ C& \text{if}\hspace{0.17em}C\ge {\theta }_C\end{array}$$ (5)

where θ_C is set at any value in the model's DD oscillation regime. This would indeed predict the desired both-off to DD transition, since I values would be prohibited from the interval (0,θ_C). However, this jump discontinuity would not be robust to noise. Alternatively, we could set the function g(C) to be a smooth approximation of Eq. 5 such that the ID regime is traversed quickly (Fig. 9A, gray curve). As discussed previously, this would not destroy the ID regime, but it could make it arbitrarily small. As a third mathematical possibility, we could replace the parameter I in Eq. 1 with a dynamical variable I:

$$\dot{I}=C-\frac{1}{3}{I}^3+\frac{m_1+m_2}{2}{I}^2-m_1{m}_{2}I$$ (6)

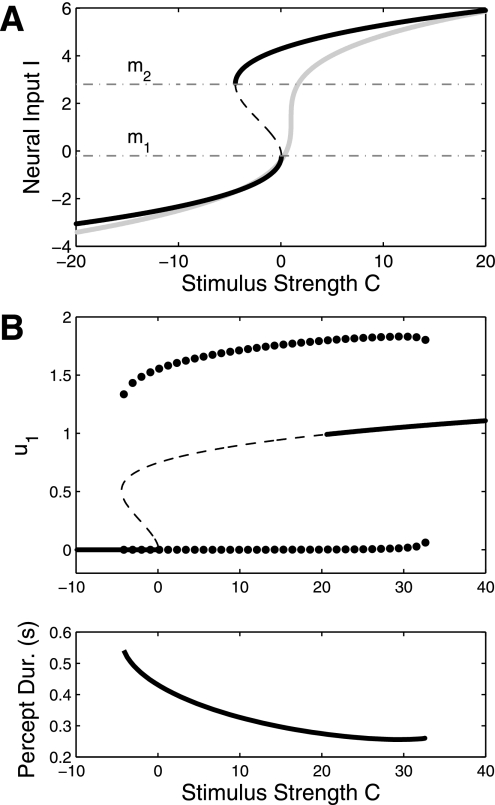
where m₁ and m₂ indicate the two limit points of the bifurcation diagram (Fig. 9A, black curve). As I evolves at some fast time constant (say, on the order of the activity variables), then I approaches either the top or bottom branch of Fig. 9A but is asymptotically restricted from values in [m₁,m₂]. We can therefore arbitrarily set [m₁,m₂] to encapsulate the ID regime of, say, the model in Fig. 6B. By setting m₁ = −0.2 and m₂ = 2.8 (vertical lines in Fig. 6B), the system exhibits the behavior seen in Fig. 9B. As input is increased, the system jumps from both-off behavior directly to DD oscillations. When I is on the bottom branch of Fig. 9A, then both-off behavior is the only attractor of the system. When I is on the top branch, the system exhibits rivalry (and for very large inputs, both-on behavior). The choice of Eq. 6 is similar to Eq. 5 in that it restricts I values from an interval, but Eq. 6 contains no mathematical discontinuities. However, both equations require tuning the parameters to skip the ID regime. Equation 6 might be considered an explicit model for contrast detection, where the difference between the two branches represents a perceptual threshold. The form of Eq. 6 was chosen for mathematical simplicity. Alternative forms with the same qualitative behavior could be chosen such that the abscissa of Fig. 9A has appropriate quantitative values (e.g., C from 0 to 1). An experimental consequence of Eq. 6 is that there will be coexistence of rivalry and no perception over a range of contrasts and the transition between the two behaviors will exhibit hysteresis. The qualitative relationship between C and I seen in Fig. 9A is general and may result from various biological mechanisms. In Multiple populations, we show how the same input control can be achieved through simple extensions to the mutual inhibition model.

Fig. 9.

A: relation between external stimulus strength C and neural input I as described by a simple dynamical system given by Eq. 6 (black curve). For a given stimulus strength, the neural input simply takes on the value of one stable attractors (solid lines). In the bistable regime, the value of neural input depends on its initial condition (above or below the unstable fixed point, dashed line). Gray curve shows a hypothetical preprocessing I = g(C) that would not destroy the ID regime, but would make it very small. B: The dynamical behavior for the model given in Fig. 6B {f(x) = ${\sqrt{\left[x\right]}}_{*}$ with c = 0.05 and adaptation only} when the parameter I is replaced with the variable I from Eq. 6. m₁ = −0.2 and m₂ = 2.8 as to encapsulate the ID regime of Fig. 6B (see vertical lines of Fig. 6B).

Multiple populations.

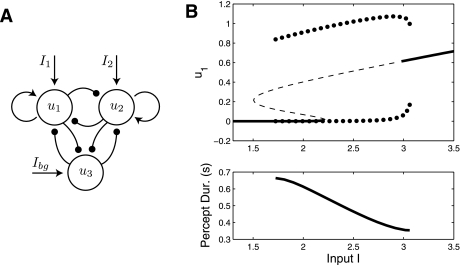
The ID regime can be removed by suppression from a background population consisting of one or more populations (see Fig. 10A). As an example, consider a single additional population that is responsive to other features of the visual field and has mutually inhibitory connections to both rivalry populations. Suppression from this background activity prohibits activity in the rivalry circuits for low contrast while allowing rivalry activity for higher contrast. The three populations obey

$$\begin{array}{l}{\tau }_u{\dot{u}}_1=-u_1+f_1\left(-{\beta }_1{u}_2{d}_2-{\beta }_2{u}_3-\gamma a_1+I_1\right)\hfill \\ {\tau }_u{\dot{u}}_2=-u_2+f_1\left(-{\beta }_1{u}_1{d}_1-{\beta }_2{u}_3-\gamma a_2+I_2\right)\hfill \\ {\tau }_u{\dot{u}}_3=-u_3+f_2\left(-{\beta }_2\left(u_1+u_2\right)+I_{bg}\right)\hfill \end{array}$$ (7)

where β₁ is the inhibition strength between the rivaling populations and β₂ is the inhibition strength of the connections to and from a third population. We use different firing rate functions, f₁ and f₂, for the rivaling populations and the third population, respectively. I_bg represents a constant input to the third population, although mathematically we could omit this and just replace f₂(x) with f₂(x − I_bg). Figure 10B shows an example bifurcation diagram. Note the similarity of Figs. 9B and 10B. In particular, the entire ID regime is destroyed due to the suppression by the third population. This three population model also includes a bistable regime between both-off and DD oscillations for low I. The features of Eq. 7 can be understood with a simple analysis. The total external input to populations one and two can be taken to be I −β₂u₃. Due to the connectivity of the network, u₃ is bistable between active and inactive states. The I_bg term assures that u₃ is active when the rivalry populations are not activated. As I increases, input to populations one and two will overcome the suppression of population three, causing u₃ to shut off. The state of u₃ is analogous to the dynamical variable I from Eq. 6.

Fig. 10.

A: 3-population model architecture. Populations 1 and 2 encode the rivalry percepts, while population 3 represents background activity. Third population receives a small background input I_bg to ensure it remains active when I₁ = I₂ = 0. Inhibition from population three prevents activity in u₁ and u₂ when I₁ = I₂ is low. This prevents the circuit from operating in the ID oscillation regime. Inhibition to the third population allows u₁ and u₂ to assume activity when I₁ = I₂ become sufficiently high. B: dynamical behavior of the model. In terms of general dynamical behavior, Figs. 9B and 10B are identical. We set β₁ = 2, β₂ = 4, δ = 1, and γ = 3. Firing-rate functions are f₁(x) = ${\sqrt{\left[x\right]}}_{*}$ with c = 0.05 and f₂(x) is a sigmoid with r = 1.5 (see appendix).

This multiple population solution is identical to the preprocessing solution in terms of perceptual behavior as a function of increasing contrast. They both yield sharp transitions from the both-off to DD oscillations. The form of input control captured qualitatively by Eq. 6 may have other possible implementations. The central idea is that mutual inhibition dynamics serve as the substrate of the rivalry process while external components can mediate access to the input regimes. A feature of these models is that their ability to resolve the L4 problem is robust to noise as long as noisy inputs are themselves not strong enough to bridge the gap between inactive and active states (of I in Eq. 6 or of u₃). This is notable because as we have mentioned previously, adding noise in the mutual inhibition model generally broadens the ID regime, even if it was made to vanish through parametric manipulations (see Control of ID Region Through the Gain Function).

Energy Well Models

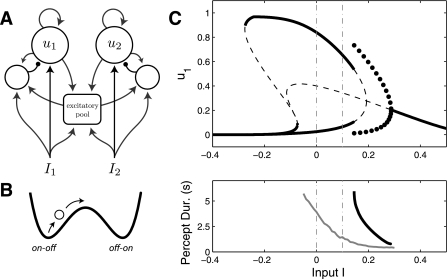
A number of recent studies (Moreno-Bote et al. 2010; Kang 2009; Moreno-Bote et al. 2007; Suzuki and Grabowecky 2002; Brascamp et al. 2006) employ an energy well scheme to describe the dynamics of rivalry (Fig. 11B). Since such models have been shown to be capable of solving the L4 problem (Moreno-Bote et al. 2007), we examine how they relate to our current findings. The idea is that the energy landscape of the rivalry circuit can be described by a double well potential. The system evolves to the bottom of one of the two wells, which represent WTA states of one percept active and the other suppressed. The system switches between states via noise or adaptation effects that modulate the energy landscape.

Fig. 11.

A: global-excitation, local inhibition (GELI) architecture. B: energy well model. C: dynamical behavior for the GELI model. Vertical lines are set at I = 0 and I = 0.1, showing the range of inputs studied in Moreno-Bote et al. (2007). Noise case is given by σ = 0.07.

Energy well models are often presented as a normative framework of rivalry. Equations can be prescribed to the energy landscape that governs the dynamics of the system (Moreno-Bote et al. 2007), and this can be done without supposing which cortical mechanisms might be responsible for generating these dynamics. Arguably, the simplest way to implement energy well dynamics (i.e., two attractor states) in a mechanistic model is mutual inhibition. Any Lyapunov function of the neural activity equations (Eq. 1) would represent two potential wells in the u₁–u₂ domain, thus retrieving the same schematic in Fig. 11B, but in two dimensions. That is, mutual inhibition models (Eqs. 1–3) are energy well models. However, there is a distinction between one-dimensional energy well models [e.g., Moreno-Bote et al. (2007)] and the neural activity equations (Eq. 1) in that energy well models have a one-dimensional activity space, while mutual inhibition models have two dimensions (i.e., the firing rates of the 2 populations are individually described). Therefore, one-dimensional energy well models describe only the WTA on-off and off-on states. Alternatively, the two-dimensional rate equations (Eq. 1) can describe both-off and both-on states in addition to the two WTA states. Therefore, any one-dimensional energy well model that gives L4 also assumes rivalrous activity in the absence of a stimulus. Thus the energy well solution to the L4 problem presented in Moreno-Bote et al. (2007) falls within the realm of solutions to the mutual inhibition model via restriction of input (see Restriction of input).

Moreno-Bote et al. (2007) also used the energy well framework to motivate a more general global-excitation, local inhibition (GELI) model (Fig. 11A). The equations for the GELI model are similar to Eqs. 1–2 (and thus can describe the both-off state). The GELI architecture is one example in which two attractor states can be achieved without strict mutual inhibition, although the effect of mutual inhibition is present indirectly via connectivity with a shared excitatory pool [therefore, it might be appropriate to call this an indirect mutual inhibition model, as in Moreno-Bote et al. (2010)]. The GELI model yields only DD oscillations (Fig. 11C). Since a cortical model not based on mutual inhibition can yield L4 for all input values, this has been taken as evidence against the standard mutual inhibition architecture (Moreno-Bote et al. 2007). However, the dynamics of the GELI model (seen in Fig. 11C) are qualitatively identical to the mutual inhibition model with strong recurrent excitation (Fig. 8B). Namely, both transition from the both-off regime to the WTA regime (such that the ID regime is surpassed) and then to the DD oscillation regime. Strong recurrent excitation is also present in the GELI model, which is how the model achieves WTA states for I = 0. We claim that the lack of an ID regime is exclusively due to recurrent excitation, and this can be also be achieved in a strict mutual inhibition framework (see Control of ID Region Through Recurrent Excitation). Nevertheless, the GELI model emphasizes that “mutual inhibition” need not imply direct connectivity between perceptual neurons.

The GELI model and our recurrent excitation model assume WTA activity for I = 0. This implies that switching between the two percepts can occur in the presence of noise. This is similar to the restriction of input solution; here, rivalrous activity in the absence of a stimulus is enforced via recurrent excitation as opposed to a shift in accessible I values. If we consider negative I values as well, then these models exhibit a both-off to WTA transition (Figs. 8B and 11C) instead of the both-off to DD transition we presented in previous sections. Although input noise induces rivalrous switching in WTA regimes, typical input noise strengths produce unreasonably long dominance durations near the center of the WTA regime, while higher noise strengths can reintroduce ID behavior. Thus it is unclear whether these models can capture realistic both-off to oscillation transitions. Nevertheless, due to the qualitative effect of removing the ID regime, recurrent excitation might be worth exploring further through implementations different from a linear αu_i term. One example could be with spatially extended connectivity (Laing and Chow 2002; Kilpatrick and Bressloff 2010).

Moreno-Bote et al. (2007) also emphasized the role of noise in their models, distinguishing between “noise-only” and “adaptation-only” models. As we mentioned earlier (general mutual inhibition model), mutual inhibition models produce the general L1–L4 behavior regardless of whether it is noise, adaptation, or a combination of the two that facilitate switches. The same observation applies to other two-attractor (i.e., energy well) models.

Although the energy well model from Moreno-Bote et al. (2007) assumes rivalrous activity in the absence of input, it may offer may offer important insights into the dynamics of rivalry. An interesting result from Moreno-Bote et al. (2010) is that when the contrast of one eye is held constant and the other changed, then the maximum alternation frequency occurs when C₁ = C₂ [note that this is not a trivial consequence of L1–L3; see Moreno-Bote et al. (2010) for details]. The authors found that the energy well model developed in Moreno-Bote et al. (2007) matched perfectly with this “alternation rate is maximal at equi-dominance” result. Mutual inhibition models, as well as the GELI model, were also capable of replicating the result, but only after a rescaling (normalization) of the asymmetric inputs. The energy well framework has also been useful in describing the effect of perceptual “trapping” in binocular rivalry (Suzuki and Grabowecky 2002).

DISCUSSION

Our work was primarily motivated by Shpiro et al. (2007), which showed that mutual inhibition models disobey L4 at low contrasts. Since mutual inhibition architecture remains an attractive candidate for modeling perceptual bistability phenomena, we have proposed simple modifications to the general mutual inhibition model that resolve this discrepancy. Our proposals are quite general and would apply to any circuit with mutual inhibition.

One focus of our work was on how rivalry models behave in the absence of stimuli. If we presume that significant neural activity in the model explicitly represents a percept then this would constrain activity to be below the perceptual threshold for blank stimuli. This can take the form of the both-off regime, where background spontaneous activity would resemble stationary noisy activity (since u₁ and u₂ are generally small but nonzero in this regime). Alternatively, blank stimuli may correspond to an oscillation regime, where the circuit rivals in the absence of any stimuli (implying highly structured, large amplitude spontaneous activity). Mathematically, the models of Moreno-Bote et al. (2007) and Ashwin and Lavric (2010) follow the latter assumption, although they were generally presented as capturing the dynamics of rivalry for only nonblank stimuli. Such an approach may indeed be beneficial as evident by general insights offered by the energy well framework (Moreno- Bote et al. 2010; Hohwy et al. 2008; Suzuki and Grabowecky 2002). Nevertheless, the distinction is important because the L4 problem arises precisely because of the transition from both-off to oscillations. By also assuming rivalrous activity in the absence of a stimulus, the mutual inhibition model can indeed fully account for L4 via the “restriction of input” (see Restriction of input) or strong recurrent excitation (see Control of ID Region Through Recurrent Excitation). This implies that nonmutual inhibition models that give L4 but also assume rivalrous activity in the absence of stimuli cannot be taken as evidence against mutual inhibition (with regard to L4). Our proposed solutions that allow the mutual inhibition model to transition directly from both-off to DD oscillations could also be applied to other models.

Understanding how rivalry models behave in the absence of stimuli is important for replicating psychophysics experiments incorporating on/off presentations of ambiguous images. For example, the Wilson (2003) model replicates results from Logothetis et al. (1996) that use flicker and switch stimuli, where ambiguous images are presented in an on/off cycle of 18 Hz (and images are swapped between the eyes three times per second). Also, the Wilson (2007) and Noest et al. (2007) models replicate rivalry memory, a phenomena that emerges when continuous presentations are interrupted by a blank stimulus for a second or more; upon reintroduction of the ambiguous images the previously dominant percept tends to reappear (Leopold et al. 2002). This phenomena is novel because on/off timings can be set such that one percept remains dominant for minutes at a time. All of these models assume the both-off attractor for the blank portions of the on/off cycles, and results could not be replicated in these models otherwise. To see this, consider rivalry memory. The Noest et al. (2007) and Wilson (2007) mutual inhibition models include facilitation terms that bias the previously active percept to regain dominance. The activity variables quickly decay to the both-off attractor during the blank stimulus interval. When the images are reintroduced, the system immediately assumes two WTA attractors, and the model must “choose” one of the two states. A memory trace from the previously active percept is incorporated into facilitation terms that ensure that the both-off “initial condition” falls within the basin of attraction of the appropriate (i.e., previously dominant) state. These facilitation inputs are weak enough that they do not significantly affect the rivalry process but are strong enough to successfully bias the value of the both-off attractor state. Alternatively, models that assume rivalrous activity in the absence of a stimulus would not predict rivalry memory. For a blank interval lasting several seconds, the model would simply continue to rival (presumably below some perceptual threshold) and not replicate the ability of certain on/off timings to reliably stabilize a single percept for minutes at a time.

The Wilson (2007) and Noest et al. (2007) models are extensions of general mutual inhibition models, and the extensions that account for rivalry memory do not significantly affect the dynamics of standard rivalry. The extensions are necessary because Eqs. 1–3 do not, in themselves, predict rivalry memory. The habituation variables during blank intervals bias the previously suppressed percept to attain dominance. This phenomena is indeed observed experimentally when blank intervals are sufficiently short (less than ∼500 ms), whereas the rivalry memory effect requires longer blank durations. Importantly, the Noest et al. (2007) model successfully captures both experimental features: forced percept switches for short blank durations and percept stabilization for long blank durations.

The Noest et al. (2007) model is a mathematical variation of Eqs. 1–2 involving the same general dynamics, i.e., mutual inhibition enforces two attractor states where switches can occur due to adaptation or noise. Under the presence of noise, the Noest et al. (2007) formulation indeed includes both ID and DD behaviors (data not shown). Our input preprocessing solution or its biophysical implementations would allow this model to transition from both-off to DD oscillations to comply with L4. These extensions would not affect the model's ability to replicate phenomena that utilize on/off sequences, since these solutions only affect behavior for contrasts near detection threshold. Importantly, these solutions would not affect the “memory trace” of the model. The facilitation variable would still be allowed to grow and decay across a continuum of values, allowing it to replicate experimental features not captured by the binary memory trace of the Wilson (2007) model [see Pearson and Brascamp (2008)]. Our extensions also do not conflict with other variations of the Noest et al. (2007) model that allow it to account for flash suppression and flash facilitation (Brascamp et al. 2007), memory effects across multiple time scales (Brascamp et al. 2008), and the effects of voluntary control on the percept-choice process (Klink et al. 2008). The general idea is that the Noest et al. (2007) model incorporates a mathematically parsimonious extension to mutual inhibition models to account for various phenomena involving on/off presentations, and our solutions to the L4 problem fit in nicely with the Noest et al. (2007) framework because they do not affect the evolution of the model's facilitation variable.

In binocular rivalry, fused percepts or fusion (i.e., a superposition of both left- and right-eye stimuli) may occur for a significant portion of viewing duration, even when steps are taken to minimize their occurrence. For example, van Ee (2009) used stimuli that yielded a 2% occurrence of fusion for high contrast stimuli and up to a 30% occurrence for low contrast stimuli [other experiments also show that the predominance of fused percepts decrease with increasing contrast (Hollins 1980)]. It is unclear how fused percepts should be modeled in a mutual inhibition framework. A natural assumption is that the both-on state corresponds to fusion. However, this state only occurs for high contrast stimuli in the mutual inhibition model, which raises the question of what could represent fusion for low contrast. One possibility is that this is represented by a third population in the multipopulation model. This hypothesis would predict that high contrast and low contrast fusion are inherently different. High contrast fusion is a coexistence of the two percepts, whereas low contrast fusion is a combination of the two stimuli into a different distinct percept. Another prediction would be that low contrast fusion would form more easily if the combination of the two stimuli more naturally form a single gestalt such as oblique gratings (i.e., parallel lines) into a plaid, whereas high contrast fusion would be relatively independent of the congruity of the two stimuli. In experiments, high contrast fusion occurs reliably if stimulus presentations are very short (∼100 ms; Wolfe 1983), and this effect is captured by mutual inhibition models if u₁ ≈ u₂ > 0 is assumed to yield a fused percept [upon stimulus introduction, u₁ and u₂ increase simultaneously for a brief duration until the system chooses one of the two WTA states; see Noest et al. (2007)].

Although our work showed how mutual inhibition models can fully comply with L4, it is possible that L4 itself is invalid at low contrasts. Although published data on L4 is sparse, DD behavior does appear to hold down to the contrast detection threshold for oriented gratings [e.g., Fig. 1B of van Ee (2009)]. However, convincing confirmation of L4 would require high resolution sampling of contrast values just above detection threshold (where one would expect ID behavior to occur, if it exists). Liu et al. (1992) examined ambiguous oriented gratings at very low contrasts and reported that at stimulus onset, subjects initially perceive a fused overlap of the two gratings. The fused percept lasts several seconds but eventually rivalry occurs. This could be modeled by a third population representing the fused percept competing with the two others representing the two stimuli. The authors did not report on dominance durations during rivalry, but they did show that in this very low contrast regime, an increase in contrast resulted in a monotonic decrease in the transient duration of the initial fused percept. This result might be taken as evidence that L4 holds down to contrast detection threshold. That is, we may suppose that for increases in contrast, the reported decrease in stability of the initial fused percept would imply a similar decrease in stability for the individual percepts once rivalry begins. This would imply faster perceptual switches or L4. Therefore, solutions to the L4 problem in the mutual inhibition model that eliminate the ID regime altogether may be favorable to the solutions that merely minimize the regime.

We considered models with adaptation and/or synaptic depression (with and without noise). Shpiro et al. (2009) showed that both a deterministic adaptation process and noise are required to reproduce the gamma distribution of dominance durations seen experimentally. A consequence of an adaptation process is that it produces successive correlations in dominance durations. Although early studies have shown such correlations (Fox and Herrmann 1967; Lehky 1995; Leopold and Logothetis 1996), they have been regarded as too small to be significant, implying that adaptation is not involved in rivalry. On the other hand, noise-only models (Moreno-Bote et al. 2007) while showing no correlations, yield an exponential distribution of dominance durations that is not observed. A recent study from van Ee (2009) showed significant nonzero correlations for successive dominance durations by accounting for previously ignored experimental impurities (reaction time, drift, and incomplete percepts). Several other experimental studies (van Ee 2011; Alais et al. 2010; Kang and Blake 2010; Kim et al. 2006; Suzuki and Grabowecky 2002) suggest that adaptation mechanisms play a role in rivalry. This is in contrast to other modeling efforts that emphasize the role of noise in causing perceptual switches (Moreno-Bote et al. 2007; Gigante et al. 2009). As we stated earlier, the L1–L4 dynamics of the mutual inhibition model are independent of whether it is noise or adaptation (or both) that facilitate switches. For example, if we removed adaptation and included only noise in the model of Fig. 4, then all plots (average dominance duration as a function of I) would remain qualitatively unchanged. The main difference is that noise induces perceptual switches in WTA regimes. If both noise and adaptation are indeed involved in rivalry, then one question is which of the two ultimately “causes” each perceptual switch. If noise is the primary switching mechanism, then switches would not occur if noise was removed. If switches are due to adaptation, then a noise-free system would oscillate with perfect periodicity. In our current study, we focused primarily on the deterministic dynamics so as to capture the qualitative ID/DD behavior of the model as clearly as possible. However, if noise is the primary “cause” of perceptual switches, then we could account for that with a broader WTA regime by increasing inhibition strength or reducing adaptation strength. For a set of parameters that produces an intermediate WTA regime, our input preprocessing and multiple population solutions to the L4 problem still hold as long as input is restricted from the “noisy” ID regime (e.g., gray curves in Figs. 4A, 6C, and 8A). Hence, our solutions hold even if we require the model to operate in a regime where noise is the primary cause of switches.

The input preprocessing solution and its implementations predict that as image contrast is increased from subthreshold detection levels, the images will “pop in” at the detection threshold and give way to rivalry [although our model does not capture the initial summation period (Liu et al. 1992)]. Percepts will “pop out” of perception at a lower threshold when contrast is approached from above. The models predict that a similar perceptual hysteresis occurs for nonambiguous stimuli. This has been observed by Kleinschmidt et al. (2002) who increased and decreased the contrast of an object (the letter “K”) against a noisy background and observers reported perceptual hysteresis: the object “popped in” to perception at a higher contrast than when it “popped out.” This study suggests that existence of a percept cannot be captured by a fixed detection threshold. For our assumption that sufficient neural activity in our model's populations corresponds to a percept, the results of Kleinschmidt et al. (2002) suggest we cannot model the I = g(C) relationship as a smooth, increasing function. Rather, a hysteretic relationship between C and I, such as that given by Eq. 6 or with a multiple population model, would fit the Kleinschmidt et al. (2002) results and, as we have shown, is also capable of solving the L4 problem.

There is increasing evidence that binocular rivalry shares several key characteristics with other bistable stimuli. For example, Klink et al. (2008) used a rotating structure-from-motion sphere, where the stimulus could be perceived as either rotating clockwise or counterclockwise. Here, parametric changes in dot luminance can alter the average dominance durations of the percepts (e.g., higher luminance for left-moving dots biases the clockwise percept). Klink et al. (2008) showed that all four of Levelt's (revised) propositions held. Interestingly, although the averaged data for the five subjects in Klink et al. (2008) followed L4, two of the subjects exhibited ID regimes. It is unclear whether these ID regimes are due to statistical variation or represent actual perceptual dynamics. Also, their data show only modest changes in dominance durations down the C₁ = C₂ diagonal (L4) compared with changes along vertical or horizontal cross-sections (C₁ or C₂ fixed, i.e., L1–L3). This is similar to observations for binocular rivalry (Moreno-Bote et al. 2010) and mutual inhibition dynamics (Fig. 4C). This suggests that if ID behavior indeed occurs, it may be relatively difficult to observe experimentally. It may be fruitful to find a class of stimuli (whether in binocular rivalry or other bistable stimuli) that reliably produces ID behavior for low stimulus strengths. This would lend evidence toward mutual inhibition as a mechanism for perceptual rivalry, since by default they do predict an ID regime. Though for cases where only DD behavior occurs for all accessible stimulus strengths (as it appears to be the case in binocular rivalry), our current study provides plausible mechanisms to account for this.

Finally, we note that the modifications made to the mutual inhibition model in this study are not mutually exclusive. The multiple population model is a biophysical implementation of the input preprocessing solution, but the parametric manipulations that minimize the ID regime fit nicely with this form of input control. If the ID regime is minimized via the gain function or choice of habituation mechanism, then this implies that the input need only skip over a small range of values to comply with L4.

GRANTS

This work was supported by the National Institute of Diabetes and Digestive and Kidney Diseases, NIH Intramural Research Program.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

APPENDIX

Linear Threshold Gain Function

Here we show how the dynamics of Eqs. 1–2 behave when f(x) is taken to be a linear threshold gain function:

$$f\left(x\right)={\left[x\right]}_{+}\equiv \{\begin{array}{cc}0& \text{if}\hspace{0.17em}x<0\\ x& \text{if}\hspace{0.17em}x\ge 0\end{array}$$ (8)

We omit recurrent excitation and synaptic depression, but include adaptation, which is the case that was presented in Wilson (2007). Assume that population one is active and is suppressing population two. The switch threshold is at x = 0, but the choice of gain function precludes release switches. This is because u₁ has an asymptotic value that is above threshold. Specifically,

$$u_1\left(\infty \right)=\frac{I}{1+\gamma }>0$$

[see Wilson (2007)]. Therefore, switches only occur when the off population crosses threshold, i.e., when

$$I-\beta u_1-\gamma a_2=0$$

The adaptation variables obey

$$\begin{array}{l}{a}_1\left(t\right)=\left(a_1\left(0\right)-\frac{1}{1+\gamma }\right)e^{-{\left(1+\gamma \right)}^{t/\tau }}+\frac{I}{1+\gamma }\hfill \\ a_2\left(t\right)=a_2\left(0\right)e^{-t/\tau }\hfill \end{array}$$

Then using u₁ = I − a₁ we could solve for T(I), but due to the different time constants in a₁(t) and a₂(t) there is no closed form expression. As in Wilson (2007), a useful approximation is to assume that u₁ is at its asymptotic value at the time of the switch, i.e., u₁(T) ≈ u₁(∞). This assumption also gives the value for a₂(0), namely a₂(0) = u₁(∞) = a₁(∞), since we also assume that u₂ was at its asymptotic value before the switch at t = 0. Therefore, the condition for switches is given by

$$I-\beta u_1\left(\infty \right)-\gamma u_1\left(\infty \right)e^{-T/\tau }=0$$

Solving for T(I) yields

$$T=-\tau \log \left(\frac{I-\beta u_1\left(\infty \right)}{\gamma u_1\left(\infty \right)}\right)=-\tau \log \left(\frac{I}{\gamma u_1\left(\infty \right)}-\frac{\beta }{\gamma }\right)$$ (9)

[Note: this is a special case of Eq. 8 from Wilson (2007).] Notice that the u₁(∞) = I/(1+γ) term has a single factor of I, therefore, all factors of I cancel and T is constant with respect to I. Through simulation we can confirm that the above two assumptions [i.e., τ_u ≈ 0 and u₁(T) ≈ u₁(∞)] do not affect this result. Even changing the slope of the linear threshold function for x ≥ 0 does not affect this result (since the multiplicative factor would just absorb into the parameters I, β, and γ). Interestingly, despite the flat T(I) curve, a linear threshold function can still predict L1–L3 (Wilson 2007). That is, asymmetric changes in I₁ and I₂ follow L1–L3, yet predict no change in percept duration when I₁ = I₂.

To produce DD oscillations, we need to ensure that u₁(∞) is not linearly dependent on I (but monotonically increases with I), so that the terms in Eq. 9 do not cancel. Therefore, we can replace the linear threshold function with f(x) = ${\sqrt{\left[x\right]}}_{+}$. The function T(I) is still given by Eq. 9, but now u₁(∞) is determined by x. Specifically,

$$u_1\left(\infty \right)=\frac{-\gamma +\sqrt{{\gamma }^2+4I}}{2}$$

which we can plug back into Eq. 9. Hence, dominance time is now a monotonically decreasing function of I. Therefore, choosing a square root gain function and including adaptation yields purely decreasing-duration oscillations in Eqs. 1–2.

Equations

In Figs. 4 and 10, the choice of firing rate function is a sigmoid:

$$f\left(x\right)=1/\left(1+e^{-rx}\right)$$ (10)

with r = 10. Note that in all of our functions, we could also include a threshold parameter, θ, and replace x with x − θ. We omit θ since it is simply an additive mechanism, like I, and thus does not change the qualitative behavior of the model with respect to changes in I (i.e., it would simply shift the abscissa of our bifurcation diagrams by an amount θ).

We also considered a smooth variant of the linear threshold gain function given by

$$f\left(x\right)={\left[x\right]}_{*}\equiv c\log \left(1+e^{-x/c}\right)$$ (11)

The parameter c determines the level of “smoothing” around x = 0. As c → 0, [x]_* → [x]₊.

Finally, as in recent rivalry studies (Moreno-Bote et al. 2007; Shpiro et al. 2009), we model input noise as an Ornstein-Uhlenbeck process:

$$\dot{\eta }=-\frac{\eta }{{\tau }_s}+\sigma \sqrt{\frac{2}{{\tau }_s}}\xi \left(t\right)$$ (12)

where τ_s = 100 ms in our simulations and ξ(t) is a white noise process with zero mean. The parameter σ determines the strength of the noise and assumes different values across our simulations. Two independent noise processes, η₁ and η₂, are simply added to the net inputs of each population.