Clustering Fiber Traces Using Normalized Cuts

Abstract

In this paper we present a framework for unsupervised segmentation of white matter fiber traces obtained from diffusion weighted MRI data. Fiber traces are compared pairwise to create a weighted undirected graph which is partitioned into coherent sets using the normalized cut (N cut) criterion. A simple and yet effective method for pairwise comparison of fiber traces is presented which in combination with the N cut criterion is shown to produce plausible segmentations of both synthetic and real fiber trace data. Segmentations are visualized as colored stream-tubes or transformed to a segmentation of voxel space, revealing structures in a way that looks promising for future explorative studies of diffusion weighted MRI data.

1 Introduction

Diffusion Weighted MRI (DWI) makes it possible to non-invasively measure water diffusion within tissue. In a volume acquired using DWI, each voxel contains a diffusion tensor or other higher order descriptor for the local water diffusion. In fibrous tissue such as muscles and human brain white matter, water tend to diffuse less in the directions perpendicular to the fiber structure. This makes it possible to study the local fiber orientations indirectly by interpreting the water diffusion within the voxel. From DWI data it is therefore possible to create so called fiber traces from virtual particles, traveling along the direction of maximum diffusion, starting from a set of seed points [1,2,13], a.k.a fiber tracking. Performing fiber tracking in DWI data from the human brain gives valuable insights about fiber tract connectivity, useful in for instance surgical planning and for the study of various diseases such as schizophrenia.

In our experiments we have exclusively used data from so called diffusion tensor MRI (DT-MRI) [9], where the diffusion inside a voxelis described by a second order symmetric positive definite 3 × 3 tensor, which may be thought of as an ellipsoid. An elongated ellipsoid represent high diffusivity in a particular direction, which may be interpreted as the dominant orientation of the fibers going thru that particular voxel. From this data, fiber traces were created within the white matter areas using a standard fiber tracking algorithm following the principal direction of diffusion based on a fourth-order Runge-Kutta integration scheme.

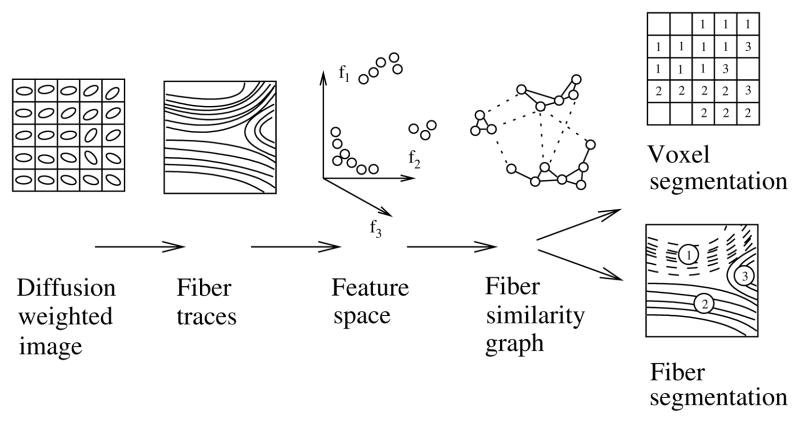
The contribution of this paper is a novel post processing method for clustering or segmentation of such fiber traces. Fiber traces are grouped according to a pairwise similarity function which takes into account the shape and connectivity of fiber traces. The clustering method we propose builds on so called normalized cuts, which have previously been introduced in the computer vision community by Shi and Malik [10] for automatic segmentation of digital images. This results in an unsupervised segmentation of human brain white matter, in which fiber traces are grouped into coherent bundles, applicable to any DWI technology able to produce fiber traces. For an overview of the method, see figure 1.

Fig. 1.

An overview of the proposed method. Whether the result should be in voxels or fiber traces depends highly on the application. Fiber traces are flexible, they are for instance able to represent multiple fiber directions going thru a point in space. Voxels are on the other hand more suitable for volume rendering.

1.1 Previous Work

There are numerous examples where fiber traces from DWI have successfully revealed fiber tracts in the human brain, see for instance [2,3,13]. Stream-tubes have often been used for visualization [14], sometimes in combination with coloring schemes and variation of the stream-tube thickness according to some aspect of the underlying local diffusion descriptor. The idea of using fiber traces to obtain segmentations of white matter fiber tracts, as well as gray matter areas, have been explored in a number of papers recently. In [3] a segmentation of deep gray matter structures is performed using probabilistic fiber tracking, which connects pre-segmented areas of the human cortex with the thalamus. There also exist manual approaches to organize fiber traces into fiber bundles, such as the virtual dissection proposed in [5]. In [4] the idea of pseudo-coloring (soft clustering) fiber traces to enhance the perception of connectivity in visualizations of human brain white matter was presented. Some unsupervised approaches to clustering of fiber traces, similar to the one in this paper, have also been reported. For instance fuzzy c-means clustering [11] and K nearest neighbors [6]. Outside the area of medical image processing, clustering of curves [8] has been reported.

2 Determining Fiber Similarity

Many clustering methods, including the N Cut being used in this paper, operate on a graph with undirected weighted edges describing the pairwise similarity of the objects to be clustered. This graph may be described using a weight matrix W, which is symmetric and has values ranging from 0 (dissimilar) to 1 (similar).

A fiber trace, represented as an ordered set of points in space, is a fairly high-dimensional object. Therefore the pairwise comparison of all fiber traces could potentially be a time-demanding task if fiber trace similarity is cumbersome to calculate and the number of fiber traces is high. In this paper we propose to split the computation of similarity into two steps:

1. Mapping high-dimensional fiber traces to a relatively low-dimensional Euclidean feature space, preserving some but not all information about fiber shape and fiber connectivity. This mapping is oblivious, acting on each fiber separately.

2. The use of a Gaussian kernel for comparison of points in the Euclidean feature space. This function acts on pairs of fiber traces.

It is important to point out early that even though the above mapping to a feature space may seem to be crude at a first glance, it works surprisingly well for fiber traces in practice. For a set of N fiber traces the first calculation above cost O(N), while the second calculation cost O(N²) operations. This is also the reason for pre-processing the fiber data in the first step, making the second calculation more computationally efficient.

2.1 Mapping Fiber Traces to an Euclidean Feature Space

The position, shape and connectivity are important properties of a fiber trace to preserve in the mapping to a feature space. If we regard a fiber trace as just a set of points in space, we capture a sketch of these properties by calculating the mean vector m and the covariance matrix C of the points building up the fiber trace. In order to avoid non-linear scaling behavior, we take the square root of the covariance matrix, $\mathbf{G}=\sqrt{\mathbf{C}}$ Now the mapping of a fiber F may be described

$$\mathrm{\Phi }(F)={(m_x,m_y,m_z,g_{xx},g_{xy},g_{xz},g_{yy},g_{yz},g_{zz})}^T,$$ (1)

which is a 9-dimensional vector. This mapping has the desirable property that it is rotation and translation invariant in the sense that the Euclidean distance between two fiber traces mapped to the 9-dimensional space is invariant to any rotations or translations in the original space. For applications where mean and covariance is not enough to discriminate between different clusters of fiber traces, higher order central moments [12] could add more feature dimensions to the above mapping. Also, in cases when fiber connectivity is more important than shape, a higher weight could be given to the fiber trace end-points in the calculation of the mean vector and covariance matrix above. Different weights could also be given to the mean vector and the covariance components in the mapping in eq (1).

2.2 Using the Gaussian Kernel for Pairwise Comparison

When fiber traces have been mapped to points in a Euclidean feature space, they may be compared relatively easy for similarity. We choose Gaussian kernels (a.k.a. Radial Basis Functions in Neural Networks literature)

$$K(x,y)=exp(-\frac{{\left|\right|x-y\left|\right|}^2}{2{\sigma }^2})$$ (2)

which are symmetric and contain a parameter σ which we may use to adjust the sensitivity of the similarity function. This function maps similar points in feature space to unity and dissimilar points to zero.

2.3 Constructing W

By combining the mapping to a Euclidean feature space with the Gaussian kernel, we obtain the weights of an undirected graph describing the similarity between all pairs of fiber traces. The weights are stored in a matrix W defined as

$$w_{ab}=K(\mathrm{\Phi }(F_a),\mathrm{\Phi }(F_b)).$$ (3)

This matrix is expected to be sparse, having most of the values close to zero.

3 Normalized Cut and Clustering

Clustering, segmentation and perceptual grouping using normalized cuts was introduced to the computer vision community by Shi and Malik in [10]. The points to be clustered are represented by a undirected graph G = (V, E), where the nodes correspond to the points to be clustered and each edge has weight w(i, j) which represent the similarity between point i and j. The cut is a graph theoretical concept which for a partition of the nodes into two disjunct sets A and B bipartitioning V is defined as

$$\mathit{cut}(A,B)=\sum _{u\in A,v\in B}w(u,v)$$ (4)

Using the cut, an optimal partitioning of the nodes may be defined as one that minimizes the cut. Intuitively this could be used for segmentation, while the minimum cut corresponds to a partitioning which keeps well connected components of the graph together. However, there is no bias in the minimum cut which says it should partition the graph in two parts of equal size. Shi and Malik therefore defined the normalized cut, which is defined as

$$N\mathit{cut}(A,B)=\frac{\mathit{cut}(A,B)}{\mathit{asso}(A,V)}+\frac{\mathit{cut}(A,B)}{\mathit{asso}(B,V)}$$ (5)

where asso(A, V) = Σ_u∈A,t∈V w(u, t). This new measure N cut tries to minimize the cut, while at the same time penalizing partitions in which one set of nodes is only loosely connected to the graph at large. If we define x_i = 1 when node i ∈ A, x_i = −1 when node i ∈ B, d(i) = Σ_j w(i, j), $k=\frac{{\sum }_{x_i>0}{d}_i}{{\sum }_i{d}_i}$, D is a matrix with d = d(i) in it’s diagonal and W is the matrix defined by w(i, j) then it is shown in [10] that

$$N\mathit{cut}=\frac{{(1+x)}^T(D-W)(1+x)}{k{\overline{1}}^{T}D\overline{1}}+\frac{{(1-x)}^T(D-W)(1-x)}{(1-k){\overline{1}}^{T}D\overline{1}}.$$ (6)

which can be shown to be equivalent to

$$N\mathit{cut}=\frac{y^T(D-W)y}{y^{T}Dy}$$ (7)

where y_i ∈ {1, −b}, b = k/(1 − k), for y = (1 + x) − b(1 − x) while y^T d = 0. Relaxing the problem by allowing y to take any real values results in the minimization of the so called Rayleigh quotient, which can be minimized by solving

$$(D-W)y=\lambda Dy$$ (8)

It is shown in [10] that the second smallest eigenvector of eq. (8) minimizes the real valued version of the normalized cut.

In our implementation we used the second smallest eigenvector to obtain a 1-d ordering of the vertices of the graph. A random search was then performed to determine a good threshold for the bipartitioning of the graph. To test the goodness of a specific threshold the true discrete N cut was calculated. When the graph has been split into two, [10] recommends the partitioning continues recursively until the N cut raises above a certain value.

4 Results

The method was tested on both synthetic datasets and fiber traces from real diffusion weighted MRI. Results are visualized using both stream-tubes and color coded voxel data. All algorithms were implemented in Matlab.

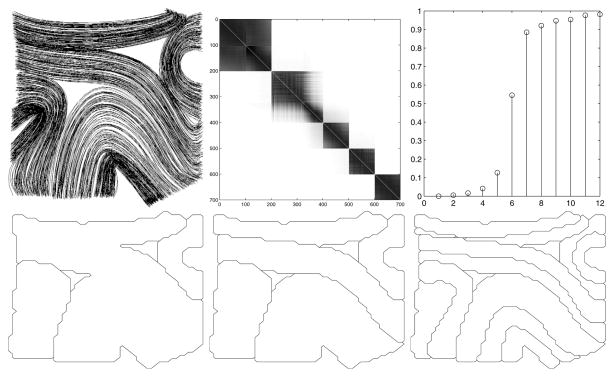
• – In figure 2 the method is tested on synthetically generated fiber traces in 2-D.

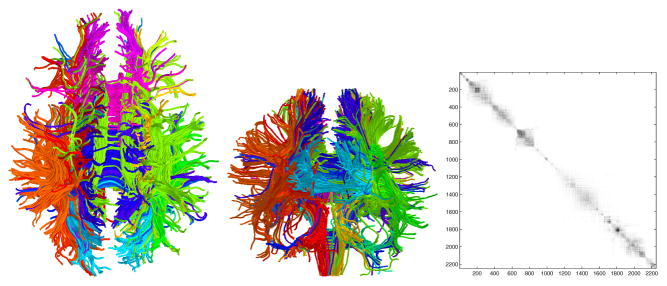
• – In figure 3 real fiber traces obtained from DT-MRI was used as input.

• – In figure 4 the method was tested with a very large value of σ and direct mapping of the second, third and fourth eigenvector to colors similar to the approach described in [4].

Fig. 2.

Top left A set of synthetic fiber traces in 2-D. Top middle: The matrix W. Rows and columns sorted according to the second smallest eigenvector. The Gaussian kernel have been chosen so that five clusters present themselves naturally. Top right: The 15 smallest eigenvalues of (D − W)/D. Bottom: Segmentation obtained from recursive bipartitioning of the fiber traces. Maximum value of the N cut set to 0.2, 2.5 and 4.5 respectively.

Fig. 3.

Left: Axial view of a segmentation obtained from recursive bipartitioning of the white matter fiber traces. Maximum value of the N cut was set to 1.5 and Gaussian kernel σ = 20. . The colors of fiber traces indicate cluster membership. Middle: Coronal view. Right: The matrix W. Rows and columns sorted according to the second smallest eigenvector.

Fig. 4.

Pseudo-coloring of fiber traces. RGB colors are derived directly from scaled versions of the 2nd, 3rd and 4th eigenvector of (D − W)/D. Using a very large Gaussian kernel, σ = 100, results in a soft clustering effect. Note the enhanced perception of fiber connectivity and shape, despite the lack of discrete clusters. Left: Whole brain white matter visualized using pseudo-colored fiber traces. Middle: A subset of the white matter fiber traces visualized using pseudo-colored fiber traces. Right: Pseudo-coloring of voxels belonging to white matter enhance perception of connectivity in slices or volumes. To fill in holes in white matter when fiber traces were transformed to voxels, a nearest-neighbor approach combined with a white matter mask was used.

5 Discussion

We have not yet investigated the effects of noise to the clustering. Also, the maximum number of fiber traces we have analyzed so far is only about 5000, due to the current implementation in Matlab which does not fully exploit the sparsity of W. Never the less, the experiments show the potential of the N Cut criterion and the proposed measure of fiber similarity.

One insight from the experiments is that pseudo-coloring of fiber traces is very effective to reveal errors in fiber tracking algorithms. A collection of fiber traces may look ok at a first glance, but after pseudo-coloring, the anomalies are easily spotted. One example of this is in figure 4 (middle) where the red fiber traces may be identified instantly as outliers because they have a very different color than surrounding fiber traces.

In our experiments we have segmented fiber traces and then sometimes transformed the results back to voxel space. One may ask if it would be possible to segment voxels directly, and what features to use to discriminate voxels. A solution with obvious similarities to the approach presented in this paper would be to perform fiber tracking, possibly stochastic [3], from each voxel inside white matter and regard the fiber traces as a non-local features of the voxels – macro features.

The continuous coloring in figure 4 appears to be more visually pleasing than the discrete coloring according to the segmentation in figure 3. One may in fact ask if a structure such as the corpus callosum is meaningful to partition into several clusters or whether it is better described as one fiber bundle parameterized by a coordinate system going from anterior to posterior. One could think of the smoothly varying colors in figure 4 as coordinate systems, parameterizing all fiber traces in the cross bundle directions. It is in fact then also natural to add a parameterization of each bundle in the fiber direction.

In conclusion the proposed clustering method seems to be a promising new way to automatically reveal the global structure of white matter by segmentation of fiber traces obtained from DWI data. We believe this to be useful in for instance explorative studies of the brain and for visualization of DWI data in surgical planning applications. Important to note though is that all post processing methods for fiber traces share the same weakness: they all rely on a good fiber tracking algorithm to perform well.