Compensation method for obtaining accurate, sub-micrometer displacement measurements of immersed specimens using electronic speckle interferometry

Abstract

We proposed and validated a compensation method that accounts for the optical distortion inherent in measuring displacements on specimens immersed in aqueous solution. A spherically-shaped rubber specimen was mounted and pressurized on a custom apparatus, with the resulting surface displacements recorded using electronic speckle pattern interferometry (ESPI). Point-to-point light direction computation is achieved by a ray-tracing strategy coupled with customized B-spline-based analytical representation of the specimen shape. The compensation method reduced the mean magnitude of the displacement error induced by the optical distortion from 35% to 3%, and ESPI displacement measurement repeatability showed a mean variance of 16 nm at the 95% confidence level for immersed specimens. The ESPI interferometer and numerical data analysis procedure presented herein provide reliable, accurate, and repeatable measurement of sub-micrometer deformations obtained from pressurization tests of spherically-shaped specimens immersed in aqueous salt solution. This method can be used to quantify small deformations in biological tissue samples under load, while maintaining the hydration necessary to ensure accurate material property assessment.

1. Introduction

Optical measurement techniques can provide fast, full-field, and highly accurate measurements of specimen displacements. These techniques do not provide a direct measurement of the specimen deformation, but record light intensity data as a function of the displacement field and the sensitivity of the optical set-up. Digital Image Correlation (DIC) and Electronic Speckle Pattern Interferometry (ESPI) are two of the most common optical techniques used for analyzing specimens, prototypes, and real components subjected to mechanical deformation.

DIC-based measuring techniques, when properly compensated for refractive distortion where applicable, can adequately measure relatively homogeneous deformation fields under a variety of conditions. DIC displacement calculations are derived from pixel-based tracking of the variation of light intensity using correlation analysis and a reconstruction process that relates point projections in the cameras’ CCD plane to 3D space. Deformation resolution is limited by the field of view, resolution of the camera(s), and correlation sub-set size [1]. Measurement accuracy and repeatability are affected by sub-set shape functions [2], grayscale image value interpolation [3], speckle pattern distribution [4], and intensity pattern noise [5], all of which can introduce considerable measurement uncertainty. Out-of-plane displacement components are particularly susceptible to intensity pattern noise [5].

When analyzing the mechanical behavior of anisotropic specimens where estimation of local material properties and/or strain must be based on measurements of small displacements relative to immediately adjacent regions, the high spatial resolution, local measurement accuracy, and repeatability of ESPI make it a more suitable measurement technique than 3D DIC. ESPI has been used to measure displacements in posterior scleral shells from monkey eyes subjected to experimental inflation tests [6]. ESPI displacement calculations are based on recording a phase shift of a laser wavefront created by the deformation of the specimen surface [Eq. (1)], and by considering the sensitivity direction of the optical set-up, the displacement vectors can be calculated [Eq. (2)]. ESPI measurement resolution is limited only by the laser wavelength, and spatial resolution is limited by the optical sensor resolution [7]. Noise and decorrelation effects can affect accuracy and spatial resolution [8,9], although decorrelation effects can be sharply reduced by avoiding rigid body motion and limiting in-plane displacements. Decorrelation errors are negligible for specimens similar to that used in the present work that are fully constrained against rigid body motion and subjected to predominantly sub-micrometer out-of-plane displacement.

Mechanical testing of specimens immersed in water or salt solution is common for offshore structures (e.g., water-immersed pipelines) or biological tissues, whose hydration must be preserved during testing. Investigating the biomechanical behavior of biological tissues commonly involves displacement measurements of a specimen immersed in an aqueous solution (phosphate-buffered saline or PBS) while the recording device (CCD camera) is in air. Immersion of tissues in PBS or cell media keeps cells viable and preserves tissue hydration, which is necessary to maintain tissue mechanical properties as close to the in vivo state as possible [10,11]. This measurement set-up, however, involves a change of refractive index of the media present in optical path as depicted in Fig. 1 , which imparts optical distortions and changes the focal plane. Appropriate optical [12] or numerical compensation must be used to avoid large errors in the reconstruction of the displacement field.

Fig. 1.

Geometry for determining the sensitivity vector$\tilde{K}=({\widehat{K}}_i-{\widehat{K}}_o)$ when the specimen is illuminated by a spherical wavefront generated by the light source and observed at the view point. Refraction implies the bending of the light when passing from air to phosphate-buffered saline solution (PBS). Dimensions are in mm and are not to scale.

Extensive work has been done on developing effective numerical compensation methods for underwater measurements using DIC [13,14], but these methods have not been fully developed for ESPI.

An ESPI set-up for pure in-plane measurement doesn’t require compensation for change of refractive index in the optic media. In contrast, an ESPI set-up for out-of-plane measurement requires that the effective laser wavelength (shortened by the change of refractive index) has to be taken into account. The ESPI technique has been used to analyze mechanical deformation of biological tissues tested underwater [15,16] although this compensation was not employed. Zaslansky et al. used a commercial ESPI (Q300, Ettemeyer, Germany) to perform underwater deformation measurements on equine cortical bones using two different interferometer configurations, one for measuring pure in-plane displacement, and one for pure out-of-plane displacement [15]. No compensation for refractive index change of the optical media was used for the out-of-plane displacement in this work. Rivera et al. investigated the effects of underwater testing on ESPI measurements by comparing displacement fields obtained for both air- and water-immersed mechanical testing of a deformed cantilever beam [16], and the displacement fields were reconstructed using in-house software. Their results clearly show different phase values obtained for in-air and underwater tests, but the authors did not specify if (or how) any compensation was performed. In summary, previous studies either did not require compensation due to the nature of the experiment (different interferometers to measure different components of the displacement) or did not use compensation when it was needed.

We have therefore proposed and validated a numerical compensation method that aims to account for the optical distortions inherent in the mechanical testing of specimens immersed in aqueous solutions. The proposed compensation method is based on a ray-tracing algorithm that accounts for the change in refractive index that alters the optical path and wavelength of the illumination and observation light, taking into account the real geometry of the optical set-up and using a customized B-spline based parameterization of the specimen shape. The same customized B-spline formulation is also used to fit the reconstructed displacement field, which results in a continuous and differentiable analytical system of functions describing the specimen deformation. In addition, we assessed the measurement repeatability of the ESPI technique on an immersed rubber specimen, and validated the compensation technique proposed herein by comparing the displacement fields obtained between identical tests performed while the specimen was immersed in either air or phosphate-buffered saline (PBS).

2. Methods

The sensitivity direction of the ESPI technique is function of the illumination and observation directions. When the illuminating laser and observation light pass through media with significantly different refractive indices, the bending of the light rays must be taken into account in order to accurately evaluate the sensitivity directions and compute the measured displacement. The compensation method consisted of computing the actual direction of the laser beam incident to the specimen and the actual direction back to the viewpoint (lens entrance pupil) for every sample point on the specimen surface. This was accomplished by accounting for refraction and wavelength changes induced by the PBS and silica window. Point-to-point light direction computation is achieved by a ray-tracing strategy coupled with B-spline based analytical representation of the specimen shape. The compensation method aims to account for the differences in the information recorded by the ESPI when the test is performed with the specimen immersed in PBS instead of air such that one can obtain the same displacement field for specimens in air as that from specimens immersed in water.

The company provided the specifications of the optical features of the commercial ESPI used in this study, such as lens focal length and diffusers on the laser as it exits the optical fiber. The system came factory-calibrated, and light source and viewpoint were assumed to conform to the pinhole model. Correctness of the assumed optical position of the light sources and viewpoint were verified by comparing displacement maps obtained by a test in air and processed with the commercial software provided with the ESPI with those processed with the proposed method.

2.1. Theoretical aspects of the compensation method

The interferometer used in the present work allows us to measure three orthogonal displacement components, each of which can be evaluated by the well-known holographic interferometry formula:

$$\varphi =\frac{2\pi }{\lambda }({\widehat{K}}_i-{\widehat{K}}_o)\cdot \tilde{d}=\frac{2\pi }{\lambda }(K{}_{x}d{}_x+K{}_{y}d{}_y+K{}_{z}d{}_z),$$ (1)

where λ is the wavelength of the light source, $\tilde{d}$is the displacement occurring at the generic point, ${\widehat{K}}_i$ and ${\widehat{K}}_o$ are the unit vectors identifying the illumination and observation directions, respectively, $\tilde{K}$is the sensitivity vector, and ϕ is the phase variation induced by the displacement. Thus, if at least three linearly independent measurements of the phase are available (i.e., three sensitivity vectors) the displacement vector can be directly retrieved; in the case of four phase measurements, the displacement vector is evaluated accordingly to the following relation:

$$\left\{\begin{array}{c}{d}_x\\ d_y\\ d_z\end{array}\right\}=\frac{\lambda }{2\pi }{\left[\tilde{K}\right]}^{\ast }\left\{\begin{array}{l}{\varphi }_1\\ {\varphi }_2\\ {\varphi }_3\\ {\varphi }_4\end{array}\right\},$$ (2)

where_{${\varphi }_i$}is the absolute phase in the i-direction, and _{${\left[\tilde{K}\right]}^{\ast }$}represents the pseudo-inverse of the 4x3 matrix obtained with the four sensitivity vectors.

The sensitivity vector can be considered constant over the investigated area, provided that the illuminating beam is collimated and the anterior principal plane of the object is sufficiently far from the observed surface. In the present application, the operating conditions do not allow this simplification, so it is necessary to take into account the real locations of light sources and of the viewpoint. This operation was accomplished by considering the real geometry of the interferometer point-to-point by taking into account both the location of the light sources and the optics of the camera.

The presence of two different refractive media through which the light travels during the experiment requires taking into account both the bending of the light rays and the shortening of the wavelength in the medium where the displacements occur [Eq. (3)]. The wavelength change can be evaluated by considering that the ratio of the wavelengths λ₁ and λ₂ of the light travelling in the two media is

$$\frac{{\lambda }_2}{{\lambda }_1}=\frac{n_1}{n_2}=\frac{\sin {\theta }_2}{\sin {\theta }_1},$$ (3)

where n₁ and n₂ are the refractive indices of the optical media, respectively, and θ₁ and θ₂ are the incident angles of the illumination direction before and after the air-water interface. Light ray bending can be compensated using Snell’s Law [Eq. (3)]. Figure 1 reports a schematic emphasizing the geometrical quantities necessary to carry on these calculations. If the shape of the specimen is known, the sensitivity vectors can be accurately evaluated point-by-point.

An ESPI configured for measuring pure in-plane displacements with collimated illumination direction doesn’t require refractive index change compensation. By considering a decomposition along three orthogonal directions (k,1,3), and by substituting in Eq. (1) λ/n for λ and $K_{ik}\arcsin (\sin {\theta }_{ik}/n)$ for_{${\widehat{K}}_i$}it can be seen that shortening of the wavelength that increases displacement sensitivity due to the higher refractive index of the water (here n) is perfectly compensated by the inclination change of the illumination direction at the air-water interface that decreases in-plane displacement sensitivity.

The experimental data obtained by the interferometer used in this study consists of four phase maps for each load step. A typical set of experimental data is shown in Fig. 2 , which represent the four wrapped phase maps recorded by the interferometer with the specimen immersed in PBS (upper row) and in air (lower row) for an identical loading step. Increased magnification (5x) of the specimen image obtained while immersed in PBS effectively increased the spatial resolution and the signal/noise level. Hence, a sub-set of 450x450 pixels (in PBS) was used to image the area of the rubber specimen in this study.

Fig. 2.

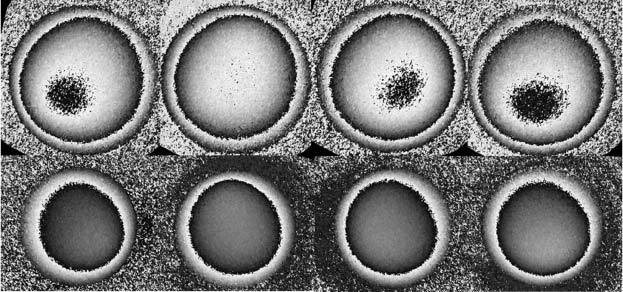
The wrapped fringes recorded by the ESPI for a pressure step of 0.5 mmHg in both air and PBS. Each image represents the information recorded for one of the four lasers of the ESPI. The images in the top row were obtained by performing the test in PBS, while the 4 images in the bottom row are recorded for the identical test performed in air. Note that the speckle data for these identical deformation tests are significantly different due to the presence of different optical media.

2.2. Experimental setup

The testing set-up used in this work (Fig. 3 ) was described in a previous study reporting results from testing scleral tissue [6]. Briefly, this set-up consists of

Fig. 3.

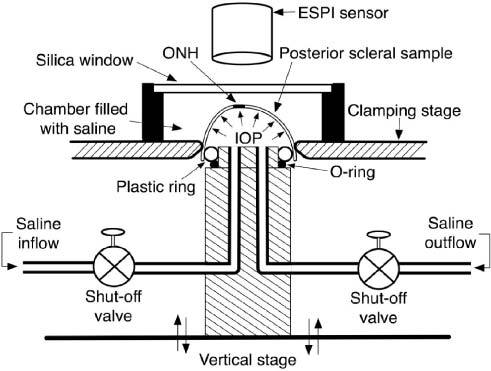
Pressurization apparatus for mechanical inflation test of spherically-shaped specimens. Reproduced with permission from Girard and colleagues [6].

• • A stainless steel support (clamping stage, and vertical stage) that clamped a rubber hemispherical specimen (1.5 mm thickness and 12 mm radius).
• • A hydraulic system that allowed the specimen to be pressurized with PBS solution.
• • A sealed chamber with a silica window needed to perform the test with the specimen immersed in PBS while allowing optical access to the specimen.
• • A commercial speckle interferometer (ESPI; Q-100, Dantec Dynamics A/S, Denmark). The interferometer consists of a unit containing four lasers (λ = 780nm) symmetrically positioned around the CCD camera (768x576 pixels, 8.2 μm pixel size) of the device, and of a central unit controlling the lasers and the camera.

A 3D mechanical digitizer (MicroScribe G2X, Immersion, San Jose, CA) was used to collect a cloud of about 2 thousand points on the outer surface of the specimen, which were used to define specimen geometry.

2.3. Inflation test procedure

Repeatability of the measurement system was assessed by measuring surface displacement of a spherically-shaped rubber specimen that was mounted and pressurized on the apparatus shown in Fig. 3. The specimen was subjected to preconditioning, consisting of 20 pressure cycles of 5 to 30 mmHg at a rate of 5 mmHg per second, and then allowed to recover for 10 minutes. The specimen was pressurized to 25 mmHg, then 10 additional cyclical pressure loadings of 0.5 mmHg were applied with the specimen immersed in air and in PBS at room temperature. A very small pressure load step was used to ensure a linear elastic response of the rubber specimen, which also ensures that the resulting deformation is a function of the pressure difference between internal and external surfaces of the rubber.

2.4. Assessment of measurement repeatability and compensation effectiveness

Random variability in the reconstructed displacement vector fields for different pressure steps is intrinsic to experimental measurements. Random changes in the sensitivity direction reduce measurement repeatability, while systematic changes in the sensitivity direction reduce measurement accuracy. The systematic difference in the phase maps shown in Fig. 2 is due to the variation of the sensitivity vector directions and the change of laser wavelength when test is performed in water rather than in air.

Measurement repeatability of the system was assessed by evaluating the mean variance [Eq. (4)] per load step of the absolute displacement recorded at 3000 equally-spaced sample points on the specimen surface.

A one-to-one comparison of all the 45 possible combinations of deformation fields obtained per load step was performed.

Effectiveness of the compensation method was assessed by comparing 10 load steps from tests performed in air with 10 load steps from identical tests performed in PBS. A one-to-one comparison of all 100 possible combinations of deformation fields obtained in the load steps performed in air and in water was performed by computing the mean absolute difference of the displacement magnitude and of the angle between the displacement vectors over 3000 sample points on the specimen surface. Compensation effectiveness was assessed by considering three different levels of compensation as follows:

• • No Compensation: no compensation for light ray bending or wavelength changes associated with transitions in the refractive index of the optical media.
• • Effective Wavelength Compensation: sensitivity vector directions are computed considering light bending and wavelength shortening due to refractive index transitions, but not accounting for the non-planar geometry of the specimen.
• • Full Compensation: sensitivity vector directions are computed considering light bending and wavelength shortening due to refractive index transitions, as well as the non-planar geometry of the specimen.

Variation of the difference (reconstruction error) between displacement vector fields reconstructed in air and water is considered at different compensation conditions. Measurement repeatability of the system was assessed by

$$MeanVariance=\frac{{\displaystyle \sum _{s=1}^{s.points}\sqrt{\frac{{\displaystyle \sum _{l=1}^{l.steps}{(\left|{\tilde{d}}_l^s\right|-\left|\overline{d^s}\right|)}^2}}{l.steps}}}}{s.points},$$ (4)

where_{$\left|\overline{d^s}\right|={\displaystyle \sum _{l=1}^{l.steps}\left|{\tilde{d}}_l^s\right|}/l.steps$}is the mean absolute displacements of the 10 load steps computed at a generic sample point.

2.5. B-spline based fitting

As mentioned in the introduction, noise in the phase maps affect accuracy [17] and repeatability [18] of the measurements. Filtering phase maps before the unwrapping procedure introduces systematic errors that reduce the spatial resolution of the measurement system [17]. We used a strategy wherein phase maps were unwrapped with an algorithm robust to noise (Flynn’s minimum discontinuity) [19] and then B-spline fitting was applied to the absolute phase maps with the aim of preserving a high spatial displacement resolution. This resulted in a continuous and differentiable analytical formulation defining the specimen displacement field.

The strategy used to build the B-spline system is conceptually based on the formulation proposed in [20], where a set of functions based on the B-spline formulation are linearly combined to define the entire fitted domain. The fitting system reported in [20] is directly applicable to a rectangular domain and it works well in a rectangular reference system. The posterior scleral shell is a cap sphere, and therefore fitting based on a polar coordinate system is a more reasonable choice. In this case, the B-spline functions were used only for modeling the variation in the radial direction, while sinusoidal functions were used in the circumferential direction. The overall number of functions (N_n) that are linearly combined is equal to the control points chosen along the radius multiplied by the number of sinusoidal functions used in the circumferential direction.

Figure 4 shows the shapes of cubic polynomials that define the functions along the radial direction, which were defined such that they assume a zero value at the maximum radius of the region of interest. This assumption is consistent with the loading configuration of the investigated specimen, which is clamped at the outer radius by the pressurization apparatus described in the previous section. The order of the polynomials shown in Fig. 4 was used in the fitting of experimental data analyzed herein. In the circumferential direction, we obtain 2h + 1 terms if the first h integer harmonics were used, a sine and a cosine term for each harmonic, plus the constant term.

Fig. 4.

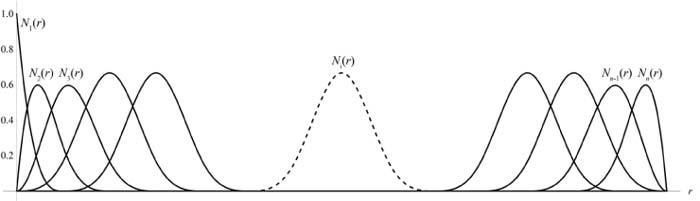
Cubic functions (N_n) of the B-spline fitting system defined in the radial direction (r).

Hence, the generic overall fitting function F(r,θ) for n control points along the radial coordinates (r) and for h integer harmonics along the circumferential direction (θ) assumes the following form:

$$\begin{array}{c}F(r,\theta )=w_1{N}_1(r)+\cdots +w_n{N}_n(r)\\ +[w_{n+1}{N}_1(r)+\cdots +w_{2n}{N}_n(r)]\cos \theta +[w_{2n+1}{N}_1(r)+\cdots +w_{3n}{N}_n(r)]\sin \theta +\cdots \\ +[w_{n(2h-1)+1}{N}_1(r)+\cdots +w_{n(2h-1)+n}{N}_n(r)]\cos h\theta \\ +[w_{n(2h)+1}{N}_1(r)+\cdots +w_{n(2h)+n}{N}_n(r)]\sin h\theta ,\end{array}$$ (5)

where w_i are the n × (2h + 1) weights to be evaluated by an optimization procedure based on the least-squares method.

After the computation of the pseudo-inverse of the matrix whose elements are the values that the functions to be linearly combined assume at each experimental point, the weights w_i are estimated by multiplying this new matrix by the experimental data. Thus if m experimental data are available, the matrix for which the pseudo-inverse must be evaluated assumes the following form:

$$\left[\begin{array}{cccccccccccccccc}{N}_1(r_1)& \cdots & N_n(r_1)& N_1(r_1)\cos {\theta }_1& \cdots & N_n(r_1)\cos {\theta }_1& N_1(r_1)\sin {\theta }_1& \cdots & N_n(r_1)\sin {\theta }_1& \cdots \cdots & N_1(r_1)\cos h{\theta }_1& \cdots & N_n(r_1)\cos h{\theta }_1& N_1(r_1)\sin h{\theta }_1& \cdots & N_n(r_1)\sin h{\theta }_1\\ ⋮& & ⋮& ⋮& & ⋮& ⋮& & ⋮& & ⋮& & ⋮& ⋮& & ⋮\\ N_1(r_m)& \cdots & N_n(r_m)& N_1(r_m)\cos {\theta }_m& \cdots & N_n(r_m)\cos {\theta }_m& N_1(r_m)\sin {\theta }_m& \cdots & N_n(r_m)\sin {\theta }_m& \cdots \cdots & N_1(r_m)\cos h{\theta }_m& \cdots & N_n(r_m)\cos h{\theta }_m& N_1(r_m)\sin h{\theta }_m& \cdots & N_n(r_m)\sin h{\theta }_m\end{array}\right]$$

where (r_i) represents the coordinates in a polar coordinate system of the i-th point at which the experimental datum is retrieved. Reliable optimization requires that the number of experimental data points is much greater than the number of the parameters to be estimated.

In this case, we chose n = 3 and h = 3 to obtain an analytical expression of the specimen shape and therefore the overall fitting function was formed by 21 terms. The specimen surface was represented by approximately 2000 sample points as described above.

We have chosen n = 6 and h = 4 to fit displacement maps in this example and hence the overall fitting function is formed by 54 terms. The displacement maps to be fitted consist of approximately 450x450 pixels for a test performed on a PBS-immersed specimen.

3. Results

3.1. Compensation method effectiveness

No compensation resulted in unacceptable mean displacement magnitude error (34.8%) and to an average angular error of 6.2°. Full compensation (evaluated with the one-to-one comparison method described in section 2.4) reduced the mean displacement magnitude error to approximately 3%, and the average angular error to 5.0°. Not accounting for the real geometry of the specimen slightly increased mean displacement magnitude error and average angular error to 3.3% and 5.4°, respectively.

3.2. ESPI measurement repeatability

Measurement repeatability assessments for identical tests performed in air (evaluated with the one-to-one comparison method) show that random fluctuation of the absolute phase values led to a mean displacement magnitude difference of 2.1%, and an average angular difference of 3.3°. Measurement repeatability with the specimen immersed in PBS was 1.8% of mean displacement magnitude and 2.5° of average angular difference.

Measurement repeatability evaluated with the variance at sample points method yielded a displacement field repeatability of ±16 nm at the 95% confidence level for the test performed in air, which slightly improved to ±15 nm when the test was performed in PBS. Measurement repeatability was slightly worse when the actual specimen geometry was not taken into account.

4. Discussion

The ESPI interferometer and numerical data analysis procedure presented herein provide reliable, accurate, and repeatable measurement of nanometer-scale deformations obtained from pressurization tests on a spherically-shaped rubber specimen immersed in aqueous salt solution (PBS). This numerical compensation method greatly reduced the systematic error induced by measurement of specimens in a PBS bath. Point-to-point compensation for the bending of the optical path and laser wavelength changes accounted for the majority of the correction, while the addition of geometric compensation for the non-planar specimen shape conferred relatively little additional error reduction. Geometric compensation becomes increasingly important as the distance between the laser sources and CCD gets shorter, which could prove important for some optical systems. The commercial ESPI device we used incorporates measurement distances that are sufficiently large to avoid the majority of the potential geometric error. Using this method, a custom system with shorter CCD-to-specimen distances could achieve higher spatial resolution while preserving displacement measurement accuracy.

Preserving local displacement measurement accuracy on aqueous solution-immersed soft tissue specimens is a basic requirement in biomechanics because dehydration alters the specimen’s mechanical properties. Incorporation of the numerical compensation and the customized B-spline fitting method for measurement in a PBS bath allows reconstruction of the local continuous deformation field at the nanometer-scale, which is important to determine the point-to-point surface deformations associated with inhomogeneous biological tissue hyperelasticity and anisotropy. The customized B-spline fitting method used to analytically express the specimen shape and displacement field provides a flexible tool to fit noisy experimental data. In addition, using the same functional form to describe specimen shape and displacement allows direct surface deformation analysis to calculate strains without any intermediate finite element modeling.

This work should be considered with the following limitations in mind. First, Fig. 5 shows that the bulk of the displacement magnitude error is due to reconstruction difficulties at the outer edge of the specimen. This is unavoidable for cap sphere geometries such as this, but it does create considerable uncertainty in those locations. However, the studies of scleral shell biomechanics for which these methods were designed, require accurate measurements at the center (apex) of the specimen, so this is less of a concern. Second, the pinhole model assumption could be a source of error that limits the presented method’s capabilities. Better ray tracing performance can be achieved by using a more realistic behavior of the optical system as proposed by Lin et al. [21]. Third, systematic error arising from uncertainty of the nominal sensitivity vector directions due to optical system misalignments can reduce measurement accuracy [22]. The commercial ESPI used for this work had a fixed optical geometry for which we had inexact specifications, so there is some uncertainty in the parameters used for the calculations (i.e., position of the light source and view point). However, factory calibration of our ESPI system should ensure measurement accuracy in this study. Finally, errors in the specified locations of the optical interfaces of the device and in the optical geometry of the experimental set-up itself could cause deviations in the sensitivity vector direction that lead to systematic displacement reconstruction errors. This could affect measurement accuracy, but should not affect the reported repeatability.

Fig. 5.

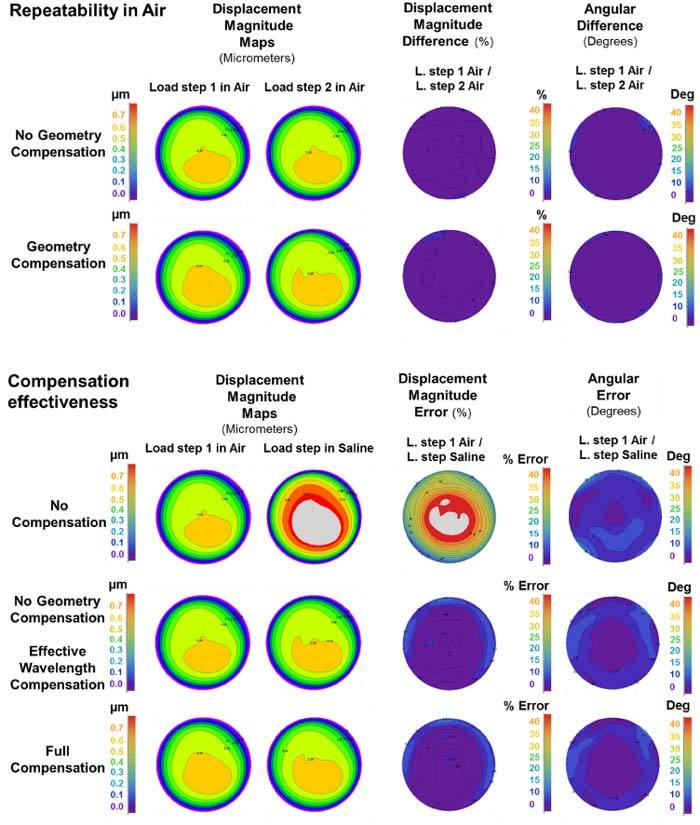
Point-to-point comparison and difference maps for the displacement magnitude and displacement vector angle for different tests in air (repeatability) and different methods of compensation for optical distortion due to in PBS (compensation).

Use of a measurement technique and testing set-up that exhibits good displacement measurement repeatability is crucial when performing mechanical tests. Known measurement repeatability is especially important when comparing biologic specimens that have been subjected to different diseases, conditions or treatments, as it is important to ascertain whether the measured mechanical differences are due to disease/treatment/condition effects or uncertainty in the measurement system itself. The system described herein has been optimized to measure small displacements in pressurized scleral shells with excellent repeatability and spatial resolution, both of which are necessary to elucidate the hyperelastic and highly anisotropic behavior of this tissue in normal, aged, and diseased eyes.