Nuclear Inelastic Scattering and Mössbauer Spectroscopy as Local Probes for Ligand Binding Modes and Electronic Properties in Proteins: Vibrational Behavior of a Ferriheme Center Inside a β-Barrel Protein

Abstract

In this work we present a study of the influence of the protein matrix on its ability to tune the binding of small ligands such as NO, cyanide (CN^-) and histamine to the ferric heme iron center in the NO-storage and -transport protein Nitrophorin 2 (NP2) from the salivary glands of the blood-sucking insect Rhodnius prolixus. Conventional Mössbauer spectroscopy shows a diamagnetic ground state of the NP2-NO complex and Type I and II electronic ground states of the NP2-CN^- and NP2-histamine complex, respectively. The change in the vibrational signature of the protein upon ligand binding has been monitored by Nuclear Inelastic Scattering (NIS), also called Nuclear Resonant Vibrational Spectroscopy (NRVS). The NIS data thus obtained have also been calculated by quantum mechanical (QM) density functional theory (DFT) coupled with Molecular Mechanics (MM) methods. The calculations presented here show that the heme ruffling in NP2 is a consequence of the interaction with the protein matrix. Structure optimizations of the heme and its ligands with DFT retain the characteristic saddling and ruffling only if the protein matrix is taken into account. Furthermore, simulations of the NIS data by QM/MM calculations suggest that the pH dependence of the binding of NO, but not of CN^– and histamine, might be a consequence of the protonation state of the heme carboxyls.

Introduction

The diatomic molecule nitric oxide, NO, plays an essential role as a signal molecule for cardiovascular regulation, the regulation of cell function and as a neurotransmitter in vertebrates, as well as a toxic defense substance for eliminating invading organisms.^1-9 In mammals, to aid in defense against microbes, immune cells such as neutrophils and activated macrophages produce large amounts of NO,^10,11 which helps to kill phagocytosed bacteria and parasites.¹² Since NO is toxic in high concentration its production and transport are strongly regulated.

Insects such as the Amazon river-based kissing bug Rhodnius prolixus have developed the strategy of causing vasodilation by injecting the suite of NO-transporter heme proteins, the nitrophorins (NP) into the tissues and capillaries of their victims.^13-16 NO dissociates upon dilution and pH rise from ~5-6 in the salivary glands of the insect to ~7.3-7.4 when the saliva is injected into the victim’s tissues. The NO can pass through cell walls to reach the capillaries, and there interact with soluble guanylyl cyclase to cause their dilation.⁶ At the same time, the insect’s bite triggers release of histamine by the victim’s mast cells and platelets. Histamine causes itching and the beginning of the immune response, which is supposed to alert the victim to the presence of the biting insect. However, histamine readily binds to the distal site of the heme of the nitrophorins with a larger binding constant than NO (at the pH of the victim’s tissues),¹⁷ thus preventing histamine from warning the victim.^8,9 Both of these actions permit the insect to remain at the site of the bite for a longer period of time, to obtain a sufficient blood meal before detection.

A cDNA library was produced from R. prolixus salivary glands and the gene for the most abundant nitrophorin, NP1, was cloned¹⁶ and expressed.¹⁸ The genes for NP2, NP3 and NP4 have also been cloned, sequenced, and found to be similar in sequence to NP1.¹⁹ NP1 and NP4 are 91% identical in sequence, while NP2 and NP3 have 78% sequence identity. Overall, the four major NP proteins of the adult insect have only 39% sequence identity. The rates of NO release fall into two groups, with NP1 and NP4 having much larger K_ds than NP2 and NP3.²⁰

The Rhodnius NPs have a molecular mass of about 20 kDa. Crystallographic data show that the tertiary structure of the Rhodnius NPs is that of β-barrel proteins, with a histidine residue that serves as the proximal ligand to the heme.²¹ The 3-dimensional structures of various ligand complexes of recombinant NP1,^22,23 NP2^24,25 and NP4^26-30 obtained by X-ray crystallography show that the protein fold of the nitrophorins belongs to a diverse class of proteins called lipocalins,^31,32 a family of relatively small secreted proteins that typically bind small, principally hydrophobic molecules such as e.g. pheromones,^33-35 retinol,^36,37 prostaglandins,^36,38 retinoic acid,³⁹ and biliverdin.^36,40-44 In the nitrophorins, ferrihemin b is bound to the protein via the imidazole nitrogen of His59 in NP1 and NP4 (His57 in NP2 and NP3). The immediate heme distal ligand-binding pocket is hydrophobic, although there are several glutamate and aspartate amino acid side chains at a somewhat greater distance which have a significant influence on the midpoint potential of the protein.⁴⁵ At present, these are the only known heme proteins with the heme inside a β-barrel.

In the notation of Enemark and Feltham,⁴⁶ the NO complexes of the NPs have {FeNO}⁶ centers, which are expected to be EPR silent. In fact, the appearance of the high-spin Fe(III) EPR signal when argon was blown over a sample of homogenized R. prolixus salivary glands, and its disappearance when NO was blown over the same sample¹⁴ provided the initial clue as to how NO could be released upon dilution of the protein, because Fe(II)NO centers, having the {FeNO}⁷ electron configuration,⁴⁶ have dissociation constants in the pico- to femtomolar range⁴⁷ and would thus not release NO upon dilution by a factor of ~100.

As mentioned above, the NPs provide an additional means of assuring the insect a sufficient blood meal, by binding histamine,^22,48 which is produced by the victim in response to the wound. The histamine complex dissociation constant of wt NP1 is 9.1 nM,¹⁷ while the NO complex dissociation constant is 830 nM, both at pH 7.5, 25 °C, about 90 times larger. For NP4 and wt NP2 the histamine K_ds are 6.6 and 10 nM, respectively, while the NO K_ds are 120 and 20 nM, respectively,¹⁷ or about 18 and 2 times larger, respectively, all at pH 7.5, 25 °C. In contrast, wt NP3 has a K_d for histamine that is 25 nM at pH 7.5, 25 °C,¹⁷ while the K_d for NO is estimated to be 10 nM at pH 8.0, 25 °C, and is thus smaller than that for histamine.⁴⁹ Hence, histamine can displace NO from the Fe(III) form of three of the major nitrophorins, and the tight binding of histamine provides yet another means of insuring a successful meal for the insect.

The binding of histamine, which leads to the insect’s not being detected for long periods of time during feeding, is clearly a contributing factor in the potential infection of the victim with Trypanosoma cruzi, because this protozoan is carried by Rhodnius prolixus, and is left at the site of the bite in the feces of the insect after feeding.²¹ Later, secretion by the victim of more histamine than can be bound by the nitrophorins injected by the insect, causes itching and the beginning of the immune response, which may lead the victim to scratch the bite and then rub his/her eyes, nose or mouth. By this means, the trypanosome may be introduced into the mucous membranes and eventually the blood stream and distant cells. T. cruzi causes Chagas’ disease, a debilitating disease that leads to weakening of the heart and/or gut muscles on a very slow time-scale, and in some cases to death after periods of tens of years.^50-53 Both the insect and the trypanosome are found in tropical areas of the New World, and now as far north as southern Texas and Arizona.⁵²

Since the NPs represent the first examples of proteins with stable Fe(III)-NO complexes, which allow storage of NO for long periods of time, yet release upon dilution and pH rise, they represent an ideal system for study of the dynamic and electronic properties of the heme Fe-NO bond. Spectroscopic techniques that have been utilized to characterize nitrosylheme proteins in general include magnetic circular dichroism (MCD),^54,55 infrared (IR),^23,56-60 resonance Raman (rR),^61-67 Mössbauer,^68-75 and electron paramagnetic resonance (EPR or ESR).^14,23,76-91

Infrared (IR) spectroscopy has been used to characterize the N-O stretching frequencies of ferro- (1675 and 1618-1635 cm^-1 for 5- and 6-coordinate model hemes, respectively,⁵⁷ 1615-1617 cm^-1 for HbA^56,58 and 1611 cm^-1 for reduced NP1²³) and ferrihemes (1925 cm^-1 for HbA,^58,60 1917 and 1904 cm^-1 for oxidized NP1,²³ and 1865-1910 cm^-1 for related Fe(III)-NO centers⁶⁰). Resonance Raman (rR) spectroscopy has been used to characterize not only this stretch^61,62 but also the low-energy Fe-NO stretch for ferrous (522-527 cm^-1 for model hemes⁶⁵ and 551-554 cm^-1 for HbA⁶¹) and ferric heme centers (601-603 cm^-1 for models,⁶⁵ 595 cm^-1 for HbA⁶² and 591 cm^-1 for NP1⁶⁷), as well as porphyrin ring vibrations. It should be noted with respect to the N-O stretching frequencies that those of the nitrophorin-NO complexes (and other ferric-NO complexes, 1865-1917 cm^-1) are somewhat similar to those of ferrous-CO stretching frequencies (1936, 1960 cm^-1),²³ which lends support to the suggestion that the electron configuration is Fe(II)-NO⁺, although the Fe(III)-NO frequencies are 40-70 cm^-1 lower than those of the Fe(II)-CO stretches.

Nuclear inelastic scattering of synchrotron radiation (NIS, also known as NRVS, Nuclear Resonant Vibrational Spectroscopy^92,93) detects iron-involved molecular vibrations. It is sensitive to the displacement of the ⁵⁷Fe Mössbauer nucleus, and for this reason it is complementary to other methods such as IR or Raman spectroscopy. NIS measurements allow identification of individual modes at the iron, and therefore are sensitive to iron-ligand distances which are in turn related to the formal oxidation state of the iron. For heme-containing systems, NIS was used early^94,95 and more recently⁹⁶ to investigate myoglobin samples, and has been used to investigate the interplay of structure and vibrational dynamics in five-⁹⁷ and six-coordinate ferrous heme nitrosyls,^98-101 as a local probe to investigate the NO activation in model hemes¹⁰² and in myoglobin,^103,104 and the Fe(IV)=O (Compound II) state of myoglobin,¹⁰⁵ and the Fe(II) and Fe(III) states of horse heart cytochrome c.¹⁰⁶ However, it has so far not been used to characterize {FeNO}⁶ centers such as those in the nitrophorins, either in proteins or in corresponding model complexes, although DFT-calculated frequencies for a 5-coordinate (without imidazole or other sixth axial ligand) model heme {FeNO}⁶ complex have been reported.¹⁰²

DFT calculations are being employed intensively to study the electronic and dynamic properties of iron centers in proteins and iron complexes.¹⁰⁷ Quantum-mechanical calculations of iron centers in proteins cannot currently be performed by including the entire protein matrix (due to the immense demand of computer power). Thus, it is commonly accepted to treat only the metal sites, including practically-chosen ligand spheres, with DFT methods,¹⁰⁸ or to employ combined quantum-mechanics/molecular-mechanics (QM/MM) approaches in order to account for the effects of the protein matrix.¹⁰⁹ Nitrophorin 2 is an ideal system to study the effects of the protein matrix on the properties of heme proteins, since it is still a matter of debate whether the protein matrix induces the very strongly ruffled heme conformation or whether it may be an effect of just a special orientation of the axial histidine to the heme. Therefore, in this work we present a study of the influence of the protein matrix on its ability to tune the binding of small ligands such as NO, cyanide (CN^–) and histamine to the heme center of Nitrophorin 2. The electronic properties of the heme iron are measured and interpreted by conventional Mössbauer spectroscopy, as well as by synchrotron-based Nuclear Forward Scattering (NFS). The change of the vibrational signature of the protein upon ligand binding is monitored by Nuclear Inelastic Scattering (NIS), and calculated via quantum-mechanical DFT methods, coupled with Molecular Mechanics (QM/MM) methods. The analysis of the NFS data during data collection at the synchrotron show no radiation damage due to the exposure to the synchrotron beam.

The QM/MM calculations presented here show that the heme ruffling in NP2 is a consequence of the interaction with the protein matrix. In this work we show that treating the protein matrix with the MM approach and the heme, including its axial ligands, with DFT methods, retains the heme ruffling of the NO, CN^- and histamine complexes of NP2. If the protein matrix is not included, energy minimization of just the heme including its axial ligands always leads to almost flat, non-ruffled heme structures. Furthermore, simulations of the NIS data by QM/MM calculations suggest that the protonation state of the heme propionates might be a contributing factor in the pH-dependent release of NO from nitrophorins.

Experimental

Sample preparation

Except where indicated, materials were obtained from Sigma Aldrich and used without further purification. The method of biosynthetic production of protohemin IX used BL21(DE3) E. coli cells (Novagen), transformed with a pET-28a expression plasmid (Novagen) which encoded the expression of the soluble heme-containing nitrophorin from Cimex lectularius¹¹⁰ with an N-terminal His₆-tag to facilitate purification and subsequent protohemin IX extraction. In this case a ⁵⁷Fe-enriched defined culture medium for the E. coli cells was used. A 50 mg quantity of ⁵⁷Fe-enriched metal powder (enrichment of ⁵⁴Fe, ⁵⁶Fe, ⁵⁷Fe, and ⁵⁸Fe at 0.01%, 2.70%, 95.30%, and 1.99%, respectively, obtained from Advanced Materials Technologies, Israel) was dissolved in 1 mL of concentrated HCl with magnetic stirring overnight. This was then neutralized with 12 M KOH and used to make the defined growth medium, with 2.5 mg ⁵⁷Fe per L, and constituted the sole significant source of iron. The growth medium was adjusted to pH 7.4 and was based on one described previously.¹¹¹ In addition to the 44 μM ⁵⁷Fe, the growth medium also contained 50 mM sodium chloride, 40 mM 3-morpholinopropane-1-sulfonic acid, 22.2 mM D-glucose, 18.7 mM ammonium chloride, 10 mM sodium carbonate, 4 mM tricine, 1.32 mM dipotassium phosphate, 0.53 mM magnesium chloride, 0.28 mM potassium sulfate, 0.77 mM L-alanine, 0.5 mM L-arginine, 1 mM L-asparagine, 1.3 mM L-aspartic acid, 0.91 mM L-glutamine (Calbiochem), 0.85 mM L-glutamic acid (Mallinckrodt), 1 mM glycine, 0.54 mM L-histidine, 0.58 mM L-isoleucine, 1.7 mM L-leucine, 1.3 mM L-lysine, 0.26 mM L-methionine, 0.86 mM L-phenylalanine, 0.88 mM L-proline, 1.5 mM L-serine, 1.2 mM L-threonine, 0.27 mM L-tryptophan, 0.74 mM L-tyrosine, 1.1 mM L-valine, 64 μM L-cystine (the disulfide-bonded dimer of cysteine), 4 μM boric acid, 0.8 μM manganese dichloride, 0.3 μM cobalt dichloride, 0.1 μM copper(II) sulfate, 0.1 μM zinc sulfate, 0.72 μM sodium molybdate, 10 μM thiamine, 10 μM pantothenic acid, 10 μM 4-hydroxybenzoic acid, 10 μM 4-aminobenzoic acid, 10 μM 2,3-dihydroxybenzoic acid, and 51 μM kanamycin sulfate. A 300 mL quantity of this ⁵⁷Fe enriched, defined culture medium was inoculated, grown overnight at 37 °C in a shaker incubator, and used to inoculate a further 16 L. This was grown at 25 °C with oxygen sparging in two 10 L flasks, with the addition of 0.5 mL of antifoam 204 (Aldrich). At an OD₆₀₀ of 0.5 (~6 hours), 1 mM isopropyl β-D-1-thiogalactopyranoside (IPTG, Research Products International Corp.) and 0.1 mM of 5-aminolevulinic acid (Sigma-Aldrich) was added, and growth was continued overnight before harvesting the cells. The isotopically-enriched ⁵⁷Fe protoporphyrin IX was extracted into 2-butanone under acidic conditions (pH <4) as reported previously,¹¹² evaporated to dryness, and used in the preparation of holo-NP2 as described previously.^113,114

The method used for apo-NP2 production utilized BL21(DE3) E. coli cells (Novagen) transformed with a pET-24a expression plasmid (Novagen) which encoded the expression of wild-type nitrophorin 2 from Rhodnius prolixus as inclusion bodies. These inclusion bodies were solublized and refolded according to methods described previously¹¹⁵ to produce soluble apo-NP2. The isolated apo-NP2 was first purified by size-exclusion chromatography (using a High-Prep™ 26/60 Sephacryl S-100 column (GE Healthcare Biosciences) at pH 7.5, with 100 mM sodium phosphate buffer containing 100 mM NaCl) before titration with the ⁵⁷Fe-enriched protoporphyrin IX (dissolved in dimethylsulfoxide) to an A_402nm/A_280nm ratio of 3.0, and further purified by size exclusion chromatography (at pH 5.0, with 100 mM sodium acetate buffer containing 100 mM NaCl). The ⁵⁷Fe-enriched NP2 was preliminarily characterized by UV-visible spectroscopy and by mass spectrometry using MALDI–TOF (Matrix Assisted Laser Desorption-Time-of-Flight), which confirmed the expected absorbance spectrum and mass for holo-NP2. High-resolution electrospray mass spectrometry was also used to establish that the ratio of ⁵⁶Fe to ⁵⁷Fe in the extracted protoporphyrin IX was the same as that in the ⁵⁷Fe-enriched metal powder used in the growth medium (⁵⁶Fe/⁵⁷Fe ratio was 1:34.9 and 1:35.3, for the extracted ⁵⁷Fe protoporphyrin IX and the ⁵⁷Fe enriched metal powder, respectively); thus no significant dilution from trace natural abundance iron in the growth medium components occurred.

Three conventional Mössbauer samples were prepared with approximately 3 mM ⁵⁷Fe-enriched NP2, 100 mM sodium phosphate and appropriate ligand at a molar ratio of 1.5; (i) NO-bound (NP2-NO) at pH 5.5, (ii) CN^--bound (NP2-CN) at pH 7.5 and (iii) histamine-bound (NP2-Hm) at pH 7.5. In the case of the NP2-NO sample, diethylamine NONOate (DEANO, Cayman Chemical Company) was used as the source of NO ligand. (DEANO dissociates in solution to liberate 1.5 moles of NO per mole of parent compound.¹¹⁶) A 650 μL quantity of each sample was introduced into conventional Mössbauer sample holders and frozen in liquid nitrogen, and in the case of NP2-NO, was prepared under anaerobic conditions. Three NIS/NFS samples, one each of a saturated solution (~10 mM) of ⁵⁷Fe-enriched NP2 bound to the above-mentioned ligands, were also prepared, each in a 150 μL NIS/NFS sample holder, and each under the pH conditions listed above.

Nuclear inelastic scattering (NIS), nuclear forward scattering (NFS) and field-dependent Mössbauer spectroscopy

The NIS and NFS spectra were recorded at the Nuclear Resonance Beamline ID 18¹¹⁷ of the European Synchrotron Radiation Facility (ESRF) in Grenoble, France. The 6 GeV electron storage ring was operated in 16-bunch mode with a purity of the filling better than 10^-9. The incident beam was monochromatized by a Si(111) double-crystal premonochromator to a bandwidth of 2.1 eV. A further decrease of bandwidth down to 2 meV was obtained with a refractive beryllium collimator and a high-resolution monochromator. Thus the experimental resolution was 2 meV, which corresponds to 16 cm^-1 in wave number units. The relatively coarse energy resolution was chosen deliberately in order to increase scattering intensity. This beam with an intensity of ~1.8·10⁹ photons per second after refill was used to excite the 14.413 keV nuclear level of ⁵⁷Fe in the sample. An avalanche photodiode with a time resolution of less than 1 ns has been used as detector. The NIS data were collected during 11 energy scans for NP2-NO, 8 for NP2-CN and 13 for NP2-Hm with 160 steps on average, each with 0.5 meV step size and 10 s measuring time. The NFS data were collected in 2048 channels up to 164 ns after the synchrotron pulse. The samples were mounted in a closed-cycle cryostat to permit measurements at low temperatures.

Mössbauer spectra were recorded using a conventional spectrometer in the constant-acceleration mode. Isomer shifts are given relative to α-Fe at room temperature. Field dependent conventional Mössbauer spectra were recorded with a closed-cycle cryostat from CRYO Industries of America, Inc. Magnetically split spectra were simulated in the spin-Hamiltonian approximation described below; otherwise spectra were analyzed by least-square fits using Lorentzian line shapes.

The Zeeman interaction of a spin with an applied field $\overrightarrow{B}$ and $\overleftrightarrow{g}$ describing the electronic g tensor is given by the Hamiltonian

$${\widehat{H}}_{\mathit{el}}={\mu }_B\overrightarrow{S}\overleftrightarrow{g}\overrightarrow{B}.$$ (1)

where μ_B denotes the Bohr magneton. Magnetic Mössbauer spectra were simulated using Eq. (1) for a S=1/2 spin system together with the nuclear Hamiltonian¹¹⁸

$${\widehat{H}}_N=\frac{\mathit{eQ}{V}_{\mathit{zz}}}{\mathit{4}I(\mathit{2}I-\mathit{1})}\left[\mathit{3}{\widehat{I}}_z^{\mathit{2}}-I(I+\mathit{1})+\eta ({\widehat{I}}_x^{\mathit{2}}-{\widehat{I}}_y^{\mathit{2}})\right]-g_N{\mu }_N\overrightarrow{I}\overrightarrow{B}+<\overrightarrow{S}>\overleftrightarrow{A}\overrightarrow{I}.$$ (2)

Here I denotes the nuclear spin quantum number, Q the nuclear quadrupole moment of the excited nuclear state, V_zz the z-component of the electric-field gradient (EFG) tensor and η = (V_xx - V_yy)/V_zz the asymmetry parameter of the EFG, g_N the nuclear g-factor, $<\overrightarrow{S}>$ the electron spin expectation value, and μ_N the nuclear magneton. Note that the axis system being used for the EFG is that of the g- and A-tensors, i.e., with z along the normal to the porphyrin plane and x, y axes in the porphyrin plane.^119-121

Computational methods

Geometry optimizations and frequency calculations were performed with GAUSSIAN 03.¹²² As input for the calculations, structural data for NP2-NO, NP2-CN and NP2-Hm were taken from the PDB entries 1T68, 2HYS, and 1PEE.²⁵ The crystal structure 1PEE has an imidazole ligand. It was taken as an approximation for the structure of NP2-Hm. Hydrogen atoms were added to the structural data from the PDB-files with the program GaussView 4.1.2.

DFT calculations were first performed on the heme moiety only (heme + ligands, with propionates of heme replaced by propyls) using the functional B3LYP¹²³ and the basis set CEP-31G.^124-126 In order to investigate the influence of the protein matrix on the heme structure, in a second step QM/MM calculations were performed on the whole protein by applying the method ONIOM,¹²⁷ which is implemented in GAUSSIAN 03. Within these calculations the heme moiety and its ligands were treated with DFT (B3LYP with CEP-31G) and the rest of the protein with the universal force field UFF.¹²⁸ As the protonation state of the carboxylates of the heme group is not definitely known, calculations performed with the ONIOM method were carried out both for structures with protonated and with unprotonated (i.e. charged) carboxylates.

For the optimized structures the frequency calculations were subsequently performed with GAUSSIAN 03 (B3LYP/CEP-31G, or B3LYP/CEP-31G and UFF combination, of isolated heme or heme plus entire protein, respectively), yielding the normal vibrational modes and their frequencies. On the basis of the latter the vibrational density of states of the iron atom (DOS) was calculated according to

$$\mathit{DOS}(\stackrel{\sim }{v})=\sum _{\alpha }{e}_{\mathit{Fe\alpha }}^{2}L(\stackrel{\sim }{v}-{\stackrel{\sim }{v}}_{\alpha })$$ (3)

where e²Feα is the mode composition factor and represents the fraction of vibrational energy of mode ṽ_α associated with the motion of the iron atom:

$$e_{\mathit{Fe\alpha }}^2=\frac{m_{\mathit{Fe}}{r}_{\mathit{Fe\alpha }}^2}{\sum _j{m}_j{r}_{\mathit{j\alpha }}^2}$$ (4)

Thereby r _ja is the calculated contribution of atom j to normal mode α. The function L(ṽ − ṽ_α) in equation (3) is a Lorentzian with a width corresponding to the experimental resolution.

Results and Discussion

NIS Spectra

Figure 1a shows the NIS spectrum of NP2–NO up to an energy of 650 cm^-1. The data exhibit a dominant peak at 594 cm^-1 with a shoulder at about 581 cm^-1. An earlier resonance Raman spectral investigation of NP1–NO assigned a mode at 591 cm^-1 to a Fe–NO stretching mode and a mode at 578 cm^-1 to a Fe–NO bending mode.⁶⁷ However, these bands are only barely visible in the resonance Raman spectra, and ¹⁵NO isotope labeling had to be used to confirm the assignments.⁶⁷ In contrast, in the NIS spectrum of Figure 1a the Fe–NO modes clearly dominate the experimental data.

Figure 1.

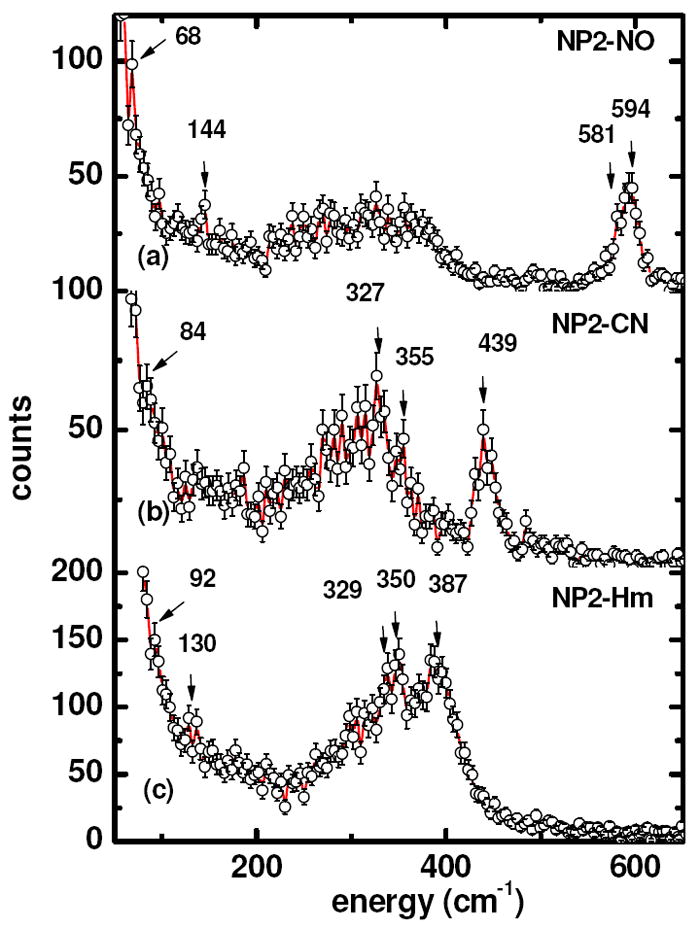
Experimental NIS spectra obtained from NP2 under three different conditions, from top to bottom: (a) NO-bound (NP2–NO) obtained at 67 K, (b) CN^–-bound (NP2–CN) obtained at 51 K, (c) Histamine-bound (NP2–Hm) obtained at 250 K. The protein concentration was ~10 mM in all three cases. The solid lines are guides to the eye.

The spectral region between 200 and 400 cm^-1 shows a quasi-continuous spectral pattern with no well-resolved, localized modes. Within this region, in-plane iron vibrations against the four pyrrole nitrogen atoms of the heme have been observed for deoxygenated and CO-ligated myoglobin.¹⁰⁴ In addition, a mode at 144 cm^-1 is observed in Figure 1a. This spectral feature may possibly be attributed to an iron-histidine stretching mode, based on recently-reported NIS experiments on myoglobin compound II, where a feature resolved near 147 cm^-1 has been assigned to Fe–His vibration.¹⁰⁴ This assignment was based on DFT calculations, which predicted 119 cm^-1 for this stretch.¹⁰⁴ Imidazole ring translation dominates this mode, which may explain the reduced frequency in comparison with 220 – 230 cm^-1 observed for ferrous deoxymyoglobin,¹⁰³ and met-myoglobin hydroxide, with Fe-His at 234 cm^-1.¹⁰⁴ Also, NIS single crystal studies of metmyoglobin report two strong orientation-dependent modes, an in-plane mode at 264 cm^-1 and an out-of-plane iron mode at 172 cm^-1, the latter of which is a good candidate for a Fe–His mode.⁹⁶ However these reported assignments should be treated with some skepticism, since the QM/MM calculations presented in this work do not point to a specific Fe-His mode in this spectral region, as will be discussed further below. In addition, a well-defined peak at 68 cm^-1 is observed in Fig. 1a. Recently Scheidt and coworkers reported modes with substantial doming character in Fe(II)OEP-NO which have been calculated by DFT methods to occur at 37, 41 and 47 cm^-1. They also identified a mode at 139 cm^-1 which has doming character.¹²⁹

In the very low frequency region, there is a shoulder at 28 cm^-1 (see Supporting Information Figure S1). Modes in this region have also been observed near 25 cm^-1 in MbCO and deoxyMb, and have been assigned to translational modes in response to torsional oscillations of the polypeptide backbone and side chains.¹⁰³ This assignment was confirmed by Achterhold and Parak,⁹⁶ who identified heme sliding motions in single crystal metMb in the region of 32-40 cm^-1. In addition, low frequency vibrations involving nonplanar conformational modes (ruffling, saddling) of hemes and related macrocycles are expected in the 15-25 cm^-1 region,¹³⁰ although these may not involve much, if any, movement of the iron.

For NP2–CN, an intense Fe–CN stretching mode is observed at 439 cm^-1. The decrease in the frequency of the iron ligand stretching mode of ~140 cm^-1 compared to NP2–NO is a consequence of the lower bond order of the Fe–CN bond as compared to the Fe–NO bond. In fact, NP4–NO, a Fe(III)–NO structure (PDB entry 1X80) has Fe–N bond length 1.69 Å and NP2–CN has a Fe–C bond length of 1.99 Å (PDB file 2HYS). Confirmation of this assignment comes from resonance Raman data, which show modes at 454 and 443 cm^-1. These modes have been attributed to the ν(Fe–CN) stretching vibrations of a linear (175°) and a bent (155°) Fe(III)CN linkage,⁶⁷ respectively. Based on CN isotope difference spectra it has been claimed that these two populations coexist in the isoform NP1, with the linear Fe(III)CN configuration having a δ(Fe–C–N) bending mode at 397 cm^-1 and the bent Fe(III)CN configuration having a δ(Fe–C–N) bending mode at 357 cm^-1.⁶⁷ Closer inspection of the NIS data of NP2–CN indeed yields a mode at 355 cm^-1, but the absence of the proposed bending mode at 397 cm^-1 of the linear Fe(III)CN configuration. Instead, a mode at 327 cm^-1 is observed which has also been observed to have a cyanide isotope dependence in the resonance Raman experiments.⁶⁷ In comparison, the only metMb-anion complex that has been studied by NIS techniques is metMb-OH, which has a Fe-O stretch at 556 cm^-1 and additional bands at 376, 343 and 277 cm^-1,¹⁰⁵ all of which are proportionately higher in frequency than the NP2–CN modes mentioned above, even though the Fe-O bond length is undoubtedly quite similar to that of the Fe-C bond length. The spin state of metMb-OH, however, is not purely low-spin.¹³¹

In the histamine (Hm) complex of NP2, both axial ligands bind to Fe(III) through an imidazole nitrogen (His57 and Hm), and thus this is the first heme protein complex thus far that has been studied by NIS techniques that has two axial ligands of nearly equal donor strength. However, NMR investigations have suggested that histamine has a slightly greater donor strength (albeit π donor strength) than does His57,^132,133 possibly because the imidazole ring N-H of Hm is hydrogen-bonded (2.79 Å) to the oxygen of a water molecule (water 1), which is in turn hydrogen-bonded to the carbonyl oxygen of Ile120 (2.72 Å). However, the H57 imidazole ring N-H is hydrogen-bonded (2.73 Å) to a water molecule as well (water 2), which is in turn hydrogen-bonded to the side-chain carbonyl of Asn68 (2.70 Å). These two structural water molecules are seen in all published and unpublished X-ray crystal structures of NP1,2,4-Hm, with extremely similar bond distances between the mentioned atoms in each case.^22,25,27 NMR spectra of the NP2-Hm complex show that Hm is the stronger-field ligand,¹³⁴ as compared to His57. Binding of histamine to NP2 leads to the observation of a mode at 387 cm^-1 (Figure 1c). This mode might correspond to the Fe(III)-histamine stretching frequency in NP2–Hm. In addition, bands at 350 and 329 cm^-1 increase in intensity and might be attributed to Fe(III) histamine bending modes, or an interaction between His57 and Hm in this complex, which has two nearly equal donor strength axial ligands.

Density Of vibrational States (DOS)

So far we have considered experimental NIS spectra which have been obtained from the summation of 8-13 scans, depending on sample. The experimental NIS spectra depend on the occupation of the density of vibrational states (DOS) at a given temperature. The DOS, which describes all vibrational states involving movement of the iron, is an intrinsic property of the investigated sample, and can be obtained from the experimental data by a formalism developed previously.^93,135

The DOS of NP2–NO, NP2–CN and NP2–Hm are presented in Figure 2, and exhibit all previously discussed vibrational bands. Note that the bands in the DOS of the high-energy ironligand modes are much more pronounced in comparison to the low-frequency modes, in contrast to the experimental spectra displayed in Figure 1. This is because the experimental NIS spectra are basically proportional to atomic displacements which, in addition to the density of states include also the Bose-Einstein occupation factor divided by the vibrational frequency. As reported previously, deoxyMb shows a much larger DOS at very low frequency (20-30 cm^-1) than do ferro- or ferricytochrome c,¹⁰⁶ and the three NP2 complexes all have small DOS values similar to cytochrome c in this low frequency region.

Figure 2.

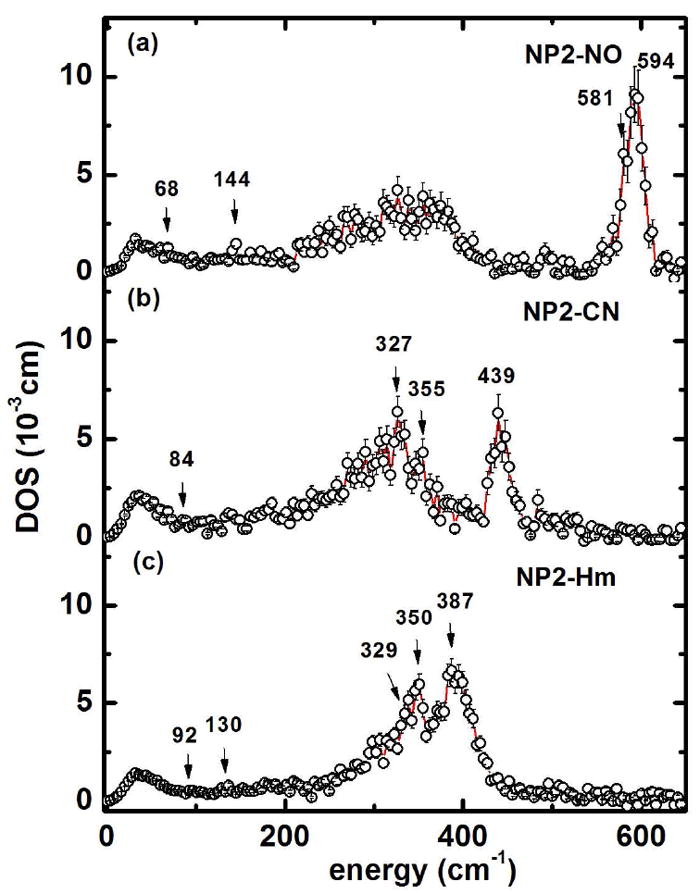
Iron density of states obtained from the experimental NIS spectra in Figure 1, from top to bottom: (a) NO-bound (NP2–NO), (b) CN^--bound (NP2–CN), (c) Histamine-bound (NP2–Hm). The solid lines are guides to the eye.

Nuclear Forward Scattering (NFS) and field-dependent Mössbauer spectra

In order to perform quantum chemical calculations to simulate the DOS of NP2–NO, NP2–CN and NP2–Hm displayed in Figure 2, one needs to know the spin states as well as the oxidation state of the heme moiety. Therefore we have performed a temperature- and field-dependent Mössbauer study of each of the three ligand complexes of NP2. In addition, in order to check whether the samples suffered radiation damage during exposure to the synchrotron radiation, Nuclear Forward Scattering (NFS) spectra have also been recorded during the collection of the NIS data.

The NFS spectra shown in Figure 3 display a periodic structure (also called “quantum beats”), which reflects the quadrupole splitting ΔE_Q of the ⁵⁷Fe nuclei in the sample. A least-squares fit using the software package MOTIF¹³⁶ yields ΔE_Q = 1.89 ± 0.05 mms^-1 for NP2–NO (Figure 3a), 1.03 ± 0.10 mms^-1 for NP2–CN (Figure 3b) and 2.18 ± 0.05 mms^-1 for NP2–Hm (Figure 3c). The ΔE_Q values obtained in this manner are in excellent agreement with the values obtained from the analysis of the conventional Mössbauer spectra also shown in Figure 3. These Mössbauer spectra yield δ = -0.01 ± 0.02 mms^-1, ΔE_Q = 1.86 ± 0.02 mms^-1 for NP2–NO (Figure 3d), δ = 0.17 ± 0.04 mms^-1 and ΔE_Q = 1.03 ± 0.04 mms^-1 for NP2–CN (Figure 3e) and δ = 0.24 ± 0.04 mms^-1 and ΔE_Q = 2.25 ± 0.04 mms^-1 for NP2–Hm (Figure 3f).

Figure 3.

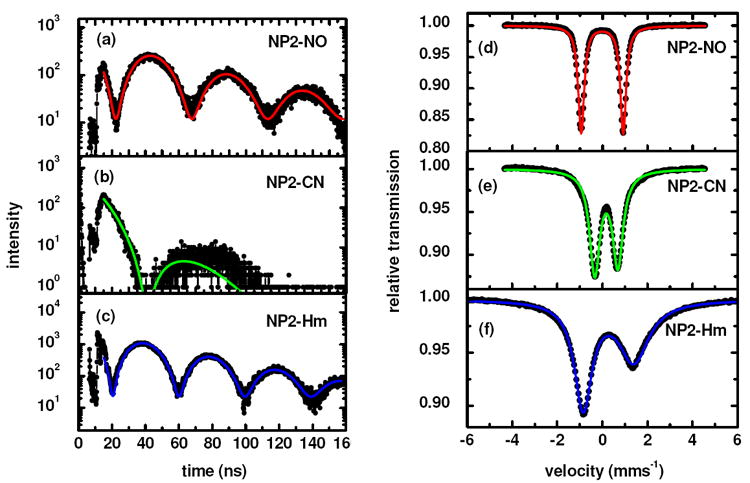
Nuclear forward scattering (NFS) spectra (a-c) and conventional Mössbauer spectra (taken at T=77 K) (d-f) of the three NP2 complexes. The NFS spectra have been obtained during the NIS scans at T = 67 K (a), T = 51 K (b) and T = 250 K (c). The solid line in (a-c) is a fit with the software MOTIF¹³⁶ yielding ΔE_Q = 1.89 ± 0.05 mms^-1 for NP2–NO, 1.03 ± 0.10 mms^-1 for NP2–CN and 2.18 ± 0.05 mms^-1 for NP2–Hm. The effective thicknesses are t_eff = 1.80 for NP2–NO, 1.86 NP2–CN and 1.19 for NP2–Hm. The solid line in (d-f) represents a Lorentzian fit of the Mössbauer data with the following parameters: NP2–NO: δ = −0.01 ± 0.01 mms^-1, ΔE_Q = 1.86 ± 0.01 mms^-1, Γ = 0.40 ± 0.01 mms^-1. NP2–CN: δ = - 0.17 ± 0.01 mms^-1, ΔE_Q = 1.03 ± 0.01 mms^-1, Γ₁ = 0.64 ± 0.01 mms^-1, Γ₂ = 0.66 ± 0.01 mms^-1. NP2–Hm: δ = 0.27 ± 0.01 mms^-1, ΔE_Q = 2.25 ± 0.01 mms^-1, Γ₁ = 0.96 ± 0.01 mms^-1, Γ₂ = 1.72 ± 0.01 mms^-1.

The Mössbauer spectrum of NP2–NO, obtained at 5 T and displayed in Figure 4 shows a magnetic splitting due only to the external magnetic field, which leads to the conclusion that the Fe–NO entity has a diamagnetic ground state. This has also been shown to be the case for the NO complex of the isoform NP4.⁷⁴

Figure 4.

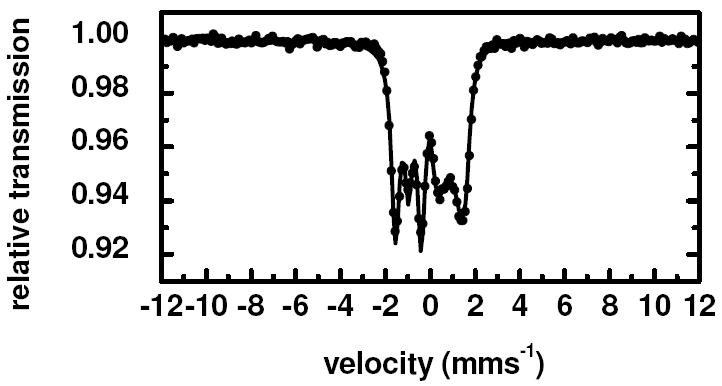
Mössbauer spectrum of NP2–NO obtained at 11 K in the presence of a 5 T magnetic field applied perpendicular to the γ-beam. The solid line is a simulation with parameters given in Table 1, assuming a diamagnetic ground state for NP2–NO.

Figure 5 shows the Mössbauer spectra of NP2–CN obtained at fields up to 5 T. Electron paramagnetic resonance investigations of NP2–CN yield a “large g_max” or Type I¹¹⁹ spectrum with observable g-values at 3.55 and 1.96 typical for a Type I ferric low-spin heme center, with S = 1/2 and a (d_xy)²(d_xz,d_yz)³ ground state,¹³⁴ very similar to that for met-MbCN.¹³⁷ Inspection of Figure 5 leads to the conclusion that the magnetic hyperfine splitting increases with increasing external field, which indicates that the product of the largest components of the hyperfine coupling tensor A_zz and of the g-tensor g_zz is positive. This is indeed the case, because the simulation of the spectra by means of the spin Hamiltonian (Equations 1 and 2) yields a g-tensor $\overleftrightarrow{g}=(0.67,1.96,3.55)$ and a hyperfine coupling tensor $\overleftrightarrow{A}/g_N{\mu }_N=(­41.1,44.3,47.1)$. For this fitting procedure the g-tensor normalization condition g_xx² + g_yy² + g_zz² = 16 was used.^121,138,139

Figure 5.

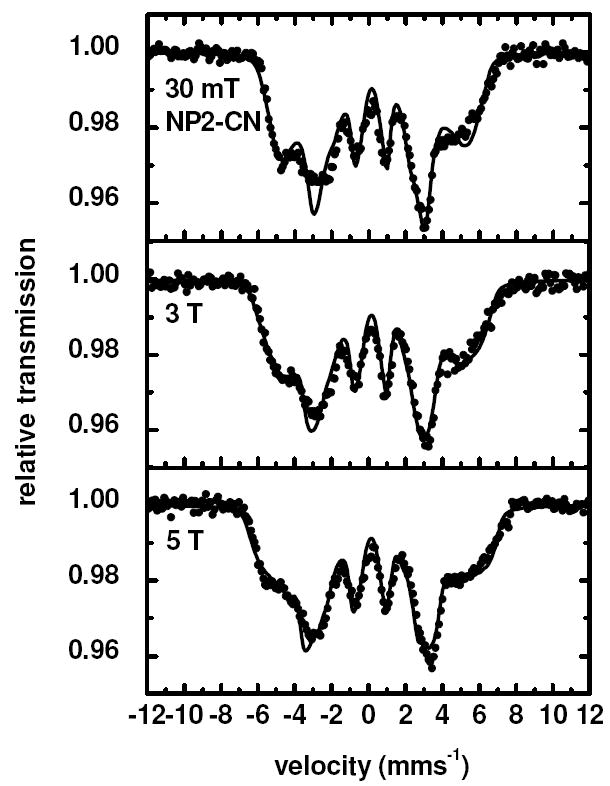
Mössbauer spectra of NP2–CN obtained at 5 K in the presence of several different magnetic fields up to 5 T applied perpendicular to the γ-beam. The solid lines are fits performed in the limit of slow relaxation with parameters given in Table 1.

Whereas the isomer shift δ = 0.17 mm/s is in the range for S = 1/2 systems, the obtained quadrupole splitting, ΔE_Q = 1.03 mms^-1, is remarkably small for Type I heme centers¹¹⁹ (see Table 1). It is also unusual for Type III centers,¹¹⁹ although there the quadrupole splitting is negative. Even Type III complexes have |ΔE_Q| ~1.7−1.8 mm/s.^119,140 NMR investigations of NP2–CN have led to the conclusion that at ambient temperatures, where nonplanar vibrational modes are more highly populated, this complex has a mainly (d_xz,d_yz)⁴(d_xy)¹ ground state.¹³⁴

Table 1.

Mössbauer parameters of the simulations shown in Figures 4-6. Values in square brackets given for the hyperfine coupling tensor $\overleftrightarrow{A}$ and the asymmetry parameter η have been calculated according to Oosterhuis and Lang⁶⁹ in the reference frame of Taylor¹²¹ using P = 62 T and κ = 0.35.

	S	δ (mms-1)	ΔEQ (mms-1)	η	g	A/gNμN (T)
NP2–NO	0	−0.01	1.86	0	–	–
NP2–CN	½	0.17	1.03	−1.74	(0.67,1.96,3.55)	(−41,44,47)1
				[−1.71]		[−36,27.6,85.3]
NP2–Hm	½	0.27	2.25	−1.57	(1.52,2.24,2.92)	(−27,19,60)
				[−2.59]		[−40.5,16.7,50]

¹The A-tensor is turned with respect to the electric field gradient tensor by the Euler angles α = 25° and β = 56°.

On the basis of EPR studies, NP2–Hm has been reported to be a Type II¹¹⁹ ferric low-spin heme center with $\overleftrightarrow{g}=(1.52,2.24,2.92)$ and a (d_xy)²(d_xz,d_yz)³ electronic ground state.¹⁴¹ This is consistent with the Mössbauer parameters deduced from the field-dependent Mössbauer spectra shown in Figure 6 (δ = 0.27 mms^-1, ΔE_Q = 2.25 mms^-1 and $\overleftrightarrow{A}/g_N{\mu }_N=(-27.3,19.4,60.0)$ T (Table 1)).

Figure 6.

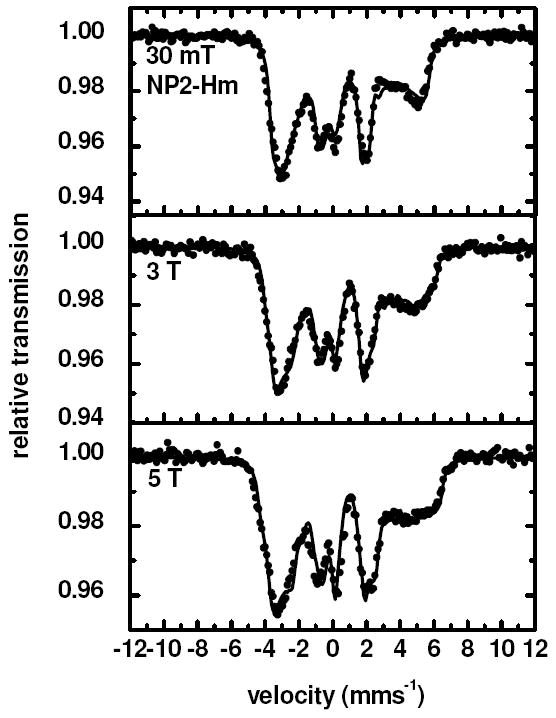
Mössbauer spectra of NP2–Hm obtained at 5 K in the presence of several different magnetic fields up to 5 T applied perpendicular to the γ-beam. The solid lines are fits performed with parameters given in Table 1.

In conclusion, the Mössbauer study presented above shows unambiguously that NP2–NO is diamagnetic and that both NP2–CN and NP2–Hm have S = 1/2. All three iron centers have a ferric low-spin d⁵ electronic structure. Together with the crystallographic data these information have been used in order to perform quantum mechanical DFT calculations and to obtain a quantitative picture of the observed iron modes.

DFT calculations and the influence of the protein matrix on heme structure

The heme structures of NP2–NO, NP2–CN and NP2–Hm obtained after energy minimization via DFT calculations of just the heme moiety plus its axial ligands are shown in Figure 7 a-c. From simple inspection of this figure it is evident that energy minimization of just the heme including its proximal histidine and the three different axial ligands leads to a nearly flat heme structure in all three cases. This is in contradiction with the fact that the nitrophorins have strongly nonplanar hemes. Therefore, we have used combined quantum mechanical/molecular mechanics (QM/MM) calculations, and have treated the heme moiety and its ligands with DFT, and calculated the rest of the protein with molecular mechanics using the Gaussian03 ONIOM approach.¹²⁷ Inspection of Figure 7 d-f indeed shows that the structures optimized with the ONIOM method have ruffling and saddling contributions similar to those of the crystal structures.

Figure 7.

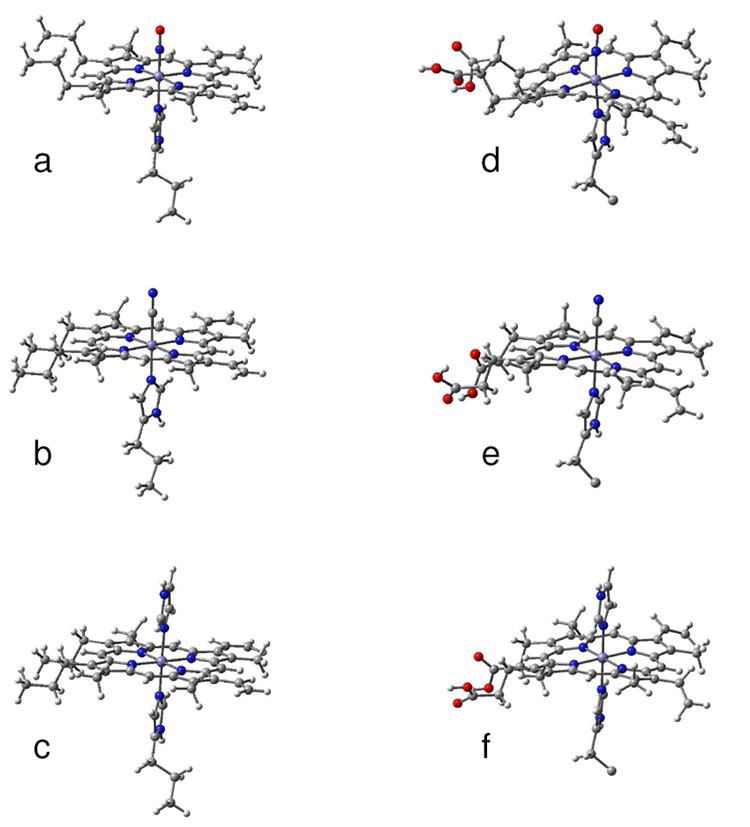
Optimized structures of the heme group and its ligand of (a) NP2–NO, (b) NP2–CN and (c) NP2-Hm which were obtained from DFT calculation on the shown molecular structures only. The functional groups of the heme and the histidine ligand were replaced by methyl groups. For comparison the optimized molecular structures calculated with the ONIOM method of (d) NP2–NO, (e) NP2–CN and (f) NP2-Hm are shown. Only the parts of the molecules treated with DFT are displayed. The residual parts of the protein, which were taken into account by force field calculations, are not shown.

The discrepancies between the crystal structures, the DFT- and the QM/MM-optimized structures can best be quantified by a normal-coordinate structure decomposition (NSD) analysis.¹⁴² NSD is a method for quantitatively describing the three-dimensional conformation of heme groups. It is based on the observation, that the deviations from ideal, planar D_4h symmetry of most porphyrin rings of heme groups are static displacements along the lowest-energy normal coordinates of the macrocycle. This is reasonable, since deformations along the lowest-energy normal coordinates require the least energy, for example, to relieve steric stress. Hence the idea of the NSD method is to describe the deviations of a given heme group from ideal D_4h symmetry in the basis of the low-energy normal coordinates of a macrocycle with D_4h symmetry. Thus heme structures can be classified by the symmetry type of the modes which contribute predominantly to their three-dimensional structure.¹⁴²

Our NSD analyses of the crystal structures of NP2 reveal that their porphyrin rings show mainly ruffling and saddling distortions. Ruffling and saddling are terms for the lowest-energy B_1u and B_2u modes of the porphyrin ring with D_4h symmetry. Schematic representations of them are given in Supporting Information Figure S2.

Figure 8 a-c shows NSD analyses of the optimized structures in comparison to the crystal structures for NP2–NO, NP2–CN, and NP2–Im. The analyses were performed with the NSD program developed by Sun and Shelnutt.¹⁴³ They confirm that heme structures optimized without regard to the protein environment are markedly less ruffled and saddled than the respective crystal structures. Thus it is the protein matrix which is essential for maintaining the strong ruffling of the heme structure in nitrophorins, and is very likely as well for cytochromes c,¹⁴⁴ and likely in certain other heme-containing proteins as well. In the case of the nitrophorins, NMR investigations also suggest that the entire β-barrel backbone of the protein, and especially the side chains of I120¹⁴⁵ and the “belt” residues F27, Y38, Y85, and the set of four residues F42, E53, Y81 and Y104, the latter three of which are hydrogen-bonded to each other,¹³³ are the most important in causing the ruffling of the heme.

Figure 8.

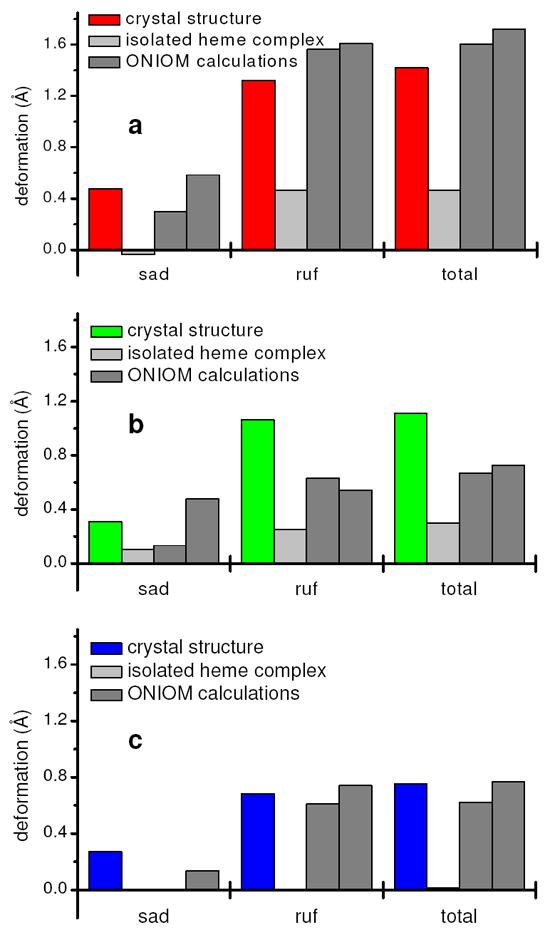
NSD analyses¹⁴³ of the optimized heme structures of NP2–NO (a), NP2–CN (b) and NP2–Hm (c) in comparison to NSD analyses¹⁴³ of the heme groups of the crystal structures which were taken as input for the calculations. sad stands for saddling and ruf for ruffling, total denotes the total out-of-plane deformation. The two bars for the ONIOM calculations stand for the optimized structures with deprotonated (left) and protonated carboxylates (right), respectively.

DFT-based normal mode analysis and density of states (DOS)

In Supporting Information Figure S3 the DOS calculated on the basis of the planar heme complexes in Figure 7a-c are presented. Even though the molecular structures in Figure 7a-c are only very crude models for NP2, the high-energy region of the DOS is well represented by calculations performed on these model systems (compare to Figure 2). Whereas the calculated Fe–NO stretching mode at 665 cm^-1 is different than the experimentally-observed value of 594 cm^-1 (see Supporting Information Figure S3a and Table S1) the NP2–CN pattern is reproduced quite well, with the Fe–CN stretch being calculated at 463 cm^-1 and a mode which involves bending at 438 cm^-1 (Figure S3b). The histamine in NP2–Hm was modeled by an imidazole (NP2–Im) and this simulation yields reasonable agreement with the experiment (Figure S3c). Here three modes involving strong iron–ring contributions have been calculated at 412, 418 and 426 cm^-1.

The low-energy part of the experimental DOS, however, is only poorly reproduced by these calculations. This may be due to the missing ruffling and saddling of the heme structure, but more likely to the neglect of the atoms in the protein environment of the heme. In fact, as will be shown below, the low energy range molecular vibrations always involve large parts of the protein.

Figure 9 displays the QM/MM simulation of the DOS of NP2–NO, based on its crystal structure (PDB filename 1T68) in comparison to the experimentally determined DOS of NP2-NO (Figure 9a). The simulation shown in Figure 9b has been performed with the heme carboxylates of NP2–NO both being protonated. This was motivated by the low pH of the NP2–NO sample (pH 5.5), which was chosen to be similar to that of the saliva of R. prolixus. A mode with considerable Fe–NO stretching contribution occurs at 630 cm^-1 and a band consisting of two Fe–N–O bending modes at 582 and 591 cm^-1 is visible at 580 cm^-1 (Table 2). See NP2-NO Movies in the Supporting Information. Comparing these values to the experimentally observed 594 cm^-1 for the ν(Fe–NO) stretching and 581 cm^-1 for δ(Fe–N–O) bending leads to a reasonable agreement. Since raising the pH to 7.5 leads to release of NO from the protein we were interested in whether the possible deprotonation of the heme carboxylates at neutral pH would influence the Fe–NO modes.

Figure 9.

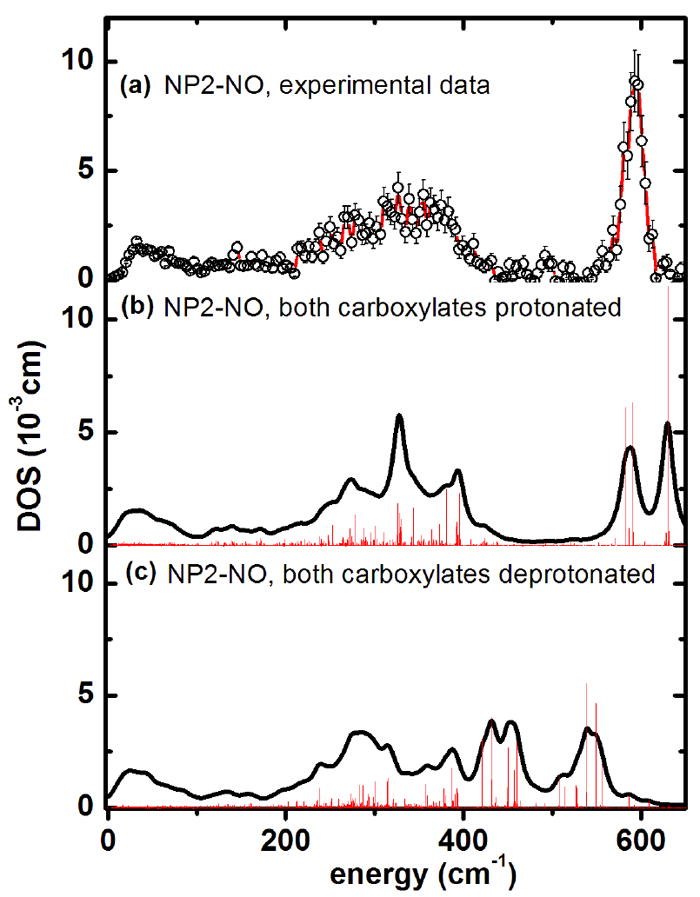
Iron vibrational density of states obtained from calculations for NP2–NO (a) experimental data. (b) Simulation with the ONIOM approach¹²⁷ with both heme carboxylates protonated, and (c) with both heme carboxylates deprotonated. The bar graphs display the calculated mode composition factor e², scaled by a factor of 0.11.

Table 2.

Structural parameters of the iron-ligand-bond in the ONIOM-optimized molecular structures of NP2 on which the calculations of the DOS presented in Figures 9-11 are based and comparison of calculated and observed iron ligand modes from NIS

	Heme carboxylates	Fe-Ligand distance [Å]	Fe-Ligand angle [°]	Fe-Ligand vibrations (calculated) [cm-1]	NIS characteristic bands at [cm-1]
NP2-NO	protonated	1.651	167.9	Fe-NO-stretch (630)	594, 581
				Fe-N-O-bend (591, 582)
	deprotonated	1.697	159.3	Fe-NO-stretch (539,549)
				Fe-N-O-bend (431, 421, 450, 460)
NP2-CN	protonated	1.936	178.2	Fe-CN-stretch (468)	439, 355, 327
				Fe-C-N-bend (443, 446, 406)
	deprotonated	1.947	176.9	Fe-CN-stretch (455)
				Fe-C-N-bend (451, 379)
NP2-Im	protonated	2.010	-	-	387, 350, 329
	deprotonated	2.022	-	-

This is indeed found to be the case, as the simulation of the DOS displayed in Figure 9c shows that deprotonation of the heme carboxylates leads to a downshift of the ν(Fe–NO) mode to 538 cm^-1. Thus, deprotonation of the heme carboxyls leads to a redshift in the calculated Fe–NO stretching mode, which is consistent with a weakening of the Fe-NO bond. Whether this effect actually contributes to triggering the NO release may be speculative at this point, but the crystal structures of all NP–NO complexes show that in fact the heme carboxylates are freely accessible to solvent and therefore may well act as pH-dependent NO release switches. This effect is expected to be particularly important for NP2 (and probably NP3 as well), where there is little change in A-B and G-H loop conformation upon pH rise to 7.7,^24,25,146 as compared to the large conformational changes observed for NP4 as a function of pH.^18,22,26-29 Correspondingly, there is only a factor of 3 increase in the dissociation rate of NO on pH rise from 5.0 to 7.5, whereas NP4 shows a factor of 80 increase in k_d for NO release over this same pH range.²⁰

At low energies, below 100 cm^-1, about 300 protein modes have been calculated using the PDB entry 1T68 and assuming protonated heme carboxyls. 55 of these calculated protein modes have a mode composition factor e² > 0.0001 and their frequencies are listed in Table S2 (supporting information). Among the most intense seven modes are four at 69, 70, 72 and 74 cm^-1, all of which involve considerable heme doming (see also NP2-NO Movies in the Supporting Information). It is striking that the experimental NIS spectrum of NP2-NO also has an intense band at 68 cm^-1 (see Figure 1a). Therefore, based on the simulations presented here, this band can be assigned to protein modes involving strong heme doming character. The remaining three modes with the highest iron displacement below 100 cm^-1 are at 17, 36, and 29 cm^-1. These modes represent mainly heme sliding motions, which is e.g. at 36 cm^-1 coupled to a twisting of the β-barrel subunits (see Movie in the Supplemental Information). Indeed, there is also an experimentally observed band at around 32 cm^-1 (see Figure S1a). Thus, heme sliding motions can also be directly monitored by measuring NIS in the very low energy region, below 50 cm^-1.

The QM/MM simulation of the DOS of NP2–CN (based on PDB entry 2HYS), with both heme carboxylates being protonated (Figure 10 b) displays a splitting of the Fe–CN modes into two nearly degenerate modes, with significant δ(Fe–CN) contributions at 443 cm^-1 and 446 cm^-1, and a mode with both δ(Fe–C–N) and ν(Fe–CN) contributions at 468 cm^-1 (Table 2). Since the NP2–CN sample was prepared at pH 7.5, which (although the pK_a value of the heme carboxylates is not yet known) may lead to deprotonation of the carboxylates, a further QM/MM simulation was performed with deprotonated carboxylates (Figure 10c). The so-calculated DOS shows a band centered at 450 cm^-1, which is also in good agreement with the experimentally observed 439 cm^-1 (Figure 1b and 10a). This band represents a pair of a nearly degenerate ν(Fe–CN) stretch at 455 cm^-1 and a δ(Fe–C–N) bend at 451 cm^-1 (see NP2-CN Movies in the Supporting Information). Therefore it cannot be ruled out that a mixture of protonated and deprotonated heme carboxylates are present. For example, the structure of the NP2(D1A)-CN complex (PDB file 2HYS) shows that one carboxylate has each oxygen H-bonded to a water molecule, while the other carboxylate has no H-bonded waters.

Figure 10.

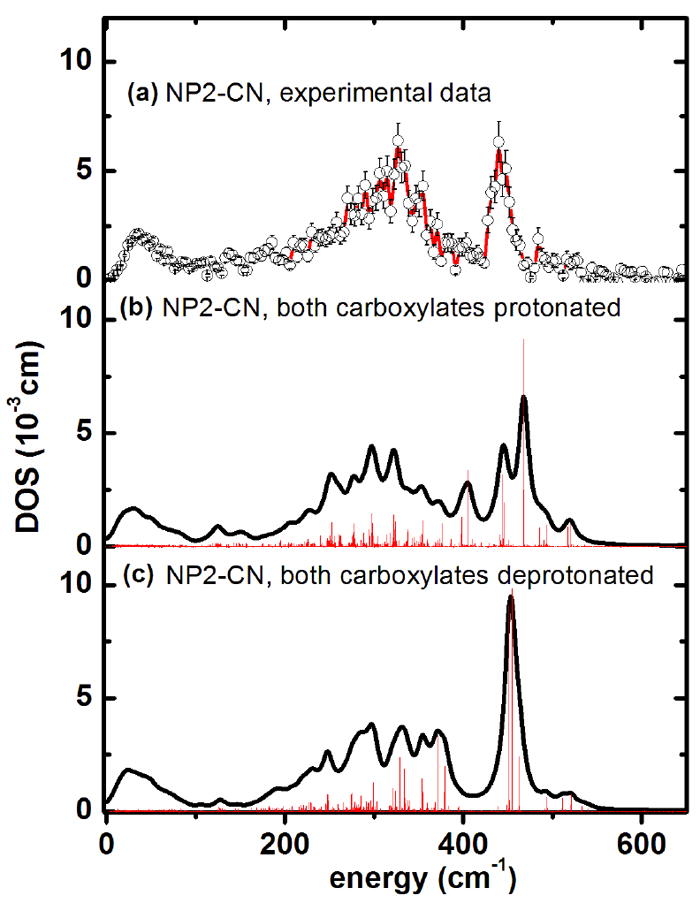
Iron vibrational density of states obtained from calculations for NP2–CN (a) experimental data. (b) Simulation with the ONIOM¹²⁷ approach with both heme carboxylates protonated, and (c) with both heme carboxylates deprotonated. The bar graphs display the calculated mode composition factor e², scaled by a factor of 0.11. The possibility that the experimental spectrum (DOS) could be a superposition of protonated and deprotonated forms cannot be excluded.

Assuming deprotonated heme carboxyls, the most intense calculated modes below 100 cm^-1 with considerable heme sliding have been calculated to occur at 12, 21 and 35 cm^-1, which is in partial agreement with the experimentally observed broad band at 24 cm^-1 (Fig. S1b). Modes with significant heme doming have been calculated to be at 47, 74, 76 and 83 cm^-1.

The experimental DOS of NP2-Hm shows two broad bands around 350 cm^-1 and 400 cm^-1 (Figure 1c and 11a) which are well reproduced by the simulated DOS assuming both heme carboxylates being protonated (Figure 11 b). The latter simulation leads to defined bands with maxima at 345 cm^-1 and 410 cm^-1 (Table 2). Calculation of the DOS, assuming both heme carboxylates to be deprotonated, leads to a pattern which is dominated by a band at 385 cm^-1. Thus, comparing the simulated DOS in Figure 11b and c with the experimental DOS displayed in Figure 11a suggests that NP2-Hm might display a mixture of NP2s with protonated and unprotonated heme carboxyls at pH = 7.5. There are three dominant modes which contribute significantly to the DOS: (i) in-plane iron modes along CHB and CHD coupled to rotation of the imidazole rings (both ligand and distal histidine) around the ring normal at 389 cm^-1. (ii) out-of-plane movements of the iron and inversely phased doming of the heme ring at 422 cm^-1. (iii) in-plane iron movement along the CHA-CHC-axis coupled to a slight tilting of the imidazole rings at 383 cm^-1. Movies of these modes for NP2-Hm are available in the Supporting Information.

Figure 11.

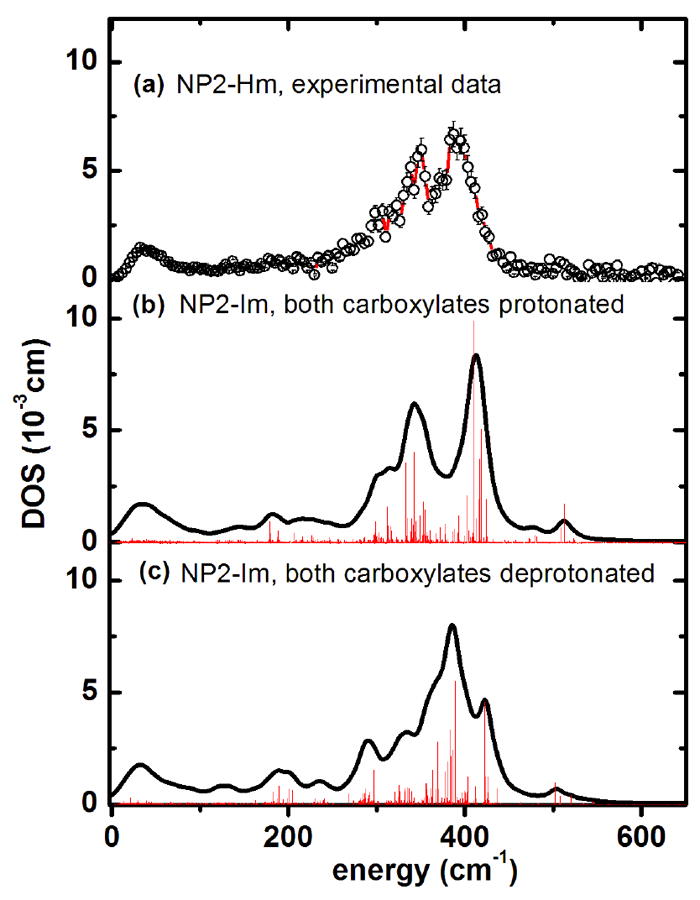
Iron vibrational density of states obtained from calculations for NP2–Hm (a) experimental data. (b) Simulation of NP2–Im with the ONIOM approach¹²⁷ with both heme carboxylates protonated, and (c) with both heme carboxylates deprotonated. The bar graphs display the calculated mode composition factor e², scaled by a factor of 0.11. The possibility that the experimental spectrum (DOS) could be a superposition of protonated and deprotonated forms cannot be excluded.

For the low-energy region of NP2-Hm a characteristic mode pattern different from those of NP2-NO and NP2-CN has been obtained: the most intense mode is at 21 cm^-1, followed by modes at 13, 29 and 39 cm^-1. All of them have strong heme sliding character and are also visible in the experiment (see band at 32 cm^-1 in Figure S1c). There are two modes at 66 and 85 cm^-1 which involve considerable heme doming, but whether these are responsible for the experimentally-observed band at 92 cm^-1 (see Figure 1c) remains a subject for further investigation.

Conclusions

The present study shows that Nuclear Inelastic Scattering (NIS), also called Nuclear Resonant Vibrational Spectroscopy (NRVS),^97-105 coupled with QM/MM calculations, provide an excellent means of understanding the unique ruffling of the heme in NP2. NIS gives deep insight not only into iron-ligand binding modes, but also into possibly functionally-relevant low-energy modes at energies down to 10 cm^-1. If Nuclear Forward Scattering (NFS) techniques are coupled with conventional Mössbauer spectroscopy and/or Nuclear Forward Scattering (NFS), spin and oxidation states of the iron centers are obtained. By means of conventional Mössbauer spectroscopy we have shown that NP2-NO has a diamagnetic ground state, whereas the NP2-CN and NP2-Hm complexes have Type I and II low spin ferriheme centers,¹¹⁹ respectively. This knowledge, together with crystal structure data, allowed us to perform QM/MM calculations on the whole protein molecule, and the experimentally-observed modes could be assigned. The QM/MM calculations also show that it is the protein matrix of the β-barrel protein, and not the axial heme ligand, which is responsible for the strong non-planarity in nitrophorins, and most probably as well in other heme proteins, especially some of the cytochromes c.¹⁴⁴