Selection for mitonuclear co-adaptation could favour the evolution of two sexes

Abstract

Mitochondria are descended from free-living bacteria that were engulfed by another cell between one and a half to two billion years ago. A redistribution of DNA led to most genetic information being lost or transferred to a large central genome in the nucleus, leaving a residual genome in each mitochondrion. Oxidative phosphorylation, the most critical function of mitochondria, depends on the functional compatibility of proteins encoded by both the nucleus and mitochondria. We investigate whether selection for adaptation between the nuclear and mitochondrial genomes (mitonuclear co-adaptation) could, in principle, have promoted uniparental inheritance of mitochondria and thereby the evolution of two mating types or sexes. Using a mathematical model, we explore the importance of the radical differences in ploidy levels, sexual and asexual modes of inheritance, and mutation rates of the nucleus and mitochondria. We show that the major features of mitochondrial inheritance, notably uniparental inheritance and bottlenecking, enhance the co-adaptation of mitochondrial and nuclear genes and therefore improve fitness. We conclude that, under a wide range of conditions, selection for mitonuclear co-adaptation favours the evolution of two distinct mating types or sexes in sexual species.

1. Introduction

The advantages and disadvantages of sexual reproduction are well known, if disputed [1]. The reason for the existence of two sexes in the vast majority of sexual organisms is less celebrated and understood. While sex requires two parents, there is no obvious need for these parents to be of different sexes. At face value, two sexes seem to be the worst of all possible worlds: individuals are restricted to mating with half the population, which must have a selective cost if there is any difficulty in finding a mate. Either a single sex or multiple sexes should be better, as both would enable individuals to mate with a larger proportion of the population.

Sexual dimorphism is grounded in anisogamy, in which one sex, by definition the female, produces a few large, immobile eggs, while the male produces greater quantities of small, motile sperm. Parker et al. [2] proposed that anisogamy evolved from an isogamous population via disruptive selection. The hypothesis assumes that zygote fitness increases with size, and that gamete production has a number-size trade-off. While this may be true, such trade-offs cannot explain the existence of two sexes (or strictly, mating types) in isogamous species. Thus, the basis of two sexes precedes the evolution of anisogamy and sexual dimorphism, and cannot be ascribed solely to disruptive selection.

The distinction between the two mating types in isogamous species typically relates to the inheritance of cytoplasmic genes [3]. One ‘sex’ passes on mitochondrial genes, the other does not. The few exceptions typically conform to the spirit of this generality. For example, the multiple sexes of some slime moulds such as Physarum polycephalum, and the thousands of mating types in fungi such as Schizophyllum commune, do not contravene the principle of uniparental inheritance of mitochondria [4,5]. Likewise, the doubly uniparental inheritance system of bivalve mussels, males receive mitochondria from both parents, but these then segregate, with male mitochondria entering the gonads and female mitochondria committed to the soma [6]. From this point of view, the best explanation for the asymmetry of the sexes lies in the selective forces that led to uniparental cytoplasmic inheritance.

Most theoretical work on the evolution of uniparental cytoplasmic inheritance has concentrated on its role as a mechanism to minimize selfish conflict between cytoplasmic elements [7–10]. It is argued that mixing cytoplasmic elements from different parents may result in conflict among them [8] or selection for good competitors [9], in both cases at the cost of cell fitness. Various authors have modelled these frameworks and concluded that nuclear mutations which enforce uniparental transmission of the cytoplasm are favoured by selection, thereby eliminating the opportunity for conflict in the zygote or the spread of selfish mutants [8–10]. This seems reasonable even though there are some constraints on the models. For instance, as noted by Birky [11] and Hoekstra [12], mutations that induce uniparental inheritance are only selected during the brief time window when a selfish mutant is present, and before it spreads to fixation. If such selection only operates occasionally, selfish conflict might fall short of a general explanation for the near-universality of uniparental inheritance.

In this paper, we explore a novel hypothesis for the evolution of uniparental inheritance. In the early evolution of mitochondrial symbiosis, a large fraction of the mitochondrial genome migrated to the nucleus [13,14]. This means that adaptive evolution of the key mitochondrial function, oxidative phosphorylation, depends on proteins encoded by two different genomes. There is strong evidence across many eukaryotic orders, from fungi and plants to invertebrates and mammals (including humans) that the mitochondrial and nuclear genomes have adapted to each other over evolutionary time [15,16]. This evidence includes a concordance between the evolutionary rates of mitochondrial and nuclear genes encoding respiratory-chain subunits, a decline in respiratory function in nuclear-cytoplasmic hybrids (cybrids) and hybrid breakdown in introgressed populations caused by mitonuclear incompatibilities [17,18].

Could uniparental inheritance of mitochondria have arisen to facilitate better co-adaptation of mitochondrial and nuclear genes, and so explain the evolution of two sexes [17,19]? Here, we explore this possibility using a mathematical model of evolution in a unicellular organism with the ancestral state of biparental inheritance of mitochondria. Our model explores the different modes and tempi of inheritance and evolution of nuclear and mitochondrial genes: different copy number (1 or 2 in the nucleus versus many in mitochondria), different mutation rates (typically lower in the nucleus) and different patterns of inheritance (Mendelian in the nucleus; uni/biparental and bottlenecks in mitochondria).

The model allows us to consider the consequences of selection for mitonuclear co-adaptation. We do not consider direct competition between uni- and biparental inheritance of mitochondria here, as the dynamics of the two modes of inheritance are known to be complex [9]. Here, we demonstrate that mitonuclear co-adaptation is indeed improved with uniparental inheritance and mitochondrial bottlenecks under a wide range of conditions. This shows that the requirement for co-adaptation could have been an important force in the evolution of two sexes.

(a). Model of mitonuclear co-adaptation

To model co-adaptation between the nucleus and mitochondria, we consider a single gene in the nucleus that interacts with a single gene in the mitochondria (see box 1 for model terminology). Both genes have two allelic states, 0 and 1. We assume that each cell contains a fixed number M of haploid mitochondria. Let the diploid nuclear state i = 1, 2, 3 represent the three possible genotypes (00), (01) and (11), respectively. Let the mitochondrial state j, where j ∈ {0, 1, …, M}, represent a cell with j mitochondria in state 1 and M − j mitochondria in state 0. Under this model, there exist three possible nuclear states and M + 1 mitochondrial states. It follows that any cell in the population can be in 3(M + 1) possible mitonuclear states. Fitness is a function of the degree of matching between genes in the nucleus and the mitochondria defined by:

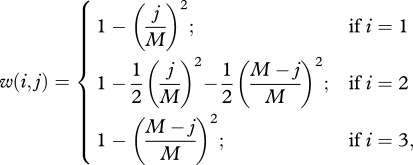1.1

where i is the nuclear state and j the mitochondrial state. Since a cell contains many mitochondria, mitonuclear mismatches that are present in only a few of a cell's mitochondria are likely to have a very minor fitness effect, as is borne out by the relatively high threshold of mitochondrial mutations within a cell required to cause a significant decline in oxidative phosphorylation in mitochondrial diseases [20]. The decline in fitness should become increasingly steep with greater mismatch, which justifies the choice of the quadratic functions in equation (1.1) to describe fitness (electronic supplementary material, figure S1). Optimal fitness is achieved when the mitochondrial and nuclear genes are fully matched.

Box 1. Terms and definitions.

w

fitness

M

number of mitochondria

B

bottleneck size

μ

mitochondrial mutation rate

ν

nuclear mutation rate

p

proportion of allele 1 in the nucleus

q

average proportion of allele 1 in the mitochondria

average population fitness

σ²

variance in population fitness

P_w

proportion of the population with fitness greater than or equal to w

To model the evolution of the system, we suppose a life cycle composed of five steps (figure 1). The population of unicellular organisms undergoes clonal expansion during which it is subject to mutation and selection (the model's logic also applies to multi-cellular organisms). We do not explicitly model this, but for simplicity impose mutation (step one) followed by selection (step two). The pair of nuclear genes mutates independently of each other and of the mitochondrial genes with probability ν. Mitochondrial genes mutate independently of each other and of the nuclear genes with probability μ. After mutation, selection is imposed, with the change in the relative frequency of each mitonuclear genotype being proportional to its fitness as defined in equation (1.1).

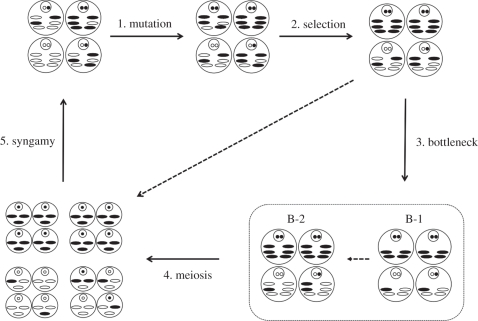
Figure 1.

Schematic of the life cycle. A representative sample of unicellular organisms (large circles) containing a number of haploid mitochondria (ovals) and a diploid nucleus (smaller circle) undergo steps 1–5 described in the main text. The mitochondria are shaded or left blank to represent the two states the mitochondrial genes may assume. The smallest circles in the nucleus represent nuclear genes that are shaded or left blank to represent the two states genes may assume. B-1 and B-2 are the two bottleneck stages as described in the main text. The dashed arrow represents the case where no bottleneck is assumed.

Surviving cells then enter the sexual phase in which they undergo meiosis and syngamy to produce the next generation. We assume that there is a mitochondrial bottleneck before meiosis (step three). This imposes two rounds of sampling: the first without replacement from a mitochondrial population of size M down to the bottleneck size B, and the second with replacement from B up to M. The bottleneck is simply a process of sampling and amplification in the mitochondrial population of a cell, and the precise mechanism by which this is achieved (e.g. physical bottleneck or non-random segregation) is not relevant.

Each cell then undergoes meiosis (step four). The cell's population of mitochondria is doubled to 2M and then reduced through two cell divisions to produce four haploid gametes, each with M/2 mitochondria. At each meiotic cell division, the mitochondrial genotypes of the parent cell are randomly segregated between the two daughter cells (i.e. sampling without replacement). Gametes then randomly fuse with each other to form the next generation of cells that re-enter the life cycle (step five). Depending on the mode of mitochondrial inheritance assumed, only one (uniparental inheritance) or both (biparental inheritance) parents transmit their mitochondrial genomes to the offspring (new cell). With uniparental inheritance, the M/2 mitochondria inherited from the transmitting sex are sampled with replacement to restore the original number M. With biparental inheritance, the mitochondrial genomes of the two parents are conjoined to form a set of M mitochondria.

We assume an infinite population of cells thus neglecting drift in nuclear genes. Note, however, that the population of mitochondrial genes is of finite size, M, and drift in the mitochondria is explicitly considered. This life cycle can be described mathematically in an exact manner (see the electronic supplementary material, appendix). However, the complexity encompassed by the biological process prevents us from solving analytically for the equilibrium states. In order to investigate the asymptotic behaviour of the system we used numerical simulation. The initial frequency of each mitonuclear genotype was assigned from a uniform distribution Uni(0,1) and then normalized so that the frequencies sum to 1. We let the population evolve according to steps 1–5. We assume that equilibrium has been reached when the maximum of all changes in relative genotype frequency across a generation is smaller than an appropriately small value ɛ (see the electronic supplementary material, appendix).

2. Results

We ran simulations for a variety of parameter values (see the electronic supplementary material, appendix for more details) and compared the genotype distributions at equilibrium under uniparental and biparental mitochondrial inheritance. Depending on p₀, the initial frequency of allele 1 in the nucleus, and q₀, the initial frequency of allele 1 in the mitochondria, the population converged on either nuclear state (11) or (00) (electronic supplementary material, figure S2). This was the case with both uniparental and biparental inheritance of mitochondria. The heterozygous case (01) was never found to be attractive within the parameter sets employed in our study. This outcome follows from the assumption of additive effects, as the mitochondria can match a homozygous nucleus better than a heterozygote (see equation (1.1)). With a heterozygous nucleus, mitochondrial and nuclear genes can never be in full agreement. As a result, the nucleus always converges to one of the homozygous states along with matching mitochondria, dependent on initial conditions (electronic supplementary material, figure S2).

In order to compare the fitness under uniparental or biparental inheritance of mitochondria we plotted the population fitness distributions at equilibrium. These were generally skewed to the right (the fittest states, figure 2). A number of statistical measures were calculated in order to capture the distribution of genotypes at equilibrium, in particular, the population mean fitness and variance (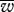 and σ², respectively), as well as P_w, the percentage of the population having fitness greater than a value w (e.g. w = 0.9 or 0.95). The latter measures act as good indicators of the population concentration around the fittest state. We also measured the average mitochondrial variation within individuals in the population, h. This is a measure of mitochondrial heteroplasmy in the population. The values of these statistics are given for a wide range of parameter values in table 1.

Figure 2.

Population fitness density under uniparental (red lines) and biparental (black lines) mitochondrial inheritance for μ = 0.01; ν = 0.001 and different values for the pair (M, B). (a–c) Parameter values with no bottleneck (M, B) equal to (200,—), (100,—) and (50,—), respectively. (d–f) Parameter values with bottlenecks (M, B) equal to (100,10), (50, 10) and (50, 5), respectively.

Table 1.

Summary statistics for different parameter sets (M, B, μ, ν). (The statistics 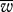and σ² are the mean and variance of the population fitness, and P_0.95 and P_0.9 are the proportion of the population with fitness greater than 0.95 and 0.9, respectively. h is the within cell variance in the mitochondria.)

	uniparental					biparental
(M,B,μ,ν)		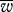σ2	P0.95	P0.9	h		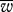σ2	P0.95	P0.9	h
(a) simple model with no bottleneck
1. (200, —, 0.01, 0.001)	0.945	0.0034	61.6	83.8	0.151	0.826	0.0013	1.06 × 10−4	1.04	0.242
2. (150, —, 0.01, 0.001)	0.951	0.0036	66.2	85.6	0.138	0.841	0.0016	0.113	5.33	0.238
3. (100, —, 0.01, 0.001)	0.965	0.0042	79.7	89.8	0.119	0.865	0.0020	0.728	21.2	0.230
4. (50, —, 0.01, 0.001)	0.972	0.0048	85.9	91.5	0.0866	0.904	0.0026	19.0	56.6	0.208
(b) effect of bottleneck
5. (200, 100, 0.01, 0.001)	0.960	0.0039	75.7	88.5	0.113	0.871	0.0021	1.42	29.2	0.225
6. (200, 50, 0.01, 0.001)	0.966	0.0042	80.5	90.0	0.0930	0.896	0.0025	11.0	53.7	0.210
7. (200, 10, 0.01, 0.001)	0.978	0.0059	89.9	93.6	0.0396	0.950	0.0035	64.8	85.7	0.139
8. (100, 50, 0.01, 0.001)	0.969	0.0045	83.3	90.4	0.0821	0.909	0.0027	22.2	63.4	0.2008
9. (100, 25, 0.01, 0.001)	0.973	0.0050	86.4	91.7	0.0639	0.928	0.0030	42.9	76.2	0.179
10. (100, 10, 0.01, 0.001)	0.978	0.0060	90.5	93.9	0.0388	0.952	0.0035	67.2	85.9	0.136
11. (50, 25, 0.01, 0.001)	0.977	0.0056	89.2	92.9	0.0466	0.938	0.0032	55.0	79.9	0.167
12. (50, 10, 0.01, 0.001)	0.979	0.0063	91.5	94.1	0.0320	0.955	0.0034	71.2	86.2	0.129
(c) varying μ and ν
13. (50, 10, 0.001, 0.001)	0.997	0.0011	98.9	99.2	0.00352	0.993	0.00074	97.5	99.2	0.0358
14. (50, 10, 0.001, 0.01)	0.988	0.0055	97.1	97.4	0.00359	0.983	0.0051	95.1	97.0	0.0391
15. (50, 10, 0.1, 0.01)	0.821	0.040	37.6	48.3	0.163	0.778	0.15	7.17	17.3	0.228
16. (50, 10, 0.5, 0.01)	0.711	0.022	4.97	9.48	0.214	0.734	0.0095	1.11	4.22	0.237

(a). Simple model with no bottleneck

In the absence of a bottleneck, uniparental inheritance always gave a higher mean and variance of the population fitness (table 1a). The values of P_w were also higher with uniparental inheritance and this can be seen from the heavy skewedness of the distribution under uniparental inheritance (figure 2a–c). So the higher variance under uniparental inheritance was owing to a highly skewed distribution with a high concentration of genotypes in the fittest states plus a long tail. By contrast, biparental inheritance generated a more normally distributed range of fitness around the mean. Finally, mitochondrial heteroplasmy was notably lower under uniparental inheritance (table 1a) as has been shown previously [21].

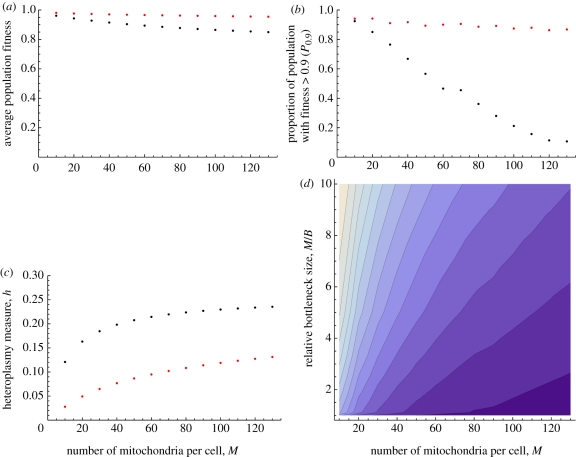
Mean fitness decreased with larger numbers of mitochondria per cell (M) under both modes of inheritance (table 1a). Likewise, P_w values dropped and heteroplasmy increased (table 1). Uniparental inheritance, unlike biparental inheritance, maintained high levels of mitonuclear matching for larger values of M (figure 3a,b). The fitness advantage of uniparental inheritance, both in mean fitness and P_0.9, P_0.95 increased with M (figure 3a,b). Likewise, the heteroplasmy measure h, increased with M, under both modes of inheritance, albeit substantially faster with biparental than with uniparental inheritance (figure 3c).

Figure 3.

Fitness advantage of uniparental inheritance over biparental inheritance. (a–c) Contrasting values of 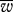, P_0.9 and h for variable numbers of mitochondria per cell (M) with no bottleneck (red points for uniparental inheritance and black for biparental inheritance). Other parameter values, μ = 0.01; ν = 0.001. (d) Contour plot for the difference in 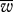for different numbers of mitochondria per cell (M) and the relative bottleneck size (M/B); bright, small difference (min = 0.008378), dark purple, large difference (max = 0.1046). Other parameter values, μ = 0.01; ν = 0.001.

(b). Effect of a bottleneck

When a bottleneck was included in the model, the population fitness distribution improved under both modes of inheritance. The tighter the bottleneck, the higher the resulting fitness distribution (both 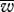and P_0.9, P_0.95) and the lower the level of mitochondrial heteroplasmy (table 1) under both modes of inheritance. Bottlenecks had the general effect of decreasing the distinction between uniparental and biparental inheritance (figure 2d–f and table 1b). Interestingly, when a very tight bottleneck was assumed, the number of mitochondria per cell seemed to have less of an effect on the fitness distribution. This can be seen with a bottleneck B = 10, contrasting the number of mitochondria M = 200, 100 and 50 (table 1b, rows 7, 10 and 12, respectively). There was little difference in mean fitness under uniparental and biparental inheritance with this very tight bottleneck. The opposite was the case without a bottleneck (table 1a; rows 1, 3 and 4). To illustrate the dynamic effect of the coupling (M, B) on the distinction between the two modes of inheritance, we generated a contour plot for the difference in mean fitness (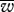) under the two modes of inheritance (uniparental minus biparental), for different values of M and relative bottleneck size M/B (figure 3d). This shows that the advantage of uniparental inheritance is greater for high values of M and less tight bottlenecks.

(c). Varying µ and ν

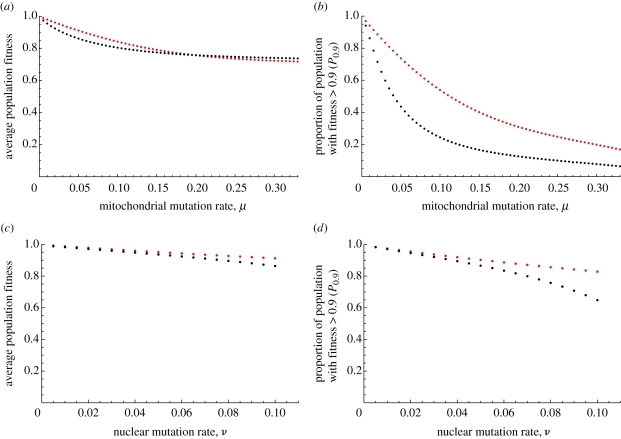
In the analysis above, we assumed that the mitochondrial mutation rate (μ) exceeded the nuclear mutation rate (ν). When this pattern of mutation was reversed (table 1c; row 13 ν = μ, row 14 ν > μ), the advantage of uniparental over biparental inheritance was smaller (figure 4). On the other hand, increasing μ while keeping ν fixed resulted in a greater advantage of uniparental inheritance (table 1c; row 14,15). However, when μ was increased beyond a threshold value, the distinction between uniparental and biparental inheritance decreased and biparental inheritance gave higher average fitness, although the value of P_0.9 and P_0.95 were always higher for uniparental inheritance (table 1c, row 16; figure 4).

Figure 4.

Fitness under uniparental (red points) and biparental (black points) inheritance given variation in the mutation rates. (a,b) Variation in mitochondria mutation rate μ given a fixed nuclear mutation rate ν = 0.001. (c,d) Variation in nuclear mutation rate ν given a fixed mitochondria mutation rate μ = 0.001. Other parameter values, M = 50; B = 10.

This initially puzzling result can be explained as follows. When the mitochondrial mutation rate becomes very high, all cells are kept in a state of considerable mitochondrial heteroplasmy (table 1). This selects for heterozygosity in the nucleus. Even though segregation of the nuclear genes results in a high frequency of homozygotes, net selection can favour a more even representation of the 0 and 1 alleles in the mitochondria of progeny. So above a high threshold of mitochondrial mutation rate, biparental inheritance is favoured over uniparental inheritance. This is unlikely to be of relevance under natural circumstances.

3. Discussion

Our results suggest that uniparental inheritance of mitochondria improves mitonuclear co-adaptation. Uniparental inheritance increased the mean population fitness () and the proportion of the population with high-fitness genotypes (P_0.9 and P_0.95; table 1 and figure 2a–c). These outcomes can be explained in two ways. Biparental inheritance reduces the variance in mitochondrial states between cells, which increases heteroplasmy in zygotes. This is disadvantageous as it interferes with co-adaptation, which requires matching of the mitochondria population to the nuclear background. In our model, the optimal state towards which the population evolves contains a homozygous nucleus (either (00) or (11)) with corresponding homoplasy in the mitochondria (state 0 or 1, respectively), to complete co-adaptation between the nucleus and mitochondria. Once a population is near to this state, fitness is improved if heteroplasmy is minimized. This is better achieved by uniparental inheritance, which precludes the mixing of mitochondrial populations in the zygote. A second way of formulating this advantage is to note that the higher variance between individuals generated under uniparental inheritance improves the efficiency of selection. This permits selection to amplify the frequency of optimal genotypes, allowing the population to evolve closer to the optimal state. We can see this in the skewed distribution of fitness under uniparental inheritance with a high frequency of individuals attaining maximum fitness (figure 2a–c). This outcome follows from our assumption that selection is concave down and so reaches a plateau as the number of matching mitochondria increases (electronic supplementary material, figure S1 and equation (1.1)).

We also examined the effect of a mitochondrial bottleneck before meiosis. This had a beneficial effect on mitonuclear co-adaptation under both modes of inheritance (figure 2). Both the mean population fitness (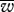) and the proportion of the population with high-fitness genotypes (P_0.9 and P_0.95) were improved when a bottleneck was assumed (table 1). Decreasing the bottleneck size had a positive effect on the fitness distribution (table 1 and figure 2d–f). The effects of a bottleneck were similar to those generated by uniparental inheritance. Bottlenecks are a sampling process that reduce heteroplasmy and increase the variation between zygotes, and so increase the efficiency of selection (table 1), a conclusion drawn before in other modelling contexts [21,22]. In general, bottlenecks had larger effects on biparental inheritance, reducing the advantage of uniparental over biparental inheritance. This was especially true when the bottleneck was very tight (figure 3d, high M/B).

Our model explicitly considers an idealized unicellular life cycle (figure 1). In this context, we can interpret the bottleneck step as equivalent to mitochondrial segregation during cell division in the clonal expansion phase of the life cycle. The results, therefore, suggest that if unicellular species originally had few mitochondria and biparental inheritance, there would only have been weak selection in favour of the evolution of uniparental inheritance. Mitochondrial segregation during cell division might have been sufficient to restrict heteroplasmy and so maintain adaptation. However, in lineages where the number of mitochondria per cell increased, there would have been a much greater advantage generated by the switch to uniparental inheritance. Thus, uniparental inheritance may have been a prerequisite for mitonuclear co-adaptation in multi-cellular organisms with higher energy requirements and larger populations of mitochondria per cell. It is notable that organisms such as yeast (Saccharomyces cerevisiae and Schizosaccharomyces pombe) have a small number of mitochondria (less than 100) and do indeed lack uniparental inheritance [11,23,24]. Their mode of inheritance involves biparental inheritance of mitochondria followed by mitochondrial segregation. Plainly, this is sufficient to maintain mitonuclear function, as predicted by our model.

Our model also has implications for multi-cellular organisms, where true germline bottlenecking occurs [21,22]. In line with our results, true bottlenecks are only observed in large organisms with large numbers of mitochondria [25–27]. The tightness of the bottleneck varies across species and correlates with litter size (species with small litters having tighter bottlenecks) [28]. This fits our expectations, because the smaller the litter, the greater the need for offspring fitness to be assured, hence likewise for mitonuclear co-adaptation. From our results, we also predict that species with higher aerobic capacity, such as birds with powered flight, should also exhibit very tight bottlenecks [17,18,29].

In our model, optimal fitness can only be achieved by the homozygote states. This relates to our assumption that the nuclear genes are additive in their effect on mitochondria and both alleles are equally active. The additive assumption seems a natural one, as the population of mitochondria are likely to interact with the gene products of both nuclear alleles. To ensure that the preference for homozygous states was not an artefact of the additive assumption in our model, we considered a situation in which there was an advantage for heterozygotes (see the electronic supplementary material, appendix). Even in these cases, the population converged to the homozygous state. This is related to the pattern of Mendelian inheritance. A population can never be fully heterozygous because heterozygous parents will always give rise to 50 per cent of homozygous children. Therefore, even if the heterozygotes reach optimum fitness, their homozygous offspring will be significantly less fit, eventually pushing the population to one of the homozygous states.

We focused on mutation rates in which the mitochondrial rate (μ) was 10 times faster than the nuclear rate (ν). This difference seems appropriate for animals and fungi, where mitochondrial evolution rates are typically an order of magnitude greater than nuclear rates [30,31]. Note that a mutation in our model signifies a shift from one state to another, and is therefore commensurate with long-term evolutionary rates rather than mutations in nucleotide sequence, which can range over several orders of magnitude. In general, we found that uniparental inheritance was favoured whenever the mitochondrial mutation rate was greater than the nuclear mutation rate (table 1 and figure 4a,c). We also considered the reverse case (table 1 and figure 4b,d), which is perhaps more representative of plants, where nucleotide substitution rates are lower in the mitochondria than in the nucleus [32,33]. In this case, the benefit of uniparental inheritance was lower. This might help to explain why heteroplasmy is more common in angiosperms [34].

In conclusion, our model suggests that selection for mitonuclear co-adaptation may favour the evolution of uniparental inheritance in unicellular organisms, particularly when the number of mitochondria is large. Likewise, our model predicts the combination of uniparental inheritance with germline bottlenecking in larger multi-cellular organisms. Such asymmetric passage of mitochondria in the germline is the deepest evolutionary distinction between the two sexes. Our work illustrates a fundamental principle of uniparental inheritance, namely the capacity to generate greater variation and so facilitate selection for mitonuclear co-adaptation. Conversely, biparental inheritance, by mixing different populations of mitochondria, restricts the evolution of optimal mitonuclear combinations. While these findings can explain the evolution of two sexes in principle, further work exploring the evolutionary invasion of uniparental mutants in biparental populations is needed. We expect that, given the difference in fitness between the two modes of inheritance illustrated here, the requirement for mitonuclear co-adaptation will be an important force favouring the establishment of uniparental inheritance and the evolution of two distinct sexes.