A general model for effects of temperature on ectotherm ontogenetic growth and development

Abstract

The temperature size rule (TSR) is the tendency for ectotherms to develop faster but mature at smaller body sizes at higher temperatures. It can be explained by a simple model in which the rate of growth or biomass accumulation and the rate of development have different temperature dependence. The model accounts for both TSR and the less frequently observed reverse-TSR, predicts the fraction of energy allocated to maintenance and synthesis over the course of development, and also predicts that less total energy is expended when developing at warmer temperatures for TSR and vice versa for reverse-TSR. It has important implications for effects of climate change on ectothermic animals.

1. Introduction

Changes in environmental temperature regimes pose potentially severe problems for ectothermic organisms. Their body temperatures fluctuate with environmental temperatures and the rates of most biochemical reactions and biological processes increase approximately exponentially with temperature. So changing temperature literally changes the pace of life.

The rates of ontogenetic growth and development are not exceptions. Ectothermic animals develop faster at warmer temperatures [1], and they usually mature at smaller body sizes—as much as 20 per cent smaller for a 10°C temperature increase. This phenomenon has been called the ‘temperature size rule’ (TSR) [2]. Like most biological ‘rules’, however, there are exceptions, including well-documented cases of the reverse-TSR, where the mature body sizes are larger at higher temperatures. Different compilations give about 15 per cent (13–17%) of reverse-TSR cases [2,3].

Here, we develop a simple model for the effects of temperature on ontogenetic development of ectothermic animals. The model extends an earlier model for allocation of energy and biomass to growth on endotherms [4] by explicitly incorporating the temperature dependence of the rate of development and the rate of somatic growth. Any imbalance in these two rates results in either the TSR or reverse-TSR, depending on which process is more sensitive to temperature. The model predicts the fractions of energy allocated to maintenance and biomass synthesis at a given developmental stage, including the total quantity of energy expended during development. We model explicitly the case of post-hatching development, where an animal consumes food to fuel its metabolism. Later, we consider the case of embryonic development, where the organism fuels its metabolism from energy reserves stored in the egg.

2. The model

Growth and development are fuelled by metabolism. It is well known that within the normal temperature range, metabolic rate increases approximately exponentially with temperature [5]. This relationship can be described by the Boltzmann relation, 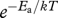, where E_a is an ‘activation energy’ that reflects the kinetics of the underlying biochemical reactions and quantifies the temperature dependence, k is Boltzmann's constant and T is absolute temperature ([1,6], but see [7]). For processes governed by aerobic respiration, such as growth and development of most ectothermic animals, E_a is typically approximately 0.65 eV (corresponding to a Q₁₀ of approx. 2.5 or a 2.5-fold increase in development rate for a 10°C increase in temperature) [1].

The effect of temperature on body size at maturity, however, depends on how energy and materials are allocated during ontogeny. The body mass m(t, T) at any time, t, during development depends on the magnitude of two different processes that can have different temperature dependence: (i) growth rate or rate of biomass accumulation, ∂m/∂t, with temperature dependence 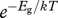and (ii) development rate or rate of ontogenetic differentiation, ∂μ′/∂t, with temperature dependence 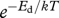, where E_g and E_d are the respective ‘activation energies’ (figure 1). The relative developmental stage, μ′ ≡ t/t_dev, is defined in terms of the time to the current developmental stage, t, relative to the total development time, t_dev. Similarly, the relative body mass, μ ≡ m/M, is the body size at any time, t, relative to adult body size [4]. Since ∂μ′/∂t = 1/t_dev, the total time of development 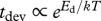. The relative developmental stage is a simple way to standardize the overall ontogenetic trajectory on a 0–1 scale, so μ′ = 0.1 means 10 per cent of time to adulthood. The adult mass, 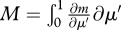, is proportional to 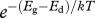. It can also be calculated as 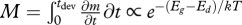. Unless these two processes, growth and development, have exactly the same temperature dependence (E_g ≡ E_d), size at maturity will vary with temperature (figure 1).

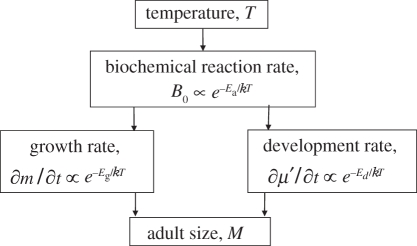
Figure 1.

Flow chart showing the effects of temperature on energy allocation during ontogenetic development. Metabolic rate, B, varies with body mass, m, and absolute temperature, T, as 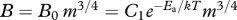, where B₀ is a temperature-dependent constant for a given species, E_a is the activation energy and k is Boltzmann's constant. Other variables: t is time, E_g and E_d are the activation energies for biomass accumulation rate and development rate, respectively.

The animal consumes food to fuel growth and development from hatchling to adult. We use an extended ontogenetic growth model [4] to capture the energy allocation during growth. The rate of food assimilation, A, is the sum of the rates of energy consumption for maintenance and growth. So

2.1

and

2.2

where B_maint is the rate of energy expended on maintenance, B_syn is the rate of energy used to synthesize the new biomass, B is the total metabolic rate, S is the rate of energy allocation to storage in new biomass and B_syn + S is the rate of energy expended on growth. Assuming that the energy content per unit of biomass, E_c, remains constant over ontogeny and is independent of temperature, these equations reflect energy and mass balance at any time, t. The integrated form over the entire development period is

2.3

where Q_tot is the total quantity of energy expended, Q_maint is energy expended on maintenance, Q_syn is energy expended to synthesize new biomass and Q_sto is energy stored in new biomass.

To incorporate effects of body size and temperature into equation (2.1), we make two assumptions:

• — Throughout ontogeny, metabolic rate, B, scales with body mass as B = B₀m^3/4, where B₀ is constant within and among individuals of the same species developing at the same temperature, but varies with temperature and species. The generality of m^3/4 scaling of metabolic rate has been questioned (but see [4,8–10]). It is straightforward to substitute a generic scaling exponent, α, or a different numerical value when there is compelling evidence for deviation from three-quarter-power scaling.

• — The temperature dependencies of the component processes can be characterized by Boltzmann relations as indicated above and below.

Rewriting equation (2.2) to explicitly incorporate body mass dependence gives

2.4

Additionally, B_maint = mB_m, where B_m = B₀M^−1/4 is the mass-specific rate of energy expenditure for maintenance, M is the body mass at maturity, B_syn = E_m(∂m/∂t), and E_m is the quantity of energy expended to synthesize a unit of biomass, assumed here to be independent of temperature. Dividing both sides of equation (2.4) by m^3/4 gives

2.5

Now incorporating the temperature dependencies in figure 1 and 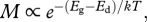equation (2.5) gives

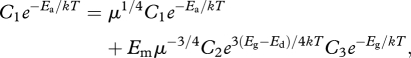2.6

where μ ≡ m/M is the relative body mass at any time, t, which is temperature-independent; E_a, E_g and E_d are the activation energies for the rates of overall metabolism, growth and development, respectively; and C₁, C₂ and C₃, are temperature-independent coefficients. Therefore, equation (2.6) gives the relationship among the temperature dependencies of rates of metabolism, growth and development

2.7

The model predicts the trajectories of biomass accumulation rate and development rate over ontogeny from hatching to maturity. Rewriting equation (2.4) by normalizing with respect to M, the body mass at maturity, gives a normalized biomass accumulation rate (see electronic supplementary material, appendix A)

2.8

where C₁ is a temperature-independent coefficient. Normalizing with respect to the effect of temperature, 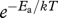, in equation (2.8), predicts the biomass accumulation rate normalized to both temperature and body mass at maturity

2.9

This model makes two additional predictions for the energy budgets of ectotherms during ontogeny. First, introducing effects of temperature into equation (2.2) gives (see electronic supplementary material, appendix B)

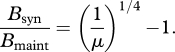2.10

This predicts that the same fraction of metabolic energy is allocated to maintenance and synthesis at any given relative body mass, regardless of temperature and taxon. Second, integrating equation (2.1) with respect to time gives equation (2.3), and introducing effects of temperature gives

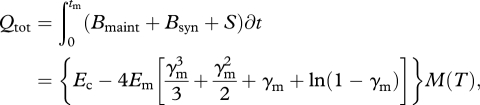2.11

where t_m is the time to reach some near-asymptotic adult size, m_adult = (1 − ɛ)M with ɛ ≪ 1 and γ_m = (m_adult/M)^1/4 [11]. In equation (2.11), E_c, E_m and γ_m are all independent of temperature, so the total quantity of energy consumed, Q_tot, during ontogeny varies predictably with temperature as 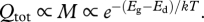The model predicts that when developing at higher temperatures, TSR ectotherms should consume less energy and reverse-TSR ectotherms should consume more energy.

3. Empirical evaluation

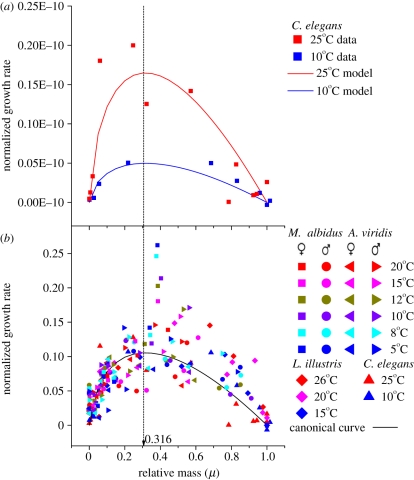
Experimental data for a variety of ectotherm taxa, such as nematodes, molluscs, crustaceans, insects and amphibians (table 1) support the model. The activation energy for metabolic rate, E_a, for each organism has been calculated based on equation (2.7). The average calculated E_a is 0.62 ± 0.03 eV. This average and most of the individual values are close to the predicted 0.65 eV, but a few outliers in table 1 and earlier studies [1,12] encompass a total range from 0.15 to 1.2 eV. Equation (2.9) predicts that all organisms should exhibit identical ‘canonical’ curves for normalized rates of biomass accumulation over ontogeny. Data for several organisms generally support this prediction. As predicted, the absolute rates, normalized only with respect to mass, increase with increasing temperature (figure 2a), but when normalized with respect to both mass and temperature, these curves all converge on the same shape with a peak at μ ≈ 0.3 (figure 2b). So, the highest rate of growth or biomass accumulation occurs at about 1/3 of adult mass, independent of temperature. This peak occurs at the same fraction of adult mass in ectotherms as it does in endotherms [4].

Table 1.

Effects of temperature on rate of development, biomass accumulation and metabolism and on body size at maturity. Experimental studies conducted at different temperatures provide data on development rate (E_d in 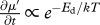) and body size (E_g − E_d in 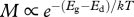) of different species. Effects of temperature on growth rate (E_g in 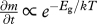) and metabolic rate (E_a in 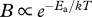) are calculated by E_a − (1/4)E_g − (3/4)E_d = 0 from the model. (Original data are in electronic supplementary material, appendix D.)

taxon	species	sex	development rate,	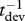adult size, M	biomass accumulation rate, ∂m/∂t	metabolic rate, B
			Ed (eV) (empirical)	Eg − Ed (eV) (empirical)	Eg (eV) (calculated)	Ea (eV) (calculated)
nematode	C. elegans	n.a.	0.61	−0.14	0.47	0.58
mollusc	Crepidula plana	n.a.	0.45	−0.16	0.29	0.41
crustacean	Acanthocyclops viridis	F	0.66	−0.13	0.53	0.63
		M	0.73	−0.14	0.60	0.69
	Macrocyclops albidus	F	0.78	−0.20	0.57	0.73
		M	0.77	−0.13	0.64	0.74
	Acanthocyclops vernalis	F	0.83	−0.14	0.69	0.80
		M	0.86	−0.24	0.62	0.80
insect	Drosophila willistoni	M	0.63	−0.26	0.37	0.57
		F	0.63	−0.15	0.48	0.59
	Drosophila equinoxialis	M	0.70	−0.12	0.58	0.67
		F	0.70	−0.16	0.54	0.66
	Drosophila pseudoobscura	M	0.62	−0.3	0.32	0.55
		F	0.62	−0.3	0.32	0.55
	Drosophila persimilis	M	0.59	−0.19	0.4	0.54
		F	0.59	−0.17	0.42	0.55
	Drosophila melanogaster	n.a.	0.81	−0.17	0.64	0.77
	Chaoborus flavicans	n.a.	0.53	−0.46	0.07	0.42
	Lucilia illustris	n.a.	0.63	0.05	0.68	0.64
	Chorthippus brunneus	F	0.73	0.41	1.15	0.84
	Omocestus viridulus	F	0.11	0.18	0.29	0.15
	Myrmeleotettix maculatus	F	0.43	0.31	0.75	0.51
	Stenobothrus lineatus	F	0.57	0.33	0.90	0.66
amphibian	Rana sylvatica	n.a.	1	−0.86	0.14	0.79

Figure 2.

Different species of ectotherms developing at different temperatures follow the same canonical curve of biomass accumulation rate. (a) Normalized for differences in adult mass, rates of biomass accumulation are higher at higher temperatures, but the trajectories differ only in absolute rates (heights). (b) So, when normalized with respect to temperature as well as mass, the rates for different species and temperatures all cluster closely around the theoretically predicted curve, which peaks at 31.6% of adult body mass. Species are Macrocyclops albidus, Acanthocyclops viridis, Lucilia illustris and Caenorhabditis elegans. Macrocyclops albidus, A. viridis and C. elegans are temperature size rule (TSR) species; L. illustris is a reverse-TSR species. (Original data and calculations are in electronic supplementary material, appendix C.)

4. Discussion

It is well documented that, in ectotherms, rates of both somatic growth and ontogenetic development increase with increasing temperature, so time to maturity is shorter at higher temperatures. Whether body size at maturity is smaller or larger, however, depends on the difference in the temperature dependence between these two rates: the TSR occurs when development rate is more temperature-sensitive, the reverse-TSR when biomass accumulation rate is more sensitive.

The TSR and reverse-TSR are necessary consequences of differences in the temperature dependence of somatic growth rate and development rate. Growth is the trajectory of increase in somatic mass owing to the uptake, transformation and allocation of materials, so it must obey mass balance. Development is the trajectory of differentiation from fertilized egg or some later stage to adult, regulated by gene-by-environment interactions and physiological and biochemical signals. Growth and development usually occur together during ontogeny, but do not necessarily proceed at the same rates. For example, in arthropods, the pace of post-embryonic development is marked by moulting through a series of instars, and in holometabolous insects, the final stage, pupa, undergoes differentiation (development) but no growth (since the pupa metabolizes but does not feed, mass actually decreases) [13].

Many investigators have studied the temperature dependence of these two processes [2,14–17]. It is now well documented that differences in size at maturity after developing at different temperatures can be due to differences in cell size, number of cells or some combination of these. For example, Caenorhabditis elegans, other nematodes, rotifers and some arthropods, have a determinate fixed number of cells at maturity, so variation in adult body size is due entirely to variation in cell size. In Drosophila, however, differences in adult body size after developing at different temperatures may be due primarily to differences in either cell size or cell number [18,19].

The current study appears to offer four important advances over previous theoretical and empirical treatments of the TSR. First, we present an analytical model that is both very simple and very general. It incorporates a minimum number of assumptions, parameters and functions required to characterize the primary effect of temperature on the two critical processes: rate of biomass accumulation and rate of development. These can all potentially be measured to evaluate the model, its assumptions, and its predictions empirically. Model predictions provide a quantitative baseline against which to compare data for different kinds of animals developing under different physiological and environmental conditions. The assumptions can be relaxed to generate more complicated models for animals where they may not apply. This level of simplicity and generality stands in contrast to studies using a Sharpe–Schoolfield model [17,20], which incorporates multiple parameters of enzyme kinetics that may be only indirectly relevant and are difficult to measure directly, and to studies on other aspects of development, such as hormonal regulation [15,21,22].

Second, our model easily accommodates cases where differences in adult body size after developing at different temperatures are due to any combination of variation in cell size or cell number. In organisms with a fixed number of cells at maturity, such as C. elegans, variation in adult body size depends on the amount of somatic growth and hence the increase in cell size. This case can be analysed quantitatively by modifying the model to define the relative developmental stage by relative number of cells rather than relative time.

Third, our model not only accounts for how temperature gives rise to both the TSR and reverse-TSR, it also predicts the effect of developmental temperature on three other important aspects of development. The first is the trajectory of biomass accumulation rate over ontogeny (equations (2.8) and (2.9); figure 2). The model predicts that after normalizing for body mass at maturity, all ectotherms should exhibit quantitatively similar trajectories of ontogenetic growth, with temperature affecting only the absolute growth rate. The second prediction is that the proportion of energy allocated to maintenance as opposed to biosynthesis at a given relative size is independent of temperature (equation 2.10). So the net growth efficiency [23] at any given relative mass, μ, is independent of temperature, although it decreases over ontogeny (see electronic supplementary material, appendix E). The third novel prediction is how temperature affects the total quantity of energy used at each stage of development (equation 2.11). We know of no other model that predicts these important unifying features of ontogeny. They are relevant to understanding effects of environmental temperature on the life history, ecology and evolution of ectotherms. And again, when deviations from model predictions are observed empirically, these cases call attention to the importance of other factors left out of our deliberately very simple model.

Fourth, although developed above explicitly for the case of post-embryonic development, the model can easily be modified for the case of an embryonic development. An embryo developing within an egg is fuelled by energy reserves stored in yolk, so the total quantity of energy available is fixed by egg size. The model predicts that when eggs of the same size are incubated at higher temperatures, a TSR ectotherm consumes less energy during incubation and may hatch with unused yolk, whereas a reverse-TSR ectotherm uses more energy, consumes more yolk and may hatch at a less-developed stage. Actually, some TSR ectotherms appear to compensate by producing smaller eggs at higher temperatures [24–29], supporting the prediction that they consume less total energy during development [30]. More complicated treatments may be required to incorporate other features of embryonic development, such as: (i) cell size usually decreases over ontogeny with the multiple of cycles of cell division as a single-celled zygote develops into a multi-cellular hatchling and (ii) relative water content of the embryo may decrease and energy density of accumulated biomass may increase over ontogeny [31,32].

It remains to be explained why the majority of ectotherms follow the TSR, whereas only a minority exhibit the reverse-TSR. Several authors have proposed adaptive explanations for the preponderance of the TSR [23,33–42], and many other studies in the context of geographical variation in ectotherm body size in gradients of environmental temperature, especially in Drosophila. Usually selection can be expected to minimize the time and the total energy consumed during ontogeny. Time can be minimized by behavioural temperature regulation, selecting higher temperatures for both incubation and post-hatching development. This tendency for ‘warmer to be better’ [43] should translate into a TSR. Selection to incorporate a margin of safety so that embryos do not run out of yolk should also favour TSR. A reverse-TSR should be expected only in rare cases when it is advantageous to develop at colder temperatures, such as to behaviourally select cold microclimates to avoid predators or to prolong development owing to constraints of environmental seasonality [42]. The theory developed here should also apply to special cases, such as when temperature dependence of solubility and diffusion of oxygen in aqueous media limit egg size and development of aquatic organisms [44,45].

The phenomenon of ‘Bergman's Rule’ in ectotherms is consistent with the TSR. In latitudinal and elevational gradients of increasing temperature, both aquatic and terrestrial arthropods and other ectotherms are often smaller in warmer environments [46]. So this pattern could potentially be just a direct phenotypic response to environmental temperature. Alternatively, if the TSR is most often adaptive for any of the above reasons, then the Bergmann's rule phenomenon may reflect selection for decreased developmental time and energy consumption in warmer environments. Application of our model should allow predictions for effects of global warming on ectotherm development.

Our model is generally consistent with the above adaptive hypotheses, but offers additional insights. Both growth rate and development rate vary approximately exponentially with temperature, and the magnitude of the temperature dependence of each rate is subject to natural selection. In general, natural selection should tend to keep the temperature dependence of these rates very nearly equal, so that the developmental programme buffers size at maturity against perturbations owing to differences in temperature. However, equation (2.7) shows that E_g − E_d is very sensitive to E_a and E_d (e.g. Δ(E_g − E_d) = 4(ΔE_a −ΔE_d)), and consequently body mass at maturity, M, is extremely sensitive to these temperature dependencies.

One other interesting application of the theory is to organisms that have temperature-dependent sex determination, which occurs in many reptiles and amphibians, some fish, and at least one bird [47–50]. Small differences in temperature during development should potentially affect not only the gender of the hatchling, but also the time of development and body size at hatching. It is known that warmer temperatures during development can produce either males or females, depending on taxon: for example, generally males in crocodilians and females in turtles. In the Australian brush turkey (Alectura lathami), higher temperatures during incubation of eggs result in proportionately more females with larger body mass at hatching [48], consistent with reverse-TSR. Temperature-induced sex-related differences in development time and body size at hatching should have potentially important consequences for subsequent life history and ecology.

The quantitative model developed here, and more complicated analytical mathematical or computer simulation versions that could be developed for cases that do not meet the simplifying assumptions, provide a theoretical basis for assessing responses of ectothermic organisms to changes in environmental temperature regimes [51]. The magnitude of recent anthropogenic global warming is already substantial and likely to increase for decades and perhaps centuries [52]. The impacts on ectothermic animals and their ecology will undoubtedly be profound. Many of these impacts can be understood in a general theoretical context that is based on the fundamental effect of temperature on metabolism, and the effects of metabolism on many aspects of organism structure and function, population and ecosystem ecology, and biological evolution [53–55]. It will be impossible to conduct the detailed studies, on one species at a time, to predict effects of climate change on the abundance, distribution and diversity of species. A practical alternative will be to start by developing general theory, like the model presented here, which is based on fundamental biological principles and can make testable quantitative predictions.