Fitness consequences of centrality in mutualistic individual-based networks

Abstract

The relationships among the members of a population can be visualized using individual networks, where each individual is a node connected to each other by means of links describing the interactions. The centrality of a given node captures its importance within the network. We hypothesize that in mutualistic networks, the centrality of a node should benefit its fitness. We test this idea studying eight individual-based networks originated from the interaction between Erysimum mediohispanicum and its flower visitors. In these networks, each plant was considered a node and was connected to conspecifics sharing flower visitors. Centrality indicates how well connected is a given E. mediohispanicum individual with the rest of the co-occurring conspecifics because of sharing flower visitors. The centrality was estimated by three network metrics: betweenness, closeness and degree. The complex relationship between centrality, phenotype and fitness was explored by structural equation modelling. We found that the centrality of a plant was related to its fitness, with plants occupying central positions having higher fitness than those occupying peripheral positions. The structural equation models (SEMs) indicated that the centrality effect on fitness was not merely an effect of the abundance of visits and the species richness of visitors. Centrality has an effect even when simultaneously accounting for these predictors. The SEMs also indicated that the centrality effect on fitness was because of the specific phenotype of each plant, with attractive plants occupying central positions in networks, in relation to the distribution of conspecific phenotypes. This finding suggests that centrality, owing to its dependence on social interactions, may be an appropriate surrogate for the interacting phenotype of individuals.

1. Introduction

Individuals belonging to a group or population interact with each other positively (i.e. mating, mutualistic sharing, etc.) and negatively (i.e. parasite transmission, competitive interactions, etc.). The relationships among all members of a group may be visualized as a network where nodes are the individuals and the links connecting those nodes are the interactions among them [1,2]. Most real-world networks, from biological to social to chemical networks, are scale-free. In these networks, the number of links per node is not randomly distributed, but follows a power law where a few nodes are highly connected (hubs) and the rest are sparsely connected [3]. In scale-free networks, nodes also differ in their location within the network. Although some nodes are located in central positions and quickly connect to most other nodes, many other nodes occupy peripheral positions, from where they cannot interact easily with the rest of the nodes [4,5]. The centrality of a given node captures its importance within a network [6–8]. Thus, the robustness of gene and protein networks depends almost exclusively on the highly connected elements, whereas peripheral nodes are negligible for the functioning of these networks [4,9]. In ecological networks, the most abundant species, as well as the most generalist ones, occupy central positions and are proportionally more important for the stability and functioning of the whole system than peripheral species [10,11]. Similarly, the position of an individual within a social network determines its importance for the maintenance of the network structure, with central individuals having higher importance than peripheral ones [2,8,12,13].

The position of a given node within a network may not only affect the functioning of the whole system, but may also entail crucial consequences for the performance of those given nodes. That is, it can be predicted that nodes may benefit from occupying specific positions within the network. For example, when organizing the management of business, it is acknowledged that organizational units occupying central network positions enjoy better performance and innovation because they have easier access to new knowledge developed by other units [14,15]. In the same way, leaders and most efficient actors in terrorist networks tend to occupy central positions [13,16]. Despite the architecture and topology of ecological networks being well known [1,17–19], little information exists about the consequences for the fitness or performance of individuals occupying specific network positions. In networks generated by negative interactions, such as parasite transmission networks, individuals occupying central positions would have a higher probability of being infested and presumably will have a lower fitness [20,21]. In individual-based networks generated by positive interactions, in contrast, individuals occupying central positions will surely benefit from quick connections to most other conspecifics. We thereby hypothesize that these central individuals will show higher fitness than peripheral ones as a consequence of this higher frequency of intraspecific interactions. In this study, we explore this hypothesis, and estimate the benefit of occupying central positions in individual plant–pollinator networks. Specifically, we (i) quantify the correlation between centrality values and flower visitor assemblage visiting each individual plant, (ii) determine the relationship between local and global centrality and plant fitness, and (iii) disentangle the direct and network-mediated indirect effects of phenotype on fitness.

2. Material and methods

(a). Study system

This study was carried out in eight localities from the Sierra Nevada (Granada province, Spain). In each locality, we studied the interaction occurring between individuals of the monocarpic hermaphroditic herb Erysimum mediohispanicum through sharing flower visitors. For this, 90 plants per population were marked at the onset of the 2005 flowering period (720 plants in total).

(b). Flower visitor abundance, identity and diversity

During peak bloom (10–15 days per population), we conducted five to seven surveys per population. In these surveys, we noted during five-minute intervals the number of open flowers in each labelled plant, and the number and identity of insects that landed on the flowers and touched plants' sexual organs. Thus, each survey lasted 450 min, and we conducted more than 1500 min of observation per population. Insects were identified in the field, and some specimens were captured for further identification in the laboratory. Some rare flower visitors could not be captured and thus we identified them only to the level of genus or family [22]. The number of samples per population was fitted to the local abundance of flower visitors by means of accumulation curves generated with EstimateS software [23]. The results indicated that 130–150 insects per population provided an accurate estimate of the pollinator assemblage.

We grouped the flower visitors in seven functional groups, depending on their similarity in size, proboscis length, foraging behaviour and feeding habits: (i) large bees (mostly pollen- and nectar-collecting females greater than or equal to 10 mm in body length); (ii) small bees (mostly pollen- and nectar-collecting females less than 10 mm); (iii) wasps (aculeate wasps, large parasitic wasps and cleptoparasitic bees collecting only nectar); (iv) bee flies (long-tongued nectar-collecting Bombyliidae); (v) hover-flies (nectar- and pollen-collecting Syrphidae, and short-tongued Bombyliidae); (vi) beetles (including species collecting nectar and/or pollen); and (vii) butterflies (mostly Rhopalocera, all nectar collectors) [24].

(c). Network centrality

For each plant population, we constructed a bipartite unweighted network of interacting plant individuals and flower visitor species [24]. These bipartite networks were built by connecting each individual plant with the insects visiting its flowers. We considered only plants censused for more than 15 min and receiving at least one visit. Consequently, we studied a different number of plants per population, although our initial number of plants was 90 per population [24]. Afterwards, we obtained the unipartite projections of each bipartite network, depicting the pattern of shared pollinator species among individual plants in each population [24]. That is, in the resulting unipartite networks, two individual plants were connected if they shared at least one flower visitor. This is a study based on individual plants linked by species of presumptive pollinators, not linked by observations of plant-to-plant movements of individual animals.

Centrality indicates how well connected is a given E. mediohispanicum individual with the rest of the co-occurring conspecifics owing to sharing flower visitors. Centrality does not indicate any spatial position of the plants, but their topological position in the resulting network. Centrality was estimated using three metrics: degree centrality (Cd(i)), closeness centrality (Cc(i)) and betweenness centrality (Cb(i)) [25,26]. Degree centrality is the simplest form of centrality, and it assesses the importance of a node according to its normalized degree in the interaction graph [8]. The degree of a node is defined by the number of links that are connected to that node [25]. This measure provides a description of network connectivity based on the individual components. Closeness centrality is positively related to the shortest number of direct and indirect interactions between one node and all other nodes in the network (shortest paths) [27]; a node is central because it is close to most other nodes within the network and can thereby interact with any other node using no or few intermediaries [10]. Betweenness centrality is the number of shortest paths between two nodes that pass through a node of interest [28,29]. Therefore, nodes with high site betweenness act as bridges, connecting one part of a network to another [25]. Networks' structure was drawn, and centrality measures were computed with the software Pajek [27] (see [24] for further explanations).

(d). Plant phenotypic traits

For each labelled plant, we quantified the following phenotypic traits: (i) stalk height (the height in centimetres of the tallest stalk, from the ground to the top of the highest open flower); (ii) flower number (the entire production of flowers in each plant); (iii) corolla diameter (the distance between the edges of two opposite petals, measured with a digital caliper; ±0.1 mm error); (iv) corolla tube length (the distance between the corolla tube aperture and the base of the sepals); (v) corolla tube width (the diameter of the corolla tube aperture as the distance between the bases of two opposite petals); and (vi) corolla shape (determined in each plant by means of geometric morphometric tools, using a landmark-based methodology) [30] (see [31] for a detailed description of landmark locations). To describe corolla shape, we used the four first relative warps (RW) [31]. Each RW explains a given variation in shape among specimens, and their scores can be used as a data matrix to perform standard statistical analyses [30].

(e). Plant fitness

Fitness was estimated as the net reproductive rate R₀, the number of adults produced during the next generation per ovule produced by each studied plant. For this, we calculated several consecutive fitness components. First, we determined the number of seeds produced per fruit by counting in five fruits per plant the number of ovules setting seeds (SO ratio). Second, we estimated the number of seeds produced per plant during its entire life by counting the number of ripe fruits per plant and multiplying number of fruits per plant by number of seeds per fruit. Third, we quantified seed germination and emergence by collecting 30–40 seeds per plant at the end of the season, when seeds are mature but prior to dispersal (September). We planted 10 seeds per maternal plant on October 2005 in a greenhouse of the University of Granada (UGR). Seeds were placed in individual pots 15 cm apart to avoid competition. To avoid environmental covariance, pots were distributed according to a completely randomized design. We registered seedling emergence during the first month after planting, until no new seedlings emerged. Fourth, we quantified seedling survival. In order to do this, seedlings were transferred to an UGR outdoor common garden when they had produced the cotyledons, but before true leaf development. Plants were watered once weekly during winter (October–January), twice weekly during spring (February–May) and daily during summer (June–September). The watering regime was identical for all plants. We surveyed these plants until they flowered in April–May 2007, when they were 2 years old. In total, 1675 plants belonging to 332 families reached adulthood. Our R₀ estimate probably overestimates actual fitness because seeds germinated and seedlings developed in the benign conditions of the greenhouse rather than the more rigorous conditions experienced in the natural populations. However, since seeds belonging to all plants and populations experienced the same greenhouse conditions, we think this does not alter the main conclusions of our study.

(f). Statistical analysis

The relationship between pollinator assemblage and network position of the plants was checked by correlating the centrality of the plants, and the abundance and diversity of the insects visiting their flowers. We did these analyses separately per population and, because outcomes were consistent, we then pooled plants from all populations.

The effect of centrality on plant fitness was tested using two complementary analyses. First, we performed a generalized linear mixed model (GLMM) including as dependent variable the plant fitness and as independent variables the three centrality metrics. In this model, to control for potential external confounding factors, we included also the plant phenotypic traits, the plant population identity and their interactions with centrality estimates. Population and its interaction with the centrality estimates were considered as random factors. Consequently, their significance values were tested by comparing the full models including only the fixed variables with models including random factors and each interaction by means of likelihood ratio tests [32]. Models were compared using maximum-likelihood estimation because they had different fixed effect structures [33]. All analyses were performed using nlme package in R [34].

In addition, to accurately establish the importance of centrality for fitness, for each plant population we built causal structural equation models (SEMs) connecting centrality metrics, plant phenotypic traits, flower visitors and fitness. We first created three latent variables, called centrality, flower visitor and phenotype. We connected centrality to the three centrality metrics calculated per plant, flower visitor to the abundance and diversity of insects per plant, and phenotype to the six phenotypic traits measured in each plant. In the case of corolla shape, we built a fourth latent variable called corolla shape and connected to the four RWs. Plant phenotype was connected to plant fitness, flower visitors and centrality. Flower visitor was connected to plant fitness and centrality. Finally, centrality was connected to fitness. We compared three models: the full model described above (model 1), a nested model built by constraining to zero the path between centrality and fitness (model 2), and another model built constraining to zero the path between phenotype and centrality (model 3). To decide which model was more appropriate, we compared the magnitude of their Bayesian information criteria (BIC) by means of a likelihood ratio test [35]. If they were significantly different, we chose the one bearing a smaller BIC value [35]. All analyses have been performed using sem package in R [34].

3. Results

The three centrality estimates were significantly correlated with each other in each of the eight populations (r values ranging between 0.594 and 0.786, all p-values < 0.006, product–moment correlations). The centrality of the plants was significantly and positively associated with both the number of insect visits as well as the number of insect species visiting their flowers (table 1). In addition, the proportion of visits made by bee flies correlated positively with the three centrality indices (table 1), whereas large bees, small bees and beetles were positively correlated with closeness centrality and degree centrality.

Table 1.

Product–moment correlations between the three centrality estimates used in this study and the per-plant abundance and diversity of insects (n = 502 plants, all populations pooled). *p < 0.05, **p < 0.01, ***p < 0.001. The population-wise analyses showed similar results, and we show only the overall analysis.

	degree	closeness	betweenness
pollinator richness	0.0741 ± 0.0049***	0.0522 ± 0.0053***	0.0120 ± 0.0009***
pollinator visitation rate (visit h−1)	0.0028 ± 0.0012*	0.0026 ± 0.0013 n.s.	−0.0006 ± 0.0002*
large bees (%)	0.1784 ± 0.0378 n.s.	0.2099 ± 0.0410***	0.0108 ± 0.0068 n.s.
small bees (%)	0.2367 ± 0.0381***	0.2560 ± 0.0412***	0.0094 ± 0.0068 n.s.
wasps (%)	0.1032 ± 0.0532 n.s.	0.0560 ± 0.0577 n.s.	0.0129 ± 0.0095 n.s.
bee flies (%)	0.2996 ± 0.0378***	0.3063 ± 0.0410***	0.0135 ± 0.0068*
hover-flies (%)	0.0711 ± 0.0550 n.s.	0.1206 ± 0.0596*	0.0047 ± 0.0099 n.s.
beetles (%)	0.1190 ± 0.0376**	0.1693 ± 0.0408***	0.0124 ± 0.0067 n.s.
butterflies (%)	0.0409 ± 0.0482 n.s.	0.0770 ± 0.0523 n.s.	0.0018 ± 0.0087 n.s.

The GLMMs show that the fitness of the plants was significantly associated with betweenness centrality (table 2). This effect was significant even when statistically controlling for the phenotype of the plants (table 2). Furthermore, no significant interaction was found between betweenness and population (electronic supplementary material, appendix S1), indicating that the positive effect of betweenness was consistent across populations. The other centrality estimates (closeness and degree) did not significantly affect plant fitness according to the GLMMs with all predictors (table 2).

Table 2.

Summary of the GLMM showing the effect of plant phenotype and network position on plant fitness, quantified as the number of offspring reaching adulthood next generation (R₀). Population and the centrality × population interactions were tested by likelihood ratio tests (see electronic supplementary material, table S1).

	parameter ±1 s.e.	t-value	p-value
degree	0.272 ± 0.477	0.272	0.569
closeness	−0.176 ± 0.666	0.263	0.792
betweenness	7.787 ± 2.334	3.336	0.001
number of flowers (log)	1.668 ± 0.339	1.668	0.001
stalk height (log)	0.310 ± 0.155	1.998	0.046
stalk diameter (log)	0.026 ± 0.549	0.026	0.963
number of stalks (log)	−0.188 ± 0.304	0.188	0.536
flower diameter (log)	0.489 ± 0.983	0.489	0.619
corolla tube length (log)	2.782 ± 0.912	2.782	0.002
corolla tube width (log)	−0.387 ± 0.506	0.387	0.444
corolla shape component RW1	−0.217 ± 0.409	0.217	0.595
corolla shape component RW2	0.263 ± 0.578	0.263	0.649
corolla shape component RW3	−0.206 ± 0.777	0.206	0.791
corolla shape component RW4	−0.198 ± 1.035	0.198	0.848

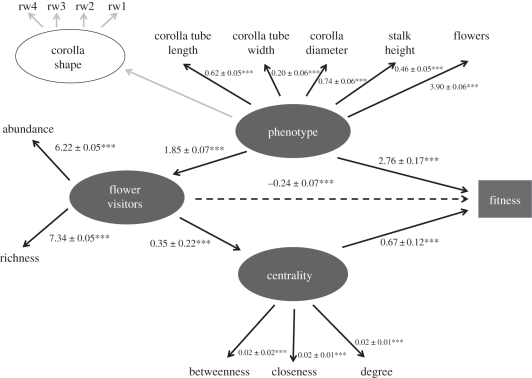
SEM analysis also indicates that centrality affected plant fitness. Thus, when comparing the model linking centrality and plant fitness (model 1) against the model with this path constrained to zero (model 2), the former was statistically better than the latter, both for every population analysed separately as well as for all populations pooled together (table 3). This suggests that centrality of the individual plants positively affected plant fitness not only as a consequence of its relationship with flower visitors and plant phenotype but also because of some other factors independent of its own measured phenotype (figure 1). The SEM indicates that the three centrality estimates significantly contributed to plant fitness (figure 1). Finally, the model disrupting the path between phenotype and centrality (model 3) was as adequate as the model allowing it (model 1), both when all populations were pooled together and in seven out of the eight plant populations (table 3). According to these models (figure 1), plant phenotype has both a direct and an indirect (animal-mediated) effect on plant fitness, whereas flower visitors affected fitness both directly and indirectly, through its effect on centrality (figure 1). The direct effect of flower visitors on fitness, after controlling for indirect effects, was negative (figure 1), suggesting that the positive effects of flower visitors are mostly expressed through their effect on plant centrality.

Table 3.

Comparison between structural equation models with (model 1) and without (model 2) centrality effect on fitness, and without phenotype effect on centrality (model 3). BIC, bayesian information criterion; LRT, likelihood ratio test.

population	BICmodel 1	BICmodel 2	BICmodel 3	likelihood tests comparing model 1 versus model 2			likelihood tests comparing model 1 versus model 3
				LRT	d.f.	p-value	LRT	d.f.	p-value
overall	1249.10	1375.40	1244	132.56	1	0.00001	1.08	1	0.299
Em01	9.68	2.78	5.59	17.24	1	0.00001	0.06	1	0.813
Em02	−46.81	−18.79	−50.84	36.48	1	0.00001	0.20	1	0.652
Em08	7.61	52.97	4.14	53.82	1	0.0001	0.76	1	0.383
Em21	89.07	162.70	86.06	48.91	1	0.00001	1.37	1	0.241
Em22	−123.94	−110.29	−110.80	17.70	1	0.00001	21.26	1	0.0001
Em23	45.25	64.38	41.28	23.30	1	0.00001	0.19	1	0.659
Em24	−81.60	−69.72	−83.85	15.73	1	0.00001	1.60	1	0.205
Em25	−7.50	−0.22	−11.44	11.23	1	0.00001	0.01	1	0.916

Figure 1.

Most parsimonious model showing the relationship between plant phenotype, network centrality and individual fitness (model 3). This model corresponds to all populations pooled. Significant paths are indicated in black and non-significant paths in grey. All path coefficients are ×10⁻¹.

4. Discussion

Our study found that individual plants differ in centrality within individual-based networks. The species occupying central positions in ecological community networks connect otherwise unconnected subnetworks and increase the cohesion of the entire network [10,36,37]. If this role maintains for individual networks, such as the one studied here, the cohesion of the entire population is mostly due to the activity of a subgroup of well-connected individuals that share genes via mutualistic interactions with most of the other conspecific plants in the population [1]. The effect of contrasting architectures on the fragility of networks in which nodes are individuals connected by mating is still unknown. It would be interesting to explore whether, as occurs in ecological community networks, the disappearance of central individuals would cause a reduction in fitness or even the loss of most of their conspecifics [38,39], or, alternatively, if it would produce a switch of interaction partners [40].

In ecological networks, species occupying central positions tend to be the most generalist ones [10]. Similarly, the centrality of an individual plant was related to the abundance and diversity of insects that visit its flowers. Central plants received more visits and were visited by a higher number of insect species. Consequently, agreeing with community studies [10,11], the most generalist plants at the individual level were also those located in central positions in individual networks. That is, the centrality value of a given individual plant in an individual pollination network may be related to its individual generalization level. This finding suggests that, by having different centrality values, different individual plants in the same population have different generalization levels. This finding agrees with previous network- and non-network-oriented studies that indicate that individual plants belonging to the same population may interact with a different number of insect species [19,41]. Herrera [41] suggested that generalization, rather than being a species property, may be considered a local phenomenon. Our outcomes indicate that, in some systems, generalization may even be considered an individual attribute.

Centrality of the individual plants was influenced by the identity of the insects visiting their flowers. In fact, it seems that, in our system, centrality was positively related with bee fly abundance at flowers. That is, those plants receiving more visits by bee flies were also those occupying more central positions in the networks. This outcome agrees with our previous findings about the positive effect of bee flies on the connectivity and functioning of whole population networks [24]. As indicated by Gómez et al. [24], this is a consequence of the foraging behaviour displayed by bee flies, which move indiscriminately across the complete set of plants of a given population. Thus, plants visited by bee flies are probably more connected, occupying central positions in the networks, than plants visited by other insects.

Our results strongly suggest that the network position occupied by a given plant is related to its fitness, with plants located in central positions of the networks having higher fitness than individuals located in peripheral positions. Centrality's effect on fitness was not merely an effect of the abundance of visits and the species richness of visitors. It is not just that plants that receive more visits and more kinds of visitors produce more seeds. Centrality has an effect even when simultaneously accounting for these predictors. By attracting more insects, a plant increases its chance of intercrossing with a higher number of conspecifics. Similarly, by attracting a higher diversity of complementary pollinators [42], each with a slightly different foraging pattern, there is also a high possibility of receiving pollen from many different conspecific plants. Consequently, in our generalist system, central plants surely crossed with a high diversity of mates, and probably received a high diversity of pollen. This would entail the production of a more abundant progeny, also displaying higher genetic vigour. However, we need to be cautious in extrapolating this finding to other kinds of networks, since the advantage of being central would surely depend on the type of interaction mediating the links among individuals. In networks generated by antagonistic interactions (e.g. AIDS networks, parasite transmission networks, etc.), to be central probably entails a decrease in fitness, because central individuals would probably have a higher probability of infestation and mortality [20,21].

This centrality effect on fitness is, obviously, partially due to the specific phenotype of each individual plant. In our pollination networks, plants displaying some traits attract more insects and occupy central positions in mating networks [31]. This phenotype-mediated centrality effect on fitness is frequent in individual-based networks. However, this study also suggests that the advantage of being central is not exclusively due to the phenotype of the own individual. In fact, the GLMMs suggest that, after controlling for individual phenotype, there is still an effect of centrality on fitness. Similarly, the SEMs constraining to zero the path between centrality and fitness (model 2) were always much less appropriate than the models allowing this path (model 1), whereas the models constraining to zero the path between phenotype and centrality (model 3) were equally appropriate in most populations. These outcomes suggest that fitness increase of individuals is not only a consequence of their phenotypes. There have to be some additional advantages of occupying central positions. Central plants would attract more efficient pollinators than peripheral ones, a phenomenon that may explain why, after controlling for centrality, the effect of flower visitor abundance and diversity was negative for the plant. Krause et al. [43] suggested that the centrality of a given individual in mating, parasitic, social and other individual-based networks depends on both its own phenotype and the phenotype of the other conspecifics contributing to the interaction network. For example, the susceptibility of a given individual to be infested by pathogens or preyed upon by predators is a function of its own defense traits averaged by the defense traits of its co-occurring conspecifics. Analogously, pollinator preference is context-dependent in many systems [44]. In fact, many polymorphic traits in plants (such as flower colour, style size, etc.) are usually maintained by frequency-dependent pollinator preference [45]. The fitness gain of plant traits depends in these scenarios on the trait distribution of the plant population. Under a network perspective, these findings indicate that the same individual plant may occupy a central position in a given network but a peripheral position in an alternative network, even though its phenotype remains the same, only by changing the phenotype distribution of the conspecifics. These traits influenced by interactions with conspecifics are called interacting phenotypes [46]. We believe that network-based individual properties, like centrality, due to its dependence on social interactions, may be considered an appropriate proxy of the interacting phenotype of the individuals. Consequently, centrality's effect on fitness may be determined not only by the own phenotype of the focal individual but also by the conspecifics' phenotypes, suggesting the occurrence of a collective component of fitness [47–49]. Network metrics may be related to indirect genetic effects, a phenomenon occurring when the phenotype and fitness of an individual depends partially on the genetic composition of the co-occurring conspecifics [50,51]. Under this perspective, our results suggest that natural selection may act not only on individual phenotypes but also on network properties. Further studies, including information on both the spatial and genetic components of centrality, may help us to unveil this intriguing question.