The Magnetic Field Dependence of Water T₁ in Tissues

Abstract

The magnetic field dependence of the composite ¹H₂O NMR signal T₁ was measured for excised samples of rat liver, muscle, and kidney over the field range from 0.7 to 7 T (35 MHz to 300 MHz) with a NMR spectrometer using sample-shuttle methods. Based on extensive measurements on simpler component systems, the magnetic field dependence of T₁ of all tissues studied are readily fitted at Larmor frequencies above 1 MHz with a simple relaxation equation consisting of three contributions: a power law, A*ω^−0.60 related to the interaction of water with long-lived-protein binding sites, a logarithmic term B*τ_d*log(1+1/(ωτ_d)²) related to water diffusion at macromolecular interfacial regions, and a constant term associated with the high frequency limit of water-spin-lattice relaxation. The parameters A and B include the concentration and surface area dependences respectively. The logarithmic diffusion term becomes significant at high magnetic fields and is consistent with rapid translational dynamics at macromolecular surfaces. The data are fitted well with translational correlation times of approximately 15 ps for human brain white matter, but with a B value three times larger than gray matter tissues. This analysis suggests that the water-surface translational correlation time is approximately three times longer than gray matter.

Introduction

The spin-lattice-relaxation time, T₁, is a central parameter in MRI and is critical for design of data acquisition protocols. The magnetic field dependence of T₁ is well studied at low magnetic field strengths in excised tissues using fast field cycling methods (1–5). Systematic measurements at fields between approximately 30 MHz and 300 MHz have been more difficult to obtain; however, sample-shuttle spectrometers provide a means for collecting data sets over a decade or more in magnetic field strength on the same sample without the complications of carrying the sample between different instruments operating at different magnetic field strengths (6–8) and temperature. We report here measurements of ¹H T₁ on excised rat muscle, liver, and kidney from Larmor frequencies of 35 MHz to 300 MHz. The data may be fitted to several models; however, we show that experiments on pure component systems suggest a simple linear combination of relaxation contributions that provides an excellent fit to the data over this range of Larmor frequencies. This analytical approach requires few adjustable parameters, is simple to implement, and rests on physically clear origins. Muscle, liver and kidney are fitted with similar relaxation contributions; however, application of this approach to published data for in vivo human brain demonstrates a fundamental difference from other tissues and between gray and white matter.

Experimental

Male Sprague Dawley rats weighing 250–350 g were sacrificed by guillotine after isoflurane anesthesia. Tissue samples, each approximately 0.5 g obtained on different days from five different rats, were excised and promptly placed in a 5 mm thick-walled tube affixed to the sample shuttle and sealed. Kidney samples consisted of cortex and medulla, muscle was taken from the thigh. Spin-lattice-relaxation time measurements (6–8) were made by polarizing the spins at the isocenter of the magnet, applying a 180° pulse, then pneumatically transporting the sample to different calibrated positions in the fringe-field of the superconducting 7 T solenoid magnet where the spins relaxed for a variable delay period before return to the isocenter of the field where the magnetization was detected promptly using a 90° pulse. The spin-lattice-relaxation-rate constants were obtained using 30 logarithmically spaced delay periods. Although the longitudinal relaxation of tissue is generally not exponential, the slow shuttling times required for sample movement between magnetic fields (170–230 ms one way) precluded measurement of rapidly decaying components. The slow relaxation components detected in these experiments were exponential within experimental error of 3% or less. To check for time dependence the magnetic field dependence was sampled in a pseudo-random order and measurements at the highest and lowest fields were repeated at the end of each acquisition sequence. Measurements below 35 MHz were made using a Stelar fast field cycling NMR spectrometer FFC-2000 (Stelar s.r.l., Mede, Italy).

Results

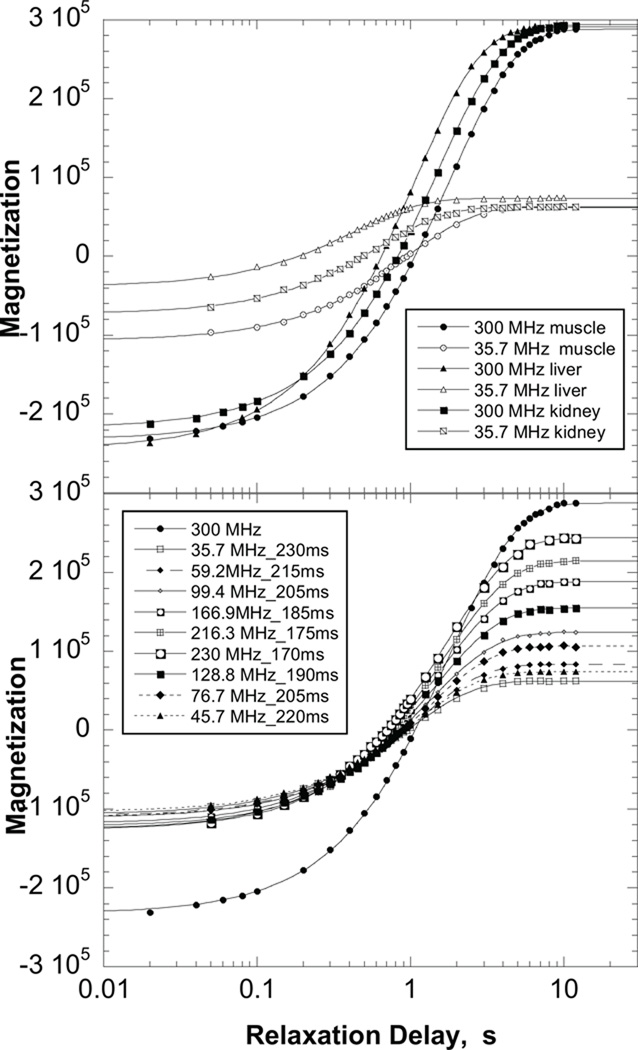
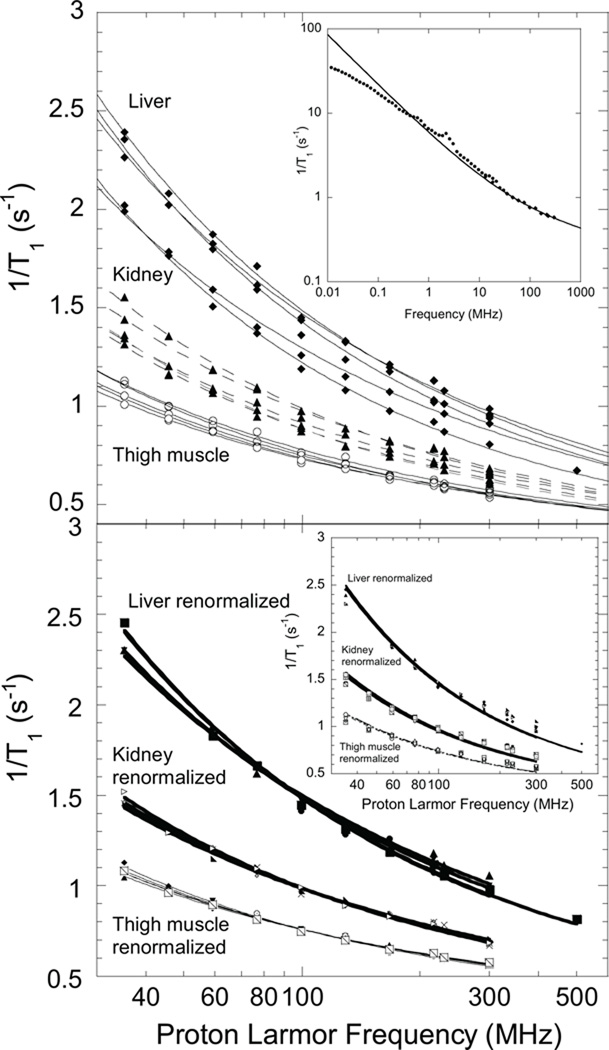
Representative magnetization recovery curves are shown in Fig. 1; the magnitude of short delay- time magnetizations are somewhat smaller than the longest delay-time magnetizations because of pulse-sequence delays incorporated for sample movement. Water-proton-spin-lattice-relaxation-rate constants for five samples of each tissue are shown in Fig. 2. There is a monotonic decrease in the relaxation-rate constant 1/T₁ with increasing magnetic field. The magnetic field dependence is relatively weak and without sharp features that permit easy distinction between different analytical approaches. At lower magnetic field strengths, the relaxation rate constants are reasonably described by a power law in the Larmor frequency, which derives in large part from the protein contributions (1–3,9–20). Indeed, a power law was among the earliest suggestions for understanding the magnetic field dependence of T₁ (21). The present data may be represented by the equation,

$$\frac{1}{T_1}=A{\omega }^{-b}+C$$ [1]

Figure 1.

Top: Representative magnetization recovery curves for muscle, liver, and kidney shown for relaxation fields of 300 MHz and 35.7 MHz as a function of relaxation delay. Bottom: representative magnetization recovery curves for muscle tissue at each magnetic field as a function of relaxation delay.

Figure 2.

Top: ¹H nuclear spin-lattice-relaxation-rate constants as a function of magnetic field strength shown as the proton Larmor frequency for five samples of excised rat muscle, kidney, and liver at ambient laboratory temperature( 295±2 K). Solid lines are least squares fits to Eqn. 2. The inset shows the magnetic field dependence for a muscle sample from 0.01 MHz to 300 MHz; the solid line was computed with Eq. 2 and the parameters A= 6.4×10⁴ s^−1.6 and B = 2.6×10⁻⁸ s⁻². Bottom: Renormalized tissue data; parameters summarized in Table I. The inset shows fits of tissue data to Eq. 1.

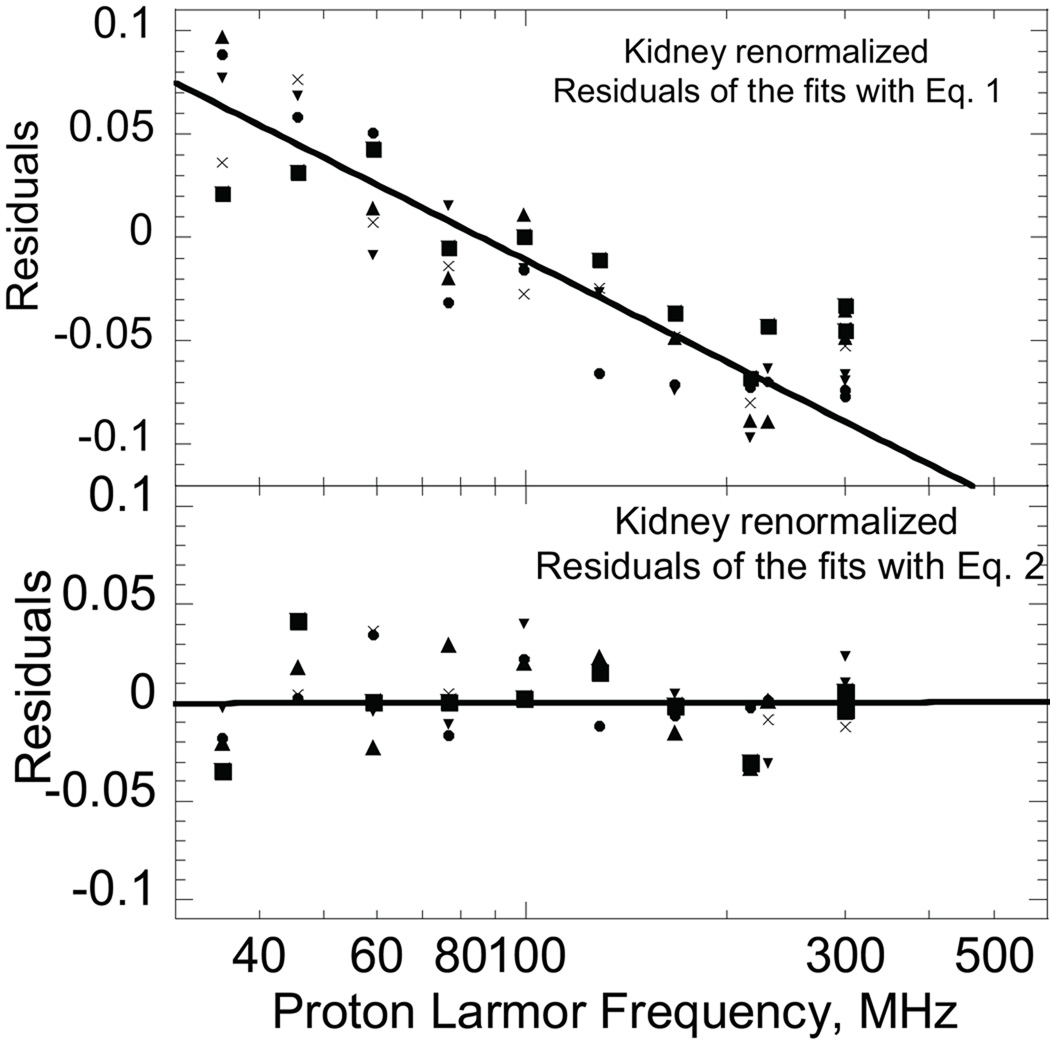
A is a constant related to the strength of the dipolar couplings driving relaxation, b a number of order 0.5–0.8, and C a constant. A practical problem with Eq. [1] is that the value of the exponent b is remarkably sensitive to the choice of the constant C which presumes that the high-field relaxation-rate constant is independent of magnetic field. If the observations are essentially of water protons in the tissue and there is a bulk water pool in exchange with the multiple macromolecular environments, which is the usual class of model, the limiting value for C should be 0.28 s⁻¹ at 25°C or 0.22 at 37°C, the value for pure water, but weak additional contributions may elevate this value for the complex aqueous environment of a tissue. Using Eq. [1] for muscle, the values of b range from 0.51–0.65 for the range of C from 0.3 to 0.4. Similar problems are found for kidney and liver analysis. The difficulty of knowing precisely what the constant term should be in the high frequency limit may be mathematically eliminated by examining the derivative of the relaxation rate constant with respect to frequency. This procedure yields b values of 0.6±0.1. The bottom panel inset of Fig. 2 shows fits of the tissue data to Eq. 1 and Fig. 3 shows residuals for fits of the kidney data to Eq. 1 and Eq. 2 introduced below. The residual pattern associated with Eq. 1 shows systematic deviations (Fig. 3) which demonstrate that Eq. [1] is incomplete.

Figure 3.

Residuals for fits of kidney data sets to Eq. 1 and Eq. 2.

A power law in the Larmor frequency is expected for the 1/T₁(ω) in tissues at low magnetic field strengths based on the observations that proton-spin-lattice relaxation of both dry and hydrated proteins is a power law in the Larmor frequency with an exponent of 0.78 (1–3,9–18). We emphasize that at Larmor frequencies below approximately 1 MHz, the effects of finite magnetic exchange rates with the protein protons as well as limitations in water molecule or proton exchange rates may alter the magnetic field dependence as shown by the inset in Fig. 2. In the lower magnetic field range, it is necessary to solve coupled differential equations that relate the macromolecule spin-lattice relaxation rate constants to the detected water-proton-spin-lattice-relaxation-rate constant. However, at higher magnetic field strengths, the water spins are in the fast magnetic exchange limit, which simplifies the relaxation models to a population weighted sum of contributions.

In liquids, it is convenient to separate effects of intramolecular from intermolecular relaxation. For water, the intramolecular contribution derives from the dipolar coupling of neighboring proton on the oxygen atom which is modulated by rotational diffusion or somewhat larger angular jumps. The intermolecular contribution includes the dipolar couplings to all other protons in the solution and is modulated by the relative translational motions of the water spins. These two contributions have different magnetic field dependences. In a rigid solid, the local dipolar fields from the spin moments are not averaged by rotational or translational motion. In consequence, the local magnetic field from the adjacent protons is substantial, and the spins are strongly coupled to provide efficient spin-spin communication and a large linewidth. In a non-rotating protein, for example, the proton linewidth is approximately 35 kHz corresponding to an apparent transverse relaxation time of approximately 10 µs. If a water molecule is rigidly bound to a protein site, it is problematic to separate the effects of the neighboring proton on the oxygen atom from the others because of the strong coupling. The protons form a coupled population and are generally relaxed by what remaining motions there are, typically stochastically rotating methyl groups (22–24). If there is local motion of the bound water molecule, for example, small wiggles in a geometrically constrained binding site or multiply constrained hydrogen bonded site, then the bound water may provide a relaxation path for the protein protons. However, the magnitude of the intramolecular relaxation rate constant is substantially attenuated from that associated with isotropic reorientation because of the restricted angular excursions imposed by the spatial constraints of a strong binding site. Although intramolecular relaxation may be approached using either protons or deuterons in protein containing systems, it is simplest to utilize deuterons because the complication of efficient magnetic coupling between water protons and the protein protons is removed. At magnetic fields corresponding to deuteron Larmor frequencies above 0.1 MHz, the deuteron relaxation rate constant is a power law in the Larmor frequency with an exponent of approximately 0.5, and the same result is found for the intramolecular proton contribution in cross-linked protein gels (25–30). Thus, in the magnetic field range 30–300 MHz, which is the focus of this discussion, the power law is justified by both inter and intramolecular contributions that derive from water spins interacting with the macromolecules of the system. We note that the origins of the power law for inter- and intramolecular spin dynamics are quite different. For the protons, the coupling between the water protons and the macromolecule protons tie the power law of the non-rotating macromolecule protons to the water-spin-lattice-relaxation-field dependence. The intramolecular relaxation rate constant for the intramolecular contribution is independent of magnetic field strength at low fields as shown by the deuteron relaxation dispersion profiles as well as the intramolecular parts of the proton dispersion; it is a power law at higher field strengths (27–30). However, a relatively sharp feature associated with the low field plateau is not generally found for water protons in cross-linked protein models or in the tissue relaxation profiles, for example Fig. 2.

At high magnetic fields, the relaxation rate constant for water protons in a solution of pure protein is a logarithmic function of the Larmor frequency which is attributed to the effects of localized translational diffusion at the macromolecular interface (31). A logarithmic field dependence is common for high surface area systems and derives from diffusive exploration geometrically restricted by the excluded volume of the interface (32–34). In tissues, the macromolecular concentration is high and molecular crowding an issue; therefore, macromolecular interfacial effects are significant. We assume that proton spin-lattice relaxation is dominated by rapid mixing of water among different environments on a molecular scale, i.e., the usual fast exchange approximation. We propose a relaxation equation that is a sum of contributions: a macromolecular power-law term associated with exchange of water and protons from long-lived binding sites, a logarithmic term associated with water diffusing in the restricted space of all interfaces, and a constant for the high frequency plateau presumed in the case that there is a bulk water pool.

$$\frac{1}{T_1}=A*{\omega }^{-0.06}+B{\tau }_d*[\mathit{\text{ln}}(1+\frac{1}{{({\tau }_d*\omega )}^2})+4\mathit{\text{ln}}(1+\frac{1}{{(2{\tau }_d*\omega )}^2})]+C.$$ [2]

A and B are constants characterizing the strength of the dipolar interactions driving spin relaxation, as well as the concentration dependent probabilities for these interactions in various environments. τ_d is the translational correlation time for water in the interfacial region (31). The exponent for the power law is set to 0.6 based on the derivative fit discussed above, although there is an argument for the value of 0.78 based on protein measurements by several laboratories (9,12,15–17,35). For oxygen-free pure water at 25µC, C = 0.28 s⁻¹. However, if the surface area in the tissue is very high, the population of the bulk water pool may decrease and in the limit that there is no bulk phase, the constant term could become inappropriate. Similarly, the power law observed in the water-spin relaxation derives in large measure from exchange of water molecules between the protein-bound sites which relax with a power-law dependence on magnetic field strength. If no protein-bound-water molecules or bound protons exchange with the bulk water pool, then the power-law term is unimportant and the surface diffusion contribution dominates. There are two terms for the surface contribution corresponding to spectral density functions at the Larmor frequency and twice the Larmor frequency. Although similar contributions are made to the first term of Eq. (2), the power law incorporates the magnetic field dependence for both (15).

Application of Eq. [2] results in the lines shown in Fig. 2 computed with the parameters summarized in Table I. The coefficient B and the correlation time τ_d enter as the product, which may create a difficulty in fitting procedures. However, B does not enter the logarithmic argument that determines the frequency dependence. To minimize this problem, the value of τ_d was set to 15 ps based on measurements in protein solutions for the surface translational correlation times (31), then the value of B adjusted. The weighting coefficients A and B do not alter the underlying magnetic field dependence, but vary somewhat with different animals and tissues because of differences in concentration and composition. If the underlying magnetic field dependence is the same, then a multiplicative constant will scale all the data from a particular tissue to the same curve as shown in Fig. 2 (bottom). The appropriate scaling factors are readily deduced by dividing the data for each tissue by a particular reference data set point by point at each frequency and taking the average of the resulting ratios over the complete frequency range. Although the ratio is different for different animals, the standard deviation for the ratio between two data sets is small. Applying this procedure yields the nearly coincident curves shown in the bottom panel of Fig. 2. Thus, while the concentration factors may vary between different animals, the frequency dependence is essentially constant. Equation [2] thus describes the data of Fig. 2 efficiently and incorporates a physically sound but weak magnetic field dependence in the high field region. The residual pattern shown in Fig. 3 demonstrates the improvement over Eq. 1 in accounting for these data.

Table I.

Tissue Parameters for renormalized rat tissue^†

Sample	Muscle	Muscle	Kidney	Kidney	Liver	Liver
	A (104 s−1.6)	B (109 s−2)	A (104 s−1.6)	B (109 s−2)	A (104 s−1.6)	B (109 s−2)
1	6.9	0.19	9.0	0.37	19	0.35
2	5.4	0.32	8.7	0.40	14	0.76
3	5.8	0.28	8.3	0.44	16	0.63
4	6.3	0.24	9.9	0.30	19	0.31
5	5.9	0.27	11	0.22	18	0.38
Mean	6.1	0.26	9.4	0.35	17	0.49
Std Dev	0.6	0.05	1.1	0.09	2.2	0.20

^†Fits to equation [2] with τ_d = 15 ps and C=0.28 (s⁻¹).

No term is explicitly included for the effects of paramagnetic components of the tissue, which are expected to vary. However, for rotationally immobilized paramagnets rigidly bound to proteins, the magnetic field dependence of the ¹H spin-lattice-relaxation-rate constant is similar to that in Eq. [2] at high magnetic field, i.e., a power law in the Larmor frequency; the surface diffusive paramagnetic contributions will be described by a logarithmic dependence as well, but the scaling coefficient B will be larger (36,37). Thus, in the high frequency regime, above the relaxation dispersion associated with free metals or protein-bound metal ions (38), the form of equation 2 is appropriate for diamagnetic as well as diffusive and rigidly bound paramagnetic contributions. The larger dipolar couplings associated with the paramagnetic contributions essentially increase the magnitude of A or B in the high frequency range.

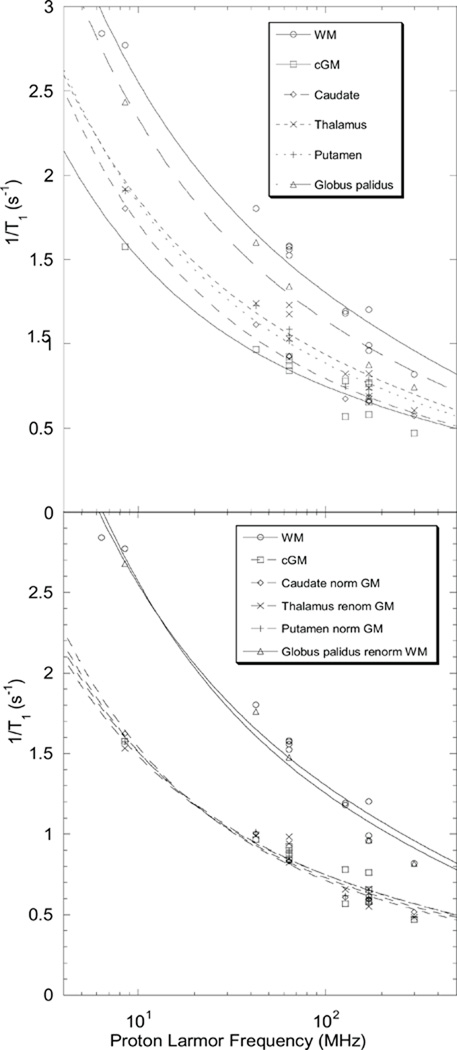
Measurements on brain tissue with this apparatus were made and while they are in reasonable agreement with the reports of Rooney and collaborators (18), the data are not reported because the impact of the shuttle movement altered the apparent integrity of the tissue. In vivo measurements of spin-lattice-relaxation rates for human brain have been reported and summarized by Rooney and collaborators (18) where a power law was used to fit the data well with a small exponent. We re-examine the data summarized in Table I of this reference. We note that the ratio of the relaxation rate constants reported for the different brain tissues is in a constant ratio to either the gray or white matter value over the whole range of field strengths. As in the bottom of Fig. 2, the brain tissue data can be renormalized or scaled by these factors as shown in Fig. 4. The parameters associated with these fits are summarized in Table 2. The values of A are somewhat smaller than those for muscle and much smaller than those for liver; the values of B are comparable. For white matter structures, however, the value of B is much larger than for gray matter structures, which may reflect differences in the effective interfacial concentration or topography. However, this result may reflect regions of increased translational correlation time or slower diffusion in the interfaces of these tissues compared than the others because the coefficient of the logarithmic terms is proportional to the translational correlation time. Direct evidence for the increase in the translational correlation time for the white matter when compared with the gray matter is the increase in the slope of the Larmor frequency dependence shown in Fig. 4 for the white matter. Although the time scales for the measurements are quite different, these translational correlation time differences in brain tissues are consistent with diffusion weighted MRI measurements reported by Le Bihan and coworkers (39).

Figure 4.

Brain tissue proton relaxation rates (18) unnormalized (top) and renormalized (bottom) to either the gray or white matter average value. Lines are fits to Eqn. 2 and the parameters summarized in Table II.

Table II.

Renormalized Brain Data^†

Sample	A (s−1.6)	B (s−2)
White matter	5.0 ×104	1.3 ×109
Gray Matter	3.6 ×104	0.54 ×109
Caudate	4.3 ×104	0.43 ×109
Thalamus	3.4 ×104	0.56 ×109
Putamen	3.9 ×104	0.49 ×109
Globus Palidus	5.8 ×104	1.2 ×109

^†C=0.22 (s⁻¹); τ_d = 15 ps

Conclusion

For ¹H Larmor frequencies in the range (30–300 MHz), the effects of complex magnetic coupling mechanisms to macromolecular components in tissues are in the fast exchange limit which simplifies the relaxation equation for the magnetic field dependence of water proton 1/T₁ to macromolecule-based-power-law contribution, and a logarithmic term identified with restricted diffusive exploration at macromolecular interfaces. Although the power law dominates at low magnetic field strengths, both contributions are important at higher magnetic fields. The data are consistent with a short translational correlation time for interfacial water, in the range of 15 ps. Brain white matter is distinct from gray matter in that the weighting factor for the diffusion contribution is three times larger than for gray matter structures that may reflect regions of increased translational correlation time or slower diffusion in the interfaces of these tissues.