Skip to main content
PMC home page
Springer logoLink to Springer
. 2011 Nov 12;22(4):891–899. doi: 10.1007/s00330-011-2313-1

Effects of microperfusion in hepatic diffusion weighted imaging

Hildebrand Dijkstra 1,✉, Paul Baron 2, Peter Kappert 2, Matthijs Oudkerk 1, Paul E Sijens 2
PMCID: PMC3297749  PMID: 22080250

Abstract

Objective

Clinical hepatic diffusion weighted imaging (DWI) generally relies on mono-exponential diffusion. The aim was to demonstrate that mono-exponential diffusion in the liver is contaminated by microperfusion and that the bi-exponential model is required.

Methods

Nineteen fasting healthy volunteers were examined with DWI (seven b-values) using fat suppression and respiratory triggering (1.5 T). Five different regions in the liver were analysed regarding the mono-exponentially fitted apparent diffusion coefficient (ADC), and the bi-exponential model: molecular diffusion (D slow), microperfusion (D fast) and the respective fractions (f slow/fast). Data were compared using ANOVA and Kruskal–Wallis tests. Simulations were performed by repeating our data analyses, using just the DWI series acquired with b-values approximating those of previous studies.

Results

Median mono-exponentially fitted ADCs varied significantly (P < 0.001) between 1.107 and 1.423 × 10−3 mm2/s for the five regions. Bi-exponential fitted Dslow varied between 0.923 and 1.062 × 10−3 mm2/s without significant differences (P = 0.140). D fast varied significantly, between 17.8 and 46.8 × 10−3 mm2/s (P < 0.001). F-tests showed that the diffusion data fitted the bi-exponential model significantly better than the mono-exponential model (F > 21.4, P < 0.010). These results were confirmed by the simulations.

Conclusion

ADCs of normal liver tissue are significantly dependent on the measurement location because of substantial microperfusion contamination; therefore the bi-exponential model should be used.

Key Points

  • Diffusion weighted MR imaging helps clinicians to differentiate tumours by diffusion properties

  • Fast moving water molecules experience microperfusion, slow molecules diffusion

  • Hepatic diffusion should be measured by bi-exponential models to avoid microperfusion contamination

  • Mono-exponential models are contaminated with microperfusion, resulting in apparent regional diffusion differences

  • Bi-exponential models are necessary to measure diffusion and microperfusion in the liver

Keywords: Diffusion weighted imaging, IVIM, Liver parenchyma, Microperfusion, ADC variability

Introduction

Diffusion weighted imaging (DWI) started with the introduction of intravoxel incoherent motion (IVIM) imaging by Le Bihan et al. in the late 1980s [1]. IVIM was developed to quantify microscopic translational motions in a voxel by defining the apparent diffusion coefficient (ADC), which integrates the effects of both molecular diffusion and microperfusion of blood in the capillary network [2]. The ADC is sensitive to all intravoxel incoherent motions and equals the diffusion coefficient D slow if only molecular diffusion is present. However, ADCs of brain tissue were often higher than expected because of microperfusion contamination. Therefore, the IVIM theory was extended to a bi-exponential model that was used to obtain pure and separate images of molecular diffusion D slow and microperfusion D fast [3]. DWI was introduced in the abdominal organs from the early 1990s [4]; before that, it was primarily limited to the brain [1–3, 5]. Subsequently, DWI of liver parenchyma and liver abnormalities was performed, however mainly by application of ADC quantification using the mono-exponential model [6–8]. Yamada et al. then demonstrated that the effect of microperfusion significantly contributes to the ADCs of abdominal organs and hepatic lesions [9]. They concluded by application of the bi-exponential model that the molecular diffusion coefficient D slow and microperfusion fraction f are useful parameters for the characterisation of hepatic lesions. This was supported by later studies that showed the additional value of using the bi-exponential model for the clinical evaluation of hepatic parenchyma and hepatic lesions [10–14].

However, we noticed that most liver studies up to now rely on the ADC as a measure for molecular diffusion without taking into account microperfusion contamination [15–17]. Only a few liver studies avoided microperfusion contamination by choosing only higher b-values starting from 50 mm2/s for the calculation of ADCs [18–23]. Others showed that besides the MRI technique and field strength, the location of the measurement can influence the ADC significantly [21, 24–26]. We, however, suspected that the variation of ADCs in different regions of the liver was due to microperfusion contamination. Thus, the purpose of this study was to demonstrate that mono-exponential diffusion in the liver is contaminated by microperfusion and that the bi-exponential model is required.

Methods and materials

Study population

The protocol of the study was approved by the hospital’s institutional review board, and informed consent was obtained from all subjects. The study population comprised 10 men and 9 women (n = 19) ranging from 20 to 62 years old (mean 32.9 years). All subjects were healthy volunteers, without relevant medical history, with a body mass index (BMI) ranging from 20 to 32 kg/m2. The only preparation before the examination was an 8-h fasting period.

MR protocols

All subjects were prospectively examined using MR imaging at 1.5 T (Magnetom Avanto, Siemens Medical Solutions, Erlangen, Germany). The body coil served as a transmitter and a six element spine matrix coil in combination with the body matrix as a receiver. After routine localiser- and T2-weighted imaging a series (b = 0, 50, 100, 250, 500, 750, 1000 s/mm2) of isotropic diffusion weighted images (DWI) were acquired using a spin echo based echo-planar imaging (EPI) sequence in combination with spectral adiabatic inversion recovery (SPAIR) fat suppression. The acquisition was gated using PACE respiratory triggering (TR = 3100–6500 ms) and was tuned with the following parameters: TE 75 ms; slice-thickness 6 mm; slice-gap 18 mm; FOV 379 × 284 mm; matrix 192 × 144; bandwidth 1735 Hz/pixel; averages 2 and parallel acquisition technique GRAPPA with acceleration factor 2. Diffusion gradients (25 mT/m) were applied in the phase, read, and z-directions separately. In total 9 transverse slices were acquired with an 18 mm slice gap to cover the whole liver within an average total acquisition time of 8.1 min (range; 4.7–11.1 min). The image acquisition took place in an interleaved mode; first slices 1, 4 and 7 were consecutively acquired with b = 0 value, then the same slices with b = 50 value and so on up to b = 1000. Subsequently, slices 2, 5 and 8 were acquired in the same way, and finally slices 3, 6 and 9 also.

Image analysis

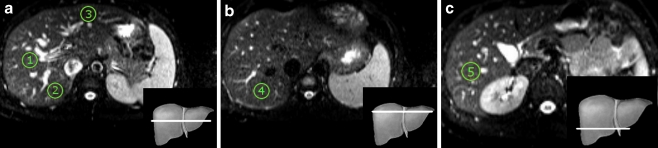
A programmable graphical and calculus environment was used (Matlab, The Mathworks, Natick, MA, USA) to develop a tool for analysing the DWI series using mono- and bi-exponential fitting procedures. First, the DWI data were loaded and the five liver regions were defined for all 19 datasets by drawing circular regions-of-interest (ROIs) with a diameter of 22.3 mm on selected transverse 6-mm slices (Fig. 1). For each dataset three slices at three different levels were selected; medial at the level of the right portal vein, cranial above the level of the left portal vein and caudal at the level of the splenic vein. The first three regions were drawn in the medial liver slice: central in the right lobe (ROI 1, segments 5/8), dorso-lateral in the right lobe (ROI 2, segments 6/7) and ventral in the left lobe (ROI 3, segments 2/3). The fourth region was drawn in the cranial liver slice, dorso-lateral in the right lobe (ROI 4, segment 7), and the last region in the caudal liver slice, near the gallbladder (ROI 5, segment 5). Any nearby visible vascular and biliary structures were avoided. For each ROI and all seven b-values the average signal intensity S was calculated and stored. Then, the signal intensities S and all seven b-values were fitted to the bi-exponential model [3]:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \frac{S}{{{S_0}}} = {f_{{fast}}} \cdot \exp ( - b \cdot {D_{{fast}}}) + {f_{{slow}}} \cdot \exp ( - b \cdot {D_{{slow}}}) $$\end{document} 1

where S 0 is the maximum signal intensity, D fast is the fast component representing microperfusion, f fast is the fraction of microperfusion, D slow is the slow component representing molecular diffusion and f slow is the fraction of molecular diffusion (f slow  = 1 - f fast). Equation 1 was fitted by the Nelder-Mead simplex direct search method with bound constraints (Table 1), which performs a constrained non-linear minimisation of the sum of the squared residuals [27, 28]. Finally, the conventional ADC was determined using linear regression analysis of the natural log of signal intensities S versus all seven b-values [2]:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ S = A\exp ( - b \cdot ADC) $$\end{document} 2

where A is the intercept of the signal.

Fig. 1.

Fig. 1

Open in a new tab

Diffusion in the liver was measured in five locations (ROI 1 to 5) with a diameter of 22.3 mm. a Transverse plane of the medial liver with ROI 1 central in the right lobe (segments 5/8), ROI 2 dorso-lateral in the right lobe (segments 6/7) and ROI 3 ventral in the left lobe (segments 2/3). b Transverse plane of the cranial liver with ROI 4 dorso-lateral in the right lobe (segment 7) c Transverse plane of the caudal liver with ROI 5 near the gallbladder (segment 5)

Table 1.

Fitting parameters

Bi-exponential fit (p = 3)a Lower-bound Higher-bound Initial guess
f fast (unitless) 1e-8 1 0.4
D fast (×10−3 mm2/s) 1e-5 100 10
D slow (×10−3 mm2/s) 1e-5 10 1
Open in a new tab

aNumber of parameters

Parametric maps

For one subject, parametric maps of ADC and D slow were calculated by fitting the diffusion signal of a 4 by 4 pixels area to the mono- and bi-exponential model. The area was then moved 4 pixels until the whole liver matrix (192 × 144) was covered, resulting in a parametric map of 48 × 36. Subsequently, the parametric map was rescaled to the original matrix size by linear interpolation.

Influence of blood vessels

To illustrate the effects of microperfusion on the mono- and bi-exponential models, an ROI was drawn in one subject and blood vessels were included in the ROI. Then the same ROI was moved slightly until the blood vessels were excluded from the ROI. In both cases ADC, D slow, D fast and f were calculated and the curves presented in a figure for comparison.

Simulation study

A systematic literature search was performed in order to compare our results with previous findings. We included multi-region DWI liver studies that determined the ADC for healthy liver tissue for at least 20 patients and published a P-value for the significance of the ADC difference among the regions. Then the results of the reviewed studies were simulated by performing mono- and bi-exponential analyses on our data using the b-values and regions mentioned in the review studies. The ADC, D slow, D fast, f slow and f fast resulting from the simulation were then compared with those of the reviewed studies.

Statistical analysis

Statistical analysis was performed using SPSS (SPSS 18, Chicago, IL, USA). All data were tested for normality using Shapiro–Wilk tests. For normally distributed data (ADC and D slow) one-way ANOVA tests were used to compare measurements between different liver regions. For non-normally distributed data (D fast and f) the differences between liver regions were determined using non-parametric Kruskal–Wallis tests. The central tendency and variability of the data were quantified by the median \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\mu_{{1/2}}} $$\end{document} and the median deviation \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\sigma_{{1/2}}} $$\end{document} [29] where

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\sigma_{{1/2}}} = median(|{x_i} - {\mu_{{1/2}}}|) $$\end{document} 3

For each individual fitting procedure the coefficient of correlation (goodness-of-fit) R 2 was adjusted for the number of parameters p and the number of data points n:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ R_{{adj}}^2 = 1 - \frac{{(1 - {R^2}) \cdot (n - 1)}}{{n - p}} $$\end{document} 4

where n = 7 for seven b-values and p = 2 or 3 for mono- and bi-exponential models respectively. F-tests were performed to evaluate whether the bi-exponential model was justified over a mono-exponential model:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ F = \frac{{(SS{E_{{mono}}} - SS{E_{{bi}}})/(D{F_{{mono}}} - D{F_{{bi}}})}}{{SS{E_{{bi}}}/D{F_{{bi}}}}} $$\end{document} 5

where SSE mono and SSE bi are the sum-of-squared errors (SSE) of the mono- and bi-exponential fits respectively, and DF mono and DF bi are the degrees of freedom of both analyses (DF = n – p). All statistical analyses had a significance level of 5%.

Results

The mono-exponentially fitted ADCs were significantly different (P < 0.001) among the five regions and normally distributed (Tables 2 and 3). The left lobe showed the highest ADC (1.423 × 10−3 mm2/s) and the lowest ADC was found centrally in the medial right lobe (1.107 × 10−3 mm2/s).

Table 2.

Tests of normality

Region Segment ADC D slow D fast f slow/fast
1 5/8 0.798 0.929 0.022* 0.761
2 6/7 0.895 0.708 0.086 0.005*
3 2/3 0.814 0.309 0.007* 0.900
4 7 0.208 0.523 0.563 0.023*
5 5 0.230 0.735 0.167 0.663
Open in a new tab

P values (Shapiro–Wilk tests) indicate deviations from normal distribution (P < 0.05). Measurements of D fast and f fractions were non-normally distributed, D slow values were normally distributed

Table 3.

Mono- and bi-exponential fitting results for five regions in the liver

Mono-exponential fit Bi-exponential fit
R 2adj ≥ 0.479 R 2adj ≥ 0.969
Region Segment ADC (×10−3 mm2/s) f fast (%) D fast (×10−3 mm2/s) f slow (%) D slow (×10−3 mm2/s)
1 5/8 1.107 ± 0.101 29 ± 5 33.5 ± 12.1 71 ± 5 0.923 ± 0.148
2 6/7 1.204 ± 0.055 24 ± 3 37.8 ± 11.0 76 ± 3 1.038 ± 0.052
3 2/3 1.423 ± 0.118 47 ± 9 17.8 ± 7.1 53 ± 9 0.900 ± 0.228
4 7 1.239 ± 0.090 24 ± 5 46.8 ± 19.8 76 ± 5 1.062 ± 0.118
5 5 1.107 ± 0.102 29 ± 4 43.6 ± 9.7 71 ± 4 0.954 ± 0.120
P-value <0.001* <0.001† <0.001† <0.001† 0.140*
Open in a new tab

Data are medians ± median absolute deviations. Both mono- and bi-exponential fits were determined with seven b-values (0, 50, 100, 250, 500, 750 and 1000). R 2adj is the goodness-of-fit correlation coefficient. P values indicate the significance of differences between different regions in the liver. *One-way ANOVA. †Non-parametric Kruskal–Wallis

The bi-exponentially fitted D slow was not shown to be significantly different (P = 0.140) among the five regions and were normally distributed (Tables 2 and 3). The median of the D slow components varied between 0.923 and 1.062 × 10−3 mm2/s for each of the five regions.

The bi-exponentially fitted D fast was significantly different (P < 0.001) between the five regions and non-normally distributed (Tables 2 and 3). The median of the D fast components varied between 17.8 and 46.8 × 10−3 mm2/s for the five regions.

The left lobe showed the highest fraction of microperfusion f fast (47%) and the lowest fraction of diffusion f slow (53%). The dorso-lateral right lobe showed the lowest fraction of microperfusion f fast (24%) and the highest fraction of molecular diffusion f slow (76%). The f slow and f fast fractions were significantly different among the five regions (P < 0.001) (Table 3).

The adjusted R 2 showed that the bi-exponential model fitted better to the diffusion data than the mono-exponential model for each liver region (R 2adj, bi > R 2adj, mono). Furthermore, the F-tests showed that the diffusion data fitted significantly better to the bi-exponential model (F > 21.4, P < 0.010) than to the mono-exponential model in all individual fitting procedures.

Parametric maps

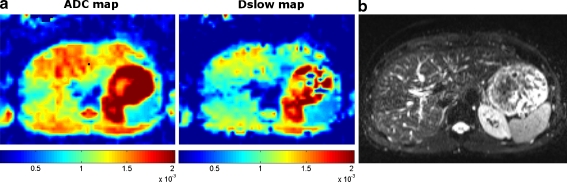
Diffusion weighted imaging data of the medial liver of one subject were used to calculate ADC and D slow maps (Fig. 2). The D slow map showed a more homogeneous distribution of the bi-exponential fitted slow diffusion throughout the liver. The ADC map showed more differing values between different regions of the liver, especially near blood vessels and in the left lobe.

Fig. 2.

Fig. 2

Open in a new tab

An example of ADC and D slow maps of the medial liver. a ADC map (left) and D slow map (right) of the medial liver which were scaled equally from 0.1 × 10−3 to 2 × 10−3 mm2/s. The D slow map shows a more homogeneous distribution of the bi-exponential fitted slow diffusion component throughout the liver. The ADC map shows significantly different values between different regions of the liver, especially near blood vessels and in the left lobe. b The anatomical position of the ADC and D slow maps

Influence of blood vessels

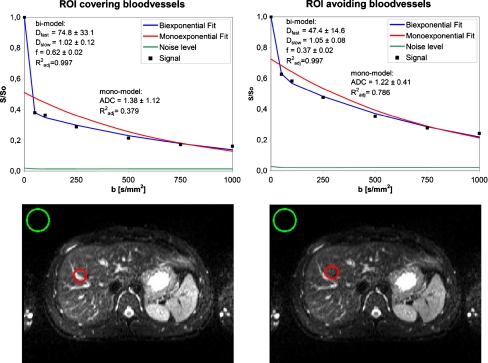
In one subject, the effects of microperfusion on the mono- and bi-exponential models were illustrated by including blood vessels in the ROI; this showed a large influence of microperfusion on the ADC (Fig. 3). When the blood vessels were excluded from the ROI a decreased ADC was observed. However, D slow was similar to when blood vessels were included in the ROI.

Fig. 3.

Fig. 3

Open in a new tab

An example of the effects of microperfusion on DWI measurements. To illustrate the effects of microperfusion on the mono- and bi-exponential model, blood vessels were included in the ROI (left) which showed a large influence of microperfusion on the ADC. Then the same ROI was moved slightly until the blood vessels were excluded from the ROI (right) which showed a decreased ADC, however D slow was similar to when blood vessels were included in the ROI. The noise was defined as the average signal measured in air (green ROI), away from any visible artefacts

Simulation study

The systematic literature search resulted in six multi-region DWI studies of the liver in which a minimal of 20 patients were included and in which between two and four different regions of healthy liver parenchyma were analysed [13, 19, 21, 25, 26, 30]. Studies in which mono-exponential analyses were performed showed ADCs between 1.00 and 2.69 × 10−3 mm2/s using sets of two, three or five b-value combinations between 0 and 1300 s/mm2 (Table 4). We found ADCs between 0.94 and 2.39 × 10−3 mm2/s when using the same b-value combinations. All mono-exponential studies reported significantly (P < 0.05) different ADCs between the different liver regions, this was confirmed by our simulation study (P < 0.001).

Table 4.

Reviewed data simulated with mono-exponential analysis

Reviewed data Simulated on our data
Ref. n b-values (s/mm2) #regions ADC (range) P value b-values (s/mm2) ADC (range) P value
Nasu et al. [25] 30 0, 500 2 1.98–2.69 <0.001 0, 500 1.64–2.39 <0.001
Yoshikawa et al. [30] 45 0, 600 4 1.55–1.63 <0.05† 0, 750 1.38–1.91 <0.001
Kiliçkesmez et al. [26] 50 0, 500 ,600 4 1.34–1.77 <0.01 0, 500, 750 1.42–1.98 <0.001
Bruegel et al. [21] 90 50, 300, 600 4 1.12–1.44 <0.001 50, 250, 750 1.02–1.41 <0.001
Mürtz et al. [19] 36 50, 300, 700, 1000, 1300 3 1.00–1.16 <0.05† 50, 250, 750, 1000 0.94–1.10 (only RL)a 0.001
Open in a new tab

ADCs are means in units of 10−3 mm2/s. P values (one-way ANOVA) indicate the significance of differences between different regions in the liver. † P value was not mentioned; however the significance level was 5%. aMürtz et al. [19] did not evaluate regions in the left lobe; therefore we excluded ROI 3 (left lobe) from the simulation

In one study a bi-exponential analysis of two different regions of liver parenchyma was performed using a series of ten b-values between 0 and 800 s/mm2 (Table 5) [13]. They did not find significantly different D slow components among different liver regions (P = 0.5); this was confirmed by our simulation study (P = 0.105).

Table 5.

Reviewed data simulated with bi-exponential analysis

Reviewed data [13] Simulated on our data
N 25 19
b-values (s/mm2) 0, 10, 20, 30, 50, 80, 100, 200, 400, 800 0, 50, 100, 250, 500, 750
#regions 2 5
Mean (range) P value Mean (range) P value
f fast (%) 26–31 0.07 26– 43 0.000b
D fast (×10−3 mm2/s) 71.0–85.1 0.1 27.9–57.2 0.001b
f slow (%) 69–74 0.07 57–74 0.000b
D slow (×10−3 mm2/s) 1.02–1.16 0.5 0.98–1.18 0.105a
Open in a new tab

Data are means. P values indicate the significance of differences between different regions in the liver. aOne-way ANOVA. bNon-parametric Kruskal–Wallis

Discussion

The aim of this study was to demonstrate that mono-exponential diffusion in the liver is contaminated by microperfusion. We suspected that variation of ADCs in different regions of the liver is due to microperfusion contamination and that therefore the bi-exponential model is required. We found that the ADC of normal liver tissue is substantially dependent on the location; however, the bi-exponentially fitted D slow is not dependent on the location of the measurement. We used terminology according to the suggestions of Guiu and Cercueil who convincingly advocated for the use of D slow to describe molecular diffusion properties and D fast to describe microperfusion [31].

Our results agree with earlier studies reporting significant differences among ADCs obtained in different regions in the liver [19, 21, 25, 26, 30]. ADCs in our study (1.107 to 1.423 × 10−3 mm2/s) were consistent with those of previous reports, which showed a large range (0.69 to 2.69 × 10−3 mm2/s) of ADCs for normal liver tissue [15, 25, 32]. The results on D slow were supported by Luciani et al.; they also found no significant differences between D slow of normal liver tissue [13]. They found that D slow varied between 1.02 and 1.16 × 10−3 mm2/s; this is comparable to our range (0.98 to 1.18 × 10−3 mm2/s) when we simulated their results using our data and similar b-values.

The demonstrated regional dependence of the ADC contrary to the non-regional dependence of D slow can be explained from the differences between the mono- and the bi-exponential models. The mono-exponentially fitted ADC is to a high degree sensitive to microperfusion, which was already shown by Le Bihan et al. in the brain [2]. When the DWI sequence contains b-values in the microperfusion range, and the microperfusion is relatively high compared with the diffusion component, then the model will result in a high ADC compared with D slow. When there is no microperfusion, which has been reported for fibroglandular breast tissue, the ADC will be comparable to D slow [33]. Hence the ADC of the liver is to a large extent dependent on microperfusion, especially when the DWI sequence contains several b-values in the microperfusion range [14]. This is why in some studies researchers tried to choose b-values not within the microperfusion range [18–23]. For example, Perman et al. observed that the ADC value for liver decreased from 1.36 to 0.98 × 10−3 mm2/s when the b = 0 value was omitted; this is similar to the range of D slow that we found. In a recent consensus report on DWI, it was recommended to use two b-values (>100 and between 500 and 1000 mm2/s) for ADC assessments [34]. It is, however, difficult to choose b-values such that microperfusion contamination of the ADC is avoided, because the microperfusion effects of the tissue are not known beforehand. We demonstrated in our simulation study that, although low b-values were excluded, the ADC of liver tissue was to a large extent contaminated by microperfusion and that this resulted in apparent differences of the diffusion between liver regions. The simulation study also showed that the variety of ADC values of healthy liver tissue published in the literature, were probably caused by the choice of b-values, and the mono-exponential model itself. This is a pitfall of using the ADC as a measure for molecular diffusion; there is no optimal combination of b-values, because the amount of microperfusion determines the optimal sequence of b-values and this is not known a priori. Recently, a similar simulation study was performed in the kidneys; they also found that the variability of the ADC in the kidneys is caused by the use of the mono-exponential model [35].

The microperfusion component D fast of the bi-exponential model significantly depends on the location of the measurement. This contradicts with the results of Luciani et al., who did not find a location dependency of D fast, possibly because they compared just two regions (left and right lobe) [13]. The range (71.0–85.1 × 10−3 mm2/s) was higher than what we found (27.9–57.2 × 10−3 mm2/s) when we simulated their results using our data and similar b-values. This may reflect the use of different calculation methods. In our study f, D fast and D slow of an ROI were calculated by taking the medians of the underlying b-maps as an input for the fitting procedure, where Luciani et al. first calculated D fast, D slow and f maps on a pixel-by-pixel based fitting procedure, after which the average of an ROI was calculated. In addition, they used six b-values under 100 s/mm2 (versus two in our study), which tends to decrease the uncertainty of the fitting algorithm, and increase the slope of the curve close to zero. This might explain the higher D fast and the decreased range of D fast in their study. However, we have shown that even with seven (rather than 16 b-values) the bi-exponential fits are already extremely accurate, which is supported by the nearly identical values of D slow in their study and our simulation study. Too little b-values under b = 100 s/mm2 can however hamper an accurate determination of D fast, especially when analysing tissues with high D fast values, which can be expected in pathology or near blood vessels.

The increase in the ADC in the left lobe, which was demonstrated in Fig. 2, is usually explained from the increased cardiac motion in the left lobe [19, 25, 36–38]. However, we found that the fraction of microperfusion f fast in the left lobe was almost a factor two higher than in other liver locations. Although pseudo-anisotropy is a known artefact of respiratory triggering in the liver [39], we suspect that the increased ADC in the left lobe may be caused by extensive microperfusion contamination of the ADC and to a lesser extent by either cardiac or respiratory artefacts. This is supported by a study on the hepatic perfusion of eight hepatic segments by dual-source computed tomography [40]. They found that the hepatic perfusion index (HPI) was significantly higher in segment 3 (left lobe) than in segments 5 to 8 (right lobe), and suggested that this might be related to the anatomy of the liver vessels. Another study using pharmacokinetic analysis of dynamic contrast-enhanced MRI demonstrated that regional variations in liver microcirculation can be displayed by colour-coded parameter maps [41]. They found a minor variation of perfusion in an apical section of a transplanted liver. The left part of the liver, corresponding to segment 2, showed a different perfusion rate than the right part of the liver. In an experimental study on rats using perfusion CT, the relative blood flow in the left lobe was 17% higher than in the right lobe of the liver [42]. We suspect that these regional variations in the density of small blood vessels and capillaries caused the heterogeneous appearance of microperfusion throughout the liver. This is supported by our analysis of including a blood vessel in the ROI, which resulted in more microperfusion contamination than when blood vessels were avoided.

Some studies have reported on age-related changes in liver structure and function [43, 44]. However, Pasquinelli et al. showed no significant variations in liver DWI quantitative parameters according to the age of the subject [45]. Therefore, we assumed that the possible effects of age in our cohort are far smaller than the demonstrated significant region dependency of the ADC in the liver. Although the conclusions in this study are drawn from healthy volunteers, we suspect that the effects of microperfusion are much larger in pathology, and should therefore be applicable to patient data also.

In conclusion, the ADC of normal liver tissue is significantly dependent on the measurement location because of substantial microperfusion contamination; therefore the bi-exponential model should be used. Currently, the diagnostic use of DWI for discriminating hepatic masses, liver cirrhosis and fibrosis is mainly based on the ADC, and the discrimination between diseased and healthy tissue may therefore be hampered [6–8, 15–18, 20, 21, 23, 30, 37, 46]. Thus, the bi-exponential model is essential for the future development of the clinical diagnostic application of DWI in the liver.

Acknowledgments

Open Access

This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.

References

  • 1.Le Bihan D, Breton E, Lallemand D, Grenier P, Cabanis E, Laval-Jeantet M. MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders. Radiology. 1986;161:401–407. doi: 10.1148/radiology.161.2.3763909. [DOI] [PubMed] [Google Scholar]
  • 2.Le Bihan D, Breton E, Lallemand D, Aubin ML, Vignaud J, Laval-Jeantet M. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology. 1988;168:497–505. doi: 10.1148/radiology.168.2.3393671. [DOI] [PubMed] [Google Scholar]
  • 3.Le Bihan D, Turner R, Moonen CT, Pekar J. Imaging of diffusion and microcirculation with gradient sensitization: design, strategy, and significance. J Magn Reson Imaging. 1991;1:7–28. doi: 10.1002/jmri.1880010103. [DOI] [PubMed] [Google Scholar]
  • 4.Müller MF, Prasad P, Siewert B, Nissenbaum MA, Raptopoulos V, Edelman RR. Abdominal diffusion mapping with use of a whole-body echo-planar system. Radiology. 1994;190:475–478. doi: 10.1148/radiology.190.2.8284402. [DOI] [PubMed] [Google Scholar]
  • 5.Turner R, Le Bihan D, Maier J, Vavrek R, Hedges LK, Pekar J. Echo-planar imaging of intravoxel incoherent motion. Radiology. 1990;177:407–414. doi: 10.1148/radiology.177.2.2217777. [DOI] [PubMed] [Google Scholar]
  • 6.Namimoto T, Yamashita Y, Sumi S, Tang Y, Takahashi M. Focal liver masses: characterization with diffusion-weighted echo-planar MR imaging. Radiology. 1997;204:739–744. doi: 10.1148/radiology.204.3.9280252. [DOI] [PubMed] [Google Scholar]
  • 7.Ichikawa T, Haradome H, Hachiya J, Nitatori T, Araki T. Diffusion-weighted MR imaging with single-shot echo-planar imaging in the upper abdomen: preliminary clinical experience in 61 patients. Abdom Imaging. 1999;24:456–461. doi: 10.1007/s002619900539. [DOI] [PubMed] [Google Scholar]
  • 8.Kim T, Murakami T, Takahashi S, Hori M, Tsuda K, Nakamura H. Diffusion-weighted single-shot echoplanar MR imaging for liver disease. AJR Am J Roentgenol. 1999;173:393–398. doi: 10.2214/ajr.173.2.10430143. [DOI] [PubMed] [Google Scholar]
  • 9.Yamada I, Aung W, Himeno Y, Nakagawa T, Shibuya H. Diffusion coefficients in abdominal organs and hepatic lesions: evaluation with intravoxel incoherent motion echo-planar MR imaging. Radiology. 1999;210:617–623. doi: 10.1148/radiology.210.3.r99fe17617. [DOI] [PubMed] [Google Scholar]
  • 10.Moteki T, Horikoshi H, Oya N, Aoki J, Endo K. Evaluation of hepatic lesions and hepatic parenchyma using diffusion-weighted reordered turboFLASH magnetic resonance images. J Magn Reson Imaging. 2002;15:564–572. doi: 10.1002/jmri.10101. [DOI] [PubMed] [Google Scholar]
  • 11.Moteki T, Horikoshi H. Evaluation of hepatic lesions and hepatic parenchyma using diffusion-weighted echo-planar MR with three values of gradient b-factor. J Magn Reson Imaging. 2006;24:637–645. doi: 10.1002/jmri.20682. [DOI] [PubMed] [Google Scholar]
  • 12.Coenegrachts K, Delanote J, Ter Beek L, et al. Evaluation of true diffusion, perfusion factor, and apparent diffusion coefficient in non-necrotic liver metastases and uncomplicated liver hemangiomas using black-blood echo planar imaging. Eur J Radiol. 2009;69:131–138. doi: 10.1016/j.ejrad.2007.09.013. [DOI] [PubMed] [Google Scholar]
  • 13.Luciani A, Vignaud A, Cavet M, et al. Liver cirrhosis: intravoxel incoherent motion MR imaging–pilot study. Radiology. 2008;249:891–899. doi: 10.1148/radiol.2493080080. [DOI] [PubMed] [Google Scholar]
  • 14.Moteki T, Horikoshi H. Evaluation of noncirrhotic hepatic parenchyma with and without significant portal vein stenosis using diffusion-weighted echo-planar MR on the basis of multiple-perfusion-components theory. Magn Reson Imaging. 2011;29:64–73. doi: 10.1016/j.mri.2010.07.008. [DOI] [PubMed] [Google Scholar]
  • 15.Taouli B, Koh DM. Diffusion-weighted MR imaging of the liver. Radiology. 2010;254:47–66. doi: 10.1148/radiol.09090021. [DOI] [PubMed] [Google Scholar]
  • 16.Taouli B, Vilgrain V, Dumont E, Daire JL, Fan B, Menu Y. Evaluation of liver diffusion isotropy and characterization of focal hepatic lesions with two single-shot echo-planar MR imaging sequences: prospective study in 66 patients. Radiology. 2003;226:71–78. doi: 10.1148/radiol.2261011904. [DOI] [PubMed] [Google Scholar]
  • 17.Talwalkar JA, Yin M, Fidler JL, Sanderson SO, Kamath PS, Ehman RL. Magnetic resonance imaging of hepatic fibrosis: emerging clinical applications. Hepatology. 2008;47:332–342. doi: 10.1002/hep.21972. [DOI] [PubMed] [Google Scholar]
  • 18.Chan JH, Tsui EY, Luk SH, et al. Diffusion-weighted MR imaging of the liver: distinguishing hepatic abscess from cystic or necrotic tumor. Abdom Imaging. 2001;26:161–165. doi: 10.1007/s002610000122. [DOI] [PubMed] [Google Scholar]
  • 19.Mürtz P, Flacke S, Träber F, van den Brink JS, Gieseke J, Schild HH. Abdomen: diffusion-weighted MR imaging with pulse-triggered single-shot sequences. Radiology. 2002;224:258–264. doi: 10.1148/radiol.2241011117. [DOI] [PubMed] [Google Scholar]
  • 20.Boulanger Y, Amara M, Lepanto L, et al. Diffusion-weighted MR imaging of the liver of hepatitis C patients. NMR Biomed. 2003;16:132–136. doi: 10.1002/nbm.818. [DOI] [PubMed] [Google Scholar]
  • 21.Bruegel M, Holzapfel K, Gaa J, et al. Characterization of focal liver lesions by ADC measurements using a respiratory triggered diffusion-weighted single-shot echo-planar MR imaging technique. Eur Radiol. 2008;18:477–485. doi: 10.1007/s00330-007-0785-9. [DOI] [PubMed] [Google Scholar]
  • 22.Perman WH, Balci NC, Akduman I, Kuntz E. Magnetic resonance measurement of diffusion in the abdomen. Top Magn Reson Imaging. 2009;20:99–104. doi: 10.1097/RMR.0b013e3181c0d772. [DOI] [PubMed] [Google Scholar]
  • 23.Sandrasegaran K, Akisik FM, Lin C, et al. Value of diffusion-weighted MRI for assessing liver fibrosis and cirrhosis. AJR Am J Roentgenol. 2009;193:1556–1560. doi: 10.2214/AJR.09.2436. [DOI] [PubMed] [Google Scholar]
  • 24.Dale BM, Braithwaite AC, Boll DT, Merkle EM. Field strength and diffusion encoding technique affect the apparent diffusion coefficient measurements in diffusion-weighted imaging of the abdomen. Invest Radiol. 2010;45:104–108. doi: 10.1097/RLI.0b013e3181c8ceac. [DOI] [PubMed] [Google Scholar]
  • 25.Nasu K, Kuroki Y, Sekiguchi R, Kazama T, Nakajima H. Measurement of the apparent diffusion coefficient in the liver: is it a reliable index for hepatic disease diagnosis? Radiat Med. 2006;24:438–444. doi: 10.1007/s11604-006-0053-y. [DOI] [PubMed] [Google Scholar]
  • 26.Kiliçkesmez O, Yirik G, Bayramoğlu S, Cimilli T, Aydin S. Non-breath-hold high b-value diffusion-weighted MRI with parallel imaging technique: apparent diffusion coefficient determination in normal abdominal organs. Diagn Interv Radiol. 2008;14:83–87. [PubMed] [Google Scholar]
  • 27.D’Errico J (2006) Understanding fminsearchbnd, MATLAB Central File Exchange. Available via http://www.mathworks.com/matlabcentral/fileexchange/8277-fminsearchbnd. Accessed 4 May 2011
  • 28.Lagarias JC, Reeds JA, Wright MH, Wright PE. Convergence properties of the Nelder-Mead Simplex method in low dimensions. SIAM J Optim. 1998;9:112–147. doi: 10.1137/S1052623496303470. [DOI] [Google Scholar]
  • 29.Hampel FR. The influence curve and its role in robust estimation. J Am Statist Assoc. 1974;69:383–393. doi: 10.2307/2285666. [DOI] [Google Scholar]
  • 30.Yoshikawa T, Kawamitsu H, Mitchell DG, et al. ADC measurement of abdominal organs and lesions using parallel imaging technique. AJR Am J Roentgenol. 2006;187:1521–1530. doi: 10.2214/AJR.05.0778. [DOI] [PubMed] [Google Scholar]
  • 31.Guiu B, Cercueil JP. Liver diffusion-weighted MR imaging: the tower of Babel? Eur Radiol. 2011;21:463–467. doi: 10.1007/s00330-010-2017-y. [DOI] [PubMed] [Google Scholar]
  • 32.Chow LC, Bammer R, Moseley ME, Sommer FG. Single breath-hold diffusion-weighted imaging of the abdomen. J Magn Reson Imaging. 2003;18:377–382. doi: 10.1002/jmri.10353. [DOI] [PubMed] [Google Scholar]
  • 33.Baron P, Dorrius MD, Kappert P, Oudkerk M, Sijens PE. Diffusion-weighted imaging of normal fibroglandular breast tissue: influence of microperfusion and fat suppression technique on the apparent diffusion coefficient. NMR Biomed. 2010;23:399–405. doi: 10.1002/nbm.1475. [DOI] [PubMed] [Google Scholar]
  • 34.Padhani AR, Liu G, Koh DM, et al. Diffusion-weighted magnetic resonance imaging as a cancer biomarker: consensus and recommendations. Neoplasia. 2009;11:102–125. doi: 10.1593/neo.81328. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Zhang JL, Sigmund EE, Chandarana H, et al. Variability of renal apparent diffusion coefficients: limitations of the monoexponential model for diffusion quantification. Radiology. 2010;254:783–792. doi: 10.1148/radiol.09090891. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Koh DM, Scurr E, Collins DJ, et al. Colorectal hepatic metastases: quantitative measurements using single-shot echo-planar diffusion-weighted MR imaging. Eur Radiol. 2006;16:1898–1905. doi: 10.1007/s00330-006-0201-x. [DOI] [PubMed] [Google Scholar]
  • 37.Kandpal H, Sharma R, Madhusudhan KS, Kapoor KS. Respiratory-triggered versus breath-hold diffusion-weighted MRI of liver lesions: comparison of image quality and apparent diffusion coefficient values. AJR Am J Roentgenol. 2009;192:915–922. doi: 10.2214/AJR.08.1260. [DOI] [PubMed] [Google Scholar]
  • 38.Kwee TC, Takahara T, Niwa T, et al. Influence of cardiac motion on diffusion-weighted magnetic resonance imaging of the liver. MAGMA. 2009;22:319–325. doi: 10.1007/s10334-009-0183-1. [DOI] [PubMed] [Google Scholar]
  • 39.Nasu K, Kuroki Y, Fujii H, Minami M. Hepatic pseudo-anisotropy: a specific artifact in hepatic diffusion-weighted images obtained with respiratory triggering. MAGMA. 2007;20:205–211. doi: 10.1007/s10334-007-0084-0. [DOI] [PubMed] [Google Scholar]
  • 40.Su BY, Jin ZY, Liu W, et al. Features of eight segments of liver perfusion with the second generation dual-source computed tomography. Acta Acad Med Sin. 2010;32:655–658. doi: 10.3881/j.issn.1000.503X.2010.06.013. [DOI] [PubMed] [Google Scholar]
  • 41.Scharf J, Kemmling A, Hess T, Mehrabi A, Kauffmann G, Groden C, Brix G. Assessment of hepatic perfusion in transplanted livers by pharmacokinetic analysis of dynamic magnetic resonance measurements. Invest Radiol. 2007;42:224–229. doi: 10.1097/01.rli.0000255892.07208.f2. [DOI] [PubMed] [Google Scholar]
  • 42.Tutcu S, Serter S, Kaya Y, Kara E, Neşe N, Pekindil G, Coşkun T. Hepatic perfusion changes in an experimental model of acute pancreatitis: evaluation by perfusion CT. Eur J Radiol. 2010;75:203–206. doi: 10.1016/j.ejrad.2009.04.072. [DOI] [PubMed] [Google Scholar]
  • 43.Schmucker DL. Age-related changes in liver structure and function: implications for disease? Exp Gerontol. 2005;40:650–659. doi: 10.1016/j.exger.2005.06.009. [DOI] [PubMed] [Google Scholar]
  • 44.Schmucker DL. Aging and the liver: an update. J Gerontol A Biol Sci Med Sci. 1998;53:B315–B320. doi: 10.1093/gerona/53A.5.B315. [DOI] [PubMed] [Google Scholar]
  • 45.Pasquinelli F, Belli G, Mazzoni LN, Grazioli L, Colagrande S. Magnetic resonance diffusion-weighted imaging: quantitative evaluation of age-related changes in healthy liver parenchyma. Magn Reson Imaging. 2011;29:805–812. doi: 10.1016/j.mri.2011.02.014. [DOI] [PubMed] [Google Scholar]
  • 46.Gourtsoyianni S, Papanikolaou N, Yarmenitis S, Maris T, Karantanas A, Gourtsoyiannis N. Respiratory gated diffusion-weighted imaging of the liver: value of apparent diffusion coefficient measurements in the differentiation between most commonly encountered benign and malignant focal liver lesions. Eur Radiol. 2008;18:486–492. doi: 10.1007/s00330-007-0798-4. [DOI] [PubMed] [Google Scholar]

Articles from European Radiology are provided here courtesy of Springer

RESOURCES