Permeation and Block of the Kv1.2 Channel Examined Using Brownian and Molecular Dynamics

Abstract

Using both Brownian and molecular dynamics, we replicate many of the salient features of Kv1.2, including the current-voltage-concentration profiles and the binding affinity and binding mechanisms of charybdotoxin, a scorpion venom. We also elucidate how structural differences in the inner vestibule can give rise to significant differences in its permeation characteristics. Current-voltage-concentration profiles are constructed using Brownian dynamics simulations, based on the crystal structure 2A79. The results are compatible with experimental data, showing similar conductance, rectification, and saturation with current. Unlike KcsA, for example, the inner pore of Kv1.2 is mainly hydrophobic and neutral, and to explore the consequences of this, we investigate the effect of mutating neutral proline residues at the mouth of the inner vestibule to charged aspartate residues. We find an increased conductance, less inward rectification, and quicker saturation of the current-voltage profile. Our simulations use modifications to our Brownian dynamics program that extend the range of channels that can be usefully modeled. Using molecular dynamics, we investigate the binding of the charybdotoxin scorpion venom to the outer vestibule of the channel. A potential of mean force is derived using umbrella sampling, giving a dissociation constant within a factor of ∼2 to experimentally derived constants. The residues involved in the toxin binding are in agreement with experimental mutagenesis studies. We thus show that the experimental observations on the voltage-gated channel, including the toxin-channel interaction, can reliably be replicated by using the two widely used computational tools.

Introduction

The Kv1.2 channel is a member of the Shaker subfamily of delayed rectifier voltage-gated potassium channels. Present in a variety of nerve and muscle cells, it is a slowly inactivating channel whose function is to help regulate and modulate the repolarization of excitable cells during the period following an action potential (1,2). Kv1.2 is the first eukaryotic delayed rectifier potassium channel to have had its structure solved (3). The availability of a crystal structure presents a good opportunity for computational modeling. In this study, we show how a range of structure-function relationships for the channel can be computationally characterized using a combination of Brownian and molecular dynamics (MD). We can replicate many of the salient features of Kv1.2, including the current-voltage-concentration profiles and the binding affinity and binding mechanisms of charybdotoxin, a scorpion venom. We also explore the means by which structural modifications to the inner vestibule of Kv1.2 can lead to differences in permeation function.

Channels in the Kv1.x (Shaker) family typically show single channel permeation characteristics that include conductances around the 18–30 pS range (4–7) and currents that exhibit half maximum saturation around 200 mM (4). Starting with the crystal structure of the open state Kv1.2 channel (2A79) (3) and using an improved Brownian dynamics (BD) code, we conduct BD simulations of ion permeation. Our results are compatible with these experimental permeation data. The conduction of the channel is strongly dependent on the width of the inner vestibule (1), in agreement with other experimental (8) and theoretical (9) work. Transport of ions through the inner vestibule is a rate-limiting step in the conduction kinetics, due to the presence of largely nonpolar neutral residues lining the inner pore. In this sense, the channel is rather different in its properties to KcsA, which exhibits a larger conductance and no inward rectification, and whose inner cavity contains several charged and polar residues, unlike the mainly hydrophobic pore of Kv1.2. We show that mutating particular residues that line the inner vestibule from nonpolar proline to charged aspartate increases the current of the channel and removes the inward rectification, thus making the channel more comparable to KcsA (9). We also note that the saturation of conductance with increasing concentration is reduced in the modified channel.

The Kv1.2 channel is blocked by a variety of polypeptide toxins, including charybdotoxin (ChTX) in the nanomolar range (7,10–12). Various experimental (11,13–16) and theoretical (17–19) studies have provided evidence that charybdotoxin, with a charge of +5 e, is electrostatically attracted to negatively charged acidic residues in the S5-S6 linker region forming the outer vestibule of the pore. It then binds to the pore by means of a positively charged lysine residue entering the top of the pore while another lysine and arginine bind to the negatively charged aspartate residues surrounding the pore; other positively charged residues in the toxin also interact to some extent with other negatively charged residues around the pore and turret regions of the channel's outer vestibule. We investigate the interaction between charybdotoxin and the outer vestibule of the channel using MD. The toxin binds strongly to the outer vestibule of the channel in the manner indicated previously. We use umbrella sampling to derive a potential of mean force (PMF) for the toxin as it binds to the pore, with a binding constant that is in good agreement with experimental data. In addition, we note that the prediction of which particular residues are most strongly involved with the binding agrees with experimental mutagenesis studies (11,13).

Methods

Channel model

We use the open state crystal structure for Kv1.2 (2A79) (3) as a basis for all of our models. The VMD molecular viewing and modeling program (20) and the NAMD MD program (21) are used to build the model systems. We use only the region around the pore: residue numbers 288–420 inclusive. A tetramer is first constructed, based on crystallographic symmetry operations. For MD calculations, potassium ions, separated by single water molecules, are then placed in the selectivity filter, at binding sites S0 (just above Tyr-377), S2 (between Val-375 and Gly-376), and S4 (between Thr-374 and Thr-373) (22).

The use of a truncated channel for building our models could potentially raise questions about whether we have accurately captured the electrostatics. Much of our modeling is done at concentrations of around 300 mM, giving a Debye length of around 6 Å; therefore any truncated residues, which lie at a much greater distance from the pore, should normally be well screened. Residual effects, for example from the gating charges, would correspond to very small forces distributed over a large volume, with the bulk of the effect being neutralized by the flow of a small number of counterions also acting at a large distance. It is our experience that permeation in ion channels is controlled by charges that can act locally (therefore giving rise to large forces) on the ions inside the channel or vestibules, where the enclosed space precludes the flow of counterions, and that the presence of nonlocal charges has little effect. For these reasons, and as being able to use a truncated model gives a great computational advantage in Brownian and molecular dynamics, we have not attempted to model the gating segments and β-subunit.

Brownian dynamics

The BD system is represented in Fig. 1. The simulation cell is a cylinder whose axis runs in the z direction. For the simulations described in this work, we use a cylinder with a radius and length of 30 and 105 Å, respectively. The channel and surrounding lipid is modeled as a low dielectric region running across the center of the simulation cell. Only the ions in the system are explicitly modeled as spherical charged particles; water is implicit. Forces present in the system are: Macroscopic electrostatic forces describing various dielectric-mediated interactions between the ions and the channel, Coulomb ion-ion forces, short range fitted ion-ion forces, and short range repulsive forces from the channel boundary (9). The BD is solved using the algorithm of van Gunsteren and Berendsen (23). The timestep is 100 ns for ions in the reservoirs and 2 ns for ions inside the channel.

Figure 1.

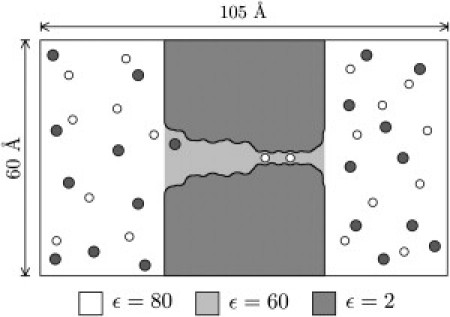
Schematic of the BD simulation cell.

In the past, we have modeled the dielectric boundary as a cylindrically symmetric surface (9). This is a good approximation for channels such as KcsA, and allows Poisson's equation to be solved extremely efficiently. The solutions to Poisson's equation are stored in precalculated lookup tables that contain the electric field at discrete points. These tables are then used to derive the forces on the ions during the simulation. The need to include the effects of the protein partial charges, applied electric field, and image charges of ions means that three types of lookup tables are required: a 2-d table, a 3-d table, and a 5-d table, named after their dimensionality (see Table 1).

Table 1.

Old lookup tables

Table	Field function	Reaction field source	Evaluated at	Boundary
2-d	$E\left(z,r\right)$	Ion at $\left(z,r\right)$	$\left(z,r\right)$	Cyl. sym.
3-d	$E\left(z,r,\theta \right)$	Protein + appl. elect. field	$\left(z,r,\theta \right)$	Cyl. sym.
5-d	$E\left(z,r,\theta ,r^{\prime },{\theta }^{\prime }-\theta \right)$	Ion at $\left(z^{\prime },r^{\prime },{\theta }^{\prime }\right)$	$\left(z,r,\theta \right)$	Cyl. sym.

However, Kv1.2 and related channels contain four turret regions, linking S5 and the pore helix, that protrude into the extracellular solution (see Fig. 6 A); their presence means that not all of the channel can be accurately approximated using a cylindrically symmetric boundary. Thus, we find it desirable to find some other means to deal with the electrostatics. We therefore proceed as follows: First, a cylindrically symmetric dielectric boundary is defined as previously, except that the turret regions and other isolated protrusions into the intracellular and extracellular solutions are excluded from the set of atoms used to generate the pore outline. Second, the 2-d, 3-d, and 5-d tables are calculated as above, except that the 3-d table now only includes the effect of the applied electric field; the protein partial charges are excluded from the calculation. Third, the Adaptive Poisson-Boltzmann Solver program (24) is used to solve Poisson's equation with a nonsymmetrized dielectric boundary and including all the protein partial charges, to define an extra 3-d table representing the self-generated field of the protein. The boundary is modified by adding a dielectric slab representing the lipid bilayer around the channel, having a thickness of 27 Å and with a z center of mass determined from our MD simulation. The bulk water is given a dielectric constant $\epsilon =80$, the water inside the channel is given a dielectric constant $\epsilon =60,$ and the interior of the protein/lipid region is given a dielectric constant $\epsilon =2$. The situation is set out in Table 2. These choices of ε used are based on a systematic study (25) that matches computational results to experimental data. The values used should be considered a phenomenological choice, which takes into account the deviation from a homogenous and linear dielectric of water. Because such a deviation is also implicit in MD simulations, our choice of ε is consistent with our MD modeling.

Figure 6.

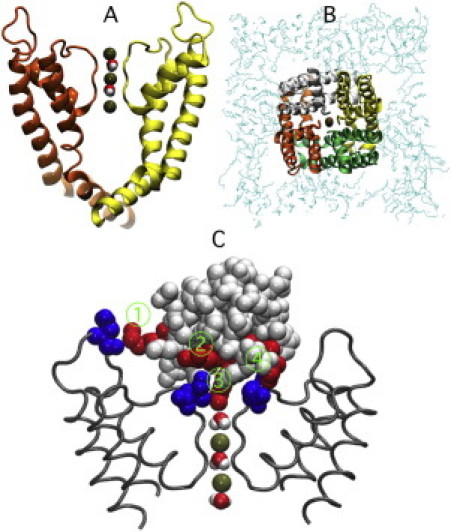
(A) Side (left-hand side) and (B) top (right-hand side) views of the channel system equilibrated for 10 ns with MD simulations. The selectivity filter contains three ions (green) and two water molecules. For clarity, only two of the four subunits are shown for the side view of the channel. (C) Bound configuration for the charybdotoxin molecule to the channel. The arginine and lysine residues on the ChTX molecule that are involved in the binding are shown in red. The corresponding channel aspartate residues are shown in blue. Water and potassium ions inside the selectivity filter are also shown. Close contacts are labeled 1–4: 1), ChTX Lys-31 interacts with channel Asp-355. 2), ChTX Arg-34 interacts with channel Asp-379. 3), ChTX Lys-27 enters the pore. 4), ChTX Arg-25 interacts with channel Asp-379.

Table 2.

New lookup tables

Table	Field function	Reaction field source	Eval. at	Boundary
2-d	$E\left(z,r\right)$	Ion at $\left(z,r\right)$	$\left(z,r\right)$	Cyl., pore region only
3-d	$E\left(z,r,\theta \right)$	Appl. elect. field	$\left(z,r,\theta \right)$	Cyl., pore region only
3-d APBS∗	$E\left(x,y,z\right)$	Protein	$\left(x,y,z\right)$	Full molec. surf.
5-d	$E\left(z,r,\theta ,r^{\prime },{\theta }^{\prime }-\theta \right)$	Ion at $\left(z^{\prime },r^{\prime },{\theta }^{\prime }\right)$	$\left(z,r,\theta \right)$	Cyl., pore region only

^∗Adaptive Poisson-Boltzmann Solver.

The input data for constructing a channel model are the atomic coordinates, partial charges, and radii. In the current study, the crystal structure (see above) provides the initial atomic coordinates. Partial charges are taken from the CHARMM22 force field. For the purpose of calculating solutions to Poisson's equation, we use radii optimized for macroscopic electrostatics taken from Nina et al. (26); for the purposes of defining a hard sphere exclusion radius between protein atoms and ions, we use the zero-energy isosurface of the Lennard-Jones potential, equal to $0.89\times r_{\text{min}}/2$, where $r_{\text{min}}/2$ is the CHARMM22 Lennard-Jones radius.

Because the BD channel model is rigid, the selectivity filter of the channel needs to be slightly expanded (by roughly 0.2 Å) so that the ions can fit inside it. We have verified that the results are not greatly sensitive to the exact amount of expansion used and we have used a minimal radius to accommodate a potassium ion, around 1.4 Å. The expansion itself is accomplished by highly constrained minimization of the protein in MD, with large outward force acting radially outward on all atoms that enter within a certain minimum distance of the z axis. Other molding of the channel to explore various scenarios may be accomplished at this stage by using further constrained minimization.

Nonpolar hydrogens ($q\le 0.1e$) are combined with their parent atoms, so that only polar hydrogens are explicitly represented. Finally, the partial charges and symmetric dielectric boundary are then used to produce lookup tables, describing the solutions to Poisson's equation in the presence of the channel.

For the current-voltage curves, 16 cations and 16 anions are placed in the top reservoir and the same number in the bottom reservoir; an additional two ions are placed in the selectivity filter. The system size is then set to give a KCl concentration of 320 mM. Multiple runs, of a few μs each, are then carried out for each voltage and the curve is constructed. For the current-concentration curves, the system size is kept constant while adjusting the number of ions in each reservoir to give the desired concentration.

Molecular dynamics

The initial channel (see above) is embedded in a lipid layer containing 91 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine molecules. The system is then hydrated with a 250 mM solution of KCl; our final system contains 13,823 water molecules, 57 potassium ions, and 77 chloride ions, to maintain neutrality. The initial size of the unit cell is 90 Å × 90 Å × 100 Å.

The system is equilibrated using NAMD with the CHARMM 22/27/CMAP force field. A Langevin thermostat is used to control the temperature, with a damping constant of 1 ps^–1 and a temperature of 310 K. We use constant pressure dynamics at 1 atm using a Nosé-Hoover Langevin piston, with the cell shape fixed to a square in the x-y plane. Periodic boundary conditions are incorporated using particle mesh Ewald electrostatics. To confine it to the center of the simulation cell, we constrain the lipid center of mass in the z direction, using a harmonic force with a spring constant 0.2 kcal/(mol Å)². The x-y motion of the protein center of mass is likewise constrained, using the same spring constant. Initially, the protein is fixed and the lipids, water, and ions are allowed to equilibrate around the fixed protein. Following this, some 10 ns of equilibration are performed using only the constraints described previously.

Similar to Chen and Kuyucak (18,19), we also perform PMF umbrella sampling simulations of the charybdotoxin (ChTX) polypeptide interacting with the channel. The coordinates for this toxin are obtained from RCSB PDB entry 2A9H (27), which contain a complex between ChTX and the KcsA channel. ChTX has a nonstandard N-terminal residue, namely pyroglutamic acid, which is a cyclized form of glutamic acid that shares features of proline. For this residue we use parameters obtained by others and documented on the CHARM users group (28) using a combination of analogy, CHARMM model compounds, and some fitting of dihedrals to quantum calculations.

For the PMF reaction coordinate we use the distance along the z axis between the channel and the blocker: more precisely, the displacement vector between the centers of mass of the C_α atoms in the channel and those in the blocker projected onto the z axis. For each umbrella sampling window W_i, a harmonic bias potential is applied to the reaction coordinate, centered at the given value z_0i and with a spring constant of 5 kcal/mol Ų.

The umbrella sampling simulations require a series of starting configurations of the ChTX-Kv1.2 system to be built. Each window W_i requires the ChTX molecule to be positioned above the entrance to the pore with a reaction coordinate z_0i. The initial orientation of the ChTX molecule is chosen to conform to the published orientation (RCSB PDB entry 2A9H) for the KcsA/ChTX complex, as determined from NMR (27). To ensure that the orientation with respect to the equilibrated Kv1.2 channel is similar to that of the initial complex 2A9H, the orientation of the former is first transformed to bring the selectivity filters of the two channels in line with each other, the ChTX molecule is placed in the aligned system, and the reverse transformation is applied to the new system containing the ChTX molecule.

In addition to the umbrella sampling simulations, we carry out an unconstrained run where the ChTX molecule is initially placed with a reaction coordinate of 28 Å above the mouth of the channel pore and is then allowed to freely bind to the pore.

Results and Discussion

Permeation characteristics from BD

As illustrated schematically in Fig. 2 A, the pore-forming segment of the channel, composed of the selectivity filter and inner conduit, is connected to a shallow outer vestibule on the extracellular side and a deeper inner vestibule on the intracellular side. Four negatively charged aspartate residues surround the entrance to the selectivity filter. In addition, there are four visible turret regions, see Fig. 6 A, which protrude into the extracellular region, each containing a further aspartate residue facing the pore axis. Thus, the inner vestibule region is surrounded by eight negatively charged residues, meaning that there is an enhanced concentration of K⁺ ions near the outer mouth of the selectivity filter. The inner region of the channel, in contrast, is lined with many nonpolar, hydrophobic residues that repel ions due to image charge effects. Unlike in KcsA (29), there is normally no resident ion in the intracellular region in the Kv1.2 channel. Occasionally in our simulations an ion moves in and out of the filter binding site S4 to site S5, just outside the filter and in the inner vestibule; this behavior is consistent with the small x-ray peak at S5 and with other modeling (30). Note that the region immediately on the cytoplasmic side of the filter contains polar residues, unlike the rest of the inner vestibule, which is hydrophobic. The passage of potassium ions toward the selectivity filter is thus critically dependent on the size of the intracellular cavity. This may be related to the observations of Jensen et al. (30), who see a hydrophobic gating mechanism in their MD simulations that seems to be dependent on pore size.

Figure 2.

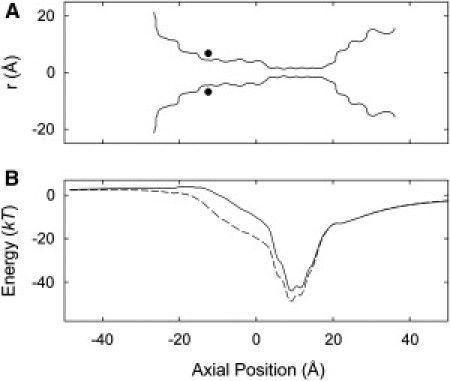
(A) Pore profile of the Kv1.2 channel. The black circles indicate the location of the P407D mutation. (B) Energy profile of a single ion moving along the z axis of the channel. The solid line is for the unmodified channel, and the broken line is for the P407D mutation.

We illustrate in Fig. 2 B the one-dimensional PMF of a potassium ion brought into the channel from the intracellular reservoir in the absence of other ions. The curves are obtained from the original (solid line) and a mutant (broken line, to be discussed later) Kv1.2 channels. In the region outside the pore, where the 1-d PMF is not well defined for an unconstrained ion, the ion is confined to lie within 8 Å of the pore axis. For the unmodified channel, the energy well experienced by a single ion is deep, reaching 48 kT within the selectivity filter ($z=10$ Å). The well results mainly from the effect of the carbonyl oxygens in the selectivity filter and is augmented by the presence of negatively charged residues around the mouth of the channel. The depth of this well is dramatically reduced when the pore is occupied by more than one ion; this effect is compounded by the fact that the presence of the dielectric boundary focuses the electric field lines along the axis of the channel. The deep energy well attracts two resident ions in the channel. With two ions in the selectivity filter, a third ion entering the channel from the intracellular space encounters a small, rising energy landscape as it moves toward the selectivity filter. Once it moves near the two resident ions, the outermost ion is ejected, and a conduction event takes place via a three ion knock-on mechanism (31). The presence of this small energy barrier for the third ion is expected to give rise to inward rectification. Although the conduction process typically can involve three or more ions, it can be illustrated by considering a two-ion PMF, see Fig. 3. The knock-on conduction pathway follows a valley floor through the two-dimensional energy landscape, as illustrated by the arrows in the figure; the barrier encountered is now around 12 kT.

Figure 3.

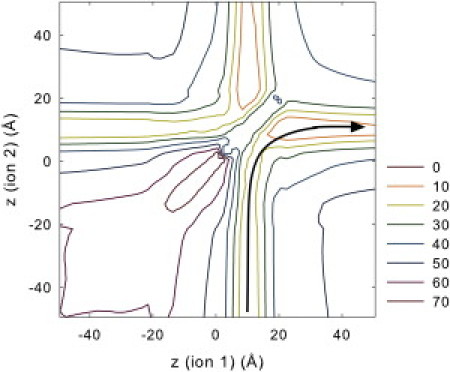
Two-ion PMF for the wild-type Kv1.2 channel. The x and y axes indicate the distance along the pore axis of each ion; the ions are confined to lie within a cylinder of radius 8 Å oriented along the pore axis. The black arrow in the lower right quadrant of the plot indicates a minimum energy trajectory leading to conduction via the knock-on mechanism; initially ion 2 starts in the intracellular reservoir and ion 1 in the filter. Ion 2 approaches to about z = 0 Å before causing the second ion to begin to move out of the filter. Real conductions typically involve the movement of three or more ions, and the energy barrier in these cases could be relatively small.

Fig. 4 A shows the current-voltage curve for BD. The chord conductance between 0 and 100 mV is 20 pS at a concentration of 320 mM. Experimental conductances quoted in the literature range from 18 pS for Kv1.2 (5–7) to 33 pS at 300 mM for Shaker (Kv1.0) (4). In their long timescale all-atom MD simulation, Jensen et al. (30) obtained a value of 233 pS at 600 mM. Similar to experimental results for Shaker (4), the channel is inwardly rectifying; the conductance at −150 mV is 58 pS, whereas that at +150 mV is 20 pS. This suggests a rate-limiting barrier for an ion entering the inner vestibule, perhaps accentuated by an enhanced concentration of cations at the mouth of the pore.

Figure 4.

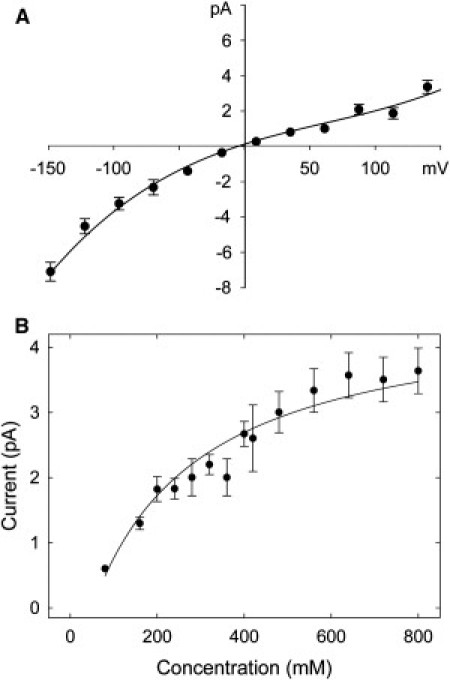
Current-voltage and current-concentration relationships as calculated from BD. The current-voltage relationships were obtained with a symmetric concentration of 320 mM KCl, whereas the current-concentration curves were derived with the applied potential of 120 mV. The lines fitted through the data points in B are fitted with the Michaelis-Menten equation. Error bars have a length of 1 mean ± SE and are not shown when they are smaller than the data points.

The current-concentration curve, at a voltage of 116 mV, is shown in Fig. 4 B. There is a rather slow saturation of current with increasing concentration. Saturation occurs as the occupation probability at the entrance to or inside the inner vestibule approaches one. Above this point, the rate-limiting step becomes the time taken for the actual conduction of ions across the channel rather than the replenishment of the channel from the reservoirs. From the fitted Michaelis-Menten curve, we derive a half-saturation concentration of 250 mM, which appears to approximately fit the data measured for Shaker by Heginbotham et al. (4).

The results above can be contrasted with KcsA, where the experimental conductance is somewhat higher, with various experimental values existing around the 100 pS mark (32–34), and the channel is not inward rectifying. KcsA contains a complex network of charged, polar and ionizable residues in its inner vestibule and cavity, of which several are thought to play a role in the pH sensitive gating mechanism (35,36), and which are to be contrasted with the mainly hydrophobic inner pore of Kv1.2. To investigate the effects of the hydrophobic, neutral inner cavity of Kv1.2, we carry out a theoretical site-directed mutagenesis and construct the current-voltage-concentration profiles. In the mutant channel, we replace two of the four proline residues at position 407, which is located near the intracellular pore mouth, to charged aspartate residues. The approximate location of the mutated residue is shown by the filled circles in Fig. 2 A.

Referring back to Fig. 2 B (broken line), we see that the mutation makes the inner vestibule much more energetically favorable to permeant ions. The depth of the energy well at $z=10$ Å is increased by 5 kT. More importantly, there appears a pronounced dip in the energy profile at $z=-8$ Å, resulting from the charge of −0.5 e carried by each aspartate residue. With two resident ions in the selectivity filter, a third ion sees an energy well, extending from $z=-20$ to $z=-10$ Å. This well is occupied on average by 0.9 K⁺ ions. With this mutation, the main rate limiting step in the wild-type Kv1.2 channel is eliminated. The third ion in this well move toward the selectivity filter under the influence of an applied potential, and the outermost ion in the selectivity filter is ejected from the channel, so causing a conduction event to take place.

We construct the current-voltage-concentration curves in the P407D mutant channel by performing BD simulations. The results are illustrated in Fig. 5. We see that the mutation has the effect of increasing the conductance fivefold, removing the inward rectification of the channel, and causing the current-concentration curve to saturate much faster, with the half saturation current concentration being 110 mM. This value is slightly higher than the experimentally determined values for other potassium channels (37,38) and is somewhat lower than that determined from KcsA using BD simulations (39). The conductance at ±100 mV is 88 pS, corresponding to that observed experimentally from KcsA. We surmise that adding negatively charged residues to the intracellular entrance removes the barrier to a third ion entering the pore from the intracellular side, which is a necessary step for conduction to take place. The lowering of the barrier leads to the increased conductance. The usual presence of an ion in the inner vestibule also accounts for the rapid saturation of current with concentration.

Figure 5.

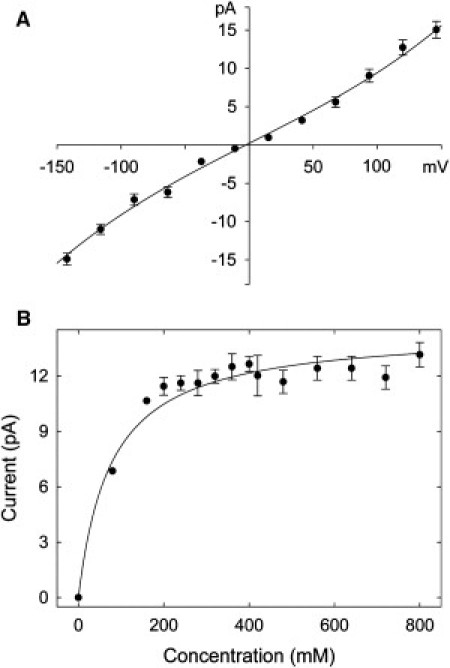
Current-voltage and current-concentration relationships obtained after the proline residue at position 407 was replaced with aspartate in two out of the four monomers.

Although BD, being an implicit solvent model, will not excel at modeling hydration effects, hydrogen bonding, and the like, we are mainly concerned with the movement of very small, highly charged particles (ions) through narrow pores, where multi-ion electrostatics appear to play the dominant role. Our model accordingly concentrates on modeling this aspect of the physics in a sophisticated manner. Other effects are to some extent incorporated in a phenomenological manner—for example, the microscopic details of frictional effects in the channel (40) are incorporated into the diffusion coefficients inside the pore, and the details of the water structure inside the channel are incorporated into the choice of $\epsilon =60$ for the dielectric constant that optimizes the conductance to experimental data (25). The usefulness of this approach, both as a predictive model and a means of elucidating the essential physics of ion permeation, is demonstrated by previous success in reproducing and elucidating the conduction of ions through various channels (9,29,41,42).

Toxin binding from MD

We first consider the equilibration of the system containing the channel, lipids, water, and ions. After 10 ns, the unit cell has a final size of 90 Å × 90 Å × 100 Å. The channel structure is stable throughout the simulation. The time-averaged backbone root mean-square deviation (RMSD) for the entire channel is 0.94 Å. The selectivity filter (residues 374–377) has an average RMSD of just 0.6 Å, and importantly the glutamate oxygens face the pore for the entire simulation. The extracellular loops (residues 351–360) are far more mobile, with an average RMSD of 2.1 Å. The pore K⁺ ions, which were initially placed in binding positions S0 (just above Tyr-377), S2 (between Val-375 and Gly-376), and S4 (between Thr-374 and Thr-373), are stable throughout the equilibration, a result that is compatible with previous studies (27,30,31). The final equilibrated system is shown in Fig. 6, A and B, showing three K⁺ ions in positions S0, S2, S4, and water ions in positions S1 and S3.

The equilibrated system is then used as a starting point for constructing umbrella sampling simulations of ChTX binding to the pore. In addition, a further unconstrained run is performed, with the ChTX molecule placed in binding position with Lys-27 just entering the pore.

We first describe the results from this unconstrained run. Fig. 6 C shows the results after 10 ns of simulation time. During the simulation, Lys-27 of ChTX quickly enters the pore and stays there due to a strong electrostatic attraction from the carbonyl oxygens of Tyr-377 that line the entrance to the pore as well as the ring of four Asp-379 residues that surround the outer mouth of the pore; this is what actually blocks conduction through the ion channel (see Fig. 6 C). Arg-25 of ChTX is seen to make a more or less permanent salt bridge with Asp-27 in the channel (Fig. 6 D). Arg-34 makes and breaks periodic contact with Asp-379 (Fig. 6 B). Although ChTX Lys-31 remains within a few ångströms of Asp-355 (Fig. 6 A), it does not make contact and no hydrogen bonds or salt bridges are formed. Fig. 7 shows the radial pair distribution function between the contact atoms HH12 atom of ChTX Arg-25 and the OC atom of Asp-379, and between the HH11 atom of ChTX Arg-34 and O of Asp-379; the former is seen to spend all of its time in close contact, whereas the latter frequently breaks contact.

Figure 7.

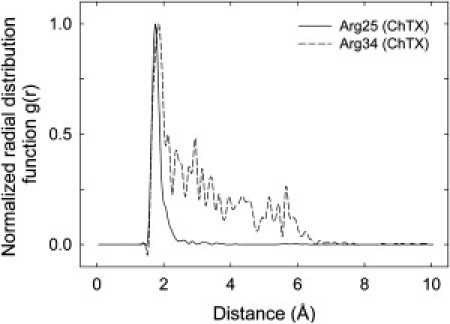
Radial pair distribution functions showing the probability distribution $g\left(r\right)$ of two atoms lying at a given radius r for contacts between ChTX and the channel. Both curves have been normalized to have a maximum value of one. The solid line shows $g\left(r\right)$ between the HH12 atom of ChTX Arg-25 and the OC atom of Asp-379, and the broken line is $g\left(r\right)$ between the HH11 atom of ChTX Arg-34 and O of Asp-379.

These results are consistent with the findings of Park and Miller (11), who investigated the effects of mutating the charged residues on the ChTX molecule to neutral glutamine residues. They reported a large effect for the mutations involving Arg-25, Lys-27, and Arg-34. The largest attenuation of block was seen for the Lys-27 mutation, followed by Arg-25, Arg-34, and Lys-31 in that order; these relative strengths of attenuation are also consistent with our observations of the strength of binding between the various residues as described previously. The effect of shortening the pore blocking lysine (Lys-27) while retaining its charge has also been investigated experimentally (15); interestingly, the blocker is still seen to bind strongly to the pore for the modified toxins.

To derive the PMF, the first 2 ns of each window are discarded from the analysis to let the system properly equilibrate. A total of 10 ns, including this equilibration time, are used for each window. The PMF is shown in Fig. 8. The well depth is ∼19 kT. The kink at z = 28 Å occurs as the protein unbinds from the pore. As this unbinding occurs, the protein experiences large forces and one must be careful to maintain good sampling for all positions z; we did so by adding extra umbrella sampling windows and adding windows with a larger constraint force of 15 kcal/mol Ų. After these windows had been added, we obtained reasonable sampling for all values of z. To test the convergence of the PMF, we derive separate PMFs for times between 2 and 6 ns and between 6 and 10 ns. The results are also shown in Fig. 8; the curves agree to within a couple of kT indicating a reasonable level of convergence on the timescales tested.

Figure 8.

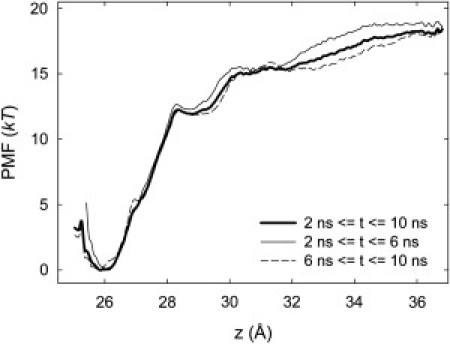
PMF for ChTX binding to Kv1.2.

To relate the PMF to the dissociation constant K_d, we note that K_d is the free toxin concentration at which the binding probability will be 1/2. The toxin is constrained to lie within a cylinder of radius R = 8 Å aligned along the z -axis, so that if we are far from the channel, we can calculate the binding probability according to the usual relation as

$$K_{\mathrm{d}}^{-1}=1000\pi R^2{N}_{\mathrm{A}}\underset{z_1}{\overset{z_2}{\int }}\exp \left(-W\left(z\right)/kT\right)dz,$$ (1)

where z₁ and z₂ give the limits of the binding site, $W\left(z\right)$is the one-dimensional PMF, with the zero point of energy set to be zero in the bulk, N_A is Avagadro's number, k is Boltzmann's constant, and T is the temperature. The factor of $1000N_{\mathrm{A}}$ is a conversion from m³ to L/mol. For the PMF curve derived here, we arrive at a value of $K_{\mathrm{d}}\approx$ 57 nM, which is in reasonable agreement with experimental values, which lie in the 10–30 nM range (7,43).

Conclusions

We have used both an improved BD code and MD to model the ion permeation and susceptibility to blocking by the charybdotoxin of the Kv1.2 channel. On the basis of the crystal structure of the channel, we have constructed a BD model of the channel that exhibits conduction that is compatible with the existing permeation data on several fronts. The channel is inward rectifying, has a conductance of 20 pS at 320 mM, and saturates relatively slowly with increasing ion concentration. We contrast this to the KcsA channel, which shows a greater conductance and no inward rectification. To examine how the mainly hydrophobic and neutral inner vestibule can help to explain these differences in permeation, we have explored the effect of mutating a neutral proline residue lying near the entrance to the inner vestibule to a charged aspartate residue. The mutated channel shows a fivefold increase in conductance (putting it closer to the range of KcsA), is no longer inward rectifying, and shows a faster saturation of current with increasing concentration.

We have also used MD simulations to explore the block of this channel by the charybdotoxin peptide. Our results indicate that the toxin binds in a manner that agrees with existing experimental mutation studies. We have derived a PMF for the binding/unbinding of the charybdotoxin molecule from the channel, and find a binding constant that agrees reasonably well with experimental values.

We have therefore been able to develop a computational model of the Kv1.2 channel and show that by using both Brownian and molecular dynamics we are able to match a variety of experimental data and have the ability to explore various what-if scenarios. This model should be valuable in the future, both as a benchmark for developing homology models of other voltage-gated potassium channels, as a means to test novel blockers, and as a starting point for other theoretical investigations, including the development of rigid body BD simulations, on which we are currently working.