Intermembrane Docking Reactions Are Regulated by Membrane Curvature

Abstract

The polymorphism of eukaryotic cellular membranes is a tightly regulated and well-conserved phenotype. Recent data have revealed important regulatory roles of membrane curvature on the spatio-temporal localization of proteins and in membrane fusion. Here we quantified the influence of membrane curvature on the efficiency of intermembrane docking reactions. Using fluorescence microscopy, we monitored the docking of single vesicle–vesicle pairs of different diameter (30–200 nm) and therefore curvature, as mediated by neuronal soluble N-ethylmaleimide-sensitive factor attachment protein receptors (SNAREs) and streptavidin-biotin. Surprisingly, the intermembrane docking efficiency exhibited an ∼30–60 fold enhancement as a function of curvature. In comparison, synaptotagmin and calcium accelerate SNARE-mediated fusion in vitro by a factor of 2–10. To explain this finding, we formulated a biophysical model. On the basis of our findings, we propose that membrane curvature can regulate intermembrane tethering reactions and consequently any downstream process, including the fusion of vesicles and possibly viruses with their target membranes.

Introduction

The process of vesicle docking on other membranes is a vital biological reaction because it precedes all membrane fusion events. Thus, any factors that modulate the docking reaction will de facto propagate to downstream processes such as membrane trafficking or neurotransmission. Because systematic variation of the experimental factors that affect vesicle docking and fusion is challenging in cell-based assays, investigators have devised a wealth of in vitro assays to dissect the mechanism of membrane fusion (1,2). In the majority of in vitro studies of intermembrane reactions, researchers relied on ensemble-based measurements in which two distinct populations of fusogenic vesicles were mixed, and subsequently monitored the onset of the fusion reaction by applying time-lapse spectroscopy (e.g., fluorescence dequenching or Förster resonance energy transfer) of the intensity signal (3–5). Despite its merits, this approach is limited to monitoring only the end-point of the reaction, i.e., membrane fusion. Consequently, information regarding the initial docking stage is inevitably lost, which renders interpretation of a kinetic curve less straightforward (for example, did the experimental variable affect only the docking step or the fusion step, or both?).

To overcome this challenge, investigators devised a new generation of experiments that, in contrast to ensemble measurements, allow them to study single vesicles directly by applying fluorescence microscopy (6–10). Docking and fusion can be monitored independently, thus enabling a more detailed understanding of the complete intermembrane reaction pathway. For example, it was found that neuronal synaptotagmin-1 (syt), a soluble N-ethylmaleimide-sensitive factor attachment protein receptor (SNARE)-interaction partner, influenced both docking and fusion in a calcium-dependent manner (6). So far, researchers have focused their attention on reproducing and refining the results from the ensemble-based fusion assays, thus resolving the mechanics of membrane fusion to an unparalleled extent but leaving the mechanics of docking unresolved.

Here we present a biophysical model (along with data in support of the model) that describes the vesicle-docking process in detail and reveals a substantial energetic barrier that exclusively depends on membrane shape. We employed time-resolved fluorescence microscopy to monitor the kinetics of single small unilamellar vesicles (SUVs) undergoing docking on apposed membranes of different geometries. We measured the shape of the apposing membranes with a precision of ∼5 nm from their fluorescence intensity signal (11–14), which enabled us to correlate the SUV docking kinetics with membrane curvature. We measured the reaction kinetics as a function of membrane curvature radius for two distinct docking-mediators (receptor/ligand), NeutrAvidin (NAv)/biotin and neuronal SNAREs, both of which exhibit size-dependent docking. We found that, depending on the intermembrane geometry, the docking efficiency could be increased up to 60 times for otherwise chemically identical vesicles.

Up to now, the putative regulatory roles of membrane curvature in lipid (15) and protein (16) sorting, as well as membrane fusion efficiency (17), have been rationalized by its influence on intrabilayer structure. In this work, we show how this curvature also modulates the long-range interactions between membranes. The curvature-dependent docking kinetics we documented originates from the curvature dependence of both long-range repulsive intermembrane forces and receptor/ligand membrane abundance. The dramatic influence of membrane curvature on docking kinetics even surpasses the response of protein-mediated membrane fusion in vitro, i.e., a 2–10-fold acceleration of fusion in the presence of synaptotagmin/Ca²⁺ (18–20). This led us to hypothesize that membrane curvature may be relevant in vivo, where, for example, vesicles and organelles of different sizes or shapes may exhibit different docking curvature preferences, thus imparting an additional layer of regulation in the efficiency of vesicle fusion.

Materials and Methods

Vesicle preparation

We prepared SUVs by applying the thin-film rehydration technique. Lipids dissolved in chloroform were mixed in the desired ratio, followed by evaporation of the solvent under nitrogen flow, thus producing a thin lipid film on the side of the glass vessel. The film was stored in vacuum for 2 h to remove residual solvent and then gently rehydrated in the appropriate buffer to a total lipid concentration of 1.0 g/l to form a vesicle suspension. The suspension was thoroughly vortexed and subjected to five freeze/thaw cycles before it was extruded through polycarbonate membranes with a pore diameter of 50 nm (SUV₅₀ or SUV_SLB; see Table S1 in the Supporting Material) or 200 nm (SUV₂₀₀; Table S1) via a pressurized extrusion device (Northern Lipids, Burnaby, British Columbia, Canada). Details about the SNARE-reconstitution protocol and lipid compositions can be found in the Supporting Material and Table S2.

Microscopy

All fluorescence micrographs were acquired with an inverted confocal microscope (TCS SP5; Leica, Solms, Germany) with an oil immersion objective HCX PL APO, ×100 magnification, and numerical aperture 1.4. Images were typically acquired at a resolution of 1024 × 1024 pixels, physical pixel size of 60 × 60 nm², and a temporal resolution of 0.5 frame/s. Laser light wavelengths of 458 nm, 543 nm, and 633 nm were used to excite vesicles labeled with DiO, DiI, and DiD, respectively. The emitted fluorescence signal was collected with photomultiplier tubes. We measured the axial point-spread function of the objective by operating the microscope in reflection mode, and used it to calibrate the SUV size and NAv density.

For additional information about the materials and experimental methods used, see the Supporting Material.

Theory

Biophysical model of SUV docking

For simplicity, we model the docking process as two distinct steps: 1), a SUV is brought into proximity to its complementary surface (here defined as the binding distance δ); and 2), tether complexes are formed upon contact, as sketched in Fig. 1 A.

Figure 1.

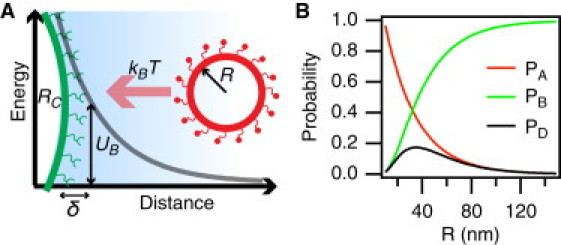
Impact of membrane curvature on SUV docking. (A) A sketch illustrating the docking process. An SUV from the bulk under Brownian motion probes the potential energy landscape of the immobilized docking partner. (B) The two dominant contributions to the docking efficiency (black) are depicted as a function of the SUV radius. P_A and P_B are plotted as red and green lines, respectively. Curves were constructed with the following parameters: R_C = inf., δ = 2 nm, A_CS = 2 nm², N₀ = 2, [Na⁺] = 100 mM, ρ_L = 1.0 mol %, and ρ_R = 10.0 mol% (see also Table S3). The membrane charge was set to 40.0 and 10.0 mol % of negatively charged lipids, corresponding to surface potentials of 204 mV and 51 mV, respectively.

Intermembrane proximity

Due to a variety of intermembrane forces (21), there is an energy cost associated with bringing a SUV close to any other membrane surface. The three most prominent interaction potentials are the hydration repulsion (U_H) (22), the van der Waals attraction (U_V) (23), and the electrostatic double-layer repulsion (U_E) (24). Evaluating the sum of the three potentials at the binding distance δ provides the total energy barrier (U_B) associated with bringing two curved membranes into apposition, which in turn provides the probability to surmount this barrier (P_A) only by thermal motion, i.e.,

$$P_A=\exp \left(-\frac{U_H\left(\delta \right)+U_V\left(\delta \right)+U_E\left(\delta \right)}{k_{\text{B}}T}\right)=\exp \left(-\frac{U_B}{k_{\text{B}}T}\right),$$ (1)

where k_B and T are the Boltzmann's constant and the absolute temperature, respectively. Functional expressions for U_H, U_V, and U_E are provided below. For the hydration repulsion (U_H) we have (25):

$$U_H\left(\delta \right)=2\pi B{\lambda }_H\frac{R{R}_C}{R+R_C}\exp \left(-\frac{\delta }{{\lambda }_H}\right),$$ (2)

where B and λ_H are two phenomenological constants that describe the potential energy profile (Table S3). The van der Waals attractive force exhibits a longer interaction range than the hydration repulsion, and for a pair of vesicles the interaction energy (U_V) is given as (23):

$$U_V\left(\delta \right)=-\frac{A_H\left(\delta \right)}{6}\left[\frac{R{R}_C}{R+R_C}\left(\frac{1}{\delta +2t}-\frac{1}{\delta +t}+\frac{1}{\delta }\right)-\text{ln}\left(\frac{\delta \left(\delta 2t\right)}{{\left(\delta +t\right)}^2}\right)\right],$$ (3)

where t is the bilayer thickness and A_H is the nonretarded Hamaker constant given as (21):

$$A_H\left(\delta \right)=2\kappa \delta A_0\exp \left(-2\kappa \delta \right)+A_1,$$ (4)

where κ is the inverse Debye-screening length, and A₀ and A₁ are the zero-frequency and dispersion contribution to the Hamaker constant, respectively. Lastly, the electrostatic double-layer repulsion (U_E) between lipid bilayers that possess charged headgroups assumes the following profile (24):

$$U_E\left(\delta \right)=\frac{\epsilon {\epsilon }_{0}R{R}_C}{4\left(R+R_C\right)}\left(2\Psi {\Psi }_C\text{ln}\left(\frac{1+\exp \left(-\kappa \delta \right)}{1-\exp \left(-\kappa \delta \right)}\right)+\left({\Psi }^2+{\Psi }_C^2\right)\text{ln}\left(1-\exp \left(-\kappa \delta \right)\right)\right),$$ (5)

where Ψ and Ψ_C represent the surface potentials of the two apposing membranes, _e is the dielectric constant of the buffer, and _e0 is the permittivity of vacuum. The surface potentials are calculated as $\epsilon =2q\chi /A_{LH}\epsilon {\epsilon }_0\kappa$, where q is the electronic charge, ε₀ is the molar fraction of charged lipid in the membrane, and A_LH is the lipid headgroup area.

The expression for P_A contains parameters relating to all external environmental factors (e.g., buffer ionic strength, temperature, and membrane composition), but of importance, all of the terms carry an intrinsic size-dependent prefactor $\left(R{R}_C/\left(R+R_C\right)\right)$ that originates from the Derjaguin approximation. In Fig. 1 B we plot P_A for a range of SUVs undergoing docking onto a planar substrate-supported lipid bilayer (SLB; i.e., R_C = ∞) under our experimental conditions. It can be seen that P_A is a monotonously decreasing function of R, mainly due to the contribution from U_E.

Bond formation

We now turn to calculating the probability to form bonds (P_B) upon contact. In contrast to P_A, P_B does not depend on environmental parameters but on intrinsic molecular properties that govern the binding process. Here we use one characteristic parameter, the binding cross section (A_CS), to exclusively determine binding efficiency. We define A_CS in terms of the binding probability (P_R,L) of a single receptor/ligand pair. If the pair occupies an area A < A_CS, then a bond will be formed with P_R,L = 1; otherwise, if A > A_CS, then P_R,L = A_CS /A. Using this definition, we can model the bond-formation process as a random process wherein N_R receptors attempt to bind to N_L ligands with P_R,L chance to succeed per bond.

From geometry we arrive at a closed expression for the contact area (see sketch in Fig. 2 A):

$$A_C=\pi R_{CA}^2=\pi {\left(R+\delta \right)}^2{\sin }^2\left(\arccos \left(\frac{{\left(R+\delta \right)}^2+R^2+2R\left(R_C+\delta \right)}{2\left(R+\delta \right)\left(R+R_C+\delta \right)}\right)\right).$$ (6)

Figure 2.

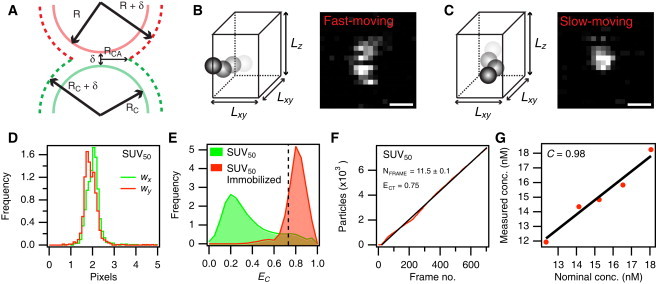
Quantification of SUV concentration. (A) Sketch of the contact area between two apposing SUVs. The contact area is defined by the circle of radius R_CA, which lies in a plane perpendicular to the center-to-center line between the SUVs. (B and C) Sketch of a diffusing particle (B) escaping and (C) remaining inside a rectangular box during the microscope acquisition time of a single particle. The corresponding micrographs are shown to illustrate how the eccentricity values of the particles are changed by their movement. Scale bars are 300 nm. (D) Distribution of w_x and w_y obtained from a calibration sample of the immobilized SUV₅₀ population. The discrepancy between widths along the x- and y-axes is due to a minor aberration of the microscope objective. (E) Distribution of E_C-values obtained from a diffusing SUV₅₀ population (green) and the same population, but immobilized (red). The dashed line indicates the eccentricity threshold applied to all experiments, i.e., E_CT = 0.75. The fraction of missed detections (F_MD) corresponds to the part of the red curve with E_C < E_CT. (F) Accumulated number of SUVs diffusing inside the field of view during an experiment. The SUVs were selected to exhibit eccentricity values greater than E_CT. The black line indicates a linear fit to the curve with slope N_FRAME. (G) Correlation between the measured concentration of colloidal beads with R = 18 nm. The Pearson sample correlation coefficient (C) was calculated to be 0.98.

For the limiting case of an SUV in contact with an SLB, the area is $A_C=\pi \delta \left(2R+\delta \right)$. We denote the number of available tether molecules in the apposing membrane as $N_{R,L}={\rho }_{R,L}{A}_C$, where ${\rho }_{R,L}$ is the membrane density and subscripts R and L denote the receptor and ligand, respectively. As shown in the Supporting Material, P_B is calculated as

$$P_B=1-\frac{1}{2}\lfloor \frac{\text{erf}\left(\frac{N_0-x_R}{\sqrt{2}{\sigma }_R}\right)-\text{erf}\left(-\frac{x_R}{\sqrt{2}{\sigma }_R}\right)}{1-\text{erf}\left(-\frac{x_R}{\sqrt{2}{\sigma }_R}\right)}+\frac{\text{erf}\left(\frac{N_0-x_L}{\sqrt{2}{\sigma }_L}\right)-\text{erf}\left(-\frac{x_L}{\sqrt{2}{\sigma }_L}\right)}{1-\text{erf}\left(-\frac{x_L}{\sqrt{2}{\sigma }_L}\right)}\rfloor ,$$ (7)

where x_R,L = N_R,L P_L,R = A_Cρ_Rρ_LA_CS and ${\sigma }_{R,L}=\sqrt{x_{R,L}\left(1-{\rho }_{L,R}{A}_{CS}\right)}$. In contrast to P_A, then P_B is an increasing function of R (Fig. 1 B). This is because greater radii result in greater contact areas, thus increasing the likelihood that at least N₀ bonds will form upon contact. The docking probability (P_D) is now found as the joint probability that a vesicle will approach its complementary membrane at the binding distance (P_A) and simultaneously form minimum N₀ bonds upon contact (P_B), i.e.,

$$P_D\left(R,R_C\right)=P_A\left(R,R_C\right)\times P_B\left(R,R_C\right).$$ (8)

Because P_D is a composite of an increasing and a decreasing function, it experiences a global maximum value, suggesting a particular set of R and R_C to be the best-suited geometry for efficient docking (Fig. 1 B). We find it interesting to speculate that this biophysical effect might provide a passive targeting mechanism in vivo, and could explain the fact that trafficking vesicles exhibit characteristic diameters depending on which pathway they are upholding (26,27).

Measuring SUV docking probabilities

We now describe how one can directly obtain values for P_D from particle-tracking experiments for freely diffusing SUVs docking onto immobilized SUVs and an SLB. We start by noting that the number of diffusing SUVs that are impinging onto the surface of an immobilized vesicle (N_DIF) is given as (28,29):

$$N_{DIF}=2\pi D\left(R+R_C\right)C_{V}t,$$ (9)

where D is the diffusion coefficient of the SUV, R_C is the radius of the diffusing SUV, R is the radius of the immobilized SUV, C_V is the bulk SUV concentration, and t is time elapsed. A similar expression can be obtained for an SLB (see Supporting Material):

$$N_{DIF}=3D{A}_{SLB}{C}_V^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}t,$$ (10)

where A_SLB is the area of the SLB. The docking probability is inversely proportional to N_DIF, i.e., a high P_D-value leads to a short time elapsed before docking, whereas a low P_D-value gives rise to an extended time duration before docking. For a docking experiment, we collect two observables: the total number of docked SUVs (N_D) and the docking time duration. Our goal is now to convert these observables to the docking probability. We start by considering the case of SUV/SLB docking.

SUV/SLB

Initially, we assume that the SUV population is monodisperse with radius R. Our experimental observables are the total number of SUVs docked to the SLB (N_D) and the experimental time duration (t). The docking probability is obtained by dividing N_D with the total number of SUVs that impinge onto the SLB during the experiment. Thus, using Eq. 10, we arrive at

$$P_D=\frac{N_D}{N_{DIF}}=\frac{N_D}{3D{A}_{SLB}{C}_V^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}t}.$$ (11)

We now adapt a more realistic scenario by replacing the monodisperse population with a polydisperse one. With f(R) we denote the normalized size distribution function of the SUV population and can thus modify Eq. 10 to obtain N_DIF as a function of R:

$$N_{DIF}\left(R\right)=3D{A}_{SLB}{\left(f\left(R\right){\overline{C}}_V\right)}^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}t,$$ (12)

where ${\overline{C}}_V$ indicates the average bulk concentration of SUVs. Thus, we can immediately obtain P_D as a function of R, applying Eqs. 11 and 12:

$$P_D\left(R\right)=\frac{N_D\left(R\right)}{N_{DIF}\left(R\right)}=\frac{N_D\left(R\right)}{3D{A}_{SLB}{\left(f\left(R\right){\overline{C}}_V\right)}^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}t}.$$ (13)

SUV/SUV

The SUV/SUV scenario differs from the SUV/SLB experiment in one important aspect: Each time a diffusing SUV docks onto an immobilized vesicle, the local membrane environment is perturbed, thus creating correlations between successive docking events. For example, P_D for the first docking event is different from that for the next event, because a smaller area of the immobilized SUV's membrane is accessible for docking and the electrostatic potential is changed by the presence of the previous docked SUV. Hence, to circumvent this experimental challenge, we decided to only record the time duration to the first docking event (t₁) for each immobilized SUV. Thus, the experimental observables in this case are t₁, N_D, and the total number of immobilized SUVs that are available for docking (N_I). As a first approximation, we can obtain P_D simply by calculating the average docking probability of all immobilized SUVs:

$$P_D=\frac{1}{N_I}\sum _{i=1}^{N_I}\frac{1}{N_{DIF}^i}=\frac{1}{N_I}\sum _{i=1}^{N_I}\frac{1}{2\pi D\left(R+R_C\right)C_V{t}_1^i}.$$ (14)

Here, the index i runs over all immobilized SUVs that experienced a docking event during the experimental time frame. However, we chose to apply a more accurate maximum likelihood (ML) approach to also take into account the SUVs on the sample, which did not experience a docking event due to the finite time span of the experiment.

To implement the ML approach, we assume the docking to be a random process, and thus the probability to observe a docking after t₁ is $P_D{\left(1-P_D\right)}^{N_{DIF}\left(t_1\right)-1}$. Conversely, the probability to observe an immobilized SUV, which did not experience docking during the experiment, is ${\left(1-P_D\right)}^{N_{DIF}\left(T\right)}$. Here, N_DIF(T) indicates the total number of unsuccessful docking attempts that impinge on the immobilized SUV during the experimental time duration T (cf. Eq. 9). If we consider the entire immobilized population, we can calculate the joint probability (P_J) to observe that particular sequence of docking events:

$$P_J\left(P_D\right)=\prod _{\text{Docked}\text{SUVs}}{P}_D{\left(1-P_D\right)}^{2\pi D\left(R+R_C\right)C_V{t}_1^i-1}\prod _{\text{Non}\mathrm{-}\text{docked}\text{SUVs}}{\left(1-P_D\right)}^{2\pi D\left(R+R_C\right)C_{V}T}.$$ (15)

P_J is a function of P_D, and it is thus straightforward to obtain an accurate value for P_D by plotting P_J from 0 to 1 and locate the maximum, i.e., the P_D-value that maximizes the likelihood of obtaining these particular experimental observables.

Results and Discussion

Online measurements of SUV concentration

To use Eqs. 13 and 15 to measure the docking probabilities, it is necessary to know the bulk concentration of diffusing SUVs. As a first approximation, we could use the nominal value of C_V as estimated from the SUV preparation procedure and the volume of the sample. Nevertheless, due to the extrusion process, significant amounts of lipids are lost during the preparation (i.e., adsorption on surfaces and extrusion filters), and as a result of sample handling, the C_V-values might even differ among identically prepared samples. Furthermore, in the case of SUV/SLB experiments, the docking reaction might be diffusion-limited, thus inducing concentration gradients to build up adjacent to the SLB. For these two reasons, we do not consider it sufficiently accurate to simply estimate C_V based on lipid mass and sample volume. Instead, we developed a scheme to convert the number of detectable diffusing SUVs to C_V-values, thus enabling an online measurement of concentration, while simultaneously recording docking events.

In a typical docking experiment, we consider an SUV to be docked if its center position does not change >5 pixels for three consecutive frames. For each frame, we thus partition all detected particles into two categories: docked and diffusing. If we also know the detection volume (depth of field) of the microscope (V_D), we can calculate C_V as

$$C_V=\frac{N_{FRAME}}{V_D}=\frac{N_{FRAME}}{A_{FW}{L}_Z},$$ (16)

where N_FRAME is the average number of diffusing SUVs per frame. We have replaced V_D with the sum of the field-of-view area (A_FW) and the confocal detection length along the z-axis (L_z). The latter can be evaluated by measuring the microscope point-spread function (see Eq. S9). However, many SUVs diffuse too rapidly to be detectable on a microscope image, and thus we have to modify Eq. 16 to also include the fast-moving particles:

$$C_V=\frac{1}{F_D}\frac{N_{FRAME}}{A_{FW}{L}_Z},$$ (17)

where F_D represents the probability that an SUV will move slowly enough to become detectable. The total amount of SUVs that are present during an exposure is thus N_FRAME/F_D. We can consider slow-moving particles to reside in a rectangular box of height L_z and widths L_xy during the time (t_P) it takes for the confocal microscope to acquire an image of the particle. A fast-moving particle will break out of the imaginary box during the time span t_P and thus appear elongated, as illustrated in Fig. 2, B and C. In the Supporting Material we show that F_D is calculated as

$$F_D={\left(\text{erf}\left({\alpha }_{xy}\right)+\frac{\exp \left(-{\alpha }_{xy}^2\right)-1}{{\alpha }_{xy}\sqrt{\pi }}\right)}^2\times \left(\text{erf}\left(2{\alpha }_z\right)+\frac{\exp \left(-4{\alpha }_z^2\right)-1}{2{\alpha }_z\sqrt{\pi }}\right),$$ (18)

where ${\alpha }_{xy}=L_{xy}/\sqrt{4D{t}_P}$ and ${\alpha }_z=L_z/\sqrt{4D{t}_P}$ are characteristic parameters that relate particle diffusion to the microscope acquisition time.

To calibrate particle motion, we imaged a sample of immobilized vesicles and fitted the intensity distributions of individual particles to 2D Gaussian functions of the following form to obtain the particle eccentricity (E_C):

$$G\left(x,y\right)=I_{BG}+A\exp \left(-\frac{x_R^2}{w_x^2}-\frac{y_R^2}{w_y^2}\right).$$ (19)

Here x_R = (x − x₀) cosθ − (y − y₀) sinθ and y_R = (x − x₀) sinθ − (y − y₀) cosθ, where x₀ and y₀ are the particle center coordinates and θ is the angle of rotation relative to the x-axis. I_BG is the background intensity, A is the signal amplitude, and w_x and w_y are the widths along the x- and y-axis, respectively. We thus define eccentricity as the ratio of y-width to the x-width, i.e., E_C = w_y/w_x (see Fig. 2 D).

Next, we imaged and extracted E_C-values for a sample of freely diffusing vesicles. Not surprisingly, the diffusing vesicles exhibited lower E_C-values than the immobilized ones (Fig. 2 E). We set a threshold eccentricity value (E_CT) of 0.75 to distinguish between fast- and slow-moving particles. In this way, we consider a slow-moving (detectable) particle to exhibit an E_C-value > E_CT, whereas a fast-moving (nondetectable) particle exhibits E_C-values < E_CT. The result of this classification is shown in Fig. 2 F as a graph of the cumulated count of detectable particles for a sequence of fluorescence micrographs. We obtained a value for N_FRAME as the slope of the graph.

However, as shown in Fig. 2 E, even completely immobilized particles can exhibit E_C-values < E_CT due to noise. To correct for this, we introduce the parameter F_MD, which is the fraction of missed detections, i.e., slow-moving particles that due to noise are not detected. F_MD is directly obtained from the E_C distribution of immobilized vesicles by integrating the part of the graph to the left of E_CT. Eq. 17 is thus recast as

$$C_V=\frac{1}{F_D\left(1-F_{MD}\right)}\frac{N_{FRAME}}{A_{FW}{L}_z}.$$ (20)

To validate Eqs. 18 and 20, we prepared five solutions of fluorescence-labeled, 36-nm-diameter colloid beads, for which the particle concentration was known in advance from the manufacturer's specifications. We imaged a reference sample of immobilized beads and also acquired time-lapse micrograph sequences of freely diffusing colloids. Setting an E_CT-value of 0.75 allowed us to extract N_FRAME and calculate F_D, thus evaluating the particle bulk concentration (Fig. 2 G). For the five samples tested, we found a good agreement between the nominal and the measured particle concentration, yielding a Pearson sample correlation coefficient of 0.98.

Quantification of the reaction efficiency for SUV/SUV and SUV/SLB docking

To quantify how nanoscale membrane curvature influenced a docking reaction, we applied two distinct experimental assays involving fluorescence-labeled SUVs, as sketched in Fig. 3, A and B. In one assay, we functionalized SUVs of various sizes (and thus curvatures) with a coat of fluorescence-labeled NAv, and subsequently immobilized them on a polyethylene-glycol-passivated glass substrate. Next, we initiated docking by adding a biotinylated SUV population (SUV₅₀) with a narrow size distribution and average radius of R_C = 28 nm (as obtained from dynamic light scattering). In the second assay, we docked a polydisperse population of biotinylated SUVs (SUV₂₀₀) on an SLB functionalized with NAv. In this way we were able to compare docking reactions between SUVs of various radii (R = 20–150 nm) and another surface of fixed complementary curvature at either R_C = 28 nm or R_C = ∞.

Figure 3.

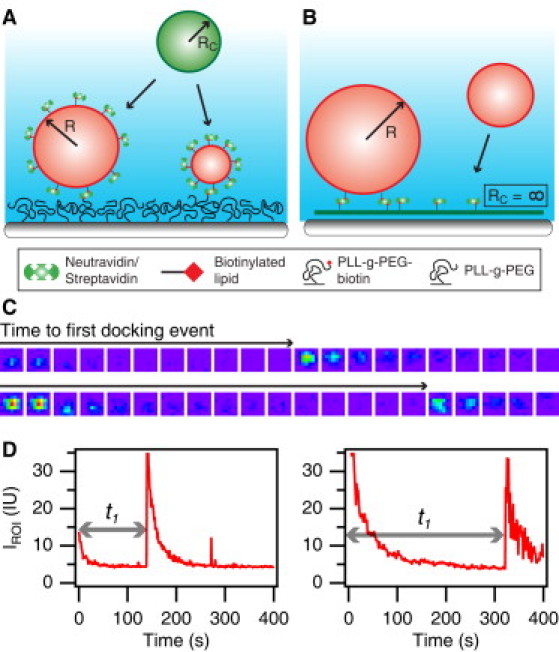
Measurements of single-vesicle-docking kinetics on membranes of variable curvature obtained by time-resolved fluorescence microscopy. (A) Vesicles with a coat of NAv and of various radii were immobilized on a glass substrate functionalized with biotin conjugates of polyethylene glycol. Extruded, monodisperse SUVs with DOPE-biotin included in the membrane were allowed to dock onto their surface-immobilized partners. Surface-attached and diffusing SUVs contained 2.0 mol % of the lipophilic fluorescent probe DiD-C₁₈. (B) Docking reactions between a SLB functionalized with NAv and a polydisperse population of biotinylated diffusing SUVs labeled with DiD-C₁₈. Membranes of fixed curvature (R_C) are labeled in green, and membranes of variable curvature are labeled in red. The red SUV population remained the same in both SUV/SUV and SUV/SLB experiments. (C) False-colored micrograph series after docking events at the site of two immobilized SUVs from the setup in panel A. (D) Time-resolved intensity signal extracted from the micrograph sequences in C showing bleaching of an immobilized SUV and then docking of another SUV from solution after time (t₁), as indicated by an arrow.

We measured the kinetics for docking reactions that took place between two highly curved SUV membranes, as sketched in Fig. 3 A. The low density of immobilized NAv-coated SUVs on the surface enabled us to resolve single vesicles, and thus we were able to follow the docking reaction by monitoring the fluorescence intensity trajectory at the site of individual SUVs, as shown in Fig. 3 C. Initially, the intensity from the membrane label 1,1′-dioctadecyl-3,3,3′,3′-tetramethyl-indodicarbocyanine (DiD-C₁₈) decreased exponentially as a footprint of photobleaching (Fig. 3 D). The moment a docking reaction took place, the DiD-C₁₈ intensity increased abruptly due to the presence of the docked SUV, which subsequently also underwent photobleaching. From the intensity trajectories, we extracted the docking time (t₁), here defined as the time elapsed until the occurrence of the first intensity peak (illustrated with gray arrows in Fig. 3 D).

In analogy to our recently published work (29), we converted the list of t₁-values into the number of unsuccessful docking attempts (N_DIF) before docking. Briefly, we counted the number of detectable diffusing SUVs that appeared during the entire experimental time course (Fig. 4 A) and converted this number to actual concentration (C_V) by applying Eq. 20. For SUV/SUV docking, we obtained the docking efficiency (P_D) from an ML fit to the t₁ list according to Eq. 15 (Fig. 4 B). For SUV/SLB docking, we obtained P_D-values by recording and analyzing micrograph sequences of the docking process (Fig. 4 C), and thus extracted the total number of docked (N_D) SUVs during the experimental time as well as C_V. We resolved both N_DIF and N_D as a function of the SUV radius (Fig. 4, D and E), and thus calculated the docking efficiency as P_D = N_D / N_DIF according to Eq. 13.

Figure 4.

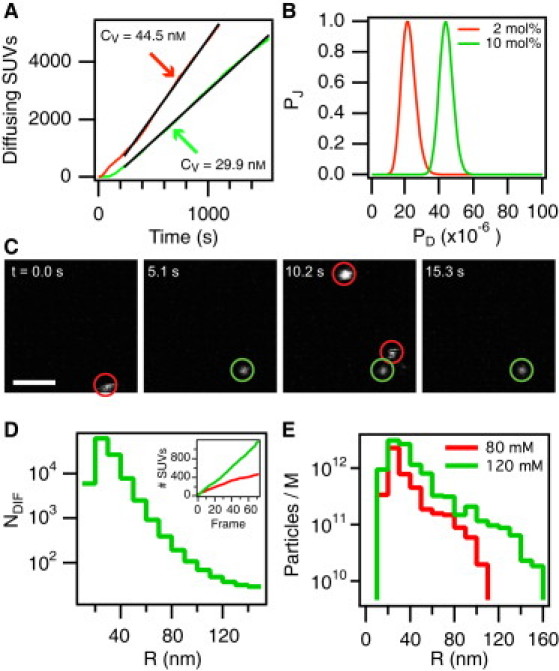
Docking efficiency measured for NAv-coated SUVs. (A) Concentration measurement of single diffusing SUVs. The C_V-values were 44.1 ± 0.1 nM (red line) and 29.8 ± 0.1 nM (green line). Black lines indicate a linear fit to the data. (B) Direct extraction of docking efficiency (P_D) by a global maximum-likelihood fit to the complete set of experiments performed with SUVs displaying 2.0 mol % (red line) or 10 mol % (green line) DOPE-biotin in the membrane. From Eq. 15 we found P_D = (2.2 ± 0.6) × 10⁻⁵ and P_D = (4.4 ± 0.5) × 10⁻⁵ for 2 mol % and 10 mol % DOPE-biotin, respectively. (C) Confocal fluorescence micrograph sequence displaying DiD-C₁₈-stained diffusing biotinylated SUVs docking onto an SLB presenting NAv. Red circles indicate diffusing SUVs probing the SLB interface, and the green circle identifies a successfully docked vesicle. Scale bar is 5.0 μm. (D) Distribution of SUV docking attempts (N_DIF) experienced by the SLB resolved as a function of vesicle radius R. The inset shows the number of diffusing SUVs for two different experiments with [Na⁺] = 80 mM (red) and [Na⁺] = 120 mM (green) corresponding to ${\overline{C}}_V$ = 0.10 nM and ${\overline{C}}_V$ = 0.21 nM, respectively. (E) The size distribution of all SUVs that successfully docked after t = 358 s normalized by the average bulk concentration of SUVs (${\overline{C}}_V$) for direct comparison among experiments. Docking reactions took place in buffers with [Na⁺] = 80 mM (green) and [Na⁺] = 120 mM (red).

Membrane ligand density and electrostatic screening regulates docking efficiency

In Fig. 4 B we compare two SUV/SUV-docking experiments in which we increased the membrane density of 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-(biotinyl) (DOPE-biotin) from 2 to 10 mol %. Not surprisingly, we obtained a corresponding increase from P_D = (2.2 ± 0.6) × 10⁻⁵ to P_D = (4.4 ± 0.5) × 10⁻⁵. In Fig. 4 E we compare two SUV/SLB-docking experiments in which we decreased the counterion concentration of the buffer from 120 mM to 80 mM but otherwise kept all settings identical. Mainly due to the increased electrostatic repulsion in the 80 mM experiment, we observed a consistent decrease in N_D. In particular, large SUVs (R > 120 nm) were not permitted to dock onto the SLB during the experimental time course of ∼10 min. From these four types of experiments, it is evident that both the density of receptors/ligands available in the SUV contact area (A_C) and the potential energy of establishing the intermembrane junction affect the docking efficiency, in qualitative agreement with Eqs. 1 and 7 for P_A and P_B, respectively.

SUV/SLB-docking efficiency depends on membrane curvature

From the data shown in Fig. 4, we can extract the full relationship between SUV docking efficiency and membrane curvature, thus testing the predictions of Eq. 8. For the case of SUV/SLB docking, we calculate P_D(R) simply by dividing the docked SUV size distribution (Fig. 4 E) with the docking-attempt size distribution (Fig. 4 D), i.e., Eq. 13. The resulting docking efficiency profiles are shown in Fig. 5 A for two different buffer ionic strengths. Both P_D(R) profiles exhibit a clear trend of increasing efficiency for larger SUV radii; however, the measured P_D-values are overall smaller for the low ionic strength ([Na⁺] = 80 mM) than for the higher ionic strength ([Na⁺] = 120 mM), consistent with the predicted decrease of the potential energy barrier U_B in Eq. 1.

Figure 5.

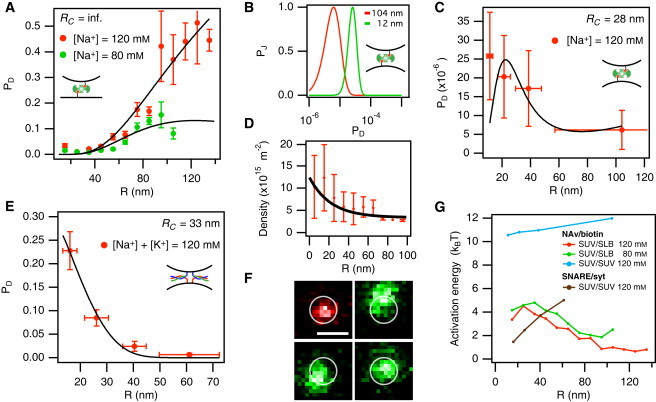
Vesicle-docking reactions are dramatically influenced by membrane curvature. (A) Efficiency profile of a NAv/biotin-mediated SUV/SLB-docking reaction as a function of SUV radius for [Na⁺] = 120 mM (red markers) and [Na⁺] = 80 mM (green markers). Black lines indicate a global fit of the data to Eq. 8 (for input parameters see Table S3). (B) Maximum-likelihood fit to extract P_D for NAv/biotin-mediated SUV/SUV-docking reactions shown for two immobilized SUV subpopulations with average radius 104 nm (red line) and 12 nm (green line). (C) Efficiency profile of a NAv/biotin-mediated SUV/SUV-docking reaction as a function of SUV radius. The black line indicates a plot of Eq. 8 with the values of A_CS and δ obtained from the fits shown in A and with a size-dependent NAv density as obtained from D. (D) Density profile of NAv bound to SUV membranes as a function of SUV radius. (E) Size-dependent efficiency of a SNARE/syt-mediated SUV/SUV-docking reaction. The black line is a fit to Eq. 8. (F) False-color micrograph of an SUV/SUV complex stably docked by the formation of SNARE/syt-complexes. The SUV originating from the bulk solution (green color) diffuses on the membrane surface of the immobilized SUV (red). Scale bar is 500 nm. (G) Energy barriers associated with forming a stable intermembrane junction through docking of SUVs is shown for NAv/biotin-mediated docking on SLB at [Na⁺] = 120 mM (red) and 80 mM (green), and for SUV/SUV docking at [Na⁺] = 120 mM (blue). The curve in black corresponds to SNARE/syt-mediated docking of SUVs.

The feature of increasing P_D-values for larger SUVs suggests that the bond-formation process (P_B) is the rate-limiting step of the docking reaction, i.e., smaller SUVs have less chance to create bonds upon contact. Of interest, by decreasing [Na⁺] to 80 mM, we were able to enhance the electrostatic repulsion and thus observed a maximum in the P_D(R) profile at R = 90 nm, suggesting a transition from bond formation to SUV proximity as the rate-limiting step, i.e., P_A(R > 90 nm) < P_B(R > 90 nm). To gain a more detailed insight into the docking process, we conducted a global fit of the data in Fig. 5 A to Eq. 8 keeping δ, A_CS, and N₀ as the only free parameters. From the global fit we obtained δ = 3.78 ± 0.07 nm, A_CS = 2.8 ± 0.6 nm², and N₀ = 2.7 ± 0.5. The binding distance of 3.78 nm agrees well with published values on the molecular dimensions of streptavidin (30), a homotetramer that is similar in structure to NAv.

For the range of SUVs shown in Fig. 5 A, the contact areas span 400–3600 nm² corresponding to 5–42 NAv tetramers within (Table S3), thus yielding on average 10–84 binding sites available for docking. However, the low A_CS-value of 2.8 nm² corresponds to an optimal density of 0.2 NAv/nm², which is ∼15 times larger than the experimental density of binding sites, thus supporting the notion that bond formation is indeed the rate-limiting step of SUV/SLB docking.

NAv-mediated SUV/SUV-docking efficiency depends on membrane curvature

To further test the predictions of Eq. 8, we constructed a P_D(R) profile for the data on SUV/SUV docking shown in Fig. 4 B. We first partitioned the immobilized population of SUVs into bins depending on their size, and then applied Eq. 15 to each of the four subpopulations (Fig. 5 B). The resulting profile is shown in Fig. 5 C, which shows a consistent decrease in docking efficiency as R increases. Of interest, the overall P_D for a SUV docking with another SUV (R_C = 28 nm) is ∼100,000 times smaller than that for the same SUV docking onto a SLB (R_C = infinite). Our model, which predicted only an ∼1000-fold decrease in docking efficiency, could not immediately explain this large difference. However, in all of our NAv-mediated docking experiments, we simultaneously measured the membrane NAv density using a fluorescence intensity calibration scheme as described previously (12) and in the Supporting Material. In this way, we found that single SUVs bind NAv to a lesser extent than does an SLB (Table S3), most likely due to differences in the membrane composition (i.e., the SLB contained four times less charged lipids than the SUV membrane; Table S1). This difference in electrostatic potential may modulate the interfacial concentration of NAv, resulting in a different membrane density. We also observed that NAv binding to the biotinylated SUV membranes takes place in a mildly (∼3-fold) curvature-dependent manner (Fig. 5 D). By combining Eq. 8 with the measured NAv-density profile, i.e., ρ_R = ρ_R(R), we obtained theoretical P_D-values that matched the magnitude of the experimentally recorded ones (Fig. 5 C, black line) and described the curvature dependence within uncertainties.

The efficiency of SNARE-mediated docking depends on membrane curvature

To investigate a more biologically relevant system, we reconstituted rat neuronal synaptobrevin, syntaxin, and SNAP-25 into SUV membranes. The reconstitution protocol we used is described in detail elsewhere (29,31) and was not changed. We conducted experiments involving docking between surface-immobilized SUVs displaying syntaxin/SNAP-25 and freely diffusing SUVs displaying synaptobrevin. Upon addition of the water-soluble domain of syt and Ca²⁺, SUVs from the bulk successfully docked on their counterparts at the surface, which allowed us to extract the docking times and the corresponding P_D(R) profile shown in Fig. 5 E. Again, we found a strongly size-dependent docking efficiency that exhibited a 34-fold decrease from R = 16 nm to R = 61 nm.

Stable SUV/SUV membrane junctions could only be formed in the presence of syt and Ca²⁺, and were irreversible on an experimental timescale. The docked synaptobrevin-functionalized SUVs that did not undergo immediate fusion were able to execute a random walk on the surface of the immobilized syntaxin/SNAP-25 SUVs (Fig. 5 F), suggesting that the SNARE/syt-complex remained mobile in the membrane even after docking. According to previous studies (9), a single SNARE complex is sufficient to mediate stable docking. This allowed us to set N₀ = 1 and consequently fit the P_D(R) profile in Fig. 5 F to Eq. 8, and thus obtain values for δ and A_CS. Because the syt fragment we used here was previously shown to exhibit size-dependent binding to SUV membranes (31), we used the published density profile of syt (reproduced in Fig. S1 B) to enable the fitting.

The SNARE/syt system yielded a significantly smaller binding distance (δ = 1.8 ± 0.1 nm), as well as a greater binding cross section (A_CS = 60 ± 25 nm²), compared with NAv. The δ-value of 1.8 nm suggests that SNARE/syt-mediated docking is enabled only when the intermembrane separation is comparable to the short axis of the folded SNARE complex (∼1–2 nm) (32). The surprisingly high binding cross section indicates that SNARE/syt assembles 22 times more readily than NAv/biotin, which implies that fast association kinetics dominate the high SNARE-complex binding energy (∼30 k_BT), in contrast to the off-rate controlled binding energy of NAv/biotin.

We find it worthwhile to compare our results with previous bulk experiments by Cypionka et al. (33) on the docking and fusion kinetics of SNARE-functionalized vesicles. In their experiments, the authors compared the docking rate (k_D) between two complementary SUV populations with an average radius of 15 nm with that of two other complementary populations with an average radius of 50 nm. They concluded that the two k_D-values were almost identical, resulting in at least a threefold difference between the corresponding P_D-values due to the threefold greater diffusion of the smaller SUVs. In reality, even carefully extruded SUV preparations exhibit a substantial degree of polydispersity as the extrusion filter pores get larger (13), which can mask any size-dependent effect measured in an ensemble-based assay. However, to enable comparison with our results, we applied our experimentally obtained values of δ and A_CS along with Eq. 8 to calculate P_D (15 nm, 15 nm) and P_D (50 nm, 50 nm), which yielded a three- to fourfold difference depending on the exact electrostatic conditions (e.g., membrane composition and ionic strength). Consequently, our single-vesicle results are in good agreement with the previously published bulk experiments.

As shown in Fig. S2, A–C, we extracted, processed, and replotted data from Grabner et al.'s (34) electrophysiological study of exocytosis in chromaffin cells. Of interest, Fig. S2 C shows an ∼250–450% decrease in exocytic efficiency as the vesicle radius increased. Cell-based assays that cannot measure the biochemical composition of individual native vesicles cannot decouple the contributions of membrane curvature and vesicle composition on the docking and fusion efficiency, and thus cannot establish the origin of the trend underlying the data of Fig. S2 C. However, because this trend is qualitatively similar to our in vitro data on SNAREs (Fig. 5 F), we suggest that it may be an example of rate-limiting, curvature-sensitive docking and its influence on fusion kinetics in vivo.

Comparison of docking mechanisms

We illustrate the differences in docking mechanism among the four different experiments presented in Fig. 5, A, C, and E, by converting the docking efficiency into activation energy (E_A), which indicates the minimum energy required to dock, where

$$E_A=-k_{\mathrm{B}}T\text{ln}\left(P_D\right)=-k_{\mathrm{B}}T\left(\text{ln}\left(P_A\right)+\text{ln}\left(P_B\right)\right).$$ (21)

The E_A-values are shown in Fig. 5 G and span a wide range from ∼1–12 k_BT. E_A is a composite of the repulsive potential experienced by the two opposing surfaces and the combinatorial process of initiating receptor/ligand complexation. NAv/biotin-mediated SUV/SUV-docking reactions are least probable and thus attain the highest E_A-value, which is entirely due to the small number of available binding sites in the contact area combined with the low A_CS-value. It is worth noting that due to the differences in NAv density on SUV and SLB membranes, the E_A-values for SUV/SUV docking do not asymptotically approach (for R → ∞) those of SUV/SLB docking. For SNARE/syt-mediated docking, the overall activation energy is low but exhibits a substantial increase with SUV size, which we mainly attribute to the size-dependent syt density.

Conclusion

The shape of cellular membranes is a tightly regulated and well-conserved phenotype; however, to date, investigators have largely ignored the effects of membrane shape/curvature on biological functions that make this shape so critical for sustaining life. Recent data revealed putative regulatory roles of membrane curvature in lipid (15) and protein (16) sorting, as well as membrane fusion efficiency (17). Here we show that apart from influencing intrabilayer structure, curvature causes dramatic changes in the long-range interactions between membranes and thus in the membrane docking kinetics. The magnitude of the dependence of docking rates on curvature that we observed in purified in vitro systems (up to 5000% and energy barriers up to 12 k_BT; Fig. 5, A–E) suggests that this mechanism may play an important, heretofore unrecognized role in cellular biology. As shown here, however, docking rates can in principle either increase or decrease with curvature depending on a number of molecular parameters (e.g., tether density, tether length, and surface charge), allowing for diversity and adaptability of this mechanism. Most importantly, long-range, membrane-shape-induced effects that can control the yield of intermembrane tethering reactions would de facto propagate to numerous downstream biological processes, including viral infection, membrane trafficking, neurotransmitter release at the synapse, and even juxtacrine signaling (35).