Active Trans-Plasma Membrane Water Cycling in Yeast Is Revealed by NMR

Abstract

Plasma membrane water transport is a crucial cellular phenomenon. Net water movement in response to an osmotic gradient changes cell volume. Steady-state exchange of water molecules, with no net flux or volume change, occurs by passive diffusion through the phospholipid bilayer and passage through membrane proteins. The hypothesis is tested that plasma membrane water exchange also correlates with ATP-driven membrane transport activity in yeast (Saccharomyces cerevisiae). Longitudinal ¹H₂O NMR relaxation time constant (T₁) values were measured in yeast suspensions containing extracellular relaxation reagent. Two-site-exchange analysis quantified the reversible exchange kinetics as the mean intracellular water lifetime (τ_i), where τ_i⁻¹ is the pseudo-first-order rate constant for water efflux. To modulate cellular ATP, yeast suspensions were bubbled with 95%O₂/5%CO₂ (O₂) or 95%N₂/5%CO₂ (N₂). ATP was high during O₂, and τ_i⁻¹ was 3.1 s⁻¹ at 25°C. After changing to N₂, ATP decreased and τ_i⁻¹ was 1.8 s⁻¹. The principal active yeast ion transport protein is the plasma membrane H⁺-ATPase. Studies using the H⁺-ATPase inhibitor ebselen or a yeast genetic strain with reduced H⁺-ATPase found reduced τ_i⁻¹, notwithstanding high ATP. Steady-state water exchange correlates with H⁺-ATPase activity. At volume steady state, water is cycling across the plasma membrane in response to metabolic transport activity.

Introduction

Water transport across the plasma membrane is crucial to cell function. This is often characterized as a pseudo-first-order process, measured by the permeability coefficient (P), an intrinsic membrane property. The osmotic coefficient (P_f) is measured when net transmembrane water movement responds to an extra- and intracellular water chemical potential difference. Cell and tissue osmotic water fluxes and volume changes are measured using several techniques, a number of them optical (1). The proteins that mediate and the molecular mechanisms that regulate water transport are of great interest. A second process, steady-state transmembrane water molecule exchange (no net water flux or volume change), occurs even in the absence of osmotic gradients. This is characterized by the diffusional water permeability coefficient (P_d). Steady-state exchange occurs by passive diffusion through the phospholipid bilayer and membrane proteins.

Transmembrane exchange was originally detected in cell suspensions using isotopically labeled water (2). NMR approaches have also long been used to measure reversible water-exchange kinetics in cell suspensions. Generally a paramagnetic relaxation reagent (RR_e) alters the extracellular ¹H₂O relaxation time constant (T₁ or T₂). The T₂ method was introduced by Conlon and Outhred (3) and has been widely employed (4). Longitudinal magnetic resonance relaxography (MRR) distinguishes intra- (¹H₂O_i) and extracellular (¹H₂O_e) signals by their T₁ difference (¹H₂O T₁ MRR/RR_e) (5). These data can yield accurate intra- and extracellular mole fractions (p_i and p_e) and the mean intracellular water molecule lifetime (τ_i) if equilibrium transmembrane water exchange kinetics are quantified with two-site exchange (2SX) analysis (5–7). The inverse (τ_i⁻¹) is the equilibrium water efflux pseudo-first-order rate constant (k_ie). Mass balance gives the influx rate constant (k_ei). To aid the reader, Table 1 lists the symbols and abbreviations.

Table 1.

Definition of symbols and abbreviations

Abbreviations/acronyms	Definition
MRS	Magnetic resonance spectroscopy.
MRR	Magnetic resonance relaxography.
T1	Longitudinal relaxation time constant.
R1 (≡ T1−1)	Longitudinal relaxation rate constant.
T2	Transverse relaxation time constant.
RRe	Extracellular relaxation reagent.
GdDTPA2−	Gadolinium diethylenetriamine penta-acetate.
IR	Inversion recovery experiment for T1 measurement.
tI	Delay time between 180° and 90° RF pulses in IR experiment.
R1L	Apparent R1 of component with larger T1 value.
R1S	Apparent R1 of component with smaller T1 value.
aL	Apparent population of component with larger T1 value.
aS	Apparent population of component with smaller T1 value.
2SX	Two-site exchange analysis model used to measure equilibrium transmembrane water exchange kinetics.
R10	Measured 1H2O R1 of a sample in absence of RRe.
R1i	R1 of intracellular water.
R1e0	R1 of extracellular water before RRe.
r1e	RRe relaxivity.
τi	Mean intracellular water molecule lifetime.
τe	Mean extracellular water molecule lifetime.
kie (≡ τi−1)	Pseudo-first-order rate constant for equilibrium water efflux.
kei	Pseudo-first-order rate constant for equilibrium water influx.
pi	Intracellular water mole fraction.
pe	Extracellular water mole fraction.
Pf	Osmotic or hydraulic water permeability coefficient.
Pd	Diffusional water permeability coefficient.
Pw	Steady-state water permeability coefficient with active and passive components: Pw = Pw(active) + Pw(passive).
V	Yeast cell volume.
A	Yeast cell surface area.
r	Yeast cell radius (modeled as a sphere).

At 37°C, the T₂ method has measured a τ_i value of 8.2 ms in human erythrocytes (3) and 4.5 ms in agile wallaby erythrocytes (4). The T₁ approach has been applied to yeast cell suspensions (5) and rat thigh muscle in vivo (8). In densely packed yeasts, τ_i was 672 ms and p_i was 0.35 (5). Resting rat thigh muscle data yielded τ_i = 1.1 s and the p_e was 0.11 (8). We studied isolated rat hearts during perfusion with Krebs Henseleit buffer containing RR_e and found that τ_i = 184 ms (9). Interestingly, during no-flow ischemia, τ_i increased to 280 ms. Although water exchange is thought of as a passive process, i.e., not requiring energy, the increase in τ_i led us to speculate that, because ischemia decreases ATP concentration, τ_i may be sensitive to cellular energetics. Because ATP is required for membrane ion pump activity and the development of the primary ion gradient, which powers secondary active symporters and antiporters, we hypothesized that transport activity may affect transmembrane water exchange or cycling.

Accordingly, the ¹H₂O T₁ MRR/RR_e method was used to measure p_i and τ_i in yeast cell suspensions maintained in different oxygenation states, which altered cellular energetics. ATP was measured by ³¹P MRS and HPLC. We found that τ_i⁻¹ (≡ k_ie) strongly correlates with cellular ATP and, more importantly, specifically with the activity of the major ion transport plasma membrane protein, a P-type H⁺-ATPase. These results demonstrate an active transmembrane water cycling in yeast. To our knowledge, this is the first such observation.

Materials and Methods

Yeast strains and suspensions

Four Saccharomyces cerevisiae strains were used. Bakers yeast, Fleischmann's Fresh Active, locally purchased was washed in minimal medium twice before use. The yeast D273-10B (No. 2465) was obtained from ATCC (Manassas, VA). These yeast cells were grown in YPD medium: 1% yeast extract, 1% peptone, and 2% glucose, and harvested at midstationary phase. BY4743 yeast (ATCC: 4024376), which are heterozygous for the gene encoding P-type H⁺-ATPase, PMA1, (PMA1^+/−), were grown in YPD to midstationary phase, harvested, and resuspended in phosphate-free media (10), shaken for 7 h, and harvested. PMA1^+/− cells have reduced H⁺-ATPase activity (11). MR6 ρ+ yeast cells (12) were grown in YPD plus adenine and harvested at midstationary phase.

Before MR experiments, yeast were washed twice with cold minimal medium (MM) and resuspended in MM to achieve a cell density of 30% wet weight/volume (w/v). MM contains 4 mM MgSO₄, 13 mM KCl, 13 mM Na⁺ (from NaOH), 50 mM MOPs; final pH = 6.6. The ¹H₂O_e RR_e, Na₂GdDTPA, was synthesized from Gd₂O₃ and H₂DTPA (13). An aliquot of 100 mM Na₂GdDTPA stock solution was added to the MM before making up the 30% (w/v) yeast suspension. The final [RR_e] was 9.3 mM.

MR measurements were done in a 20 mm O.D. MR tube fitted with two tubes that extended to near the tube bottom (7). Gas, 95% O₂ (O₂, aerobic), or 95% N₂ (N₂, anaerobic), each 5% CO₂, flowed constantly through the tubes. Gas flow was adjusted to suspend yeast cells during MR studies, which were done at 25°C.

Studies with ebselen (2-phenyl-1,2-benzisoselenazol-3(2H)-one)

D273-10B cells 30% (w/v) were suspended in a solution containing 4.04 mM MgSO₄, 13.4 mM KCl (pH = 6.24). Suspensions were bubbled with N₂ for 50 min while ³¹P MRS and ¹H MRS IR data sets were acquired. Then a volume of ebselen in dimethyl sulfoxide (DMSO), to yield a final extracellular concentration of 3 mM or an equal volume of DMSO, was added 2 min before the switch to O₂ and ³¹P and ¹H IR data were acquired. Parallel studies were done to measure suspension extracellular pH (pH_e) using a pH electrode and to obtain aliquots for HPLC ATP measurements.

MR measurements and data analyses

All MR data were acquired with an Inova 9.4T spectrometer (Varian, Palo Alto, CA). Water proton, ¹H₂O, (398.8 MHz) longitudinal relaxation rate constants (R₁ ≡ T₁⁻¹) were measured using an IR pulse sequence: sw = 8000 Hz, 2048 complex points, 64 delay increments (t_I) between the 180° (composite) pulse and 90° RF pulse, total time 4 min. The t_I values are listed in the Supporting Material. The longitudinal magnetization (M_z) was quantified using Bayesian analysis software, which analyzes the free induction decay (14). The midpoint of the entire IR acquisition is reported as the measurement time. Each ¹H₂O IR T₁ measurement was followed by a ³¹P MRS acquisition (161.8 MHz) with a one-pulse sequence; free induction decays result from 208 45° pulses with a recycle time of 0.9 s averaged for 3.5 min. The ATP amount was measured using Bayesian analysis software.

Relaxographic data analyses

Fully relaxed magnetization M_Z(∞) was the average of the last two IR M_z(t_I) values and the quantity [(M_Z(∞) – M_Z(t_I))/2M_Z(∞)] calculated. To measure the equilibrium trans-plasma membrane water exchange kinetics, we used the 2SX model for ¹H₂O T₁ relaxation affected by water exchange (5,8). The major 2SX assumption is that water mixing within each compartment (site) is complete; i.e., fast compared with equilibrium exchange between sites. This is an excellent assumption. With a conservatively small water diffusion coefficient (1.5 μm²/s), an intracellular water molecule will translate 10 μm in 11 ms (15). Because 10 μm is significantly larger than the yeast cell radius, and τ_i is hundreds of milliseconds (see below), water molecules sample the entire cell interior many times during a lifetime, meaning they are “well mixed”.

The model predicts that, under some conditions, the experimental recovery of longitudinal magnetization after inversion can be analyzed as biexponential. This is expressed in

$$M_z\left(t_I\right)=M_Z(\infty )\left[1-2\left[a_L\text{exp}\left(-t_I{R}_{1L}\right)+a_S\text{exp}\left(-t_I{R}_{1S}\right)\right]\right],$$ (1)

where a_L and R_1L are the apparent population and relaxation rate constant, respectively, of the component with the larger T₁ value, and a_S and R_1S are the analogous quantities for the smaller T₁ value component.

The 2SX model for ¹H₂O T₁ relaxation has seven model parameters, of which only five are independent (5). These are: r_1e (extracellular RR relaxivity), T_1e0⁻¹ (R_1e0, for ¹H₂O_e before RR_e), T_1i⁻¹ (R_1i, for ¹H₂O_i), τ_i (mean intracellular water molecule lifetime), and p_i (intracellular water mole fraction or population). Assuming the fast exchange limit condition before RR_e arrival (a very good assumption), one could estimate a value for R_1e0 using R₁₀ as

$$R_{1e0}=\frac{\left(R_{10}-p_i{R}_{1i}\right)}{\left(1-p_i\right)},$$ (2)

where R₁₀ is the measured ¹H₂O R₁ for the suspension before RR_e. This leaves only four parameters (16). The first two are MR quantities (dependent on B₀ and temperature). The last two are physiological parameters (dependent on temperature and cell density for p_i), which are related to the τ_e (mean extracellular water molecule lifetime) and p_e (extracellular water mole fraction) values by equilibrium mass balance:

$$\left[{\tau }_e={\tau }_i\times \left(\frac{p_e}{p_i}\right);p_e=1-p_i\right].$$ (3)

R_1L, R_1S, a_S, and a_L can be expressed in terms of the five intrinsic system parameters, R_1i, r_1e, R_1e0, τ_i, and p_i in Eqs. 4–6:

$$R_{1L}=1/2\left[R_{1i}+r_{1e}\left[R{R}_e\right]+R_{1e0}+{\tau }_i^{-1}+\frac{p_i}{{\tau }_i\left(1-p_i\right)}\right]-1/2{\left\{{\left[R_{1i}-r_{1e}\left[R{R}_e\right]-R_{1e0}+{\tau }_i^{-1}-\frac{p_i}{{\tau }_i\left(1-p_i\right)}\right]}^2+\frac{4p_i}{{\tau }_i^2\left(1-p_i\right)}\right\}}^{1/2},$$ (4)

$$R_{1S}=1/2\left[R_{1i}+r_{1e}\left[R{R}_e\right]+R_{1e0}+{\tau }_i^{-1}+\frac{p_i}{{\tau }_i\left(1-p_i\right)}\right]+1/2{\left\{{\left[R_{1i}-r_{1e}\left[R{R}_e\right]-R_{1e0}+{\tau }_i^{-1}-\frac{p_i}{{\tau }_i\left(1-p_i\right)}\right]}^2+\frac{4p_i}{{\tau }_i^2\left(1-p_i\right)}\right\}}^{1/2},$$ (5)

$$\frac{a_S}{a_S+a_L}=1/2-1/2\left[\frac{\left(R_{1i}-r_{1e}\left[R{R}_e\right]-R_{1e0}\right)\left(1-2p_i\right)+{\tau }_i^{-1}+\frac{p_i}{{\tau }_i\left(1-p_i\right)}}{{\left\{{\left[R_{1i}-r_{1e}\left[R{R}_e\right]-R_{1e0}+{\tau }_i^{-1}-\frac{p_i}{{\tau }_i\left(1-p_i\right)}\right]}^2+\frac{4p_i}{{\tau }_i^2\left(1-p_i\right)}\right\}}^{1/2}}\right].$$ (6)

A method we term “2SX fitting” was used to extract exchange parameters from the MRR data by rearranging Eq. 1 as Eq. 7. Equations 4–6 are substituted into the right-hand side,

$$\left[\frac{\left(M_Z(\infty )-M_Z\left(t_I\right)\right)}{2M_Z(\infty )}\right]=a_L\text{exp}\left(-t_I{R}_{1L}\right)+a_s\text{exp}\left(-t_{\text{I}}{R}_{1s}\right),$$ (7)

and τ_i, p_i, and r_1e (with fixed R_1i and R_1e0) are adjusted to match the IR time-course, [(M_Z(∞) – M_Z(t_I))/2M_Z(∞)], observed at a single [RR_e] value. The value for R₁ was determined at 25°C in cell-free MM to be 0.48 s⁻¹ with O₂, and 0.42 s⁻¹ with N₂ bubbling. The R₁₀ of an RR_e-free 30% w/v yeast suspension bubbled with O₂ is 0.48 s⁻¹, and bubbled with N₂ is 0.42 s⁻¹. Changing the R_1i value, which was fixed in Eqs. 4–6 between 0.78 and 0.42 s⁻¹, does not change the resulting fitted t_i or p_i values; the fitted r_1e value changes <1%. R_1i > 0.83 s⁻¹ does not produce satisfactory fittings of Eq. 7 to data. Although R_1e0 is surely smaller than R_1i, both values were fixed at 0.48 s⁻¹. This is consistent with Eq. 2 because realistic values for these are too small to influence the fittings. Thus, only τ_i, p_i, and r_1e parameter values were varied to optimize the fitting. The RR_e relaxivity, r_1e, was varied because it was anticipated to differ from the cell-free value (5). See the Results in the Supporting Material for more on r_1e. Water exchange parameters in Figs. 1–4 were obtained from 2SX fittings of MRR data with 9.3 mM RR_e.

Figure 1.

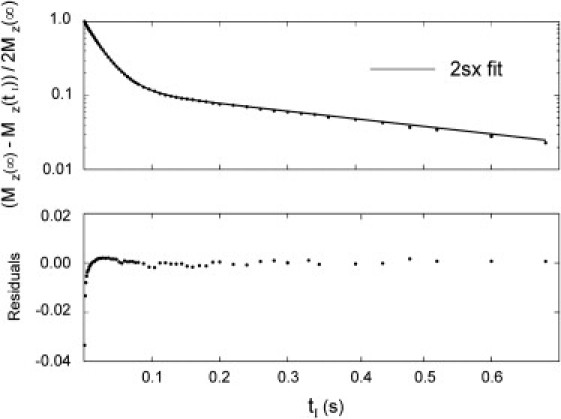
¹H₂O T₁ MRR/RR_e data and analyses. (Upper panel) 2SX fitting (solid curve) of the t_I-dependence of log [(M_Z(∞)–M_Z(t_I))/2M_Z(∞)] (●) from an anaerobic (N₂) yeast suspension with 9.3 mM RR_e. Equations 4–7 were fitted to the data by adjusting τ_i, p_i, and r_1e. The values were: τ_i, 0.536 s, p_i = 0.113, and r_1e = 4.07 s⁻¹ mM⁻¹. (Lower panel) Fitting residuals (residual = fitted curve − experiment data).

Figure 2.

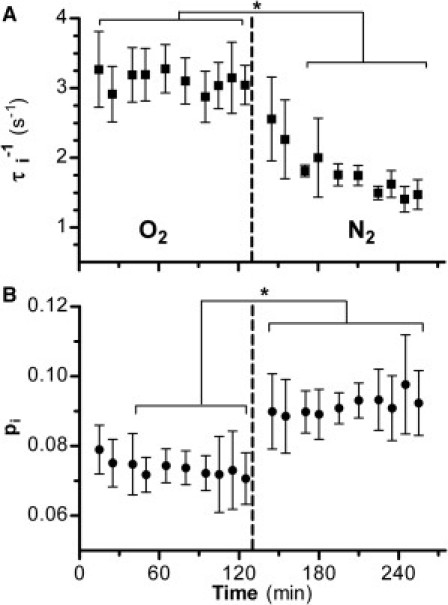
(A) Time-dependence of τ_i⁻¹ (s⁻¹), the pseudo-first-order rate constant for equilibrium water efflux (k_ie), for 30% w/v yeast suspensions during bubbling with O₂ (aerobic) and after switching (dashed line) to N₂ (anaerobic). (B) Time-dependence of p_i, the intracellular water mole fraction. Mean (± SD) of (n = 6) D273-10B yeast cell suspensions. (Asterisk) p < 0.05 repeated measures ANOVA.

Figure 3.

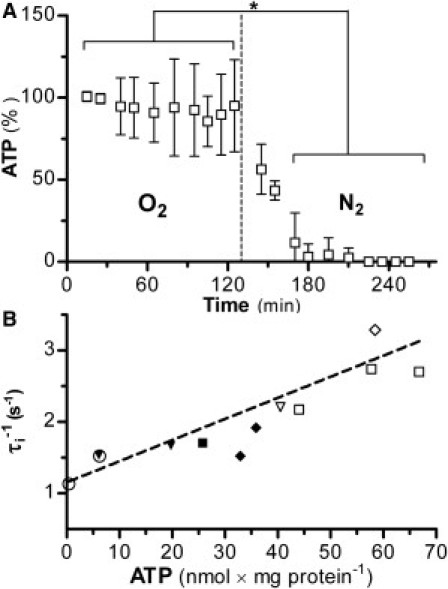
(A) Time-dependence of ³¹P MR-measured ATP content of 30% w/v suspensions of yeast bubbled with O₂ (aerobic) and after switching (dashed line) to N₂ (anaerobic). The ³¹P MR measures were interleaved with the ¹H IR measurements used to calculate τ_i⁻¹ and p_i (Fig. 2). The first two ATP measures during O₂ for each suspension were averaged and used to normalize all amounts as a percentage (%) of those measures. Mean (± SD) of (n = 6) D273-10B yeast cell suspensions. (Asterisk) p < 0.05 repeated measures ANOVA. (B) HPLC-measured ATP [nmol × (mg protein)⁻¹] dependence of τ_i⁻¹ (s⁻¹) for yeast suspensions grown and studied under various conditions. M6 ρ+ yeasts were grown with different adenine concentrations: 10 (○), 20 (▾), and, 40 mg/L (▿), and τ_i⁻¹ measured in aerobic condition. Bakers yeast was measured in aerobic (□) and anaerobic (■) conditions. D273-10B yeast were measured in aerobic (⋄) and anaerobic (♦) conditions. The best fitted line is shown: intercept, 1.2 (± 0.3) s⁻¹; slope, 0.30 (± 0.01) (s⁻¹ × [nmol × (mg protein)⁻¹]⁻¹); R² = 0.615.

Figure 4.

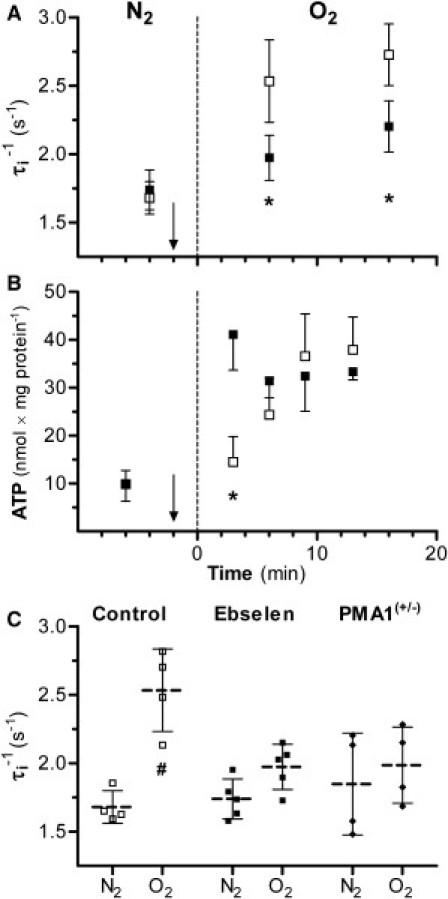
(A and B) Effect of increasing yeast plasma membrane H⁺-ATPase activity by switching from N₂ to O₂ (dashed line) at t = 0. (Arrows) At −2 min, either DMSO alone (control) or a DMSO solution of ebselen (2-phenyl-1,2-benzisoselenazol-3(2H), an H⁺-ATPase inhibitor) was added to the suspension. Mean (± SD); (asterisk) p < 0.05 ebselen versus control. (A) τ_i⁻¹ for control (□, n = 4) and ebselen-treated (■, n = 5) suspensions. (B) HPLC ATP measurements plotted from separate studies of control (□, n = 4) and ebselen-treated (■, n = 4) suspensions. (C) τ_i⁻¹ for (□) control, (■) ebselen-treated, and (♦) PMA1^+/− yeast suspensions in the N₂ (4 min before O₂) and O₂ conditions (6 min after N₂). τ_i⁻¹ for control yeast suspensions increased going from N₂ to O₂ (p < 0.001), whereas the ebselen-treated and PMA1^+/− yeast τ_i⁻¹ values were unchanged. Control and ebselen-treated τ_i⁻¹ are from panel A. The individual measurement values as well as the mean (dashed) and SD (solid) horizontal lines are shown. (Pound sign) p < 0.05 O₂ versus N₂ same group.

Another method for extracting exchange parameters, which we term “relaxivity fitting”, adjusts Eq. 4 and/or Eq. 5 to match the [RR_e]-dependences of R_1L and R_1S quantities determined from relaxograms (5,8). Results from relaxivity fitting are shown in Fig. S4 and Table S3 in the Supporting Material, and compared with those from 2SX fitting in Table S1 and Table S2.

Yeast suspension intra- and extracellular volumes

Suspension total intra- and extracellular water volume values were calculated using the MR measured p_i = 0.075 (±0.007) (n = 6) and p_e = 0.925. Note that, even in a yeast cell pellet, the p_e ∼ 0.64. The yeast cell pellet dry-weight/wet-weight ratio was 0.17 (±0.02). Thus, 3 g wet yeast equals 0.51 g dry. Final suspension total volume was 10 mL. Correcting for yeast cell mass gives water mass (10 – 0.51 = 9.49 g)—assuming unit density, this is 9.49 mL; 9.49 × 0.925 (p_e, O₂) = 8.78 mL ≈ 8.8 mL = extracellular water volume, which was used to calculate [RR_e]; and, 9.49 × 0.075 (p_i, O₂) = 0.71 mL = intracellular water volume.

Yeast cell volume and surface area

To estimate the P_W, we used P_W = τ_i⁻¹(V/A), where V and A are the individual cell volume and surface area values, respectively (5). We modeled the yeast cell as a sphere of radius r, V = (4/3)πr³, A = 4πr², V/A = r/3, and P_W = r/(3τ_i). We used a reported yeast cell intracellular water V of 42 fL (fL = 10⁻¹⁵ L; 1fL = 1 μm³) (17). It was assumed that this V measurement, made at low cell density, reflects the aerobic condition. The calculation returned an r value = 2.16 μm. To adjust for the p_i increase during N₂, V was multiplied by p_i(N₂)/p_i(O₂) = 1.24, and this returned an r of 2.32 μm.

HPLC analyses

ATP content was measured in perchloric acid extracts of yeast cell pellets from suspensions rapidly filtered, and frozen in liquid N₂. A Macherey-Nagel nucleosil 4000-7 PEI column was employed, using a buffer A (2.5 mM Trisphosphate, pH 7.2) with 5–95% buffer B (2.5 mM Trisphosphate, 1 M KCl, pH 8.0) gradient over 20 min. The ATP retention time was 12.5 min. Protein content was determined using the Lowry method (18).

Statistical analyses

Data are presented as the mean (±1 SD). Statistical computations used the software Statistica (Ver. 6.1, StatSoft, Tulsa, OK). An analysis of variance (ANOVA) compared measurements among all groups. Repeated measures ANOVA were used where appropriate. A posthoc Bonferroni test was used to compare means. Differences were declared statistically significant if p < 0.05. GraphPad Prism (5.0 for Windows, GraphPad Software, San Diego, CA) was used for plots.

Results

Relaxographic data and analyses

The quantity [(M₀(∞) − M_z(t_I))/2M₀(∞)] is calculated from the IR measurement data and 2SX fitting analyzes the data (points) with the Bloch equations modified for two-site-exchange, Eqs. 4–7 (Fig. 1, upper panel). The solid curve results from the 2SX fitting with the variables returned: τ_i = 0.54 s, p_i = 0.11, and r_1e = 4.07 s⁻¹ mM⁻¹. As is seen, the quality of the fitting is quite high. Except at very small t_I values (likely due to imperfect inversion and/or magnetization transfer from yeast macromolecular ¹H resonances), the fitting residuals (lower panel) are essentially zero.

Oxygenation dependence of water exchange kinetics

R_1L was found to depend on oxygenation state, e.g., Fig. S1 and Fig. S3 in the Supporting Material. To explore this observation, τ_i⁻¹(s⁻¹), which equals k_ie (19), was determined under aerobic and anaerobic conditions (Fig. 2 A). During O₂ bubbling at 25°C, τ_i⁻¹ was constant at 3.1 (±0.08) s⁻¹; after changing to N₂, τ_i⁻¹ decreased exponentially until, after 95 min, it reached 1.5 (±0.09) s⁻¹, an ∼50% decrease.

The H₂O_i mole fraction, p_i, was 0.074 (±0.005) during the aerobic period; after the switch to N₂, p_i increased by 23%, to 0.092 (±0.006) (p < 0.05) (Fig. 2 B). The p_i change was essentially complete by 15 min, i.e., at the first postswitch measurement. This is much faster, and smaller, percentagewise, than the τ_i⁻¹ change.

The quantity τ_i⁻¹ can be expressed as P_W(A/V), where P_W is the water permeability coefficient, and V and A are the individual cell volume and surface area values, respectively (5). The N₂-induced τ_i⁻¹ decrease (Fig. 2 A) may thus reflect decreases in P_W, (A/V), or both. To examine this, we modeled the yeast cell as a sphere, so τ_i⁻¹ = 3P_W/r (radius r). After switching to N₂, 3/r decreases by only ∼7% (assumes V ∝ p_i). This suggests the N₂-induced 50% τ_i⁻¹ reduction is dominated by a P_w decrease.

Oxygenation dependence of ATP level

With no exogenous glucose, changing suspension oxygenation alters cellular energetics (20). ³¹P MR measured yeast ATP content decreases rapidly after the switch to N₂ (Fig. 3 A), correlating with the τ_i⁻¹ decrease (Fig. 2 A). Although ³¹P MR measurements are dynamic, rigorous quantifications are difficult because polyphosphate and ATP signals overlap (20). Thus, ATP content was also measured by HPLC. Three yeast strains, D273-10B, BY, and MR6 ρ+ (lacks the ade2 gene), were used. Because MR6 ρ+ yeast requires adenine in the growth medium for purine biosynthesis, adjusting its concentration allows experimental control of steady-state aerobic ATP content. A strong correlation between τ_i⁻¹ and HPLC-measured ATP is observed (Fig. 3 B), which encompasses three yeast strains, both aerobic and anaerobic. The τ_i⁻¹ value increases at least linearly with ATP content, over almost two orders of magnitude.

Involvement of the plasma membrane H⁺-ATPase

The τ_i⁻¹ ATP correlation suggests that equilibrium trans-plasma membrane water kinetics have contributions from active processes in addition to passive diffusion. The active yeast plasma membrane ion transport protein is a P-type H⁺-ATPase, which uses ATP hydrolysis energy to pump H⁺ out of the cell. This creates an electrochemical proton gradient that establishes the membrane potential and drives much of the other transport via H⁺-dependent cotransporters. To test a H⁺-ATPase activity link to equilibrium water exchange, anaerobic suspensions were treated with ebselen, a cell membrane H⁺-ATPase inhibitor (11), and then energized with O₂. The control suspension τ_i⁻¹ (Fig. 4 A) increased from 1.7 (±0.1) s⁻¹ to 2.5 (±0.3) s⁻¹ 6 min after the O₂ switch (p < 0.001). In contrast, the ebselen-treated yeast τ_i⁻¹ was only 2.0 (±0.2) s⁻¹ at 6 min (p = 0.65), and its τ_i⁻¹ value at 16 min was still less than the control yeast. Thus, ebselen suppressed the O₂-induced τ_i⁻¹ increase. The p_i value initially decreased during O₂ in ebselen-treated and control cells (see Fig. S5 A). By 16 min, however, the ebselen-treated p_i had returned to its anaerobic value, whereas the control p_i remained small. Because V/A follows as the cube root of p_i (see above), we conclude that O₂ induces a P_W increase in control but not ebselen-treated yeast. Ebselen does not inhibit ATP synthesis. Three min after the O₂ switch, the ATP content of the ebselen-treated yeast exceeded that of the control yeast (Fig. 4 B). By the first τ_i⁻¹ measurement (6 min), however, the ATP contents of the control and ebselen-treated yeast were equal. Thus, the reduced water exchange kinetics in ebselen-treated yeast does not result from reduced ATP. This is consistent with τ_i⁻¹ being associated with H⁺-ATPase activity.

PMA1^(+/−) diploid yeasts underwent the same protocol, without ebselen. These cells are deficient in one copy of the PMA1 gene, which encodes the P-type H⁺-ATPase. The O₂ τ_i⁻¹ responses of PMA1^(+/−) and ebselen-treated yeast suspensions are remarkably similar (Fig. 4 C). This lends support to the notion that H⁺-ATPase activity is responsible for a significant portion of the τ_i⁻¹ and P_w increase with yeast cell energization.

Discussion

Water is usually in thermodynamic equilibrium (steady state) across the cell plasma membrane: i.e., the extra- and intracellular water chemical potentials are equal. Although our method measures steady-state trans-plasma membrane water exchange, it also detects net cellular water fluxes. A water influx causing an ∼20% yeast cell volume increase occurs after switching from O₂ to N₂ (Fig. 2 B). This must reflect a net influx of solutes (ions) and/or production of intracellular metabolic osmolytes; most probably an intracellular osmolarity increase associated with anaerobic metabolism. It represents a regulatory volume increase and is complete within 15 min of the gas change. The pseudo-first-order rate constant for this net influx equals 0.012 min⁻¹ (2.0 × 10⁻⁴ s⁻¹). This net water flux is described by the hydraulic permeability coefficient, P_f, to distinguish it from the equilibrium coefficient (P_d, termed P_w here) for which there is no net flux. Simultaneously, ¹H₂O T₁ MRR/RR_e 2SX analysis, and other NMR methods (21), measure diffusional water exchange kinetics, i.e., for equilibrium (steady state, reversible) trans-plasma membrane water molecule interchange. The rate constant equals k_ie + k_ei and when ATP > 50 nmol/mg protein (Fig. 3 B), it equals 3.2 s⁻¹, four orders-of-magnitude larger than net influx rate constant. This rapid water exchange persists before, during, and after any net water flux.

The results demonstrate that τ_i⁻¹ correlates (at least linearly) with cellular ATP content. The ATP = 0 intercept of the Fig. 3 B line is τ_i⁻¹ = 1.2 s⁻¹. Using 2.3 μm as anaerobic r (see Materials and Methods), the expression P_W = r/(3τ_i) yields P_W = 9.2 × 10⁻⁵ cm/s. This value is bracketed by the P_d values of 8.1 × 10⁻⁵ and 57.3 × 10⁻⁵ cm/s for sphingomyelin/cholesterol and phosphatidylcholine/cholesterol bilayer membranes, respectively, at the same temperature, 25°C (22). These values are for model bilayer membranes containing no proteins. This indicates that, in the absence of ATP and an osmotic gradient, water crosses the yeast cell membrane by simple, passive, unfacilitated diffusion directly across the plasma membrane lipid bilayer. The ATP = 0 intercept corresponds to a τ_i value of 830 ms, which agrees with the τ_i values of 700 ms (21) and 670 ms (5) reported in previous NMR studies of Bakers yeasts at similar temperatures and likely almost as ATP depleted. The method employed by Tanner (21) was different from that of Labadie (5).

One can use the rate constant τ_i⁻¹ (k_ie), 1.2 s⁻¹, (Fig. 3 B), for simple, passive, unfacilitated diffusion across the plasma membrane lipid bilayer to calculate the steady-state efflux of water molecules from the yeast cells at near minimum velocity. Thus, an anaerobic cell volume of 52.1 fL and an [H₂O_i] of 50 mol/L yields 1.57 × 10¹² molecules/cell; multiplying by 1.2 s⁻¹ yields an efflux of 1.9 × 10¹² water molecules/s/cell. Likewise, using the aerobic condition rate constant τ_i⁻¹ (k_ie), ∼3 s⁻¹ (Figs. 2 A and 3 B), with an aerobic cell volume of 42.2 fL, yields an efflux of 3.8 × 10¹² water molecules/s/cell. For both conditions there must be equal numbers of water molecules entering the cell per second. Thus, the velocity of yeast water efflux (and influx) increases by a factor of 2 (∼1.9 × 10¹² water molecules/s/cell) going from passive, unfacilitated diffusion across the plasma membrane lipid bilayer to the active component, with cellular ATP ≅ 70 nmol/mg protein, during oxidative metabolism.

With cellular ATP >35 nmol/mg protein, yeast trans-plasma membrane equilibrium water exchange has an active component (a good reason to use P_W instead of P_d): P_W = P_W(passive) + P_W(active). The most obvious way for ATP to influence water exchange is for water to accompany active trans-plasma membrane transport, ion pumping, and/or secondary cotransport. Our finding that reducing H⁺-ATPase activity with an inhibitor or genetic modification of H⁺-ATPase expression reduces τ_i⁻¹, even with adequate ATP, supports this idea. We are not aware that an active water cycling consequent to transport activity has been previously described.

The P-type H⁺-ATPase utilizes the Gibbs free energy of ATP hydrolysis, ΔG_ATP, to transport H⁺ out of the cell in an osmogenic, electrogenic reaction. This generates the electrochemical H⁺ gradient (23) that is the primary energy source for secondary transport in the yeast. The observed increase in τ_i⁻¹ (∼P_W) associated with H⁺-ATPase activity (Fig. 4) could result from water cotransport with its primary process (H_i⁺ → H_e⁺) and/or with secondary transport processes, such as of other ions (e.g., Na⁺ and K⁺), driven by the H⁺ electrochemical gradient. This is suggested in the Fig. 5 cartoon, which indicates selected proteins: the H⁺-ATPase (Pma1), the H⁺/K⁺,Na⁺ antiporter (Nha1), and the K⁺ transporter (Trk1) (24). It is possible that any, or all, of these proteins (as well as others) enable transmembrane water movement (25). The dashed membrane-spanning ovals in Fig. 5 suggest water cotransported or facilitated water diffusion with the activities of these proteins. Together, they constitute an active, equilibrium transmembrane water cycling consequent to homeostatic ion or metabolite transport processes.

Figure 5.

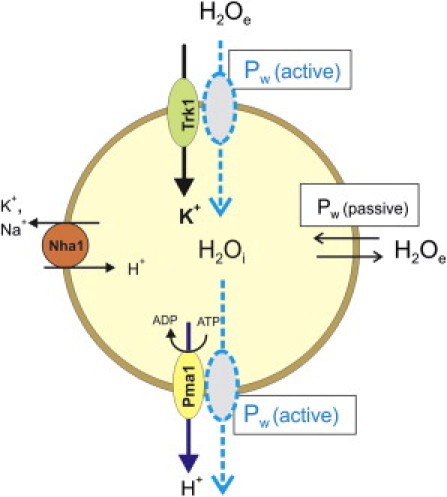
Cartoon depicting transmembrane water cycling in a yeast cell. Several plasma membrane ion transporters with hypothetical water cotransport or facilitated diffusion (dashed ovals) are shown. The major ion transport protein is the electrogenic P-type H⁺-ATPase (Pma1), which pumps H⁺ out of the cell at the expense of ATP. Also shown are the K⁺ uniporter (Trk1) and the H⁺/K⁺, Na⁺ antiporter (Nha1). Water-facilitated diffusion or cotransport could be through one or both of the following: 1), water cavities in the ion transporter molecules or 2), the ion channels themselves. Integrated over the entire cell, this represents active transmembrane water cycling accompanying the ion transport of the membrane transport enzymes. The active components, P_w(active), associated with protein activity, and passive components, P_w(passive), associated with the membrane, of the total membrane water permeability (P_w) are also indicated. Because cellular volume does not vary, at least on the macroscopic timescale, the membrane water cotransport or facilitated diffusion mechanisms requires that the entire cellular ensemble of water transporters must function in a balanced manner. Alternatively, it is possible that the dashed ovals represent intra- and extracellular water exchanging (i.e., the dashed oval arrows would be bidirectional) during protein transport activity. Because this mechanism involves water exchange and not transport, volume is unaffected.

Water cotransport describes the secondary active transport of water (25). The sodium-dependent glucose cotransporter, SGLTl (26), has been reported to conduct secondary active water cotransport (27). The energy for this was obtained from that released by the substrate flux. Others have contested water cotransport by SGLTl, finding that water transport was passive and required the osmotic gradient created by sodium and glucose transport (28). SGLT1-expressing oocytes displayed a twofold increase in passive water permeability that was sensitive to the specific inhibitor phlorizin (28). The protein acted as a conduit for the water driven by the osmotic gradient. We denote the protein-mediated increase in water permeability resulting from local osmotic gradients as facilitated water diffusion.

Although it is reasonable that the Fig. 5 dashed ovals represent water cotransported (or experiencing facilitated diffusion) with the ions or molecules transported by membrane transporter enzymes, cellular volume does not vary. Consequently, the entire cellular ensemble of membrane water transporter proteins would have to work in concert transporting water in opposite directions in a perfectly balanced manner. We know that the cell does this for the ions. Alternatively, it is possible that the dashed ovals in Fig. 5 represent an enhanced exchange of intra- and extracellular water that occurs during protein transport activity. Because this mechanism involves water exchange and not cotransport or facilitated diffusion, volume is unaffected.

Water can also move through aquaporins, membrane water channel proteins. Aquaporin-1 increases net water permeation 10- to 100-fold, in response to an osmotic gradient (29). Although aquaporin-1 can catalyze passive water exchange, as in the erythrocyte, it does not itself facilitate active water exchange (25). In most laboratory S. cerevisiae strains, the aquaporin-encoding genes (AQY1 and AQY2) contain inactivating mutations (30) and, thus, aquaporins are not normally active as water channels. For the phenomenon we observe, the Fig. 5 dashed ovals almost certainly are not aquaporins.

Pma1 contains a central aqueous cavity that is connected via columns of water molecules, which function as proton (H⁺) wires, to the inlet and outlet sides of the protein (31). It is possible that Pma1 activity increases fusion of the central-water-filled cavity with the inlet and outlets, thus increasing transmembrane H₂O cotransport or exchange. Lactose permease (LacY), a lactose proton symporter, and other major facilitator superfamily proteins, include an interior aqueous cavity (32). This cavity contains the H⁺ and lactose binding sites; is large enough to hold >400 water molecules; and, is alternately accessible to the intra- and extracellular environments during transport activity, favoring transmembrane H₂O exchange or facilitated diffusion. Because LacY uses the electrochemical H⁺ gradient to transport lactose, amplified water exchange, i.e., active water cycling, during activity could be a general characteristic of many transporters. Aqueous cavities exist in a number of membrane channels and pumps (33).

The H⁺-ATPase of plants and fungi and the related P-type ATPase (the Na⁺/K⁺ ATPase) of animal cells each create the primary ion gradient used as an energy source for secondary transport. It is possible that water also cycles across the mammalian plasma membrane in concert with Na⁺ ion pumping and exchange.

Possible implications of active water cycling for ¹H MRI

Mean human tissue τ_i values have been estimated in vivo from minimally invasive Dynamic-Contrast-Enhanced-MRI data (6,19), where the contrast reagent acts as an RR_e. The τ_i parameter is averaged over a region-of-interest or, if signal/noise permits, an image voxel. Parametric τ_i maps of a human MS lesion (34), an osteosarcoma (34), and malignant breast (34,35) tumors have been reported. Note that τ_i is proportional to a one-dimensional measure of individual cell size (and inversely proportional to P_W), and not the intravoxel cell volume fraction. It is an intensive property, independent of the number of cells in the voxel (cellularity). This is elaborated in Strijkers et al. (15). Tissues accessible to RR_e (heart, liver, kidney, skeletal muscle) provide pathologies amenable to investigation. It is tempting to speculate that τ_i⁻¹ may provide a means to differentiate pathologies, based on their transmembrane water exchange kinetics as a measure of metabolic activity (membrane exchange activity) and/or cell volume changes.

The brain parenchyma is not normally RR accessible due to the relative impermeability of the brain blood barrier. However, the mean capillary (blood) water lifetime, τ_b, can be determined in DCE-MRI studies, and mapped, and varies in MS pathology (36). Thus, τ_b⁻¹ = (P_W)_capillary(2/r)_capillary, where (P_W)_capillary is the water permeability coefficient for the vessel wall, which is comprised chiefly of endothelial cells. Their plasma membranes are surely engaged in homeostatic ion cycling.

Our finding of an active component of τ_i⁻¹ (P_w) may have implications for understanding the changes in diffusion-weighted MRI seen after stroke (37). The early decrease (30%) in the cerebral tissue water apparent water diffusion coefficient (ADC) was ascribed to a net water influx (or cell swelling) mechanism and large differences between intra- and extracellular water ADC values (38). It is now known that these ADC values are not sufficiently different and a metabolically related intracellular water (ADC_i) decrease appears more plausible (39). A model of water diffusion in axons predicts a compartmental membrane permeation rate-limiting step (40). It is possible that diffusion of intracellular water in normally energized cells includes water cycling across organelle (mitochondria, endoplasmic reticula, etc.) as well as plasma membranes. As O₂ deprivation in stroke causes rapid ATP depletion, active ion pumping will quickly cease. A concomitant transmembrane water cycling decrease could be reflected as an ADC_i decrease. Alternatively, organelle swelling could occur upon deoxygenation. From the principles elucidated here, 1/τ_organelle ∝ (P_W)_organelle(A/V)_organelle. Possibly both effects occur, each factor decreases, and a τ_organelle increase causes an ADC_i decrease.

Conclusions

Water actively cycles across the yeast plasma membrane consequent to membrane protein transport activity. Active water cycling during such activity may be a general characteristic of cells. It is an interesting question as to why nonaquaporin protein water transport capacity exists. Erythrocytes contain abundant aquaporin and display very rapid water exchange. Kuchel and Benga (41) proposed two hypotheses to explain natural selection for high erythrocyte water permeability via aquaporin: 1), the membrane has energy-dependent undulations and the energy expended is minimized by avoiding water displacement; and 2), the rapid facilitated diffusion of glucose, chloride, and bicarbonate across the membrane would cause volume change if water was not displaced. Erythrocyte water exchange is, however, reduced only ∼50% by aquaporin inhibition (4). Facilitated diffusion of water by membrane transport proteins may provide an explanation for some of the substantial nonaquaporin erythrocyte water permeability.

Noting that aquaporin is not crucial for whole body water homeostasis, Zeuthen (25) claims that much transepithelial water transport occurs through other proteins by the cotransport and/or facilitated diffusion mechanisms. Active water cycling may be a mechanism that enables cells to minimize (or avoid) transmembrane osmotic pressure gradients resulting from metabolic transport activity. With its rapid kinetics the active transmembrane water cycle has the capacity to handle rapid changes in intra- or extracellular osmotic pressure, i.e., the small-scale local osmotic gradients that are inherent in many transport and/or metabolic processes. This mechanism would keep the transmembrane osmotic pressure gradient at a minimum (or zero) and maintain steady-state cellular volume, which is important for cellular homeostasis. The proteins that mediate the water cycle may also be a component of the system that transports water in response to large-scale osmotic pressure differences.