Removing technical variability in RNA-seq data using conditional quantile normalization

Abstract

The ability to measure gene expression on a genome-wide scale is one of the most promising accomplishments in molecular biology. Microarrays, the technology that first permitted this, were riddled with problems due to unwanted sources of variability. Many of these problems are now mitigated, after a decade's worth of statistical methodology development. The recently developed RNA sequencing (RNA-seq) technology has generated much excitement in part due to claims of reduced variability in comparison to microarrays. However, we show that RNA-seq data demonstrate unwanted and obscuring variability similar to what was first observed in microarrays. In particular, we find guanine-cytosine content (GC-content) has a strong sample-specific effect on gene expression measurements that, if left uncorrected, leads to false positives in downstream results. We also report on commonly observed data distortions that demonstrate the need for data normalization. Here, we describe a statistical methodology that improves precision by 42% without loss of accuracy. Our resulting conditional quantile normalization algorithm combines robust generalized regression to remove systematic bias introduced by deterministic features such as GC-content and quantile normalization to correct for global distortions.

1. INTRODUCTION

High-throughput sequencing technology is currently being used to quantify gene expression levels on a genome-wide scale. This is done by first converting RNA transcripts into complementary DNA (cDNA) fragments, and then sequencing these fragments to produce millions of sequences of length 35–150 basepairs (bps), referred to as “reads.” Gene expression is quantified by counting the number of these reads that map back to each gene. The conventional wisdom is that this approach is an improvement over microarrays as it is a direct measurement of RNA levels and does not rely on hybridization, a process known for its lack of specificity (Wu and others, 2004; Zhang and others, 2003; Naef and Magnasco, 2003). Early studies, based on a small number of samples in highly controlled conditions, found that RNA sequencing (RNA-seq) has excellent technical reproducibility (Mortazavi and others, 2008; Marioni and others, 2008; Bullard and others, 2010). Furthermore, in a review article, Wang and others (2009) claimed that analysis of RNA-seq data does not require “sophisticated normalization.” This view was widely accepted because, unlike in microarray technology, sequencing was not affected by the culprits of nonlinear distortions, namely, chemical saturation due to hybridization and optical saturation due to scanner limitations. However, RNA-seq's sample preparation protocol includes multiple procedures that are susceptible to experimental conditions, for example, RNA extraction, reverse transcription, amplification, and fragmentation that may introduce nonlinear effects. As more data became available, problems such as sequence-specific biases were reported (Hansen and others, 2010; Li and others, 2010; Pickrell and others, 2010). Here, we make use of 3 large and 1 small, publicly available, RNA-seq data sets to demonstrate that sample-specific systematic biases, along with distortions that affect the overall distribution of count data, introduce unwanted variation in RNA-seq data that obscures the underlying biological signal.

RNA-seq technology permits applications not previously possible with microarrays. However, determining whether the expression level of a genomic unit (such as a gene, exon, or junction) differs across experimental conditions continues to be an important question in functional genomics. Therefore, to demonstrate the importance of normalization in RNA-seq data, we focus on the application of differential expression detection (Bottomly and others, 2011; wu and others, 2010; Lefebvre and others, 2011; Anders and others, 2010; Robinson and others, 2010; Eveland and others, 2010).

We start by counting the number of reads in predetermined genomic regions, such as those defined by the Ensembl database (Flicek and others, 2011), for each sample to form gene expression matrices with rows representing genes and columns representing samples as with microarray data. Because most tests developed for differential expression testing in microarray data depend on assumptions not necessarily applicable to the count data produced by RNA-seq, alternative statistical methodologies have been proposed (Anders and Huber, 2010; Robinson and others, 2010; Robinson and Smyth, 2007, 2008). Similarly, alternative normalization approaches have been proposed. The first normalization approach described in the literature was to simply correct each sample for the number of mapped reads produced for each sample, referred to as “sequencing depth,” and each gene for its length (Mortazavi and others, 2008). Because variability in sequencing depth was observed in technical replicates, it was assumed to be a technical artifact, and because longer genes are expected to have higher counts, Mortazavi and others (2008) defined the widely used “reads per kilobase per million” (RPKM) measure as the number of reads mapped to a gene in a sample divided by the product of the length of the gene in kilobases and the total number of reads mapped in the sample in millions. Various authors then showed that sequencing depth is not a stable scaling factor and a number of more robust alternatives were suggested (Bullard and others, 2010), (Robinson and Oshlack, 2010), (Anders and Huber, 2010), with Langmead and others (2010) suggesting that there might be a gene-specific linear effect of the sample-specific scaling factor. However, in Section 3, we demonstrate that, even with improved scaling, the use of the RPKM measure is not a general solution to the unwanted variability problem. In Section 2, we describe the data sets used throughout the paper, including the data set from Pickrell and others (2010) who first noticed a sample-specific guanine-cytosine content (GC-content) effect and proposed a normalization by GC-strata to remove such effects. In Section 3, we motivate our approach. In Section 4, we present a useful statistical model and use it to motivate our normalization algorithm. In Section 5, we present results illustrating the improvements made possible by our approach. Finally, in Section 6, we discuss future directions and connections to existing methodology for differential expression detection.

2. DATA DESCRIPTION

We examined the 3 currently available RNA-seq data sets with the largest number of samples (Pickrell and others, 2010; Montgomery and others, 2010; Cheung and others, 2010). In all 3 studies, the samples are lymphoblastoid cell lines from unrelated individuals in the HapMap project (International HapMap Consortium, 2003). Montgomery and others (2010) sequenced 60 individuals from the Utah residents with ancestry from northern and western Europe collected by Centre d'Etude du Polymorphisme Humain (CEPH). Cheung and others (2010) sequenced 41 individuals also from the same population with 29 in common with Montgomery and others (2010). Pickrell and others (2010) sequenced 69 individuals from Yoruba in Ibadan, Nigeria. All 3 studies, hereafter referred to as Montgomery, Pickrell, and Cheung, were designed to study the effect of genetics on gene expression and subjects were considered interchangeable. We therefore used these data to assess improvements in precision. The samples that were done in replicate across 2 studies were particularly useful for this purpose.

We also examined 6 human samples from Pai and others (2011). This study sequenced 3 male and 3 female livers and compared the results to other primate species. The samples were from primary tissues, as opposed to cell lines which are generally associated with more stable RNA data. This data set, which we refer to as Pai, served as an example of a small study based on a controlled experiment.

To assess accuracy, we used samples from Bullard and others (2010), in which 2 samples from the microarray quality control study (MAQC Consortium, 2006) were sequenced. These 2 samples are Stratagene's universal human reference RNA (UHR), which is a commercial pool of RNA from 15 different cell lines, and Ambion's human brain reference RNA. The same samples have been assayed extensively on microarrays, and we used data from the MAQC Consortium (2006), in which each of the 2 samples was hybridized to 5 different Affymetrix U133 Plus 2.0 arrays (Affymetrix, Santa Clara, CA). The microarrays served as an independent measurement that permitted an assessment of accuracy. This data set has no biological replicates, and the technical replicates are based on commercially available RNA, making the technical noise smaller than what would be expected from tissue samples.

For all data sets, the original reads were downloaded, mapped, and the gene expression count matrix created as follows. Reads were aligned to the human reference genome sequence (version hg19) using Bowtie (Langmead and others, 2009), allowing up to 2 mismatches. All reads were trimmed from the 3^′ end to be 35-bp long, and for the Montgomery data, we used the first read of the paired-end reads. To assign reads to genes, we followed essentially the same procedure used by Bullard and others (2010), except for (a) we determined overlap between a read and a genomic region based on the center base of the trimmed read and not the 5^′ end and (b) we used union gene representations instead of union–intersection gene representation as discussed in Bullard and others (2010). Sequencing depth was determined as the number of reads mapped to the genome.

3. MOTIVATION

The need for a normalization technique more complex than scaling is first motivated by simply noting that the distribution of counts across different samples differs (Figure 1(a)). Since the raw counts are affected by sequencing depth, we also compared the distribution of reads per million (RPM) (not shown). The locations of the peaks of the RPM densities of these replicates became closer, but both the shape and scale of the distributions still vary. This demonstrates that a scaling normalization, that is, a shift in log-scale expression, is not sufficient to completely normalize counts between samples.

Fig. 1.

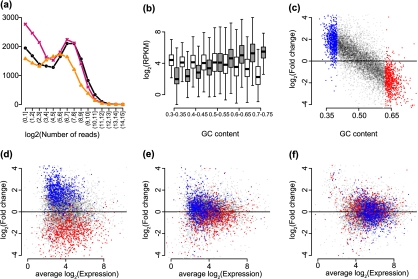
Exploratory plots. (a) The points show the frequency of counts in the bins shown on the x-axis. The 3 colors represent 3 samples (NA12812, NA12874, and NA11993) from the Montgomery data. (b) log₂-RPKM values are stratified by GC-content for 2 biological replicates from the Montgomery data (NA11918 and NA12761) and are summarized by boxplots. The 2 samples are distinguished by the 2 colors (colors can be seen in the online version). Genes with average (across all 60 samples) log₂-RPKM values below 2 are not shown. (c) Log fold changes between RPKM values from the 2 samples and the same genes shown in (b) were computed and are plotted against GC-content. Red is used to show the genes with the 10% highest GC-content and blue is used to show the genes with the 10% lowest GC-content. (d) RPKM log fold changes are plotted against average log₂ counts for the samples and genes shown in (b), with the same color coding as in (c). (e) As (d) but from values corrected using the method proposed by Pickrell and others (2010). (f) As (d) but for values normalized using our approach (see Section 4).

Contrary to an early expectation of RNA-seq technology, the number of reads from a given gene is not simply determined by the gene expression level. Rather, certain fragments are preferentially detected in the RNA-seq data acquisition process, leading to nonuniform detection of expression between genes. We refer to this bias in measurement as “counting efficiency.” The best documented example is the effect of the percent of C or G nucleotides in a gene: the so-called “GC-content” effect. GC-content has been shown to influence a number of DNA-related measurements. Examples include gene expression microarrays (Wu and others, 2004; Zhang and others, 2003; Naef and Magnasco, 2003), copy number arrays (Nannya and others, 2005; Carvalho and others, 2007), sequencing coverage (Dohm and others, 2008), and RNA-seq (Pickrell and others, 2010). The difference in counting efficiency between genes means that expression levels cannot be compared between genes directly. A more subtle and detrimental problem is that these systematic biases affect different samples differently, thus, even within gene, comparison between 2 samples becomes problematic. In fact, Pickrell and others (2010) demonstrated that the GC-content effect can change from sample to sample. Here, we demonstrate that this appears to be a general problem. In Figure 1(b), we show the distribution of log₂-RPKM for various strata of gene GC-content for 2 biological replicates from the Montgomery study. For illustration purposes, we selected one sample in which a higher GC-content leads to increased counting efficiency and another in which there is little impact. This problem has downstream consequences since observed fold changes are obscured by the variability introduced by GC-content effects (Figure 1(c) and (d)).

Some work has been done to address these effects. Pickrell and others (2010) suggested stratifying predefined genomic regions by GC-content and then for each stratum, dividing the sample counts by the sum of the counts across all samples. This fraction is considered an enrichment factor for that GC-content stratum, which is then smoothed by GC-content for each sample separately. Counts are then adjusted by the smoothed enrichment factor. Finally, they did this at the exon level, adding adjusted counts across all exons from a gene in order to obtain gene-level adjusted counts. We found 2 problems with this approach that we decided to improve. First, the enrichment scores are computed for each sample relative to all samples in an experiment, thus, this adjustment does not remove the GC-content effect but rather equalizes the effect across samples. As a consequence, adjustments vary depending on what samples are processed together. Second, the GC-content effect is estimated based on the direct summation of counts on different genes in different samples, ignoring the fact that genes with higher expected counts also have greater variance. As a result, GC-content effects are not entirely removed (Figure 1(e)). To study the effect of genotype on gene expression, Pickrell and others (2010) also employed 2 rounds of quantile normalization on the GC-corrected gene by sample matrix, first on the genes such that each gene ends up with a standard Gaussian distribution across samples and then on the samples. Between these 2 rounds of normalization, they also corrected for the effect of differing sequencing centers and sample concentrations and removed the first 16 principal components. In addition, Roberts and others (2011) address bias removal within the Cufflinks transcript assembly framework (Trapnell and others, 2010) and show improvements in comparisons between sequencing technologies but do not address variation between biological replicates.

4. METHODS

We present a normalization algorithm motivated by a statistical model that accounts for both the need to correct systematic biases and the need to adjust for distributional distortions. We denote the log gene expression level for gene g at sample i with θ_g,i, which we consider a random variable. For most g, θ_g,i are independent and identically distributed across i. We assume that the marginal distribution of the θ_g,i is the same for all samples i and denote it by G. Note that this variability accounts for the difference in gene expression across different genes. The p covariates thought to cause systematic errors are denoted with X_g = (X_g,1,…,X_g,p)^′. Examples of covariates considered here are GC-content, gene length, and gene mappability defined as the percentage of uniquely mapping subreads of a gene. To model the observed counts Y_g,i for gene g in sample i, we write:

with

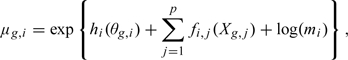with $f_{i,j}({\stackrel{-}{X}}_{.j})=0\forall j$ for identifiability. Here, the h_is are nondecreasing functions that account for the fact that count distributions are distorted in nonlinear ways across the different samples (Figure 2(a)). The f_i,js account for sample-dependent systematic biases. Data exploration suggested that these are smooth functions, so for tractability, we model these as (parametric) natural cubic splines with known degrees of freedom and knot locations. If there is no technical variability, h_i is the identity function and ∑_{j = 1}^pf_i,j(X_g,j) = 0, then the distribution of Y_gi for a given i reduces to a G-Poisson mixture. Finally, m_i is the sequencing depth in millions.

Fig. 2.

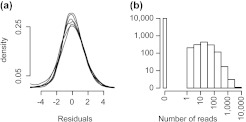
Empirical distributions. (a) Empirical density estimates of $\text{log}(Y_{g,i})-{\widehat{f}}_{i,j}\left(X_{g,j}\right)$ are shown for 6 samples from the Montgomery data. (b) A histogram of counts in a single sample for genes with a GC-content of 45 ± 1% and with a length between 500 and 2000 bp is shown.

With the model in place, obtaining normalized counts is equivalent to estimating θ_g,i. To do this, we needed to estimate the nonparametric h_i functions along with the linear parameters that define the splines. Note that the distribution of the θ_g,i in a sample is determined by the biological system, which varies greatly between species, tissue types, and developmental stages. Thus, it is unrealistic to restrict it to a particular parametric family of distributions. This makes estimation requiring full likelihood, including maximum likelihood estimation and Bayesian approaches unsuitable. In addition, outliers can arise because of either biological activity or technical artifacts. Since both h and f represent the global impact of systematic effects on all genes in general, it is crucial to define estimation procedures that are robust to outliers. We take advantage of the large amount of data for each sample and our parsimonious model to define a stable algorithm, which we now motivate and describe.

For any given i, the distribution of h_i(θ_g,i) is unspecified, and Figure 2(b) shows that values can range from − ∞ to 8. First, we use the delta method and note that when μ_g,i is large, log(Y_g,i)|μ_g,i is approximately normal with mean log(μ_g,i) and variance 1/μ_g,i. The small variance implies that for large μ_g,i,

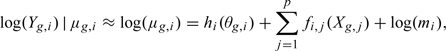showing that for a fixed i and large μ_g,i, the distribution of log(Y_g,i) is equal to h_i(θ_g,i) except for a location shift given by ∑_{j = 1}^pf_i,j(X_g,j). Even though the shape of h_i(G) is left unspecified, the quantiles of log(Y_g,i) shift by ∑_{j = 1}^pf_i,j(X_g,j). We therefore use quantile regression to estimate the f_i,js. To assure the large μ_g,i assumption is satisfied, instead of fixing the quantile choice, we use median regression on a subset of genes with average counts beyond a lower bound.

To estimate the h_is, we take advantage of the fact that

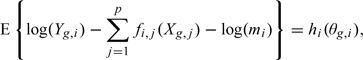and that the distribution of θ_g,i does not depend on i, to use quantile normalization (Bolstad and others, 2003), (Wu and Aryee, 2010).

The specifics of our algorithm are as follows with all the details available in the open source code:

1. Select a subset of genes with ${\stackrel{-}{Y}}_{g,.}>50$. Then, for the genes satisfying this cutoff, we assume log(Y_g,i + 1) − log(m_i) = ∑_{j = 1}^pf_i,j(X_g,j) + ϵ_g,i where the fs are natural cubic splines. For the results shown in the paper for GC-content and gene length, we used the R function “ns” from the “splines” package with 5 knots at the (0.025,0.25,0.5,0.75,0.975)-quantiles. Then, for each sample i, we estimate the spline parameters using median regression via the “rq” function in the “quantreg” package (Koenker, 2011). With these parameter estimates, we then define ${\widehat{f}}_{i,j}$.

2. A modified quantile normalization is applied to the residuals ${\widehat{ϵ}}_{g,i}\equiv \text{log}(Y_{g,i}+1)-\text{log}(m_i)-\sum _{j=1}^p{\widehat{f}}_{i,j}\left(X_{g,j}\right)$. The default algorithm implementing quantile normalization (Bolstad and others, 2003) maps the distribution of each sample, estimated by the empirical cumulative distribution function (CDF) of each sample, to a target distribution, estimated by the empirical distribution of the averaged order statistics. To normalize the genes not included in the subset defined in Step 1, we modified this algorithm by estimating the CDFs as a weighted average of the empirical CDF and a parametric estimate based on a Gaussian mixture, as described in Wu and Aryee (2010). Finally, we define ${\widehat{h}}_i^{-1}$ as the function that maps the sample-specific residuals to the reference distribution.

3. For each gene g on each sample i, define a “normalization offset” as

   

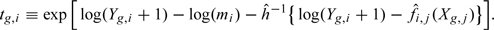
The algorithm returns an offset rather than normalized data for 2 reasons. First, for interpretability, we want to preserve the data as counts, that is, integer numbers. Due to the large sampling error, small counts should be treated with caution, and thus, users of the algorithm benefit from access to these original counts. Second, the most widely used methodologies for identifying differentially expressed genes from RNA-seq data model the counts in a way that sampling error from counting process (such as Poisson) and variation in gene expression (θ) are taken into account (Robinson and others, 2010; Anders and Huber, 2010). Providing an offset allows direct application of these existing methods, which take counts as input and can be easily adapted to adjust for offsets. For example, in designed experiments, we recommend the modular approach generally used in microarray experiments. Specifically, first apply conditional quantile normalization (CQN), without consideration of the experimental design, to obtain the normalization offsets. Then, fit a generalized linear model (GLM) that does take into account the design, as done by McCarthy and others (2012), by assuming log(μ_gi/t_gi) = Zβ_g with μ and t as defined above, Z the design matrix, and β the parameters of interest.

While the algorithm allows one to correct for a variety of systematic biases, we have consistently used GC-content and gene length. An R package (“cqn”) implementing the method is available from “Bioconductor” (http://bioconductor.org).

5. RESULTS

Because experimentally controlling for the amount of RNA extracted from a sample is difficult, the total number of counts varies across samples and manifests itself as between sample differences in the locations of the log read count distributions (Figure 1(a)). This unwanted technical variability is further augmented by the differences in cDNA amplification efficiency (Aird and others, 2011) and other technical artifacts, and differences in distribution shapes and scales persist after library size is taken into account. Scaling normalization based on more robust estimates of the shift in location (Bullard and others, 2010; Robinson and Oshlack, 2010; Anders and Huber, 2010) can provide further improvement, although improvement is limited in the samples we have analyzed (as an example, results for trimmed median of M-values from Robinson and Oshlack, 2010, are shown in Figure 4). In contrast, our normalization approach (CQN) results in sample distributions with comparable scales and shapes, as discussed below.

Fig. 4.

Improved precision provided by CQN on comparisons across studies. (a) We show boxplots of the estimated log fold change between the 2 groups of 5 samples (the same 2 groups as in Figure 3) from the Montgomery data using standard RPKM, expression values normalized by TMM (trimmed median of M-values, the method proposed in Robinson and Oshlack, 2010), the method proposed in Pickrell and others (2010), and CQN with and without quantile normalization. We show genes with length greater than 100 bp and average (across all samples) log₂-RPKM greater or equal to 2. (b) We normalized the 29 samples assayed in both Montgomery and Cheung. For each gene, we computed the mean squared difference between the expression measure based on the Montgomery and the Cheung data. The boxplots show the distribution of these precision measures for the highly expressed genes, for each of the 4 choices of normalization: standard RPKM, TMM, the method proposed in Pickrell and others (2010), and CQN. We show genes with length greater than 100 bp and average (across all samples) log₂-RPKM greater or equal to 2. (c) For the MicroArray Quality Control data, we obtained fold change estimates between UHR and brain based on RNA-Seq and microarrays. For RNA-seq, we used 2 samples. For the microarrays, we used a 5 versus 5 comparison. The microarray data were normalized using Robust Multiarray Analysis, and the RNA-seq data were normalized by CQN.

To demonstrate the downstream advantages of our algorithm, we first considered comparisons between 2 samples. For illustrative purposes, we selected 2 samples with very different systematic bias patterns (f_i,js). For the assessment, we focused on fold change as it is considered the basic unit for differential expression analysis. We computed log fold change for each gene after both RPKM normalization and CQN, and a substantial improvement was observed (Figure 1(e) and (f)). Specifically, while the RPKM showed a strong dependence between fold change and GC-content, CQN eliminated it.

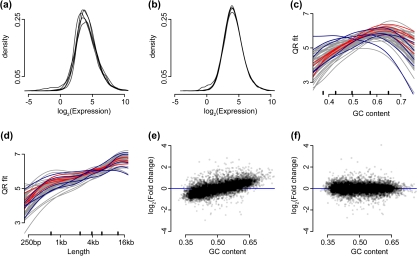
The resulting estimates of ${\widehat{f}}_{i,j}$ provided a useful quality assessment since plotting these demonstrated a wide range of GC-content and gene length effects (Figure 3(c) and (d)). In the data sets we analyzed, length effects were more consistent between samples than GC-effects. For many samples, the length effect is close to linear with a constant slope for genes shorter than 5000 bp. This result implies that dividing by gene length, as done by the RPKM approach, is suitable in most circumstances. However, we observed that for genes shorter than 1000 bp, the length effect appears to be stronger, while for genes beyond 5000 bp, the length effect plateaus. This suggests that dividing by gene length may not always be appropriate. A sample-specific gene length effect may capture sample-specific fragmentation bias as well as differences in size selection.

Fig. 3.

Results from normalizing 60 samples. In these plots, we only show genes with a length greater than 100 bp and an average (across all 60 samples) standard log₂-RPKM of 2 or greater. (a) Empirical density estimates of log₂-RPKM for 5 different biological replicates from the Montgomery data are shown. (b) As (a) but CQN-normalized expression values on the log₂-scale are shown. (c) The estimated GC-content effect are shown as curves for all 60 biological replicates in the Montgomery study. We created a 5 versus 5 comparison using the samples highlighted in blue (group 1) and red (group 2) (colors can be seen in the online version). (d) As (c) but curves are shown for the gene length effect instead of GC-content. (e) Average log fold change is plotted against GC-content. Here, we used RPKM values and compared group 2 to group 1. (f) Average log fold change is plotted against GC-content using CQN-normalized expression measures.

We have illustrated the potential downstream consequences of not normalizing with a comparison of 2 samples (Figure 1). To demonstrate the advantages of CQN in a study with replicates, we performed a 5 versus 5 comparison of biological replicates, between which we expect little difference. Systematic bias was observed in the average log fold changes with a strong dependence on GC-content, using standard RPKM (Figure 3(e)). These problems were removed by CQN (Figure 3(f)). The log fold variation was noticeably reduced by CQN (Figure 4(a)). We also observed systematic bias in the Pai data, a small controlled experiment (see supplementary Figure 1 available at Biostatistics online).

To perform a global assessment of precision, we compared the 29 Hapmap samples processed by both the Cheung and the Montgomery studies. For each gene, we computed the mean squared difference between the expression measures from the 2 technical replicates. Our approach improved precision greatly as shown in Figure 4(b): The median mean squared difference was reduced by 42% after normalization. This comparison also shows that most of the improvement offered by CQN is due to removing the effect of the gene-specific covariates, not the quantile normalization. Note that this shows improvements in across study comparisons.

Finally, to assure that the gains in precision were not achieved by simply reducing overall dynamic range, we assessed accuracy by comparing RNA-seq counts to measurements from microarrays. Specifically, we computed log fold change values between UHR and brain and averaged these across all replicates. We did this for both microarrays and sequencing counts and then compared the agreement with microarrays to sequencing counts after RPKM normalization or CQN. We found similar accuracy (Figure 4(c)): Between technology, correlations were 0.84 using CQN normalization compared to 0.85 using standard RPKM. Indeed, using standard RPKM instead of CQN normalization produced a plot very similar to Figure 4(c) (not shown).

6. DISCUSSION

Unlike previous reports based on small samples, by examining large data sets processed from 4 different studies, we found RNA-seq data to be greatly affected by bias and systematic errors. We also observed these effects in a small controlled experiment. Previously developed normalization methods (Bullard and others, 2010; Robinson and Oshlack, 2010; Anders and Huber, 2010) consider the sample effect as common for all genes, and thus, only one scaling factor is estimated in a sample. Although RPKM takes gene length into account, the effect is considered static and constant for all samples. By studying 4 different RNA-seq data sets, we found that these assumptions do not always hold. In fact, the GC-content effect may vary substantially between samples as does the gene length effect, although to a lesser degree. Just as with microarrays, we found that lack of proper normalization can lead to false positives in a differential expression analysis. Particularly, sample-specific GC-content effects led to confounding of GC-content and observed log fold change values.

To remove these unwanted sources of variation, we developed a normalization procedure for RNA-seq data that greatly improved precision without affecting accuracy. We demonstrated the improvements with comparisons of 2 biological samples and a 5 versus 5 example. Although in a comparison with many biological replicates, the observed sample-specific biases may cancel out, large studies are not the norm due to the cost and current optimistic view of the technology's precision (Hansen and others, 2011). More importantly, we show a great increase in precision across studies using CQN. Removing the GC-content effect was the primary source of the improvement. Quantile normalization provided additional improvements, but we recommend that one guide the decision to implement this feature using data exploration (Figure 2(a)). Note that although CQN does not take experimental design into consideration, it is designed to work in conjunction with analysis methods that do, for example, McCarthy and others (2012). We recommend a modular approach, in which CQN preprocessing is followed by linear modeling. Note that CQN returns a sample-/gene-specific normalization offset that can be readily used with the current implementations of the most widely used GLM-based frameworks: edgeR (Robinson and others, 2010) and DEseq (Anders and Huber, 2010).

CQN is not the first attempt to remove sample-specific GC bias. As mentioned above, Pickrell and others (2010) equalize the GC-content effect across all samples but leave an average experiment-wide effect in the normalized data. In contrast, CQN removes the GC-content effect under the assumption that the distribution of true expression values does not depend on GC-content. Although it is possible that the association between GC-content and absolute gene expression is not an artifact but due to a real biological event, we conjecture that associations with relative levels are much more likely to be due to unwanted variation. In fact, we observed strong GC-content effects across different parts of the same gene (see supplementary Figure 2, available at Biostatistics online), a result that points to the variability being technical as opposed to biological. We therefore conclude that applying CQN will improve downstream results much more than it will remove interesting variation.

For the results presented here, we considered only 2 covariates, GC-content and gene length, but our model permits the inclusion of others: for example, mappability or more elaborate models of sequence effects. Although the biochemical and technical mechanisms for the inconsistent systematic biases between samples are not fully explained, these biases can be estimated and adjusted for because of the high-throughput nature of RNA-seq technology.

SUPPLEMENTARY MATERIAL

Supplementary material is available at http://biostatistics.oxfordjournals.org.

FUNDING

National Institutes of Health (R01HG004059) and National Science Foundation (DBI-1054905).