Family-based association tests using genotype data with uncertainty

Abstract

Family-based association studies have been widely used to identify association between diseases and genetic markers. It is known that genotyping uncertainty is inherent in both directly genotyped or sequenced DNA variations and imputed data in silico. The uncertainty can lead to genotyping errors and missingness and can negatively impact the power and Type I error rates of family-based association studies even if the uncertainty is independent of disease status. Compared with studies using unrelated subjects, there are very few methods that address the issue of genotyping uncertainty for family-based designs. The limited attempts have mostly been made to correct the bias caused by genotyping errors. Without properly addressing the issue, the conventional testing strategy, i.e. family-based association tests using called genotypes, can yield invalid statistical inferences. Here, we propose a new test to address the challenges in analyzing case-parents data by using calls with high accuracy and modeling genotype-specific call rates. Our simulations show that compared with the conventional strategy and an alternative test, our new test has an improved performance in the presence of substantial uncertainty and has a similar performance when the uncertainty level is low. We also demonstrate the advantages of our new method by applying it to imputed markers from a genome-wide case-parents association study.

1. INTRODUCTION

Genotyping uncertainty is inherent in both directly genotyped/sequenced DNA variations and imputed data in silico. In directly genotyped data, the fully automated clustering algorithms adopted by current high-throughput technologies are unavoidable to errors and missingness in assigning genotypes when the clouds of fluorescence signals are not perfectly separated or when a rare cluster has few data points. Analyzing genotype data with uncertainty is also increasingly encountered with the growing popularity of testing association using low-coverage sequencing data (Li and others, 2011) and imputed genotypes (Browning and Browning, 2009; Li and others, 2010; Lin and others, 2008; Marchini and others, 2007; Nicolae, 2006; Servin and Stephens, 2007; Zaitlen and others, 2007).

Genotyping uncertainty causes both genotyping errors and missingness. The consequence of genotyping errors on genetic association studies has been extensively studied (Pompanon and others, 2005). Random genotyping errors, i.e. errors not relying on disease status, may reduce the power (Gordon and Ott, 2001) but are unlikely to affect the false-positive rates of case–control studies. For family-based studies, however, genotyping errors not only affect the power but also inflate the false-positive rate (Gordon and others, 2001; Heath, 1998; Mitchell and others, 2003). As a result, different approaches have been proposed to correct the inflation due to genotyping errors for the case-parents design (Cheng and Chen, 2007; Gordon and others, 2001; Morris and Kaplan, 2004) and for general pedigrees (Gordon and others, 2004).

Genotyping errors can be prevented by using a stringent cutoff in genotype calling and it is believed that the impact of genotyping errors on different genetic studies is unlikely to be an important factor with the improvement of genotyping technologies (Laird and Lange, 2006). However, genotype-specific missingness cannot be eliminated by using a stringent cutoff in genotype calling. Despite the high genotyping accuracy and the overall high call rate of currently used genotyping and sequencing technologies, genotype-specific missingness still exists (Fu and others, 2009; Illumina, 2010). Compared with the impact of genotyping errors that of genotype-specific missingness is much less studied. For family-based association studies, there are only a few published articles related to the problem of genotype-specific missingness. (Hirschhorn and Daly, 2005) found that genotype-specific call rates can cause false positives in the case-parents design, and the impact is the largest when the minor allele frequency (MAF) is small enough to avoid Hardy–Weinberg disequilibrium (HWE) but large enough to cause false positives. Other relevant work includes methods that aim to reduce the bias caused by informative missingness of parental data (Allen and others, 2003; Chen, 2004). However, the missingness they consider is caused by the unavailability of parental DNA samples.

Because the bias caused by genotyping errors has been well studied, here we examine the bias caused by genotype-specific missingness in family-based association studies. Consider a single nucleotide polymorphism (SNP) with alleles A and B. For simplicity, we assume that case-parents trios are sampled from a random mating population. (Curtis and Sham, 1995) suggested that, to avoid bias, trios with one missing parent should be excluded from the calculation of the transmission disequilibrium test (TDT) (Spielman and others, 1993) statistic. Let b denote the number of heterozygous parents who transmitted allele A to his/her offspring; let c denote the number of heterozygous parents who transmitted allele B to his/her offspring. The TDT, which is a McNemar test, is defined as 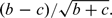Among the 3 genotypes of a SNP, the rare homozygous genotype is usually more difficult to be called because it has fewer data points, and the common homozygous genotype is usually easier to be called because it has more data points. Under these conditions, ($b-c$) has a positive expectation when $p>$ 1/2 and a negative expectation when $p<$ 1/2, where p is the frequency of allele A. Full details of the direction of bias are in Section A of the supplementary material available at Biostatistics online. This implies that the unequal missingness leads to overtransmission of the common allele. (Mitchell and others, 2003) found that genotyping errors also lead to overtransmission of the common allele. This suggests that the bias reported by (Mitchell and others, 2003) is caused probably not only by genotyping errors but also by genotype-specific missingness.

The bias caused by genotype-specific missingness and genotyping errors demonstrates that it is of great importance to develop association testing strategies that can take into account uncertainty in genotyped, sequenced, or imputed genetic data for family-based association studies. Methods to incorporate genotyping uncertainty have been proposed and studied for samples with unrelated subjects (Allen and others, 2010; Guan and Stephens, 2008; Kutalik and others, 2011; Lin and others, 2008; Marchini and others, 2007). However, there are few family-based association methods that systematically and efficiently take uncertainty into consideration in imputed data. One exception is (Chen and Abecasis, 2007), which deals with the situation that only a subset of individuals in each pedigree was genotyped in a high resolution. As both genotyping error and genotype-specific missingness caused by genotyping uncertainty can inflate the false-positive rates of family-based association tests (FBATs), a strategy that can simultaneously address the 2 difficulties would be desirable. In this article, we discuss strategies to analyze uncertain genotype data for family-based studies and propose a new FBAT that incorporates genotyping uncertainty. Using simulated data, we demonstrate that our new method improves Type I error rates and power in the presence of substantial uncertainty. We also demonstrate the advantage of our new method by applying it to imputed markers from a genome-wide association study using case-parents trios. The software that implements our new method is available upon request.

2. METHODS

In this section, we first briefly describe the original FBAT for genotype data without uncertainty. We will then provide testing strategies that can incorporate genotyping uncertainty.

2.1. The original FBAT

Suppose there are $n_i$ assayed members in the ith family and we use $G_i=(G_{i1},\dots ,G_{i{n}_i})$ to denote the genotype vector of the assayed members, with i = 1, . , n. Let $T_{ij}$ be the trait value, and $X_{ij}\left(G_i\right)$ be the count of the risk alleles of the jth nonfounder in the ith family, with$j=1,\dots ,n_i^{\prime }$. Here, we assume that the nonfounders are a subset of the assayed members in a family. For example, for the ith case-parents trio, the number of assayed members $n_i$ is 3 and the number of nonfounders $n_i^{\prime }$ is 1. Here, the genotype vector $G_i$ is required to be free from Mendelian errors, and we call such genotype vectors as compatible genotypes. To conduct the original FBAT (Horvath and others, 2001; Rabinowitz and Laird, 2000), we first compute the score U and the variance V for each family, respectively:

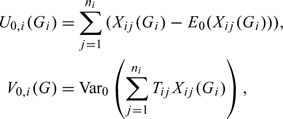where $E_0(·)$ and ${Var}_0(·)$ denote the expectation and variance, respectively, under the null hypothesis of no association between the testing marker and the trait. The mathematical formula of the null expectation of the score can be found in (Horvath and others, 2001). The formula of the null variance depends on whether association is tested in the absence or presence of linkage (Horvath and others, 2001; Lazzeroni and Lange, 1998; Martin and others, 2000; Rabinowitz and Laird, 2000). When testing association in the absence of linkage, its formula for general nuclear families was given by (Horvath and others, 2001). To test association in the presence of linkage, one can use the empirical variance (Lake and others, 2000), i.e. $V_{0,i}\left(G_i)=U_{0,i}^2\right(G_i)$. Once the scores and variances are computed, the test statistic can be computed as follows:

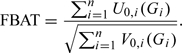Under the null hypothesis of no genetic effects, the test statistic follows a standard normal distribution approximately. Because we define $X_{ij}\left(G_i\right)$ as the count of the risk alleles of the jth nonfounder in the ith family, our tests assume log-additive genetic effects. Other genetic effects can be tested by changing the definition of $X_{ij}\left(G_i\right)$.

2.2. The FBAT that takes uncertainty into account by weighting (${\text{FBAT}}_{\text{weight}}$)

The first method we examine is to take uncertainty into account by weighting. The idea of incorporating weights into likelihood has been proposed for testing imputed markers using unrelated subjects (Guan and Stephens, 2008; Kutalik and others, 2011; Marchini and Howie, 2010). In these methods, quantifying uncertainty, such as computing genotype probabilities, is first conducted, then these probabilities are treated as known values in the association testing stage using weighted likelihood. Here, we adopt the idea of weighting to studies using families. In the presence of genotyping uncertainty, such as imputed genotypes, genotypes are usually not directly observed. Instead, it is the individual genotype probabilities that are available. Let $P(G_{ij}\parallel S_{ij})$ be the genotype probability for the jth assayed member of the ith family, where $S_{ij}$ denote the observed signal intensities in genotype data, read counts in sequence data, or the information that allows to impute an ungenotyped SNP such as genotyped SNPs and the linkage disequilibrium pattern of an independent panel of samples. These individual genotype probabilities are provided by many genotype calling packages (Bravo and Irizarry, 2010; Browning and Yu, 2009; Carvalho and others, 2010; Teo and others, 2007; WTCCC Consortium, 2007) or packages that impute ungenotyped SNPs (Browning and Browning, 2009; Li and others, 2010; Marchini and others, 2007). For a compatible genotype of the ith family $G_i=(G_{i1},\dots ,G_{i{n}_i})$ with the corresponding $S_i=(S_{i1},\dots ,S_{i{n}_i})$, the genotype probability $P(G_i\parallel S_i)$ equals the product of individual genotype probabilities, subject to standardization by a constant:

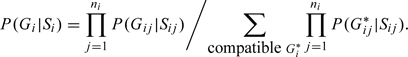As derived in Section B of the supplementary material available at Biostatistics online, using weighted likelihood for the ith family leads to the following score and variance:

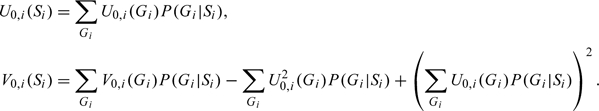(2.1)

We denote the FBAT test based on the above score and variance as ${\text{FBAT}}_{\text{weight}}$, which uses the test statistic 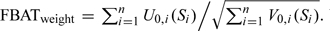When the null hypothesis is true, assuming that the weights are known and the uncertainty level is independent of genotypes, this test statistic is expected to follow the standard normal distribution asymptotically.

2.3. A likelihood ratio test that assumes genotype-specific call rates (${\text{FBAT}}_{LRT}$)

Motivated by the fact that both genotype errors and genotype-specific call rates can cause bias, we propose a likelihood ratio test that uses genotype-specific call rates as nuisance parameters. At a single SNP, estimating genotype-specific call rates is an unidentifiable problem for unrelated subjects. Fortunately, with the familial structure and the resulting constraints on the genotypes of family data, genotype-specific call rates can be incorporated into likelihood function. Here, we present the method applicable to the case-parents design.

For data with uncertainty, we first use a cutoff value of 0.9 to make genotype calls. This step protects against large genotyping error rates of calls when data quality is not high, such as when imputed genotypes are used. Let $g_i$ and $G_i$ denote the observed and the underlying true genotype vectors for the ith trio, respectively. Note that $g_i$ can contain up to 3 missing genotypes. To follow the FBAT framework, we assume the log-additive genetic effects. Let BB genotype be the baseline genotype, and β be the log of the relative risk (Schaid and Sommer, 1993) of the AB genotype. The log-additive assumption implies that

Let $c=(c_{\text{AA}},c_{\text{AB}},c_{\text{BB}})$ denote the vector of call rates, and $\mu =({\mu }_1,\dots ,{\mu }_9)$ denote the 9 mating type probabilities. To make the presentation of the method easier, we let $\theta =({\theta }_1,\dots ,{\theta }_{15})$ be the frequencies of the 15 possible trio types (see Table S2 of the supplementary material available at Biostatistics online). As shown in Table S2 of the supplementary material available at Biostatistics online, θ is not an additional vector of parameters, as it is completely determined by μ and β. Assuming no genotyping error, then the complete- and observed-data likelihood functions contributed by the ith trio are, respectively,

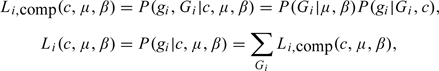where

and $I(·)$ is the indicator function. The EM algorithm (Dempster and others, 1977) is used to estimate parameters. We derive the expectation and maximization steps. The details of the steps can be found in Section C of the supplementary material available at Biostatistics online.

Let Λ denote the likelihood ratio statistic, defined as the ratio of the maximized likelihood under the null hypothesis to that obtained under the alternative. To examine the direction of bias, we use 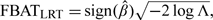where $\hat{\beta }$ is the maximum likelihood estimate of β. Under the null hypothesis, the test statistic follows the standard normal distribution asymptotically, as -2log Λ follows the chi-square distribution with 1 degree of freedom asymptotically. The method does not make assumptions of genotype probabilities at population level, such as HWE. Thus, it is fully robust against population stratification.

3. SIMULATIONS AND RESULTS

3.1. Methods of simulations

To compare the performance of different methods, we simulate case-parents genotype data under the null hypothesis $H_0$: β = 0 or under an alternative hypothesis $H_1$: β = ln(1.2). The genotypes of case-parents trios are simulated from a random mating population with the frequency of the allele A varying from 0.1 to 0.9. To mimic the situation of genotyping uncertainty, we consider normally distributed 1-dimension signal data with fixed cluster means: 0 for AA genotype, 1 for AB genotype, and 2 for BB genotype. We assume that the 3 genotype clusters have the same variance and use ${\sigma }^2$= 0.03 and ${\sigma }^2$= 0.05 to reflect different levels of genotyping uncertainty. Using 1-dimension simulation is justified by the fact that signal data from commonly used platforms can be transformed into 1-dimension data. The assumption of equal variance across genotypes may be violated in practice; however, when that happens, more genotyping errors and/or genotype-specific missingness are often expected. Once signal data are generated, we use the EM algorithm (Dempster and others, 1977) to fit a 3-component normal mixture model. After the EM algorithm converges, the posterior probabilities computed in the E-step are used as genotype data with uncertainty to examine the performance of the difference methods.

To evaluate the performance of ${\text{FBAT}}_{\text{weight}}$ and ${\text{FBAT}}_{\text{LRT}}$, we compare them with ${\text{FBAT}}_{\text{call}}$, which denotes the association test based upon called genotypes. In ${\text{FBAT}}_{\text{call}}$, each signal data point is either assigned to a genotype call or no-call, depending on whether the largest posterior probability is greater than a prespecified cutoff (here, we use 0.9). Then, families with Mendelian errors or at least one no-call are removed and the remaining “cleaned” data are used to perform FBATs. We also provide the “gold standard” by conducting association test using the true genotypes (${\text{FBAT}}_{\text{true}}$). The computation of the Type I error rate or power is based on 1000 simulations, 1000 trios sampled from a random mating population, and the nominal p value cutoff of 0.05.

3.2. Simulation results

We first examine call rates and accuracy under the 2 different levels of genotyping uncertainty. The results for data simulated under the null hypothesis are summarized in Tables 1 and 2. With the high threshold (0.9) we use to make genotype calls, the genotyping accuracy is satisfying: >99.9% and 99.5% for ${\sigma }^2$= 0.03 and ${\sigma }^2$= 0.05, respectively, for all allele frequencies. The overall call rates are >99% and 94% for ${\sigma }^2$= 0.03 and ${\sigma }^2$= 0.05, respectively, for all allele frequencies. Despite the high call rates and genotyping accuracy, notable difference exists among genotype-specific call rates. For example, when allele frequency p is 0.1 and ${\sigma }^2$= 0.05, the call rate of BB genotype is 98.23%, whereas that of AA genotype is only 89.25%. As we have shown in Section 1, this genotype-specific missingness can lead to bias in FBATs.

Table 1.

Accuracy and call rates (%) for simulated data when σ² = 0.03, for different allele frequencies

Allele frequency	p = 0.1	p = 0.2	p = 0.3	p = 0.4	p = 0.5	p = 0.6	p = 0.7	p = 0.8	p = 0.9
Accuracy	99.95	99.94	99.93	99.92	99.92	99.92	99.93	99.94	99.95
Call rate	99.54	99.38	99.30	99.24	99.22	99.24	99.29	99.39	99.54
Call rate	(BB) 99.73	99.60	99.50	99.37	99.24	99.12	98.93	98.70	98.33
by genotype	(AB) 98.76	99.04	99.15	99.19	99.21	99.19	99.14	99.03	98.75
	(AA) 98.29	98.65	98.94	99.08	99.22	99.36	99.49	99.61	99.73

Table 2.

Accuracy and call rates (%) for simulated data when σ² = 0.05, for different allele frequencies

Allele frequency	p = 0.1	p = 0.2	p = 0.3	p = 0.4	p = 0.5	p = 0.6	p = 0.7	p = 0.8	p = 0.9
Accuracy	99.72	99.62	99.56	99.52	99.51	99.52	99.56	99.61	99.71
Call rate	96.99	95.87	95.25	94.91	94.78	94.91	95.24	95.89	97.00
Call rate	(BB) 98.23	97.33	96.53	95.82	94.93	94.13	92.94	91.41	89.25
by genotype	(AB) 91.87	93.50	94.24	94.52	94.61	94.49	94.22	93.55	91.86
	(AA) 89.25	91.37	93.00	94.03	94.98	95.81	96.54	97.34	98.24

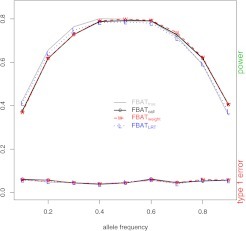
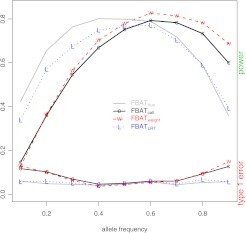
In the respect of Type I error rates, at a lower level of genotyping uncertainty, the Type I error rates of the 3 different tests are all close to those of the gold standard as illustrated in Figure 1. However, at a higher level of genotyping uncertainty, the Type I error rates of the 3 different tests are quite different: ${\text{FBAT}}_{\text{LRT}}$ is close to the gold standard ${\text{FBAT}}_{\text{true}}$ at all allele frequencies with the maximum difference being 0.01. In contrast, the Type I error rates of ${\text{FBAT}}_{\text{call}}$ and ${\text{FBAT}}_{\text{weight}}$ are >0.1 for small MAF as illustrated in Figure 2. ${\text{FBAT}}_{\text{call}}$ and ${\text{FBAT}}_{\text{weight}}$ tend to be negative when the frequency of the risk allele is <0.5 and positive when the frequency is >0.5. Box plots of the test statistics under the null hypothesis β = 0 (Figure S1 of the supplementary material available at Biostatistics online) show that both ${\text{FBAT}}_{\text{call}}$ and ${\text{FBAT}}_{\text{weight}}$ are biased toward overtransmission of the common allele. All these results indicate that the common allele appears to be overtransmitted using ${\text{FBAT}}_{\text{call}}$ or ${\text{FBAT}}_{\text{weight}}$. Mitchell et al. (Mitchell and others, 2003) reported that undetected genotyping errors also tend to predict the common allele to be overtransmitted. Thus, genotyping errors and genotype-specific missingness can not only cause transmission distortions but also pull transmission distortion toward the same direction.

Fig. 1.

The power (top) and Type I error rates (bottom) of the four tests when ${\sigma }^2=0.03$ for different frequencies of the risk allele. ${\text{FBAT}}_{\text{true}}$, TDT using true genotypes; ${\text{FBAT}}_{\text{call}}$, TDT using complete trios; ${\text{FBAT}}_{\text{weight}}$, TDT using the weighting strategy; and ${\text{FBAT}}_{\text{LRT}}$, the likelihood ratio test that assumes genotype-specific call rates.

Fig. 2.

The power (top) and Type I error rates (bottom) of the four tests when ${\sigma }^2=0.05$ for different frequencies of the risk allele. ${\text{FBAT}}_{\text{true}}$, TDT using true genotypes; ${\text{FBAT}}_{\text{call}}$, TDT using complete trios; ${\text{FBAT}}_{\text{weight}}$, TDT using the weighting strategy; and ${\text{FBAT}}_{\text{LRT}}$, the likelihood ratio test that assumes genotype-specific call rates.

In the respect of statistical power, ${\text{FBAT}}_{\text{LRT}}$ also has better performance than the other 2 tests. It has closer power to the gold standard ${\text{FBAT}}_{\text{true}}$ than both ${\text{FBAT}}_{\text{call}}$ and ${\text{FBAT}}_{\text{weight}}$ in most situations. The difference is especially clear when the frequency of the risk allele is small and the genotyping uncertainty is high. For example, when p = 0.1 and ${\sigma }^2$= 0.05 (Figure 2), the power of ${\text{FBAT}}_{\text{true}}$, ${\text{FBAT}}_{\text{LRT}}$, ${\text{FBAT}}_{\text{weight}}$, and ${\text{FBAT}}_{\text{call}}$ is 0.42, 0.34, 0.13, and 0.15, respectively. With the decrease of genotyping uncertainty, the power of the 4 methods tends to be closer (Figure 1) as expected. However, the performance of ${\text{FBAT}}_{\text{LRT}}$ is still better than ${\text{FBAT}}_{\text{call}}$ and ${\text{FBAT}}_{\text{weight}}$ in most situations. Note that when the risk allele is the common allele, ${\text{FBAT}}_{\text{call}}$ and ${\text{FBAT}}_{\text{weight}}$ seem to have higher power than ${\text{FBAT}}_{\text{true}}$. However, the seemingly “higher” power in ${\text{FBAT}}_{\text{call}}$ and ${\text{FBAT}}_{\text{weight}}$ should not be interpreted as greater efficiency than the gold standard. Rather, the results once again confirm that the resulted bias is toward predicting the common allele to be overtransmitted.

One may argue that these problematic SNPs, i.e. SNPs with high genotyping uncertainty, can be filtered out by testing HWE on the called genotypes. However, we found that the inflation in false positives and the incorrect power still persist even after filtering out those data sets that show deviation from HWE at level 0.05. In addition, filtering out SNPs can lead to loss of a substantial proportion of SNPs.

Since the methods we examine here do not make assumptions with regard to population genotype frequencies, such as HWE, they are all robust against population stratification. To confirm this, we simulated trios from 2 random mating subpopulations. The results (presented in Section D of the supplementary material available at Biostatistics online) demonstrate that they are indeed robust against population stratification.

4. APPLICATION TO A REAL DATA SET

We applied ${\text{FBAT}}_{\text{LRT}}$, ${\text{FBAT}}_{\text{weight}}$, and ${\text{FBAT}}_{\text{call}}$ to data collected by the International Consortium to Identify Genes and Interactions Controlling Oral Clefts. The genome-wide analysis of assayed SNPs was reported in (Beaty and others, 2010). Besides genotype data of assayed SNPs, imputed genotypes obtained using BEAGLE (Browning and Browning, 2009) are also provided by the database of Genotypes and Phenotypes (dbGaP). According to “OralClefts_imputation_report_final.pdf” downloaded from the dbGaP, phased HapMap genotype data from Phase III release 2, with base pair positions of SNPs based on NCBI build 36, were used for the imputation. The report also states that relatedness among subjects was ignored in the imputation. We used the 47 475 imputed markers on chromosome 8 from 856 case-parents trios of European descendants. Because the imputation was based on only 234 phased haplotypes in the HapMap Phase III, the imputation accuracy for SNPs with small MAF is likely to be low; thus, we only considered imputed SNPs with ≥5% MAF. We also exclude SNPs showing large deviation from HWE (chi-square statistic >10), with more than 1 Mendelian error or having <90% call rate. The remaining 23 524 SNPs are analyzed. Here, the MAF and other characteristics, such as HWE chi-square statistic, number of Mendelian errors, and call rate of the imputed SNPs are computed using called genotypes based on the cutoff 0.9.

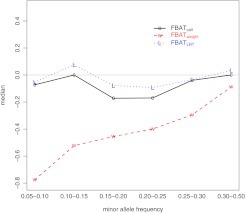
To show the difference of the 3 tests in false positives, we present results from SNPs with call rates between 0.9 and 0.99 as SNPs with call rates below 0.9 are not reliable and SNPs with call rates above 0.99 do not show much uncertainty. One useful measure of false positives in analyzing real data is the inflation factor introduced by (Devlin and Roeder, 1999). However, inflation factors are based on squared statistics and they do not show the direction of bias. To investigate the direction of bias, we compute the FBAT test statistics by treating the minor allele as the risk allele and examine the medians of the 3 tests. In our way of computing test statistics, a negative value implies predicting the common allele to be the risk allele. The results of MAF-stratified medians are presented in Figure 3, where the median for a specific MAF category is the median of the test statistics of all SNPs that fall into this category. All the medians of ${\text{FBAT}}_{\text{weight}}$ are negative and the smaller the MAF, the larger the bias. Although ${\text{FBAT}}_{\text{call}}$ has less bias than ${\text{FBAT}}_{\text{weight}}$, most of its medians are still negative. In contrast, ${\text{FBAT}}_{\text{LRT}}$ has both negative and positive medians and most of them are close to 0. These results not only agree with our theoretical prediction that genotyping uncertainty can lead to overtransmission of the common allele but also imply that our new approach ${\text{FBAT}}_{\text{LRT}}$ can reduce bias caused by genotyping uncertainty.

Fig. 3.

MAF-stratified medians of the three tests on the imputed SNPs from the Oral Clefts project. ${\text{FBAT}}_{\text{call}}$, TDT using complete trios; ${\text{FBAT}}_{\text{wight}}$, TDT using the weighting strategy; and ${\text{FBAT}}_{\text{LRT}}$, the likelihood ratio test that assumes genotype-specific call rates.

Next, we examine the 3 most significant SNPs among the imputed SNPs. The results in Table 3 indicate that the 3 tests provide similar statistic values. The small difference is presumably due to low uncertainty level at the 3 SNPs as reflected by the large call rates. Nevertheless, compared with the 2 most significant SNPs that are directly assayed, i.e. rs1519847 and rs12542837 (with the same TDT statistic 5.83), the 3 SNPs in Table 3 have greater values. Note that the top 2 assayed and the top 3 imputed SNPs are within a 50 kb region at chromosome 8q24, indicating that they are probably in the same functional region. These results reveal the efficiency of imputing genetic markers and incorporating genotyping uncertainty into FBATs.

Table 3.

The top three imputed SNPs

Marker	MAF	Position (bp)	Call rate (%)	FBATcall	FBATweight	FBATLRT
rs997310	0.31	129989462	99.96	6.59	6.59	6.69
rs17241908	0.24	130014058	99.84	6.78	6.80	6.78
rs17242358	0.24	130034055	98.60	6.77	6.86	6.85

5. DISCUSSION

In this article, we investigated 3 FBATs for uncertain genotype data. Among them, ${\text{FBAT}}_{\text{call}}$ is the conventional method that uses called genotypes; ${\text{FBAT}}_{\text{weight}}$ is a weighted test with the idea of weighting borrowed from association tests for studies using unrelated subjects. It is surprising to find that these ideas, which have been widely used and shown to perform well in studies using unrelated subjects, have unsatisfactory performance for the case-parents design. ${\text{FBAT}}_{\text{call}}$ can be biased by genotype-specific call rates even when a stringent threshold is used to rule out most genotyping errors. ${\text{FBAT}}_{\text{weight}}$ can be biased by both genotype-specific uncertainty levels and genotyping errors that are Mendelian consistent and therefore cannot be eliminated by weighting. The novelty of our new test, ${\text{FBAT}}_{\text{LRT}}$, is that by using genotype calls with a high quality and incorporating genotype-specific call rates, we can simultaneously correct bias due to both genotyping errors and genotype-specific missingness. Simulation results show that our new method ${\text{FBAT}}_{\text{LRT}}$ reduces the false-positive rates of the methods using called genotypes (${\text{FBAT}}_{\text{call}}$) and the weighting approach (${\text{FBAT}}_{\text{weight}}$).

The proposed method may be extended in several respects. First, because ${\text{FBAT}}_{\text{LRT}}$ concentrates on the case-parents design, it would be helpful to develop methods that are applicable to families of arbitrary structures and other types of traits. One difficulty in extending the case-parents design to families with multiple children is that the number of family types, which are defined as combinations of genotypes and phenotypes, can be very large; as a result, assumptions such as HWE might need to be used (Dudbridge, 2008), which can lead to inflated false positives in the presence of population stratification. Second, ${\text{FBAT}}_{\text{LRT}}$ can be extended to analyze other types of traits, such as quantitative traits. To do so, genotype risks need to be replaced by density functions for a quantitative trait. For families of arbitrary structures and general types of traits, we are currently developing methods that can efficiently correct the uncertainty-caused bias with minimum sacrifice of robustness.

SUPPLEMENTARY MATERIAL

Supplementary material is available at http://biostatistics.oxfordjournals.org.

FUNDING

National Institute of Health (grant R01-HG004960).