Abstract
Identifying brain regions with high differential response under multiple experimental conditions is a fundamental goal of functional imaging. In many studies, regions of interest (ROIs) are not determined a priori but are instead discovered from the data, a process that requires care because of the great potential for false discovery. An additional challenge is that magnetoencephalography/electroencephalography sensor signals are very noisy, and brain source images are usually produced by averaging sensor signals across trials. As a consequence, for a given subject, there is only one source data vector for each condition, making it impossible to apply testing methods such as analysis of variance. We solve these problems in several steps. (1) To obtain within-condition uncertainty, we apply the bootstrap across trials, producing many bootstrap source images. To discover ‘hot spots’ in space and time that could become ROIs, (2) we find source locations where likelihood ratio statistics take unusually large values. We are not interested in isolated brain locations where a test statistic might happen to be large. Instead, (3) we apply a clustering algorithm to identify sources that are contiguous in space and time where the test statistic takes an ‘excursion’ above some threshold. Having identified possible spatiotemporal ROIs, (4) we evaluate global statistical significance of ROIs by using a permutation test. After these steps, we check performance via simulation, and then illustrate their application in a magnetoencephalography study of four-direction center-out wrist movement, showing that this approach identifies statistically significant spatiotemporal ROIs in the motor and visual cortices of individual subjects.
Keywords: ROI, global statistical significance, spatiotemporal clustering, bootstrap, MEG/EEG, source localization
1. Introduction
Magnetoencephalography (MEG) and electroencephalography (EEG) are non-invasive techniques that record effects of brain activity with millisecond precision. They provide brain activity images when signals recorded from sensors are mapped to activation levels on a grid of possible source locations in selected parts of the brain. There are typically many more source locations than sensor signals, which makes source localization an ill-posed inverse problem. Common methods of solving this inverse problem apply L1 and L2 constrained linear regression [1, 2]. MEG and EEG experiments typically involve two or more alternative experimental conditions, with the goal of identifying brain regions having strong differential activation levels. Such ‘hot spots’ of differential activity are often called regions of interest (ROIs). Sometimes, ROIs are determined a priori from substantive scientific hypotheses, but it is often desirable to identify them empirically. Because there are usually hundreds or thousands of possible source locations over hundreds or thousands of time points in MEG and EEG, there are substantial opportunities to find spurious ROIs because of chance alone. This paper presents a new method of discovering ROIs in space and time simultaneously by using an excursion algorithm via spatiotemporal clustering, and global significance tests (p-values) for discovered ROIs. The method may be applied to source images of individual subjects.
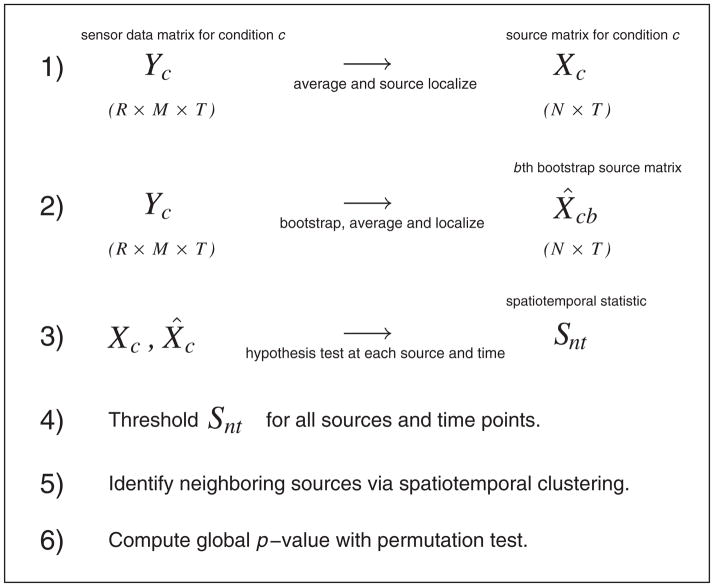
There are three main components of our work. First, because MEG and EEG signals are extremely noisy, source localization requires averaging across many experimental trials. With only a single trial in each experimental condition, the usual methods of comparing responses across treatments (analysis of variance (ANOVA) or multivariate analysis of variance) cannot be applied in source space. To overcome this limitation, we apply the bootstrap [3], repeatedly resampling from the trials in the sensor space, thereby generating multiple images that reflect variability of the source localization procedure. Second, complex brain activities during continuous recording yield high variability in brain modulations across space and time. To become candidate ROIs, hot spots of differential rates of activity should consist of many source locations that are contiguous in space and time. We apply a likelihood ratio test to the bootstrapped images, computing the test statistic at every location in both space and time, and then threshold the test statistics and cluster the results in terms of both test statistic values and space–time coordinates. As we show, this identifies candidate regions of modulated activity. Finally, to overcome problems with multiple comparisons, we apply a permutation test, repeatedly permuting the resampled images across conditions while computing the likelihood ratio test and performing clustering for each set of permuted images. This provides a valid global p-value. Figure 1 summarizes the methodology in six steps. For the clustering step, we apply Bayesian hierarchical clustering (BHC) [4] because, from our previous experience, we have found it an effective method that automatically determines the number of clusters to examine.
Figure 1.
Flow diagram of methodology. The data for condition c consist of M sensor signals at each of T time points across R replications (trials). In step 1, we average the sensor signals across trials and then localize (see text) to N sources in the brain. Step 2 repeats this process for bootstrapped set of trials. At step 3, we perform hypothesis tests at every source and time point to test the null hypothesis that the mean source activities are equal across conditions. We threshold these test statistics at step 4 and then identify spatiotemporal neighbors as clusters, representing potential ‘hot spots’ at step 5. We carry out a global significance test in step 6.
In Section 2, we describe our procedures. In Section 3, we evaluate our algorithms in simulation studies and then illustrate the methodology in the context of a MEG study of hand movement, in which brain activities of human subjects were recorded while they performed a visually cued four-direction center-out wrist movement task [5, 6]. In this case, we had four alternative experimental conditions corresponding to four movement directions, and the goal was to identify regions on the cortical surface containing neural activity exhibiting differential modulations across the movement directions. By using the discovered ROI, we show highly distinguishable patterns among the directions. In Section 4, we discuss further issues and draw conclusions.
2. Methods
Suppose we have MEG or EEG recordings from M sensors at T time points for R trials under C conditions. If we index time by t = 1, …, T, trial by r = 1, …, R, condition by c = 1, …, C and let Ycr be a M × T matrix representing recordings at trial r under condition c, then the ensemble recordings Y can be represented as follows:
| (1) |
To map these sensor recordings to the cortical surface, MEG source localization algorithms such as minimum current estimate (MCE) [2] typically average sensor signals across many trials and then solve the inverse problem via constrained optimization
| (2) |
where (i.e., row averages of Y in Equation (1)) is the sensor trial mean under condition c, A is specified by the forward model from the quasi-static solution to Maxwell’s equations [1], Xc (N × T, assuming there are N sources indexed by n) is the transformed source currents on the cortical surface where each row in Xc is the time course of a source, and E is the additive noise. Because the number of sources far exceeds that of the sensors, the inverse problem is ill posed [1] (it is a p ≫ n problem). MCE offers a sparse solution to the inverse problem via weighted L1 regularization, effectively assuming that there are only a few sources that are activated at one time point (e.g., an image of the cortex with very few hot spots).
Solving the inverse problem based on averaged trials yields only a single trial under each experimental condition; hence, it is difficult to carry out statistical analysis on these sparse data. To resolve this issue, we use bootstrap to generate multiple samples of source images under each condition. We utilize these bootstrap samples as our data and apply hypothesis tests in the brain source space. We then apply an excursion algorithm to find statistically significant and nearby spatiotemporal points (hot spots)—it turns out that the excursion can be implemented in terms of a clustering algorithm. Finally, we use a permutation test to evaluate the significance of these ROIs. In the following sections, we describe each of these procedures in detail.
2.1. Bootstrapped source images
To produce multiple ‘copies’ of trials in the source space, we resample the trials under condition c by B times. For bootstrap sample b with b = 1, …, B, we then let Ycrb be the resulting sensor signal vector, take and write
| (3) |
By bootstrapping, we generate uncertainty under each experimental condition—each of these samples is a slight variant of the original source image based on trial averages. By solving the inverse problem (Equation (3)), we obtain X̂cb as an estimate of Xcs and thereby obtain the ensemble of source signals (or time-varying source images)
| (4) |
2.2. Likelihood ratio test
To examine whether any individual brain regions are modulated under differing experimental conditions, we perform hypothesis tests making use of the bootstrapped source data (Section 2.1). It should be emphasized that in reality, any standard testing methods such as ANOVA would be applicable, although here, we choose to use a likelihood ratio test similar to that described in [7], which does not assume that the conditions have equal variance and explicitly takes that variability into account. We write the likelihood ratio test in extension to bootstrapped data following [7]. A likelihood ratio test has the form
| (5) |
where f (x|θ) is the likelihood parameterized by θ, and Θ0 and Θ are the parameter space under the null and in the unrestricted hypothesis, respectively. Following Equation (4), we denote the signal from a source at a single time t from bootstrapped source trials in all conditions as x = [x11, …, x1B, …, xC1, …, xCB]T, where xcb is the signal strength in trial b under condition c. Assuming that the mean signal under condition c, , is normally distributed and under the null hypothesis H0 that the source current has equal mean strength under all conditions, we construct the following test:
| (6) |
where it can be easily shown that the following is the maximum likelihood estimate under H0:
| (7) |
where is the variance of x estimated from the bootstrapped data. It also follows that μc * = xc is the maximum likelihood estimate in the unrestricted parameter space. Equation (6) can thus be simplified to
| (8) |
which, if all σc were known, would follow a χ2 with C − 1 degrees of freedom. We perform this likelihood ratio test for each source at each time point and repeat across time. Assuming there are T′ points after smoothing, we write the log LR test statistic for source n at time t as snt with n = 1, …, N and t = 1, …, T′. In practice, we can smooth the signals by averaging them over a small window every few time points to reduce the number of tests. We then obtain a matrix of smoothed log LR statistics for every source across time. We then collect these into the following matrix:
| (9) |
We also obtain a corresponding matrix of p-values (P), based on the χ2 distribution.
2.3. Spatiotemporal excursion algorithm
After obtaining the log LR statistical map S (Equation (9)) from the likelihood ratio tests, we wish to locate ROIs by identifying spatiotemporal clusters that have significant modulations. In this section, we describe a spatiotemporal excursion (STE) algorithm that achieves this.
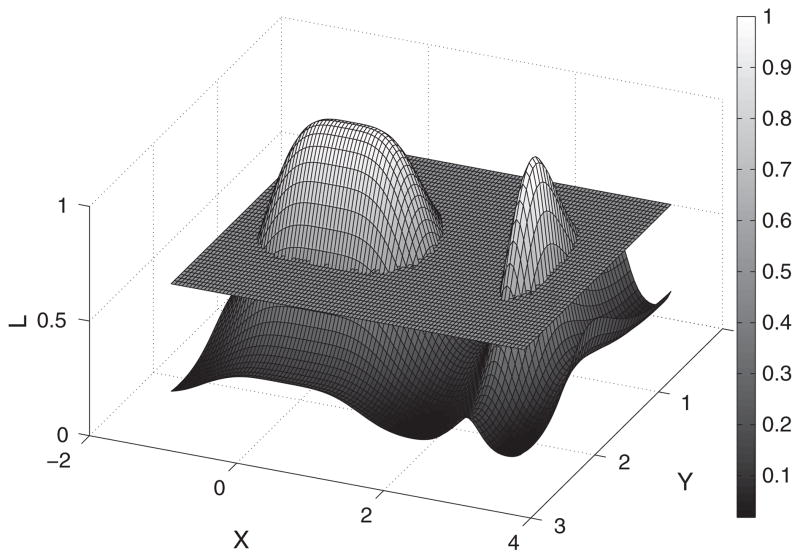
The STE algorithm finds the peaks in the spatiotemporal map of the log LR statistics defined in Equation (9). Because peaks of interest occur across contiguous points in time and space, we cluster and threshold these spatiotemporal events. The STE follows three main steps. (1) We prune ‘insignificant’ cortical sources at a pre-defined αthresh level (e.g., αthresh = 0.01) based on the likelihood ratio test statistics. (2) We partition the rest of the sources via a clustering algorithm where the inputs are four-dimensional vectors (3-D for spatial source coordinates and 1-D for a specific time instance). (3) We locate the hot spots by finding large aggregated source statistics within the obtained clusters. We illustrate our algorithm in a simplified 3-D example shown in Figure 2. The height on L-axis indicates the magnitude of the test statistic, and the X and Y axes represent space and time. In step 1, we threshold using a sectioning plane at L = 0.5 and prune those points that are under the threshold. In step 2, we partition the remaining areas into contiguous clusters (i.e., the two peaks in Figure 2). In step 3, we localize ROIs by finding spatiotemporal clusters that have large statistics summed over the individual sources (i.e., the cluster with the larger area in this particular example). As a result, we obtain a spatiotemporal representation of ROIs where significant activities may take place. We summarize the STE algorithm as Algorithm 1. Specifically, the STE algorithm calls three subroutines, which are fully described in Algorithms 2–4.
Figure 2.
Illustration of the excursion algorithm in a 2-D space. The curved surface represents the magnitude of statistic from the hypothesis tests. The sectioning plane prunes insignificant sources at a pre-defined threshold level. We subsequently grouped the remaining two peaks into two distinct clusters based on their neighboring profiles.
Algorithm 1.
Spatial–temporal excursion algorithm
| input: threshold, averaging window, source signals and coordinates |
| run likelihood ratio test and threshold (Algorithm 2 – Hyptest) |
| cluster spatiotemporal sources (Algorithm 3 – BHC) |
| compute ROI statistics (Algorithm 4 – ROIstats) |
| output: ROI coordinates, time points and statistics |
Algorithm 2.
Routine Hyptest
| input: signals X (N sources) and coordinates POS (N × 3), threshold level αthresh, averaging window δ |
| for n = 1 to N do |
| run likelihood ratio test on source n in time step δ (T steps) |
| compute statistics sn = [sn1, …, snT] and corresponding p-values pn = [pn1, …, pnT] |
| for t = 1 to T do |
| if pnt < αthresh then |
| obtain 3-D coordinates POSn = [x, y, z]n |
| store cnt = [t, POSn] in C |
| store n and t in N* and T*, respectively |
| end if |
| t ← t + 1 |
| end for |
| n ← n + 1 |
| end for |
| output: 4-D spatiotemporal coordinates C = {cnt |n ∈ N*, t ∈ T*} |
It turns out that the excursion procedure can be implemented in the vehicle of a clustering algorithm. Specifically, if we treat the spatial and temporal coordinates of individual sources as the input, then a clustering algorithm defined with some measure of similarity metric would serve the purpose of grouping these sources based on their spatiotemporal ‘closeness’. To cluster the spatiotemporal sources, we use an algorithm (Algorithm 3) that partitions the sources based on their spatial and temporal coordinates. In our analysis, we use BHC [4]. It is worth mentioning that in principle, any clustering method (e.g., K-means, spectral-clustering) would work for excursion, and BHC is only one of these methods. The strength of BHC, however, is that it automatically determines the number of clusters in the data and has been proven to perform well in general. In the following section, we describe the BHC algorithm following [4].
Algorithm 3.
Routine BHC
| input: spatiotemporal source coordinates C = {cnt |n ∈ N*, t ∈ T*} |
| initialize: number of clusters m = |N*| × |T*| where each cluster contains a single 4-D coordinate |
| cnt in C |
| while m > 1 do |
| Merge pair of coordinates with the highest probability of the merged hypothesis (see Section 2.3.1) |
| end while |
| output: clustered coordinates in space and time A = [A1, …, AK ] |
2.3.1. Bayesian hierarchical clustering
Consider a data set
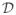 = {x(1), …, x(n)} and tree T where
= {x(1), …, x(n)} and tree T where
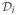 ⊂
⊂
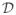 is the set of data points at the leaves of the subtree Ti of T. In our context, each data point corresponds to a four-element vector containing the spatial coordinates of a source and its time instance. BHC is similar to traditional agglomerative clustering in that it is a bottom-up agglomerative method that initializes n clusters (leaves of the hierarchy), each containing a single data point
is the set of data points at the leaves of the subtree Ti of T. In our context, each data point corresponds to a four-element vector containing the spatial coordinates of a source and its time instance. BHC is similar to traditional agglomerative clustering in that it is a bottom-up agglomerative method that initializes n clusters (leaves of the hierarchy), each containing a single data point
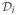 = {x(i)}. It then iteratively merges pairs of clusters to construct a hierarchical binary tree. The main difference between BHC and traditional hierarchical clustering methods is that BHC uses a statistical hypothesis test to choose which clusters to merge based on the odds ratio of posterior probabilities [8], instead of a distance metric.
= {x(i)}. It then iteratively merges pairs of clusters to construct a hierarchical binary tree. The main difference between BHC and traditional hierarchical clustering methods is that BHC uses a statistical hypothesis test to choose which clusters to merge based on the odds ratio of posterior probabilities [8], instead of a distance metric.
In considering each merge, we compare two hypotheses. The first hypothesis (
) is that all the data in
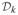 were generated independently and identically from the same probabilistic model (i.e., the merged hypothesis), p(x|θ) with unknown parameters θ (e.g., a Gaussian with θ = (μ, Σ)). We compute the probability of data
were generated independently and identically from the same probabilistic model (i.e., the merged hypothesis), p(x|θ) with unknown parameters θ (e.g., a Gaussian with θ = (μ, Σ)). We compute the probability of data
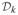 under
by specifying a prior over the parameters of the model (if we use conjugate priors, the following integral is tractable):
under
by specifying a prior over the parameters of the model (if we use conjugate priors, the following integral is tractable):
The alternative hypothesis (
) would be that
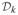 has two or more clusters in it (i.e., the split hypothesis). Summing over the exponentially many possible ways of dividing
has two or more clusters in it (i.e., the split hypothesis). Summing over the exponentially many possible ways of dividing
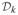 into two or more clusters is intractable. However, if we consider only clusterings that partition the data consistent with the subtrees Ti and Tj, which are built from the agglomerative bottom-up process, we can efficiently sum over exponentially many alternative clusterings by using recursion. The probability of the data under the alternative hypothesis is then simply
. The marginal probability of the data in any subtree Tk is computed as follows:
into two or more clusters is intractable. However, if we consider only clusterings that partition the data consistent with the subtrees Ti and Tj, which are built from the agglomerative bottom-up process, we can efficiently sum over exponentially many alternative clusterings by using recursion. The probability of the data under the alternative hypothesis is then simply
. The marginal probability of the data in any subtree Tk is computed as follows:
| (10) |
where
. Note that this equation is defined recursively, where the first term considers the hypothesis that there is a single cluster in
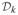 and the second term efficiently sums over all other clusterings in
and the second term efficiently sums over all other clusterings in
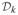 , which are consistent with the tree structure. At each iteration, BHC merges the two clusters that have the highest posterior probability of the merged hypothesis
, which is defined by the Bayes rule:
, which are consistent with the tree structure. At each iteration, BHC merges the two clusters that have the highest posterior probability of the merged hypothesis
, which is defined by the Bayes rule:
| (11) |
The quantity πk, which can also be computed bottom up as the tree is built, is defined to be the relative prior mass in a Dirichlet process mixture (DPM) model with hyperparameter α, of the partition where all data points are in one cluster, versus all the other partitions consistent with the subtrees. As shown in [4], where dk = αΓ (nk) + dleftk drightk, right (left) refer to the children of internal node k, and at the leaves, di = α, πi = 1. BHC automatically infers the number of clusters by cutting the tree at rk < 0.5. We summarize the BHC in Algorithm 3.
Although BHC is a greedy algorithm (i.e., it iteratively merges the two most probabilistically similar clusters), at each iteration, it performs model selection by evaluating the odds ratio of the marginal likelihoods under the merged and the split hypotheses (i.e., Bayes factor of the two hypotheses). Because the algorithm is recursive, the marginal likelihood sums over configurations that are consistent with the tree structure, which takes into account a large space of partitioning of the data (the resulting hierarchical tree is a rich mixture model). The algorithm can be understood as performing iterative hypothesis tests that evaluate the odds of merging or splitting the pair of clusters as it builds up the tree, and the number of clusters is determined where the merged odds is lower than the split odds that cuts the tree. Work in [4,9] relates BHC with DPMs, a clustering model that considers the space of all possible partitions of the data yet is computationally intractable, by proving that BHC provides a theoretical lower bound on the marginal likelihood of DPM. The work also empirically demonstrates that BHC offers superior clustering performance and tighter bound compared with other alternative approximate methods to DPM. It is worth mentioning, however, that because BHC outputs a single binary tree, it is possible that it may not capture fully the uncertainty associated with alternative clusterings. Xu et al. [9] show how BHC can be modified to consider alternative clusterings, although the gain of incorporating uncertainty seems only marginal, suggesting that BHC generally yields good clustering results. We demonstrate the algorithm in Section 3.1.1. It is worth mentioning that the computational complexity of BHC is quadratic in the number of data points; hence, the algorithm can be computationally demanding with very large data sets. In such cases, simpler algorithms such as K-means might serve as an alternative for practical purposes.
2.3.2. Computing the region of interest statistic
Within each of the partitioned cortical areas clustered by BHC, we compute the cluster statistics by summing over time and space, and assign the clusters that have large statistics as the ROI. Suppose BHC partitions the sources into K clusters (including those pruned by thresholding, which have zero integral) and let A = [A1, …, AK], then ROI can be defined as
| (12) |
where snt is the log LR statistic for source n at time t. Intuitively, this means that ROI is the region that contains contiguous sources that have the largest statistics summed over time and space. We summarize the algorithm in Algorithm 4. It should be noted that there are a variety of choices for ROI statistic, for example, mean or median of the clustered sources, and the aggregated statistic defined in Equation (12) is only one possibility. In the case of single-point sources, for example, using maximal or mean statistic within the clusters may be more appropriate than aggregated statistics. Our method, however, uses a modular approach that potentially allows different choices of statistic to be plugged into the algorithm for studying the ROIs.
Algorithm 4.
Routine ROIstats
| input: partitioned spatiotemporal source coordinates A = [A1, …, AK] |
| for k = 1 to K do |
| compute cluster statistic i nt (Ak) = ∫n∈Ak ∫t∈Ak snt d ndt |
| k ← k + 1 |
| end for |
| ROI ← arg maxk* i nt (Ak) and Sobs = arg maxk* i nt (Ak) |
| output: ROI topography {POSn|n ∈ Ak*}, time points {t|t ∈ Ak*} and statistic Sobs |
2.4. Computing global statistical significance
The likelihood ratio test described in Section 2.2 involves testing at a large number of source locations and time instances. To account for multiple comparisons, we use a permutation test that characterizes the statistical significance globally. Nichols and Holmes [10] first introduced permutation test in ROI analysis in fMRI. Here, we apply the idea to spatiotemporal events in MEG/EEG.
In standard ANOVA permutation tests, we test the null hypothesis that the data distributions are the same across conditions. Here, we consider the analogous null hypothesis that the multivariate source distributions across conditions are identical. In our context, once we find an ROI by using the STE algorithm (Algorithm 1), we compute a p-value that quantifies the global significance by considering the sources in the ROI clusters as a whole. To do this, we use a permutation test where the null hypothesis is that the trials are identically distributed across conditions. In other words, we compute the ROI statistic (Equation (12)) for each set of permuted trials and compute the number of permutations where that statistic exceeds the observed ROI statistic calculated from the original data. Specifically, we reject the null at level if in J* out of Np permutations, the ROI statistic found by permuting the trials across conditions is larger than that of the observed ROI. If we denote the statistic of observed ROI as Sobs and that of permuted trials j where j = {1, …, J} as Sj, we can approximate the global p-value
| (13) |
where each Sj can be calculated from the STE algorithm (Section 2.3). We summarize the complete procedures for computing the global p-value in Algorithm 5.
Algorithm 5.
Global p-value of ROI
| input: MEG/EEG sensor signals Y |
| bootstrap Y under each condition |
| store source-localized bootstrapped signals in X |
| run STE (Algorithm 1) on X and compute ROI statistic Sobs |
| for j = 1 to J do |
| permute source signals across conditions and obtain |
| run STE on and tally I(Sj ≥ Sobs) |
| j ← j + 1 |
| end for |
| compute p-value |
| output: approximate global p-value |
3. Results
In this section, we first evaluate our algorithms in three separate simulation studies. We then apply our method to a MEG study of center-out wrist movement where we discover statistically significant spatiotemporal ROIs in the motor and visual areas of cortex. Finally, we use the discovered ROIs to visualize the within and between condition variability based on the bootstrap.
3.1. Simulation
3.1.1. Clustering spatiotemporal events
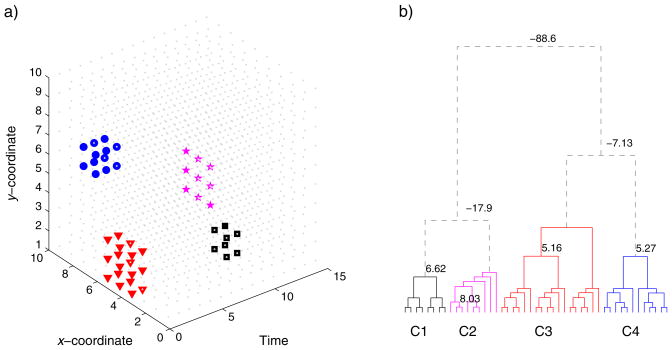
We simulated a 3-D space (two spatial dimensions (x, y) and one temporal dimension (t)) with contiguous spatiotemporal ‘hot spots’ and used BHC to automatically group these events based on their coordinates. Figure 3a shows the true events in symbols of different shapes. The cluster of squares has eight points that lie at 4: 5, 1: 2 and 10: 11 in x, y and t axes. The cluster of stars consists of nine points and occurs at a single time point, lying at 6: 8 and 1: 3 in x and y axes. The cluster of triangles has 18 points that lie at 4: 6, 1: 3 and 1: 2 in x, y and t axes. Finally, the cluster of circles contains 12 points and lie at 7: 8, 6: 7 and 1: 3 in x, y and t axes. Note that the triangle and square clusters of points are spatially overlapped (the square cluster constitutes a subset of the triangle cluster spatially) but occur at different time points. The triangle and circle clusters overlap temporally but are discrete in space. The star cluster is relatively isolated on its own. Figure 3b shows the clustering results from BHC over these points. The algorithm identifies exactly the clusters despite the overlap in space and time. The negative weights on the dendrogram suggest that the ratio of the merged hypothesis against the split hypothesis is less than 1, and hence, the tree could be cut off at these places, automatically yielding four distinct clusters.
Figure 3.
Demonstration of spatiotemporal clustering in a 3-D space. a) We set up four ‘hot spots’ in different shapes that extend through space and time (see text for details). b) Clustering in the hierarchical tree. The algorithm prunes the tree where the odds ratio of the merged hypothesis falls below the split hypothesis, identifying four distinct clusters.
3.1.2. Uniform p-values under null hypothesis
We used a simulation study to show that the p-values defined in Section 2.4 are roughly uniformly distributed under the null hypothesis for randomly generated data. We generated 1000 synthetic data sets in the MEG source space. For each source (853 in total in MCE software), we used three conditions, each of which has 25 trials. Each trial is a flat 5-point time series of random amplitude between 1 and 100, where each point is subject to a Gaussian noise with μ = 0 and σ = 5. In each of 1000 data sets, we applied the algorithm described in Section 2 to compute a global p-value by permuting 10, 000 times in the permutation test. The histogram of the resulting 1000 p-values roughly follow a uniform distribution.
3.2. A magnetoencephalography study
3.2.1. Experimental setup and data pre-processing
The experiment involved a center-out wrist movement task. We set up a screen in front of the subjects to provide visual feedback throughout the behavioral task. We used a 306-channel Elekta Neuromag (Helsinki, Finland) MEG system to record their brain activities. We asked two right-handed subjects to perform wrist movement by manipulating a joystick with their right hand following one out of four directions (radial and ulnar deviations, flexion and extension) indicated by a corresponding visual cursor cue (up and down, left and right). We asked each subject to perform the task in repeated trials (120 in each direction). Meanwhile, we used electrooculography to detect eye movement to remove any artifacts. The Institutional Review Board at the University of Pitts-burgh approved all experimental procedures, and we performed all experiments in accordance with the approved protocol. The subjects gave informed consent before the experiments. We performed spatial filtering on the raw MEG data by using signal space separation [11]. We discarded trials with apparent eye movement detected by electrooculography. We aligned each trial to recorded movement onset, which was defined as the first time when 15% of maximal cursor speed was reached. We used MCE for source localization.
3.2.2. Experimental results
We applied our method to the center-out wrist movement study. For each subject, we bootstrapped the trial average of sensor signals within each of the four directions 50 times (i.e., 200 trials in total; to reduce computation, we used a small sample size, although by examining the samples, we found that the non-zero source currents follow the normality requirement of hypothesis tests) using the procedure described in Section 2.1. We then source localized each bootstrapped sample via MCE, obtaining 200 images of source currents. For each source (853 in total) given by MCE, we ran the likelihood ratio test (the null hypothesis is that the mean source current is equivalent under four movement directions) through time by averaging the signal every 10 ms. The entire time course is 1000 ms, so there are 100 time steps after averaging. In each source and time step, we computed the log LR statistic and p-value, forming a statistical map as in Equation (9). We note that the bootstrap variance across conditions varied as much as 20-fold; hence, the standard ANOVA assumption would not be valid in this case.
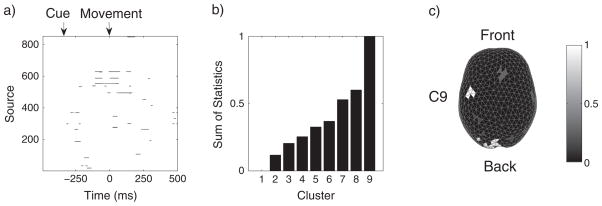
We applied the STE algorithm to the log LR statistical map thresholding at p = 0.01. Figure 4 shows the results for subject S1. Figure 4a illustrates the log LR map where the black dots indicate above-threshold test statistics. The onset of subject movement is at 0 ms, and the onset of visual cue is at approximately −300 ms. We observed that significant modulations occur at about 100 ms prior to movement and persist for 200 ms through movement. These activities mostly occur in the motor cortex, and they correspond to the motor planning and execution stages. In addition to modulation in the motor cortex, we also observed significant modulations at about −260 ms in the occipital visual area after the cue onset, which are presumably due to processing of visual stimuli. Figure 4b shows that the normalized sum of ROI statistics of nine clusters discovered using STE. We see that cluster 9 (C9) has the largest ROI statistic, whereas cluster 0 has zero ROI statistic corresponding to the under-threshold sources. Figure 4c maps these clusters topographically on the cortex, although it is worth mentioning that the sum of ROI statistics also integrates over time (Equation (12)). We see that C9 with maximal ROI statistic is in the contralateral motor region, and large ROIs also occurs in the occipital and frontal areas. Figures 5 and 6 further demonstrate the results for the two subjects (S1 and S2), respectively. We note that both subjects have similar patterns of modulation with contralateral motor region owning the maximal ROIs and less significant modulations in the visual and frontal areas. These observations suggest that the motor cortex encodes differing directional information, which agrees with the phenomenon of directional tuning observed in single-neuron studies [12–14]. Our observation is also consistent with the results in a recent MEG study of decoding center-out movement via motor-related sensors [5].
Figure 4.
Spatiotemporal region of interest analysis of a magnetoencephalography study in a visuomotor task. a) Map of time-evolving chi-square statistics of 853 sources thresholded at αthresh = 0.01 for subject S1. The black dots indicate test statistics that exceed threshold. b) Normalized sums of statistics of nine spatiotemporal clusters found using the STE algorithm for S1. Cluster 1 consists of under-threshold space–time events. Cluster 9 has the maximal sum of statistics and corresponds to the contralateral motor area (on the right). c) Spatial visualization of ROI on the cortical surface. The white area indicates the cluster with the maximal sum of statistics.
Figure 5.
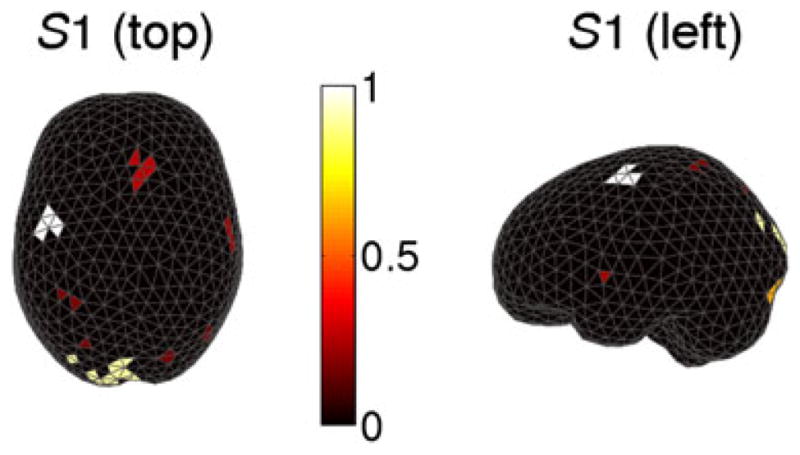
Clusters of spatiotemporal ‘hot spots’ in subject S1 in the left hemisphere viewed from the top. The intensity of the bar indicates the magnitude of the normalized sum of statistic (white for large values).
Figure 6.
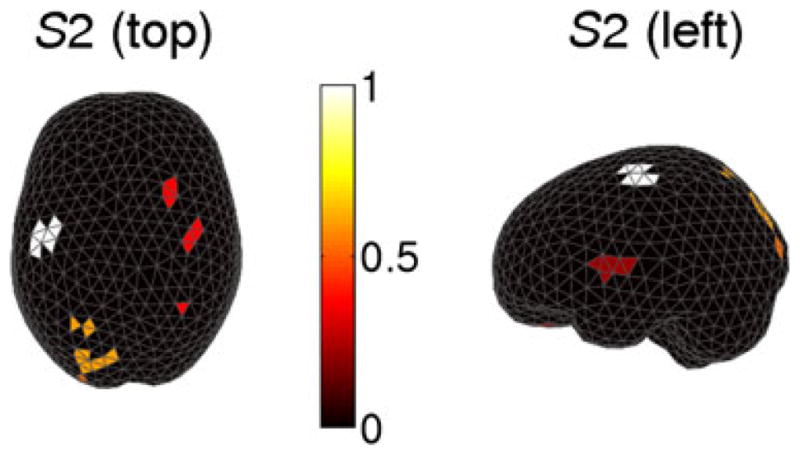
Clusters of spatiotemporal ‘hot spots’ in subject S2 in the left hemisphere viewed from the top. The intensity of the bar indicates the magnitude of the normalized sum of statistic (white for large values).
To evaluate the global significance of the observed ROI (i.e., the contralateral motor clusters), we permuted the bootstrapped source trials 100,000 times and used STE to compute the sum of ROI statistics for each permutation. For both subjects, there were zero cases where the permuted ROI statistic exceeded that of the original ROI. Hence, concluded that the ROI in both cases was statistically significant with a global p-value p < 10−5. To account for multiple ROIs, we repeated the entire permutation procedure and compared instead with the smallest ROI in the clusters partitioned from BHC, hence obtained a more conservative estimate for p-value. The intuition is that if the ROI with the smallest statistic is found significant, then those that have larger statistics would be also significant. Thus, we are able to establish the significance for multiple clusters. In these experiments, we also found that p < 10−5. Finally, to visualize spatiotemporal modulations, we took four snapshots across the time course to see how the modulations varied spatially on the cortex (Figure 7). We observed that the modulations start from the occipital visual area during the cue onset and transit to the motor area before the movement onset and persist through the movement, which matches the observed log LR map in Figure 4a and intuitively explains the process in this visuomotor task.
Figure 7.
Snapshots of ‘hot spots’ that migrate from the occipital visual area to motor area during the time course in a center-out visually cued motor task. The movement onset starts at 0 ms.
3.3. Visualizing the variability
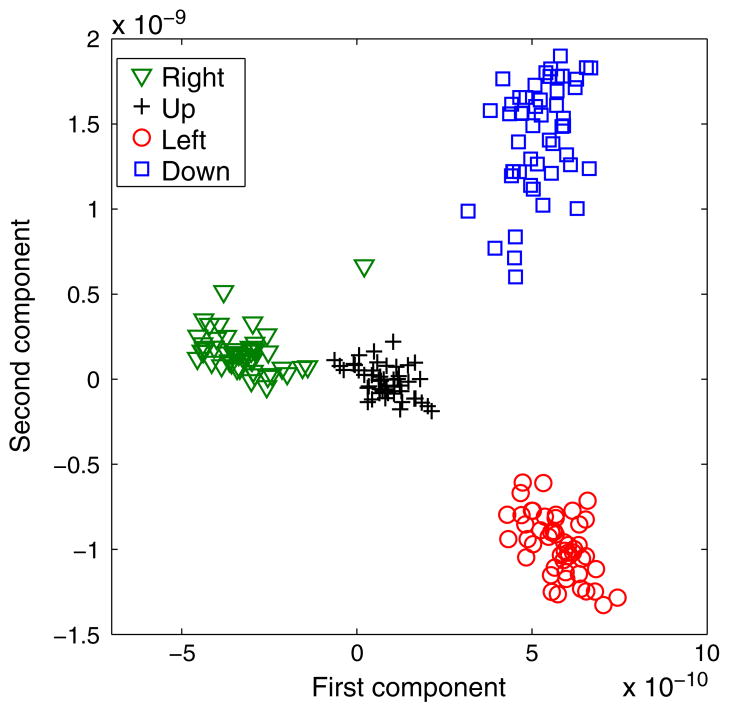
We extracted the signals in the ROI in the contralateral motor area (Section 3.2.2) and examined the variation within and across the four movement directions. To do this, we projected the bootstrapped source signals at locations inside the ROI cluster discovered by our algorithm (these occurred 100 to 0 ms prior to movement onset) onto a lower-dimensional space via PCA. Figure 8 visualizes these trials in a 2-D space spanned by the eigenvectors that correspond to the two largest eigenvalues in PCA. We observed that although the trials in each of four directions form their own clusters in the projected space, there is also noticeable trial–trial variation within each movement direction.
Figure 8.
Visualization of 200 bootstrapped trials in four movement directions (50 in each direction). The signals from the ROI in each trial are projected onto the first two principal components via PCA.
4. Discussion
To solve the problem of discovering brain regions having differential activity under varying experimental conditions, within subjects, from MEG or EEG data, we have pursued two ideas. The first uses bootstrap resampling of trials to produce uncertainty in source-localized images, within conditions. This is analogous to performing a somewhat unusual but valid bootstrap when solving an ordinary ANOVA problem. The usual bootstrap solution to ANOVA is to combine the data across conditions, and resample the whole, assigning at random each resampled observation to an experimental condition—each resampled set of data leading to a single bootstrapped F statistic. An alternative is to begin with the data means under each condition, compute a standard error of each mean by resampling the observations under each condition separately and then apply a likelihood ratio test by assuming each mean to be normally distributed. This latter bootstrap would be unnecessary in the ordinary ANOVA problem because the same standard errors may be obtained analytically. In the case of MEG, however, we are not working with a sample mean but rather with the source-localized image strength at each source, and for this, particularly in the case of L1-penalized source localization, the bootstrap is very helpful.
The second idea was to apply a clustering method to thresholded likelihood ratio values in order to find contiguous spatiotemporal sources of high differential activity and then to evaluate global significance using a permutation test. We used BHC as our clustering method, but this is not essential to the logic of our approach. We illustrated the methodology using data taken from subjects during wrist movement. Elsewhere, we have shown that directionality can be decoded from individual trials based on MEG signals [6, 15]. The point, here, has been to discover regions responsible for this ability to decode while producing a p-value that assesses the strength of the evidence against the rate of spurious null results. We have emphasized that the methodology applies to source images produced from individual subjects. Using this approach to examine inter-group differences by combining results across subjects is a topic for future research.
Acknowledgments
This research was partially supported by NIH grants R01 MH064537 and R01EB005847. Additional support was provided by NIH grants from NIBIB (1R01EB007749) and NINDS (1R21NS056136). Y. X. was supported by the Richard King Mellon Foundation. We thank the Center for Advanced Brain Magnetic Source Imaging (CABMSI) and Magnetic Resonance Research Center (MRRC) at University of Pittsburgh Medical Center for providing the scanning time for MEG and MRI data collection. We specifically thank Anna Haridis at CABMSI for her assistance in MEG setup and data collection. We also thank the reviewers for their helpful comments, which improved the manuscript.
References
- 1.Hamalainen M, Hari R, Ilmoniemi RJ, Knuutila J, Lounasmaa OV. Magnetoencephalography—theory, instrumentation, and applications to noninvasive studies of the working human brain. Reviews of Modern Physics. 1993;65(2):413–498. [Google Scholar]
- 2.Uutela K, Hamalainen M, Somersalo E. Visualization of magnetoencephalographic data using minimum current estimates. NeuroImage. 1999;10:173–180. doi: 10.1006/nimg.1999.0454. [DOI] [PubMed] [Google Scholar]
- 3.Efron B. Bootstrap methods: another look at the jackknife. Annals of Statistics. 1979;7:1–26. [Google Scholar]
- 4.Heller KA, Ghahramani Z. Bayesian hierarchical clustering. Proceedings of the 22nd International Conference on Machine Learning; 2005. [Google Scholar]
- 5.Waldert S, Preissl H, Demandt E, Braun C, Birbaumer D, Aertsen A, Mehring C. Hand movement direction decoded from MEG and EEG. Journal of Neuroscience. 2008;28(4):1000–1008. doi: 10.1523/JNEUROSCI.5171-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wang W, Sudre GP, Xu Y, Kass RE, Collinger JL, Degenhart AD, Bagic AI, Weber DJ. Decoding and cortical source localization for intended movement direction with MEG. Journal of Neurophysiology. 2010;104(5):2451–2461. doi: 10.1152/jn.00239.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Behseta S, Kass RE, Moorman D, Olson C. Testing equality of several functions: analysis of single-unit firing rate curves across multiple experimental conditions. Statistics in Medicine. 2007;26:3958–3975. doi: 10.1002/sim.2940. [DOI] [PubMed] [Google Scholar]
- 8.Kass RE, Raftery A. Bayes factors. Journal of the American Statistical Association. 1995;90:773–795. [Google Scholar]
- 9.Xu Y, Heller KA, Ghahramani Z. Tree-based inference for Dirichlet process mixtures. Proceedings of the 12th International Conference on Artificial Intelligence and Statistics; 2009. [Google Scholar]
- 10.Nichols TE, Holmes AP. Nonparametric permutation tests for functional neuroimaging: a primer with examples. Human Brain Mapping. 2001;15:1–25. doi: 10.1002/hbm.1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Taulu S, Simola J, Kajola M. Applications of the signal space separation method. IEEE Transactions on Signal Processing. 2005;53(9):3359–3372. [Google Scholar]
- 12.Georgopoulos AP, Schwartz AB, Kettner RE. Neuronal population coding of movement direction. Science. 1986;233:1416–1419. doi: 10.1126/science.3749885. [DOI] [PubMed] [Google Scholar]
- 13.Georgopoulos AP, Caminiti R, Kalaska JF, Massey JT. Spatial coding of movement: a hypothesis concerning the coding of movement direction by motor cortical populations. Experimental Brain Research. 1983;7:327–336. [Google Scholar]
- 14.Georgopoulos AP, Kalaska JF, Caminiti R, Massey JT. On the relations between the direction of two-dimensional arm movements and cell discharge in primate motor cortex. Journal of Neuroscience. 1982;2:1527–1537. doi: 10.1523/JNEUROSCI.02-11-01527.1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sudre G, Xu Y, Kass R, Weber DJ, Wang W. Cluster-based algorithm for ROI analysis and cognitive state decoding using single-trial source MEG data. Proceedings of the 17th International Conference on Biomagnetism; 2010. [Google Scholar]