A Splitting-Based Iterative Algorithm for Accelerated Statistical X-Ray CT Reconstruction

Abstract

Statistical image reconstruction using penalized weighted least-squares (PWLS) criteria can improve image-quality in X-ray CT. However, the huge dynamic range of the statistical weights leads to a highly shift-variant inverse problem making it difficult to precondition and accelerate existing iterative algorithms that attack the statistical model directly. We propose to alleviate the problem by using a variable-splitting scheme that separates the shift-variant and (“nearly”) invariant components of the statistical data model and also decouples the regularization term. This leads to an equivalent constrained problem that we tackle using the classical method-of-multipliers framework with alternating minimization. The specific form of our splitting yields an alternating direction method of multipliers (ADMM) algorithm with an inner-step involving a “nearly” shift-invariant linear system that is suitable for FFT-based preconditioning using cone-type filters. The proposed method can efficiently handle a variety of convex regularization criteria including smooth edge-preserving regularizers and nonsmooth sparsity-promoting ones based on the ℓ₁-norm and total variation. Numerical experiments with synthetic and real in vivo human data illustrate that cone-filter preconditioners accelerate the proposed ADMM resulting in fast convergence of ADMM compared to conventional (nonlinear conjugate gradient, ordered subsets) and state-of-the-art (MFISTA, split-Bregman) algorithms that are applicable for CT.

I. Introduction

Statistical image reconstruction methods in X-ray CT minimize a cost function consisting of a data-fidelity term that accommodates the measurement statistics and the geometry of the data-acquisition process, and a regularization term that reduces noise. For example, PWLS cost functions for X-ray CT use a (statistically) weighted quadratic data-fidelity term [1], [2] and can provide improved image-quality compared to filtered back-projection (FBP) [1], [2]. However, computation-intensive iterative methods are needed to minimize such cost functions. This paper describes a new minimization algorithm that uses variable splitting to provide accelerated convergence.

Several types of iterative algorithms have been proposed for statistical image reconstruction in X-ray CT, including iterative coordinate descent (ICD) methods [1], block-based coordinate descent [3], ordered subsets (OS) algorithms based on separable quadratic surrogates (SQS) [4], [5] and (preconditioned) nonlinear conjugate gradient (NCG) methods [6]. For fast computation on multiprocessor computers, (P)NCG-type methods appear to be particularly amenable to efficient parallelization because they update all voxels simultaneously using all measurements.

Developing suitable preconditioners for (P)NCG is challenging for X-ray CT because the enormous dynamic range of the transmission data causes the Hessian of the statistical data-fidelity term to be highly shift-variant [6]. Clinthorne et al. [7] showed that for unweighted least-squares reconstruction, one can precondition the problem effectively using FFTs with a kind of cone filter. This cone filter amplifies high spatial frequencies, helping to accelerate convergence. But that cone filter is ineffective for (P)NCG in the PWLS case [6]. Delaney et al. [8] considered a very special type of shift-invariant weighting and also demonstrated accelerated convergence, but for low-dose X-ray CT the appropriate statistical weighting does not satisfy the assumptions in [8]. Shift-variant pre-conditioners based on multiple FFTs were proposed in [6] for 2D transmission tomography, but never became popular due to their complexity and were never investigated for 3D problems. Another way to introduce a cone filter is the iterative FBP approach [9], [10]. Initially these algorithms “converge” rapidly compared to (P)NCG methods, but typically they do not have any theoretical convergence properties and “too many” iterations lead to undesirably noisy images. Furthermore, it is unclear how to include regularization while ensuring convergence.

The challenges described above apply regardless of the form of the regularizer. Additional difficulties arise when one uses nonsmooth regularizers such as total variation (TV) [11] and sparsity-promoting ones based on the ℓ₁-norm [12]. These regularizers are not differentiable everywhere precluding optimization by conventional gradient-descent methods (e.g., NCG). Differentiable approximations (e.g., using “corner-rounding” [12, Sec. VI.A], [13, App. A]) can be employed, but even with such modifications the Hessian of the regularizer can have very high curvature leading to slow convergence of conventional gradient-descent methods [14]. While some state-of-the-art algorithms such as (M)FISTA [15], [16] and split-Bregman-type schemes (that split only the regularization term) [17], [18] are able to handle nonsmooth regularizers exactly (i.e., without corner rounding), when applied to X-ray CT, they must minimize a cost function that involves the original statistical data-fidelity term and are in turn hindered by the shift-variance of its Hessian (see Sections II-B, IV).

In this work, we propose to use a variable-splitting technique that not only decouples the regularization term in the spirit of [17], but also dissociates the statistical and geometrical components in the data-fidelity term. This forms the key feature of our approach that enables us to “isolate” the shift-variant element in the statistical data-fidelity term thereby alleviating the problem. Our splitting procedure uses auxiliary constraint variables to transform the original PWLS problem into an equivalent constrained optimization task that we solve using the classical method-of-multipliers [19], [20] and alternating direction optimization [21]–[23] frameworks. This leads to an alternating direction method of multipliers (ADMM) algorithm for solving the original PWLS problem that, apart from requiring simple operations (such as inverting a diagonal matrix, solving 1D denoising problems), involves the solving of a “nearly” shift-invariant linear system, which is amenable to FFT-based preconditioning using cone-type filters [7]. Experimental results with synthetic and real in vivo human data indicate that the proposed ADMM converges faster than conventional (NCG and ordered subsets) and state-of-the-art (MFISTA and split-Bregman) methods, illustrating the efficacy of our splitting scheme and the potential of cone-filter preconditioners for accelerating the proposed ADMM. The proposed ADMM can also be used with a variety of convex regularization criteria (see Section VI-A) including smooth edge-preserving regularizers and nonsmooth ones such as TV and ℓ₁-regularization.

The paper is organized as follows. In Section II, we mathematically formulate X-ray CT reconstruction as a PWLS problem and briefly discuss drawbacks of some existing algorithms for X-ray CT. Section III discusses the proposed splitting strategy and the development of the ADMM algorithm in detail. In Section IV, we compare our ADMM algorithm with the split-Bregman technique applied for CT, schematically. Section V is dedicated to numerical experiments and results, while Section VI discusses possible extensions of this work to 3D CT and other statistical models. Finally, we draw our conclusions in Section VII.

II. Statistical X-ray CT Reconstruction

A. Problem Formulation

For CT, an accurate statistical model for the data is quite complicated [24], [25] and is often replaced by a Gaussian approximation [1], [2] with a suitable diagonal weighting term W whose components {w_i} are inversely proportional to the measurement variances [1], [2]. We consider a penalized weighted least-squares (PWLS) formulation of statistical CT reconstruction [1]:

$$\mathbf{P}\mathbf{0}:arg\underset{\mathbf{x}}{min}\left\{J(\mathbf{x})\triangleq J_{\text{data}}(\mathbf{y},\mathbf{Ax})+\mathrm{\Psi }(\mathbf{Rx})\right\},$$ (1)

$$J_{\text{data}}(\mathbf{y},\mathbf{Ax})\triangleq \frac{1}{2}{\left|\right|\mathbf{y}-\mathbf{Ax}\left|\right|}_{\mathbf{W}}^2,$$ (2)

where y is the M × 1 data vector (log of transmission data), A is the M × N system matrix, Ax represents the forward projection operation (e.g., line integrals), W = diag{w_i} is a M × M diagonal matrix consisting of statistical weights,¹ and ${\left|\right|\mathbf{u}\left|\right|}_{\mathbf{W}}^{\mathbf{2}}\triangleq {\mathbf{u}}^{\top }\mathbf{Wu}$. We use a general family of regularizers of the form [12]

$$\mathrm{\Psi }(\mathbf{Rx})=\lambda \sum _r{\kappa }_r{\mathrm{\Phi }}_r\left(\sum _{p=1}^P{\mid {[{\mathbf{R}}_p\mathbf{x}]}_r\mid }^m\right),$$ (3)

where λ > 0 is the regularization parameter, κ_r > 0 ∀r are user-provided weights that govern the spatial resolution in the reconstructed output [26], Φ_r are potential functions, the R × N matrix R ≜ [R₁^⊤ ··· R_P^⊤]^⊤ constitutes regularization operators R_p (e.g., finite differences, frames, etc) of size L × N, where R = PL. We concentrate on values of m and instances of Φ that result in a convex regularizer Ψ in (3).

The above general regularizer is in the “analysis” form [27], i.e., Ψ is specified as a function of the reconstructed image x. The method proposed in this paper can also be easily extended to handle “synthesis” forms [27], e.g., by writing x = Sθ and considering J(θ) = J_data(y, ASθ) + Φ(θ) in P0, for some potential function Φ and synthesis operator S. We focus on the analysis form (3) as it includes popular nonsmooth criteria such as TV (for ${\mathrm{\Phi }}_r(x)=\sqrt{x}$ and m = 2), analysis ℓ₁-wavelets (for Φ_r(x) = x, m = 1) and a variety of smooth convex edge-preserving regularizers (e.g., Huber [28], [29], Fair [6], [30] etc).

B. Previous Approaches

Conventional gradient-descent methods, e.g., NCG, for P0 depend on the Hessian of J_data: H_data = A^⊤WA, which is highly shift-variant in CT particularly due to the large dynamic range of W. As a result, it becomes difficult to precondition and accelerate such methods [6]. Fessler et al. [6] directly attacked P0 using NCG and proposed a shift-variant preconditioner to tackle H_data. But their preconditioner is data-dependent and requires at least one pair of FFT-iFFT operations per NCG-iteration.

Iterative shrinkage-thresholding (IST) [31] and its variants ((M)FISTA [15], [16], and (M)TWIST [32]) that are applicable to P0 depend on the Lipschitz constant L_data of J_data(y, Ax):

$$L_{\text{data}}={\sigma }_{max}\{{\mathbf{A}}^{\top }\mathbf{WA}\},$$ (4)

where σ_max represents the maximum eigenvalue. The convergence speed of these algorithms is primarily determined by (4): A large value of L_data results in small gradient steps [15, Sec. 1.1] leading to slow convergence. Since W has a large dynamic range and due to the (approximately) 1/r-type decay of the elements of A^⊤A, L_data can be large for CT decreasing convergence speed of IST-type algorithms. Optimization transfer-based methods (e.g., [33, Sec. IV-B.1]) face a similar issue in that the surrogate functions end up having high curvature [5] due to W, which again leads to small update-steps and slow convergence.

In summary, the weighting term W, although crucial for improving reconstruction quality, poses a challenge for optimization. Compared to A^⊤WA, the term A^⊤A is “more” shift-invariant and is appropriate for preconditioning using cone filters. This property has been used to accelerate un-weighted least-squares reconstruction for tomographic image reconstruction [7]. Therefore, our idea to mitigate the shift-variance of H_data is to untangle W from H_data thereby making the resulting problem “more” shift-invariant and suitable to circulant preconditioning. To do so, we adopt a variable-splitting strategy.

Variable splitting (VS) refers to the process of introducing auxiliary constraint variables to separate coupled components in the cost function [12], [17], [18], [34]–[42]. This procedure transforms the original minimization problem into an equivalent constrained optimization problem that can be effectively solved using classical constrained optimization schemes [19], [20]. The VS approach is appealing as it renders the resulting constrained problem tractable to alternating minimization schemes that decouple it in terms of the auxiliary variables and simplify optimization [12], [17], [18], [34], [36], [37], [39]–[42].

The VS approach has become popular recently for solving reconstruction problems in image processing [17], [34]–[37], MRI [12], [39], [40] and CT [18], [41], [42]. Many authors have focussed on splitting the regularization term [17], [18], [34], [37], [39]–[41] as it is hard to tackle in inverse problems (especially nonsmooth ones such as TV and ℓ₁-regularization). Splitting the regularization term enables one to handle it exactly (i.e., without the need for “corner-rounding” [12, Sec. VI.A], [13, App. A] for nonsmooth criteria) via simple denoising problems [12], [17], [37], [42]. However, in PWLS problems for CT, the data-term adds to the complexity (as it leads to a shift-variant hessian H_data) and therefore demands attention. So in this work, besides splitting the regularization term, we also split the data-term.

III. Proposed Method

A. Equivalent Constrained Optimization Problem

We introduce auxiliary constraint variables u ∈ ℝ^M and v ∈ ℝ^R and write P0 as the following equivalent constrained problem:

$$\begin{array}{l}arg\underset{\mathbf{x},\mathbf{u},\mathbf{v}}{min}\{f(\mathbf{u},\mathbf{v})\triangleq J_{\text{data}}(\mathbf{y},\mathbf{u})+\mathrm{\Psi }(\mathbf{v})\}\\ \text{s}.\text{t}.\mathbf{u}=\mathbf{Ax},\mathbf{v}=\mathbf{Rx},\end{array}$$ (5)

where u separates the effect of W on Ax and v splits the regularization term as in [17]. Afonso et al. [36] and Figueiredo et al. [38] have utilized data-term-splitting in the context of image restoration [36], [38] and reconstruction from partial Fourier observations [36]. However, our emphasis here is on CT reconstruction where u plays an important role: It leads to a sub-problem that is “nearly” shift-invariant and suitable to preconditioning using cone filters [42] as explained in Section III-C.

In general, the proposed splitting strategy (5) can be applied to any PWLS problem of the form P0 so as to exploit shift-invariant features in the data-model, e.g., deconvolution of blurred images corrupted with non-stationary noise.

Before proceeding, we rewrite (5) concisely as

$$\mathbf{P}\mathbf{1}:arg\underset{\mathbf{x},\mathbf{z}}{min}f(\mathbf{z})\text{s}.\text{t}.\mathbf{z}=\mathbf{Cx},$$ (6)

where

$$\mathbf{z}\triangleq \left[\begin{array}{c}\mathbf{u}\\ \mathbf{v}\end{array}\right],\mathbf{C}\triangleq \left[\begin{array}{c}\mathbf{A}\\ \mathbf{R}\end{array}\right].$$ (7)

Since P1 is equivalent to P0, solving P1 for x yields the desired reconstruction in (1).

B. Method of Multipliers

To solve P1, we use the classical framework of the method of multipliers [19], [20] and construct an augmented Lagrangian (AL) function [12], [19], [20], [42]

$$\mathcal{L}(\mathbf{x},\mathbf{z},\mathit{\gamma })\triangleq f(\mathbf{z})+{\mathit{\gamma }}^{\top }(\mathbf{z}-\mathbf{Cx})+\frac{\mu }{2}{\left|\right|\mathbf{z}-\mathbf{Cx}\left|\right|}_{\mathbf{\Lambda }}^2$$ (8)

that combines a multiplier term γ^⊤(z − Cx) with Lagrange multiplier $\mathit{\gamma }\triangleq {[\begin{array}{ll}{{\mathit{\gamma }}_{\mathbf{u}}}^{\top }\hfill & {{\mathit{\gamma }}_{\mathbf{v}}}^{\top }\hfill \end{array}]}^{\top }\in {\mathbb{R}}^{M+R}$ and a quadratic penalty term $\frac{\mu }{2}{\left|\right|\mathbf{z}-\mathbf{Cx}\left|\right|}_{\mathbf{\Lambda }}^2$, where μ > 0 is the AL penalty parameter and Λ ≻ 0 is a symmetric weighting matrix. The multiplier term can be absorbed into the penalty term in (8) (by completing the square) for ease of manipulation leading to

$$\mathcal{L}(\mathbf{x},\mathbf{z},\mathit{\eta })\triangleq f(\mathbf{z})+\frac{\mu }{2}{\left|\right|\mathbf{z}-\mathbf{Cx}-\mathit{\eta }\left|\right|}_{\mathbf{\Lambda }}^2+{\mathfrak{c}}_{\mathit{\eta }},$$ (9)

where $\mathit{\eta }\triangleq {[\begin{array}{ll}{{\mathit{\eta }}_{\mathbf{u}}}^{\top }\hfill & {{\mathit{\eta }}_{\mathbf{v}}}^{\top }\hfill \end{array}]}^{\top }=-\frac{1}{\mu }{\mathbf{\Lambda }}^{-1}\mathit{\gamma }$ and ${\mathfrak{c}}_{\mathit{\eta }}\triangleq -\frac{\mu }{2}{\left|\right|\mathit{\eta }\left|\right|}_{\mathbf{\Lambda }}^2$ is a constant independent of x and z. Unlike standard approaches [36], [38] that set Λ = I_M+R, we propose to use

$$\mathbf{\Lambda }=\left[\begin{array}{cc}{\mathbf{I}}_M& \mathbf{0}\\ \mathbf{0}& \nu {\mathbf{I}}_R\end{array}\right],$$ (10)

where ν > 0. This is crucial in CT because the elements of A and R can differ by several orders of magnitude and it is imperative to balance them to avoid numerical instabilities in the resulting algorithm and to achieve faster convergence [42].

The classical AL scheme for solving P1 alternates between a joint-minimization step and an update step [12, Sec. III]:

$$({\mathbf{x}}^{(j+1)},{\mathbf{z}}^{(j+1)})=arg\underset{\mathbf{x},\mathbf{z}}{min}\mathcal{L}(\mathbf{x},\mathbf{z},{\eta }^{(j)}),$$ (11)

$${\mathit{\eta }}^{(j+1)}={\mathit{\eta }}^{(j)}-({\mathbf{z}}^{(j+1)}-{\mathbf{C}\mathbf{x}}^{(j+1)}),$$ (12)

respectively. Unlike pure penalty methods, remarkably, the AL formalism does not require increasing μ → ∞ to ensure convergence of (11)–(12) to a solution of P1 [19].

C. Alternating Direction Minimization

It is numerically appealing to replace the more difficult joint-minimization step (11) by alternating direction optimization that decouples (11) as [21]–[23]

$${\mathbf{x}}^{(j+1)}=arg\underset{\mathbf{x}}{min}\mathcal{L}(\mathbf{x},{\mathbf{z}}^{(j)},{\mathit{\eta }}^{(j)}),$$ (13)

$${\mathbf{z}}^{(j+1)}=arg\underset{\mathbf{z}}{min}\mathcal{L}({\mathbf{x}}^{(j+1)},\mathbf{z},{\mathit{\eta }}^{(j)}).$$ (14)

Thus, at the jth iteration, instead of (11)–(12), we perform (ignoring constant terms)

$${\mathbf{x}}^{(j+1)}\stackrel{{\epsilon }_{\mathbf{x}}^{(j)}}{=}arg\underset{\mathbf{x}}{min}{\left|\right|{\mathbf{z}}^{(j)}-\mathbf{Cx}-{\mathit{\eta }}^{(j)}\left|\right|}_{\mathbf{\Lambda }}^2,$$ (15)

$${\mathbf{z}}^{(j+1)}\stackrel{{\epsilon }_{\mathbf{z}}^{(j)}}{=}arg\underset{\mathbf{z}}{min}f(\mathbf{z})+{\left|\right|\mathbf{z}-{\mathbf{C}\mathbf{x}}^{(j+1)}-{\mathit{\eta }}^{(j)}\left|\right|}_{\mathbf{\Lambda }}^2,$$ (16)

$${\mathit{\eta }}^{(j+1)}={\mathit{\eta }}^{(j)}-({\mathbf{z}}^{(j+1)}-{\mathbf{C}\mathbf{x}}^{(j+1)}),$$ (17)

where we write $\mathbf{x}\stackrel{\epsilon }{=}{\mathbf{x}}^{★}$ to mean that ||x − x^★||₂ ≤ ε, i.e., we allow for inexact updates in (15)–(16) in the spirit of [43]. Although (15)–(16) is an approximation to (11), the following theorem adapted from [43, Theorem 8] to P1 guarantees convergence of (15)–(17) to a solution of (5) (and P0).

Theorem 1

Consider P1 in (6) where f is closed, proper, convex² and C has full column-rank. Let η⁽⁰⁾ ∞ ℝ^M+R, μ > 0,

$$\sum _j{\epsilon }_{\mathbf{x}}^{(j)}<\infty ,\text{and}\sum _j{\epsilon }_{\mathbf{z}}^{(j)}<\infty .$$ (18)

If P1 has a solution (x^★, z^★), then the sequence of updates {(x^(j), z^(j))}_j generated by (15)–(17) converges to (x^★, z^★). If P1 has no solution, then at least one of the sequences {(x^(j), z^(j))}_j or {η^(j)}_j diverges.

The result of Eckstein et al. [43, Theorem 8] uses an AL function with Λ = I, so we apply [43, Theorem 8] to (9) with Λ in (10) through a simple change of variables.³ For CT, it can be readily ensured that C has full column-rank for a variety of regularization operators R. In the sequel, we explain how to perform the minimizations in (15)–(16).

Firstly, we see that due to the structure of f(z) and C, (16) further dissociates into the following:

$${\mathbf{u}}^{(j+1)}\stackrel{{\epsilon }_{\mathbf{u}}^{(j)}}{=}arg\underset{\mathbf{u}}{min}\left\{J_{\text{data}}(\mathbf{y},\mathbf{u})+\frac{\mu }{2}{\left|\right|\mathbf{u}-\mathbf{A}{\mathbf{x}}^{(j+1)}-{\mathit{\eta }}_{\mathbf{u}}^{(j)}\left|\right|}_2^2\right\},$$ (19)

$${\mathbf{v}}^{(j+1)}\stackrel{{\epsilon }_{\mathbf{v}}^{(j)}}{=}arg\underset{\mathbf{v}}{min}\left\{\mathrm{\Psi }(\mathbf{v})+\frac{\mu \nu }{2}{\left|\right|\mathbf{v}-\mathbf{R}{\mathbf{x}}^{(j+1)}-{\mathit{\eta }}_{\mathbf{v}}^{(j)}\left|\right|}_2^2\right\}.$$ (20)

These sub-problems are independent of each other and can therefore be solved simultaneously, where ${[{\epsilon }_{\mathbf{z}}^{(j)}]}^2={[{\epsilon }_{\mathbf{u}}^{(j)}]}^2+{[{\epsilon }_{\mathbf{v}}^{(j)}]}^2\forall j$. Sub-problem (19) is quadratic and has a closed form solution:

$${\mathbf{u}}^{(j+1)}={\mathbf{D}}_{\mu }^{-1}(\mathbf{Wy}+\mu (\mathbf{A}{\mathbf{x}}^{(j+1)}+{\mathit{\eta }}_{\mathbf{u}}^{(j)})),$$ (21)

where D_μ ≜ (W + μI_M). Since W is diagonal, D_μ can be inverted exactly, so that ${\epsilon }_{\mathbf{u}}^{(j)}=0$ in (19) ∀ j.

Minimization w.r.t. v (20) corresponds to a denoising problem that can be solved efficiently and/or exactly for a variety of instances of (3) including TV: This has been elucidated by many authors [12], [17], [36]–[40], [45], e.g., the techniques developed in [12, Sec. IV.A-2 – IV.A-6] can be directly applied to (20). For brevity, we concentrate on two particular instances of (3) and solve (20) exactly so that ${\epsilon }_{\mathbf{v}}^{(j)}=0$ in (20) ∀ j.

• Analysis ℓ₁-regularization [m = 1, Φ_r(x) = x ∀ r in (3)]:

  $$\mathrm{\Psi }(\mathbf{Rx})=\lambda \sum _{r=1}^R{\kappa }_r\mid {[\mathbf{Rx}]}_r\mid$$ (22)

  with the shift-invariant Haar wavelet transform (excluding the approximation level) for R, which is a sparsity-promoting criterion [12], [27], [36], [38].

• Smooth edge-preserving regularization [P = 1, m = 1, Φ_r = Φ_FP ∀ r in (3)]:

  $$\mathrm{\Psi }(\mathbf{Rx})=\lambda \sum _{r=1}^R{\kappa }_r{\mathrm{\Phi }}_{\text{FP}}(\mid {[\mathbf{Rx}]}_r\mid )$$ (23)

  using the Fair potential Φ_FP(x) = x/δ−log(1+x/δ) with δ > 0 [30] (also the smoothed Laplace function in [45, Eq. 4.11]) and finite-differences for R. This regularizer ensures a unique solution to P0 as Φ_FP is strictly convex. It has also been successfully applied to PWLS problems in tomography [6].

For these regularizers, (20) separates into R 1D minimization problems in terms of the components ${\{v_r\}}_{r=1}^R$ of v:

$$v_r^{(j+1)}=arg\underset{v_r}{min}\mathrm{\Psi }(v_r)+\frac{\mu \nu }{2}{(v_r-{\varrho }_r^{(j)})}^2,$$ (24)

where ${\varrho }_r^{(j)}$ is the rth component of ${\mathit{\varrho }}^{(j)}\triangleq \mathbf{R}{\mathbf{x}}^{(j+1)}+{\mathit{\eta }}_{\mathbf{v}}^{(j)}$. For (22), the solution of (24) is given by the shrinkage rule⁴ [46]

$$v_r^{(j+1)}=\text{sign}\{{\varrho }^{(j)}\}max\left(\mid {\varrho }^{(j)}\mid -\frac{\lambda {\kappa }_r}{\mu \nu },0\right).$$ (25)

For (23), (24) leads to a quadratic equation in v_r [45, Eq. 4.13] that yields

$$v_r^{(j+1)}=\text{sign}\{{\varrho }_r^{(j)}\}\frac{{\zeta }_r^{(j)}+\sqrt{{({\zeta }_r^{(j)})}^2+4\delta \mid {\varrho }_r^{(j)}\mid }}{2},$$ (26)

where ${\zeta }_r^{(j)}\triangleq \mid {\varrho }_r^{(j)}\mid -\delta -\lambda {\kappa }_r/(\delta \mu \nu )$.

Having addressed (16), we now consider (15) which can be easily solved analytically:

$${\mathbf{x}}^{(j+1)★}={\mathbf{G}}_{\nu }^{-1}({\mathbf{A}}^{\top }({\mathbf{u}}^{(j)}-{\mathit{\eta }}_{\mathbf{u}}^{(j)})+\nu {\mathbf{R}}^{\top }({\mathbf{v}}^{(j)}-{\mathit{\eta }}_{\mathbf{v}}^{(j)})),$$ (27)

where x^(j+1)★ represents the exact solution to (15) and

$${\mathbf{G}}_{\nu }\triangleq {\mathbf{C}}^{\top }\mathbf{\Lambda }\mathbf{C}=({\mathbf{A}}^{\top }\mathbf{A}+\nu {\mathbf{R}}^{\top }\mathbf{R})$$ (28)

is non-singular because Λ ≻ 0 and R is chosen so that C has full column-rank. Although (27) is an exact analytical solution, the enormous size of G_ν for CT makes it impossible to store and “invert” G_ν exactly. So we propose to use the conjugate gradient (CG) method for (27) and obtain an approximate update ${\mathbf{x}}^{(j+1)}\stackrel{{\epsilon }_{\mathbf{x}}^{(j)}}{=}{\mathbf{x}}^{(j+1)★}$. Since G_ν is non-singular, we have that

$${\epsilon }_{\mathbf{x}}^{(j)}\le \frac{{\rho }_{\mathbf{x}}^{(j)}}{{\sigma }_{min}\{{\mathbf{G}}_{\nu }\}},$$ (29)

where ${\rho }_{\mathbf{x}}^{(j)}$ is the corresponding residue and σ_min{G_ν} > 0 is the minimum eigenvalue of G_ν that depends only on A and R and can be precomputed e.g., using stochastic techniques [47] or the Power method.⁵ Therefore, using (29), one can monitor ${\epsilon }_{\mathbf{x}}^{(j)}$ in the CG-loop and design a suitable stopping rule to satisfy (18).

D. Preconditioning Using Cone Filter

We see that G_ν contains A^⊤A, which is “nearly” shift-invariant, so for shift-invariant⁶ R^⊤R, G_ν is amenable to preconditioning using suitable cone filters [6], [7]. We constructed a circulant matrix G̃_ν from the central column of G_ν:

$${\stackrel{\sim }{\mathbf{G}}}_{\nu }=\text{circ}\{{\mathbf{G}}_{\nu }{\mathbf{e}}_c\},$$ (30)

and used its inverse, ${\stackrel{\sim }{\mathbf{G}}}_{\nu }^{-1}$, as the preconditioner, where e_c is a standard basis vector of ℝ^N corresponding to the center pixel of the image and circ{α} represents the construction of a circulant matrix from a vector α. The proposed preconditioner ${\stackrel{\sim }{\mathbf{G}}}_{\nu }^{-1}$ corresponds to a cone-type filter that amplifies high spatial frequencies and accelerates convergence of both the CG-loop for (27) and the overall ADMM scheme as demonstrated in Section V. Implementing ${\stackrel{\sim }{\mathbf{G}}}_{\nu }^{-1}$ requires only one FFT-iFFT per CG iteration and its construction⁷ uses a product with R^⊤R and only one forward-backward projection that can be performed offline as G̃_ν is independent of W. In our experiments, we applied at most two preconditioned CG (PCG) iterations with warm starting [12] and found that ${\rho }_{\mathbf{x}}^{(j)}$ decreased sufficiently rapidly. Based on (15)–(29), we present our algorithm in Fig. 1 for solving P1 (and thus P0). In principle, Steps 4 and 5 of ADMM may be executed in parallel as they are independent of each other, but in our implementation, we chose to execute all the steps sequentially for simplicity.

Fig. 1.

ADMM for statistical X-ray CT reconstruction.

E. Selection of μ and ν

The parameters μ and ν do not affect the solution of P1, but only regulate the convergence speed of the proposed ADMM [12], [35, Sec. 4.4]. In general, choosing appropriate values for AL penalty parameters (such as μ and ν) is a nontrivial and application-dependent task. Several empirical rules have been put forth by many authors for setting AL penalty parameters (to obtain good convergence speeds for AL-based iterative reconstruction schemes) in many applications, see e.g., [37], [38] for image restoration, [17] for denoising and compressed-sensing MRI, and [12], [39] for parallel MRI reconstruction.

In this paper, Step 3 is the only inexact step of the proposed ADMM. So the computational speed of ADMM is primarily determined by how efficiently (27) is solved, which in turn is governed by ν. We use an empirical rule for selecting ν that is based on [17]: Since ν balances A^⊤A and R^⊤R in G_ν that have disjoint non-trivial null-spaces, the condition number κ(G_ν) of G_ν exhibits a minimum for some ν_min > 0: ν_min = arg min_ν κ(G_ν). It was suggested in [17] to use this property to choose AL penalty parameters to ensure quick convergence of the CG-algorithm for solving a linear system such as (27). For A implemented using the distance-driven (DD) projector [49] and R in (22)–(23), ν_min ≈ 10⁵, which yielded a very small (λ/μν) in (20) and subsequently resulted in slow convergence of ADMM in our experiments. On the other extreme, setting ν = 1 (corresponding to the standard case of Λ = I_M+R) yields a poorly conditioned G_ν that was not favorable either.

Based on our experience with 2D CT experiments, we found the empirical rule⁸ ${\nu }_{\mathit{emp}}=\frac{1}{100}arg{min}_{{\nu }_0}\kappa ({\stackrel{\sim }{\mathbf{G}}}_{{\nu }_0})$ to yield good overall convergence speeds for ADMM, where G̃_ν is the circulant matrix in (30). We also observed that ADMM was slightly more robust to the choice of μ than ν. We selected μ = median{w_i} to avoid outliers in W; this yielded a well-conditioned D_μ (with κ{D_μ} ∈ [10, 40]) that improved the numerical stability of ADMM.

IV. Comparison with the Split-Bregman Approach

The split-Bregman (SB) method [17] uses constraint variables to split the regularization term alone. For (1), this corresponds to using only v = Rx which leads to following equivalent constrained problem

$$arg\underset{\mathbf{x},\mathbf{v}}{min}\{f_{\text{SB}}(\mathbf{x},\mathbf{v})\triangleq J_{\text{data}}(\mathbf{y},\mathbf{Ax})+\mathrm{\Psi }(\mathbf{v})\}$$ (31)

$$\text{s}.\text{t}.\mathbf{v}=\mathbf{Rx}.$$ (32)

This type of splitting has been investigated for CT reconstruction in [18], [41]. Applying the Bregman iterations [17, Eq. 3.7–3.8] with alternating minimization [17, Sec. 3.1] to (31) yields the following SB scheme:⁹

$${\mathbf{x}}^{(j+1)}=arg\underset{\mathbf{x}}{min}\left\{{\left|\right|\mathbf{y}-\mathbf{Ax}\left|\right|}_{\mathbf{W}}^2+\frac{\mu }{2}{\left|\right|{\mathbf{v}}^{(j)}-\mathbf{Rx}-{\mathit{\eta }}_{\mathbf{v}}^{(j)}\left|\right|}_2^2\right\},$$ (33)

$${\mathbf{v}}^{(j+1)}=arg\underset{\mathbf{v}}{min}\left\{\mathrm{\Psi }(\mathbf{v})+\frac{\mu }{2}{\left|\right|\mathbf{v}-\mathbf{R}{\mathbf{x}}^{(j+1)}-{\mathit{\eta }}_{\mathbf{v}}^{(j)}\left|\right|}_2^2\right\},$$ (34)

$${\mathit{\eta }}_{\mathbf{v}}^{(j+1)}={\mathit{\eta }}_{\mathbf{v}}^{(j)}-({\mathbf{v}}^{(j+1)}-\mathbf{R}{\mathbf{x}}^{(j+1)}).$$ (35)

The minimization in (34) is same as that in (20), so the techniques described for (20) apply to (34) as well. The main difference between the proposed method (15)–(17) and the SB scheme (33)–(35) is in the way x is updated. The minimization in (33) leads to

$${\mathbf{x}}^{(j+1)★}={\mathbf{B}}_{\mu }^{-1}[{\mathbf{A}}^{\top }\mathbf{Wy}+\mu {\mathbf{R}}^{\top }({\mathbf{v}}^{(j)}-{\mathit{\eta }}_{\mathbf{v}}^{(j)})],$$ (36)

where x^(j+1)★ represents the exact solution to (36) and

$${\mathbf{B}}_{\mu }\triangleq ({\mathbf{A}}^{\top }\mathbf{WA}+\mu {\mathbf{R}}^{\top }\mathbf{R}).$$ (37)

The matrix B_μ contains the shift-variant component W that makes standard preconditioners (including cone filters) less effective for CG-based solving of (36). Nevertheless, we used PCG for (36) with a circulant preconditioner ${\stackrel{\sim }{\mathbf{G}}}_{\mu }^{-1}$ (obtained by setting μ ≡ ν in (30)) in our implementation of the SB scheme and found that it improved upon the standard CG method for (36). We selected¹⁰ μ = L_data/(100 σ_max{R^⊤R}) for SB¹¹ (see (4) for definitions of L_data and σ_max). This choice is motivated by the discussion pertaining to ν in Section III-E.

In principle, it is possible to construct a shift-variant preconditioner for B_μ in the spirit of [6], but such a preconditioner would invariably be data-dependent and may be computationally involved. Our approach (15)–(17) provides a simple and effective alternative using an extra constraint variable u in (5): Compared to the SB scheme (33)-(35), our method requires only an extra trivial operation of inverting a diagonal matrix D_μ in (21).

V. Experimental Results

We present numerical results for 2D CT reconstruction from simulated NCAT phantom data and in vivo human head data. The proposed ADMM is also applicable, in principle, to 3D CT reconstruction (see Section VI-A). We implemented the following algorithms in Matlab and conducted the experiments on a quad-core PC with 3.07 GHz Intel Xeon processors and 12 GB RAM.

• NCG-n: unpreconditioned nonlinear conjugate gradient algorithm with n line-search iterations that monotonically decrease the cost function J [6],

• MFISTA-n: Monotone Fast Iterative Shrinkage-Thresholding Algorithm [16] with n iterations for solving auxiliary denoising sub-problems similar to [16, Eq. 3.13],

• OS-n: Ordered subsets algorithm [5] with n blocks,

• SB-(P)CG-n: Split-Bregman scheme from Section IV with n (P)CG iterations for solving (36),

• ADMM-(P)CG-n: Proposed ADMM with n (P)CG iterations for solving (27).

MFISTA is a state-of-the-art method developed by Beck et al. [16] for image restoration that is readily applicable to P0 with the Lipschitz constant L_data in (4). Beck et al. [15] also proposed a back-tracking strategy that does not require explicit computation of L_data, but we chose to estimate and use¹¹ L_data both for ease of implementation and because it is the smallest possible value [15, Ex. 2.2] that yields the fastest convergence for MFISTA. We applied the Chambolle-type method [50] for the inner-step (i.e., computing the proximal map [16, Eq. 3.13]) of MFISTA as that does not require smoothing of (“corners” of) ℓ₁-regularizers such as (22).

Since our task is to solve P0, we fixed the cost function J (that led to a visually appealing reconstruction) and focussed on the convergence speed of the algorithms. We quantified the convergence rate using the normalized ℓ₂-distance between x^(j) and x^★:

$$\xi (j)=20{log}_{10}\left(\frac{{\left|\right|{\mathbf{x}}^{(j)}-{\mathbf{x}}^{★}\left|\right|}_2}{{\left|\right|{\mathbf{x}}^{★}\left|\right|}_2}\right),$$ (38)

where x^★ is a solution to P0 obtained numerically by running one of the above algorithms as described next. Since the algorithms have different computation load per (outer) iteration, we evaluated ξ(j) as a function of algorithm run-time¹² t_j, i.e., the time elapsed from start until iteration j. We also plot ξ(j) as a function of the iteration index j for completeness. We used the DD-projector [49] (with 8 threads) for implementing matrix-vector products such as Ax, A^⊤u and initialized all the algorithms with the image reconstructed using FBP (with the ramp filter) in all experiments.

Products with A and A^⊤ (corresponding to forward- and back-projections, respectively) are computation intensive in CT reconstruction problems and dominate the overall computation load of a reconstruction algorithm.¹³ NCG and MFISTA both require only one product with A and A^⊤, respectively, per iteration. The OS method breaks products with A and A^⊤ in terms of block-rows of A and block-columns of A^⊤, respectively, and cycles through each block once per every iteration, so effectively, OS also requires only one product with A and A^⊤, respectively, per iteration. However, for each block, the OS method demands the evaluation of the gradient of the regularization term that increases computation time per iteration as indicated in Table I. For the SB scheme, we employ (P)CG for “inverting” B_μ (that depends on A^⊤WA) in (36), so SB-(P)CG-n requires n products with A and A^⊤, respectively, per iteration of (33)-(35). In the case of ADMM, we apply (P)CG at Step 3 (see Fig.1) for “inverting” G_ν in (27), but that step also requires a product with A^⊤ in the RHS of (27), so overall ADMM-(P)CG-n uses n products with A and n + 1 products with A^⊤ per iteration of Steps 3–7 in Fig.1. Table I summarizes this discussion and also shows the mean computation time per iteration (averaged over 10 iterations) of the above algorithms. Although the proposed ADMM(-PCG) requires more forward- and back-projections per iteration (and accordingly exhibits higher computation time per iteration) compared to other algorithms (with the exception of the OS method) in Table I, we demonstrate in the sequel that it converges faster in terms of algorithm runtime.

TABLE I.

Computation Time and Number of Projections required per Iteration of Algorithms Compared in Section V

Algorithm	Time/Iteration (in seconds)		Projection operations/Iteration
	Section V-A	Section V-B	Forward (A)	Backward (A⊤)
NCG-5	1.56	4.85	1	1
NCG-10	-	8.83	1	1
MFISTA-5	2.49	8.87	1	1
MFISTA-25	5.23	-	1	1
OS-4	-	10.19	1 (effective)	1 (effective)
OS-41	-	61.84	1 (effective)	1 (effective)
SB-CG-1	2.29	6.22	1	1
SB-CG-2	3.29	8.93	2	2
SB-PCG-1	2.29	6.25	1	1
SB-PCG-2	3.30	9.07	2	2
ADMM-CG-1	3.29	8.91	1	2
ADMM-CG-2	4.31	11.61	2	3
ADMM-PCG-1	3.32	8.94	1	2
ADMM-PCG-2	4.34	11.70	2	3

A. Simulation with the NCAT Phantom

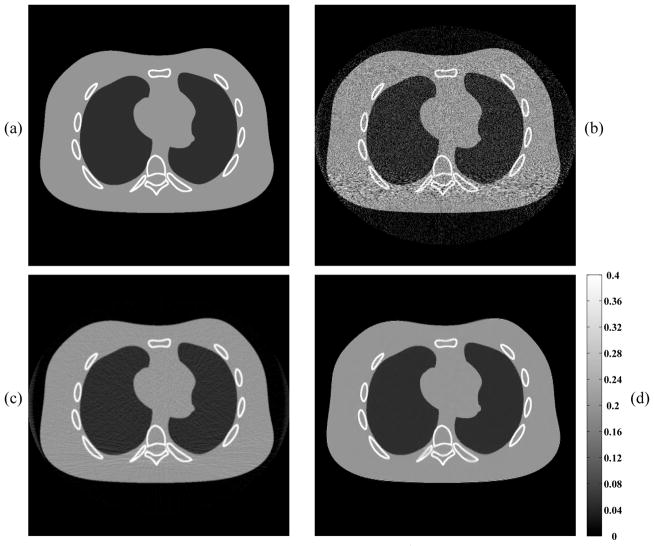
We used a 1024 × 1024 2D slice of the NCAT phantom [51] and numerically generated a 888 × 984-view noisy sinogram with GE LightSpeed fan-beam geometry [52] corresponding to a monoenergetic source with 2.5 × 10⁴ incident photons per ray and no background events. We used the ℓ₁-regularization in (22) with κ_r = ω_{(r mod N)}, where ${\omega }_n\triangleq \sqrt{{[{\mathbf{A}}^{\top }\mathbf{W}\mathbf{1}]}_n/{[{\mathbf{A}}^{\top }\mathbf{1}]}_n}$ is based on [26]. We reconstructed 512 × 512 images over a FOV of 65 cm; we obtained x^★ by running 5000 iterations of MFISTA-25 as it does not require “corner-rounding” and is therefore guaranteed to converge to a solution of P0. NCG cannot directly handle nonsmooth criteria such as (22) without smoothing it [13, App. A], so we used a smoothing value of 10⁻⁶ cm⁻¹. The FBP reconstructions in Figs. 2b, 2c corresponding to the ramp and Hanning filters, respectively, are either noisy or blurred and streaked with artifacts. The ℓ₁-regularized reconstruction x^★ in Fig. 2d preserves image features and has lower RMSE than both FBP outputs.

Fig. 2.

Simulation with the NCAT phantom: (a) Noisefree NCAT phantom (in cm⁻¹), (b) FBP reconstruction with ramp filter, also the initial guess x⁽⁰⁾ for all iterative algorithms, (c) FBP reconstruction with Hanning filter, and (d) ℓ₁-regularized reconstruction, also the solution x^★ to P0. Images in (a)–(d) have been normalized to the same color scale [as that of (a)] indicated beside (d). The ℓ₁-regularized reconstruction (d) is less noisy and has almost no streaky-artifacts compared to both FBP results.

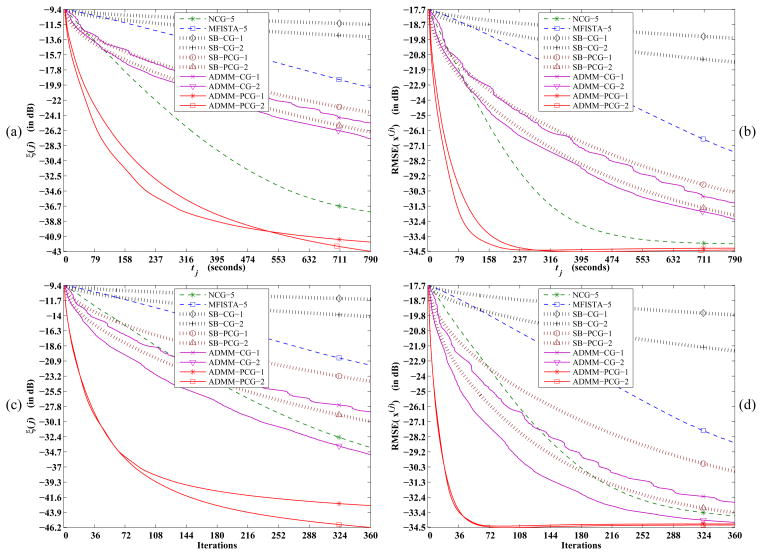
We plot ξ(j) for various algorithms as a function of time in Fig. 3a. The SB-CG scheme appears to converge the slowest, while SB-PCG is faster indicating that the circulant preconditioner ${\stackrel{\sim }{\mathbf{G}}}_{\mu }^{-1}$ provides a moderate acceleration of CG for (36). MFISTA is slower than most of the algorithms for the reason explained in Section II. The CG-version of the proposed method, ADMM-CG, is slightly faster than MFISTA and SB-(P)CG but slower than NCG. The preconditioned version ADMM-PCG is the fastest among all algorithms illustrating that the cone-filter preconditioner ${\stackrel{\sim }{\mathbf{G}}}_{\nu }^{-1}$ is very effective in accelerating convergence of CG applied to (27) and ADMM-PCG. This is also corroborated by Fig. 3c where for a given number of iterations, ADMM-PCG produces a reconstruction that is closest to x^★ in terms of ξ(j). Figs. 3b, 3d further substantiate the reconstruction speed-up of ADMM-PCG over other methods, where (both in terms of algorithm run-time and number of iterations) it rapidly leads to a RMSE-value close to RMSE(x^★).

Fig. 3.

Simulation with the NCAT phantom: (a), (b) Plot of ξ(j) and RMSE(x^(j)), respectively, as a function of time t_j and (c), (d) Plot of ξ(j) and RMSE(x^(j)), respectively, with respect to iterations, for various algorithms considered in this work. The unpreconditioned version of the proposed method, ADMM-CG, converges slightly faster than MFISTA and the split-Bregman scheme SB-(P)CG but is slower than NCG as seen in (a) and (b). But the preconditioned version, ADMM-PCG, converges rapidly both in terms of ξ(j) and RMSE indicating that the cone-filter-preconditioner ( ${\stackrel{\sim }{\mathbf{G}}}_{\nu }^{-1}$ in Section III-E) greatly accelerates convergence of the proposed ADMM.

B. Experiments with a in vivo Human Head Data-set

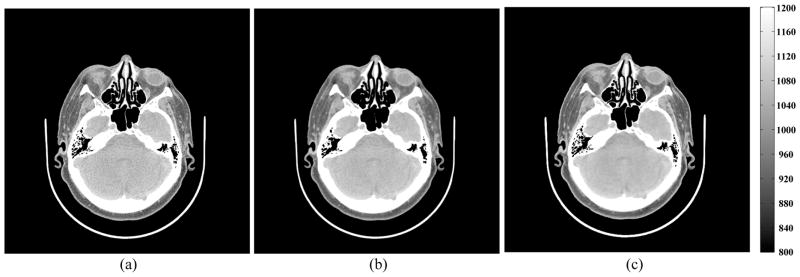
In this experiment, we used a in vivo human head data-set acquired with a GE scanner using 120 kVp source potential and 585 mA tube current with 0.6 s rotation. We reconstructed a 1024 × 1024 2D slice with 50 cm FOV and 0.625 mm thickness from a 888 × 984-view sinogram. For Ψ in (1), we used the strictly convex regularizer (23) (with δ = 10 HU) that guarantees a unique solution x^★ to P0. As NCG generally had faster convergence than MFISTA in our experiments, we obtained x^★ by running 5000 iterations of NCG-10. Fig. 4 shows the reconstruction results for this experiment. The regularized solution x^★ in Fig. 4c has reduced noise and better preserves the anatomical features compared to the FBP reconstructions in Figs. 4a, 4b obtained using the ramp and Hanning filters, respectively.

Fig. 4.

Experiment with the in vivo human head data-set: (a) FBP reconstruction with the ramp filter, also the initial guess x⁽⁰⁾ for all iterative algorithms, (b) RBP reconstruction with Hanning filter, and (c) PWLS reconstruction with the strictly convex regularizer (23), also the unique solution x^★ to P0. Images in (a)–(c) are displayed in Hounsfield units indicated beside (c). The regularized reconstruction (c) is less noisy and preserves anatomical features compared to both FBP results.

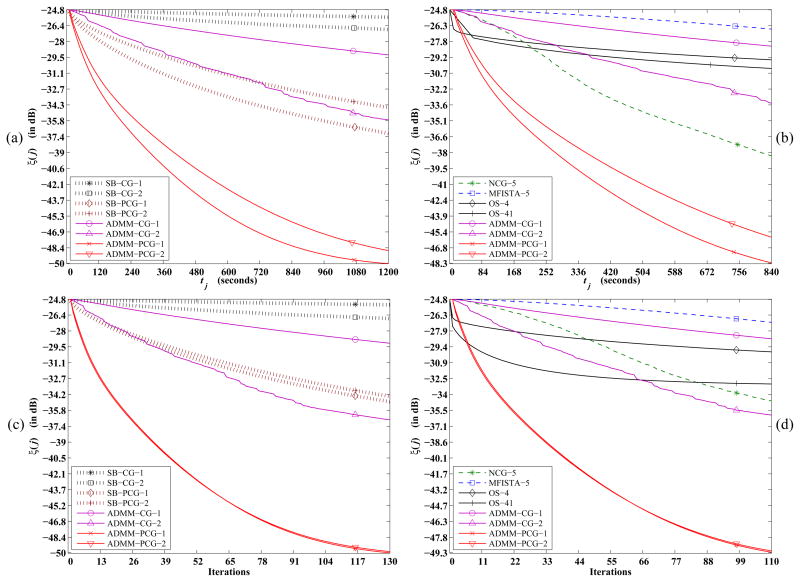
Figs. 5a–d plot ξ(j) as a function of t_j and iteration index j for all algorithms considered in this work. Here, we additionally compare the standard OS algorithm (that is not guaranteed to converge) in Figs. 5b, 5d, where we used the implementation from [53] available currently for regularization criteria such as (23). The OS algorithm is faster than all algorithms (including ADMM-PCG) for the first few iterations but it does not converge to the minimizer as expected. In practice, it may be advantageous to run a few iterations of OS and use its output to initialize a more sophisticated iterative algorithm. Figs. 5a, 5b indicate that the convergence trends for MFISTA, NCG, SB-(P)CG and ADMM-CG are generally similar to those in Figs. 3a, 3b. ADMM-PCG again provides notable reconstruction speed-up compared to all algorithms. This substantiates the potential of the cone-filter preconditioner (30) for the proposed ADMM and also demonstrates the benefit of our splitting scheme (5).

Fig. 5.

Experiment with the in vivo human head data-set: (a), (b) Plot of ξ(j) as a function of time t_j and (c), (d) Plot of ξ(j) with respect to iterations, for various algorithms considered in this work. MFISTA and SB-CG appear to be the slowest. The proposed ADMM-(P)CG is generally faster than the split-Bregman scheme SB-(P)CG as seen in (a). Although ADMM-CG converges slower than NCG as seen in (b), the preconditioned version ADMM-PCG is the fastest among the considered algorithms, illustrating the benefit of the cone-filter-based preconditioner (G̃_ν in Section III-E) for the proposed ADMM.

VI. Discussion

A. Memory Requirements

Splitting-based algorithms simplify optimization at the expense of manipulating and storing auxiliary constraint variables (and corresponding Lagrange multipliers in the AL formalism) and therefore have additional memory requirements compared to conventional algorithms such as NCG. Although this does not pose much concern for 2D reconstruction problems, it can represent a significant memory overhead for 3D problems. Specifically, the SB (Section IV) and the proposed ADMM¹⁴ (in Fig. 1) schemes use the constraint v = Rx that requires the storage of 2P vectors (v and η_v) of size L × 1. For instance, typically, the size of an image-volume in 3D CT is N = 512 × 512 × 512 (≈ 1 GB of memory when stored in double-precision format in Matlab). Then, for finite-differences with P = 13 (there are 13 nearest-neighbors on one side of any voxel), this corresponds to storing at least 26 image-volumes (≈ 26 GB of memory) that might set a practical limitation on these methods from an implementation perspective.

A quick remedy is to consider the TV regularizer with finite-differences only along the three orthogonal directions (P = 3 corresponds to 6 image-volumes) which considerably reduces the memory load. Alternatively, one could also consider using an orthonormal transform (such as orthonormal wavelets¹⁵) for R, so P = 1 and L = N. The SB and ADMM¹⁴ schemes would then require storing only 2 image-volumes (corresponding to v and η_v). Moreover, an orthonormal R satisfies R^⊤R = I_N that facilitates ADMM: G_ν in (28) becomes G_ν = (A^⊤A + νI_N) that is still “nearly” shift-invariant and can be effectively preconditioned using circulant preconditioners. With orthonormal wavelets, one also has the option of excluding the approximation coefficients from the regularization (as they are not sparse) by using scale dependent regularization parameters [50] and setting those parameters corresponding to the approximation level to zero.

B. Inclusion of Nonnegativity Constraint

In CT, a nonnegativity constraint is often imposed [1, Eq. 18], [11, Sec. 2.2] to model the positivity of the attenuation coefficient that is being reconstructed. Although we have not considered such a constraint in P0, it can be easily accommodated [38] as follows. We start with

$$arg\underset{\mathbf{x}}{min}\left\{J(\mathbf{x})\triangleq J_{\text{data}}(\mathbf{y},\mathbf{Ax})+\mathrm{\Psi }(\mathbf{Rx})+g(\mathbf{x})\right\},$$ (39)

where g is an indicator function

$$g(\mathbf{x})\triangleq \{\begin{array}{ll}0,\hfill & \text{if}\mathbf{x}\ge 0,\hfill \\ +\infty ,\hfill & \text{otherwise},\hfill \end{array}$$ (40)

that imposes the nonnegativity constraint, x ≥ 0, taken component-wise in (40). We then consider the following equivalent constrained version [38] that has an additional constraint compared to (5):

$$\begin{array}{l}arg\underset{\mathbf{x},\mathbf{u},\mathbf{v},\mathbf{w}}{min}\{f(\mathbf{u},\mathbf{v},\mathbf{w})\triangleq J_{\text{data}}(\mathbf{y},\mathbf{u})+\mathrm{\Psi }(\mathbf{v})+g(\mathbf{w})\}\\ \text{s}.\text{t}.\mathbf{u}=\mathbf{Ax},\mathbf{v}=\mathbf{Rx},\mathbf{w}=\mathbf{x}.\end{array}$$ (41)

Writing $\mathbf{z}\triangleq {[\begin{array}{lll}{\mathbf{u}}^{\top }\hfill & {\mathbf{v}}^{\top }\hfill & {\mathbf{w}}^{\top }\hfill \end{array}]}^{\top },\mathbf{C}\triangleq {[\begin{array}{lll}{\mathbf{A}}^{\top }\hfill & {\mathbf{R}}^{\top }\hfill & {\mathbf{I}}_N\hfill \end{array}]}^{\top }$ and using Λ = diag{I_M, ν₁I_R, ν₂I_N} in (9), we can design an ADMM-type algorithm similar to (15)–(17) for solving (41). It can be shown that the updates for u and v in this algorithm will be similar to (19) and (20), respectively, while the update of x would involve the “inversion” of G_ν1ν2 = (A^⊤A+ ν₁R^⊤R+ν₂I_N) and that of w would require a simple projection onto the positive orthant [38, Eq. 32]. Since G_ν1ν2 is also “nearly” shift-invariant, a cone-filter-type preconditioner similar to ${\stackrel{\sim }{\mathbf{G}}}_{\nu }^{-1}$ [see (30)] can be used for effective preconditioning of ${\mathbf{G}}_{{\nu }_1{\nu }_2}^{-1}$. Moreover, the above C has full column-rank, so this algorithm also satisfies Theorem 1 and is guaranteed to converge to a solution of (41) and (39).

C. Poisson-Likelihood Model for X-ray CT Reconstruction

The proposed strategy of splitting the data-term [i.e., the use of u in (5) and (41)] is also applicable for X-ray CT reconstruction using the Poisson-likelihood (PL) statistical model [5, Eq. 1] that may be more suitable for low-dose acquisitions. It can be shown that splitting the PL data-term yields separable 1D problems in ${\{u_i\}}_{i=1}^M$ that can be solved simultaneously similar to [38, Eq. 30]. However, the PL model for X-ray CT may preclude exact updates like (21) for {u_i}. Moreover, the general PL model [5, Eq. 1] includes background events and can be (“mildly”) nonconvex, so Theorem 1 cannot be directly applied to an ADMM-type algorithm developed for this problem. We plan to explore cost functions involving the PL model [5, Eq. 1] for transmission tomography reconstruction as part of future extensions to this work.

VII. Summary and Conclusions

Statistical X-ray CT reconstruction using penalized weighted least-squares (PWLS) criteria involve a diagonal weighting matrix W that poses a hindrance to several optimization methods due to its huge dynamic range and highly shift-variant nature. In this work, we employed a variable-splitting technique that, in addition to separating the regularization term like [17], also dissociates the statistical (W) and the system (A) components in the data term to decouple and mitigate the effect of W. We applied the method of multipliers [19] with alternating minimization [21]–[23] for the resulting equivalent constrained problem and developed an alternating direction method of multipliers (ADMM) algorithm that chiefly involves three simple operations at each iteration: (i) inverting a diagonal matrix that depends on W, (ii) minimizing a set of 1D auxiliary denoising-cost-functions that can be performed efficiently and/or exactly for a variety of regularizers, and (iii) solving a “nearly” shift-invariant linear system (involving A^⊤A) using FFT-based preconditioning with cone-type filters [7].

The proposed ADMM algorithm is guaranteed to converge to a solution of the original PWLS problem under a mild condition on the accuracy of operation (iii) above. We demonstrated using simulations and experiments with real in vivo human data that cone-filter-type preconditioners are very effective for solving the linear system in (iii) and that the preconditioned version of the proposed ADMM converges faster than conventional (NCG and ordered subsets) and state-of-the-art (MFISTA and split-Bregman) algorithms for CT. The proposed ADMM can handle a variety of regularization criteria for 2D CT reconstruction and is also applicable to 3D CT reconstruction, perhaps by using certain memory-conserving regularizers.