Abstract
To obtain structural and spectroscopic models for the diiron(II,III) centers in the active sites of diiron enzymes, the (μ-alkoxo)(μ-carboxylato)diiron(II,III) complexes [FeIIFeIII(N-Et-HPTB)(O2CPh)(NCCH3)2](ClO4)3 (1) and [FeIIFeIII(N-Et-HPTB)(O2CPh) (Cl)(HOCH3)](ClO4)2 (2) (N-Et-HPTB = N,N,N′,N′-tetrakis(2-(1-ethyl-benzimidazolylmethyl))-2-hydroxy-1,3-diamino propane), have been prepared and characterized by X-ray crystallography, EPR, and Mössbauer spectroscopy. The Fe1-Fe2 separations are 3.60 Å and 3.63 Å and the Fe1-O1-Fe2 bond angles are 128.0° and 129.4° for 1 and 2, respectively. Mössbauer and EPR studies of 1 show that the FeIII (SA = 5/2) and FeII (SB = 2) sites are antiferromagnetically coupled to yield a ground state with S = 1/2 (g = 1.75, 1.88, 1.96); Mössbauer analysis of solid 1 yields J = 22.5 ± 2 cm−1 for the exchange coupling constant (
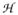 = JSA•SB convention). In addition to the S = 1/2 ground state spectrum of 1, the EPR signal for the S = 3/2 excited state of the spin ladder can also be observed, the first time such a signal has been detected for an antiferromagnetically coupled diiron(II,III) complex. The anisotropy of the 57Fe magnetic hyperfine interactions at the FeIII site is larger than normally observed in mononuclear complexes and arises from admixing S > 1/2 excited states into the S = 1/2 ground state by zero-field splittings at the two Fe sites. Analysis of the “D/J” mixing has allowed us to extract the zero-field splitting parameters, local g values, and magnetic hyperfine structural parameters for the individual Fe sites. The methodology developed and followed in this analysis is presented in detail. The spin Hamiltonian parameters of 1 are related to the molecular structure with the help of DFT calculations. Contrary to what was assumed in previous studies, our analysis demonstrates that the deviations of the g-values from the free electron value (g = 2) for the antiferromagnetically coupled diiron(II,III) core in complex
1
are predominantly determined by the anisotropy of the effective g-values of the ferrous ion, and only to a lesser extent by the admixture of excited states into ground state ZFS terms (D/J mixing). The results for 1 are discussed in the context of the data available for diiron(II,III) clusters in proteins and synthetic diiron(II,III) complexes.
= JSA•SB convention). In addition to the S = 1/2 ground state spectrum of 1, the EPR signal for the S = 3/2 excited state of the spin ladder can also be observed, the first time such a signal has been detected for an antiferromagnetically coupled diiron(II,III) complex. The anisotropy of the 57Fe magnetic hyperfine interactions at the FeIII site is larger than normally observed in mononuclear complexes and arises from admixing S > 1/2 excited states into the S = 1/2 ground state by zero-field splittings at the two Fe sites. Analysis of the “D/J” mixing has allowed us to extract the zero-field splitting parameters, local g values, and magnetic hyperfine structural parameters for the individual Fe sites. The methodology developed and followed in this analysis is presented in detail. The spin Hamiltonian parameters of 1 are related to the molecular structure with the help of DFT calculations. Contrary to what was assumed in previous studies, our analysis demonstrates that the deviations of the g-values from the free electron value (g = 2) for the antiferromagnetically coupled diiron(II,III) core in complex
1
are predominantly determined by the anisotropy of the effective g-values of the ferrous ion, and only to a lesser extent by the admixture of excited states into ground state ZFS terms (D/J mixing). The results for 1 are discussed in the context of the data available for diiron(II,III) clusters in proteins and synthetic diiron(II,III) complexes.
1. Introduction
Carboxylate-bridged nonheme diiron clusters are found in a wide array of enzymes that activate dioxygen and carry out many physiologically and environmentally important reactions.1 This ever expanding class include hemerythrin (Hr)2 and related proteins,3,4 methane monooxygenases (MMO),5,6 the R2 subunits of Class 1a ribonucleotide reductases (RNR),7,8 fatty acid desaturases,9 toluene/xylene monooxygenases,10 toluene-4-monooxygenase,11 deoxyhypusine hydroxylase,12 the arylamine N-oxygenase AurF,13,14 the amino acid β-hydroxylase CmlA,15 fatty aldehyde decarbonylases,16 tRNA hydroxylase miaE,17 ferritin,18,19 rubrerythrin,20 and symerythrin.21 To better understand their coordination environments and electronic structures, synthetic model complexes with a μ-oxo, μ-hydroxo, μ-alkoxo, or μ-phenoxo bridge have been prepared and spectroscopically characterized to mimic the diiron(II) or diiron(III) states of the enzymes. In addition to the commonly encountered diiron(II) or diiron(III) states, dinuclear iron sites can also exist in the mixed-valent diiron(II,III) state. In fact, the appearance of the characteristic EPR signal associated with diiron(II,III) clusters in the g = 2 region can be useful for the initial identification of enzymes with diiron active sites.22 While diiron(III) and diiron(II) states are well known players in the catalytic cycles and have been subjected to spectroscopic scrutiny, less attention has been devoted to the diiron(II,III) clusters due both to the greater difficulty in obtaining the diiron(II,III) state in a relative pure form22,23 and to the notion that the diiron(II,III) state may not be catalytically relevant in most O2-activating diiron enzymes.1,5
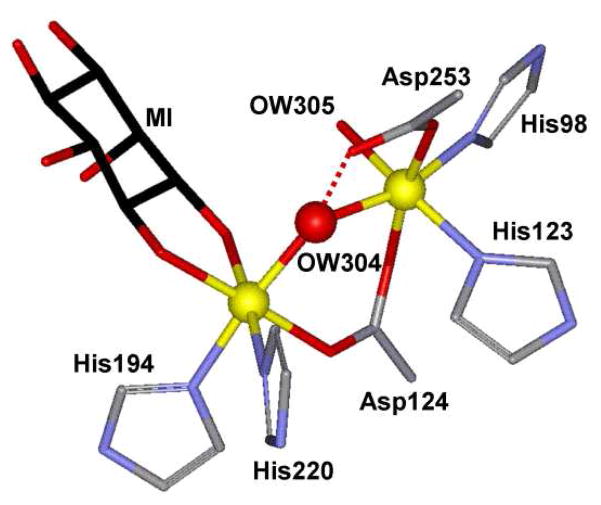
This notion was recently challenged when myo-inositol oxygenase (MIOX) was established to be a member of the family of dioxygen-activating nonheme diiron oxygenases. MIOX catalyzes the oxidative conversion of myo-inositol (MI) to D-glucuronic acid (DG) in higher eukaryotes and some bacteria,24,25 This conversion is the first step in the only known pathway in humans for the breakdown of MI,26 the depletion of which is implicated in diabetes mellitus and hepatic encephalopathy.27,28 While canonical dioxygen activation in diiron enzymes is initiated at diferrous clusters,1 MIOX diverges from this pattern and activates O2 using a mixed-valent FeIIFeIII state as the starting point.29–31 As the coordination of MI has been postulated to prime the diiron cluster for O2 activation, insight into the activation mechanism may be obtained by studying the influence of MI’s coordination on the geometric and electronic structures of the active site. Recent crystal structures for the substrate-bound complexes of mouse and human MIOX32,33 reveal that the MI substrate binds in a bidentate mode through the hydroxyl groups on C1 and C6 to the presumed FeIII site, leaving the FeII site ready for O2 binding (Figure 1).32 However these crystal structures may represent inactive diiron(III) forms of MIOX,34 leaving structural details of the active MI-bound diiron(II,III) form not fully established. Moreover, the absence of structural data for the MI-unbound form of the diiron structure precludes structural comparison between “off” and “on” states.
Figure 1.
The substrate-bound active site of mouse MIOX (2HUO).32
An alternative approach for gaining insight into the catalytically active diiron(II,III) forms of diiron enzymes is to apply spectroscopic techniques such as electron paramagnetic resonance (EPR) and Mössbauer spectroscopy. Antiferromagnetic coupling between the two iron centers of the iron(II,III) cluster affords an S = 1/2 ground state that exhibits characteristic EPR signals in the g ≤ 2 region.35 For example, active MIOX features EPR signals at g = 1.95, 1.66, 1.66, which change to 1.95, 1.81, 1.81 upon MI binding.29 Similarly, binding of phosphate to uteroferrin(II,III) elicits sizable changes in the EPR signals from (1.94, 1.73, 1.56) to (2.27, 1.51, 1.06).36–38 However, questions still remain as to how these data can be interpreted to provide better understanding into changes of electronic and even physical structures. Overcoming this difficulty requires an approach for extracting detailed information about the (electronic) structure from these data. Developing such a methodology requires first and foremost diiron(II,III) clusters that exhibit well-defined EPR and Mössbauer features. Unfortunately, poorly resolved EPR and Mössbauer spectra have persistently been a limiting factor in previous reports on diiron(II,III) clusters.29,39
In addition to providing a good starting point for establishing the relationship between spectroscopic data and electronic structure, appropriate diiron model complexes can shed light on important structural features of the active site of diiron enzymes. Different from the classic carboxylate-rich diiron active site in O2-activating enzymes,40 four His and two Asp residues coordinate to the diiron center in the active site of MIOX with the two irons bridged by a solvent-derived oxygen atom and a bidentate carboxylate from Asp-124.32,33 The nature of the single atom bridge between the iron atoms of the diiron center (i.e. OW304 in Figure 1), be it oxo, hydroxo or aqua, is difficult to ascertain from the protein crystal structures. Therefore, a comparison of the structural and spectroscopic properties of the enzyme with structurally characterized doubly bridged mixed-valent diiron(II,III) complexes may be useful. So far, only a number of mixed-valent complexes with triply bridged (μ-oxo/alkoxo/phenoxo)bis(μ-carboxylato)diiron(II,III) cores have been prepared and characterized.41–48
In this study, we have used the dinucleating ligand N,N,N′,N′-tetrakis(1-ethyl-benzimidazolyl-2-methyl)-2-hydroxy-1,3-diaminopropane (H-N-Et-HPTB) to synthesize two complexes with doubly bridged (μ-alkoxo)(μ-carboxylato)diiron(II,III) cores. These two mixed-valent complexes have been characterized by X-ray crystallography and UV-visible absorption spectroscopy, and one complex has also been analyzed in great detail with EPR and Mössbauer spectroscopies. We describe an approach, rooted in earlier contributions (see below), that allowed us to extract as many as 16 unknown spin Hamiltonian parameters, including the exchange coupling constant J, zero-field splitting parameters, local g-values, (hyper)fine structure parameters for individual irons. DFT studies further allowed us to correlate the framework of electronic structure with the coordination structure of the complex. This analysis enabled us to identify the origin of the anisotropies of the g values, in particular, whether they primarily originate from the anisotropy of the g-values for the iron(II) site, or from an admixture of excited S > 1/2 states into the ground S = 1/2 state through D/J mixing. As our approach is applicable to any antiferromagnetically coupled diiron(II,III) cluster, it may lead to a better understanding of electronic structures of such clusters in biological and synthetic systems.
2. Materials and Methods
2.1 Syntheses of complexes
Reagents and anhydrous grade solvents were purchased commercially and used as received. The dinucleating ligand N-Et-HPTB was synthesized according to a literature procedure.49 Elemental analyses were performed at Atlantic Microlab, Inc. Caution! The perchlorate salts in this study are all potentially explosive and should be handled with care.
[FeIIFeIII(N-Et-HPTB)(O2CPh)(NCCH3)2](ClO4)3 (1) was prepared under argon by dissolving PhCOOH (31 mg, 0.25 mmol), Et3N (38 mg, 0.38 mmol), and H-N-Et-HPTB (181 mg, 0.25 mmol) in 10 ml methanol and transferring the solution anaerobically to solid Fe(ClO4)2•6H2O (91 mg, 0.25 mmol) and Fe(ClO4)3•6H2O (133 mg, 0.25 mmol). A red solid precipitated from the solution within minutes. Red crystals of 1 (210 mg, 65%) of crystallographic quality were obtained by slow diffusion of diethyl ether into a CH3CN solution of 1 in a glovebox. Anal. Calc. For [FeIIFeIII(N-Et-HPTB)(O2CPh) (NCCH3)2](ClO4)3•CH3CN•2.5H2O (C52H62Cl3Fe2N11O17.5): C, 46.63; H, 4.66; N, 11.50. Found: C, 46.33; H, 4.56; N, 11.70.
[FeIIFeIII(N-Et-HPTB)(O2CPh)(Cl)(HOCH3)](ClO4)2 (2) was prepared in a glovebox by dissolving 1 (210 mg, 0.14 mmol) and [Bu4N]Cl (48 mg, 0.17mmol) in 8 ml of 1:1 mixture of CH3CN and CH3OH. The reaction mixture was stirred for four days, filtered through a filtration disk. Slow diffusion of tetrahydrofuran (THF) into the filtrate produced red crystals of 2 (90 mg, 42%) of crystallographic quality. Anal. Calc. For [FeIIFeIII(N-Et-HPTB)(O2CPh)(Cl)(HOCH3)](ClO4)2•CH3CN•H2O (C53H63Cl3Fe2N11O13): C, 49.73; H, 4.96; N, 12.04. Found: C, 49.30; H, 4.81; N, 12.13.
2.2 X-ray Crystallography
X-ray diffraction data was collected on a red cubic crystal of 1 (approximate dimensions 0.30 × 0.30 × 0.30 mm3) and a red plate crystal of 2 (0.60 × 0.30 × 0.17 mm3) by a Bruker SMART Platform CCD diffractometer for a data collection at 173(2) K in University of Minnesota Crystallography Facility. A randomly oriented region of reciprocal space was surveyed to the extent of 1.5 hemispheres and to a resolution of 0.80 Å for both structures. Three major sections of frames were collected with 0.30° steps in ω at 3 different ψ settings and a detector position of −28° in 2θ. The intensity data were corrected for absorption and decay (SADABS).50 Final cell constants were calculated from the xyz centroids of 3402 for 1 and 3210 for 2 strong reflections from the actual data collection after integration (SAINT).51 Please refer to Table 1 for additional crystal and refinement information. Structures of 1 and 2 were solved using SHELXTL-9752 and refined using SHELXTL-97.52 The space groups were determined based on systematic absences and intensity statistics. A direct-methods solution was calculated which provided most non-hydrogen atoms from the E-map. Full-matrix least squares/difference Fourier cycles were performed which located the remaining non-hydrogen atoms. All non-hydrogen atoms were refined with anisotropic displacement parameters. All hydrogen atoms were placed in ideal positions and refined as riding atoms with relative isotropic displacement parameters. There was considerable disorder associated with the three perchlorate counterions in the structure of 1. The perchlorate anion containing Cl(1) was modeled as disordered over three positions (25.5: 51.2: 23.3), the perchlorate anion containing Cl(2) was modeled as disordered over two positions (24.1: 75.9), and the perchlorate anion containing Cl(3) was modeled as disordered over three positions (48.7: 36.6: 14.7). In the structure of 2, attempts to model electron density in the vicinity of the coordinated methanol molecule (consisting essentially of O4 and C51) with THF solvent molecules resulted in a fractional molecular formula and an unsatisfactory short inter-molecular H···H distance between a hydrogen atom attached to C51 and a hydrogen atom from a THF molecule. PLATON53 located a region of disordered solvent equal to 567.9 Å3, or 16.3% of the total unit cell volume with an electron count per cell of 125. Final calculations were done after processing the data with the SQUEEZE function of PLATON. The final full matrix least squares refinement converged to R1 = 0.0391 and wR2 = 0.1188 for 1 and R1 = 0.0532 and wR2 = 0.1650 for 2. Additional information can be found in supporting information.
Table 1.
Crystal data and structure refinement for [FeIIFeIII(N-Et-HPTB)(O2CPh) (CH3CN)2](ClO4)3 (1) and [FeIIFeIII(N-Et-HPTB)(O2CPh)(Cl)(HOCH3)](ClO4)2 (2)
| Empirical formula | 1 | 2 |
|---|---|---|
| Formula weight | 1499.41 | 1450.01 |
|
| ||
| Space group | P-1 | P-1 |
|
| ||
| Unit cell dimensions | a = 12.730(1) Å | a = 12.627(1) Å |
| b = 13.881(1) Å | b = 13.524(1) Å | |
| c = 21.377(2) Å | c = 22.292(2) Å | |
| α = 100.080(2)° | α = 107.208(2)° | |
| β = 99.818(2)° | β = 90.163(2)° | |
| γ = 107.716(2)° | γ = 105.689(2)° | |
|
| ||
| Volume | 3440.5(6) Å3 | 3486.5(6) Å3 |
|
| ||
| Z | 2 | 2 |
|
| ||
| Crystal size | 0.30 × 0.30 × 0.30 mm3 | 0.60 × 0.31 × 0.17 mm3 |
|
| ||
| Reflections collected | 38153 | 38255 |
|
| ||
| Data / restraints / parameters | 14061 / 75 / 975 | 14177 / 85 / 871 |
|
| ||
| Goodness-of-fit on F2 | 1.022 | 1.066 |
|
| ||
| Final R indices | R1 = 0.0391, wR2 = 0.1045 | R1 = 0.0616, wR2 = 0.1727 |
|
| ||
| R indices (all data) | R1 = 0.0557, wR2 = 0.1188 | R1 = 0.0937, wR2 = 0.1999 |
|
| ||
| Largest diff. peak and hole | 0.471 and −0.394 e.Å−3 | 1.154 and −0.696 e.Å−3 |
2.3 Physical Methods
UV-Vis spectra of complexes in CH3CN were recorded on an HP8453A diode-array spectrometer. All samples were prepared in a N2-filled glovebox. Near IR spectra of complexes were collected on a Cary UV-Vis-IR spectrometer. EPR spectra of samples of 1 (~ 1.5 mM) in PrCN were obtained at liquid helium temperatures on a Bruker EPP 300 spectrometer equipped with an Oxford cryostat. EPR spectra were analyzed with the SpinCount developed by M. P. Hendrich. PrCN was used here rather than CH3CN to provide sharpened and better-resolved EPR signals of 1. Samples of 1 used for Mössbauer studies were prepared by selecting ~ 50 mg crystals of 1 with a single-crystal morphology, grinding the crystals to a fine powder, mixing the powder with ~0.3 mL nujol in a N2-filled glovebox until evenly distributed, and freezing the sample in a Mössbauer cup at liquid N2 temperatures. Mössbauer spectra were recorded with two spectrometers, using Janis Research Super-Varitemp dewars that allowed studies in applied magnetic fields up to 8.0 T in the temperature range from 1.5 to 200 K. Mössbauer spectral simulations were performed using the WMOSS software package (SEE Co., Edina, MN). Isomer shifts are quoted relative to Fe metal at 298 K.
2.4 DFT Calculations
DFT calculations were performed with G03,54 using the B3LYP/6-311G functional/basis set. Geometry optimizations were performed for both the ferromagnetic and broken symmetry state.
3. Results
3.1 Syntheses of diiron(II,III) complexes 1 and 2
Complex 1, [FeIIFeIII(N-Et-HPTB)(O2CPh)(NCCH3)2](ClO4)3, was prepared by reacting equimolar amounts of Fe3+, Fe2+, H-N-Et-HPTB and benzoic acid together with 1.5 equiv NEt3 in methanol and obtained in 65% recrystallized yield from CH3CN/Et2O. The self-assembly of 1 from a one-pot synthesis emphasizes the thermodynamic stability of the mixed-valent core in this system. Related complex 2, [FeIIFeIII(N-Et-HPTB)(O2CPh) (Cl)(HOCH3)]ClO4)2, was prepared by a ligand replacement reaction of 1 with a slight molar excess of chloride ion. Both complexes can be recrystallized to afford diffraction quality crystals that gave rise to high-quality X-ray structures.
3.2 Structural data
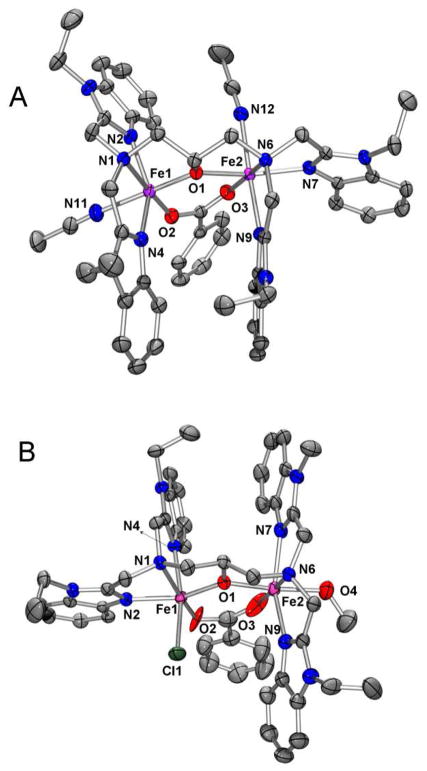
Crystals of 1 and 2 consist of the cations [FeIIFeIII(N-Et-HPTB)(O2CPh)(NCCH3)2]3+ (1) and [FeIIFeIII(N-Et-HPTB)(O2CPh)(Cl)(HOCH3)]2+ (2), respectively, and perchlorate counterions. As illustrated in Figure 2, the structures of the cations of 1 and 2 feature a (μ-alkoxo)(μ-carboxylato)diiron core with each iron ion being six-coordinate. Complexes 1 and 2 respectively exhibit Fe-Fe distances of 3.603(1) Å and 3.632(1) Å and Fe(1)-μ-O-Fe(2) angles of 128.0(1)° and 129.3(1)°. These values are larger than corresponding values for the closely related complex [FeIIFeIII(tpdb) (O2CPh)2]2+, which features a (μ-alkoxo)bis(μ-carboxylato)diiron(II,III) core,47 an Fe-Fe distance of 3.300(2) Å, and an Fe-μ-O-Fe angle of 105.8(3)°. The presence of only one carboxylate bridge in 1 and 2 as opposed to two such bridges in [FeIIFeIII(tpdb)(O2CPh)2]2+ significantly lengthens the Fe-Fe separation and enlarges Fe-O-Fe angle. Besides contributing the alkoxo oxygen O1 that bridges the two iron atoms in the complexes, the N-Et-HPTB ligand also provides each metal center with two benzimidazole donors and one tertiary amine donor. In all instances, the tertiary amines from N-Et-HPTB ligand coordinate trans to the oxygen atoms from the benzoate bridge. The iron coordination spheres are completed by two CH3CN ligands in 1 and by Cl− and CH3OH in 2.
Figure 2.
Thermal ellipsoid plots of A) [FeIIFeIII(N-Et-HPTB)(O2CPh)(NCCH3)2]3+ (1) and B) [FeIIFeIII(N-Et-HPTB)(O2CPh)(Cl)(HOCH3)]2+ (2) showing 50% probability thermal ellipsoids for all non-hydrogen atoms. H-atoms omitted for clarity. In both complex 1 and 2, Fe1 is FeIII and Fe2 is FeII.
The X-ray structural data for 1 and 2 (Figure 2, Table 2) clearly indicate that there are discrete Fe(II) and Fe(III) sites in both compounds. There are significant differences in the Fe-μ-O (O1) distances for the two iron centers: 2.088(2) and 1.919(2) Å for 1 and 2.064(3) and 1.953(3) Å for 2, reflecting a difference in oxidation state between the two iron atoms of the diiron core. The FeII-O bonds in 1 and 2 are significantly longer than those found in the corresponding diiron(II,II) complex [FeII2(N-Et-HPTB)(O2CPh)]2+ (1.966(6) Å), where each iron center has trigonal bipyramidal geometry,55 but they are in line with Fe(II)-μ-O bonds found in other diron(II,III) complexes such as [FeIIFeIIIBPMP(O2CCH2CH3)2]2+ (2.090(2) Å)56 and [FeIIFeIII(tpdb)(O2CPh)2]2+ (2.088(7) Å).43,47 The shorter lengths of the FeIII-μ-O (O1) bonds, on the other hand, compare favorably to those found for average FeIII-μ-O bond lengths in related diiron(III) complexes, such as [FeIII2(HPTB)(O2AsMe2)(Cl)(OH2)]3+ (1.956(6) Å) and [FeIII2(HPTB)(OH)(ONO2)2]2+ (1.965(8) Å).57,58 Charge balance considerations also substantiate the mixed-valent diiron(II,III) assignment for both complexes.
Table 2.
Selected bond distances (Å) for [FeIIFeIII(N-Et-HPTB)(O2CPh)(NCCH3)2]3+ (1) and [FeIIFeIII(N-Et-HPTB)(O2CPh)(Cl)(HOCH3)]2+ (2). In both 1 and 2, Fe1 is FeIII and Fe2 is FeII
| 1 | 2 | |
|---|---|---|
| Fe1···Fe2 (Å) | 3.603(1) | 3.632(1) |
| Fe1–O1–Fe2 (°) | 128.0(1) | 129.4(1) |
| Fe1–O1 (Å) | 1.919(2) | 1.953(3) |
| Fe1–O2 (Å) | 1.940(2) | 2.027(3) |
| Fe1–N1 (Å) | 2.288(2) | 2.284(3) |
| Fe1–N2 (Å) | 2.086(2) | 2.142(3) |
| Fe1–N4 (Å) | 2.083(2) | 2.130(3) |
| Fe1–N11 (Å) | 2.186(2) | - |
| Fe1–Cl1 (Å) | - | 2.300(1) |
| Fe2–O1 (Å) | 2.088(2) | 2.064(3) |
| Fe2–O3 (Å) | 2.071(2) | 2.060(3) |
| Fe2–N6 (Å) | 2.275(2) | 2.272(3) |
| Fe2–N7 (Å) | 2.135(2) | 2.142(3) |
| Fe2–N9 (Å) | 2.128(2) | 2.134(3) |
| Fe2–N12 (Å) | 2.192(2) | - |
| Fe2–O4 (Å) | - | 2.147(3) |
Interestingly, the N-Et-HPTB ligand arrangements are not identical for the two complexes. For 1, the two benzimidazole ligands are trans to each other on the FeIII site while the other two are cis to each other on the FeII site. On the other hand, two benzimidazoles are cis to each other on the FeIII site while the other two are trans to each other on the FeII site in complex 2. While previously reported diiron-HPTB structures showed that the benzimidazolyl arms of an HPTB ligand can bind to a FeIII center in either trans or cis fashion58,59 and in cis mode to a FeII center,55 complex 2 represents to the best of our knowledge the first example where benzimidazolyl arms are found to coordinate trans to each other at a FeII center. The asymmetric coordination pattern observed for metal centers in 1 and 2 is uncommon for symmetric binucleating ligands which tend to bind two metal centers in a similar fashion.43,44 It is unclear to us at this point why one isomer is favored over another.
3.3 UV-Vis-NIR characterization of 1 and 2
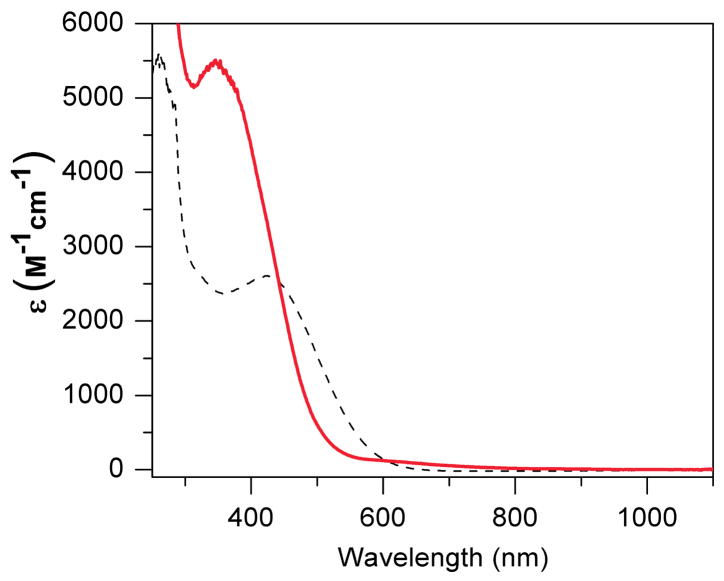
The electronic absorption spectra of 1 and 2 in CH3CN are shown in Figure 3. Both complexes exhibit a near-UV feature with λmax at 420 nm (ε = 2600 M−1cm−1) for 1 and at 350 nm (ε = 5500 M−1cm−1) for 2 that arises from charge transfer transitions. Similar bands are reported for both diiron(III) and diiron(II) complexes of HPTB. For example, [Fe2III(HPTB)(OH)(NO3)2]2+ has a λmax at 340 nm (ε = 7300 M−1cm−1) in MeOH,58 while [Fe2II(N-Et-HPTB)(O2CPh)]2+ has a λmax at 330 nm (ε = 2400 M−1cm−1) in CH3CN.55 Aside from these intense UV bands, there are also weak near IR features at 1100 nm (ε = 85 M−1cm−1) for 1 and at 880 nm (ε = 98 M−1cm−1) and 1100 nm (ε = 87 M−1cm−1) for 2. These features are likely to arise from intervalence-transfer (IT) bands, like similar bands reported for other mixed-valent diiron(II,III) complexes. For example, [FeIIFeIII(tpdb)(O2CC6H5)2]2+, another alkoxo bridged diiron(II,III) complex, exhibits IT bands at 847 nm (43 M−1cm−1) and 1123 nm (30 M−1cm−1) 47. Similar IT bands are also observed for phenolate- and hydroxo-bridged diiron(II,III) complexes but tend to be found at even lower energy.39,45,60,61
Figure 3.
Electronic spectrum of 1 (black dotted line) and 2 (red solid line) in CH3CN at 298 K.
3.4 Mössbauer, EPR and DFT Studies
3.4.1 Analysis Overview
As presented below, both EPR and Mössbauer spectroscopy show that 1 is a mixed valence complex, containing antiferromagnetically coupled high-spin (SA = 5/2) FeIII and high-spin (SB = 2) FeII sites. Before describing how information from the Mössbauer spectra was extracted, it will be useful to assemble a few expressions. The Mössbauer and EPR data were analyzed in the framework of the spin Hamiltonian (SA = 5/2, SB = 2)
| (1) |
where J (≈ +22.5 cm−1, see below) is the exchange coupling constant. DA, EA/DA and DB, EB/DB are the zero-field splitting parameters of the FeIII and FeII sites, respectively, and aA and aB area the local 57Fe magnetic hyperfine tensors.
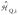 describes the quadrupole interactions and is given by
describes the quadrupole interactions and is given by
| (2) |
where ηi = (Vi,xx − Vi,yy)/Vi,zz) is the asymmetry parameter of the electric field gradient (EFG) tensor.
The exchange term of eq 1 couples the spins of the two sites, Ŝ = ŜA + ŜB, yielding a spin ladder with energies ε(S) = JS(S + 1)/2. As long as one is dealing only with the isolated S = 1/2 ground doublet, e. g. one performs studies at T ≤ 4.2 K, it is convenient the describe the spectra by the effective S = 1/2 spin Hamiltonian
| (3) |
where g,
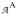 and
and
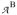 are effective tensors. In the strong coupling limit, defined by |J| ≫ |Di|, the effective tensors are given by
are effective tensors. In the strong coupling limit, defined by |J| ≫ |Di|, the effective tensors are given by
| (4) |
the minus signs reflecting the fact that SB is antiparallel to S. If J and the Di values have comparable magnitudes, the ZFS terms give a substantial admixture of the excited S = 3/2 and 5/2 manifolds into the S = 1/2 ground state (which is referred to as D/J mixing). The effect of these admixtures can be expressed by adopting g,
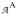 and
and
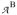 tensors in eq 3 that depend on J and the zero-field splitting parameters. D/J mixing will be important in the analysis of the data obtained for 1.
tensors in eq 3 that depend on J and the zero-field splitting parameters. D/J mixing will be important in the analysis of the data obtained for 1.
Sage and coworkers62 have given perturbation expressions that take into account this mixing, leading to modifications of eqs 4. In this treatment (mixing with S = 5/2 states was not considered by Sage et al.) D/J mixing is the source of anisotropy of the A-tensor for the ferric site,
| (5) |
where we can take aA to be isotropic. Since
 is traceless, the coupling constant for FeA is can be obtained from the expression aA = (1/7)Trace(
is traceless, the coupling constant for FeA is can be obtained from the expression aA = (1/7)Trace(
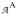 ). Similarly for site B,
). Similarly for site B,
| (6) |
where aB is generally anisotropic. (Note: Eqs 7, 8a, and 8b of Sage et al. have sign errors.62 In each expression the sign of the
 /J term has to be reversed.)
/J term has to be reversed.)
In eqs 4 and 5
 is an effective (superscript e) zero-field splitting
is an effective (superscript e) zero-field splitting
 = 8
= 8
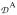 + 3
+ 3
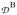 where
where
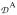 and
and
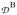 are 3×3 matrices (we will use superscripts to designate these traceless matrices).62 If
are 3×3 matrices (we will use superscripts to designate these traceless matrices).62 If
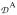 and
and
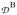 are collinear, we can write
are collinear, we can write
| (7) |
where the subscripted quantities DA,B and EA,B are the standard ZFS parameters as used in eq 1. The observation that the anisotropy of
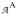 depends on
depends on
 /J allows one to determine these quantities by Mössbauer spectroscopy from the shape of the FeIII subspectrum.
/J allows one to determine these quantities by Mössbauer spectroscopy from the shape of the FeIII subspectrum.
Once the quantities (ξ = x, y, z) are determined, the g-values in the coupled representation of eq 3 can be approximated as
| (8) |
where the
 /J term is a second-order correction due to D/J mixing. Eq 8 provides insight into the contributions to g. However, for the rather large
values found here (and found in ref. 62 for uteroferrin) eq 8 is not quite accurate anymore, and in the final analysis we will calculate the g-values for the S = 1/2 ground state as usual by diagonalizing eq 1, using the ferric
(ξ = x, y, z) and the values for the diagonal elements of gB obtained by adjusting them to match the experimental g-values as given by eq 8 on the basis of the estimate for
/J term is a second-order correction due to D/J mixing. Eq 8 provides insight into the contributions to g. However, for the rather large
values found here (and found in ref. 62 for uteroferrin) eq 8 is not quite accurate anymore, and in the final analysis we will calculate the g-values for the S = 1/2 ground state as usual by diagonalizing eq 1, using the ferric
(ξ = x, y, z) and the values for the diagonal elements of gB obtained by adjusting them to match the experimental g-values as given by eq 8 on the basis of the estimate for
 /J.
/J.
In the following we have used the perturbation expressions to guide us through the parameter space of eq 1. This procedure yielded a set of parameters that gave already fairly good fits of the Mössbauer spectra. These parameters were improved by analyzing the spectra with eq 1. For the final analysis we refined the parameters by using information (presented in Section 3.4.5) obtained from decomposing the aB into contact, orbital and spin-dipolar contributions.
3.4.2 EPR studies
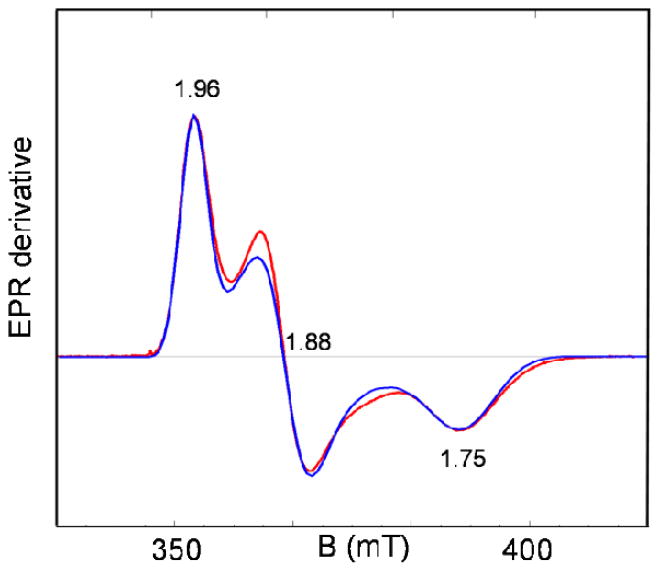
In frozen PrCN solution 1 displays EPR signals as shown in Figure 4. These features can be assigned to antiferromagnetically coupled high-spin FeIII (SA = 5/2) and FeII (SB = 2) centers with an S = 1/2 ground state with gave < 2, as observed for a variety of mixed valence FeIIIFeII complexes.29,62,63 The red line in Figure 4 represents a fit for the parameter set quoted in the caption of Figure 4.
Figure 4.
EPR spectrum of 1 in PrCN recorded at T = 8 K. The theoretical curve (red) was generated for gx = 1.75, gy = 1.88 and gz = 1.96 using the strain parameters σx = 0.025, σy = 0.015 and σz = 0.012. Below, we relate x, y, and z to the molecular frame. Conditions: 9.62 GHz; 20 μW microwave power; 1 mT modulation.
We have attempted to determine the exchange coupling constant J of complex 1 in PrCN by EPR but have not obtained sufficiently reliable results. Determination of J by power saturation did not work. Thus, the signal severely saturated at 2 K at 0.2 μW microwave power, and at 15 K the signal could not be saturated even at 200 mW. The strong temperature dependence, moreover, suggests that the T9 dependence of the Raman process dominates the Orbach term (from which J is generally extracted). We have therefore attempted to obtain the value for J by determining the temperature dependence of the spectrum of the S = 1/2 ground state, but the relaxation properties on 1 in PrCN confined these studies to temperatures between 8 K and 20 K, a range too narrow for extracting a good value for J.
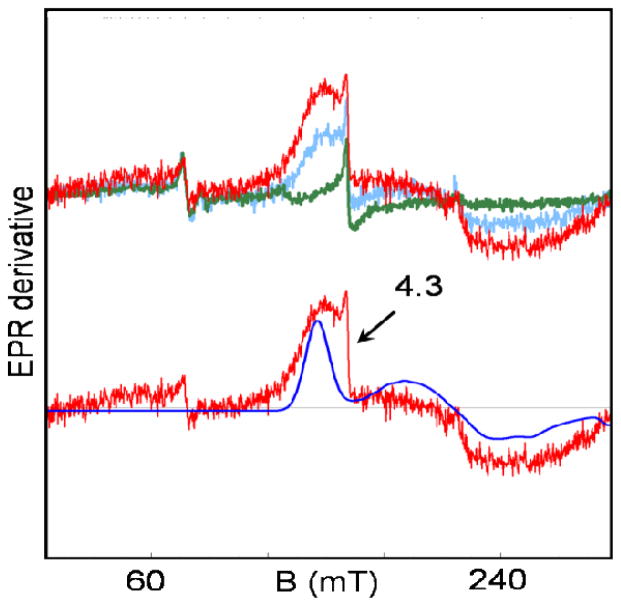
We have, however, succeeded in observing, to our knowledge for the first time, EPR signals from the first excited state, the S = 3/2 multiplet. The J-value determined by Mössbauer spectroscopy (see next section) places the S = 3/2 multiplet of 1 at 33 cm−1 above the S = 1/2 ground state. Figure 5 (upper traces) shows low-field EPR signals of 1 recorded at 8, 21, and 34 K. The amplitude of these signals, attributable to the S = 3/2 manifold, increases with temperature, showing that the signals result from excited states (there is a minor g = 4.3 contaminant). We have simulated the 34 K spectrum (blue solid curve) using for the excited state manifold the S = 3/2 Hamiltonian
Figure 5.
EPR spectra of 1 in PrCN in the low field region recorded at T = 8 K (green), 21 K (blue) and 34 K (red). The blue line in the lower trace is a simulation of the 34 K spectrum with eq 1, using the parameters listed in Table 4. To simulate the approximate line shape, EB/DB was assumed to have a Gaussian distribution with σE/D = 0.04. The feature at g = 4.3 is due to a minor S = 5/2 contaminant. Conditions: 9.62 GHz, 0.2 mW microwave power, 1 mT modulation; 1 hour accumulation time for the 34 K spectrum.
| (9) |
Due to D/J mixing, the excited state in 1 is only approximately described by an effective S = 3/2 Hamiltonian. Therefore, we have used eq 1 for our spectral simulations (solid line in Figure 5). As a first approximation, however, it is useful to consider the g-values and zero-field splittings of the S = 3/2 multiplet in the limit of strong exchange coupling. For |J/Di| ≫1 the g- and
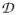 -tensors of the S = 3/2 multiplet can be expressed (see chapter 3 of ref 64) in terms of the local g- and
-tensors of the S = 3/2 multiplet can be expressed (see chapter 3 of ref 64) in terms of the local g- and
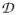 -tensors appearing in eq 1:
-tensors appearing in eq 1:
| (10) |
The expressions in eq 10 show that the g-value of the S = 3/2 state is essentially determined by gA (= 2.0) and that
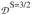 is heavily weighted toward
is heavily weighted toward
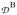 (not only due to the numerical coefficients but also because
(not only due to the numerical coefficients but also because
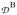 in 1 is much larger than
in 1 is much larger than
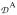 ; see Table 4). Thus, the EPR data for the S = 3/2 excited state contain information about the zero-field parameters of the ferrous site, which has been used below to narrow down the values for the local spin Hamiltonian parameters; see sections 3.4.3 and S1 in Supporting Information (SI) for how the S = 3/2 EPR data were used in our analysis.
; see Table 4). Thus, the EPR data for the S = 3/2 excited state contain information about the zero-field parameters of the ferrous site, which has been used below to narrow down the values for the local spin Hamiltonian parameters; see sections 3.4.3 and S1 in Supporting Information (SI) for how the S = 3/2 EPR data were used in our analysis.
Table 4.
Fine structure and hyperfine structure parameters for FeIII and FeII sites of 1a and the mixed-valent form of the methane monooxygenase hydroxylase component.
| D (cm−1) | E/D | gx | gy | gz | ax (T) | ay (T) | az (T) | ref | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Complex 1 | FeIII/FeA | −0.27b | 2.25b | 2 | 2 | 2 | −21.6 | −21.6 | −21.6 | * |
| FeII/FeB | 2.5 | −0.11 | 2.15 | 2.09 | 2.00 | −17.5 | −23.5 | −17.0 | ||
| Methane monooxygenase hydroxylase component d | FeIII | 0c | 0c | 2c | 2c | 2c | −21.6 | −22.1 | −20.8 | 63 |
| FeII | 3.8 | 0.02 | 2.14 | 2.10 | 2.04 | −17.3 | −20.0 | −10.9 |
Parameters for complex 1 were based on simulations with eq 1, using J = 22.5 cm−1. It is assumed that all tensors are collinear, gA = 2.00, and aA is isotropic.
In standard orientation D (along y) = 1.05 cm−1 and E/D = 0.16.
assumed.
We have changed the order of gi and ai values and units of ai values from what were reported in ref 63 for the purpose of comparison.
this work.
3.4.3 Mössbauer Studies and Our Approach for the Extraction of Spin Hamiltonian Parameters
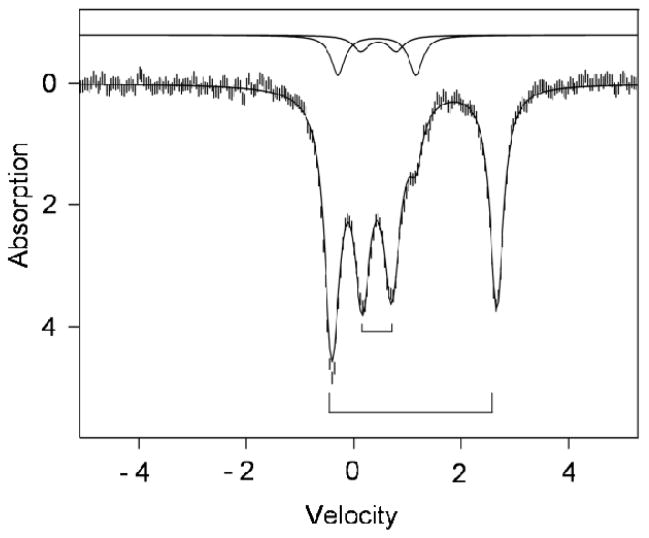
Figure 6 shows a 120 K Mössbauer spectrum of a polycrystalline sample of 1. At this temperature 1 displays, in the absence of an applied magnetic field, two major quadrupole doublets with ΔEQ = 0.52 mm/s, δ = 0.46 mm/s (high-spin ferric site FeA, ~ 43 % of Fe) and ΔEQ = 3.06 mm/s, δ = 1.12 mm/s (high-spin ferrous site FeB, ~ 43 % of Fe). At 1.8 K, where the spin-lattice relaxation is slow on the Mössbauer time scale (see below), the magnetic hyperfine splittings are still partially collapsed due to spin-dipolar relaxation between nearest neighbors. In strong applied magnetic fields (Figure 7A) these interactions are quenched and the spectra exhibit paramagnetic hyperfine structure as if the complexes were magnetically isolated. (N.B. At 4.2 K we observed separate sub spectra for the MS = −1/2 and MS = +1/2 levels of the S = ½ state, showing that the electronic spin fluctuates slowly on the Mössbauer time scale.)
Figure 6.
Mössbauer spectrum of solid 1 recorded at 120 K in zero applied field. The solid line through the data is a simulation involving doublets for ferric site A (43% of Fe, inner bracket), ferrous site B (43%, outer bracket). The solid lines shown above the data indicate the spectra of two diferric contaminants (ΔEQ = 1.40 mm/s, δ = 0.43 mm/s, 10%; ΔEQ = 0.66 mm/s, δ = 0.46 mm/s, 4%). Parameters for sites A and B are quoted in Tables 3 and 4.
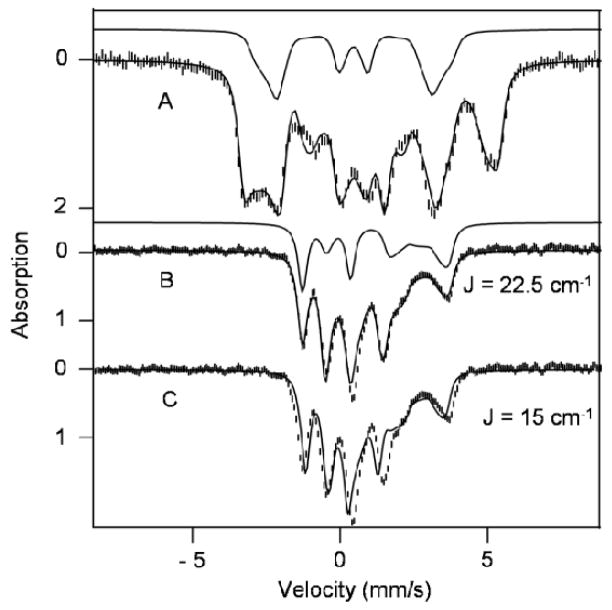
Figure 7.
Mössbauer spectra of solid 1 recorded at 1.8 K (A) and 120 K (B) in a parallel field of 7.63 T. The solid lines through the data are spectral simulations based on eq 1, using the parameters listed in Table 4. The solid line above (A) shows the contribution of the FeIII site, FeA. The solid line above (B) indicates the contribution of the ferrous site, FeB. The spectrum in (C) is the same as that shown in (B); the theoretical curve, however, was generated for J = 15 cm−1 rather than J = 22.5 cm−1.
The sample of complex 1 contains two diferric contaminants, the ΔEQ and δ values of which are given in the caption of Figure 6. One, representing ca. 10% of the Fe, is readily recognized in the spectrum of Figure 6 (shoulder at +1.1 mm/s), while a second contaminant accounts only for 3–4% of the iron content. Both contaminants were diferric species with an S = 0 ground state and with their 1.8 K spectra readily simulated.
For our analysis of solid 1 we have considered the spectra shown in Figures 6 and 7 together with a 7.63 T spectrum recorded at 4.2 K (see Figure S1 in SI). First we estimated the principal components of
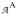 /gnβn by simulating the 1.8 K Mössbauer spectrum in coupled representation (eq 3), obtaining the values (−57.3, −43.0, −46.7) T. Using eq 5 we extracted
, and
. Then, using eq 8 we determined
from
/gnβn by simulating the 1.8 K Mössbauer spectrum in coupled representation (eq 3), obtaining the values (−57.3, −43.0, −46.7) T. Using eq 5 we extracted
, and
. Then, using eq 8 we determined
from
 /J and the experimental g-values. With the gB known we used the relationship between the ZFS tensor of the ferrous site and its g tensor obtained from second-order perturbation theory (See chapter 19 of ref 65)
/J and the experimental g-values. With the gB known we used the relationship between the ZFS tensor of the ferrous site and its g tensor obtained from second-order perturbation theory (See chapter 19 of ref 65)
| (11) |
where Δg = g −2 and where λ ≈ −80 cm−1 is the effective spin-orbit coupling constant for the ferrous ion (S = L = 2). This relation, frequently employed but rarely tested, assumes that mixing with excited S = 1 configurations of the ferrous ion do not significantly contribute to the
(and, thus, to DB and EB). Using eq 11 we obtained DB = 3.88 cm−1 and EB/DB = −0.16. From
 and
and
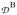 we can evaluate
we can evaluate
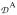 as
as
| (12) |
Next we address the determination of J for solid 1. The 7.63 T/120 K spectrum of Figure 7 was recorded under conditions for which the electronic spin system of 1 is in the fast fluctuation limit. Under these conditions the magnetic hyperfine fields at the two 57Fe nuclei, and , are proportional to the expectation values of the local spins averaged over all thermally accessible spin levels, < ŜA>therm and < ŜB>therm; (i = A or B). As the level spacing is essentially determined by J, fitting the magnetic splittings of the 7.63 T/120 K spectrum yields the exchange parameter, given that the Bint are insensitive to the ZFS parameters at 120 K. The simulation with eq 1, given by the solid line through the data of Figure 6, yields J = +22.5 cm−1 (estimated error ± 2 cm−1) as well as the sign of ΔEB,Q and the value of ηB. The simulation for FeB is shown above the data of Figure 7B. To illustrate the J-dependence of the spectrum, we show in Figure 7C a simulation for J = +15 cm−1.
Taking into account that gA = 2.0, aA is isotropic, and the principal axes of the tensors are considered to be collinear (see section 3.4.4 for details), eq 1 depends on 16 parameters. The analysis just described is summarized in the following diagram
| (13) |
where the expression numbers and data used are indicated below and above the arrows. Extracting these parameters from the EPR and Mössbauer spectra was actually a bit more involved than described here (see also section S1 in SI). Thus, the anisotropy of
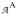 , as seen in the framework of the effective Hamiltonian eq 3, links the hyperfine parameters of FeA to the quantity
, as seen in the framework of the effective Hamiltonian eq 3, links the hyperfine parameters of FeA to the quantity
 /J. However, as the g tensor of the S = 1/2 state depends only weakly on
/J. However, as the g tensor of the S = 1/2 state depends only weakly on
 /J (the changes in g due to this term, as obtained on the basis of eq 1 rather than from the perturbation relation eq 8, are relatively minor: Δgx = −0.056, Δgy = −0.00, Δgz = −0.05) the frame of FeA is only weakly linked to the g tensor. The frame of g is essentially the frame of gB, which in turn is linked to
/J (the changes in g due to this term, as obtained on the basis of eq 1 rather than from the perturbation relation eq 8, are relatively minor: Δgx = −0.056, Δgy = −0.00, Δgz = −0.05) the frame of FeA is only weakly linked to the g tensor. The frame of g is essentially the frame of gB, which in turn is linked to
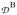 via (the assumed) relation eq 11. Further, the frame of the EFG tensor of FeB has to be assessed independently. We have done this by linking the EFG tensor of FeB to gB using the t2g orbital model presented in sections 3.4.4 and S2 of SI. This model, supported by the results of DFT calculations, will also relate the coordinate system x,y,z to the molecular structure of 1. In order to explore the spatial relations between the various coordinate frames, we had to consider the 3! = 6 permutations of the experimental g-values relative to the three components of
via (the assumed) relation eq 11. Further, the frame of the EFG tensor of FeB has to be assessed independently. We have done this by linking the EFG tensor of FeB to gB using the t2g orbital model presented in sections 3.4.4 and S2 of SI. This model, supported by the results of DFT calculations, will also relate the coordinate system x,y,z to the molecular structure of 1. In order to explore the spatial relations between the various coordinate frames, we had to consider the 3! = 6 permutations of the experimental g-values relative to the three components of
 /J and evaluate the resulting
/J and evaluate the resulting
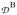 and
and
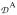 values using the relations of eq 11 and 12 (third and fourth step of eq 13). The results of this analysis are presented in Table S1 and S2. As a (better) alternative for using eq 8 in the second step of eq 13, we have evaluated the g values of 1 via simulations of the EPR spectrum of the S = 3/2 state (cf. section S1 of Supporting Information).
values using the relations of eq 11 and 12 (third and fourth step of eq 13). The results of this analysis are presented in Table S1 and S2. As a (better) alternative for using eq 8 in the second step of eq 13, we have evaluated the g values of 1 via simulations of the EPR spectrum of the S = 3/2 state (cf. section S1 of Supporting Information).
The preceding analysis was not quite as straightforward as it might appear and was developed along the way. We have at our disposal a variety of computer programs that allowed us to explore EPR and Mössbauer spectra as well as spin expectation values. Thus, once we had an estimate for
 /J, we used eq 1, rather than the perturbation expression eq 8, to calculate gB. The approximate values for the spin Hamiltonian parameters obtained from the perturbation expressions were refined in Mössbauer simulations using the Hamiltonian in eq 1. As the parameters obtained from the perturbation expression were already fairly close to their final values, refinement was quite straightforward. The parameters thus obtained are listed in Table 4. In order to provide the reader with a consistent set of S = 1/2 Hamiltonian parameters appropriate for eq 3 we have taken the theoretical spectra generated from the parameters of Table 4 and least-squares fitted them using eq 3; the resulting parameters are listed in Table 3.
/J, we used eq 1, rather than the perturbation expression eq 8, to calculate gB. The approximate values for the spin Hamiltonian parameters obtained from the perturbation expressions were refined in Mössbauer simulations using the Hamiltonian in eq 1. As the parameters obtained from the perturbation expression were already fairly close to their final values, refinement was quite straightforward. The parameters thus obtained are listed in Table 4. In order to provide the reader with a consistent set of S = 1/2 Hamiltonian parameters appropriate for eq 3 we have taken the theoretical spectra generated from the parameters of Table 4 and least-squares fitted them using eq 3; the resulting parameters are listed in Table 3.
Table 3.
Mössbauer parameters of complex 1 evaluated with the effective S = ½ Hamiltonian, eq 3, and comparison with related diiron(II,III) clusters whose parameters were previously reported.
| Ax/gnβn (T) | Ay/gnβn (T) | Az/gnβn (T) | ΔEQ (mm/s) | η | δ (mm/s) | Ref | ||
|---|---|---|---|---|---|---|---|---|
| 1a | FeII/FeB | 26.6b | 25.8 | 20.3 | 3.06 | 0.25 | 1.11 | This work |
| FeIII/FeA | −57.6 | −43.3 | −47.0 | 0.52 | 1.0 | 0.46 | ||
| MIOX(II/III)·MI a,c | FeII | 26.5d | 22.5 | 11.6 | 2.68 | 0.3 | 1.12 | 29 |
| FeIII | −43.1d | −55.8 | −53.4 | 1.11 | 7.2 f | 0.49 | ||
| uteroferrin(II,III) | FeII | 24.1 | 9.4 | 28.0 | 2.68 | 0.3 | 1.24 | 62 |
| FeIII | −43.2 | −27.9 | −64.8 | −1.85 | 0 | 0.54 | ||
| uteroferrin(II,III) phosphate | FeII | N.A. | N.A. | N.A. | 2.75 | N.A. | 1.22 | 62 |
| FeIII | N.A. | N.A. | N.A. | 0.76 | N.A. | 0.54 | ||
| methane monooxygenase hydroxylase component e | FeII | 24.8 | 26.4 | 12.9 | 2.5 | 0 | 1.24 | 63 |
| FeIII | −50.0 | −53.6 | −45.6 | −1.3 | 1.00 | 0.53 |
g-values for 1: gx = 1.75, gy = 1.88, gz = 1.96; for MIOX(II,III)·MI: g1 = 1.81, g2 = 1.81, g3 = 1.95 ref 29. The latter g-values have been labeled with numerals to indicate that their relationship with the molecular frame has not been specified.
Parameters of complex 1 were generated as described in the text.
Mössbauer features of MIOX(II,III) were poorly resolved. See ref 29.
The relationship between the (x,y,z) coordinates of the FeII and FeIII sites has not been determined.
We have changed the order of gi and ai values and units of ai values from what were reported in ref 63 for the purpose of comparison.
Reported in the A tensor frame for the FeIII site.
The parameter set listed in Table 4 is not the only one providing satisfactory simulations. Good simulations can also be obtained by using ΔEQ = −0.52 mm/s rather than ΔEQ = +0.52 mm/s for FeA. The sign change switches the signs of Vyy and Vzz (Vxx = 0 for η = 1) and as a consequence the values of
and
implied by the simulations are shifted by ≈ 0.15 in opposite directions. These shifts entail, using eq 6, changes in
of about 1.9 T in the y and z directions, which have to be compensated by complementary changes in
and
in order to retain satisfactory simulations. However, when we decomposed aB into Fermi contact, orbital and spin-dipolar contributions (as described in 3.4.5), we obtained for the traceless spin-dipolar term,
, values that were roughly a factor 2 smaller than expected for a d-orbital of the t2g set. As shown below, for the EQ = +0.52 mm/s solution we obtained acceptable values for
. Given that
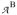 and
and
 /J both contribute to
, it is important to analyze the resulting aB along the lines described below in order to secure a solution that is admissible from a theoretical perspective.
/J both contribute to
, it is important to analyze the resulting aB along the lines described below in order to secure a solution that is admissible from a theoretical perspective.
3.4.4. Combining the Experimental Parameters with Results from DFT
The Mössbauer and EPR analysis described in the previous section has enabled us to determine with reasonable precision 16 unknown parameters of eq 1. The analysis invoked a convoluted sequence of arguments, because the anisotropy of the electronic g-tensor was insufficient for establishing the spatial correlations between the principal axes of the hyperfine tensors of the FeIII (FeA) and FeII (FeB) sites by simulation of the Mössbauer spectra. While for the FeIIIFeII state of the hydroxylase component of methane monooxygenase ENDOR data were available that related Ax and Ay of the ferric site to gx and gy. as tabulated in Table 4,63 this is not the case here. In this section, we will therefore comment on our assignments and how we relate the principal axes system x,y,z to the molecular coordinates of 1.
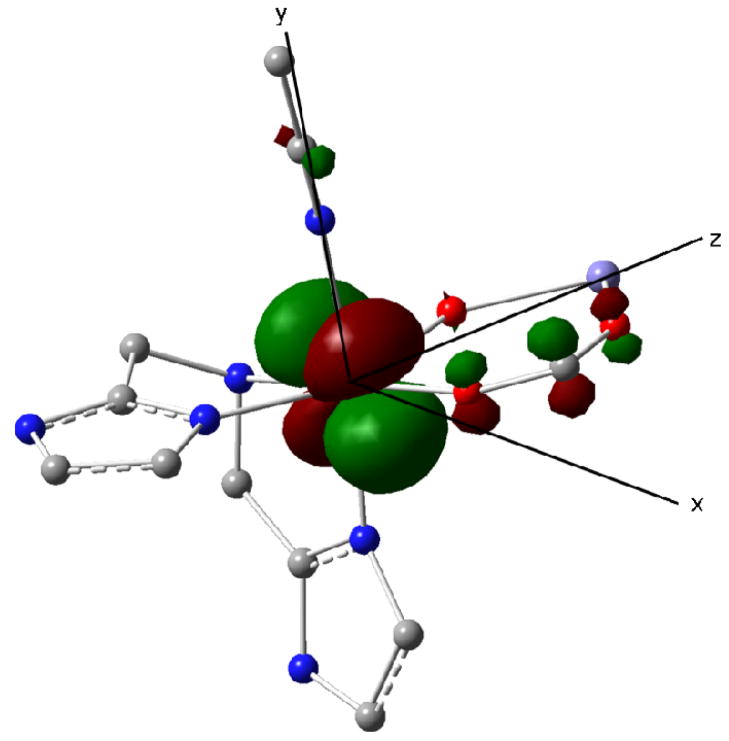
DFT geometry optimization of 1 yielded for FeB a ground state of essentially dxy symmetry (see Figure 8, Tables S6–8 in SI), in a coordinate system for which the z- axis is along the Fe-Fe direction. The β spin electron occupying this orbital provides the dominant contribution to ΔEQ,B and ηB. The DFT values ΔEQ,B = +3.68 mm/s and ηB = 0.28 are in good agreement with the experimental values ΔEQ,B = +3.10 mm/s and ηB = 0.27. The exchange-coupling constant was calculated J = 5.6 cm−1 from the difference of the ferromagnetic and broken symmetry states [J = (E(F) − E(BS))/10)]. The calculated J value represents weak antiferromagnetic coupling, and is consistent with the experimental value.
Figure 8.
Lowest 3d orbital (doubly occupied) of the FeII site of 1 obtained by DFT. The orbital has t2g parentage and has xy character when the z axis is chosen along the Fe-Fe direction and the y axis is along Fe-NMeCN. For clarity, the ligands of the FeIII site and some additional atoms have been removed.
The calculations place the major component of the ferrous EFG along the Fe-Fe direction, an observation that allows us to relate the spin Hamiltonian parameters for the FeII site to the geometrical structure of 1, i. e., the z axis of Tables 3 and 4 corresponds to the Fe-Fe direction. TD-DFT calculations for 1 place lowest 3d excitations of FeB at 2184 cm−1 (~dxz) and 3031 cm−1 (~dyz) above the lowest-lying orbital (~dxy) at 1143 cm−1.66 In a simple t2g model, this type of orbital structure implies that spin–orbit coupling gives the values
, showing that the resonance at g = 1.96 (= gz) is observed when the magnetic field is parallel to the Fe-Fe direction. (N.B. The Δgz = −0.04 shift is mainly due to D/J mixing.) The inequality
follows from the energy order ε(dxz) < ε(dyz), and implies that the g = 1.75 feature corresponds to
. Importantly, comparing the experimental g-values of 1 with the g-values calculated for the case of vanishing D/J mixing (in parentheses), i. e. for
 /J = 0, yields gx = 1.75 (1.80), gy = 1.88 (1.91) and gz = 1.96 (2.00), showing that the major shift in the g-values from g = 2.0 results from ligand field induced changes of gB (see Section 4 on its implication).67
/J = 0, yields gx = 1.75 (1.80), gy = 1.88 (1.91) and gz = 1.96 (2.00), showing that the major shift in the g-values from g = 2.0 results from ligand field induced changes of gB (see Section 4 on its implication).67
While we do not wish to overemphasize the accuracy of TD-DFT, the calculations suggest that ε(dyz) − ε(dxz) < ε(dxz) − ε(dxy), which implies that DB > 0 (in the 0 < EB/ DB < 1/3 convention), as deduced by our analysis, and that the largest component of
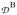 is along the z axis of Figure 8. In section 3.4.3, we deduced DB (from eq 11) = 3.88 cm−1 by employing eq 11. On a different track, we obtained DB (in Table 4) = 2.5 cm−1 by fitting the Mössbauer spectra using eq 1. The difference between the two values measures to what extent the perturbation expressions used in the analysis are applicable to the present case. For example, by using eq 11 we have implicitly assumed that contributions to DB from spin–orbit mixing with excited SB = 1 manifolds are small. We have tested this assumption by using a model in which the paramagnetic site FeIII in 1 is replaced by a diamagnetic GaIII (Table S5 of SI). The SB = 1 configurations give a small negative, nearly axial contribution to DB (along z), which reflects the contribution of admixture of excited SB =1 manifold at the FeB/FeII center. This explains why DB from Table 4 is smaller than DB from eq 11. Since the alignment of the components
and
(ξ = x, y, z) has been (approximately) established, we can now use eq 12 to evaluate
. These values for
were used as initial guess in the Mössbauer simulations, the results of which are listed in Table 4. Substitution of the fit values for
and
(obtained from Table 4 with eq 7) into the expression for
(see eq 12) yields values for these quantities that differ moderately from the values obtained with eq 5 (cf. section S1 of SI).
is along the z axis of Figure 8. In section 3.4.3, we deduced DB (from eq 11) = 3.88 cm−1 by employing eq 11. On a different track, we obtained DB (in Table 4) = 2.5 cm−1 by fitting the Mössbauer spectra using eq 1. The difference between the two values measures to what extent the perturbation expressions used in the analysis are applicable to the present case. For example, by using eq 11 we have implicitly assumed that contributions to DB from spin–orbit mixing with excited SB = 1 manifolds are small. We have tested this assumption by using a model in which the paramagnetic site FeIII in 1 is replaced by a diamagnetic GaIII (Table S5 of SI). The SB = 1 configurations give a small negative, nearly axial contribution to DB (along z), which reflects the contribution of admixture of excited SB =1 manifold at the FeB/FeII center. This explains why DB from Table 4 is smaller than DB from eq 11. Since the alignment of the components
and
(ξ = x, y, z) has been (approximately) established, we can now use eq 12 to evaluate
. These values for
were used as initial guess in the Mössbauer simulations, the results of which are listed in Table 4. Substitution of the fit values for
and
(obtained from Table 4 with eq 7) into the expression for
(see eq 12) yields values for these quantities that differ moderately from the values obtained with eq 5 (cf. section S1 of SI).
In using eq 5 for determining the components of
 /J we have assumed that aA is isotropic. This assumption is consistent with observations for a variety of octahedral high-spin FeIII complexes with N/O coordination. While we have no suitable mononuclear synthetic complex for the ferric site of 1, the DFT calculations for this complex suggest for the ferric site, FeA, a very small anisotropy, viz.
, arising from the spin-dipolar interaction.
/J we have assumed that aA is isotropic. This assumption is consistent with observations for a variety of octahedral high-spin FeIII complexes with N/O coordination. While we have no suitable mononuclear synthetic complex for the ferric site of 1, the DFT calculations for this complex suggest for the ferric site, FeA, a very small anisotropy, viz.
, arising from the spin-dipolar interaction.
3.4.5. A Special Remark on Decomposition of aB into Fermi Contact, Orbital and Spin-dipolar Contributions
As mentioned in section 3.4.3, the decomposition of the magnetic hyperfine coupling constants for the FeII site in 1 in terms of the Fermi contact (FC), the orbital term (L), and the spin-dipolar (SD) terms, , provides a check on the validity of the parameters obtained from the spectral simulations. Using the values listed in Table 4, we obtain for the isotropic term a value of −19.3 T, which is smaller than the Fermi contact coupling, aFC = −23.5 T, predicted for the free FeII ion.38 The orbital contribution is, in second-order approximation, related to the gB values as , where PL = gegnμeμn<r−3>3d. The orbital term can be split into an isotropic part and a traceless (tl) contribution: . These terms, together with the Fermi contact term and the spin-dipolar term, yield the decomposition, (ξ = x, y, z). Using the value PL = 50 T we obtained for the isotropic part of the orbital term (sometimes referred to as the pseudo-contact term) the value , which, combined with , gives for the Fermi contact term.68 Thus, the Fermi contact coupling constant for the FeII site of 1 is, as for the FeIII site, close to the free-ion value, provided the isotropic part of the orbital term is properly accounted for. [Owing to the lack of orbital moment in its 6S configuration, a correction for the pseudo contact term is not required for high-spin FeIII site.] Finally, after removing the traceless (tl) anisotropic part of the orbital term, , we obtain the spin-dipolar contribution . The components of show a pattern with a large positive component along z and two smaller, negative components along x and y, as predicted by the t2g model for a ground state with dxy symmetry. The rhombicity, , does not vanish and has a value that is slightly larger than obtained from DFT (ηSD = 0.24). The components of deduced from the decomposition are in good agreement with those predicted by DFT, (−2.8 T, −4.6 T, +7.4 T), and support the parameters of Table 4. In section 3.4.3 we mentioned that we had found another parameter set. For this set an analogous decomposition of aB yielded which is distinctly too small [In a crystal field treatment one typically uses for a t2g orbital].
4. Discussion
The two crystal structures of substrate-bound forms of MIOX reveal that the diiron centers in the MIOX active site are doubly bridged by a solvent-derived oxygen atom and the carboxylate of Asp124.32,33 The synthesis and structural characterization of 1 and 2 suggest that such a doubly bridged diiron core is also accessible in synthetic model complexes. As shown in Table 5, the Fe-Fe distances and Fe-μ-O-Fe angles of the substrate-bound forms of MIOX are comparable to those of 1 and 2, but are significantly different from those found in the triply bridged diiron(II,III) clusters in enzymes69 and in synthetic complexes such as [FeIIFeIII(Me3-TACN)(OH)(O2CiPr)2]2+, [FeIIFeIII(BPMP) (O2CCH2CH3)2]2+ and [FeIIFeIII(tpdb)(O2CPh)2]2+.45,47,61 More specifically, triply bridged diiron(II,III) clusters exhibit sizably shorter Fe···Fe distances and more acute Fe-O-Fe angles (Table 5) compared to doubly bridged diiron(II,III) cores. As we were able to mimic the essential structural features of diiron active sites of MIOX using a dinucleating ligand that provides an alkoxo bridge in addition to a carboxylate bridge, we reasoned that a hydroxo rather than an oxo or aqua group is more likely to be present as a bridge between the diiron centers in the active site of MIOX that are also bridged by an additional carboxylate group. A hydroxo bridge has also been proposed by both Baker et al. and Bollinger and Krebs et al. from mechanistic considerations.29,32
Table 5.
Core structural parameters in doubly and triply bridged diiron(II,III) cores in proteins and in model complexes.
| r(Fe···Fe) (Å) | ∠Fe-μ-O-Fe (°) | Ref | |
|---|---|---|---|
| Doubly bridged diiron centers | |||
| 1 | 3.603† | 128.0† | * |
| 2 | 3.632 | 129.3 | * |
| Mouse MIOX·MI # | 3.65 | 130 | 32 |
| Human MIOX·MI # | 3.72 | 124 | 33 |
| Triply bridged diiron centers | |||
| [FeIIFeIII(Me3-TACN)(OH) (O2CiPr)2]2+ | 3.400 | 118.1 | 45 |
| [FeIIFeIII(BPMP)(O2CCH2CH3)2]2+ | 3.365 | 113.1 | 39 |
| [FeIIFeIII(tpdb)(O2CPh)2]2+ | 3.300 | 105.8 | 47 |
| Diiron(II,III) form of DcrH | 3.34 | 115.1 | 70 |
| Pig uterroferrin # | 3.31 | 105.7 | 69 |
This work.
The crystal structure may represent a diiron(III,III) form or a diiron(II,III) state.
Abbreviations used: MIOX = myo-inositol oxygenase; MI = myo-inositol. Me3-TACN = 1,4,7-trimethyl-1,4,7-triazacyclononane; BPMP = 2,6-bis[(bis(2-pyridylmethyl)-amino)methyl]-4-methylphenolate; tpdb = N,N,N′,N′-tetrakis(2-pyridyl-methyl)-1,4-diaminobutane-2-olate. DcrH = a bacterial chemotaxis protein from Desulfovibrio vulgaris with a Hr-like domain.
DFT values: Fe···Fe = 3.701 Å (3.703 Å) and ∠Fe-OFe = 127.9° (127.4°) for broken symmetry state (ferromagnetic state).
Detailed analysis of its EPR and Mössbauer spectra reveals that 1 contains an S = 5/2 FeIII and an S = 2 FeII that are antiferromagnetically coupled, yielding an S = 1/2 ground state. From variable temperature Mössbauer studies, the exchange coupling constant J (
 = JSA•SB) was determined to be 22.5 cm−1, consistent with the presence of an alkoxo bridge that mediates the weak antiferromagnetic coupling. For such a weakly coupled system, the S = 3/2 excited state should be thermally accessible. Indeed EPR signals arising from the S = 3/2 manifold were observed in our system in addition to signals from the S = 1/2 ground state, representing the first example of such excited state signals to be detected in diiron(II,III) clusters. DFT calculations placed the major component of the ferrous EFG along the Fe-Fe direction, establishing a correlation between our spin Hamiltonian analysis and the molecular structure. Notably, from this detailed analysis of the Mössbauer and EPR data, we were able to extract all spin Hamiltonian parameters such as the zero-field splitting parameters, local g-values, the electric field gradients and the magnetic hyperfine parameters for the individual Fe sites based on some reasonable assumptions (vide supra). To the best of our knowledge this is the first time that all these electronic parameters for individual irons have been obtained from Mössbauer/EPR studies.
= JSA•SB) was determined to be 22.5 cm−1, consistent with the presence of an alkoxo bridge that mediates the weak antiferromagnetic coupling. For such a weakly coupled system, the S = 3/2 excited state should be thermally accessible. Indeed EPR signals arising from the S = 3/2 manifold were observed in our system in addition to signals from the S = 1/2 ground state, representing the first example of such excited state signals to be detected in diiron(II,III) clusters. DFT calculations placed the major component of the ferrous EFG along the Fe-Fe direction, establishing a correlation between our spin Hamiltonian analysis and the molecular structure. Notably, from this detailed analysis of the Mössbauer and EPR data, we were able to extract all spin Hamiltonian parameters such as the zero-field splitting parameters, local g-values, the electric field gradients and the magnetic hyperfine parameters for the individual Fe sites based on some reasonable assumptions (vide supra). To the best of our knowledge this is the first time that all these electronic parameters for individual irons have been obtained from Mössbauer/EPR studies.
The knowledge of the electronic structure of 1 allows us to take a closer look into the origin of the empirical correlation for FeIIFeIII complexes with S = ½ ground states where ganis (ganis = [gz−(gx+gy)/2]/3) and Δgave = 2 − gave (gave = (gx+gy+gz)/3) are found to be large when J is small, and small when J is large (cf. Table 6). It has been hypothesized that the empirical correlation arises because the anisotropy of the g-values would be primarily dictated by the
 /J term, introducing a significant dependence on the magnitude of J.71 ganis would be small because a large J gives a small
/J term, introducing a significant dependence on the magnitude of J.71 ganis would be small because a large J gives a small
 /J contribution, and vice versa, thus providing a qualitative explanation for the correlation.
/J contribution, and vice versa, thus providing a qualitative explanation for the correlation.
Table 6.
Coupling constants (J) and EPR parameters for mixed-valent diiron(II,III) form in proteins and model compounds.
| Compound | J | g-values | gave (2–gave)a | ganisb | Ref |
|---|---|---|---|---|---|
| 1 | 22.5 | 1.96, 1.88, 1.75 | 1.86 (0.14) | 0.05 | This work |
| 1 (without D/J mixing) | ∞ | 2.00, 1.91, 1.80 | 1.90 (0.10) | 0.05 | This work |
| Mouse MIOX(II,III) c | 40 | 1.95, 1.66, 1.66 | 1.76 (0.24) | 0.10 | 29 |
| Mouse MIOX(II,III)·MI c | 20 | 1.95, 1.81, 1.81 | 1.85 (0.15) | 0.05 | 29 |
| uteroferrin(II,III) | 20 | 1.94, 1.73, 1.56 | 1.74 (0.26) | 0.10 | 36,37,62 |
| uteroferrin(II,III)·phosphate | 6 | 2.27, 1.51, 1.06 | 1.61 (0.39) | 0.33 | 36,73 |
| Diiron(II,III) form of methane monooxygenases [M. trichosporium] {M. capsulatus} | ~60 | [1.94, 1.86, 1.76] {1.92, 1.86, 1.71} |
[1.85 (0.15)] {1.83 (0.17)} |
[0.04] {0.06} |
[22,74] {23} |
| Synthetic (μ-oxo)diiron(II,III) complexes | ~200 | - | ~1.93–1.96 (~0.04–0.07) | ~0.01–0.02 | 67 |
| eg. [FeII,III2(O)(O2CtBu)2(Me3-TACN)2]+ d | 238 | 1.97, 1.93, 1.90 | 1.93 (0.07) | 0.02 | 46 |
| Synthetic (μ-hydroxo)diiron(II,III) complexes | ~20 | - | >1.87 (>0.13) | >0.05 | 67 |
| eg. [FeII,III2(OH)(O2CtBu)2(Me3TACN)2]2+ d | 1.95, 1.51, 1.43 | 1.65 (0.35) | 0.16 | 45 |
gave = (gx + gy + gz)/3.
ganis = |gz−(gx+gy)/2|/3 where gz has the largest deviation from gave.
MIOX = myo-inositol oxygenase; MI = myo-inositol.
Me3-TACN = 1,4,7-trimethyl-1,4,7-triazacyclononane
The results of our study however are not consistent with the hypothesis. The g-values for 1 obtained with (in bold) and without (in parentheses) the
 /J contribution are gx = 1.75 (1.80), gy = 1.88 (1.91) and gz = 1.96 (2.00) and yield Δgave = 0.14 (0.10) and ganis = 0.05 (0.05). The comparison of the g-values obtained with and without the
/J contribution are gx = 1.75 (1.80), gy = 1.88 (1.91) and gz = 1.96 (2.00) and yield Δgave = 0.14 (0.10) and ganis = 0.05 (0.05). The comparison of the g-values obtained with and without the
 /J contribution shows that already in the case of weak coupling, as present in the alkoxo-bridged complex 1, the major contribution to Δgave, ganis, and Δgξ (Δgξ = 2 − gξ, ξ = x, y, z) originates from the ΔgBξ values for the FeII(FeB) center. This conclusion indicates that, unlike previously assumed, the
/J contribution shows that already in the case of weak coupling, as present in the alkoxo-bridged complex 1, the major contribution to Δgave, ganis, and Δgξ (Δgξ = 2 − gξ, ξ = x, y, z) originates from the ΔgBξ values for the FeII(FeB) center. This conclusion indicates that, unlike previously assumed, the
 /J term is not the major source of the large Δgave and ganis values in weakly coupled systems such as complex 1.
/J term is not the major source of the large Δgave and ganis values in weakly coupled systems such as complex 1.
Not surprisingly, the ganis and Δgave values observed for the strongly coupled oxo-bridged systems are also not consistent with the hypothesis. If the hypothesis were correct, the ganis and Δgave values for the strongly coupled oxo-bridged dimers would be approximately reproduced by substituting the large J values typically found for these systems into the expressions for these quantities in our weakly coupled complex 1. However, the values Δgave = 0.10 and ganis = 0.05 predicted for the strongly coupled species on the basis of the
 /J model for the variations in Δgξ differ by a considerable margin from the values Δgave < 0.07 and ganis < 0.02 observed for the oxo-bridged species (Table 6). Summarizing, the experimental Δg,ave and ganis
values are primarily determined by the anisotropy of the local g-values for the ferrous site, which are in turn governed by the local coordination environments of the ferrous site, and to a lesser extent by the admixture of excited S > 1/2 states into the S = 1/2 ground state for the ZFS terms (i.e. D/J mixing) as previously assumed (see eq 8 and eq 11; gA = 2.0).67
This conclusion applies both to weakly coupled systems, like the alkoxo-bridged complex
1, and strongly coupled systems, such as those that contain an oxo bridge.
/J model for the variations in Δgξ differ by a considerable margin from the values Δgave < 0.07 and ganis < 0.02 observed for the oxo-bridged species (Table 6). Summarizing, the experimental Δg,ave and ganis
values are primarily determined by the anisotropy of the local g-values for the ferrous site, which are in turn governed by the local coordination environments of the ferrous site, and to a lesser extent by the admixture of excited S > 1/2 states into the S = 1/2 ground state for the ZFS terms (i.e. D/J mixing) as previously assumed (see eq 8 and eq 11; gA = 2.0).67
This conclusion applies both to weakly coupled systems, like the alkoxo-bridged complex
1, and strongly coupled systems, such as those that contain an oxo bridge.
Given the uncertainty about the origin of the empirical Δgave/ganis vs. J correlation, it is hazardous to generalize this correlation to a larger set of systems. For example, weakly coupled dimers (no oxo bridge) do not necessarily obey the Δgave/ganis vs. J correlation, as illustrated by the example of MIOX (Table 3 and Table 6). An analysis of the anisotropy of the ferric A-tensor of MIOX(II,III)•MI analogous to that performed for complex 1 yields
 /J = −0.17,
/J = −0.17,
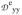 /J = −0.10,
/J = −0.10,
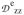 /J = +0.28, values that differ only moderately from those obtained for 1 (−0.34, +0.105, +0.235). The similarity suggests that the zero-field splitting parameters and exchange coupling constants J of both complexes are of comparable magnitude, a suggestion supported by an estimated J ≈ 20 cm−1 from power saturation studies of human MIOX(III,II)•MI reported by Gräslund and coworkers.33 We also note that the EFGs of the ferrous sites are quite similar, which indicates, following the preceding discussion, that the principal axis of the MIOX•MI EPR feature at g = 1.98 is along the Fe-Fe axis. Since the collinearity of the Fe-Fe axis and a principal axis of the ferrous EFGs is at the core of our EPR and Mössbauer analysis of 1, an analogous analysis might be equally applicable to MIOX. Notably, the binding of substrate MI shifts the EPR g-values from (1.66, 1.66, 1.95) to (1.81, 1.81, 1.95), changing the gave and ganis values from 1.76 and 0.10 to 1.85 and 0.05, respectively (see Table 6). These EPR spectral changes were interpreted in ref. 29 to be the result of an increase in the coupling constant J upon the binding of MI.29 As an alternative explanation, we propose that changes in gB induced by the substrate binding have lead to the alterations of the EPR signal. Contrary to the J-based rationalization of the g-value changes, our explanation is consistent with the conclusion of Gräslund et al. that the binding of MI actually decreases, rather than increases, the value of J based on EPR power saturation studies.33 While the crystal structures of MIOX•MI indicate that the substrate MI binds at the iron(III) center,32,33 the coordination of MI might give rise to ligand rearrangement at the iron(II) center and altered gB values. Alternatively, as the crystal structure may represent an inactive MIOX(III,III)•MI form, MI possibly binds in a bridging fashion in the catalytically relevant MIOX(II,III)•MI form, an idea supported by ENDOR studies of Hoffman and coworkers.72
/J = +0.28, values that differ only moderately from those obtained for 1 (−0.34, +0.105, +0.235). The similarity suggests that the zero-field splitting parameters and exchange coupling constants J of both complexes are of comparable magnitude, a suggestion supported by an estimated J ≈ 20 cm−1 from power saturation studies of human MIOX(III,II)•MI reported by Gräslund and coworkers.33 We also note that the EFGs of the ferrous sites are quite similar, which indicates, following the preceding discussion, that the principal axis of the MIOX•MI EPR feature at g = 1.98 is along the Fe-Fe axis. Since the collinearity of the Fe-Fe axis and a principal axis of the ferrous EFGs is at the core of our EPR and Mössbauer analysis of 1, an analogous analysis might be equally applicable to MIOX. Notably, the binding of substrate MI shifts the EPR g-values from (1.66, 1.66, 1.95) to (1.81, 1.81, 1.95), changing the gave and ganis values from 1.76 and 0.10 to 1.85 and 0.05, respectively (see Table 6). These EPR spectral changes were interpreted in ref. 29 to be the result of an increase in the coupling constant J upon the binding of MI.29 As an alternative explanation, we propose that changes in gB induced by the substrate binding have lead to the alterations of the EPR signal. Contrary to the J-based rationalization of the g-value changes, our explanation is consistent with the conclusion of Gräslund et al. that the binding of MI actually decreases, rather than increases, the value of J based on EPR power saturation studies.33 While the crystal structures of MIOX•MI indicate that the substrate MI binds at the iron(III) center,32,33 the coordination of MI might give rise to ligand rearrangement at the iron(II) center and altered gB values. Alternatively, as the crystal structure may represent an inactive MIOX(III,III)•MI form, MI possibly binds in a bridging fashion in the catalytically relevant MIOX(II,III)•MI form, an idea supported by ENDOR studies of Hoffman and coworkers.72
Next, we point out that one of the premises for our conclusion, eq 8, is a perturbation expression valid only for sufficiently small values of
 /J. To illustrate our point, we show in Figure 9 a graph of gx = gy = gperp versus
/J. To illustrate our point, we show in Figure 9 a graph of gx = gy = gperp versus
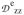 /J for a diiron(II,III) system with fixed local gA and gB values. By progressively increasing
/J for a diiron(II,III) system with fixed local gA and gB values. By progressively increasing
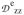 /J, the D/J mixing eventually becomes a major factor, leading to a lower gave and larger ganis. Conversely, in oxo-bridged diiron(II,III) complexes that feature a very large J, the D/J mixing effect should in principle be even smaller than in complex 1, making the criteria to be even better satisfied. As the coupling constants in strongly coupled systems are typically ten times larger than the J in 1, the
/J, the D/J mixing eventually becomes a major factor, leading to a lower gave and larger ganis. Conversely, in oxo-bridged diiron(II,III) complexes that feature a very large J, the D/J mixing effect should in principle be even smaller than in complex 1, making the criteria to be even better satisfied. As the coupling constants in strongly coupled systems are typically ten times larger than the J in 1, the
 /J term in strongly coupled systems must be practically zero. Therefore, Δgξ must result entirely from ΔgBξ in strongly coupled dimers such as oxo-bridged species, while in weakly coupled systems such as complex 1 the effects of the
/J term in strongly coupled systems must be practically zero. Therefore, Δgξ must result entirely from ΔgBξ in strongly coupled dimers such as oxo-bridged species, while in weakly coupled systems such as complex 1 the effects of the
 /J term on Δgξ are minor but not negligible. In systems where J is even smaller, such as those with aqua or only carboxylates as the bridging ligands, the
/J term on Δgξ are minor but not negligible. In systems where J is even smaller, such as those with aqua or only carboxylates as the bridging ligands, the
 /J term may play a more prominent role in dictating Δgξ and may even outweigh the effects of the ΔgBξ term. However, it should be borne in mind that the perturbational expressions (eq 8) on which the analysis is based become inaccurate when D/J ≥ 1, requiring a non-pertubative approach based on numerical diagonalization of the electronic part of the Hamiltonian in eq 1.
/J term may play a more prominent role in dictating Δgξ and may even outweigh the effects of the ΔgBξ term. However, it should be borne in mind that the perturbational expressions (eq 8) on which the analysis is based become inaccurate when D/J ≥ 1, requiring a non-pertubative approach based on numerical diagonalization of the electronic part of the Hamiltonian in eq 1.
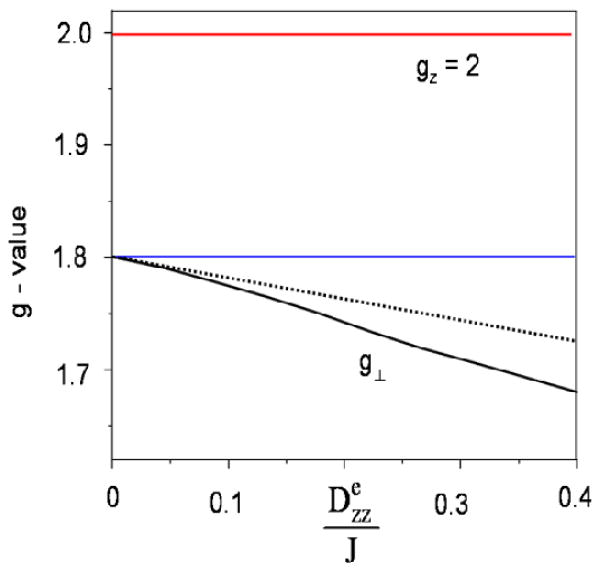
Figure 9.
Illustration of D/J mixing on the effective g-values of an FeIIIFeII system. For clarity we have made the following simplifying assumptions. . The solid lines in black and red were obtained by diagonalization of eq 1. The dashed line for gx = gy = g⊥ was generated by using the perturbation expression of eq 8. The difference between the blue horizontal line at and the solid line for g⊥ is due to D/J mixing.
Whether an oxo or a hydroxo bridge is present in the catalytically active diiron form of O2-activating diiron enzymes and complexes should have major mechanistic implications. For example, Solomon, Brunold and coworkers75 proposed that the oxygenation of deoxy-Hr involved the transfer of the μ-hydroxo proton to the dioxygen moiety as part of a transformation of the (μ-hydroxo)bis(μ-carboxylato)diiron(II) core to a (μ-oxo)bis(μ-carboxylato)diiron(III)-hydroperoxo species. The partial protonation of the dioxygen moiety by the μ-hydroxo proton was proposed to be essential for stabilizing the negative charges acquired by the dioxygen moiety after binding to the diiron center.75 As for MIOX, Hirao and Morokuma in a recent DFT and ONIOM (DFT:MM) study suggested that proton transfer between the hydroxo bridge and the iron-bound dioxygen moiety may be important for steps occurring after O2 binding in the catalytic cycle of MIOX, including C–O bond formation and O–O bond cleavage.76
In summary, we prepared a valence-localized diiron(II,III) complex that is weakly antiferromagnetically coupled (J = 22.5 cm−1) featuring a diiron core that is doubly bridged by an alkoxo and a carboxylato bridge. These features render our molecules appropriate models for diiron(II,III) centers in diiron enzymes such as MIOX. Furthermore, we presented a data analysis methodology that made possible the extraction of all spin Hamiltonian parameters from EPR and Mössbauer studies, through which we gained insight into the fine details of the electronic structures of our synthetic complex 1. Our results show that the anisotropies of the g-values of our diiron(II,III) complex are primarily dictated by the intrinsic g-values of FeII center, rather than being controlled by the magnitude of the coupling constant J, as previously suggested.
Supplementary Material
Acknowledgments
This work was supported by the National Institutes of Health grants GM-38767 to L.Q. and EB-001475 to E.M. and a dissertation fellowship to F.L. from the University of Minnesota Graduate School. We thank Dr. Victor Young Jr. and Benjamin Kucera of the University of Minnesota X-ray Crystallography Facility for helpful discussions on the crystal structure refinements as well as Mr. Andrew Wills and Prof. David Norris for their assistance in obtaining the near IR spectra.
Footnotes
Supporting Information Available: Details of Mössbauer/EPR analysis in pdf format. For complexes 1 and 2, structural reports including full tables of atom coordinates, bond distances and angles, and atomic displacement parameter in CIF format.
References
- 1.Wallar BJ, Lipscomb JD. Chem Rev. 1996;96:2625–2658. doi: 10.1021/cr9500489. [DOI] [PubMed] [Google Scholar]
- 2.Stenkamp RE. Chem Rev. 1994;94:715–726. [Google Scholar]
- 3.Xiong J, Kurtz DM, Jr, Ai J, Sanders-Loehr J. Biochemistry. 2000;39:5117–5125. doi: 10.1021/bi992796o. [DOI] [PubMed] [Google Scholar]
- 4.Salahudeen AA, Thompson JW, Ruiz JC, Ma HW, Kinch LN, Li Q, Grishin NV, Bruick RK. Science. 2009;326:722–726. doi: 10.1126/science.1176326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tinberg CE, Lippard SJ. Acc Chem Res. 2011;44:280–288. doi: 10.1021/ar1001473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sazinsky MH, Lippard SJ. Acc Chem Res. 2006;39:558–566. doi: 10.1021/ar030204v. [DOI] [PubMed] [Google Scholar]
- 7.Stubbe J, Cotruvo JA., Jr Curr Opin Chem Biol. 2011;15:284–290. doi: 10.1016/j.cbpa.2010.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Eklund H, Uhlin U, Farnegardh M, Logan DT, Nordlund P. Prog Biophyss Mol Biol. 2001;77:177–268. doi: 10.1016/s0079-6107(01)00014-1. [DOI] [PubMed] [Google Scholar]
- 9.Shanklin J, Guy JE, Mishra G, Lindqvist Y. J Biol Chem. 2009;284:18559–18563. doi: 10.1074/jbc.R900009200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Murray LJ, Lippard SJ. Acc Chem Res. 2007;40:466–474. doi: 10.1021/ar600040e. [DOI] [PubMed] [Google Scholar]
- 11.Mitchell KH, Rogge CE, Gierahn T, Fox BG. Proc Natl Acad Sci USA. 2003;100:3784–3789. doi: 10.1073/pnas.0636619100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Vu VV, Emerson JP, Martinho M, Kim YS, Münck E, Park MH, Que LJ. Proc Natl Acad Sci USA. 2009;106:14814–14819. doi: 10.1073/pnas.0904553106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Simurdiak M, Lee J, Zhao H. ChemBioChem. 2006;7:1169–1172. doi: 10.1002/cbic.200600136. [DOI] [PubMed] [Google Scholar]
- 14.Korboukh VK, Li N, Barr EW, Bollinger JM, Jr, Krebs C. J Am Chem Soc. 2009;131:13608–13609. doi: 10.1021/ja9064969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Makris TM, Chakrabarti M, Münck E, Lipscomb JD. Proc Natl Acad Sci USA. 2010;107:15391–15396. doi: 10.1073/pnas.1007953107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Krebs C, Bollinger JM, Jr, Booker SJ. Curr Opin Chem Biol. 2011;15:291–303. doi: 10.1016/j.cbpa.2011.02.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mathevon C, Pierrel F, Oddou JL, Garcia-Serres R, Blondin G, Latour JM, Ménage S, Gambarelli S, Fontecave M, Atta M. Proc Natl Acad Sci USA. 2007;104:13295–13300. doi: 10.1073/pnas.0704338104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Liu XF, Theil EC. Acc Chem Res. 2005;38:167–175. doi: 10.1021/ar0302336. [DOI] [PubMed] [Google Scholar]
- 19.Andrews SC. Biochim Biophys Acta. 2011;1800:691–705. doi: 10.1016/j.bbagen.2010.05.010. [DOI] [PubMed] [Google Scholar]
- 20.Kurtz DM., Jr J Inorg Biochem. 2006;100:679–693. doi: 10.1016/j.jinorgbio.2005.12.017. [DOI] [PubMed] [Google Scholar]
- 21.Cooley RB, Rhoads TW, Arp DJ, Karplus PA. Science. 2011;332:929. doi: 10.1126/science.1205687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fox BG, Surerus KK, Münck E, Lipscomb JD. J Biol Chem. 1988;263:10553–10556. [PubMed] [Google Scholar]
- 23.DeWitt JG, Bentsen JG, Rosenzweig AC, Hedman B, Green J, Pilkington S, Papaefthymiou GC, Dalton H, Hodgson KO, Lippard SJ. J Am Chem Soc. 1991;113:9219–9235. [Google Scholar]
- 24.Charalampous FCLC. J Biol Chem. 1957;228:1–13. [PubMed] [Google Scholar]
- 25.Charalampous FC. J Biol Chem. 1959;234:220–227. [PubMed] [Google Scholar]
- 26.Hankes LV, Politzer WM, Touster O, Anderson L. Ann NY Acad Sci. 1969;165:564–576. [PubMed] [Google Scholar]
- 27.Winegrad AI. Diabetes. 1987;36:396–406. doi: 10.2337/diab.36.3.396. [DOI] [PubMed] [Google Scholar]
- 28.Sundkvist G, Dahlin LB, Nilsson H, Eriksson KF, Lindgarde F, Rosen I, Lattimer SA, Sima AA, Sullivan K, Greene DA. Diabetes Med. 2000;17:259–268. doi: 10.1046/j.1464-5491.2000.00261.x. [DOI] [PubMed] [Google Scholar]
- 29.Xing G, Hoffart LM, Diao Y, Prabhu KS, Arner RJ, Reddy CC, Krebs C, Bollinger JM., Jr Biochemistry. 2006;45:5393–5401. doi: 10.1021/bi0519607. [DOI] [PubMed] [Google Scholar]
- 30.Xing G, Barr EW, Diao Y, Hoffart LM, Prabhu KS, Arner RJ, Reddy CC, Krebs C, Bollinger JM., Jr Biochemistry. 2006;45:5402–5412. doi: 10.1021/bi0526276. [DOI] [PubMed] [Google Scholar]
- 31.Xing G, Diao Y, Hoffart LM, Barr EW, Prabhu KS, Arner RJ, Reddy CC, Krebs C, Bollinger JM., Jr Proc Natl Acad Sci USA. 2006;103:6130–6135. doi: 10.1073/pnas.0508473103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Brown PM, Caradoc-Davies TT, Dickson JMJ, Cooper GJS, Loomes KM, Baker EN. Proc Natl Acad Sci USA. 2006;103:15032–15037. doi: 10.1073/pnas.0605143103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Thorsell APCV, Busam N, Hammarstrom RD, Graslund M, Graslund S, Hallberg ABM. J Biol Chem. 2008;283:15209–16. doi: 10.1074/jbc.M800348200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bollinger JM, Jr, Krebs C. Curr Opin Chem Biol. 2007;11:151–158. doi: 10.1016/j.cbpa.2007.02.037. [DOI] [PubMed] [Google Scholar]
- 35.Que L., Jr . Physical Methods in Bioinorganic Chemistry. Spectroscopy and Magnetism. University Science Books; Sausalito, CA: 2000. [Google Scholar]
- 36.Day EP, David SS, Peterson J, Dunham WR, Bonvoisin JJ, Sands RH, Que L., Jr J Biol Chem. 1988;263:15561–15567. [PubMed] [Google Scholar]
- 37.Averill BA, Davis JC, Burman S, Zirino T, Sanders-Loehr J, Loehr TM, Sage JT, Debrunner PC. J Am Chem Soc. 1987;109:3760–3767. [Google Scholar]
- 38.McCormick JM, Reem RC, Solomon EI. J Am Chem Soc. 1991;113:9066–9079. [Google Scholar]
- 39.Borovik AS, Murch BP, Que L., Jr J Am Chem Soc. 1987;109:7190–7191. [Google Scholar]
- 40.(a) Nordlund P, Sjöberg BM, Eklund H. Nature. 1990;345:393–398. doi: 10.1038/345593a0. [DOI] [PubMed] [Google Scholar]; (b) Rosenzweig AC, Frederick CA, Lippard SJ, Nordlund P. Nature. 1993;366:537–543. doi: 10.1038/366537a0. [DOI] [PubMed] [Google Scholar]; (c) Bailey LJ, Fox BG. Biochemistry. 2009;48:8932–8939. doi: 10.1021/bi901150a. [DOI] [PubMed] [Google Scholar]
- 41.Borovik AS, Papaefthymiou V, Taylor LF, Anderson OP, Que L., Jr J Am Chem Soc. 1989;111:6183–6195. [Google Scholar]
- 42.Mashuta MS, Webb RJ, McCusker JK, Schmitt EA, Oberhausen KJ, Richardson JF, Buchanan RM, Hendrickson DN. J Am Chem Soc. 1992;114:3815–3827. [Google Scholar]
- 43.Kanda W, Moneta W, Bardet M, Bernard E, Debaecker N, Laugier J, Bousseksou A, Chardon-Noblat S, Latour JM. Angew Chem In Ed. 1995;34:588–590. [Google Scholar]
- 44.Bossek U, Hummel H, Weyhermüller T, Bill E, Wieghardt K. Angew Chem Int Ed. 1995;34:2642–2645. [Google Scholar]
- 45.Suzuki M, Fujinami S, Hibino T, Hori H, Maeda Y, Uehara A, Suzuki M. Inorg Chim Acta. 1998;283:124–135. [Google Scholar]
- 46.Payne SC, Hagen KS. J Am Chem Soc. 2000;122:6399–6410. [Google Scholar]
- 47.Satcher JH, Droege MW, Olmstead MM, Balch AL. Inorg Chem. 2001;40:1454–1458. doi: 10.1021/ic9913177. [DOI] [PubMed] [Google Scholar]
- 48.Gouré E, Thiabaud G, Carboni M, Gon N, Dubourdeaux P, Garcia-Serres R, Clémancey M, Oddou JL, Robin AY, Jacquamet L, Dubois L, Blondin G, Latour JM. Inorg Chem. 2011;50:6408–6410. doi: 10.1021/ic2007414. [DOI] [PubMed] [Google Scholar]
- 49.McKee V, Zvagulis M, Dagdigian JV, Patch MG, Reed CA. J Am Chem Soc. 1984;106:4765–4772. [Google Scholar]
- 50.Blessing R. Acta Cryst. 1995;A51:33–38. doi: 10.1107/s0108767394005726. [DOI] [PubMed] [Google Scholar]
- 51.SAINT. Vol. 6.2. Bruker Analytical X-Ray Systems; Madison, WI: 2001. [Google Scholar]
- 52.SHELXTL. 6.10. Bruker Analyticla X-Ray Systems; Madison, WI: 2000. [Google Scholar]
- 53.Spek AL. PLATON A multipurpose crystallographic tool. Utrecht University; Utrecht, The Netherlands: 2002. [Google Scholar]
- 54.Frisch MJ, et al. Gaussian 03, Revision C.02. Gaussian, Inc; Wallingford CT: 2004. [Google Scholar]
- 55.Dong Y, Ménage S, Brennan BA, Elgren TE, Jang HG, Pearce LL, Que L., Jr J Am Chem Soc. 1993;115:1851–1859. [Google Scholar]
- 56.Other abbreviations: Me3-TACN = 1,4,7-trimethyl-1,4,7-triazacyclononane; BPMP = 2,6-bis[(bis(2-pyridylmethyl)-amino)methyl]-4-methylphenolate; tpdb = N,N,N′,N′-tetrakis(2-pyridyl-methyl)-1,4-diaminobutane-2-olate.
- 57.Eulering B, Ahlers F, Zippel F, Schmidt M, Nolting H, Krebs B. Chem Commun. 1995:1305–1307. [Google Scholar]
- 58.Brennan BA, Chen Q, Juarez-Garcia C, True AE, O’Connor CJ, Que L., Jr Inorg Chem. 1991;30:1937–1943. [Google Scholar]
- 59.Chen Q, Lynch JB, Gomez-Romero P, Ben-Hussein A, Jameson GB, O’Connor CJ, Que L., Jr Inorg Chem. 1988;27:2673–2681. [Google Scholar]
- 60.Mashuta MS, Webb RJ, Oberhausen KJ, Richardson JF, Buchanan RM, Hendrickson DN. J Am Chem Soc. 1989;111:2745–2746. [Google Scholar]
- 61.Borovik AS, Que L., Jr J Am Chem Soc. 1988;110:2345–2347. [Google Scholar]
- 62.Sage JT, Xia YM, Debrunner PG, Keough DT, de Jersey J, Zerner B. J Am Chem Soc. 1989;111:7239–7247. [Google Scholar]
- 63.Fox BG, Hendrich MP, Surerus KK, Andersson KK, Froland WA, Lipscomb JD, Münck E. J Am Chem Soc. 1993;115:3688–3701. [Google Scholar]
- 64.Bencini A, Gatteschi D. Electron Paramagnetic Resonance of Exchange Coupled Systems. Springer Verlag; Berlin: 1990. [Google Scholar]
- 65.Abragam A, Bleaney B. Electron Paramagnetic Resonance of Transition Metal Ions. Dover Publications; New York: 1986. [Google Scholar]
- 66.The excited state orbitals, ~dxz and ~dyz, are rotated relative to x,y,z by about 20° around the y and x axes, respectively, suggesting that the principal axes corresponding to gx and gy are rotated also by roughly 20° relative to x and y.
- 67.Davydov RM, Smieja J, Kikanov SA, Zang Y, Que L, Jr, Bowman MK. J Biol Inorg Chem. 1999;4:292–301. doi: 10.1007/s007750050315. [DOI] [PubMed] [Google Scholar]
- 68.Gütlich P, Link R, Trautwein AX. Mössbauer Spectroscopy of Transition Metal Chemistry. Springer; Berlin: 1978. [Google Scholar]
- 69.Guddat LW, McAlpine AS, Hume D, Hamilton S, deJersey J, Martin JL. Structure. 1999;7:757–767. doi: 10.1016/s0969-2126(99)80100-2. [DOI] [PubMed] [Google Scholar]
- 70.Onoda A, Okamoto Y, Sugimoto H, Shiro Y, Hayashi T. Inorg Chem. 2011;50:4892–4899. doi: 10.1021/ic2001267. [DOI] [PubMed] [Google Scholar]
- 71.Davydov R, Valentine AM, Komar-Panicucci S, Hoffman BM, Lippard SJ. Biochemistry. 1999;38:4188–4197. doi: 10.1021/bi982391o. [DOI] [PubMed] [Google Scholar]
- 72.Kim SH, Xing G, Bollinger JM, Jr, Krebs C, Hoffman BM. J Am Chem Soc. 2006;128:10374–10375. doi: 10.1021/ja063602c. [DOI] [PubMed] [Google Scholar]
- 73.Yang YS, McCormick JM, Solomon EI. J Am Chem Soc. 1997;119:11832–11842. [Google Scholar]
- 74.Fox BG, Liu Y, Dege JE, Lipscomb JD. J Biol Chem. 1991;266:540–550. [PubMed] [Google Scholar]
- 75.Brunold TC, Solomon EI. J Am Chem Soc. 1999;121:8288–8295. [Google Scholar]
- 76.Hirao H, Morokuma K. J Am Chem Soc. 2009;131:17206–17214. doi: 10.1021/ja905296w. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.