Abstract
In recent years, several new techniques based on the radiation force of ultrasound have been developed. Vibro-acoustography is a speckle-free ultrasound based imaging modality that can visualize normal and abnormal soft tissue through mapping the acoustic response of the object to a harmonic radiation force induced by ultrasound. In vibro-acoustography, the ultrasound energy is converted from high ultrasound frequencies to a low acoustic frequency (acoustic emission) that is often two orders of magnitude smaller than the ultrasound frequency. The acoustic emission is normally detected by a hydrophone. In medical imaging, vibroacoustography has been tested on breast, prostate, arteries, liver, and thyroid. These studies have shown that vibro-acoustic data can be used for quantitative evaluation of elastic properties. This paper presents an overview of vibro-acoustography and its applications in the areas of biomedicine.
Keywords: Ultrasound, Radiation force, Vibro-acoustography, Imaging
I. Introduction
In recent years, several new techniques for characterizing the elasticity of soft tissue based on radiation force of ultrasound have been developed. The ultimate aim of these methods is to exploit elasticity as a contrast mechanism to differentiate normal tissue from diseased tissue. Using the radiation force of ultrasound is a noninvasive mechanism to deform soft tissue so that information can be obtained by monitoring its mechanical response.
The acoustic radiation force has been studied for several decades. Acoustic waves are known to carry momentum, and radiation force is generated when the energy density of the acoustic waves changes. Numerous authors have examined the theoretical foundations of acoustic radiation force[1–7], and a review by Sarvazyan, et al., describes the use of acoustic radiation force in early applications as well as more modern biomedical applications [8]. Westervelt studied the force arising from the interaction of a plane wave with an object of arbitrary shape and boundary impedance that absorbs and scatters. The force vector, F, is given as [1]
| (1) |
where dr is the drag coefficient vector with components both parallel and perpendicular to the incident beam direction, S is the projected area of the object, and E is the energy density (E(t) = p2(t)/ρc2). The drag coefficient is given as [1]
| (2) |
where p and q are the unit vectors parallel and perpendicular to the beam direction, respectively. The quantities Πa and Πs are the total absorbed and scattered powers, respectively, γ is the scattered intensity, θ s is the angle between the incident and scattered intensity and dS is the area element. The intensities and powers are all expressed per unit incident intensity, and the drag coefficient is defined per unit incident energy density and unit projected area.
Nightingale, et al., succinctly summarized the implications of (2) as it relates to radiation force application in soft tissue [9]. It should be noted that these summarized results had been explored previously by several authors [1, 3, 6]. If the object is totally reflective, i.e., no absorption, then Πa = 0, θ s = 180°, the second integral results in a value of −Πs, and dr = 2Πs. If the object is a Rayleigh scatterer, where its size is much smaller than the wavelength of the incident acoustic wave, then scattering is assumed to occur equally in all directions and the second integral in (2) is zero leaving dr = Πa + Πs. If it is assumed that tissue can be represented as a collection of Rayleigh scatterers, one can perform the sum of the contribution of the radiation force from each scatterer. However, the power from absorption is much greater than that from scattering so dr = Πa. The radiation force attributed solely to the attenuation mechanism can be written as [5, 8–11]
| (3) |
where F is the force per unit volume, α is the attenuation coefficient of tissue, I is the acoustic intensity, and c is the speed of sound in the medium.
Silva, et al., recently proposed a way to classify acoustic radiation force by distinguishing between static and dynamic forces [12, 13]. Static radiation force is produced using continuous wave sound to exert a constant force. Dynamic radiation force is generated by modulating the amplitude of the sound through time, thereby creating a force that changes through time based on the modulation imposed. Dynamic radiation force can be generated using either pulsed or amplitude modulated sound. Dynamic radiation force has been utilized in the techniques for elasticity characterization of tissue.
Acoustic radiation force has been studied for the manipulation of objects including spheres, drops, and bubbles [14–20]. Radiation force balances have been used to calibrate the acoustic output of ultrasound transducers [21–23]. Most theoretical and experimental studies have been performed using static radiation force produced by continuous wave ultrasound. However, dynamic radiation force has been used in measuring absorption in liquids [10], measuring the power of ultrasound transducers [24], and inducing oscillation in liquid drops [25]. Theoretical studies of the dynamic radiation force have been undertaken for spheres, and spherical and cylindrical shells [13, 18, 26, 27].
The application of dynamic acoustic radiation force has been used in several elasticity measurement and imaging techniques over the past two decades [28]. Sugimoto, et al., first described using radiation force to deform tissue and using pulse-echo ultrasound to measure the mechanical response to characterize tissue hardness [29]. Sarvazyan, et al., followed this work by using ultrasound radiation force to produce propagating shear waves in a method called shear wave elasticity imaging (SWEI) that could be measured using ultrasound or magnetic resonance imaging (MRI) techniques [28, 30]. Magnetic resonance elastography is a method that uses MRI techniques to measure propagating shear waves. Normally, an external mechanical driver is used to produce the shear waves [31–34], but radiation force has also been used to create the shear waves [35–39]. Other methods have been developed stemming from the original concept of SWEI which use ultrasound systems to measure the shear wave propagation [40–46].
A method called acoustic radiation force impulse (ARFI) imaging was introduced by Nightingale and colleagues, which used short impulses (0.8–5.8 µs) of ultrasound to push tissue and then monitor the response with pulse-echo ultrasound [9, 47]. These impulses are performed at many locations in the tissue of interest to create images. Different parameters are used to characterize the tissue such as peak displacement and tissue recovery time are depicted in the images. Repeated impulses of ultrasound have also been used in characterizing tissue mimicking phantoms, ex vivo skeletal muscle, and clotting blood [48–54]. Other techniques have used an embedded sphere or bubble excited by radiation force to characterize the surrounding medium. This type of application has been studied for both elastic and viscoelastic media [55–63].
Amplitude modulated ultrasound has been used for characterization of elastic and viscoelastic media in a method called harmonic motion imaging [64–66]. The amplitude of the induced motion is used to detect differences in tissue. This method has also been used for finding the material properties of viscoelastic media [67].
Another method that uses the dynamic radiation force for soft tissue imaging and characterization is vibro-acoustography. Vibro-acoustography (VA) is a method that uses the acoustic response (acoustic emission) of an object to the harmonic radiation force of ultrasound for imaging and material characterization [68, 69].
The acoustic emission is generated by focusing two ultrasound beams of slightly different frequencies to the same spatial location and vibrating the tissue as a result of ultrasound radiation force exerted on the object at a frequency equal to the difference between the frequencies of the primary ultrasound beams. In this method the energy in the waves at high ultrasound frequencies are used to produce a low acoustic frequency wave (acoustic emission) that is often two orders of magnitude smaller than that ultrasound frequency. The acoustic emission is normally detected by a hydrophone and is used to construct the image of the object. Vibro-acoustography images have some unique characteristics that set it apart from traditional ultrasound imaging. This is partly due to the use of ultrasound beams to produce low frequency vibration of the object or tissue. For example, VA images are speckle free, which is a significant advantage over conventional pulse echo imaging.
VA may be used for a variety of imaging and characterization applications in biomedicine. In medical imaging, VA has been tested on breast, prostate, arteries, liver, and thyroid. This paper presents an overview of VA including its theoretical basis and beamforming techniques. Recent advances in various biomedical industrial applications of this technique will be described and reviewed.
II. Overview of Vibro-acoustography
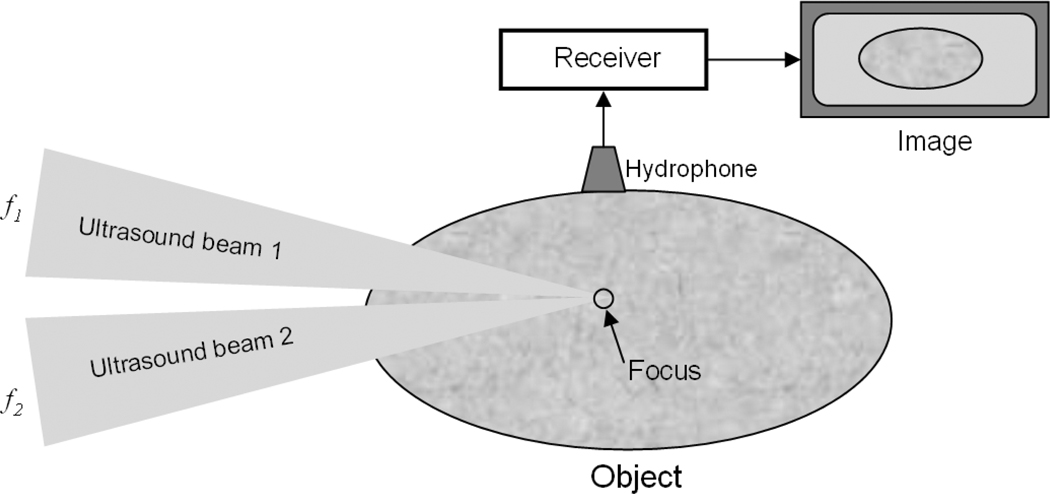
A simplified illustration of the vibro-acoustography principle is presented in the diagram shown in Fig. (1). The two co-focused ultrasound beams of slightly different frequencies f1 and f2 (Δf = f1–f2 << f1, f2) intersect at their joint focal point. For typical vibro-acoustography applications, f1 and f2 are on the order of 2–5 MHz and Δf is typically 10–70 kHz such that there are at least two orders of magnitude in difference insuring that Δf << f1, f2. The radiation force from these two beams has a component at Δf (called dynamic ultrasound radiation force), which vibrates the object. The acoustic response of the object to this force is detected by the hydrophone. The co-focus of the ultrasound beams is raster scanned across the object, and the resulting acoustic signal is recorded. An image of the object is formed by extracting the magnitude of the acoustic emission signal from the excitation point of the object and assigning that value to the image pixel.
Fig. (1).
Simplified vibro-acoustography system with two ultrasound beams focused at a common point. The excitation point is scanned within the object, and the acoustic emission is recorded by the hydrophone and an image is formed.
III. Theoretical Basis of Vibro-acoustography
The theory of vibro-acoustography has been described in [68–73]. In most cases, two spatially separate beams of ultrasound are used which are transmitting pressures, p1(t) and p2(t),
| (4) |
| (5) |
where ω i = 2πfi, (i = 1,2), Pi(r) is the pressure for the field produced by the aperture transmitting fi, (i = 1, 2), , where (x, y) is the spatial location of the object and Δϕ(r) = ϕ2(r) - ϕ1 (r) is the phase difference between the two beams, and the total pressure is p(t) = p1(t) + p2(t).
The radiation force can be found using (1)
| (6) |
| (7) |
| (8) |
where ρ is the medium density and c is the sound speed in the medium.
Using the identity cos2(b) = (1 + cos(2b))/2, the radiation force can be written as
| (9) |
where we have added the short-term time average of the energy density to evaluate the dynamic part of the radiation force. The short-term time average operator defined as
| (10) |
where 2π/ω1 ≪ T ≪ 4π/(ω2 − ω1) will retain the first three terms in the average, but the last two terms will be eliminated. The radiation force after the short-term time average is applied is
| (11) |
and the dynamic radiation force produced at Δω = ω2 − ω1 = 2πΔf is [70]
| (12) |
The radiation force is applied inside an object which causes a localized portion of the object to vibrate at frequency Δω. This vibration causes the creation of an acoustic field that propagates outward from the focal region where the force is produced. The acoustic waves, or acoustic emission, are measured by a hydrophone placed in contact or close proximity to the object.
The acoustic emission that is measured by the hydrophone can be represented by [69]
| (13) |
where a is a constant, HΔω(l) is the medium transfer function and QΔω is the total acoustic outflow by an object per unit force. The function HΔω(l) describes the acoustic environment that the acoustic emission propagates through before being measured at the hydrophone. In a laboratory setting, experiments are performed in water tanks so HΔω(l) may incorporate information related to the water and any reflections experienced at the walls or water surface. In the body, the acoustic environment is largely unpredictable. The function QΔω relates to the mechanical response to the dynamic radiation force applied to the object at frequency Δω.
The effects of the dynamic radiation force and parametric effects have been recently explored to better understand the nonlinear acoustic phenomena that contribute to the acoustic emission signal [12, 74–76]. Parametric effects arise when waves of two different frequencies, ω 1 and ω 2, interact and mix in a nonlinear acoustic medium. This mixture produces waves at the sum and difference frequencies of the original waves, ω 1 + ω 2 and ω 1 − ω 2, respectively [74, 77]. Silva, et al., explored parametric amplification of the radiation force produced in a fluid due to the interaction of sound beams of different frequencies [74]. The amplification was shown to be present and increased as Δf increased in both theoretical calculations and experimental results.
In the studies by Malcolm, et al., the ultrasound field was modeled, accounting for the geometry of the problem and nonlinearity of the medium, and the acoustic emission measured at the hydrophone was simulated [75, 78]. This model addressed the computational needs of simulating ultrasound waves at high spatial and temporal resolution in a nonlinear medium to find the radiation force and the resulting acoustic emission information at much lower frequencies. An image of an aluminum rod compared relatively well with a simulated image generated using the theory presented in this work.
IV. Vibro-acoustography Beamforming
Various studies have examined different beamforming strategies to produce radiation stress with different types of transducers [69, 79–82]. These beamforming strategies are different approaches to generate spatial distributions of the pressure P1(r) and P2(r). These studies have analyzed the image resolution and contrast that can be obtained using different beamforming geometries. In the study by Chen, et al., three different approaches were used for beamforming including, amplitude modulation with a single element transducer, confocal beams with a two-element transducer, and X-focal with two separate single element transducers. The X-focal arrangement could provide improved axial resolution, but was more complicated to align than the other two methods. All three methods could produce beams with sub-millimeter lateral resolution. Calle, et al., examined the use of annular arrays with multiple rings [76]. In this analysis, the authors investigated the field at Δf produced in the interaction region of the ultrasound beams and along the propagation path. Other types of transducers such as sector and linear arrays were explored for optimization of resolution and contrast as well as to move vibro-acoustography closer to clinical use with linear array transducers [80, 81, 83].
More recent contributions have examined the use of multiple simultaneous ultrasound signals and the resulting stress fields for image formation [59, 84]. Using multiple simultaneous ultrasound signals allows for generation of a set of difference frequencies. For example, if we have four elements, each with a different ultrasound frequency, the number of unique combinations that can arise to create a value of Δf is N(N-1)/2, where N is the number of ultrasound frequencies. By substituting N = 4, we can get up to 6 unique values of Δf. The strength of this method is that more information can be gained at many difference frequencies, thereby reducing scan times for a given amount of information acquired. In the study by Urban, et al., four ultrasound frequencies were simultaneously transmitted to produce six unique difference frequencies [59]. Hence, the data acquired in one scan produced six unique images. These images can be combined in different ways to reduce artifacts and improve visualization of different features in the images.
V. Application in Breast Imaging
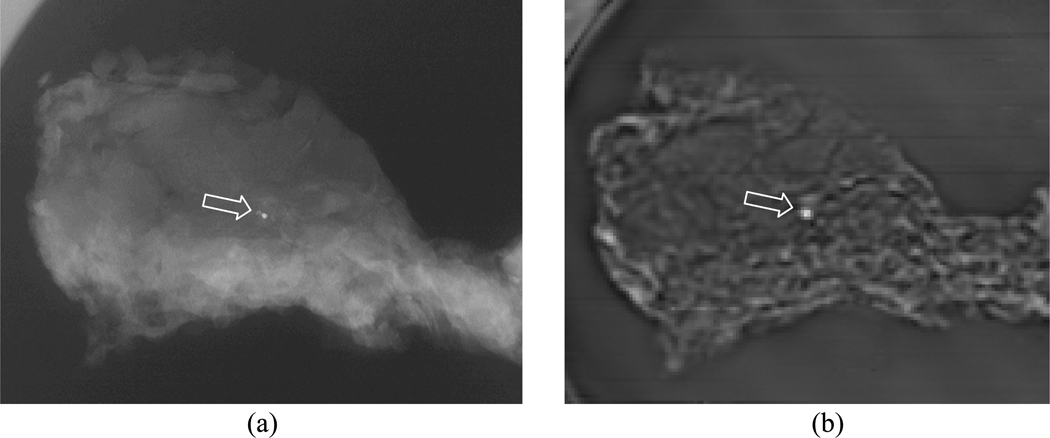
Vibro-acoustography has been studied extensively in breast imaging for detection of abnormal lesions in ex vivo [85–87]and in vivo tissue [88–90]. In testing of excised tissue samples, we have detected microcalcifications [85, 86]. The detection of microcalcifications is important because they can be indicators of the presence of benign and malignant lesions. Figure (2) shows the vibro-acoustography image of an excised human breast tissue sample with a microcalcification [86]. Although the microcalcifications may be smaller than the resolution cell of the vibro-acoustography system, it can still be detected in the image. In a previous study, it was demonstrated that microcalcifications on the order of 100 microns in diameter can be detected by vibro-acoustography [85]. In a study of 74 tissue samples, VA imaging missed 21.6% of microcalcifications (false negative) and confirmed the presence of 78.4% of microcalcifications [86]. In cases where confirmation from analyzing x-ray images and validation by histological analysis occurred, 59.5% were positively identified and 18.9% were labeled suspicious when assessed with VA.
Fig. (2).
(a) X-ray image of a breast tissue specimen. The arrow points to a microcalcification that is seen as a bright spot at the center. (b) VA image of the tissue sample. The microcalcification is clearly identified as a bright spots. The VA image also clearly shows the structure of the soft tissue. [© 2004 IEEE. Reproduced with permission from [86].]
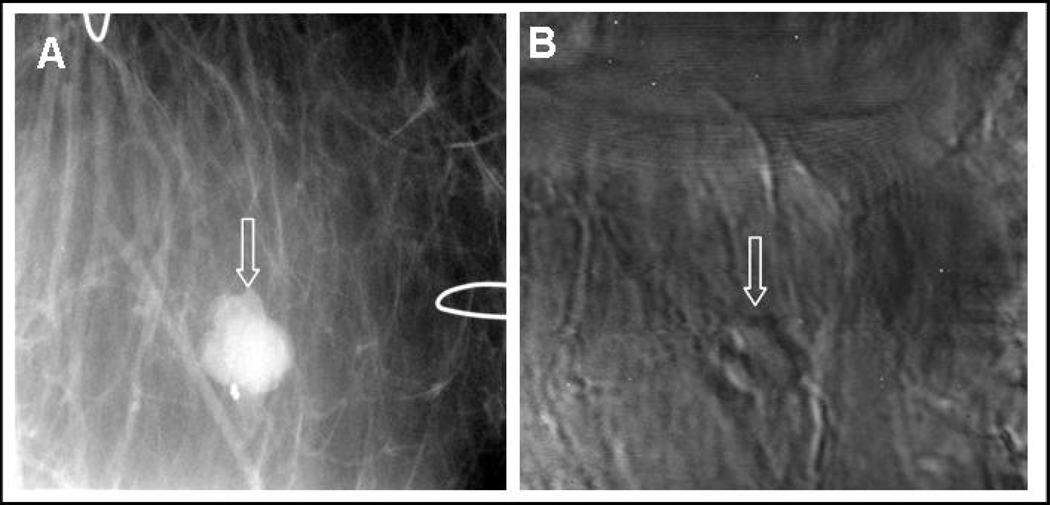
Recent in vivo human study results indicate that various types of breast lesions such as fibroadenomas as well as calcifications can be detected by VA [88]. A VA image obtained from the breast of a patient with a benign fibroadenoma mass is shown in Fig. (3). This image, which is in cranial-caudal view, clearly displays the mass. In addition, it has been demonstrated that VA may be able to detect some types of cancerous lesions that are not detectable by mammography. Lesion sizing is another important application area. Some experimental in vivo results suggest that measuring the size of breast lesions by VA may be more accurate compared to other modalities such as ultrasound or mammography. Further study on a larger cohort of patients is needed to determine the conditions under which VA may prove advantageous in lesion sizing. The study presented in [89], combines the vibro-acoustography result with mammography to maximize the clinical impact with two imaging modalities.
Fig. (3).
In vivo images of human breast. A) X-ray mammography showing partially calcified mass; B) VA scan at 40 kHz and 2 cm in depth showing the mass.
VI. Application in Prostate Imaging
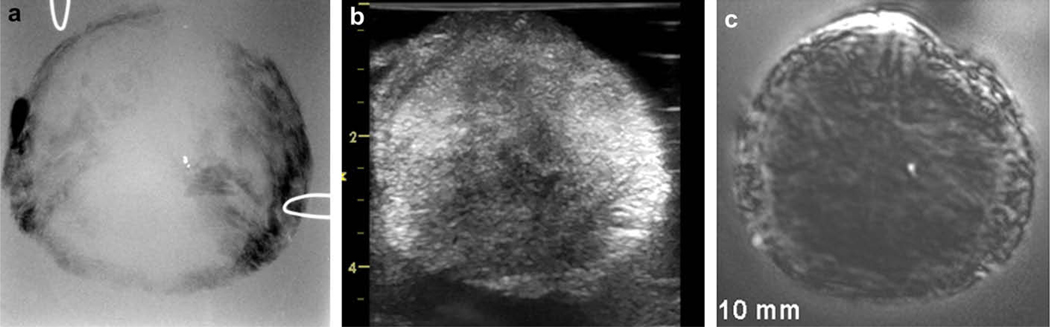
Vibro-acoustography has also been found to have potential in diagnostic and therapeutic applications in the prostate gland, particularly in detecting brachytherapy seeds and monitoring cryotherapy as evidenced from in vitro studies [91–94]. Figure (4) displays images of an excised human prostate. The x-ray image shows a calcification as a high contrast, bright point at the center of the image. Tissue structures are not clearly visible in x-ray (panel a). The traditional ultrasound image, due to its inherent speckle noise, has a low signal-to-noise ratio and low contrast. The small calcification and some of the tissue structures blend in with the speckle noise, thus hard to identify. The VA images of this prostate tissue with the ultrasound focused at the depth of 15 mm from the top surface of the sample shows detailed tissue structures as well as the calcification (panel c). Comparing the VA and ultrasound images, it is evident that VA provides speckle-free and clear images of tissue, which allows one to identify tissue structures and the small (< 1 mm) calcification [95].
Fig. (4).
a) X-ray image of an excised human prostate showing a single calcification. b) Ultrasound image of the prostate sample. This image presents an excessive amount of speckle and fails to reveal the calcification, c) Vibro-acoustography scan of the same tissue focused at 15 mm depth inside the sample. This speckle-free image shows the calcification at the center of prostate. [Reprinted from [95] with permission from Elsevier.]
The detectability of brachytherapy seeds has been shown to be enhanced compared to pulse-echo imaging techniques [93]. The integrated optical density (IOD), a measure of image intensity, was computed for both pulse-echo and VA imaging with transducer rotated at different angles with respect to the brachytherapy seeds. The VA maintained a near constant IOD for angles ranging from 20–90°, whereas the IOD for the pulse-echo measurements decreased significantly when the transducers were moved away from normal incidence with respect to the seeds.
VII. Other Biomedical Applications
Vibro-acoustography has been used for imaging lesions in excised human liver [96]. The results indicated that VA could detect lesion borders and texture with very good definition and quality. The lesions were imaged with Δf values ranging from 12.5–25.3 kHz. Using different values of Δf provided different contrast and image details in the images.
VA has been used to investigate calcifications in arteries in excised human breast tissue samples and in vivo peripheral circulation of pigs [97–99]. The calcifications appear often as bright structures and the VA images compared well with x-ray images. In the in vivo study in pigs described by Pislaru, et al., the plaque area measured by in vivo VA (1.0 ± 0.9 cm2) compared well with in vitro VA (1.1 ± 0.6 cm2) and x-ray radiography (0.9 ± 0.6 cm2) [98]. The sensitivity and specificity for calcification detection was 100% and 86%.
Calle, et al., explored the use of VA for imaging bone and compared with computed tomography and bone ultrasound attenuation imaging [100]. A variation of VA for monitoring bone fracture and fracture healing has been presented in [101]. Instead of using a hydrophone, a laser vibrometer was used to measure the frequency characteristics of the vibrating bone to assess bone fracture. Vibrational resonance frequencies shifted noticeably when the same femur was intact and then fractured [101].
The variation of the acoustic emission with temperature was investigated by Konofagou, et al. [102, 103]. This work was undertaken to use VA for monitoring the application of therapeutic ultrasound to ablate tissue. It was reported that the value of Δf that had peak amplitude shifted with temperature [103]. Additionally, the amplitude of the acoustic emission varied with temperature through heating and cooling processes [102].
Chen, et al., studied the harmonic content in ultrasound contrast microbubbles during VA excitation and found that microbubbles would produce acoustic emission at both Δf and 2Δf [104, 105]. This finding was supported by the theoretical development undertaken in these reports.
Chen, et al., have analyzed the heating that occurs from a scan of a confocal transducer to insure that the tissue of interest does not experience significant heating [106]. It was found that heating during a typical scan would be less than 0.32°C, and that the most extreme heating would come at the surface of the transducer.
VIII. Quantitative Vibro-acoustography
Although VA is primarily an imaging technique, quantitative estimation of viscoelastic parameters of tissue using inverse problem approaches have been presented in [107]. The inverse problem approach for vibro-acoustics involves using measurements of the acoustic pressure (acoustic emission) or surface motion and attempting to solve for the distribution of physical parameters, in most cases elasticity, of the object being excited by radiation force. In the approach followed by Brigham and co-workers, the inverse problem was cast in an optimization framework and the material parameters were obtained by minimizing an error functional that measured the discrepancy between modeled and measured responses. The system response was modeled using a coupled acoustic-structure interaction finite element approach [107]. These authors used both synthetic and experimental data to demonstrate that VA could be used to characterize material properties noninvasively. The results reported in [107] exhibited very good accuracy and precision (0.63–3.57% error in the inverse problem solution). It is important to point out that in the studies reported in [107] that it was assumed that the geometry of the materials and that the fluid properties were known, but the properties were unknown.
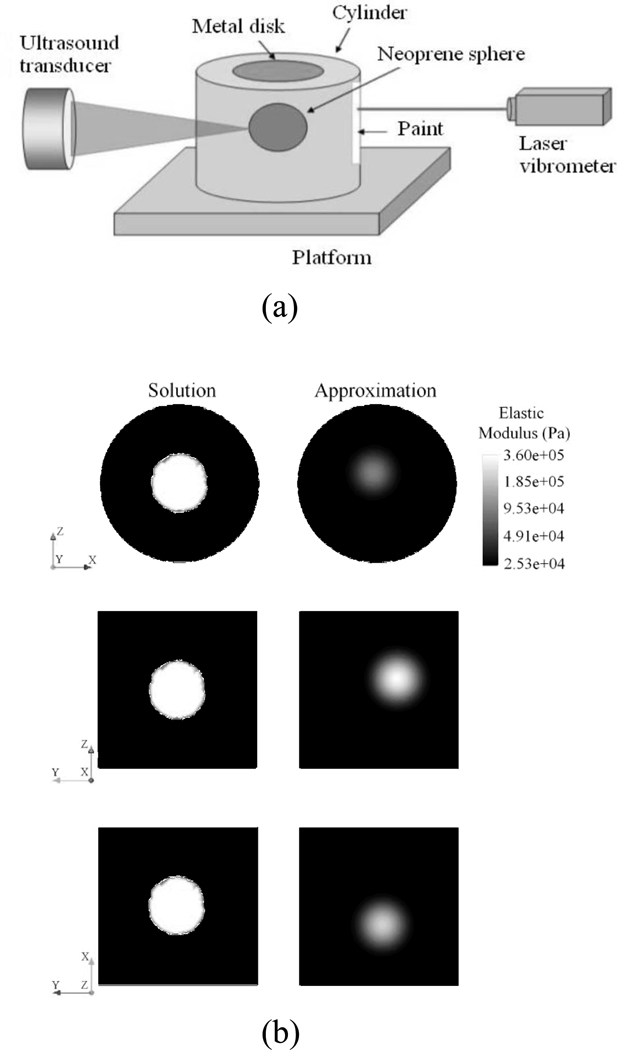
A study by Aguilo, et al., used vibro-acoustic data to estimate the spatial distribution of elastic properties of a body vibrating in a fluid [108]. These authors used both synthetic and experimental data in their studies. The coupled acoustic-structure interaction of the system was modeled using the finite element method. The inverse material identification problem was cast as an optimization problem. In their approach, the authors used either acoustic pressure fields or surface velocities to define the objective function in the optimization problem and reported the advantages and disadvantages of using these variables for materials identification in VA. Gaussian radial basis functions were used to represent the spatial variation of elastic moduli in the phantoms. In the studies that used synthetic data, both the pressure and velocity measurements yielded similar results with the surface velocity measurements providing slightly lower error in the solution of the inverse problem solution. Furthermore, an experiment was performed with an embedded neoprene sphere in an agar cylinder as shown in Fig. (5a). The sphere was excited by ultrasound radiation force, and the surface velocity of the phantom was measured with a laser vibrometer. The same phantom was modeled using FEM and the elastic properties of the model were optimized to fit the data. Good agreement was shown between the reconstructions from FEM solutions in Fig. (5b). Also, the normalized velocities from the model agreed well with the experimental data. The reconstruction from the inverse solution gave an underestimation of the elastic properties, but the results were encouraging.
Fig. (5).
a) Diagram of experimental setup, b) Plane views for the spatial distribution of elastic moduli found as solution to the inverse problem for the z-x plane, the z-y plane, and the x-y plane. [© 2010 IEEE. Reproduced with permission from [108].]
IX. Discussion
Vibro-acoustography is a unique imaging modality that uses ultrasound radiation force and the resolution of ultrasound beamforming to investigate the mechanical response of tissue at frequencies significantly lower than used in clinical ultrasound. This modality is one of many that use the radiation force of ultrasound as discussed in the Introduction, but VA is unique in that it uses multiple ultrasound beams of different frequencies to explore the physical response of tissue. Also, it is unique in the sense that it uses the acoustic response of the object to form the image. The images produced do not have the speckle present in conventional B-mode ultrasound images.
The acoustic emission signal is related to the elasticity of the tissue as well as parameters such as ultrasound reflectivity and absorption, and nonlinearity of the medium. VA has been very sensitive to depicting calcifications in tissue, in many cases, with similar contrast as an X-ray image but without the ionizing radiation.
Imaging with VA has been reported for a number of different applications as discussed above. An emerging area of focus is thyroid imaging in which some preliminary work has been reported [109, 110]. VA imaging has been used for nondestructive testing applications on non-biological objects [111–114].
Vibro-acoustography has been studied extensively in a laboratory setting, with only a few examples of in vivo studies in pig arteries and human breast [87–90, 98, 99]. To translate VA imaging to a clinical setting, we have collaborated with General Electric to modify a General Electric Vivid 7 ultrasound scanner (GE HealthCare Ultrasound Cardiology, Horton, Norway) using software and hardware modifications [115]. This system electronically scans the focus of the two ultrasound beams across the azimuthal dimension of the transducer, which speeds up the scanning procedure significantly, compared to mechanical scanning of the transducer. This implementation allows for clinical imaging of breast, prostate, and thyroid tissues.
Mechanical scanning of a confocal transducer has been employed for acquiring images in the laboratory. For a scan of a 5.0 × 5.0 cm area with 250 × 250 pixels, these scans can take up to 7 or 8 minutes. For clinical application, these times need to be reduced. Vibro-acoustography performed with electronic scanning, using a linear array transducer can make an image in less than one minute [80]. VA images are acquired in a C-scan orientation, so registering with clinical B-mode data can sometimes be challenging.
Through the course of studying VA, we have identified artifacts associated with images such as standing waves because of the long ultrasound transmissions and acoustic reverberation effects from the acoustic emission signals being reflected in the acoustic environment. Mitri, et al., has shown that by varying the ultrasound frequencies while keeping Δf constant, that the effects of the standing waves can be minimized or eliminated [116]. Urban, et al., addressed the reverberation artifact, which manifests itself as low spatial frequency variations of the image intensity, by using images formed at different Δf and summing them together yielded improved images with more homogenous backgrounds [59, 117].
X. Future Work
One of the areas with significant importance for future work is quantitative vibroacoustography for estimating viscoelastic material properties of an object. Analysis methods and modeling approaches should be refined to solve for the spatial distribution of viscoelastic material properties. Future work also should be directed toward clinical utilization of VA. Implementation of VA on a clinical ultrasound scanner will facilitate translation of this imaging modality to a clinical setting. Additional clinical studies with large cohorts of patients need to be studied for applications of VA imaging in various organs, including the prostate, breast, and thyroid.
XI. Concluding Remarks
Vibro-acoustography is an imaging and tissue characterization method with a wide range of potential applications in medicine. Vibro-acoustography images are formed using low-frequency acoustic response of the object to a harmonic excitation induced by ultrasound. Vibro-acoustography has shown to be a valuable technique in biomedical applications. Its application continues to be investigated for in vivo applications in the medical imaging field.
Acknowledgments
The authors thank Dr. Dana H. Whaley for his contribution to in vivo breast experiments, and Randall R. Kinnick for laboratory support. This work was supported in part by grants CA121579, CA127235, and CA91956 from the National Institutes of Health and BCTR0504550 from the Susan G. Komen Breast Cancer Foundation. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Cancer Institute, the National Institutes of Health, or the Susan G. Komen Breast Cancer Foundation. Disclosure of financial interests: Mayo Clinic and two of the authors (JFG and MF) have a financial interest associated with technology used in this research; the technology has been licensed in part for some specific application areas to industry.
References
- 1.Westervelt PJ. The theory of steady forces caused by sound waves. J. Acoust. Soc. Am. 1951;23:312–315. [Google Scholar]
- 2.Westervelt PJ. Acoustic radiation pressure. J. Acoust. Soc. Am. 1957;29:26–29. [Google Scholar]
- 3.Beyer RT. Radiation pressure--the history of a mislabeled tensor. J. Acoust. Soc. Am. 1978;63:1025–1030. [Google Scholar]
- 4.Chu B-T, Apfel RE. Acoustic radiation pressure produced by a beam of sound. J. Acoust. Soc. Am. 1982;72:1673–1687. [Google Scholar]
- 5.Torr GR. The acoustic radiation force. Am. J. Phys. 1984;52:402–408. [Google Scholar]
- 6.Lee CP, Wang TG. Acoustic radiation pressure. J. Acoust. Soc. Am. 1993;94:1099–1109. [Google Scholar]
- 7.Jiang ZY, Greenleaf JF. Acoustic radiation pressure in a three-dimensional lossy medium. J. Acoust. Soc. Am. 1996;100:741–747. doi: 10.1121/1.416236. [DOI] [PubMed] [Google Scholar]
- 8.Sarvazyan AP, Rudenko OV, Nyborg WL. Biomedical applications of radiation force of ultrasound: historical roots and physical basis. Ultrasound Med. Biol. 2010;36:1379–1394. doi: 10.1016/j.ultrasmedbio.2010.05.015. [DOI] [PubMed] [Google Scholar]
- 9.Nightingale KR, Palmeri ML, Nightingale RW, Trahey GE. On the feasibility of remote palpation using acoustic radiation force. J. Acoust. Soc. Am. 2001;110:625–634. doi: 10.1121/1.1378344. [DOI] [PubMed] [Google Scholar]
- 10.McNamara FL, Beyer RT. A variation of the radiation pressure method of measuring sound absorption in liquids. J. Acoust. Soc. Am. 1953;25:259–262. [Google Scholar]
- 11.Starritt HC, Duck FA, Humphrey VF. Forces acting in the direction of propagation in pulsed ultrasound fields. Phys. Med. Biol. 1991;36:1465. doi: 10.1088/0031-9155/36/11/006. [DOI] [PubMed] [Google Scholar]
- 12.Silva GT, Chen S, Greenleaf JF, Fatemi M. Dynamic ultrasound radiation force in fluids. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;71 doi: 10.1103/PhysRevE.71.056617. 056617. [DOI] [PubMed] [Google Scholar]
- 13.Chen S, Silva GT, Kinnick RR, Greenleaf JF, Fatemi M. Measurement of dynamic and static radiation force on a sphere. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;71 doi: 10.1103/PhysRevE.71.056618. 056618. [DOI] [PubMed] [Google Scholar]
- 14.Hasegawa T, Yosioka K. Acoustic-radiation force on a solid elastic sphere. J. Acoust. Soc. Am. 1969;46:1139–1143. [Google Scholar]
- 15.Crum LA. Acoustic force on a liquid droplet in an acoustic stationary wave. J. Acoust. Soc. Am. 1971;50:157–163. [Google Scholar]
- 16.Marston PL. Shape oscillation and static deformation of drops and bubbles driven by modulated radiation stresses---Theory. J. Acoust. Soc. Am. 1980;67:15–26. [Google Scholar]
- 17.Mitri FG. Acoustic radiation force acting on elastic and viscoelastic spherical shells placed in a plane standing wave field. Ultrasonics. 2005;43:681–691. doi: 10.1016/j.ultras.2005.03.002. [DOI] [PubMed] [Google Scholar]
- 18.Mitri FG, Fatemi M. Dynamic acoustic radiation force acting on cylindrical shells: theory and simulations. Ultrasonics. 2005;43:435–445. doi: 10.1016/j.ultras.2004.10.003. [DOI] [PubMed] [Google Scholar]
- 19.Mitri FG, Chen S. Theory of dynamic acoustic radiation force experienced by solid cylinders. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;71 doi: 10.1103/PhysRevE.71.016306. 016306. [DOI] [PubMed] [Google Scholar]
- 20.Lee J, Shung KK. Radiation forces exerted on arbitrarily located sphere by acoustic tweezer. J. Acoust. Soc. Am. 2006;120:1084–1094. doi: 10.1121/1.2216899. [DOI] [PubMed] [Google Scholar]
- 21.Carson PL, Fischella PR, Oughton TV. Ultrasonic power and intensities produced by diagnostic ultrasound equipment. Ultrasound Med. Biol. 1978;3:341–350. doi: 10.1016/0301-5629(78)90076-5. [DOI] [PubMed] [Google Scholar]
- 22.Fick SE, Breckenridge FR. Ultrasonic power output measurement by pulsed radiation pressure. J. Res. Natl. Inst. Stand. Technol. 1996;101:659–669. doi: 10.6028/jres.101.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Shou WD, Huang XW, Duan SM, Xia RM, Shi ZL, Geng XM, Li FQ. Acoustic power measurement of high intensity focused ultrasound in medicine based on radiation force. Ultrasonics. 2006;44:e17–e20. doi: 10.1016/j.ultras.2006.06.034. [DOI] [PubMed] [Google Scholar]
- 24.Greenspan M, Breckenridge FR, Tschiegg CE. Ultrasonic transducer power output by modulated radiation pressure. J. Acoust. Soc. Am. 1978;63:1031–1038. [Google Scholar]
- 25.Marston PL, Apfel RE. Quadrupole resonance of drops driven by modulated acoustic radiation pressure---Experimental properties. J. Acoust. Soc. Am. 1980;67:27–37. [Google Scholar]
- 26.Mitri FG, Fellah ZE. Amplitude-modulated acoustic radiation force experienced by elastic and viscoelastic spherical shells in progressive waves. Ultrasonics. 2006;44:287–296. doi: 10.1016/j.ultras.2006.03.001. [DOI] [PubMed] [Google Scholar]
- 27.Silva GT. Dynamic radiation force of acoustic waves on solid elastic spheres. Phys. Rev. E. 2006;74 doi: 10.1103/PhysRevE.74.026609. 026609. [DOI] [PubMed] [Google Scholar]
- 28.Sarvazyan A, Hall TJ, Urban MW, Fatemi M, Aglyamov SR, Garra BS. Elasticity imaging - an emerging branch of medical imaging. An overview. Curr. Med. Imaging Rev. 2011;7(4):255–282. doi: 10.2174/157340511798038684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sugimoto T, Ueha S, Itoh K. Tissue hardness measurement using the radiation force of focused ultrasound; 1990 IEEE International Ultrasonics Symposium; 1990. pp. 1377–1380. [Google Scholar]
- 30.Sarvazyan AP, Rudenko OV, Swanson SD, Fowlkes JB, Emelianov SY. Shear wave elasticity imaging: a new ultrasonic technology of medical diagnostics. Ultrasound Med. Biol. 1998;24:1419–1435. doi: 10.1016/s0301-5629(98)00110-0. [DOI] [PubMed] [Google Scholar]
- 31.Muthupillai R, Lomas DJ, Rossman PJ, Greenleaf JF, Manduca A, Ehman RL. Magnetic resonance elastography by direct visualization of propagating acoustic strain waves. Science. 1995;269:1854–1857. doi: 10.1126/science.7569924. [DOI] [PubMed] [Google Scholar]
- 32.Sinkus R, Lorenzen J, Schrader D, Lorenzen M, Dargatz M, Holz D. High-resolution tensor MR elastography for breast tumour detection. 2000;45:1649–1664. doi: 10.1088/0031-9155/45/6/317. [DOI] [PubMed] [Google Scholar]
- 33.Litwiller DV, Mariappan YK, Ehman RL. A review of magnetic resonance elastography. Curr. Med. Imaging Rev. 2012;vol. 8(1):46–55. doi: 10.2174/157340512799220562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Sinkus R, Daire J-L, Vilgrain V, Van Beers BE. Elasticity imaging via MRI: basics, overcoming the Lamb limit, and clinical liver results. Curr. Med. Imaging Rev. 2012;vol. 8(1):56–63. [Google Scholar]
- 35.Andreev VG, Dmitriev VN, Pishchalnikov YA, Rudenko OV, Sapozhnikov OA, Sarvazyan AP. Observation of shear waves excited by focused ultrasound in a rubber-like medium. Acoust. Phys. 1997;43:123–128. [Google Scholar]
- 36.Wu T, Felmlee JP, Greenleaf JF, Riederer SJ, Ehman RL. MR imaging of shear waves generated by focused ultrasound. 2000;4:111–115. doi: 10.1002/(sici)1522-2594(200001)43:1<111::aid-mrm13>3.0.co;2-d. [DOI] [PubMed] [Google Scholar]
- 37.McDannold N, Maier SE. Magnetic resonance acoustic radiation force imaging. Med. Phys. 2008;35:3748–3758. doi: 10.1118/1.2956712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Souchon R, Salomir R, Beuf O, Milot L, Grenier D, Lyonnet D, Chapelon JY, Rouviere O. Transient MR elastography (t-MRE) using ultrasound radiation force: Theory, safety, and initial experiments in vitro. Magn. Reson. Med. 2008;60:871–881. doi: 10.1002/mrm.21718. [DOI] [PubMed] [Google Scholar]
- 39.Chen J, Watkins R, Pauly KB. Optimization of encoding gradients for MR-ARFI. Magn. Reson. Med. 2010;63:1050–1058. doi: 10.1002/mrm.22299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Nightingale K, McAleavey S, Trahey G. Shear-wave generation using acoustic radiation force: in vivo and ex vivo results. Ultrasound Med. Biol. 2003;29:1715–1723. doi: 10.1016/j.ultrasmedbio.2003.08.008. [DOI] [PubMed] [Google Scholar]
- 41.Bercoff J, Tanter M, Fink M. Supersonic shear imaging: a new technique for soft tissue elasticity mapping. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2004;51:396–409. doi: 10.1109/tuffc.2004.1295425. [DOI] [PubMed] [Google Scholar]
- 42.Chen S, Fatemi M, Greenleaf JF. Quantifying elasticity and viscosity from measurement of shear wave speed dispersion. J. Acoust. Soc. Am. 2004;115:2781–2785. doi: 10.1121/1.1739480. [DOI] [PubMed] [Google Scholar]
- 43.McAleavey SA, Menon M, Orszulak J. Shear-modulus estimation by application of spatially-modulated impulsive acoustic radiation force. Ultrason. Imaging. 2007;29:87–104. doi: 10.1177/016173460702900202. [DOI] [PubMed] [Google Scholar]
- 44.Chen S, Urban MW, Pislaru C, Kinnick R, Zheng Y, Yao A, Greenleaf JF. Shearwave dispersion ultrasound vibrometry (SDUV) for measuring tissue elasticity and viscosity. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2009;56:55–62. doi: 10.1109/TUFFC.2009.1005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Fink M, Tanter M. A multiwave imaging approach for elastography. Curr. Med. Imaging Rev. 2011;7(4):340–349. [Google Scholar]
- 46.Urban MW, Chen S, Fatemi M. A review of shearwave dispersion ultrasound vibrometry (SDUV) and its applications. Curr. Med. Imaging Rev. 2012;vol. 8(1):27–36. doi: 10.2174/157340512799220625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Nightingale KR. Acoustic radiation force impulse (ARFI) imaging: a review. Curr. Med. Imaging Rev. 2011;7(4):328–339. doi: 10.2174/157340511798038657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Walker WF, Fernandez FJ, Negron LA. A method of imaging viscoelastic parameters with acoustic radiation force. Phys. Med. Biol. 2000;45:1437–1447. doi: 10.1088/0031-9155/45/6/303. [DOI] [PubMed] [Google Scholar]
- 49.Viola F, Walker WF. Radiation force imaging of viscoelastic properties with reduced artifacts. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2003;50:736–742. doi: 10.1109/tuffc.2003.1209564. [DOI] [PubMed] [Google Scholar]
- 50.Viola F, Kramer MD, Lawrence MB, Oberhauser JP, Walker WF. Sonorheometry: A noncontact method for the dynamic assessment of thrombosis. Ann. Biomed. Eng. 2004;32:696–705. doi: 10.1023/b:abme.0000030235.72255.df. [DOI] [PubMed] [Google Scholar]
- 51.Mauldin FW, Haider MA, Loboa EG, Behler RH, Euliss LE, Pfeiler TW, Gallippi CM. Monitored steady-state excitation and recovery (MSSER) radiation force imaging using viscoelastic models. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2008;55:1597–1610. doi: 10.1109/TUFFC.2008.836. [DOI] [PubMed] [Google Scholar]
- 52.Orescanin M, Toohey KS, Insana MF. Material properties from acoustic radiation force step response. J. Acoust. Soc. Am. 2009;125:2928–2936. doi: 10.1121/1.3106129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Viola F, Mauldin FW, Lin-Schmidt X, Haverstick DM, Lawrence MB, Walker WF. A novel ultrasound-based method to evaluate hemostatic function of whole blood. Clin. Chim. Acta. 2010;411:106–113. doi: 10.1016/j.cca.2009.10.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Mauldin FW, Viola F, Hamer TC, Ahmed EM, Crawford SB, Haverstick DM, Lawrence MB, Walker WF. Adaptive force sonorheometry for assessment of whole blood coagulation. Clin. Chim. Acta. 2010;411:638–644. doi: 10.1016/j.cca.2010.01.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Oestreicher HL. Field and impedance of an oscillating sphere in a viscoelastic medium with an application to biophysics. J. Acoust. Soc. Am. 1951;23:707–714. [Google Scholar]
- 56.Chen S, Fatemi M, Greenleaf JF. Remote measurement of material properties from radiation force induced vibration of an embedded sphere. J. Acoust. Soc. Am. 2002;112:884–889. doi: 10.1121/1.1501276. [DOI] [PubMed] [Google Scholar]
- 57.Ilinskii YA, Meegan GD, Zabolotskaya EA, Emelianov SY. Gas bubble and solid sphere motion in elastic media in response to acoustic radiation force. J. Acoust. Soc. Am. 2005;117:2338–2346. doi: 10.1121/1.1863672. [DOI] [PubMed] [Google Scholar]
- 58.Norris AN. Impedance of a sphere oscillating in an elastic medium with and without slip. J. Acoust. Soc. Am. 2006;119:2062–2066. doi: 10.1121/1.2171526. [DOI] [PubMed] [Google Scholar]
- 59.Urban MW, Silva GT, Fatemi M, Greenleaf JF. Multifrequency vibro-acoustography. IEEE Trans. Med. Imaging. 2006;25:1284–1295. doi: 10.1109/tmi.2006.882142. [DOI] [PubMed] [Google Scholar]
- 60.Aglyamov SR, Karpiouk AB, Ilinskii YA, Zabolotskaya EA, Emelianov SY. Motion of a solid sphere in a viscoelastic medium in response to applied acoustic radiation force: Theoretical analysis and experimental verification. J. Acoust. Soc. Am. 2007;122:1927–1936. doi: 10.1121/1.2774754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Urban MW, Greenleaf JF. Harmonic pulsed excitation and motion detection of a vibrating reflective target. J. Acoust. Soc. Am. 2008;123:519–533. doi: 10.1121/1.2805666. [DOI] [PubMed] [Google Scholar]
- 62.Karpiouk AB, Aglyamov SR, Ilinskii YA, Zabolotskaya EA, Emelianov SY. Assessment of shear modulus of tissue using ultrasound radiation force acting on a spherical acoustic inhomogeneity. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2009;56:2380–2387. doi: 10.1109/TUFFC.2009.1326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Urban MW, Fatemi M, Greenleaf JF. Modulation of ultrasound to produce multifrequency radiation force. J. Acoust. Soc. Am. 2010;127:1228–1238. doi: 10.1121/1.3294487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Konofagou EE, Maleke C. Harmonic motion imaging (HMI) for tumor imaging and treatment monitoring - A review. Curr. Med. Imaging Rev. 2012;vol. 8(1):16–26. doi: 10.2174/157340512799220616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Konofagou E, Thierman J, Hynynen K. A focused ultrasound method for simultaneous diagnostic and therapeutic applications - a simulation study. Phys Med Biol. 2001;46:2967–2984. doi: 10.1088/0031-9155/46/11/314. [DOI] [PubMed] [Google Scholar]
- 66.Konofagou EE, Hynynen K. Localized harmonic motion imaging: theory, simulations and experiments. Ultrasound Med. Biol. 2003;29:1405–1413. doi: 10.1016/s0301-5629(03)00953-0. [DOI] [PubMed] [Google Scholar]
- 67.Vappou J, Maleke C, Konofagou EE. Quantitative viscoelastic parameters measured by harmonic motion imaging. Phys. Med. Biol. 2009;54:3579–3594. doi: 10.1088/0031-9155/54/11/020. [DOI] [PubMed] [Google Scholar]
- 68.Fatemi M, Greenleaf JF. Ultrasound-stimulated vibro-acoustic spectrography. Science. 1998;280:82–85. doi: 10.1126/science.280.5360.82. [DOI] [PubMed] [Google Scholar]
- 69.Fatemi M, Greenleaf JF. Vibro-acoustography: An imaging modality based on ultrasound-stimulated acoustic emission. Proc. Natl. Acad. Sci. U. S. A. 1999;96:6603–6608. doi: 10.1073/pnas.96.12.6603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Fatemi M, Greenleaf JF. Probing the dynamics of tissue at low frequencies with the radiation force of ultrasound. Phys. Med. Biol. 2000;45:1449–1464. doi: 10.1088/0031-9155/45/6/304. [DOI] [PubMed] [Google Scholar]
- 71.Fatemi M, Manduca A, Greenleaf JF. Imaging elastic properties of biological tissues by low-frequency harmonic vibration. Proc. IEEE. 2003;91:1503–1519. [Google Scholar]
- 72.Fatemi M, Greenleaf JF. Remote acoustic emission spectrography (RAES) In: Lees S, Ferrari LA, editors. Acoustical Imaging. vol. 23. New York: Plenum Press; 1997. pp. 231–236. [Google Scholar]
- 73.Greenleaf JF, Ehman RL, Fatemi M, Muthupillai R. Imaging elastic properties of tissue. In: Duck FA, Baker AC, Starritt HZ, editors. Ultrasound in Medicine. Bristol, England: Institute of Physics Publishing; 1998. pp. 263–277. [Google Scholar]
- 74.Silva GT, Chen S, Viana LP. Parametric amplification of the dynamic radiation force of acoustic waves in fluids. Phys. Rev. Letters. 2006;96 doi: 10.1103/PhysRevLett.96.234301. [DOI] [PubMed] [Google Scholar]
- 75.Malcolm AE, Reitich F, Yang J, Greenleaf JF, Fatemi M. A combined parabolic-integral equation approach to the acoustic simulation of vibro-acoustic imaging. Ultrasonics. 2008;48:553–558. doi: 10.1016/j.ultras.2008.04.006. [DOI] [PubMed] [Google Scholar]
- 76.Calle S, Remenieras JP, Bou Matar O, Patat F. Presence of nonlinear interference effects as a source of low frequency excitation force in vibro-acoustography. Ultrasonics. 2002;40:873–878. doi: 10.1016/s0041-624x(02)00229-9. [DOI] [PubMed] [Google Scholar]
- 77.Thuras AL, Jenkins RT, O'Neil HT. Extraneous frequencies generated in air carrying intense sound waves. J. Acoust. Soc. Am. 1935;6:173–180. [Google Scholar]
- 78.Malcolm AE, Reitich F, Yang J, Fatemi M, Greenleaf JF. Numerical modeling for assessment and design of ultrasound vibroacoustography systems. In: Fatemi M, Al-Jumaily A, editors. Biomedical Applications of Vibration and Acoustics in Imaging and Characterizations. New York: ASME Press; 2008. pp. 21–40. [Google Scholar]
- 79.Chen S, Fatemi M, Kinnick R, Greenleaf JF. Comparison of stress field forming methods for vibro-acoustography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2004;51:313–321. [PubMed] [Google Scholar]
- 80.Silva GT, Greenleaf JF, Fatemi M. Linear arrays for vibro-acoustography: a numerical simulation study. Ultrason. Imaging. 2004;26:1–17. doi: 10.1177/016173460402600101. [DOI] [PubMed] [Google Scholar]
- 81.Silva GT, Chen S, Frery AC, Greenleaf JF, Fatemi M. Stress field forming of sector array transducers for vibro-acoustography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2005;52:1943–1951. doi: 10.1109/tuffc.2005.1561663. [DOI] [PubMed] [Google Scholar]
- 82.Silva GT, Frery AC, Fatemi M. Image formation in vibro-acoustography with depth-of-field effects. Comput. Med. Imaging Graph. 2006;30:321–327. doi: 10.1016/j.compmedimag.2006.08.001. [DOI] [PubMed] [Google Scholar]
- 83.Heikkila J, Hynynen K. Investigation of optimal method for inducing harmonic motion in tissue using a linear ultrasound phased array--a simulation study. Ultrason Imaging. 2006;28:97–113. doi: 10.1177/016173460602800203. [DOI] [PubMed] [Google Scholar]
- 84.Silva GT, Urban MW, Fatemi M. Multifrequency radiation force of acoustic waves in fluids. Physica D: Nonlinear Phenomena. 2007;232:53. [Google Scholar]
- 85.Fatemi M, Wold LE, Alizad A, Greenleaf JF. Vibro-acoustic tissue mammography. IEEE Trans. Med. Imaging. 2002;21:1–8. doi: 10.1109/42.981229. [DOI] [PubMed] [Google Scholar]
- 86.Alizad A, Fatemi M, Wold LE, Greenleaf JF. Performance of vibro-acoustography in detecting microcalcifications in excised human breast tissue: a study of 74 tissue samples. IEEE Trans. Med. Imaging. 2004;23:307–312. doi: 10.1109/TMI.2004.824241. [DOI] [PubMed] [Google Scholar]
- 87.Alizad A, Whaley DH, Greenleaf JF, Fatemi M. Potential applications of vibro-acoustography in breast imaging. Technol. Cancer Res. Treat. 2005;4:151–158. doi: 10.1177/153303460500400204. [DOI] [PubMed] [Google Scholar]
- 88.Alizad A, Whaley DH, Greenleaf JF, Fatemi M. Critical issues in breast imaging by vibro-acoustography. Ultrasonics. 2006;44 Suppl 1:e217–e220. doi: 10.1016/j.ultras.2006.06.021. [DOI] [PubMed] [Google Scholar]
- 89.Hosseini HG, Alizad A, Fatemi M. Integration of vibro-acoustography imaging modality with the traditional mammography. Int. J. Biomed. Imaging. 2007;2007:40980. doi: 10.1155/2007/40980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Alizad A, Fatemi M. Breast vibro-acoustography. In: Hirsekon AW, editor. Emerging Technologies in Breast Imaging and Mammography. Stevenson Ranch, CA: American Scientific Publishers; 2005. pp. 197–205. [Google Scholar]
- 91.Mitri FG, Trompette P, Chapelon JY. Improving the use of vibro-acoustography for brachytherapy metal seed imaging: a feasibility study. IEEE Trans Med Imaging. 2004;23:1–6. doi: 10.1109/TMI.2003.819934. [DOI] [PubMed] [Google Scholar]
- 92.Mitri FG, Davis BJ, Urban MW, Alizad A, Greenleaf JF, Lischer GH, Wilson TM, Fatemi M. Vibro-acoustography imaging of permanent prostate brachytherapy seeds in an excised human prostate - Preliminary results and technical feasibility. Ultrasonics. 2009;49:389–394. doi: 10.1016/j.ultras.2008.10.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Mitri FG, Davis BJ, Greenleaf JF, Fatemi M. In vitro comparative study of vibro-acoustography versus pulse-echo ultrasound in imaging permanent prostate brachytherapy seeds. Ultrasonics. 2009;49:31–38. doi: 10.1016/j.ultras.2008.04.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Mitri FG, Davis BJ, Alizad A, Greenleaf JF, Wilson TM, Mynderse LA, Fatemi M. Prostate cryotherapy monitoring using vibroacoustography: preliminary results of an ex vivo study and technical feasibility. IEEE Trans. Biomed. Eng. 2008;55:2584–2592. doi: 10.1109/TBME.2008.2001284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Alizad A, Whaley DH, Greenleaf JF, Fatemi M. Image features in medical vibro-acoustography: In vitro and in vivo results. Ultrasonics. 2008;48:559–562. doi: 10.1016/j.ultras.2008.04.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Alizad A, Wold LE, Greenleaf JF, Fatemi M. Imaging mass lesions by vibro-acoustography: modeling and experiments. IEEE Trans. Med. Imaging. 2004;23:1087–1093. doi: 10.1109/TMI.2004.828674. [DOI] [PubMed] [Google Scholar]
- 97.Alizad A, Fatemi M, Whaley DH, Greenleaf JF. Application of vibro-acoustography for detection of calcified arteries in breast tissue. J. Ultrasound Med. 2004;23:267–273. doi: 10.7863/jum.2004.23.2.267. [DOI] [PubMed] [Google Scholar]
- 98.Pislaru C, Kantor B, Kinnick RR, Anderson JL, Aubry MC, Urban MW, Fatemi M, Greenleaf JF. In vivo vibroacoustography of large peripheral arteries. Invest. Radiol. 2008;43:243–252. doi: 10.1097/RLI.0b013e31816085fc. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Pislaru C, Greenleaf JF, Kantor B, Fatemi M. Vibro-acoustography of arteries. In: Suri J, editor. Atherosclerosis Disease Management. Berlin: Springer; 2010. [Google Scholar]
- 100.Calle S, Remenieras JP, Bou Matar O, Defontaine M, Patat F. Application of nonlinear phenomena induced by focused ultrasound to bone imaging. Ultrasound Med. Biol. 2003;29:465–472. doi: 10.1016/s0301-5629(02)00729-9. [DOI] [PubMed] [Google Scholar]
- 101.Alizad A, Walch M, Greenleaf JF, Fatemi M. Vibrational characteristics of bone fracture and fracture repair: application to excised rat femur. J. Biomech. Eng. 2006;128:300–308. doi: 10.1115/1.2187037. [DOI] [PubMed] [Google Scholar]
- 102.Konofagou E, Thierman J, Karjalainen T, Hynynen K. The temperature dependence of ultrasound-stimulated acoustic emission. Ultrasound Med. Biol. 2002;28:331–338. doi: 10.1016/s0301-5629(01)00525-7. [DOI] [PubMed] [Google Scholar]
- 103.Konofagou E, Thierman J, Hynynen K. The use of ultrasound-stimulated acoustic emission in the monitoring of modulus changes with temperature. Ultrasonics. 2003;41:337–345. doi: 10.1016/s0041-624x(03)00125-2. [DOI] [PubMed] [Google Scholar]
- 104.Chen S, Kinnick R, Greenleaf JF, Fatemi M. Difference frequency and its harmonic emitted by microbubbles under dual frequency excitation. Ultrasonics. 2006;44:e123–e126. doi: 10.1016/j.ultras.2006.07.009. [DOI] [PubMed] [Google Scholar]
- 105.Chen S, Kinnick RR, Greenleaf JF, Fatemi M. Harmonic vibro-acoustography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2007;54:1346–1351. doi: 10.1109/tuffc.2007.394. [DOI] [PubMed] [Google Scholar]
- 106.Chen S, Aquino W, Alizad A, Urban MW, Kinnick RR, Greenleaf JF, Fatemi M. Thermal safety of vibro-acoustography using a confocal transducer. Ultrasound Med. Biol. 2010;36 doi: 10.1016/j.ultrasmedbio.2009.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Brigham JC, Aquino W, Mitri FG, Greenleaf JF, Fatemi M. Inverse estimation of viscoelastic material properties for solids immersed in fluids using vibroacoustic techniques. J. Appl. Phys. 2007;101:14. [Google Scholar]
- 108.Aguilo MA, Aquino W, Brigham JC, Fatemi M. An inverse problem approach for elasticity imaging through vibroacoustics. IEEE Trans. Med. Imaging. 2010;29:1012–1021. doi: 10.1109/TMI.2009.2039225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Alizad A, Mitri FG, Kinnick RR, Greenleaf JF, Fatemi M. Vibro-acoustography of thyroid. Journal of the Acoustical Society of America. 2007:3026. [Google Scholar]
- 110.Alizad A, Mitri FG, Kinnick RR, Greenleaf JF, Fatemi M. Detection of thyroid nodules by a novel acoustic imaging method. International Congress of Ultrasound. 2009:35. [Google Scholar]
- 111.Mitri FG, Eberlein U, Fatemi M. Surface roughness imaging using the acoustic emission induced by the dynamic radiation force of ultrasound. Appl. Phys. Lett. 2006;88:3. [Google Scholar]
- 112.Mitri FG, Silva GT, Greenleaf JF, Fatemi M. Simultaneous sum-frequency and vibro-acoustography imaging for nondestructive evaluation and testing applications. J. Appl. Phys. 2007;102:7. [Google Scholar]
- 113.Mitri FG, Greenleaf JF, Fatemi M. Comparison of continuous-wave (CW) and tone-burst (TB) excitation modes in vibro-acoustography: Application for the non-destructive imaging of flaws. Appl. Acoust. 2009;70:333–336. [Google Scholar]
- 114.Mitri FG, Kinnick RR, Greenleaf JF, Fatemi M. Continuous-wave ultrasound reflectometry for surface roughness imaging applications. Ultrasonics. 2009;49:10–14. doi: 10.1016/j.ultras.2008.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Urban MW, Chalek C, Kinnick RR, Kinter TM, Haider B, Greenleaf JF, Thomenius K, Fatemi M. Implementation of vibro-acoustography on a clinical ultrasound system. IEEE Trans. Ultrasonics Ferrorelect. Freq. Control. 2011;58:1169–1181. doi: 10.1109/TUFFC.2011.1927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Mitri FG, Greenleaf JF, Fatemi M. Chirp imaging vibro-acoustography for removing the ultrasound standing wave artifact. IEEE Trans. Med. Imaging. 2005;24:1249–1255. doi: 10.1109/TMI.2005.854518. [DOI] [PubMed] [Google Scholar]
- 117.Urban MW, Alizad A, Fatemi M. Medical Imaging 2009: Ultrasonic Imaging and Signal Processing. Lake Buena Vista, FL, USA: 2009. Frequency compounding in multifrequency vibroacoustography; pp. 726511–726518. [Google Scholar]