A new perspective on transition states: χ₁ separatrix

Abstract

We present a new definition of the transition state for chemical reactions, named the χ₁ separatrix. In contrast to previous transition state definitions which depend on the choice of reaction coordinates, the χ₁ separatrix is defined by choosing a time scale for observation and is connected to exact rate constants in the high friction limit. We demonstrate that this separatrix appears in the isomerization of alanine dipeptide as a stationary population in quasi-equilibrium, without assuming a particular coordinate system or reactant and product surfaces.

INTRODUCTION

The fundamental assumption in the theory of simple chemical reactions is that a separation of time scales exists such that molecular states within the reactants (or products) transform between each other rapidly, while transformations between the reactant and product states occur at the much slower reaction rate. For classical systems, the source of this separation of time scales arises strictly from the dynamics of the system, determined by the complete Hamiltonian; however, it can be largely understood in terms of the existence of a transition state, or separatrix dividing the system's conformational space into reactant and product states.

The explicit definition of the transition state separatrix is prerequisite to elucidating the relation between the transition state and reaction rate, and for designing methods to locate the transition state. It is important to stress that implicit in all transition state definitions is the assumption that there is a separation of time scales so that a single reaction rate constant is appropriate to describe the transition. Modern definitions of the transition state have origins in the classical transition state theory (TST).¹ In TST, it is assumed there are two low energy regions in configuration space, corresponding to the reactant and product states; the transition state is then defined as the saddle point along the minimum energy path connecting the two low energy regions. By assuming trajectories crossing the transition state do not recross, a close upper bound to the reaction rate could then be determined from the equilibrium flux through a surface crossing the energetic saddle point and normal to the unstable directions in the energy surface.

Although the classical transition state was well defined and proved adequate for many simple chemical reactions, the upper bound for the rate can be significantly improved by selecting a surface with minimal equilibrium flux. In theory, there exists a best dividing surface separating preselected reactant and product configurations independent of any choice of reaction coordinates.^{2, 3} In practice, one chooses the best dividing surface from among a set parametrized by a reaction coordinate. Theories based on this idea are known collectively as variational transition state theories (VTSTs).^{4, 5} In VTSTs, one identifies the reactants and products as the low free energy regions in the reaction coordinate, and the transition state with the fixed value of the coordinate between the reactant and product maximizing the free energy.

The success of VTSTs depends strongly on a priori knowledge of a “good” reaction coordinate, but VTSTs generally do not propose a means for defining a good coordinate. However, when a good definition of reactant and product volumes are known, one can define an ideal coordinate describing the motion between the surfaces as the splitting probability for a trajectory initiated from a particular configuration in the full configuration space to reach either the reactant or product surface first.^{6, 7, 8} Each probability to reach the product surface first defines an iso-committor surface corresponding to all the configurations with same probability. In the proper context, the iso-committor coordinate can be connected to exact rates between preselected configuration volumes.⁶ A new definition for the transition state can be given by the equi-committor surface, defined by the configuration of points which have equal splitting probabilities.^{8, 9, 10} It is important to note that the rate obtained by considering the equi-committor surface as the dividing surface is not necessarily the rate provided by the iso-committor approach with the theoretical scaffold of transition path theory. A method based on time-series analysis has been proposed that is equivalent to iso-committor transition state but cheaper in computational cost.^{11, 12} It is expected that a good definition of the VTST transition state will comprise states with nearly equal splitting probabilities.^{8, 9, 10} The definition of the transition state as the equi-committor has received criticism due to the fact that it does not necessarily locate the peak in the free energy when there are intermediates in the reaction.¹³ Additionally, we find that identifying reactant and product surfaces as free energy minima in one coordinate system does not lead to nearly equal splitting probabilities on the equi-committor in another coordinate system (as discussed in detail below).

In the following, we propose an alternative definition of the transition state, named the “χ₁ separatrix,” dependent only on the dynamics in the relaxation to equilibrium on a given time scale; this definition does not involve any a priori choice of reaction coordinate nor the identification of ansatz reactant and product surfaces. The techniques used here to locate the χ₁ separatrix are computationally expensive; our present intention is only to express the soundness of this idea, and in the future, more efficient techniques for its location will be explored.

We find that this definition of transition state is exactly related to the relaxation rate of the reaction in the high friction limit. To describe the χ₁ separatrix, we first present the theoretical basis of our approach, we demonstrate a set of properties that make it a good transition state, and then apply it to locate the transition state in a test system, the isomerization dynamics of all-atom alanine dipeptide in vacuum. We postulate that the χ₁ separatrix is a necessary dividing surface for “good” reactant and product volumes for iso-committor coordinates.

DEFINITION OF THE χ₁ SEPARATRIX

In systems with a separation of time scales, we define the χ₁ separatrix as the ensemble of system's configurations on which the first non-trivial eigenfunction of the Fokker-Planck operator is zero. In practice, this means that the time dependent population on this surface is static after the reactant and product have reached quasi-equilibrium. The theoretical justification for this definition is provided in the rest of this section.

We focus on systems described by the coordinates {q} and associated momenta {p}, with Hamiltonian $\mathcal{H}(q,p)$, and for which the dynamics at a given temperature T are governed by the Langevin equation,

$$\begin{array}{ccc}\hfill \frac{\partial q}{\partial t}& =& \frac{\partial \mathcal{H}}{\partial p}\hfill \\ \hfill \frac{\partial p}{\partial t}& =& -\frac{\partial \mathcal{H}}{\partial q}-\gamma p+\sqrt{2T\gamma }\eta \left(t\right),\hfill \end{array}$$ (1)

that is, we consider reactions where quantum effects are not relevant (as usually assumed in macromolecular dynamics). In Eq. 1, we have set the Boltzmann constant k_B = 1, γ is the friction constant, η(t) is a Gaussian white noise with unit variance, and t is the time variable. In the high friction, thermodynamic limit of identical such systems, the evolution of the population distribution, P(q, t) is governed by the Fokker-Planck equation (FPE),¹⁴

$$\frac{\partial P}{\partial t}=-{\mathbf{H}}_{\mathrm{FP}}P,$$ (2)

where the Fokker-Planck operator is

$${\mathbf{H}}_{\mathrm{FP}}=\frac{\partial }{\partial q}\left(T\frac{\partial }{\partial q}+\frac{\partial \mathcal{H}}{\partial q}\right).$$ (3)

Because the Fokker-Planck operator is Hermitizable, it has bi-orthogonal eigenfunctions satisfying

$${\mathbf{H}}_{\mathrm{FP}}{\psi }_i={\lambda }_i{\psi }_i$$ (4)

and

$$\int e^{E\beta }{\psi }_i{\psi }_j\mathrm{d}V={\delta }_{ij},$$ (5)

where E is the potential energy, β is the inverse temperature, and the integral is over the whole configuration space.

In terms of the Fokker-Planck eigenfunctions, the time dependent population density can be written as

$$P(q,t)=\sum _i{c}_i{\psi }_i\left(q\right)e^{-{\lambda }_{i}t},$$ (6)

where the expansion coefficients are determined by the initial conditions by

$$c_i=\int e^{\beta E}{\psi }_i\left(q\right)P(q,0)\mathrm{d}V.$$ (7)

We assume that the system is closed, so that trajectories remain in the relevant configuration space. This assumption is tantamount to the condition P(q, t) → 0 and e^−βE∇(e^βEP(q, t)) → 0 at the boundary of the configuration space. Under these conditions, the Fokker-Planck operator has an eigenspectrum of non-negative eigenvalues λ_i with λ₀ = 0 < λ₁ ⩽ λ₂ ⩽ …, and corresponding eigenfunctions ψ_i(q). In particular, there is a unique eigenfunction with eigenvalue λ₀ = 0, proportional to the Boltzmann distribution: ψ₀∝e^−βE. All other eigenfunctions satisfy ∫ψ_i dV = 0. For convenience, we choose to normalize ψ₀ such that ∫P(q, t) dV = 1, resulting in ${\psi }_0=e^{-\beta E}/\sqrt{Z}$, where Z is the canonical partition function. In the following, we denote the smallest non-zero eigenvalue as λ₁, and ψ₁ its corresponding eigenfunction.

For systems with a separation of time scales, where one slow process dominates the reaction, there exists a unique eigenfunction with eigenvalue λ₁; for these systems we define the χ₁transition state as the separatrix in configuration space where ψ₁(q) = 0. We show in Sec. 3 that this surface possesses a set of properties that make it a good transition state separatrix.

We note that this definition of the transition state depends only on assumptions common to all systems governed by the Langevin equation in the high friction limit, with no additional assumptions about reaction coordinates or a priori descriptions of reactant and product states. The transition state emerges directly from the Hamiltonian of the system.

There are (multiple) roots to the eigenfunctions with eigenvalues λ_i > λ₁, and we could refer to them as χ₂, χ₃, etc. separatrices. These separatrices become relevant when, for instance, there is a long lived intermediate (λ₂ ≈ λ₁). In that case, it no longer makes sense to speak about a phenomenological reaction rate,¹⁵ and it would become necessary to incorporate the χ₂ separatrices into our description of the reaction and reaction rate calculations. For example, in the case of an intermediate, we expect that there are two χ₂ separatrices dividing the intermediate state from the reactant and product. This problem is not particular to the χ₁ separatrix, but rather in the appropriateness of describing the time dependence of a reaction by a single rate constant calculated by any theory. Although we require a separation of time scales (λ₂ ≫ λ₁) in order for the χ₁ separatrix to be related to the reaction rate of the system, this assumption is not unique to this theory and is in fact implicitly assumed when using classical transition states to calculate a reaction rate. At present, there are no practical methods for making certain a priori that a separation of time scales exists. In order to verify the existence of a separation of time scales, one must observe the dynamics of the system explicitly, or simply assume only two dominant basins exist (as in VTST). In Appendix D, we express the breakdown of the separation of time scales analytically through Fokker-Planck eigenfunctions in the context of the reactive flux method. When multiple time scales are relevant to a reaction, the χ₁ separatrix will correspond to the slowest time scale.

Higher order separatrices also play a subtle role in our assumption that the system under consideration is closed. That is, we assumed that no trajectories escape the relevant volume of configuration space during the time scale of observation. In fact, in our observation of the c₇ to c₅ isomerization of alanine dipeptide presented below, we assume that the reaction is closed to trajectories exiting to other regions of the conformational space (such as the C_ax and D-amino isomers, that can be populated on much longer time scales¹⁶). As a consequence, the observed separatrix could be considered a χ₂ or χ₃ separatrix. The ability to observe the c₇ to c₅ isomerization as if it was a χ₁ separatrix emphasizes the robustness of this perspective in terms of its ability to characterize transition states for succeeding steps in a reaction.

PROPERTIES OF THE χ₁ SEPARATRIX

The physical interpretation of the first non-zero eigenfunction when λ₁ ≪ λ₂ can be made clear by expressing the time evolution of the population density (Eq. 6) on a time scale t ≫ 1/λ₂,

$$P(q,t)\approx \frac{{\psi }_0}{\sqrt{Z}}+c_1{e}^{-{\lambda }_{1}t}{\psi }_1\left(q\right).$$ (8)

We note that this expression of the time dependent population distribution (valid for any initial state) describes the population around each point q as monotonically approaching the Boltzmann equilibrium distribution by transferring population from regions initially in excess (c₁ψ₁(q) > 0) to regions where initially deficient (c₁ψ₁(q) < 0). Therefore, when there is a separation of time scales (λ₁ ≪ λ₂), the surface ψ₁(q) = 0 provides a natural classification of microstates as reactants or products according to whether (after a short local relaxation time ≃ 1/λ₂) their time dependent populations monotonically increase or decrease. This classification of microstates as reactants or products is one of the several properties that makes the χ₁ separatrix an intuitive and robust definition of the transition state. We use this property to find an initial approximation of the separatrix below.

Additional properties of χ₁ separatrix that we demonstrate and use in this article are the following:

• An initial population distribution on the separatrix relaxes to chemical equilibrium on the fast molecular relaxation time (≈1/λ₂).

• The escape rate from either reactants or products to this separatrix are equal to each other and to the relaxation rate for the reaction in the high friction limit.

• It is the surface of maximum net flux when the reactants and products have reached quasi-equilibrium.

• It is close to the least successfully crossed separatrix and optimum dividing surface for the reactive flux method of computing relaxation rates.

The last two properties provide further support for the conception of the χ₁ separatrix as an ideal dividing surface separating reactants and products in a simple reaction; as well as provide explicit objectives for making use of and refining the separatrix. We demonstrate these properties analytically in the Appendix.

The first two properties listed above (on the fast relaxation behavior and escape rate) are easily explained. The fast relaxation behavior follows simply from calculation of the first coefficient in Eq. 7; any distribution initially overlapping ψ₁ only on its root will have c₁ = 0, and rapidly yield a population approximating equilibrium (see Eq. 8). In the following, we make use of the fast relaxation property to refine the location of the separatrix (as detailed in the Appendix).

The escape rate property follows from Courant nodal theorem¹⁷ when we solve the FPE with absorbing boundary conditions on the χ₁ separatrix. Because ψ₁ satisfies the FPE and the boundary conditions and has no root on the domain, Courant's theorem guarantees that it is the solution associated with the smallest non-zero eigenvalue. It follows that this eigenvalue is the asymptotic rate of decay of a population absorbed at the χ₁ separatrix.

From another perspective, the usefulness of characterizing metastable states in terms of eigenfunctions of a diffusion operator has been exploited before in Perron cluster cluster analysis (PCCA).¹⁸ In PCCA, a transition matrix is derived from transition probabilities between microstates observed from a long simulation; the eigenfunctions of the matrix are then used to decompose the state space into metastable states. For a two-state reaction, PCCA characterizes metastable states divided by the root of the first eigenfunction of the transition matrix. However, because of numerical instability in this approach, modern methods in the same vein have focused on different but nearby separatrices.^{19, 20} In this work, the refined procedure for locating the surface corresponding to the root of the eigenfunction of the FPE is stable and precise as is evident from the precision of the rate calculations presented below.

Relation to the iso-committor coordinate

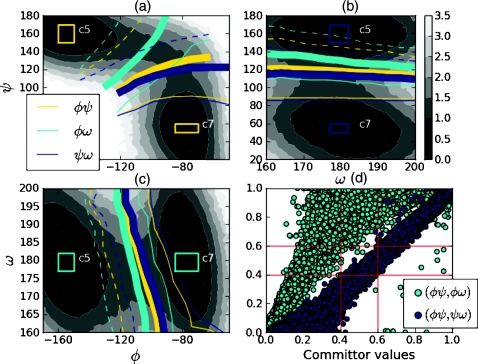
The iso-committor coordinate is known to be an ideal coordinate for describing the transition between two predefined reactant and product volumes.^{6, 8, 16, 21} However, an iso-committor coordinate can be defined for any choice of reactant and product volumes, and the freedom in choosing these volumes means that the iso-committor coordinate is not necessarily constrained to describe the simple reaction determined by the Hamiltonian itself. Indeed, in the discussion presented below, in the context of the isomerization of alanine dipeptide we find that different definitions of the iso-committor reactant and product surfaces lead to markedly different descriptions of the transition in the c₇ to c₅ isomerization reaction (see Fig. 3).

Figure 3.

Selected contours of the average iso-committor probabilities in three coordinate systems: (a) (ϕ, ψ); (b) (ω, ψ); (c) (ϕ, ω) with the free energy contours in intervals of 0.5 kT depicted in gray scale. The average iso-committor contours displayed are 0.1 (dashed), 0.5 (thick), and 0.9 (thin). The correlation between iso-committor probabilities obtained with different definition of reactants and products is reported in (d). The correlation plot shows that the different iso-committor probabilities strongly disagree about the location of the equi-committor. In the worst case, the ϕψ and ϕω equi-committor surfaces do not overlap at all. Definitions of reactants and products in each coordinate system are represented as rectangles. 3% of equilibrium population in the c₅ iso-committor reactant rectangle in the (ϕ, ω) coordinates, and 1% of the ψω c₇ iso-committor rectangle, is separated by the χ₁ separatrix. The ϕψ iso-committor rectangles do not cross the χ₁ separatrix.

A principal advantage of using the χ₁ separatrix as the dividing surface defining the reactant and product volumes of configurations space is the freedom from the requirement of a priori identification of the volumes; the χ₁ separatrix provides a definition of these volumes dependent only on the Hamiltonian of the system.

To be clear, it is necessary to explicitly distinguish iso-committor reactant and product surfaces from the reactant and product volumes defined by the χ₁ separatrix. The distinction we need to emphasize is that the iso-committor reactant and product surfaces do not intersect one another, and together do not comprise all of configuration space. The reason for this is that the iso-committor coordinate would be undefined in the intersection of the two volumes and can only take on values other than 1.0 and 0.0 in the complement of their union. Furthermore, the iso-committor reactant and product surfaces are usually determined on the base of a priori knowledge on the system. In contrast, the reactant and product volumes defined by the χ₁ separatrix share a single boundary and are defined directly by the FPE.

We posit that the χ₁ separatrix is a necessary dividing surface between iso-committor reactant and product surfaces in order for the iso-committor coordinate to be relevant to the description of the reaction. That is, good iso-committor reactant and product volumes should be constrained to be volumes with low free energy which are subsets of the volumes separated by the χ₁ separatrix. The possibility of using eigenfunctions of a diffusion operator for the automatic definition of good iso-committor reactant and product surfaces has been suggested before,⁷ but to our knowledge has not been formally developed.

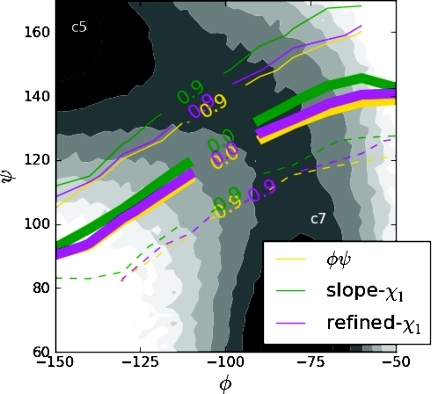
When the iso-committor reactant and product volumes are constrained to be separated by the χ₁ separatrix, the fast relaxation property of the χ₁ separatrix (noted above) implies that the χ₁ separatrix and the equi-committor separatrix are effectively identical when the equilibrium probability to be in the respective basins are equal (for instance, at the transition temperature, or in a symmetric system). Indeed, in the c₇ to c₅ isomerization reaction in the alanine dipeptide model discussed in Sec. 4, we show that the equilibrium probability to be in the respective basins are nearly equal at room temperature, and the equi-committor surface and χ₁ separatrix are very close (see Fig. 2).

Figure 2.

Two approximations to the χ₁ separatrix, and the equi-committor separatrix for the isomerization reaction of alanine dipeptide, for iso-committor reactant and product surfaces defined in (ϕ, ψ) as depicted in Fig. 3. The free energy contours in intervals of 0.5 kT depicted in gray scale in (ϕ, ψ) obtained from equilibrium simulations are shown as a reference. The dividing surfaces are obtained in the full configuration space and projected into the (ϕ, ψ) coordinate system as selected contours of the average class (the class of a reactant or product sample is −1 or 1, respectively).

When the χ₁ separatrix and the equi-committor separatrix are the same ensemble, this allows us to extend the physical properties of the χ₁ separatrix to explain the physical meaning of the equi-committor separatrix when it is not correlated with the peak free energy along good structural coordinates.¹³

When there are important intermediates, a good description of the reaction requires multiple time scales,

$$\Psi (q,t)\approx \frac{{\psi }_0}{\sqrt{Z}}+c_1{e}^{-{\lambda }_{1}t}{\psi }_1\left(q\right)+c_2{e}^{-{\lambda }_{2}t}{\psi }_2\left(q\right).$$ (9)

In this case, the escape over the intermediate barrier is related to the intermediate time scale (t ≃ 1/λ₂), while the equi-committor separatrix indicates the ideal separatrix for describing the entire intermediate as being responsible for the longer relaxation time, 1/λ₁, between the reactant and product basins.

APPLICATION TO A SIMPLE SYSTEM

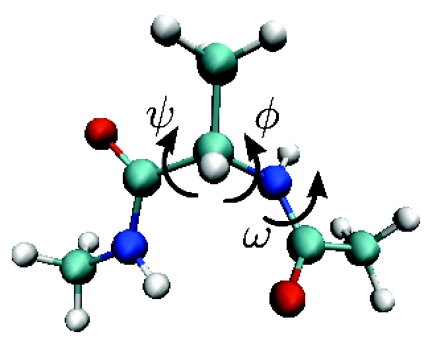
In the following, we provide an example of the practical application of the theory presented above to the characterization of the transition state and reaction rate for the well studied process of isomerization of alanine dipeptide. This system is a typical testbed for new methods in molecular dynamics problems.^{9, 16, 22} Alanine dipeptide consists in a single alanine amino acid with acetylated and methylated peptide bonds, with 22 atoms in total. Because of its small size, it is computationally feasible to sample its conformational space extensively. Additionally, the peptide backbone angles ϕ and ψ (when used together) are well known to be good coordinates, giving an effective “overhead” view of all of the relevant dynamics in only two dimensions.⁹ For comparison, we demonstrate the appearance and effect on the equi-committor separatrices developed from “bad” coordinates by combining ϕ and ψ individually with the backbone dihedral angle ω₁ (see Fig. 1). With this additional dihedral angle, we can define three different coordinate systems in which to observe the reaction: (ϕ, ψ), (ϕ, ω₁), and (ψ, ω₁). To further orient ourselves and give a benchmark for comparison, we use each of the coordinate systems to construct iso-committor coordinates and their associated equi-committor separatrices.

Figure 1.

Molecular structure of alanine dipeptide. The configuration space of the c₇ to c₅ isomerization reaction is well described by torsion of the backbone dihedral angles ϕ and ψ indicated in the figure. The additional dihedral angle ω₁ is a poor descriptor of the reaction.

Throughout the following, our goal is to describe the reaction with minimal a priori information about it; we assume only that we have an initial configuration located within the system and that there is an isolated, simple reaction on a short time scale. Although “good” coordinates are well known for this system, we refrain from using them except as a posteriori presentation of our data.

Our simulations were performed by running multiple molecular dynamics trajectories with the AMBER03 force field in vacuum. With this choice of force-field, there are three main ensembles of configurations that are populated with high probabilities and are separated by free energy barriers, these are the c₇ , c₅ , and C_ax isomers (The c₇ and c₅ isomers are also known as $C_{7\mathrm{eq}}$ and $C_{7\mathrm{eq}}^{\prime }$).^{9, 16, 22} The barrier separating the c₇ and c₅ isomers is sufficiently high that the c₇ to c₅ isomerization can be considered isolated from the C_ax minimum on the short time scales we simulate. The effective isolation from the C_ax minima allows us to observe the χ₁ separatrix separating the c₇ and c₅ isomers.

Observation of the χ₁ separatrix

A useful property of the χ₁ separatrix is its static population density in the relaxation of an out of equilibrium population (see Eq. 8). This property is observable macroscopically in the sense that it does not depend on the identity of specific trajectories in an ensemble; we are concerned only on the average number of trajectories expected in a specific volume at a given time. Here, we use this property to locate an approximation of the χ₁ separatrix in the alanine dipeptide c₇ to c₅ isomerization with minimal domain specific knowledge.

In practice, we simulate a large ensemble of short trajectories, starting from a Dirac delta distribution, and measure the time dependent changes in the population within a small radius ($0.3$ Å) around a set of test centers in the configuration space. Although this process is computationally intensive, it is trivially parallelizable, and demonstrates the existence of the separatrix directly.

We then classify each test center as being either a reactant or product according to whether, after the short local relaxation time, the slope of the time dependent population within the small least root mean square deviation (RMSD) radius around the test center during a short time interval is positive or negative.

Although we are interested only in one way transition probabilities to specific microstates, and we are not forming a matrix, this method is similar in spirit to the method used to compute an approximation to the components of the microstate transition matrix discussed in Ref. 19.

The slope of the time dependent population is determined by performing a linear fit to the population within the RMSD-ball on a time scale Δt. A linear fit for the population decay is justified after the fast molecular relaxation time when Δt ≪ 1/λ₁. When this is the case, the quasi-equilibrium population in Eq. 8 within a small RMSD-ball around the configuration x_i can be approximated by

$$\begin{array}{cc}\hfill P(x_i,t)& {\displaystyle \approx A\left(x_i\right)+B\left(x_i\right)t,\text{when}\frac{1}{{\lambda }_2}\ll t\ll \frac{1}{{\lambda }_1}.}\end{array}$$ (10)

Here, B(x_i)∝c₁ψ₁(x_i) (from the first order expansion in time of Eq. 8), thus the slope B(x_i) changes sign on the same surface as ψ₁(x_i). The surface dividing centers with slopes of opposite signs then provides us with an approximation of the χ₁ separatrix. The result is shown in Fig. 2 (green curve, indicated as “slope-χ₁” in the figure). Details on the procedure are provided in the Appendix.

Additionally, we can make use of the fast relaxation property of the χ₁ separatrix to develop a more precise characterization. The fast relaxation property tells us that when a trajectory is initiated on the χ₁ separatrix, the probability to find it in some volume after the fast relaxation time is the equilibrium probability to be in that volume (see Eq. 8). We locate a refined χ₁ separatrix by using this property in two ways, first we use the observed separatrix to learn the equilibrium distribution between the two c₇ /c₅ states of alanine dipeptide. We then refine the separatrix by considering the configurations which relax to the equilibrium distribution on the fast relaxation time scale (≃ 1/λ₂). The details of the procedure are described in the Appendix.

The resulting refined separatrix is plotted in Fig. 2 (purple curve, indicated as “refined-χ₁” in the figure), where it is projected into the (ϕ, ψ) coordinates and compared to the location of the separatrix before the refinement (green curve, indicated as “slope-χ₁” in the figure), and to the equi-committor separatrix (yellow curve, labeled as “ϕ ψ” in the figure) obtained by defining the reactants and products in the (ϕ, ψ) coordinate system (see discussion below).

Sensitivity of equi-committor surface to a priori assumptions

To our knowledge, there are no published discussions on the sensitivity of equi-committor transition state to the a priori choice of coordinates used to identify the reactant and product states. When studying the equi-committor, researchers have always focused on values calculated with respect to a single definition of the reactant and product states, with no attention given to alternative choices, or justification why their particular choice was prudent.^{8, 16, 21} We show in the following that alternative and ostensibly reasonable choices for the reactant and product states lead to markedly different iso-committor coordinates and transition states, at least for the c₇ -c₅ transition of the alanine dipeptide system considered in this study.

The approach generally used for a given chemical reaction is the following: the equilibrium population distribution is projected onto some a priori chosen coordinates (z₁, …, z_n), and a rectangular box (in z) is defined surrounding the local probability maxima where the reactant and product states are presumed to be.^{8, 10, 22} For example, in the seminal paper introducing the iso-committor approach in protein folding, p-fold,⁸ Du et al. chose as coordinates for a protein folding reaction the fraction of native contacts, Q, and total number of contacts, K, with values near the observed free energy minima obtained with these coordinates as the definition of the reactant and product. In studies of alanine dipeptide, a priori coordinates used to identify the reactant and product states are typically the peptide dihedral angles, ϕ and ψ, and reactants and products are rectangular boxes in ϕ and ψ around well known isomers.^{16, 21, 22} The chosen coordinates in these cases are well known as good coordinates for the system.

To study the effect of coordinate choice on the equi-committor surface in alanine dipeptide, we calculated the equi-committor using an intuitive definition for reactants and products in the different sets of coordinate systems presented above, that is, formed by the following different combinations of the dihedral angles: (ϕ, ω₁), (ψ, ω₁), and (ϕ, ψ). These three different choices of coordinates lead to three markedly different equi-committor transition states; for brevity, we shall refer to the distinct transition states as the “ϕψ,” “ϕω₁,” and “ψω₁”-transition states.

The free energy in each of the coordinate systems, along with indications of our choice of reactant and product states, are shown in Fig. 3. Each of the depicted coordinate systems shows two distinct free energy basins states separated by a barrier. In each coordinate system, we define a configuration of alanine dipeptide to be a reactant when the two relevant angles were in the intersection of 150° < ψ < 170°, −160° < ϕ < −150° and 177° < ω₁ < 182°. Similarly, we define the configuration of alanine dipeptide to be a product when the two relevant angles were in the intersection of 50° < ψ < 60°, −85° < ϕ < −70°, and 177° < ω₁ < 182°. The reactant and product states so defined are indicated as rectangles in the free energy profiles in Fig. 3. The comparison of the ϕψ-transition state with the χ₁ separatrix is shown in Fig. 2.

We measured the value of the iso-committor probability for each of the configurations used as centers for the observation of the χ₁ separatrix described above. The commitment probability was taken as the fraction of trajectories which reached the product surface first in 500 simulations. The results are presented in Fig. 3. The contours represent the approximation in the collective coordinates of the equi-committor separatrix, and its reactants and products, obtained by taking the average value of the iso-committor probability in each point of the collective coordinate system.

An important result emerging from Fig. 3 is that each choice of coordinate system leads to different identifications of the equi-committor surface. In the worst case, there is effectively no overlap between the equi-committor surfaces involving ψ and the other equi-committor surface. In each case, the equi-committor successfully identifies the free energy saddle point in the coordinate system in which the reactants and products are defined.

One way to understand the sensitivity of the equi-committor to the choice of reactants and products in the alanine dipeptide test case shown in Fig. 3 is that the common procedure of choosing reactant and product volumes as rectangles with low free energy can lead to bad choices for the reactant and product volumes. We expect that the location of the equi-committor would be nearly independent of the choice of reactant and product volumes as long as “good” reactant and product volumes are used; however, we are not aware of any formal requisites or methods for choosing good ones. We postulate that requiring the reactant and product volumes to be separated by the χ₁ separatrix would lead to good choices; however, full exploration of this idea is beyond the scope of this paper.

Calculation of relaxation rates

As discussed above, the χ₁ separatrix is directly related to exact reaction rates through escape rates from the reactant and product basins to the separatrix. With an ideal coordinate connecting the reactant basins to the separatrix, the conditions for the escape are identical to those in Kramer's escape formula.²³ However, use of Kramer's approximation for the escape rate requires the introduction of an effective one-dimensional coordinate and an error independent of the theory presented here. To demonstrate the relation between escape rates and relaxation rates, we simulated the escaping trajectories directly. For comparison, we measured the escape rate to each of the equi-committor separatrices in addition to the observed and refined χ₁ separatrices. The results show the unique property of identical escape rates to the χ₁ separatrix in both directions.

In practice, the rates are measured as follows. Starting with a configuration in each basin we simulated 200 000 trajectories initiated from a single configuration for a time interval of $\left(2{\mathrm{ps}}^2\right)\gamma$ (where γ is the friction constant),²⁴ noting the time at which each trajectory first crosses each separatrix. We measured the relaxation and escape rates for each separatrix by fitting a function of the form Ae^−Et + B to the population within the initial basin, and the population which had not yet crossed the respective separatrices at time t. We report the exponents, E, as the rate in Table 1. Although the escape rate converged quickly, a large number of trajectories and long simulation interval was necessary to obtain converged results for the relaxation rate.

Table 1.

Relaxation rate and the escape rates for each separatrix and a range of friction constants.

		Friction1
		5	10	20	40
Separatrix	Direction2	Ratec
ψω	Forward	12.63 ± 0.09	9.69 ± 0.26	6.48 ± 0.10	3.80 ± 0.12
	Reverse	9.44 ± 0.16	7.05 ± 0.06	4.58 ± 0.02	2.63 ± 0.01
ϕψ	Forward	11.65 ± 0.05	8.68 ± 0.13	5.66 ± 0.01	3.26 ± 0.07
	Reverse	10.51 ± 0.15	8.02 ± 0.13	5.25 ± 0.03	3.04 ± 0.03
Refined-χ1	Forward	11.47 ± 0.03	8.56 ± 0.10	5.52 ± 0.02	3.18 ± 0.07
	Reverse	10.85 ± 0.16	8.28 ± 0.16	5.44 ± 0.05	3.10 ± 0.05
Slope-χ1	Forward	11.16 ± 0.04	8.16 ± 0.10	5.20 ± 0.04	2.96 ± 0.08
	Reverse	11.99 ± 0.35	9.30 ± 0.30	6.23 ± 0.12	3.66 ± 0.07
ϕω	Forward	9.85 ± 0.26	6.72 ± 0.03	4.15 ± 0.08	2.30 ± 0.00
	Reverse	16.75 ± 0.25	13.34 ± 0.25	9.18 ± 0.06	5.48 ± 0.05
λ1	Forward	17.62 ± 0.47	10.96 ± 0.44	6.35 ± 0.10	3.25 ± 0.09
	Reverse	16.65 ± 0.86	11.04 ± 0.80	5.75 ± 0.36	3.12 ± 0.08

¹Friction constants are provided in units of  ps⁻¹.

²The forward direction is the c₇ –c₅ transition.

³Rates are provided in units of 10⁻² ps⁻¹.

Note: The refined χ₁ separatrix shows the closest agreement in the forward and reverse escape rates for all friction constants, and an escape rate nearly the relaxation rate in the high friction limit.

For the measurement of the escape rate in the c₇ to c₅ direction, we used the same starting configuration from the Dirac delta relaxation simulated to locate the χ₁ separatrix. For the reverse c₅ to c₇ escape rates, we chose the center with the largest time slope from the histograms used to observe the separatrix.

In order to evaluate the robustness of the high friction limit approximation (that is implied in the FPE), three sets of simulations were performed with different values of the friction constant ($5.0{\mathrm{ps}}^{-1}$, $10.0{\mathrm{ps}}^{-1}$, $20.0{\mathrm{ps}}^{-1}$, and $40.0{\mathrm{ps}}^{-1}$). By comparing the results obtained with different values of the friction constant, we observe that the friction constant typically used in molecular dynamics simulations (around $5{\mathrm{ps}}^{-1}$) is not large enough to give an escape rate exactly equal to the relaxation rate. The reason for the difference between the relaxation rate and the escape rate to the χ₁ separatrix with moderate friction is that in this case trajectories crossing are more likely to continue to the alternate basin than they would in the high friction limit, leading to a comparably higher relaxation rate. To demonstrate that indeed the rates converge in the high friction limit, we ran escape simulations for increasing values of the friction constant. Indeed, the results reported in Table 1 show a convergence between the χ₁ escape rates and the relaxation rate for the reaction. For low to moderate friction, we expect that a generalization of χ₁ separatrix to the eigenfunctions of the Kramer's equation (rather than the FPE) would eliminate the dependence on the friction; however, development of a computationally feasible method to observe the full phase space separatrix is beyond the scope of this paper.

CONCLUSIONS

We have presented a definition of the transition state that does not require a priori knowledge of a good coordinate system for its location or existence. We have demonstrated that the χ₁ separatrix is a useful and intuitive definition of the transition state for simple chemical reactions. In order to illustrate the validity of the theory of the χ₁ separatrix in its simplest form, we have used a brute force approach for its observation. Although this direct approach used to observe the separatrix is computationally intensive and is impractical for exact identification of the χ₁ separatrix in very long time scale problems, it is clear that other more efficient approaches can be used to locate the χ₁ separatrix. For instance, when used in conjunction with a priori information about the reaction, our refined approach locates the separatrix accurately using a relatively small number of short trajectories. We expect this approach can be made even more efficient when combined with other techniques; in particular, it has been shown that the equi-committor separatrix can be described in terms of the Fokker-Planck equation,⁷ and many of the tools developed for equi-committor calculations^{16, 25} should be portable to the problem of locating the χ₁ separatrix. Finally, it is worth mentioning that super-symmetric methods^{26, 27, 28} could be used, which allow the simulation of dynamics which anneal to regions of high net current at the same rate that regular molecular dynamics relaxes to the equilibrium population. As we demonstrate in the Appendix, the surface of maximum net current in quasi-equilibrium is the χ₁ separatrix.

APPENDIX A: χ₁ SEPARATRIX AS THE SURFACE OF MAXIMUM FLUX

At equilibrium, the net current through any surface is zero. When reactants and products have reached quasi-equilibrium, there is negligible net current within the basins, but a steady reactive current in the space dividing them. Here, we show that the separatrix through which the net current is maximized in quasi-equilibrium is the χ₁ separatrix.

When the reactants and products have reached quasi-equilibrium, the population density can be described by Eq. 8. For any separatrix χ which can be described by a smooth function D(x) such that D(x) = 0 only on the separatrix, we indicate the enclosed volume (in the direction of ∇D(x)) as |∂χ|. Then, indicating the current at position x as J(x), the separatrix χ with maximum net flux is

$$\begin{array}{cc}\hfill {\mathrm{maxarg}}_{\chi }\left|{\int }_{\partial \chi }\mathbf{J}\left(\mathbf{x}\right)·\mathrm{d}\sigma \right|& ={\mathrm{maxarg}}_{\chi }\left|{\displaystyle {\int }_{\left|\partial \chi \right|}\nabla ·\mathbf{J}\left(\mathbf{x}\right)\mathrm{d}V}\right|\end{array}$$ (A1)

by the divergence theorem. From the continuity equation, in the quasi-equilibrium 1/λ₂ ≪ t, the maximizing surface is

$$={\mathrm{maxarg}}_{\chi }\left|{\displaystyle {\int }_{\left|\partial \chi \right|}\frac{\partial P}{\partial t}\mathrm{d}V}\right|$$ (A2)

$$\begin{array}{cc}& \simeq {\mathrm{maxarg}}_{\chi }\left|{\displaystyle {\int }_{\left|\partial \chi \right|}{c}_1{\psi }_1\left(x\right)\frac{\partial e^{-{\lambda }_{1}t}}{\partial t}\mathrm{d}V}\right|.\end{array}$$ (A3)

The constants c₁ and λ₁ are independent of the dividing surface and may be taken outside the integral. Without loss of generality, we assume c₁ < 0, since it depends only on the Hamiltonian and initial distribution, and is independent of the dividing surface. With this assumption,

$$\begin{array}{cc}\hfill {\mathrm{maxarg}}_{\chi }\left|{\int }_{\partial \chi }\mathbf{J}\left(\mathbf{x}\right)·\mathrm{d}\sigma \right|& ={\mathrm{maxarg}}_{\chi }{\displaystyle {\int }_{\left|\partial \chi \right|}{\psi }_1\left(x\right)\mathrm{d}V}.\end{array}$$ (A4)

Now, we can partition the volume |∂χ| into subvolumes |∂χ|₊ = {x|x ∈ |∂χ|andψ₁(x) > 0} and |∂χ|₋ = {x|x ∈ |∂χ|andψ₁(x) < 0}, and note that

$$\begin{array}{cc}\hfill {\int }_{\left|\partial \chi \right|}{\psi }_1\left(x\right)\mathrm{d}V& ={\displaystyle {\int }_{{\left|\partial \chi \right|}_{+}}{\psi }_1\left(x\right)\mathrm{d}V}+{\displaystyle {\int }_{{\left|\partial \chi \right|}_{-}}{\psi }_1\left(x\right)\mathrm{d}V}\\ & \le {\displaystyle {\int }_{{\left|\partial \chi \right|}_{+}}{\psi }_1\left(x\right)\mathrm{d}V}\le {\displaystyle {\int }_{V_{+}}{\psi }_1\left(x\right)\mathrm{d}V},\end{array}$$

where the volume V₊ = {x|ψ₁(x) > 0}. It immediately follows that the separatrix maximizing the flux is the surface where ψ₁(x) = 0, the χ₁ separatrix.

APPENDIX B: RELATION TO VTST TRANSITION STATE

It is interesting to investigate the relationship between the χ₁ separatrix and the definition of the VTST transition state independent of any choice of reaction coordinates.², ³ As detailed in the following, we find that these transition state separatrices are not necessarily the same. To compare these states, it is useful to describe the VTST transition state in terms of Fokker-Planck eigenfunctions. To do this, we begin with the population inside some bounded volume R, of the global population initially at equilibrium,

$$P_R(x,0)=\left\{\begin{array}{cc}\hfill \frac{{\psi }_0\left(x\right)}{\sqrt{Z}},& \hfill x\in R\\ \hfill 0,& \hfill x\notin R,\end{array}\right.$$ (B1)

the instantaneous flux out of R is the equilibrium flux across its bounding surface,

$$J_{R,\mathrm{eq}}=-{\left.\frac{\partial }{\partial t}{\int }_{R}P(x,t)\mathrm{d}V\right|}_{t=0}.$$ (B2)

The time dependent behavior of the population initially on one side of R expanded in Fokker-Planck eigenfunctions is

$$\begin{array}{ccc}\hfill P_R(x,t)& =& \sum _{i=0}^{\infty }{c}_i{\psi }_i\left(x\right)e^{-{\lambda }_{i}t}\hfill \\ & =& \sum _{i=0}^{\infty }\left({\int }_R{e}^{\beta E\left(x^{\prime }\right)}\frac{{\psi }_0\left(x^{\prime }\right)}{\sqrt{Z}}{\psi }_i\left(x^{\prime }\right)\mathrm{d}{x}^{\prime }\right){\psi }_i\left(x\right)e^{-{\lambda }_{i}t}\hfill \end{array}$$ (B3)

$$\begin{array}{cc}& {\displaystyle =\frac{1}{Z}\sum _{i=0}^{\infty }\left({\int }_R{\psi }_i\left(x^{\prime }\right)\mathrm{d}{x}^{\prime }\right){\psi }_i\left(x\right)e^{-{\lambda }_{i}t},}\end{array}$$ (B4)

where we have used Eqs. 6, 7.

Defining j_{R, i} = 1/Z(∫_Rψ_i(x) dx)², substitution into Eq. B2 shows

$$J_{R,\mathrm{eq}}=\frac{1}{Z}\sum _{i=0}^{\infty }{\lambda }_i{\left({\int }_R{\psi }_i\left(x\right)\mathrm{d}x\right)}^2=\sum _{i=0}^{\infty }{\lambda }_i{j}_{R,i}.$$ (B5)

From this, we see that the surface with minimum equilibrium flux must minimize the contributions to the sum of the j_{R, i} corresponding to eigenfunctions ψ_i with large eigenvalues.

We note that, at time t = 0, the total population of P_R enclosed in R is

$${〈N_R〉}_0=\int P_R(x,0)\mathrm{d}x={〈N_R〉}_0^2+\sum _{i=1}^{\infty }{j}_{R,i},$$ (B6)

hence

$$\sum _{i=1}^{\infty }{j}_{R,i}={⟨N_R⟩}_0-{⟨N_R⟩}_0^2={⟨N_R⟩}_0{⟨N_P⟩}_0.$$ (B7)

Choosing among surfaces for a given 〈N_R〉₀, the total equilibrium flux will tend to be minimized by varying R to maximize the j_{R, i} with the smallest eigenvalues. This will tend to attract the VTST transition state toward the χ₁ separatrix, but they will in general be different.

APPENDIX C: CONFIGURATIONS ON THE χ₁ SEPARATRIX RELAX TO CHEMICAL EQUILIBRIUM ON THE FAST MOLECULAR RELAXATION TIME SCALE

Another useful property of the χ₁ separatrix giving it a direct relation to the reaction is the fast relaxation to chemical equilibrium. Normally an initial distribution needs to relax for a time t ≈ 1/λ₁ before approaching equilibrium. However, configurations initially confined to the χ₁ separatrix relax to equilibrium after only t ≈ 1/λ₂.

The coefficients for expansion of the time dependent population distribution P(x, t), (Eq. 6), are computed from

$$c_i=\int e^{\beta E}{\psi }_i\left(x\right)P(x,0)\mathrm{d}V.$$ (C1)

When the initial population is constrained to lie on the χ₁ separatrix,

$$P(x,0)\ne 0\text{if}{\psi }_i\left(x\right)=0,$$ (C2)

we find c₁ = 0, and the time dependent solutions are

$$\psi (x,t)=\frac{{\psi }_0}{\sqrt{Z}}+c_2{e}^{-{\lambda }_{2}t}{\psi }_2\left(x\right)+c_3{e}^{-{\lambda }_{3}t}{\psi }_3\left(x\right)+\cdots .$$ (C3)

Thus, after the time scale t ≈ 1/λ₂, $P(x,t)\approx {\psi }_0/\sqrt{Z}$.

APPENDIX D: THE χ₁ SEPARATRIX IS CLOSE TO THE LEAST SUCCESSFULLY CROSSED SEPARATRIX

When a simple reaction emerges in the motion of a system, there are two regions within which trajectories can move freely, but between which successful transitions are comparably rare (that is, on the time scale ≈1/λ₁). In this context, we define as optimal the separation of microstates into two volumes which produces the highest probability that a trajectory selected from the Boltzmann distribution will be found again in the same volume after the fast molecular relaxation time (≈1/λ₂ ≪ 1/λ₁). This definition is equivalent to the measure of metastability given in Refs. ¹⁹ and ²⁹. We show in Appendix E that such a division of microstates would be an optimal separation for obtaining the relaxation rate of the system via the reactive flux method. Here, we argue that when there is a sufficient separation of time scales, the χ₁ separatrix is close to such an optimal separation.

For any surface dividing the space into reactant (R) and product (P) regions, we want to know what fraction of the population initially on the R side of a separatrix will be on the P side at a time t_quasi later, with 1/λ₂ ≪ t_quasi ≪ 1/λ₁. We suppose that we have an initial population which is proportional to the Boltzmann distribution within R, and no population outside of R. That is, we assume an initial distribution of the form,

$$P_R(x,0)=\left\{\begin{array}{cc}\hfill \frac{{\psi }_0\left(x\right)}{\sqrt{Z}{〈N_R〉}_0},& \hfill x\in R\\ \hfill 0,& \hfill x\notin R,\end{array}\right.$$ (D1)

where ${〈N_R〉}_0={\int }_R{\psi }_0/\sqrt{Z}\mathrm{d}x$ normalizes the total population.

The time dependent behavior after t = 0 expanded in Fokker-Planck eigenfunctions is

$$\begin{array}{ccc}\hfill P_R(x,t)& =& \sum _{i=0}^{\infty }{c}_i{\psi }_i\left(x\right)e^{-{\lambda }_{i}t}\hfill \\ & =& \sum _{i=0}^{\infty }\left({\int }_R{e}^{\beta E\left(x^{\prime }\right)}\frac{{\psi }_0\left(x^{\prime }\right)}{\sqrt{Z}{〈N_R〉}_0}{\psi }_i\left(x^{\prime }\right)\mathrm{d}{x}^{\prime }\right){\psi }_i\left(x\right)e^{-{\lambda }_{i}t}\hfill \end{array}$$ (D2)

$$\begin{array}{cc}& {\displaystyle =\frac{1}{Z{〈N_R〉}_0}\sum _{i=0}^{\infty }\left({\int }_R{\psi }_i\left(x^{\prime }\right)\mathrm{d}{x}^{\prime }\right){\psi }_i\left(x\right)e^{-{\lambda }_{i}t},}\end{array}$$ (D3)

where we have used Eqs. 6, 7.

The portion of this population which has left R is

$$\begin{array}{cc}\hfill 〈N_P〉\left(t\right)& {\displaystyle ={\int }_P{P}_R(x,t)\mathrm{d}x}\end{array}$$ (D4)

$$\begin{array}{cc}& {\displaystyle =\frac{1}{Z{〈N_R〉}_0}\sum _{i=0}^{\infty }\left({\int }_P{\psi }_i\left(x\right)\mathrm{d}x\right)\left({\int }_R{\psi }_i\left(x\right)\mathrm{d}x\right)e^{-{\lambda }_{i}t}}\end{array}$$ (D5)

$$\begin{array}{cc}& {\displaystyle =\frac{1}{{〈N_R〉}_0}\left({〈N_P〉}_0{〈N_R〉}_0-\frac{1}{Z}\sum _{i=1}^{\infty }{\left({\int }_R{\psi }_i\left(x\right)\mathrm{d}x\right)}^2{e}^{-{\lambda }_{i}t}\right),}\end{array}$$ (D6)

where ${〈N_P〉}_0={\int }_P{\psi }_0\left(x\right)/\sqrt{Z}\mathrm{d}x$, and we have made use of the fact that (∫_Rψ_i(x) dx) + (∫_Pψ_i(x) dx) = 0, for any i > 0.

Analogously (by reversing R and P), we define 〈N_R〉(t) as the fraction of trajectories which move from an equilibrated distribution in P to R during the same time frame. Then, the total fraction of the equilibrium population which has switched sides after a time t is

$$\begin{array}{ccc}\hfill 〈N_C〉\left(t\right)& =& {〈N_R〉}_0〈N_R〉\left(t\right)+{〈N_P〉}_0〈N_P〉\left(t\right)\hfill \\ & =& 2\left({〈N_P〉}_0{〈N_R〉}_0-\frac{1}{Z}\sum _{i=1}^{\infty }{\left({\int }_R{\psi }_i\left(x\right)\mathrm{d}x\right)}^2{e}^{-{\lambda }_{i}t}\right).\hfill \end{array}$$ (D7)

As stated above, we assume there is a separation of time scales, and a time t_quasi, where reactants and products have locally equilibrated, and we can estimate $1\approx e^{-{\lambda }_1{t}_{\mathrm{quasi}}}\gg c_i{e}^{-{\lambda }_i{t}_{\mathrm{quasi}}}\approx 0$, for any i > 1, where the c_i = (∫_Rψ_i(x) dx)². At this time the population which has crossed is

$$\begin{array}{cc}\hfill 〈N_C〉\left(t_{\mathrm{quasi}}\right)& \approx 2\left({\displaystyle {〈N_P〉}_0{〈N_R〉}_0-\frac{1}{Z}{\left({\int }_R{\psi }_1\left(x\right)\mathrm{d}x\right)}^2}\right).\end{array}$$ (D8)

The separatrix minimizing 〈N_C〉(t_quasi) will be the least successfully crossed separatrix. We know from the previous section that (∫_Rψ₁(x) dx)² is maximized when the separatrix is the χ₁ separatrix, but, in principle, a different choice of separatrix produces different 〈N_P〉₀ and 〈N_R〉₀, which perturbs the optimality. However, we find that the difference between 〈N_P〉₀ and 〈N_R〉₀ for the optimal separatrix, and those for χ₁ separatrix must be negligible. That is, we assume there is an optimal separatrix separating volumes R_‡ and P_‡ such that a population initially confined to either volume relaxes to a quasi-Boltzmann distribution on the t_quasi time scale with only a minimal population reaching the complementary volume. From the χ₁ separatrix, we define analogous volumes, $R_{{\chi }_1}$ and $P_{{\chi }_1}$. We assume the reactant and product definitions associated with the χ₁ separatrix and the optimal separatrix agree in the intersecting volumes $R_{{\chi }_1}\cap R_{‡}$ and $P_{{\chi }_1}\cap P_{‡}$ and disagree in the intersecting volumes $R_{{\chi }_1}\cap P_{‡}$ and $P_{{\chi }_1}\cap R_{‡}$. The total equilibrium population in the volumes of disagreement comprises the difference in 〈N_P〉₀ and 〈N_R〉₀ between the two separatrices.

From the fast relaxation property of the χ₁ separatrix, the reaction reaches equilibrium once all of the trajectories have crossed the χ₁ separatrix once. It follows that equilibrium population inside $R_{{\chi }_1}\cap P_{‡}$ must be negligible compared to P_‡, and $P_{{\chi }_1}\cap R_{‡}$ must be negligible compared to R_‡. That is ${⟨P_{{\chi }_1}\cap R_{‡}⟩}_0/{⟨R_{{\chi }_1}\cap R_{‡}⟩}_0$ and ${⟨R_{{\chi }_1}\cap P_{‡}⟩}_0/{⟨P_{{\chi }_1}\cap P_{‡}⟩}_0$ are <λ₁t_quasi. Because both ${⟨R_{{\chi }_1}\cap R_{‡}⟩}_0$ and ${⟨P_{{\chi }_1}\cap P_{‡}⟩}_0$ are <1, both ${⟨P_{{\chi }_1}\cap R_{‡}⟩}_0$ and ${⟨R_{{\chi }_1}\cap P_{‡}⟩}_0$ are <λ₁t_quasi.

It follows that

$$\begin{array}{ccc}\hfill {⟨R_{{\chi }_1}⟩}_0{⟨P_{{\chi }_1}⟩}_0& =& ({⟨R_{{\chi }_1}\cap R_{‡}⟩}_0+{⟨R_{{\chi }_1}\cap P_{‡}⟩}_0)({⟨P_{{\chi }_1}\cap R_{‡}⟩}_0\hfill \\ & & +{⟨P_{{\chi }_1}\cap P_{‡}⟩}_0)\hfill \end{array}$$ (D9)

$$\begin{array}{cc}& ={⟨R_{{\chi }_1}\cap R_{‡}⟩}_0{⟨P_{{\chi }_1}\cap R_{‡}⟩}_0+{⟨R_{{\chi }_1}\cap R_{‡}⟩}_0{⟨P_{{\chi }_1}\cap P_{‡}⟩}_0\end{array}$$ (D10)

$$\begin{array}{cc}& +{⟨R_{{\chi }_1}\cap P_{‡}⟩}_0{⟨P_{{\chi }_1}\cap R_{‡}⟩}_0+{⟨R_{{\chi }_1}\cap P_{‡}⟩}_0{⟨P_{{\chi }_1}\cap P_{‡}⟩}_0\end{array}$$ (D11)

$$\begin{array}{cc}& <{⟨R_{{\chi }_1}\cap R_{‡}⟩}_0{⟨P_{{\chi }_1}\cap P_{‡}⟩}_0+3{\lambda }_1{t}_{\mathrm{quasi}}\end{array}$$ (D12)

$$\begin{array}{cc}& <{⟨R_{‡}⟩}_0{⟨P_{‡}⟩}_0+3{\lambda }_1{t}_{\mathrm{quasi}}.\end{array}$$ (D13)

It follows that, whenever there is an optimal separatrix giving 〈N_C〉(t_quasi) ≪ 1, and a separation of time scales giving λ₁t_quasi ≪ 1, the χ₁ separatrix will be close to the optimal separatrix.

APPENDIX E: OPTIMAL SURFACE FOR REACTIVE FLUX METHOD

The two key assumptions of the reactive flux method³⁰ are a separation of time scales and that the equilibrium time correlation function, C(t), satisfies

$$\frac{1}{{\lambda }_1}\approx \frac{1}{C\left(0\right)}{\int }_0^{\infty }C\left(t\right)\mathrm{d}t.$$ (E1)

The equilibrium time correlation function is defined by dividing configuration space into regions R and P, and taking the ensemble average over the Boltzmann distribution:

$$\begin{array}{cc}\hfill C\left(t\right)& ={〈\Delta N_R\left(x,0\right)\Delta N_R\left(x,t\right)〉}_0\end{array}$$ (E2)

$$\begin{array}{c}\hfill {\displaystyle =\int \frac{{\psi }_0\left(x\right)}{\sqrt{Z}}\Delta N_R\left(x,0\right)\Delta N_R\left(x,t\right)\mathrm{d}x}\end{array}$$ (E3)

Here, we define ΔN_R(x, t) by

$$\Delta N_R\left(x,t\right)={\int }_R{\delta }_x(x^{\prime },t)-\frac{1}{\sqrt{Z}}{\psi }_0\left(x^{\prime }\right)\mathrm{d}{x}^{\prime },$$ (E4)

where δ_x(x′, t) is the time dependent solution to the Fokker-Planck equation starting from an initial Dirac delta distribution, δ_x(x′, 0) = δ(x − x′).

The correlation function can be expressed in terms of Fokker-Planck eigenfunctions after computing the coefficients of the Dirac delta distribution at x,

$$c_i\left(x\right)=\int e^{\beta E\left(x^{\prime }\right)}{\psi }_i\left(x^{\prime }\right){\delta }_x(x^{\prime },0)\mathrm{d}{x}^{\prime }=e^{\beta E\left(x\right)}{\psi }_i\left(x\right).$$ (E5)

So that

$$\begin{array}{cc}\hfill \Delta N_R\left(x,t\right)& {\displaystyle ={\int }_R\sum _i{e}^{\beta E\left(x\right)}{\psi }_i\left(x\right){\psi }_i\left(x^{\prime }\right)e^{-{\lambda }_{i}t}-\frac{1}{\sqrt{Z}}{\psi }_0\left(x^{\prime }\right)\mathrm{d}{x}^{\prime }}\end{array}$$ (E6)

$$\begin{array}{cc}& {\displaystyle =\sum _{i=1}^{\infty }{e}^{-{\lambda }_{i}t}{e}^{\beta E\left(x\right)}{\psi }_i\left(x\right){\int }_R{\psi }_i\left(x^{\prime }\right)\mathrm{d}{x}^{\prime }.}\end{array}$$ (E7)

Carrying out the correlation integral and using the biorthognality relation shows that

$$\begin{array}{cc}\hfill C\left(t\right)& {\displaystyle =\frac{1}{Z}\sum _{i=1}^{\infty }{e}^{-{\lambda }_{i}t}{\left({\int }_R{\psi }_i\left(x\right)\mathrm{d}x\right)}^2}\end{array}$$ (E8)

$$\begin{array}{cc}& {\displaystyle ={〈N_P〉}_0{〈N_R〉}_0\sum _{i=1}^{\infty }{\xi }_i^2{e}^{-{\lambda }_{i}t},}\end{array}$$ (E9)

where the coefficients ${\xi }_i^2$ are defined as

$${\xi }_i^2=\frac{1}{Z}\frac{{\left({\int }_R{\psi }_i\left(x\right)\mathrm{d}x\right)}^2}{{〈N_P〉}_0{〈N_R〉}_0}=\frac{{\left({\int }_R{\psi }_i\left(x\right)\mathrm{d}x\right)}^2}{{\sum }_{i=1}^{\infty }{\left({\int }_R{\psi }_i\left(x\right)\mathrm{d}x\right)}^2}<1.$$ (E10)

On these terms, we see the assumption that the reactive flux method yields the relaxation rate is tantamount to

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\lambda }_1}}& {\displaystyle \approx \frac{1}{C\left(0\right)}{\int }_0^{\infty }C\left(t\right)\mathrm{d}t}\end{array}$$ (E11)

$$\begin{array}{cc}& {\displaystyle ={\int }_{t=0}^{\infty }\sum _{i=1}^{\infty }{\xi }_i^2{e}^{-{\lambda }_{i}t}\mathrm{d}t}\end{array}$$ (E12)

$$\begin{array}{cc}\hfill & {\displaystyle =\sum _{i=1}^{\infty }{\xi }_i^2\frac{1}{{\lambda }_i}}\end{array}$$ (E13)

$$\begin{array}{cc}\hfill & {\displaystyle \approx {\xi }_1^2\frac{1}{{\lambda }_1}.}\end{array}$$ (E14)

The discrepancy between the reactive flux relaxation rate and the true relaxation rate by the factor ξ₁ has been noted before.³¹, ³², ³³

This result suggests a variational approach choosing a dividing surface maximizing ${\xi }_1^2$. However, we recognize ${\xi }_1^2=1-〈N_C〉\left(t_{\mathrm{quasi}}\right)/C\left(0\right)$ from Appendix D. As we showed there, the χ₁ separatrix is close to such an optimal surface when there is a separation of time scales 1/λ₂ ≪ t_quasi ≪ 1/λ₁.

APPENDIX F: LOCALIZATION ON THE χ₁ SEPARATRIX IN THE FULL DIMENSIONAL SPACE: FIRST APPROXIMATION

As stated in the article, we use the slope of the time dependent population around a set of points to obtain a first approximation for the χ₁ separatrix. After a short local relaxation time (≈1/λ₂), we consider the time evolution of the population within a small (0.3 Å) RMSD-ball around a configuration x_i for a short time interval Δt ≪ 1/λ₁ in the form,

$$\begin{array}{cc}\hfill P(x_i,t)& {\displaystyle \approx A\left(x_i\right)+B\left(x_i\right)t\text{when}\frac{1}{{\lambda }_2}\ll t\ll \frac{1}{{\lambda }_1},}\end{array}$$ (F1)

where B(x_i)∝c₁ψ₁(x_i) and changes sign on χ₁.

In order to consider the time dependent population, we first generate a swarm of trajectories originated from a Dirac delta distribution in the configuration space. The starting point for the Dirac delta relaxation was chosen as a low energy configuration from previous exploratory simulations. The χ₁ separatrix would be observable from the diffusion initiated from an initial Dirac delta distribution almost anywhere in c₇ /c₅ configurational space of alanine dipeptide (excluding only configurations very near the separatrix itself); however, choosing an initial point which would give a large value of the coefficient c₁ increases the magnitude of the B(x_i) and makes observation of the separatrix easier. The magnitude of c₁ for an initial Dirac distribution at x is e^E(x)βψ₁(x) (from Eq. 7). The eigenfunction ψ₁(x) is the quasi-equilibrium population distribution for particles escaping at the separatrix, so e^E(x)βψ₁(x) will be large and nearly independent of x effectively anywhere inside the reactant or product basin. Since configurations within the basins mostly compose of the equilibrium population, choosing any configuration at random from a long trajectory would be a satisfactory starting point; choosing a low energy configuration improves this chance.

The centers for measuring the time dependent population were chosen as the set of final configurations from all trajectories simulated in the Dirac delta diffusion. Choosing the centers this way provides a simple means of ensuring that centers existed in the region near the separatrix.

The relaxation dynamics from the Dirac delta distribution were simulated by running 500 000 trajectories for $5.0\mathrm{ps}$, with initial velocities taken from a Maxwell distribution at temperature T = 300 K. The population of the 500 000 trajectories was histogrammed into the 0.3 ÅRMSD-balls at each test center at intervals of $0.1\mathrm{ps}$, and a linear function was fit to the time dependent population around each center which had a population greater than 10 samples at each time step. Observation of the time dependent population within test centers near the starting configuration showed an initial rapid decline over a time scale of 1.0 ps followed by much slower decline. This slower decline in the population indicated a reaction taking place on this time scale. The linear fit was then extracted considering the time interval between 3.0 and 5.0 ps in each of the 5.0 ps trajectories.

The centers were then classified according to the sign of the slope of the population in the RMSD balls around each center. Figure 2 illustrates the results obtained by projecting the χ₁ separatrix located on the full configurational space of alanine dipeptide on the (ϕ, ψ) subspace, and compares it to the equi-committor surfaces obtained by choosing the reactant and product states in the (ϕ, ψ) coordinates. We indicate the χ₁ separatrix located with this approach as the “slope-χ₁” in the following.

Although robust in principle, this method for classifying configurations is inherently noisy, particularly near the separatrix where the trajectories rarely visit. To remove some of the noise and allow us to extend the classification to other samples (for instance, in the escape simulations), we trained a support vector machine (SVM) to recognize configurations of alanine dipeptide on each side of the respective separatrices. The SVM operates by finding an optimal set of samples, {x_i} (the support vectors), with associated weights {α_i} and an offset b, producing a function,

$${\displaystyle D\left(x\right)=\sum _i{\alpha }_i\exp \left\{-{(x-x_i)}^2\right\}+b,}$$ (F2)

such that the sign of D(x) describes the class of x. In our case, the class of x is either 1 or –1 if the configuration x is in the reactant or product state. After normalizing each sample so that the maximum value of any coordinate in the training set was 1, we used the SVMLIGHT package³⁴ to train the SVM parameters. When using the SVM to classify a new sample, we rescale its coordinates with the same factor used to normalize the training set.

The SVM was then used to classify every center in the training set as either a reactant or product. The results are presented in Fig. 2.

APPENDIX G: LOCALIZATION ON THE χ₁ SEPARATRIX IN THE FULL DIMENSIONAL SPACE: REFINEMENT

As mentioned in the article, we use the fast relaxation to equilibrium of the points located on the χ₁ separatrix to refine its location. After a short time ≈1/λ₂, a distribution of trajectories starting on the χ₁ separatrix will be relaxed to the equilibrium distribution. On the contrary, distribution of trajectories starting in either the reactant or product volumes will relax to equilibrium on a longer time scale ≈1/λ₁.

In order to find the equilibrium distribution, the conventional approach is to sample a single trajectory for a time much longer than the relaxation time for the reaction. However, since the c₇ /c₅ reaction of alanine dipeptide is not completely isolated from the C_ax state, a single trajectory long enough to adequately sample the respective basins will also have a non-negligible probability to escape to the C_ax minimum. We could simply remove trajectories escaping to the C_ax minimum, but doing so requires that we use domain specific knowledge to describe this population and remove it from our sample set. In the spirit of studying the reaction without domain specific knowledge, we made use of the fast relaxation property to obtain the equilibrium c₇/c₅ populations without running trajectories long enough to enter the C_ax minimum. An added benefit is that we were able to obtain the equilibrium populations by using a large set of shorter simulations simulated massively in parallel.

If we were certain that we had a configuration on the separatrix, a short relaxation on the time scale around $1\mathrm{ps}$ would be sufficient to obtain the equilibrium distribution; what is necessary is that we go beyond any relevant intermediate time scale. The close fit of the escaping population to a single exponential indicated that there was no relevant intermediate on this time scale. However, since the observed separatrix may be slightly off, it was necessary to run simulations beyond the short relaxation time. The escape rate to the separatrix trained from the slope classes (reported in Table 1), showed that the time scale for the relaxation was on the order of 10 ps. Noting the approximate time scale for relaxation, we were ensured a relaxation time of 40 ps would produce an equilibrium distribution. We proceeded to relax a delta distribution of 200 000 trajectories from a configuration on the slope-χ₁ separatrix.

In order to confirm the accuracy of the equilibrium distribution obtained from the fast relaxation technique, we compared the distribution to one taken from a long trajectory of $20\mu \mathrm{s}$ with samples taken at 10 ps intervals. After removing the samples from the C_ax minimum, we found the population distributions matched in the (ϕ, ψ) coordinate system with the same accuracy as a second simulation of a long trajectory (both had a relative error ≈4%). Furthermore, the relative probability to be in the respective volumes separated by the SVM was accurate to within 0.2%.

After using the SVM to classify the equilibrated sample population, we found the probability to be on the c₅ side of the separatrix was ≈55%. For each configuration in our sample set, we ran 500 $1\mathrm{ps}$ trajectories, measuring the probability for the trajectory to end in the c₅ basin as determined by the SVM. We then trained a new SVM to separate configurations with probabilities above and below the 55% probability to be in the c₅ basin. This procedure produced a refined location of the χ₁ separatrix; the result is plotted in Fig. 2 (purple curve, indicated as “refined-χ₁” in the figure).

It is important to note that the key property necessary to obtain the refined separatrix by the above method is the fast relaxation to equilibrium as compared to the relaxation rate; initial delta distributions on the χ₁ separatrix relax to global equilibrium faster than delta distributions in any other part of configuration space. Thus, the property necessary to classify a configuration as being on the χ₁ separatrix is that a delta distribution located at that configuration will be found in any subvolume in the system with equilibrium probability after a much shorter time than the global relaxation rate. The volumes separated by a good transition state separatrix would be pragmatically close to ideal, since trajectories which are present in those volumes after a short time are not likely to leave until the much longer relaxation time. This makes the necessary time to converge to the equilibrium population inside the volume much shorter than the time scale necessary for complete relaxation within the volume.We use this method to refine the slope-χ₁ separatrix obtained directly from the decrease/increase of population around a set of points (as discussed in Appendix F). The whole process requires no a priori information about the reaction.