Anatomical complexity in breast parenchyma and its implications for optimal breast imaging strategies

Abstract

Purpose: The purpose of this investigation was to assess the anatomical noise in breast images using a mathematically derived parameter β as a surrogate for detection performance, across the same patient cohort but in different imaging modalities including mammography, tomosynthesis, and breast CT.

Methods: Women who were scheduled for breast biopsy were approached for participation in this IRB and HIPPA-compliant investigation. A total of 23 women had all views of each modality and represent the cohort studied in this investigation. Image data sets across all modalities were analyzed using 1000 regions of interest per image data set, and the anatomical noise power spectrum, NPS_a(f), was computed and averaged for each breast image data set. After windowing the total noise power spectrum NPS_t(f) to a specific frequency range corresponding to anatomical noise, the power-law slope (β) of the NPS_a(f) was computed where NPS_a(f) = α f^−β.

Results: The value of β was determined for breast CT data sets, and they were 1.75 (0.424), 1.83 (0.352), and 1.79 (0.397), for the coronal, sagittal, and axial views, respectively. For tomosynthesis, β was 3.06 (0.361) and 3.10 (0.315) for the craniocaudal (CC) and medial lateral oblique (MLO) views, respectively. For mammography, these values were 3.17 (0.226) and 3.30 (0.236), for the CC and MLO views, respectively. The values of β for breast CT were significantly different than those for tomosynthesis and mammography (p < 0.001, all 12 comparisons).

Conclusions: Based on the parameter β which is thought to describe anatomical noise in breast images, breast CT was shown to have a statistically significant lower β than mammography or tomosynthesis. It has been suggested in the literature that a lower β may correspond to increased cancer detection performance; however, this has yet to be demonstrated unequivocally.

INTRODUCTION

Considerable resources are spent on breast cancer screening strategies. It is estimated that in the United States alone, more than $5.2 billion dollars is spent annually for breast cancer screening.¹ Although the effectiveness of breast cancer screening in various age and risk groups remains controversial,^{2, 3, 4} there has been a significant reduction in breast cancer mortality in the past 30 years since breast cancer screening programs have been initiated. It is likely that this reduction in mortality is due both to earlier detection from screening, as well as through better surgical and therapeutic management of the disease.

Mammography is the predominant imaging modality used for breast cancer screening; however, a limited angle tomography technique (“tomosynthesis”) was recently approved by the FDA for screening as well.⁵ Our laboratory has developed fully tomographic x-ray computed tomography systems specifically designed for imaging the breast while the women lays prone on a padded table. Almost 500 women have been imaged on our two breast CT (bCT) scanners, located at two different institutions. This system and other designs for breast CT systems have been described extensively in the literature.^{6, 7, 8, 9, 10}

It is known that the patient’s normal breast anatomy can obscure the detection of a breast cancer lesion, if one is present. For women with dense breasts, this problem is even worse and this is because there is more glandular tissue in those patients. The presence of normal glandular tissue results in what is referred to as anatomical noise in the image—and in general, it is known that greater levels of anatomical noise lead to poorer detection performance.^{11, 12, 13} In this study, we computed a mathematical parameter β directly from patient’s breast images that is thought to correlate with anatomical noise, and this parameter was then compared between mammography, tomosynthesis, and breast CT images. The analysis was performed on breast images from the same 23 women who were imaged by all three modalities.

METHODS

The parameter β

The noise power spectrum (NPS) is a commonly used metric in medical imaging which is used to characterize noise texture.^{14, 15, 16} The NPS is computed as a function of spatial frequency, NPS(f), and the integral of NPS(f) over all frequencies is the image variance, σ². The NPS(f) metric has traditionally been used to characterize the quantum noise characteristics in imaging systems; however, Bochud^{11, 12} and Burgess¹⁴ have suggested that the total NPS, NPS_t(f) can be used to characterize both anatomical and quantum noise, where

$$\begin{array}{cccc}\multicolumn{1}{c}{{\mathrm{NPS}}_t(f)}& \hfill =\hfill & \hfill {\mathrm{NPS}}_a(f)\hfill & \hfill \begin{array}{cc}\multicolumn{1}{c}{+}& \hfill {\mathrm{NPS}}_q(f)\hfill \end{array}\hfill \end{array},$$

and where NPS_a(f) is noise attributed to the anatomy in the image and NPS_q(f) characterizes quantum noise power. Burgess demonstrated by using digitized screen-film mammograms that the anatomical noise power spectrum can be modeled using a mathematical power function

$$\begin{array}{cccc}\multicolumn{1}{c}{{\mathrm{NPS}}_a(f)}& \hfill =\hfill & \hfill \alpha \hfill & \hfill f^{-\beta }\hfill \end{array},$$

The parameter β is the metric of interest in this investigation. Burgess hypothesized that lower values of β would correlate with better cancer detection performance in breast images.^{15, 17} This metric has subsequently been used by a number of investigators for the analysis of mammograms.^{14, 16, 18, 19, 20}

Patient selection

Patients who had suspicious findings on routine breast screening and who as a result were scheduled for breast biopsy were approached for participation in this study. Participants underwent IRB approved and HIPPA-compliant research imaging just prior to their scheduled breast biopsy. After written consent was obtained, the patients were imaged on a prototype tomosynthesis system, which also captured a digital mammogram in the “combination” acquisition mode. The patients were then scanned by the breast CT system, which was located in an adjacent room and was developed at the medical center of University of California, Davis. All three imaging procedures were performed within a 30 min time period. Both breasts were scanned for most patients, although in this study only the images of the unaffected breast were used in the analysis. A total of 32 different women were enrolled; however, not all women had all exams for various reasons. Overall, 26 women had breast CT, 28 had tomosynthesis, and 28 had mammography. A total of 23 patients were imaged by all three modalities, and this is the cohort that is the focus of this report.

Imaging systems

Digital mammography/breast tomosynthesis

A prototype breast tomosynthesis/digital mammography system was used for this study. The system (Selenia Dimensions, Hologic Corporation, Bedford, MA) uses an x-ray tube with a tungsten anode with 0.50 mm added Al for tomosynthesis scanning. The system used in our laboratory was not FDA approved at the time of this research study but is exactly the same unit as that which has been subsequently approved by the FDA for clinical use. Automatic exposure control was used, and the auto-kV mode was also used resulting in an average of 33.5 kV for tomosynthesis (range 28–44). The system uses a selenium-based direct thin film transistor x-ray detector, with an active imaging area of 23.3 × 28.5 cm. The acquisition uses a tomographic angle of 15° and 11 images are acquired over this angular range. The tomosynthesis images were reconstructed in the axial plane for craniocaudal (CC) projection imaging, and in a tilted sagittal plane for the medial lateral oblique (MLO) view. The algorithm uses a standard limited angle cone beam reconstruction. Images were reconstructed using 0.12 mm pixel pitch in-plane sampling, and reconstructed images are spaced 1 mm apart in the z-dimension, which does not mean that they have a 1 mm slice thickness. This system was also used to acquire full field digital mammography images, and 0.050 mm Rh added filtration was used in mammography mode. The full detector array with a 0.07 mm pixel pitch was used for image formation. In mammography mode, the automatic exposure control and auto-kV was also used, with an average of 30.5 kV (range 26–36 kV).

Breast CT scanner

The prototype breast CT scanner is the second prototype cone beam CT scanner developed at our institution specifically for breast imaging. Commercial components of this scanner consist of an x-ray tube (Comet AG, Flamatt, Switzerland), an indirect detection CsI-based flat panel detector (PaxScan 4030CB Varian Medical Systems, Palo Alto, CA), and a servo motor with bearing and angle encoder (Kollmorgen, Radford, VA). This system has been well described in the literature.^{8, 21, 22, 23, 24} Briefly, 500 projection images were acquired at 30 frames per second for a 16.6 s acquisition time, while the patient was in breath-hold. These 768 × 1024 projection images were used to reconstruct breast CT volume data sets ranging up to 512 images, each 512 × 512 in format. The system uses conventional Feldkamp cone beam reconstruction methods, as discussed in the literature.^{6, 21, 22, 23, 24} Breast CT images were reconstructed using a cone beam filtered backprojection algorithm with a Shepp–Logan filter. The mean slice thickness in the natively reconstructed coronal images was 0.23 mm, and the pixel dimensions of the coronal images ranged from 0.29 to 0.38 mm depending on breast size, with an average pixel dimension of 0.37 mm in coronal view corresponding to a field of view of about 19 cm per breast.

Computation of parameter β

Region of interest selection

Each breast image data set was evaluated independently, so a total of 161 image data sets were evaluated: 23 patients × (3 bCT + 2 tomosynthesis + 2 mammography), comprising almost 40 000 breast images. For the breast CT data sets, the three orthogonal views (coronal, sagittal, axial) were evaluated, and the craniocaudal and mediolateral oblique views for both tomosynthesis and mammography were used. In each image data set, a total of 1000 regions of interest (ROIs) were randomly located on the image data. Regions on each image data set which did not include breast anatomy were excluded using a combination of algorithms and manual tracing techniques designed to delineate the breast boundary, and all ROI placements were visually inspected to insure that they were located over breast parenchyma. Areas adjacent to the chest wall and nipple were avoided. The coordinates of each ROI were selected using a random number generator, and only if all the pixels inside each selected ROI corresponded to breast parenchyma, would the ROI would be used for analysis. The selected ROI positions were marked on breast images using overlay graphics for visual verification.

Due to the properties of the fast Fourier transform, the dimensions of the ROI (in pixels) have to be powers of two, i.e., 2 ⁿ. The ROIs for bCT were 64 × 64 pixels, ranging from 18.6 to 24.3 mm in side length for coronal view, depending on the breast size. ROIs were chosen as 256 × 256 pixels (30.7 × 30.7 mm) on tomosynthesis images and 512 × 512 pixels (35.8 × 35.8 mm) on mammography images, in order to adjust the physical ROI dimensions to be as close to those of bCT as possible, given the differences in pixel dimensions on each of these modalities.

Using the nearly isotropic breast CT data sets, the influence of breast thickness integrated onto a single image on the computation of β was also studied. The breast CT data had intrinsic thickness (Δ) ranging from 0.18 to 0.28 mm per slice for the coronal plane, and from 0.29 to 0.38 mm for the sagittal and axial planes. Adjacent slices in a three dimensional block of image data were averaged together to produce two dimensional images with thicknesses corresponding to N slices, where N = 1, 2, 4, 8, 16, 32, 64, 128, and 256 slices. The corresponding physical thicknesses were then N Δ (mm).

To assess the relative contribution of quantum noise to the total NPS_t(f) [Eq. (1)], a homogeneous polyethylene cylinder of the approximate diameter as some of the breasts imaged in this study was also imaged on the breast CT scanner, using the same technique factors. Quantum noise was obtained by the subtraction of two repeat scans of the phantom positioned at the same location. The NPS_t(f) was assessed on the subtracted phantom images. Because of the subtraction, a factor of 2 was divided from the magnitude of the NPS_q(f).²³ These data, which corresponded to primarily quantum noise, were used for comparison between the NPS_t(f) compared on breast images which included both anatomical and quantum noise.

Arithmetic methods for computing β

For each two dimensional ROI selected on an image, the mean gray scale value was computed and subtracted, resulting in a zero-mean ROI. For a ROI with a side length of linear dimension of s, a Hanning window function [H(r) = 0; r > ½ s, H(r) = ½ + ½ cos(2πr/s), elsewhere] was used to suppress spectral leakage. The two dimensional Fourier transform (FT) was then computed on the ROI, resulting in NPS_t(f_x, f_y), the two dimensional noise power spectrum.^{14, 16} The 1000 2D NPS functions were averaged to produce one mean $\overline{\mathrm{NPS}}(f_x,\mathrm{\hspace{1em}\hspace{1em}}{f}_y)$. The nearly symmetrical two dimensional frequency domain data was radially averaged using $\begin{array}{c}\multicolumn{1}{c}{f_r=\sqrt{f_x^2+f_y^2}}\end{array}$, resulting in NPS_a(f_r). The NPS_a(f) data was binned and radially averaged in the frequency domain with a bin width of approximately 0.028 mm⁻¹, which was 1/50 of the Nyquist frequency for each bCT data set. The bin-widths were kept similar to bCT while radial averaging the NPS_t(f_x, f_y) of tomosynthesis and mammography. This data was used to fit the function $\begin{array}{c}\multicolumn{1}{c}{{\mathrm{NPS}}_a(f_r)=\alpha f_r^{-\beta }}\end{array}$. In order to do this fitting, the logarithm of both sides of the equation was computed, linear regression was performed, and the intercept α, and slope, −β, were assessed. The regression analysis was performed on a limited segment of data in a frequency window between frequencies f₁ on the low frequency end and f₂ on the high frequency side of the window. For each NPS_a(f_r), the values of f₁ and f₂ were selected based on the maximum r² value of the linear regression fit, where a range of f₁ and f₂ values were iterated over. The purpose of the frequency windowing is to reduce low frequency anomalies characteristic of the NPS_a(f) at the low frequency end, and to reduce the influence of quantum noise at higher frequencies. The range of values for f₁ and f₂ was selected by inspection for each imaging modality.

Statistical analysis

For each of the comparisons across modalities and projections (mammography CC and MLO, tomosynthesis CC and MLO, and breast CT coronal, sagittal, and axial), the Student’s T-test was used. Across the 23 patients, the mean and standard deviation of the parameter β was computed, and these values were used in computing the t-statistic across comparisons and p-values were computed from tables of T and the degrees of freedom. Statistical significance was assumed if p < 0.05.

RESULTS

It was found that the frequency window edges, f₁ and f₂, which produced the highest r² fit values ranged from {0.04–0.1} mm⁻¹ for f₁ to {0.25–0.50} mm⁻¹ for f₂.

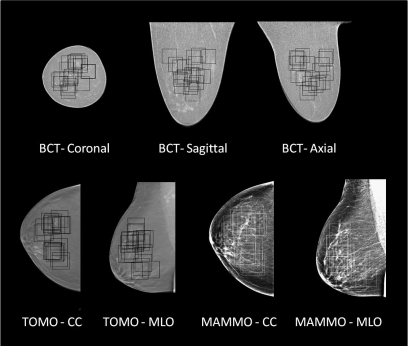
Figure 1 illustrates breast images in each projection possible from each modality. Because of the truly three dimensional characteristics of breast CT, three orthogonal images can be seen representing the coronal, sagittal, and axial planes. For mammography, images are produced by projecting the anatomical information onto the plane of the detector. For tomosynthesis imaging, the images from our prototype system are generated in the plane parallel to the detector. The CC and MLO planes are the standard projections used in screening mammography and tomosynthesis. The three breast CT image projections were produced in one acquisition, while each of the tomosynthesis and mammography projections was generated by a different image acquisition geometry. Figure 2 illustrates a mosaic of ROI patches from each modality and projection. This figure illustrates that the texture from each modality is visually different. Figure 2 shows 100 ROIs per modality for one breast in the cohort, while the NPS was computed using 1000 ROIs for each modality and projection.

Figure 1.

Images from breast CT, tomosynthesis, and mammography. Individual images from each of the three breast imaging modalities are illustrated, with each projection shown. The boxes illustrate the randomly selected ROIs for NPS measurement on these images.

Figure 2.

Image Texture: A 10 × 10 patch of ROIs from different imaging modalities for the same breast are shown. Visually, each of these mosaics of breast images illustrate differences in anatomical texture.

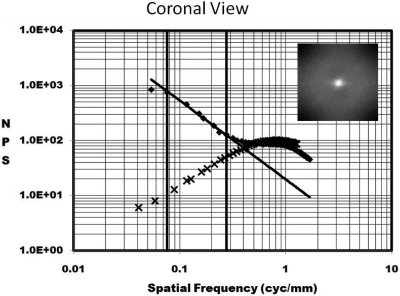
Figure 3 illustrates the NPS_a(f) as a function of f on a log–log axis plot. The two dimensional NPS data is shown for a coronal breast in the inset. Two plots are shown: the linear plot (♦ symbols) represents the NPS computed from a coronal breast CT image data set. The other plot (x symbols) shows the NPS computed from the subtraction of two repeated scans of the homogenous cylinder of polyethylene (PE), which closely mimics the x-ray attenuation properties of adipose in the breast. Because the PE has no anatomical structure, the predominant source of noise in this phantom is quantum noise. The NPS_q(f) of the PE cylinder is thought to be comparable to the NPS_q(f) for the breast that was evaluated in Fig. 3, because the diameter of the PE cylinder was matched to that of the breast and the x-ray technique factors were the same, and hence, the quantum noise levels and distribution should be approximately similar. The vertical lines in Fig. 3 illustrate the lower and upper frequency bounds (f₁ and f₂) which form the frequency window in which the slope of the NPS was computed for the breast. It is seen that the quantum noise contributes very little to the frequency window used for assessment of β. The frequency bounds for each breast were varied slightly, and the values of f₁ and f₂ which maximized the r² of the linear fit were used for each breast. The value of r² measured across all 23 breasts in each modality averaged to >0.990 in all cases.

Figure 3.

The NPS(f) is shown as a function of frequency, on a graph with log–log axes. The anatomical noise of a breast is shown as the points (♦) along the straight line fit. The NPS computed from a homogeneous polyethylene cylinder with similar dimensions to the breast is also shown (x).

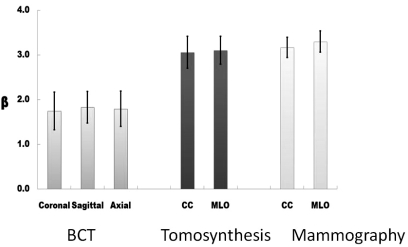
Figure 4 illustrates a bar graph showing the average value of β (±σ) for each projection of each modality. Averaged across all three projections, the mean β (standard deviation) was 1.790 (0.042) for breast CT, and was 3.235 (0.090) for mammography. Perhaps surprisingly, the mean β for tomosynthesis was measured to be 3.08 (0.032). While this value is in between the β values for true 2D mammography and true 3D breast CT, with respect to the differences in β between breast CT and mammography, the β for tomosynthesis is only 10.7% different than mammography (100% × [3.23 − 3.08]/[3.23 − 1.79]).

Figure 4.

Bar chart showing values of β for each modality and projection: The error bars represent ±1σ. These data represent averages across 23 breast image data sets for each bar.

The values of β compared across the three orthogonal projections for breast CT were not significantly different from each other (coronal/sagittal p = 0.246, coronal/axial p = 0.474, axial/sagittal p = 0.320). Similarly, compared across the MLO and CC projections, β for tomosynthesis was not significantly different (p = 0.446). The β values for MLO and CC projections for mammography, however, were significantly different from each other (p = 0.003). All statistical comparisons between breast CT projections and the other two modalities (and projections) showed significant differences with p < 0.001 (all 12 comparisons). The p-values comparing tomosynthesis with mammography showed statistical significance with p-values in the range between 0.002 and 0.039, except for the nonsignificant comparison between MLO tomosynthesis and CC mammography, where p = 0.182.

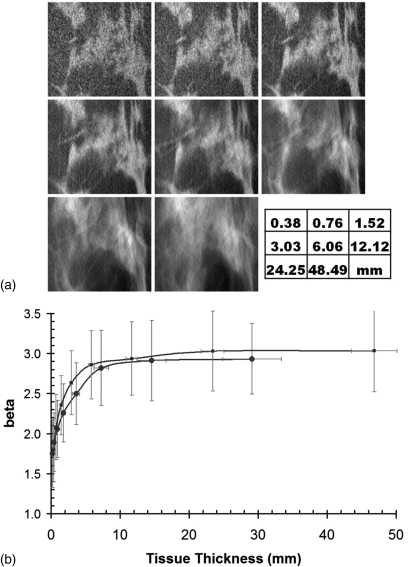
We evaluated whether the value of β was an intrinsic property of a given imaging modality, or if something more fundamental was at play in regards to the value of β. Using the isotropic thin slice breast CT data for each patient, images of differing slice thickness were generated by averaging adjacent images of thickness Δ, such as (1, 2, 4, 8, 16, 32, 64, 128) Δ. Figure 5 illustrates that β starts out low for native breast CT images (1 Δ = 0.4 mm), but the value of β measured for thicker slice breast CT images was similar to that of tomosynthesis and mammography for the thicker slices (128 Δ = 48.5 mm). This observation suggests that it is not the breast imaging modality which is the fundamental determinant of β per se, but rather it is the effective thickness of the images that are produced with each modality that is the most important determinant of detection performance, based on β. In discussing the three modalities studied here, the effective thickness of mammography is simply the compressed breast thickness, since that is the projected thickness through the breast. For breast CT images, because the slice sensitivity profile is well constrained and is nearly a RECT function defined by the sections of tissue summed together, the effective slice thickness refers to a slice thickness in the tomographic volume defined by one or more slices (n Δ as discussed above). For tomosynthesis, however, the slice sensitivity function is not defined by a RECT function but rather by a very broad distribution ranging centimeters in width. Even though the images are reconstructed with a spacing of 1 mm in the z-dimension, this does not imply that the slice thickness is 1 mm.

Figure 5.

Anatomical noise versus breast thickness (a) images are shown for the same ROI, with increasing slice thickness. (b) The value of β as a function of slice thickness is illustrated. The points (•) are for the coronal view, and the points (▪) are for the axial view.

DISCUSSION

Radiologists who read breast images have a daunting task—they are charged with detecting cancers in 3–6 women per 1000 screening examinations, but need to do this while keeping false positive rates low, which requires further workup. Radiographically, cancer in the breast can appear in multiple ways, including small clusters of microcalcifications or masses with various shapes. The parameter β discussed in this work and as proposed by Burgess relates only to the detection of mass lesions and does not currently address the issue of microcalcification detection.

Tomosynthesis is a form of limited angle tomography that has been shown in trials to increase specificity while maintaining sensitivity.²⁵ A clear advantage of tomosynthesis over breast CT is that the hardware is colocated onto a digital mammography system, and indeed, the mammogram can be acquired in the same short imaging sequence as the images required to produce a tomosynthesis data set.

This study is an extension of the previous work of Metheany.¹⁶ The analysis methodology was quite similar in this work, and the region of interest dimensions and fit ranges in the frequency dimension were approximately the same. However, the analysis software was completely rewritten. The Metheany paper did not address the important and timely issue of tomosynthesis, and there were very limited comparisons across modality on the same patients because at that time, imaging data sets across all three modalities were not available. In this work, we compared results between three modalities across a cohort of women who were imaged in a prospective clinical trial. This trial was conducted specifically for this type of comparative study. In addition, in this study we used the thin section breast CT image data set to synthesize breast images of different thicknesses [Fig. 5b]. These data provide a well sampled assessment of β as a function of breast thickness, and provides a concise conceptual understanding of how β changes with slice thickness.

Gong²⁶ used computer modeling techniques to compare mammography, tomosynthesis, and breast CT in a human observer receiver operating characteristic (ROC) curve study. The investigators used power-law noise to generate the background image data in the simulations, using a β of 3.0. In that work, tomosynthesis and breast CT compared very similarly, and both of these tomographic modalities significantly outperformed mammography. However, the assumptions used in that study were that the value of β was identical between tomosynthesis and breast CT—only the pixel size was varied between these modalities in their simulations. In the current investigation, we have demonstrated using physical breast imaging on live patients, that the value of β is quite different between tomosynthesis and breast CT. Indeed, our results suggest that the value of β is quite similar between mammography and tomosynthesis, and the β associated with both of these modalities differs significantly from that of breast CT.

The results of this study demonstrate that the anatomical noise signature of breast tomosynthesis is far closer to that of mammography than breast CT. Using the intrinsically thin section breast CT data sets, thin CT images were summed to represent images of varying slice thickness, ranging from very thin slices (Δ = 0.38 mm) to slice thicknesses more characteristic of mammography (48 mm), and the parameter β was computed from those synthesized thick images. Images of the breast with submillimeter thickness demonstrate very low values of β (β ≈ 1.8), but as CT images are summed and the thickness (T) of the breast image increases, the value of β increases rapidly—the initial slope (dβ/dT) is on the order of 0.78/mm. As the slice thickness increases to 20 mm, the slope drops to less than 0.01/mm. Anatomical noise in breast imaging, as characterized by the parameter β, is only reduced when the slice thickness of visualized tissue is less than 7 mm, and appreciable reduction in β occurs when the slice thickness is less than 1 mm. It is noted that although the tomosynthesis images are reconstructed every 1.0 mm, this does not mean that this interval corresponds to the effective slice thickness.

CONCLUSIONS

The value of β is significantly lower in the case of breast CT, compared to mammography or tomosynthesis. If the parameter is a surrogate predictor of detectability, then these results would indicate that for mass lesions (not microcalcifications), breast CT may be superior to mammography or tomosynthesis for detection of mass lesions. Such a result would be consistent with results from a study involving subjective radiologist comparison between breast CT and mammography.²¹ Analysis of trends in the value of β as a function of breast image thickness shows that lower values of β, thought to be representative of better detection performance, occurs when the imaged thickness of the breast is thin, and the value of β increases rapidly as the thickness of the breast image increases. This observation supports the hypothesis that mass lesion detection is better in thinner breast images, regardless of what the specific imaging modality is.