The Role of Atomic Level Steric Effects and Attractive Forces in Protein Folding

Abstract

Protein folding into tertiary structures is controlled by an interplay of attractive contact interactions and steric effects. We investigate the balance between these contributions using structure-based models using an all-atom representation of the structure combined with a coarse-grained contact potential. Tertiary contact interactions between atoms are collected into a single broad attractive well between the C^β atoms between each residue pair in a native contact. Through the width of these contact potentials we control their tolerance for deviations from the ideal structure and the spatial range of attractive interactions. In the compact native state dominant packing constraints limit the effects of a coarse-grained contact potential. During folding however the broad attractive potentials allow an early collapse that starts before the native local structure is completely adopted. As a consequence the folding transition is broadened and the free energy barrier is decreased. Eventually two-state folding behavior is lost completely for systems with very broad attractive potentials. The stabilization of native-like residue interactions in non-perfect geometries early in the folding process frequently leads to structural traps. Global mirror images are a notable example. These traps are penalized by the details of the repulsive interactions only after further collapse. Successful folding to the native state requires simultaneous guidance from both attractive and repulsive interactions.

Introduction

What are the relative roles of steric repulsion and attractive forces in protein folding?

Globular proteins, at the atomic level, are clearly dense objects. X-ray crystallographic images suggest there is very little free volume in protein interiors. Yet the rapid penetration of small molecule ligands such as O₂ into proteins, at often very high rates, suggests that fluctuations making room for ligand transport are not too costly in free energy ^1,2,3. Diffuse X-ray backgrounds⁴ and sophisticated multi-configuration fits to X-ray data^5,6,7 also suggest there is at least a moderate level of structural disorder (~10%) at the side-chain level in the typical globular protein.

The importance of steric effects is evidenced by the observation that accommodating mutations with increased volume in evolved native protein structures is more difficult than accommodating mutations to smaller amino acid residues. Nevertheless protein interiors have been reconstructed with side chains very different from those constructed by evolution, with some success^8,9,10,11,12. Another observation suggesting a limited role of detailed sterics in folding is that coarse grained simulations with unified residue potentials often predict protein structures reasonably well. We see that steric forces are important at the atomic level resolution but that their effects are buffered in some way by the flexibility of the folded protein structure. In this paper we explore the physics of the interplay between side chain degrees of freedom and the establishment of overall chain topology and how this interplay depends on the range of the inter-residue attractive forces.

One way of discussing this question is to use the language of macroscopic phase transitions. The final folded protein structure which is of rather low entropy can be regarded as a crystal. Should we think of the native states as nearly perfectly defined (with a few vacancies) or should we think of the native ensemble as a plastic crystal phase in which considerable side chain motion occurs? In laboratory studies near the folding midpoint, the process of folding often commences from a high entropy random coil ensemble of conformations with very sparse configurations. This ensemble is pretty clearly analogous to a gas. Many studies under more strongly nativizing conditions have revealed other dense phases of globular proteins which are only partially ordered. The term “molten globules” has long been associated with such phases, since Ptitsyn attracted attention to them and pointed out their importance.¹³

Many ways of characterizing both residual order and the disorder in molten globule phases have been developed. Many experiments show that some degree of native topology is already present in molten globules^{14,15,16,17,18} and other denatured states. One extreme view, in fact, is that the native topology is nearly perfect in the molten globule, like that seen in the X-ray structure but that side chains are mobile (like the plastic crystal phase idea for the folded ensemble mooted earlier). Another minimal view is that the molten globule is more disordered, a liquid crystalline assembly of secondary structure elements. This picture was first championed by Ptitsyn¹³ and later quantitatively analyzed by Ramirez, Luthey-Schulten and Wolynes¹⁹. The role of local secondary structure signals in further organizing the liquid crystalline globule giving rise to some native structure in the MG ensemble was highlighted by Saven and Wolynes²⁰.

A liquid crystalline phase has ample opportunities for non-native contacts to form and thus has the dynamics typical of glass-forming liquids owing to escape from local free energy minima^21,22,23. The latter, glassy, liquid crystalline view underpins many quantitative treatments of the folding free energy landscape of helical proteins^24,20.

The plethora of possible partially ordered phases of globular protein matter opens up a large number of scenarios for protein folding under different thermodynamic conditions. A very common scenario (near the folding midpoint) is a more or less direct transition from the gas-like random coil state directly to a fully ordered (nearly fully) internal crystalline native structure. This process resembles inverse sublimation going directly from a gas-like phase to a crystalline solid-like phase. In the transition state ensemble, partially ordered phases may still play a role^25,26.

In all-atom computer simulations even near T_F often a significantly populated molten-globule like phase with a large amount of non-native structure usually is seen. The large amount of non-native structure strongly suggests that even the better computer simulations carried out today at an atomistic level are based on energy landscapes more rugged than the real one²⁷, although we must acknowledge this conclusion certainly encounters controversy²⁸.

In this paper we examine another aspect of the “sublimation” versus “condensation-freezing scenarios” which hinges on the nature of the inter-residue forces. We show that very short range attractions lead to the direct scenario while broader attractive wells lead to the liquid condensation-freezing/crystallization scenario. This dichotomy depending on the range of attractions resembles what is known about the phase transformations of simple substances where very short range interactions lead to sublimation without the possibility of a liquid phase.

While we regard the present study as largely conceptual, the lessons it holds may have practical consequences. While fully accurate protein structures can be used to predict folding kinetics quite well²⁹, do lower resolution models like those obtained by homology modeling^30,31,32 or ab initio structure prediction^33,34,35 suffice for kinetic modeling? Here we show that if sufficient predictive accuracy is available short range attractive models can be used and direct transit to the folded state (like that usually found experimentally near T_F) will occur in the simulation and mechanisms near the folding midpoint properly delineated. With lower precision models, where greater tolerances must be allowed, simulations may predict additional intermediates which actually are never populated.

Constructing Structure-Based Models with Variable Resolution

To quantify the interplay between side-chain steric effects and different ranges of attractive interactions between amino acids we investigate model systems that are derived from a structure-based model(SBM)^36,25,37 with explicit representation of all heavy atoms³⁸, which contains exclusively native-centered backbone potentials and tertiary contact interactions. For the tertiary contacts we have introduced a potential based on Gaussian functions³⁹, much in the spirit of the sums of Gaussians in the associative memory hamiltonian⁴⁰. The models presented here are variations of our standard all-atom SBM^41,42,43, with the main difference that a single C^β – C^β interaction replaces several atom contacts while the excluded volume remains the same. Effectively the models combine a detailed representation of the atomic level structure with a coarse grained potential for tertiary contacts. The loss of structural information encoded in the attractive contact potential shifts the balance of control over the folding process towards the steric repulsive interactions.

We assume that attractive potentials and unspecific interactions will be relevant only for residue pairs with long sequence separations. Experience with predictive protein models shows that local structures can be determined with reasonable confidence from structural databases. Additional information may be necessary for pairs that are distant in sequence, because the available information becomes increasingly reduced and ambiguous with growing sequence distance. This information may come from different sources and may have limited structural resolution, leading to the introduction in the model of spatially broad attractive interactions. Limited spatial resolution is a trade off to limit energetic frustration, which is unavoidable because a predictive model will not be perfectly accurate.

Specifically we replace all the native attractive interactions between the atoms of any pair of residues p,q with a long sequence separation of Δ_p,q = |p−q| > 8 by a single interaction between their C^β atoms. The width of the attractive well of the potential for this residue contact is varied for the different realizations of the model, allowing us to investigate how different levels of resolution lead to different outcomes. A sketch of this procedure is shown in Fig. 1. Atom contacts between residues with a short sequence separation of Δ_p,q = |p−q| ≤ 8 are retained as in the full all-atom structure-based model. Fragments of similar length are also frequently used in several structure prediction schemes^34,44. Backbone interactions, which apply to covalently bound atoms, are also maintained unmodified from the all-atom structure-based model.

Fig. 1.

All-atom models with coarse-grained contact maps: Starting from a structure-based model with all-atom representation, atom contacts between pairs of residues with long sequence separations |p−q| > 8 are replaced by single residue contacts acting on the C^β atoms. Pairs of residues with short sequence separations |p−q| ≤ 8 retain the individual atom contacts that are also present in the full structure-based all-atom model. Multiple atom contacts between a pair of residues can fully determine the relative position of their side chains. A given single contact between their C^β atoms may be compatible with multiple configurations. Packing restrictions imposed by repulsive interactions between the side chain atoms gain in relevance.

Despite the coarse-graining of the contact interactions for residue pairs with long sequence separations, the models are still completely structure-based. All the minima of attractive contact potentials continue to be placed at the exact distances obtained from the crystal structure. Only the range (tolerance) of the geometrical deviations of tertiary contacts is increased. In the all-atom SBM multiple interactions between individual atoms of a residue pair forming a native contact can determine the distance and the relative orientations of their side chains. Within the coarse-grained contact interactions the single remaining potential between the C^β atoms of a residue pair only depends on their separating distance. The relative orientation of the side chains is not controlled by the contact potential. Modifications to the width for the single potential between their C^β atoms allow one further to control the tolerance for deviations in the contact distance adopted by the residues³⁹.

While the tertiary interactions between residues with long sequence separations are thus coarse-grained, the structure is however still represented in atomic detail. Repulsive interactions between side chains and their packing constraints therefore remain fully effective in the models. To analyze also the effects of repulsive interactions we use variants of our models that additionally replace the term for the unspecific repulsion by Weeks-Chandler-Andersen(WCA) potentials⁴⁵ with even shorter range.

In this way we can vary the range and the effectiveness of both the unspecific repulsive interactions and of the specific attraction between tertiary contact pairs to observe their respective influence on the formation of native protein structure.

All-atom structure-based model

The Hamiltonian for our structure-based model consists of bonded and non-bonded interactions.

$$V=V^{\text{bonded}}+V^{\text{non}-\text{bonded}}$$ (1)

Bonded interactions serve to determine the geometry of the protein chain and establish a local bias towards the native configuration. Non-bonded interactions provide excluded volume to the chain and provide additional stabilizing interactions between atoms that are separated in sequence but close in space in the native structure. All non-hydrogen atoms are individually represented in the model. The bonded interactions include harmonic potentials for bond lengths and bond angles. Further harmonic terms constrain peptide bonds and aromatic rings to planar geometries and maintain proper chirality.

$$V^{\text{bonded}}=\left\{\sum _{\text{bonds}}{V}^{\text{B}}+\sum _{\text{angles}}{V}^{\text{A}}+\sum _{\text{impropers}/\text{planars}}{V}^{\text{I}}+\sum _{\text{backbone}}{V}^{\text{BB}}+\sum _{\text{side}-\text{chains}}{V}^{\text{SC}}\right\}$$ (2)

Dihedral potentials V ^BB and V ^BB for backbone and side chain torsional angles use the same cosine potential

$$V^{\text{D}}(\phi )={\epsilon }_{\text{D}}\left\{\left[1-cos(\phi -{\phi }_0)\right]+\frac{1}{2}\left[1-cos(3(\phi -{\phi }_0))\right]\right\}$$ (3)

with different amplitudes ε_BB and ε_SC selected according to the scaling rules described in Ref. 38.

The non-bonded interaction between any pair of atoms i, j is selected by the corresponding element $c_{i,j}^{\text{A}}$ of the atom contact matrix C^A, which is 1 if the atoms i, j are in contact in the native structure and 0 otherwise.

$$V^{\text{non}-\text{bonded}}=V^{\text{contact}}+V^{\text{non}-\text{contact}}=\sum _{i,j}{c}_{i,j}^{\text{A}}{V}^{\text{C}}(r_{i,j})+\sum _{i,j}(1-c_{i,j}^{\text{A}})V^{\text{R}}(r_{i,j})$$ (4)

The determination is made according to the “shadow” algorithm, which generates possible contacts based on a distance cutoff, and then eliminates contacts as redundant if they are separated by interposed atoms.⁴⁶ Contacts between atoms that belong to residues p,q with a sequence separation |p−q| ≤ 3 are also excluded.

Atom pairs that do not form native contacts interact by a purely repulsive potential

$$V^{\text{R}}(r_{i,j})={\epsilon }_{\text{NC}}{(d/r_{i,j})}^{12}.$$ (5)

For simplicity a constant value of d is used for all the heavy atoms that are represented in the model. To create an alternative set of models with shorter range for the unspecific repulsion we replace V ^R by a WCA potential⁴⁵. The WCA potential is derived from a Lennard-Jones potential that is shifted up to become zero at the location of its minimum. At shorter distances than the minimum distance the WCA potential is equal to this shifted Lennard-Jones potential, at longer distances it is set to zero.

$$V^{\text{WCA}}={\epsilon }_{\text{NC}}\lfloor {\left(d/r_{i,j}\right)}^{12}-{\left(d/r_{i,j}\right)}^6+\frac{1}{4}\rfloor \text{for}{r}_{i,j}<2^{(1/6)}d\text{and}0\text{otherwise}.$$ (6)

Native contacts are stabilized by a potential V ^C with a minimum at the native distance $r_{i,j}^{\text{N}}$ and repulsive interaction at shorter distances. Typically modified Lennard-Jones potentials have been used for V ^C. For our purposes this choice is problematic because the shape of a Lennard-Jones potential is completely determined by the placement of the native minimum. We have recently introduced an alternative contact potential that offers more flexibility³⁹:

$$V^{\text{C}}(r_{i,j})=V^{\text{R}}(r_{i,j})+A_{i,j}{V}^{\text{G}}(r_{i,j})+V^{\text{R}}(r_{i,j})V^{\text{G}}(r_{i,j}),$$ (7)

$$V^{\text{G}}(r_{i,j})=exp\left[-{(r_{i,j}-r_{i,j}^{\text{N}})}^2/(2{\sigma }_{i,j}^2)\right].$$ (8)

It combines the repulsion V ^R with an attractive Gaussian function V ^G. The additional product term places the minimum of the total V ^C at the native distance at (r_{i, j},− A_{i, j}). In addition to the native distance the depth of the minimum, the width of the Gaussian, and also the atom diameter for the repulsive term remain as adjustable parameters, i.e. $V^{\text{C}}=V^{\text{C}}(r_{i,j};r_{i,j}^{\text{N}},A_{i,j},{\sigma }_{i,j},d_{i,j})$. All three values are relevant for the construction of models with coarse-grained contact maps.

Models with reduced native information

To support the introduction of a coarse-grained contact map at the residue level instead of contacts between individual atoms, the contact potential from Eq. (4) can be rewritten in terms of residues p,q and their constituent atoms A(p) and B(q) as

$$V^{\text{contact}}=\sum _{p,q}\sum _{\text{A}(p)}\sum _{\text{B}(q)}{c}_{\text{A}(p),\text{B}(q)}{V}^{\text{C}}(r_{\text{A}(p),\text{B}(q)}).$$ (9)

There is a unique correspondence between each atom A(p) and its index i used in Eq. (4).

From the atom contact map C^A we can count the number of atom contacts between a pair of residues:

$$N_{p,q}^{\text{A}}=\sum _{\text{A}(p)}\sum _{\text{B}(q)}{c}_{\text{A}(p),\text{B}(q)}^{\text{A}}.$$ (10)

We use this count to define a residue contact map C^R with elements

$$c_{p,q}^{\text{R}}=\{\begin{array}{cc}1& \text{for}{N}_{p,q}^{\text{A}}>0\\ 0& \text{for}{N}_{p,q}^{\text{A}}=0\end{array}.$$ (11)

Contacts between residues with |p−q| ≤ 3 are not part of C^A and remain excluded in C^R. As residue contacts act on the C^β atoms we further exclude contacts between glycine residues.

We now distinguish contacts between residues with short sequence separation |p−q| ≤ 8 from contacts between residues with long sequence separation |p−q| > 8and assign different contact potentials to them,

$$V^{\text{contact}}=V^{\text{short}}+V^{\text{long}}.$$ (12)

Short contacts retain the detailed contact interactions from the all-atom structure-based model,

$$V^{\text{short}}=\sum _p\sum _{q\le p+8}\sum _{\text{A}(p)}\sum _{\text{B}(q)}{c}_{\text{A}(p),\text{B}(q)}^{\text{A}}{V}^{\text{G}}(r_{\text{A}(p),\text{B}(q)};\dots ).$$ (13)

Long contacts use the coarse-grained residue contact map, with interactions acting on the C^β atoms,

$$V^{\text{long}}=\sum _p\sum _{q>p+8}{c}_{p,q}^R{V}^{\text{G}}(r_{{\text{C}}^{\beta }(p),{\text{C}}^{\beta }(q)};\text{K}).$$ (14)

The parameter d_{i, j} for the effective atom diameter in the repulsive part of the contact potential is kept identical in all cases to the value used in the purely repulsive potential for non-contacts. Especially for the residue contacts this possibility is crucial. With a Lennard-Jones contact potential between the C^β atoms the interaction would soon become repulsive at distances below the native separation. This behavior is however only desirable in a fully coarse-grained model, when the amino acid structure is not directly represented in the model. The contact repulsion then reflects the approximate sizes of the whole side chains. Our models include the all-atom structure of the residues explicitly. This detailed treatment of side chain volume and packing would only be diluted by an averaged repulsive interaction. Contact amplitudes A_{i, j} are equal for all contacts in V ^short to the value ε_C that is determined according to the procedure from Ref. 38. In V ^long we set all A_{i, j} to a new constant value that is scaled by the numbers of replaced long atom contacts and of residue contacts to conserve the total contact energy in the native configuration, $A_{i,j}={\epsilon }_{\text{C}}{N}_{\text{long}}^{\text{A}}/N_{\text{long}}^{\text{R}}$. Energetic information about the differing numbers of atom contacts between different residue pairs is thus dropped from the model together with the geometrical information contained in the atom contact distances.

The width of the Gaussian in V ^short is set proportional to the native distance, as it is done in the all-atom structure-based model to mimic the behavior of the conventional Lennard-Jones potentials: ${\sigma }_{i,j}=k_{\sigma }{r}_{i,j}^{\text{N}}$. In V ^long we use a constant width σ_{i, j} = σ_β in the Gaussian term in the residue contacts in each model. Different values for σ_β in different variants of the model represent varying degrees of assumed uncertainty in the structural input information. The values for σ_β used in this study are 0.5, 1.0, 2.0 Å.

Results

We have investigated the impact of the described coarse-grained contact maps on the folding behavior of five small proteins with different folds and structural complexity, namely the helix bundles Protein A (PrA) and 434 Repressor (434rp), an SH3 domain, and the mixed alpha-beta proteins CI2 and FtsA. They range in size from 46 amino acids for PrA to 81 for FtsA. The full structure based models contain between 311 and 714 atom contacts. In the relatively simpler helix bundles, half of the contacts are formed between residues with sequence separations up to 8 residues and half between more distant pairs. In the three proteins that contain beta structures, the fraction of contacts between residue pairs with sequence separations larger than 8 residues is between 75% and 84%, with the highest value for FtsA. FtsA also has the most complex structure according to the mean sequence separation of residue contacts, 〈δ〉 = 32. The lowest complexities according to this measure are found again for the helix bundles, with 〈δ〉 =14 for PrA. This information is collected for all treated proteins in Table I.

Table I.

List of treated proteins

Protein	PDB	N res	N A	$N_{\text{short}}^{\text{A}}$	$N_{\text{long}}^{\text{A}}$	〈σ〉
PrA	1BDD	46	311	153	158	14
434rp	1R69	63	523	261	262	18
SH3	1FMK	57	481	79	402	23
CI2	2CI2	64	481	118	363	22
FtsA	1E4F	81	714	149	565	32

To describe the folding behavior of these proteins in our models, native-like atom contact distances are used as the main geometrical criterion for determining nativeness. The fraction of formed native contacts is a natural reaction coordinate for a structure-based energy model, because it also reflects the degree of energetic stabilization through the corresponding contact potentials. For the systems with coarse grained contact maps the geometrical criterion still describes native-like local structure. For contacts between residues pairs with short sequence separations, where the atom contact potential from the full structure-based model is retained, the direct correspondence to energetic stabilization also remains. The precise correspondence to energetic stabilization is lost for residue pairs with long sequence separations, whose atom contact potentials have been replaced by a single residue contact potential. The fraction of formed contacts in both groups is plotted separately as $Q_{\text{AA}}^{\text{short}}$ and $Q_{\text{AA}}^{\text{long}}$ in Fig. 2 A for the case of 434rp. In the full structure-based model, where both groups of contacts are treated in the same way, the behavior of the two groups is similar. Both are mostly unformed at higher temperatures, and the majority of contacts from both groups are formed cooperatively at the same transition temperature. The temperature dependence for the formation of the remaining contacts at lower temperatures is also identical for both groups. Only the fraction of contacts that is already randomly formed in the unfolded state above the transition temperature differs with sequence separation. As expected the fraction of formed contacts is higher for pairs separated by shorter loops.

Fig. 2.

Structure formation and stabilization: The transition between folded and unfolded states in all-atom models with coarse-grained contact maps is characterized through the temperature-dependent fraction Q of formed contacts. A: Fractions Q_AA of atom contacts for 434 repressor: Atom contacts between pairs of residues with sequence separation |p−q| ≤ 8 are directly included in all models. Their fraction in labeled $Q_{\text{AA}}^{\text{short}}$ and shown by black curves. Data for a model with the complete all-atom contact map are labeled AA. In the coarse-grained contact maps atom contacts between residue pairs with longer sequence separations |p−q| < 8 are replaced by single contacts between the C^β atoms. The width parameter σ_β of the attractive Gaussian contact well varies between models from 0.5 to 2.0 Å. The fraction of the replaced atom contacts that are geometrically formed is labeled $Q_{\text{AA}}^{\text{long}}$ and shown in red. In the coarse-grained models Q_AA is only a measure of structure, and not of direct energetic stabilization as it is in the full structure-based model where potentials for these contacts are included. Curves for the coarse-grained models are therefore dashed. Wider curves correspond to models with broader potentials for the C^β contacts. B: Formation of the C^β contacts used in coarse-grained contact maps, for 434 repressor: Black curves for $Q_{\text{AA}}^{\text{short}}$ from panel A are repeated for reference. Green curves give the fraction $Q_{\text{AA}}^{\text{long}}$ of formed C^β contacts between residue pairs with sequence separations |p−q| > 8. C^β contacts are defined as formed when the pair distance is within 2 σ_β from the native value. The blue dashed curves use a stricter geometrical criterion: A native C^β contact is considered to be formed when the distance between the C^β atoms is within 1.0 Å of the native value.

In the models that employ coarse grained interactions for residue pairs that are distant in sequence, the transition temperatures for $Q_{\text{AA}}^{\text{short}}$ and $Q_{\text{AA}}^{\text{long}}$ still coincide in each system. The common transition temperature is higher for systems with broader potentials for the residue contacts between contact pairs with long sequence separations. For both $Q_{\text{AA}}^{\text{short}}$ and $Q_{\text{AA}}^{\text{long}}$ the fraction of atom contacts that is formed cooperatively at this transition temperature shrinks as the residue potentials used for contacts with long sequence separations are broadened. Below the transition temperature different temperature dependences of $Q_{\text{AA}}^{\text{short}}$ and $Q_{\text{AA}}^{\text{long}}$ arise from the different treatment of residue contact pairs that are close or distant in sequence. The group of atom contacts between pairs with short sequence separations, which are still stabilized by individual contact potentials, proceeds to completion with the same temperature dependence as in the full structure-based model. The fraction of formed atom contacts between residue pairs with long sequence distances, which are only stabilized indirectly via the coarse-grained contact potentials between the residues’ C^β atoms, increases more slowly below the main transition temperature, so that the transition for these contacts becomes broadened. Further broadening of the transition occurs above the transition temperature for both groups of contacts. Broader potentials for the contacts between the C^β atoms of residue pairs with long sequence separations move the onset of native-like structure formation to increasingly higher temperatures for both $Q_{\text{AA}}^{\text{short}}$ and $Q_{\text{AA}}^{\text{long}}$.

The temperature dependent formation of the residue contacts defined between C^β atoms of residue pairs with long sequence separations is plotted in Fig. 2B, again for 434rp. Their transition from low to high degrees of formation coincides with the transition monitored by the atom contacts in each system. Compared to the atom contacts, the transition for the residue contacts is more complete, when the distance cutoff for their formation is chosen to correspond to the actual width of the contact potential between the C^β atoms in each system. When a stricter constant distance cutoff is chosen for the formation of the residue contacts, monitoring more precisely the adoption of closely native-like distances instead of the onset of energetic stabilization, the formation of residue contacts goes to completion more gradually below the transition temperature, in a manner more similar to the atom contacts.

Above the transition temperature an early onset of contact formation broadens the transition for the residue contacts to an even greater extent than for the atom contacts. The broadening effect is again strongest for those models using the widest attractive contact potentials, and it is most notable when the distance cutoff used to recognize contact formation matches the width of the potentials.

Fig. 3 summarizes the behavior of the atom contacts for the set of five investigated proteins. In models with coarse grained contact maps, all five proteins show the same broadening of the folding transition that is dominated by an early onset of structure formation above the cooperative folding temperature for both the groups of contacts with short and long sequence separations. All the proteins we studied also share the separation in behavior between these groups of contacts below the folding transition, where the complete formation of atom contacts with long sequence separations is delayed in models with coarse grained contact maps.

Fig. 3.

Broadening of folding transitions for different proteins: Characteristic temperatures T_v are used to summarize the behavior of $Q_{\text{AA}}^{\text{short}}$ and $Q_{\text{AA}}^{\text{long}}$ shown in panel A for the set of five tested proteins. $T_{0.25}(Q_{\text{AA}}^{\text{short}})$ is e.g. defined as the temperature where $Q_{\text{AA}}^{\text{short}}$ equals 0.25 (see markings in panel A). Temperatures for $Q_{\text{AA}}^{\text{long}}$ are plotted against the corresponding temperatures for $Q_{\text{AA}}^{\text{short}}$ to compare the relative progress of both groups of contacts. T_0.25 and T_0.75, marked by circles and diamonds respectively, are used to describe early and advanced contact formation. Data for models with complete atom contact maps are shown in the inset. Placement of the symbols for T_0.25 close to the diagonal indicates that $Q_{\text{AA}}^{\text{short}}$ and $Q_{\text{AA}}^{\text{long}}$ reach the value 0.25 at similar temperatures. The same holds for T_0.75. Folding progresses simultaneously for both groups of contacts. Small differences between T_0.25 and T_0.75 indicate that the transition occurs cooperatively over a narrow temperature range. Data in the main plot show the behavior of models with coarse-grained contact maps for contacts between residues with long sequence separations |p−q| > 8. The relative placement of data points for models with increasingly broader potentials for the residue contacts is indicated by the black arrows. Corresponding symbols showing T_0.25 and T_0.75 for each model of SH3 are in addition indicated by blue arrows. For the systems with coarse-grained contact maps only symbols for T_0.25 are placed close to the diagonal, while those for T_0.75 are displaced from it. Both $Q_{\text{AA}}^{\text{short}}$ and $Q_{\text{AA}}^{\text{long}}$ reach the value 0.25 at similar temperatures, but progress to 0.75 occurs at lower temperatures for $Q_{\text{AA}}^{\text{long}}$. For both groups of contacts separately the difference between T_0.25 and T_0.75 is increased compared to that for the complete all-atom structure-based models. The broad and gradual character of the transition indicated by this difference grows for each tested protein with increasing width of the contact potential for the C^β contacts in the coarse-grained contact map.

The relationship between formation of native-like local structure and collapse is exhibited in Fig. 4 for 434rp. Structure formation is here quantified by the fraction of all native-like atom contacts Q_AA, without the distinction by sequence separation made above. The behavior of contact formation is compared to the temperature dependence of the radius of gyration as a measure of compactness. Protein folding is monitored by R_g as a transition from high values for extended unfolded conformations at high temperatures to a low value for the compact folded structure. For the full structure-based model this transition temperature coincides with the transition temperature for forming native contacts, and both transitions are equally sharp. For models with coarse grained contact maps, the transition in R_g becomes more gradual as the width of the contact potential is increased for residue contacts between pairs with long sequence separations. The transition is also somewhat shifted, so that native-like values of R_g are reached at higher temperatures in these models, but the onset of collapse occurs at even higher temperatures. Both effects together lead to a growing separation between contact formation and collapse. The same qualitative behavior is also seen in models with WCA potentials for the unspecific repulsive interactions between atoms. With its shorter range, the WCA potential leads to even earlier collapse, while the temperature dependence of contact formation doesn’t change.

Fig. 4.

Collapse: The transition between extended and compact states in all-atom structure-based models of 434 repressor with coarse-grained contact maps is characterized through the temperature dependence of the radius of gyration, shown in red. Black curves give the fraction Q_AA of formed atom contacts for reference. Data for a model with the complete all-atom contact map is labeled AA. In the coarse-grained contact maps atom contacts between residue pairs with sequence separations |p−q| > 8 are replaced by single contacts between their C^β atoms. The width parameter σ_β of the attractive Gaussian contact well varies between models from 0.5 to 2.0 Å. Open circles add data for models where additionally a WCA potential is substituted for the 12^th power term for the unspecific repulsive interaction between atom pairs that form no native contact.

Fig. 5 summarizes the relationship between collapse and structure formation for all five investigated proteins. The described behavior is confirmed in all cases. When the width of the attractive potentials is increased in these models, the separation in temperature between collapse and formation of native-like atom contacts increases. While the strength of the effect differs between proteins for identical models, the different models for each protein all follow a similar trend. With the coarse grained contact maps, collapse is increasingly further advanced before local structure formation even begins.

Fig. 5.

Separation of the collapse and structure formation for different proteins: Characteristic Temperatures T_0.25 are used to summarize the relationship between R_g and Q_AA, shown in Fig. 4, for all tested proteins. T_0.25 (Q_AA) is the temperature, where Q_AA equals 0.25. Similarly the normalized radius of gyration $(R_{\text{g}}-R_{\text{g}}^{\text{N}})/(R_{\text{g}}^{\text{U}}-R_{\text{g}}^{\text{N}})$ equals 0.25 at T_0.25 (R_g). Solid symbols compare T_0.25 (R_g) and T_0.25 (Q_AA) for models with complete atom contact maps. Their placement close to the diagonal indicates that compaction and formation of native structure happen together. Open symbols correspond to models with coarse-grained contact maps for residue pairs with long sequence separations |p−q| > 8. A single contact between their C^β atoms replaces all atom contacts between such pairs. The width parameter σ_β of the attractive Gaussian contact well increases between models from 0.5 to 2.0 Å. For each protein separately T_0.25 (R_g) is increasingly higher than T_0.25 (Q_AA) for models with broader potentials for the C^β contacts. Formation of native atom contacts proceeds only after collapse is already advanced.

Free energy profiles as functions of Q and R_g display a qualitative change in behavior underlying this trend. As shown for 434Rp in Fig. 6A, the profiles for the full structure-based model at the folding temperature shows two coexisting minima corresponding to the folded and unfolded states. In simple two state folders like 434Rp they are connected by a single barrier, which here measures about 5 k_BT. The folded state is restricted to a narrow range of values around the native R_g, but it covers a larger range of high values in Q. The unfolded state is located at low Q and consists of a basin that extends towards larger radii R_g. Upon the change to coarse-grained contact maps with increasingly wide residue contacts between the C^β atoms of residue pairs with sequence separations Δ_p,q > 8 both minima shift towards the barrier in the profile, and the height of the barrier is reduced. For 434Rp the barrier has shrunk to about 1 k_BT for the model using σ_β=1.0 Å for the width of the residue contacts. With still wider contacts the barrier eventually vanishes completely. Folded and unfolded states merge into a single basin that shifts along the landscape with decreasing temperature from extended unfolded states to compact native-like configurations. Compact states with low Q are adopted in between, and two destabilized branches of the basin extend towards folded and unfolded regions. For 434Rp this single state “downhill” behavior is first encountered in the model with σ_β =2.0 Å. For FtsA, where the fraction of contacts with sequence separations Δ_p,q > 8 is higher, single-state behavior is already reached at σ_β =1.0 Å. For both proteins the remaining barrier in any given model is lowered further when WCA repulsion is introduced.

Fig. 6.

Loss of two-state behavior, in two dimensional free energy-landscapes as functions on R_g and Q_AA. A: The structure-based model of 434 repressor using the complete atom contact map shows folded and unfolded basins in equilibrium separated by a barrier of 5 – 6 k_BT. In the inset, the corresponding landscape is shown for a model with a coarse grained contact map that replaces atom contacts between residue pairs with long sequence separations |p−q| > 8 by a single contact between their C^β atoms. The width parameter for the contact potential is σ_β = 2.0 Å. Here the barrier between the folded and unfolded basins is reduced to 1 – 2 k_BT. B: For FtsA two state-behavior is already replaced by a shifting single basin in the model using residue contacts with σ_β = 1.0 Å between C^β atoms. The main plot shows the situation at T=1.625, between the folded and unfolded parameter regions. The alternative landscapes for T = 1.2 and T = 2.0, given as insets, show the folded and unfolded regimes.

The loss of two-state folding behavior in our systems with unspecific interactions poses practical challenges for the application of such models. A clear transition from unfolded to native-like configurations can no longer be observed at constant temperature. For our systems folding trials were performed instead with a minimal annealing routine using linear temperature ramps. In order to emphasize possible kinetic traps a fast cooling rate has been chosen. It was adjusted to produce a small fraction of misfolded outcomes also for the simple helix bundles in the full structure-based models with all-atom contact maps. Results from 50 folding attempts for each protein indicate that using the coarse-grained contact maps also increases the likelihood for certain scenarios of misfolding. Especially with those potentials having the broadest attractive contacts, global mirror images of the native structure arise as an extreme outcome. These structures are approximate mirror images at the coarse grained level that describes the relative positions of elements of secondary structure and their connecting loops. Local constraints with chemical motivation, like the planarity of peptide bonds or of aromatic rings, which are enforced by the harmonic potentials of improper dihedral interactions, remain satisfied. Other local structures like individual helices may also be formed with the correct native-like orientation, or they may be disrupted to comply with the inverted global geometry. Such distortions are only opposed by the softer proper dihedrals. While part of the local structure is thus disrupted, such mirror images apparently satisfy nearly all constraints encoded in the broad contact potentials that form the coarse-grained contact maps of these models.

These unspecific residue contacts are able to lock in mirror images and other misfolded chain geometries through their high stabilization and their observed tendency to form early during the folding process, in spite of high energetic penalties for the completed structure from other parts of the potential.

Repulsive interactions contribute significantly to the energetic penalties that are realized in such final misfolded structures. Mostly this contribution is however indirect, apparently the excluded volume interactions distort other degrees of freedom with less steep potentials, like dihedral angles. Repulsive interactions can also not prevent the falling into such traps because of their short range, especially compared to the unspecific residue contacts that form during the early collapse.

Early collapse alone has long been identified as a cause of slow folding, since trapping is increased in compact structures.⁴⁷ Broadened contact potentials would be likely to strengthen this effect through their capacity to stabilize competing non-native topologies. This effect of the broadened contact potentials would apply to proteins that fold natively through compact intermediates with reduced native structure even without any nonspecific tendencies to induce early collapse as well.

Some of the misfolded results encountered in our folding trials could probably have been avoided by a more elaborate annealing procedure. But with the minimal annealing scheme used here to emphasize misfolding behavior, broad potentials also show some advantages. As the pie charts in Fig. 7b indicate, the fraction of native outcomes, shown in green, is highest for 434Rp with the full all-atom structure-based model. A success rate of 90% suggests that the annealing is only slightly faster than optimal. Coarse grained contact maps with increasing width of the attractive potentials decrease the number of correctly folded results found. For the structurally most complex test protein FtsA, the same annealing schedule produced only 20% native outcomes with the full structure-based all-atom model. With narrow residue potentials between the C^β atoms of residue pairs with long sequence separations only few native-like results remain. But by using the large value of σ_β =2.0 Å for the width parameter of these residue contacts, 20% native outcomes are recovered. Similar behavior is observed for SH3, where C^β contacts with σ_β = 2.0 Å again produce a higher fraction of native-like outcomes than the same coarse-grained contact map with more narrow contacts. The unspecific long contacts here confer some tolerance against kinetic traps as well as possibilities for misfolding.

Fig. 7.

Refolding outcomes: Global mirror images, shown for FtsA, arise as a telling misfolding scenario in models that use broad contact potentials between C^β atoms in coarse-grained contact maps for residue pairs with long sequence separations |p−q| > 8. A simple annealing schedule was adopted to compensate the loss of folding ability at constant T in these models. The pie charts give the number of native outcomes, of structures closer to the mirror image, of clear mirror images, and of other misfolded structures in a set of 50 folding attempts for each tested protein.

When native-like topologies are reached during the annealing procedure, the final structures that are adopted by these models at low temperature turn out to be very close to the crystal structure that is encoded in the potentials. For the native-like outcomes counted in Fig. 7 the root mean square deviation of the backbone to the native configuration is generally smaller than 0.5 Å. Within these limits the deviations are larger in models with coarse-grained contact maps, where single contact potentials between C^β atoms are used for residue pairs with sequence separations Δ_p,q > 8. Among these models the deviations furthermore increase with growing width of the potentials used for the C^β contacts that constitute the coarse-grained part of the contact maps. But the loss of precision is limited. Notably the deviations do not grow in proportion with the width of individual residue contact potentials. For practical purposes when native-like topologies are produced the low temperature minima of all tested models can be considered as identical to the crystal structure. The broad attractive interactions do not impede the realization of the encoded precise native bias.

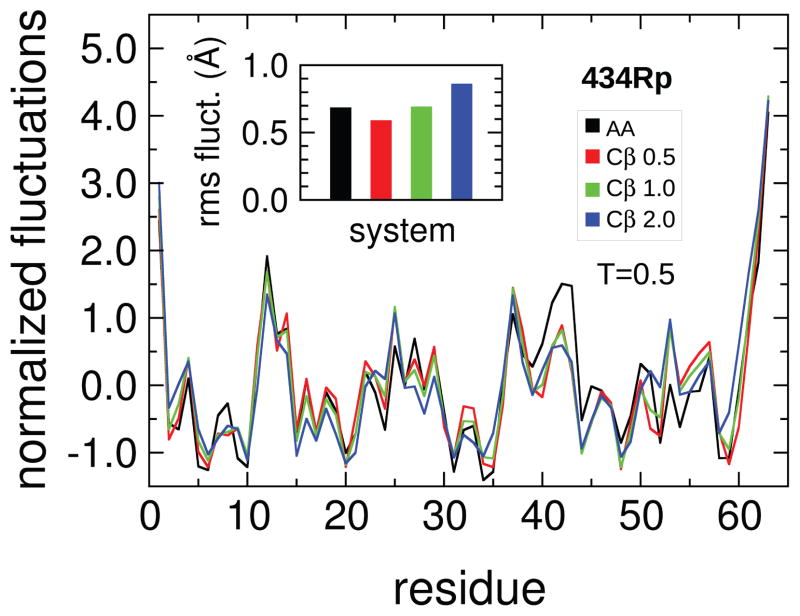
To further assess how well the native state is represented in these models we consider the root mean square fluctuations around the native configuration as a practically relevant property. It is presented in Fig. 8 for 434Rp. Fluctuation profiles are shifted to zero mean and normalized to a variance of one for easier comparison of their shapes. The data for the full structure-based model are given by the black trace. Results for the models coarse grained contact maps are shown in red, green and blue for values of σ_β = 0.5,1.0,2.0 Å respectively.

Fig. 8.

Native dynamics: RMS fluctuations around the native configuration for 434 repressor. Fluctuations of the C^β atoms at T = 0.5 are shown. Data are shifted and normalized to have zero mean and unit variance for comparison between systems. Actual RMS fluctuation amplitudes are given in the inset. The behavior of a model with the complete atom contact map is shown in black. Results for models with coarse-grained contact maps, using single contacts between the C^β atoms of residue pairs with long sequence separations |p−q| > 8, are given by the colored lines. The width parameter σ_β of the attractive Gaussian contact well for the residue contacts varies between models from 0.5 to 2.0 Å.

The unscaled amplitudes are shown in the inset as root mean square averages over all residues. Here the influence of the width chosen for the C^β contacts is apparent. Narrow contacts, with σ_β = 0.5 Å, lead to a reduced level of fluctuations. Amplitudes grow with increasing width of the contact potential. The level for σ_β =1.0 Å is very similar to that in the full structure-based model, and fluctuations are clearly larger in the model with σ_β =2.0 Å.

Meanwhile the general features of the fluctuation profile are preserved in the models with coarse grained contact maps, as for example the high peak at residue 12, the double peak around residue 40, and other features down to small maxima like the peaks around residues 8 or 32. Quantitative differences occur, most notably in the double peak around residue 40, where one of the two peaks is strongly reduced in all the models with coarse-grained contact maps. There is however no strong dependence of these quantitative changes upon the width of the residue potentials. Most of the effect seems related to the introduction of residue level contacts themselves, and not to their broadening.

Conclusions

The interplay between steric interactions and attractive contact potentials is clearly governed by the different reach of both types of interactions. Increasing the width of the attractive potential wells gives an extended range to contact interactions. This broadening of the attractive wells results in less cooperative transitions since residues start to feel each other even in the more extended structures. In its early stages the collapse, which is driven by the formation of these residue contacts, proceeds without the perfect formation of native-like local structure. Since detailed attractive interactions have been replaced by an average residue-residue interaction, less precise structures are formed. Native-like local configurations, signaled by a high fraction of native atom contact distances, only appear at the later stages of folding. The short-range attractive interactions for contacts close in chain and the repulsive interactions only influence the process once the structure is sufficiently compact.

We can conclude from the partially misfolded outcomes observed with the coarse-grained contact maps that steric effects and local contacts play significant cooperating roles in guiding the folding process in the fully detailed model. The coarse grained contacts with very broad attractive potentials are able to lock the system into partially folded global structures since they are formed at early stages of the folding process when conflicting interactions are not yet effective. Energetic penalties are imposed only at later stages of folding by steric repulsion and unsatisfied short-range attractive contacts. Under the annealing conditions chosen in this study, these penalties can not correct some folding mistakes that have already been stabilized by the broad residue contacts. But narrower long-range contacts produce less of these misfolded outcomes although on their own they would be equally suited geometrically to stabilize them. Observations with the WCA potential confirm the relevance of the relative ranges of repulsive and attractive interactions. It is interesting to notice that the repulsive WCA potential strengthens both the broadening of the collapse transition and the loss of cooperativity during folding.

Attractive contact potentials and of repulsive steric interactions both act simultaneously to control protein folding in realistic models. By modulating the range of these long-range attractive interactions we were able to identify the different roles of these two contributions. Attractive interactions provide the driving force for collapse, while steric effects exclude many unproductive folding routes. A detailed representation of the protein structure can improve the precision in the attractive contact potentials in a protein model. Naturally packing constraints are most effective in dense configurations. The compact native state is thus most tolerant against imprecise contact potentials. In extended states earlier during the folding process, the early stabilization of incorrect structures can limit access to the correct native one and therefore limit the corrective effect of steric penalties.