Abstract
Objective
The objective of this study was to compare two recently proposed methods for fast measurements of psychophysical tuning curves (fast-PTCs) in terms of resulting tuning curve features and training effects.
Design
Fast-PTCs with swept-noise (SN) and gated-noise (GN) maskers were measured at signal frequencies of 500, 1000, 2000 and 4000 Hz. The effect of amplitude modulating the signal in the GN condition was evaluated. Two PTC runs were obtained for each condition to assess training effects.
Study Sample
Eight normally-hearing young adults participated in the study.
Results
The SN and GN methods resulted in similar estimates of frequency selectivity when training effects were considered. Amplitude modulating the tone in the GN method reduced the effect of training. On average, SN-PTCs were most repeatable compared to the two other methods and they were not affected by training. Estimation of the shift in the PTC tip frequency was not affected by the measurement method or training effects. Fast-PTC methods resulted in similar estimates of tuning as compared to published notched-noise data.
Conclusions
The SN method and the GN procedure with amplitude modulated signals allowed for time-efficient estimation of frequency selectivity that was unaffected by training.
Keywords: psychophysical tuning curves, frequency selectivity, equivalent rectangular bandwidth, normally-hearing
I. Introduction
Psychophysical tuning curves (PTC) can be used to assess the frequency selectivity of the auditory system (Zwicker, 1974). Conventionally, psychophysical tuning curves are measured with a tone that is fixed in frequency and level (usually 10 dB SL), presented together with a masker (a narrow band of noise or a pure tone) at varying frequencies and levels. The masker level that causes the signal to be just audible is determined and plotted as a function of its frequency, forming a characteristic “V” shaped PTC. This shape corresponds to Wegel and Lane's (1924) observation that tones with frequencies close to the signal frequency are the most effective maskers. Thus, the PTC shape carries information about the ability of the auditory system to filter out one stimulus (the signal) from the others (the masker) on the basis of frequency (frequency selectivity). Frequency selectivity may also be evaluated by measuring the width of an auditory filter, for example, using a notched-noise method (e.g., Glasberg & Moore, 1990).
Measuring an individual's frequency selectivity could have important implications, especially in a clinical setting. Decreased hearing sensitivity is usually associated with reduced frequency selectivity (e.g., Florentine et al, 1980; Glasberg & Moore, 1986; Moore et al, 1999; Zwicker & Schorn, 1978). However, the correlation between the auditory filter width and the audiometric threshold at the test frequency is not high (Glasberg & Moore, 1986; Lutman et al, 1991; Moore et al, 1999), presumably reflecting differences in the etiology of the hearing losses across subjects. Deterioration of frequency selectivity decreases one's ability to distinguish sounds with different spectra. Accordingly, loss of frequency selectivity may contribute to impaired speech, pitch and timbre perception, reduced frequency discrimination, and altered loudness perception (reviewed in Moore, 2007). Some researchers have also suggested that frequency selectivity may play a role in auditory scene analyses (reviewed in Grimault & Gaudrain, 2006), including the ability to segregate auditory streams (Gaudrain et al, 2007). Direct assessment of frequency selectivity with PTCs may also be used to detect cochlear dead regions (Moore, 2001). Reduced frequency selectivity has also been associated with difficulties in hearing in noise by subjects with normal audiometric thresholds (Badri et al, 2011). Altogether, estimation of an individual's frequency selectivity may be used to improve the diagnostic and counseling processes (e.g., Haggard et al, 1986; Kishon-Rabin et al, 2009; Moore, 1996; Robinson et al, 2007; Zwicker & Schorn, 1978).
The classical measures of frequency selectivity based on a multiple-alternative forced-choice paradigm are very time consuming which severely limits their application beyond the laboratory setting. Several investigators have proposed ways to accelerate the measurements of either PTCs (Haggard et al, 1986; Kishon-Rabin et al, 2009; Lutman et al, 1991; Lutman & Wood, 1985) or auditory filters (Nakaichi et al, 2003; Stone et al, 1992). However, an acceptable balance between efficiency and accuracy has not been accomplished with these approaches.
More recently Sęk et al. (2005) developed a fast method to measure PTCs with a masker that continuously changes its center frequency in time (swept-noise), which has been made a publically available software program (Sęk & Moore, 2011). The masker level is adjusted for signal threshold with a Békésy-tracking paradigm. A similar approach was used by Zwicker (1974) with normally-hearing subjects and by Summers et al. (2003) with hearing-impaired subjects. Sęk et al. (2005) evaluated the effects of several parameters on the fast-PTC, including the rate of change of masker level, the masker bandwidth and the direction of masker sweep (i.e., from low to high frequencies and vice versa). The shapes of the PTCs measured with the fast and multiple-alternative forced-choice methods were very similar for both normally hearing and hearing-impaired subjects (Sęk et al, 2005; Sęk et al, 2007), suggesting that the fast-PTC method is a good substitute for the more time-consuming PTC assessment with the forced-choice paradigm.
Nevertheless, some important procedural aspects have not been tested. Several investigators used the fast-PTC paradigm with a gated-noise (GN) instead of the swept-noise (SN) masker (Malicka et al, 2009, 2010; Robinson et al, 2007). In this method the masker is pulsed on and off synchronously with the signal, while the masker center frequency changes from block to block in discrete frequency steps. Some studies have shown that auditory filter width decreases together with increasing masker-signal onset-onset delay (e.g., Bacon & Moore, 1986; Bacon et al, 2002; Bacon & Viemeister, 1985; Wright & Dai, 1994), but no such dependence was found by Moore et al. (1987). However, the effects of a gated masker have been primarily considered for short duration signals and for short onset-onset delays. The GN-PTC method uses a relatively long duration signal and onset-onset delay close to what is usually considered as a “continuous-noise condition” (Bacon & Viemeister, 1985). Thus, it could be hypothesized that differences in sharpness of tuning for GN-PTCs and SN-PTCs would be small. Whether these differences could be ignored and the methods could be used interchangeably needs further investigation, and is a topic of this study.
The GN-PTC method primarily uses an amplitude modulated tone (Malicka et al, 2009, 2010) which is not a standard procedure in PTC measurements. Amplitude modulation is assumed to decrease the risk of beat detection (Malicka et al, 2009) which may arise due to temporal interaction between the masker and the signal. Beats can provide a salient detection cue that leads to a narrowing of the PTC tip (Kluk & Moore, 2004, 2005). To the best of our knowledge, there is only one study that evaluated the effects of signal amplitude modulation on the PTC features measured using the three-alternative forced-choice method (Markessis et al, 2009). That study did not reveal significant differences between the PTCs measured with an unmodulated pure-tone signal and with a signal modulated at either a rate of 81 Hz or 88 Hz, for 1000 and 2000 Hz signal frequencies respectively. However, these results could not be directly generalized to the PTC obtained with the fast methods, since in the GN-PTC approach the 8 Hz AM rate was routinely used independently of the signal frequency (Malicka et al, 2009, 2010).
Unlike multiple-alternative forced-choice methods, a Békésy-tracking paradigm is a criterion-dependent test, meaning it does not control for the subject's judgment (i.e., internal criteria). Thus, it is crucial to establish whether the subject's performance in a fast-PTC paradigm is changing over time due to criterion adjustment (i.e., training effect). Kluk and Moore (2006) reported that stable results with SN-PTC test could be obtained with as little as one practice run. However, some elderly subjects had difficulties understanding the task and more practice was needed. The possible training effects in a fast-PTC paradigm have not been investigated.
In summary, fast-PTC methods provide promise for use in the laboratory or clinical settings as a time-efficient measure of frequency selectivity. The aim of this investigation is to make practical recommendations about the choice of the measurement method. The primary goal was to evaluate whether GN-PTC and SN-PTC methods give equivalent results in terms of the PTC features, specifically its equivalent rectangular bandwidth (ERB)1 and shift in the tip frequency (ftip). In the next step, the effect of amplitude modulating the signal was evaluated for fast-PTCs obtained with the gated-noise method. All three conditions were compared in terms of the repeatability and stability of the results obtained over a recording session. Finally, the effect of the signal frequency on various PTC features will be discussed.
II. Methods
Subjects
Eight normally-hearing subjects were recruited to participate in the study (3 females, including the first author). The mean age was 24.8 years (range 19 – 29 years). The GN-PTC program was used for hearing threshold acquisition in quiet (see Equipment and software) with a standard 5-dB bracketing procedure. One ear was selected randomly for further testing (Table 1). The testing sessions were two hours or less in duration and subjects were allowed to take breaks. The study was approved by the Northwestern University Institutional Review Board and subjects were paid an hourly rate for their participation (except the first author).
Table 1.
Subjects' pure tone thresholds (dB SPL) measured with GN-PTC program for the ears chosen for testing.
| Subject ID | Ear | Frequency (Hz) | |||
|---|---|---|---|---|---|
| 500 | 1000 | 2000 | 4000 | ||
| NH04 | Left | 10 | 10 | 10 | 10 |
|
| |||||
| NH05 | Left | 20 | 15 | 10 | 25 |
|
| |||||
| NH13 | Right | 20 | 10 | 10 | 15 |
|
| |||||
| NH14 | Right | 10 | 10 | 15 | 15 |
|
| |||||
| NH15 | Right | 15 | 10 | 15 | 20 |
|
| |||||
| NH16 | Right | 15 | 10 | 10 | 20 |
|
| |||||
| NH17 | Left | 10 | 10 | 10 | 10 |
|
| |||||
| NH18 | Left | 20 | 10 | 20 | 10 |
Equipment and software
The signals were generated and controlled by a PC with a built-in soundcard. The signals were presented monaurally via ER-3 insert earphones (Etymōtic Research, Elk Grove Village, IL). The subject was seated in a double-walled sound booth. Hardware and software setups used for PTC measurements with swept-noise and gated-noise are described below.
The setup used for SN-PTC testing consisted of a program provided by Aleksander Sęk, (Adam Mickiewicz University, Poland) installed on a PC connected to a PA5 attenuator (Tucker Davis). The maximum masker level offered in the program was 77 - 97 dB SPL which provided a sufficient dynamic range for accurate PTC measurements in our normally-hearing subjects. The SN-PTC software generated the tonal signal and the continuous masker as described in Sęk et al (2005). In brief, the signal was a 500-ms (including 20 ms rise/fall times) pure tone pulsed on and off with an interstimulus time interval of 200 ms. The masker was a narrow-band noise with continuously changing center frequency (fc). The fc was swept at a constant rate on a logarithmic scale. The total noise duration was matched to the GN-PTC test duration to make the test conditions across methods as similar as possible in terms of the rate of masker fc change in time. The masker level changed at a rate of 2 dB/sec in 0.5 dB steps.
The PTC measurements with the gated-noise method were conducted with a program written by Richard Baker (University of Manchester, United Kingdom; see http://personalpages.manchester.ac.uk/staff/richard.baker/, ver. 1.1.1.5), installed on a PC with a Realtek Sound Card. The probe signal was a pure tone lasting 500 ms (including 20 ms rise/fall time). In the first condition, the signal was a steady tone (GN-PTC condition). In the second condition, the signal was amplitude modulated at a rate of 8 Hz (GN-AM-PTC condition). The signal was presented in the middle of the duration of a 700 ms narrowband noise (the masker) with a fixed fc. The tone and the masker were pulsed together in time and the interstimulus interval between the two masker presentations was 200 ms. After each masker presentation the masker fc was changed in 3 or 5 Hz steps on a linear frequency scale for the 500-Hz and 1000-Hz signal frequency respectively, and in 10 Hz steps for both 2000-Hz and 4000-Hz signal frequency. The step size and the range of the fc change (see Procedures) defined the test duration (range 180 sec to 360 sec). The maximum masker level was set at 90 dB SPL. The masker level changed in 2 dB steps per presentation.
Procedures
The fast PTCs were collected for four signal frequencies, fsignal (500 Hz, 1000 Hz, 2000 Hz and 4000 Hz) presented in a random order. The signal was fixed in frequency and level (10 dB SL), and the masker level required to mask the signal was determined as a function of the masker fc with a tracking paradigm. The masker sweep direction appeared to have similar effects on the shift at PTC tip frequency, ftip in both fast-PTC methods (Malicka et al, 2009; Sęk et al, 2005). Malicka et al (2009) also found that the masker sweep direction did not have a significant impact on estimates of sharpness of tuning. Because the major goal of this investigation was to compare the methods, we decided to use maskers that changed fc only in one direction, namely from 0.5 fsignal to 1.5 fsignal with a rate specified for each fsignal (see Equipment and software), which greatly reduced the time needed for data collection. To minimize beat detection, the masker bandwidth was set as 20% of fsignal for the 500 Hz and 1000 Hz tones, and 320 Hz for 2000 Hz and 4000 Hz tones (Kluk & Moore, 2005; Sęk et al, 2005). The subjects were asked to press a space bar on a keyboard and hold it when the signal was audible, and release the space bar when the signal was no longer audible. Pressing/releasing the space bar caused the noise level to increase/decrease at the rate specified for each fast-PTC method. The starting noise level was set below the signal level to allow the subjects to become familiar with the signal.
For all three conditions (SN, GN and GN-AM) subjects were allowed to become familiar with the tracking paradigm by obtaining up to two “practice” runs. If the first practice fast-PTC did not resemble a V-shaped curve, instructions were repeated to make sure that the subject understood the task.
The subjects were tested with the SN-PTC, GN-PTC and GN-AM-PTC methods in random order. To evaluate the repeatability of the results and potential training effects, the subjects completed a second run of fast-PTC tests. Not all subjects participated in all testing conditions. Results were stored on a computer hard drive for offline analysis.
Data analyses
The raw fast-PTCs were smoothed with the LOESS (Locally Weighted Regression) algorithm (Cleveland, 1979) with a second degree polynomial model as suggested by Jacoby (2000). The smoothing parameter (α) was defined with the smoothing LOESS residuals strategy (for details see Cleveland, 1994; Jacoby, 2000). In brief, LOESS for each raw PTC was calculated for 6 different smoothing parameters (.15 to .65 in .10 steps) chosen in a way to contain the most commonly used α values (.25 to .5), as well as values outside this range. For each LOESS fit a graph of residuals was constructed. The largest smoothing parameter α that produced the residual graph with no patterns across the whole data set was defined as optimal for fast-PTC smoothing and in this case was equal to .25. The PTCs smoothed with LOESS2 with α = .25 were used to estimate PTC parameters (Fig. 1).
Fig. 1.
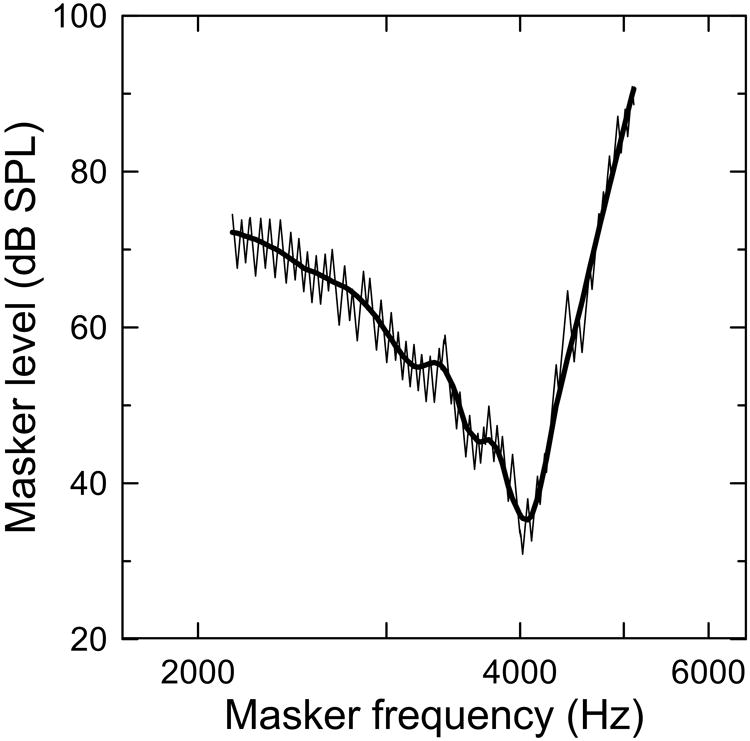
An example of a fast PTC (thin line) smoothed with the LOESS algorithm with smoothing parameter α set at .25 (bold line).
The dependent measures were equivalent rectangular bandwidth (ERB) and the shift of the ftip expressed as a percent of fsignal. The ftip of the modeled PTC was defined as the frequency at the minimum of the curve. The shift at the tip of the PTC is of special interest, since it is used to diagnose cochlear dead regions (e.g., Kluk & Moore, 2006; Malicka et al, 2010; Sęk et al, 2005). The ERB was chosen in place of the quality factor QERB because the ERB is not confounded by the shift at the ftip, which is expected to occur in the direction of the noise fc change in the fast-PTC paradigm (Malicka et al, 2009; Sęk et al, 2005; Sęk et al, 2007). The modeled PTCs were inverted for the purpose of computing ERBs. The raw PTC modeling and parameterization was executed with a custom script written in MATLAB (MathWorks).
Data from only the first run were considered for comparisons across methods. This most closely approximates the likely application of the method in a clinical setting. Data obtained during the second run were used to estimate the repeatability and stability of the results. Statistical analyses were performed with a within-subject ANOVA using SPSS (SPSS Inc., Chicago IL) with the subjects treated as a random factor and the combination of specific recoding conditions (e.g., type of noise, AM-probe, signal frequency, run) as fixed factors. The model included main effects and up to 2-way interactions (if available). Post hoc tests (Fisher's LSD test) were performed if needed. This statistical model was chosen because it allowed for analyses in cases of missing data points (see Table 2). The significance level was set at .05.
Table 2.
Mean and individual equivalent rectangular bandwidth (ERB) values (Hz) calculated for PTCs smoothed with LOESS (α = .25).
| Signal frequency | Subject ID | SN-PTC | GN-PTC | GN-AM-PTC | |||
|---|---|---|---|---|---|---|---|
| Run 1 | Run 2 | Run 1 | Run 2 | Run 1 | Run 2 | ||
| 500 Hz | NH04 | 64 | 73 | 62 | 69 | 55 | 64 |
| NH05 | 62 | 50 | 41 | - | 110 | - | |
| NH13 | 38 | 62 | 135 | - | 79 | - | |
| NH14 | 72 | 52 | 107 | 57 | 58 | 39 | |
| NH15 | 62 | 72 | - | - | 30 | 29 | |
| NH16 | 77 | 91 | 77 | - | 57 | 72 | |
| NH17 | 101 | 99 | 62 | 84 | 104 | 106 | |
| NH18 | 85 | 110 | 111 | 87 | 126 | 98 | |
| Mean (SD) | 70 (19) | 76 (22) | 85 (33) | 74 (14) | 77 (33) | 68 (31) | |
|
| |||||||
| 1000 Hz | NH04 | 130 | 113 | 210 | 134 | 90 | 139 |
| NH05 | 188 | 101 | 160 | 122 | 157 | - | |
| NH13 | 162 | 153 | 272 | 283 | 229 | - | |
| NH14 | 163 | 152 | 135 | 129 | 183 | 136 | |
| NH15 | 87 | 121 | - | - | 153 | 186 | |
| NH16 | 144 | 166 | 186 | 184 | 153 | 152 | |
| NH17 | 179 | 98 | 140 | 119 | 104 | - | |
| NH18 | 134 | 162 | 129 | 149 | 136 | 217 | |
| Mean (SD) | 148 (32) | 133 (28) | 176 (51) | 160 (58) | 151 (44) | 166 (35) | |
|
| |||||||
| 2000 Hz | NH04 | 219 | 175 | 338 | 273 | 308 | 259 |
| NH05 | 350 | 283 | 245 | 274 | 206 | 321 | |
| NH13 | 216 | 253 | 330 | - | 256 | 201 | |
| NH14 | 213 | 273 | 372 | 256 | 285 | 202 | |
| NH15 | 236 | 175 | - | - | 220 | 308 | |
| NH16 | 221 | 229 | 393 | 283 | 170 | 233 | |
| NH17 | 224 | 157 | 277 | 217 | 282 | 223 | |
| NH18 | 256 | 202 | 235 | 243 | 336 | 259 | |
| Mean (SD) | 242 (46) | 218 (48) | 313 (62) | 258 (25) | 258 (56) | 251 (45) | |
|
| |||||||
| 4000 Hz | NH04 | 307 | 265 | 379 | 411 | 312 | 301 |
| NH05 | 277 | 366 | 465 | 312 | 418 | 373 | |
| NH13 | 297 | 328 | 496 | 319 | 323 | 374 | |
| NH14 | 276 | 299 | 472 | 256 | 539 | 486 | |
| NH15 | 371 | 418 | - | - | 370 | 353 | |
| NH16 | 325 | 349 | 319 | 380 | 388 | 528 | |
| NH17 | 320 | 334 | 372 | 366 | 255 | 309 | |
| NH18 | 377 | 434 | 666 | 336 | 353 | 456 | |
| Mean (SD) | 319 (39) | 349 (57) | 453 (114) | 340 (51) | 370 (85) | 397 (83) | |
III. Results
Even after practice runs, in a few cases curves contained very few data points around the tip of the PTC or the tip was not clearly identifiable, obstructing interpretation of the PTC width. These curves were excluded from the analyses and, if time allowed, additional recordings were made. In total, 64 curves were included in the analysis of the SN-PTC method (32 for the first and 32 for the second run) and 7 curves (10% of the total of curves collected) were rejected. For the GN-PTC method, 52 curves (28 for the first run and 24 for second run) were included and 5 curves (10%) were rejected. For the GN-AM-PTC method, 59 curves were included (32 for the first run and 27 for second run) and one curve (2%) was rejected. Fig. 2 shows a typical data set for one subject. The GN-PTCs and GN-AM-PTCs contained fewer points on the low frequency side of the curves than SN-PTCs, which was an expected consequence of using a linear rather than logarithmic scale for the masker fc sweep.
Fig. 2.
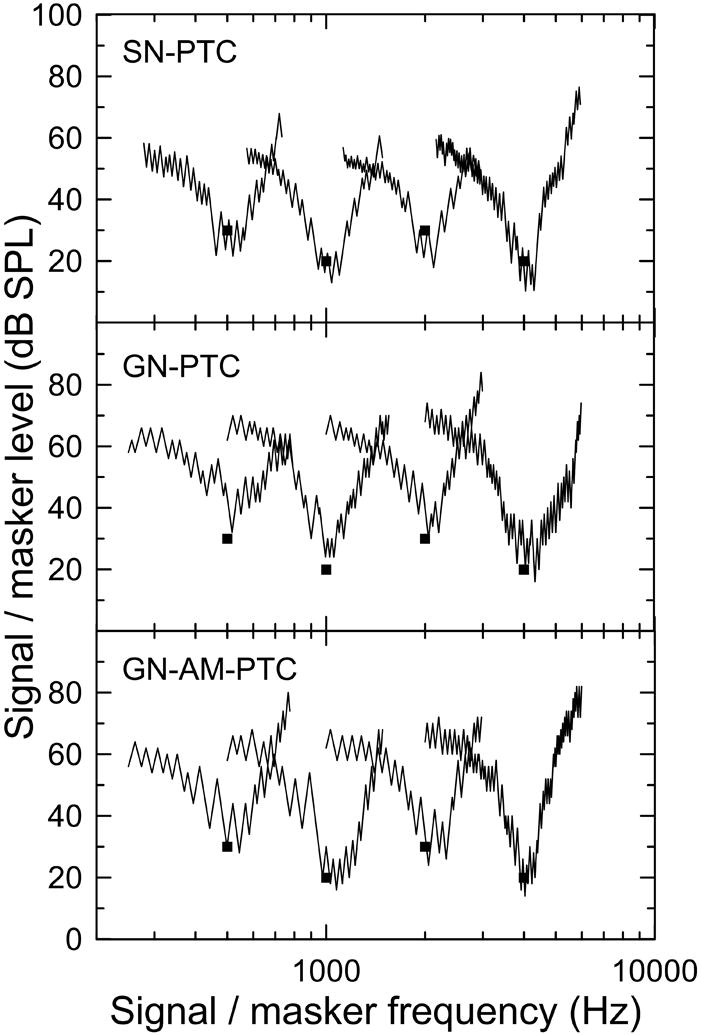
The PTCs collected with the SN-PTC, GN-PTC and GN-AM-PTC methods for subject NH18. The filled squares indicate the probe level and frequency. Data for the first run are shown.
The tip of the PTCs was usually shifted in the direction of the upward masker sweep (ftip > fsignal). This trend was observed in 80% of SN-PTC data, 81% of GN-PTC data and in 88% of GN-AM-PTC data. The individual and mean ERB values across methods, runs and fsignal are presented in Table 2.
Comparison of fast-PTC methods (effect of the masker type)
A within-subject ANOVA with masker type (GN vs. SN) and fsignal set as fixed factors was performed on ERBs and shifts at the ftip. In both conditions the probe signals had the same duration and were not amplitude modulated. There was a significant main effect of the masker type and the signal frequency on ERB (F1,6 = 13.7, p < .02, F3,23.5 = 82.0, p < .001, respectively). The only significant interaction was for fsignal and masker type (F3,18 = 3.89, p < .05). As shown in Fig. 3 SN-PTC resulted in smaller ERBs (sharper tuning) than GN-PTC with a difference between the two methods increasing with increasing fsignal (compare squares to circles). The main effects as well as the interactions were insignificant when the shift at the tip was considered (Fig. 4, squares and circles).
Fig. 3.
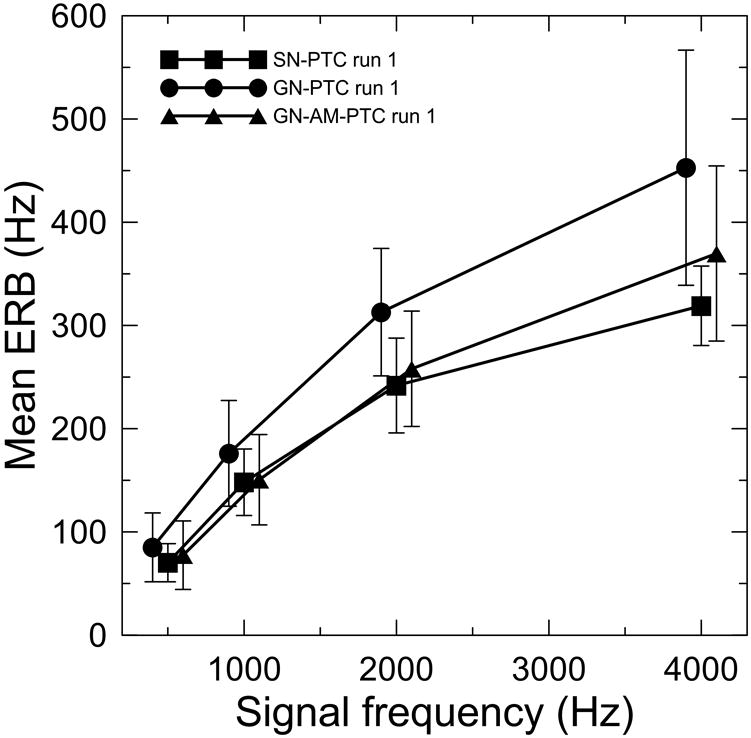
Mean equivalent rectangular bandwidths (ERB) derived from the data collected using SN-PTC (squares), GN-PTC (circles), and GN-AM-PTC (triangles) methods for run 1 as a function of the signal frequency. Data points are offset slightly for clarity. Error bars represent ±1 standard deviation.
Fig. 4.
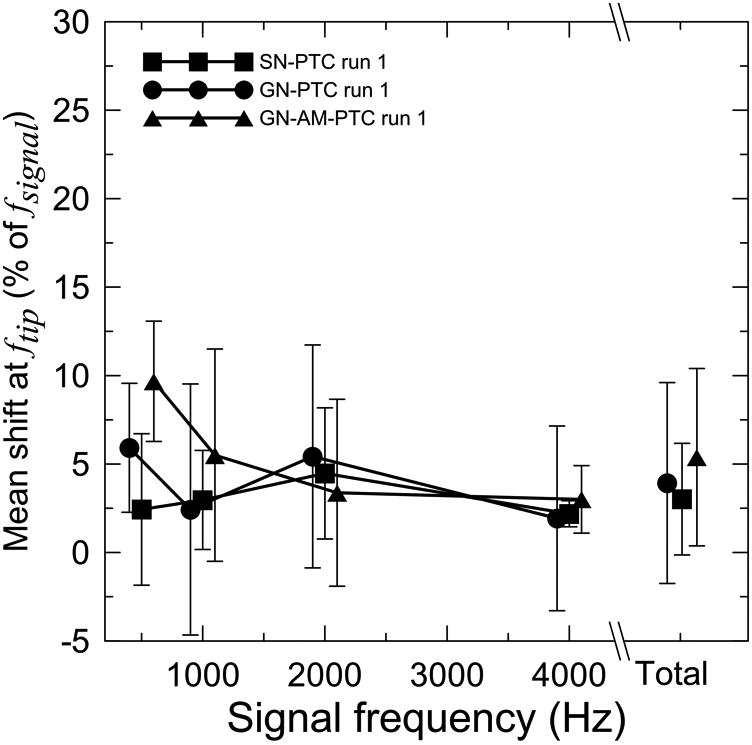
Mean shifts in the tip frequency of the PTC (in percent of signal frequency) for the SN-PTC (squares), GN-PTC (circles) and GN-AM-PTC (triangles) methods (run 1) as a function of the signal frequency. The total represents the global mean across fsignal for a given method. Data points are offset slightly for clarity. Error bars represent ±1 standard deviation.
Effect of signal amplitude modulation in the GN-PTC method
Analogous analyses were performed for data acquired with GN-PTC and GN-AM-PTC conditions. The ERBs were significantly smaller (on average by 42 Hz, see Fig. 3, circles and triangles) when an amplitude modulated tone probe was used as compared to the condition with an unmodulated probe (F1,6 = 12.9, p < .02). This suggests that the AM probe was not reducing the detection of beats. As expected, there was also a significant main effect of fsignal on ERB (F3,24.3 = 76.8, p < .001). The interactions did not reach the significance level.
With regard to the shift at the ftip, there was no significant main effect of the AM probe (F1,6 = .92, p = .38) and no significant interactions (Fig. 4), but unexpectedly there was an effect of fsignal (F3,25.3 = 3.87, p < .03). A post hoc test showed that the shift at 4000 Hz was significantly smaller than the shift at 500 Hz by 5.4% on average (p < .02), which was most probably driven by the relatively large mean shift at the ftip observed at 500 Hz for the GN-AM-PTC method (see Fig. 4, triangles). No other comparisons reached the significance level.
Repeatability and training effects
To assess if any of the fast-PTC methods provide more repeatable results, the mean absolute differences (MAD) between ftip and ERB obtained during the first and the second runs were calculated separately for each condition. Since both runs were collected within a single session large MAD values indicated that the subjects' performance was unstable over the recording time.
The results are presented in Table 3 (MAD values for ftip) and in Table 4 (MAD values for ERBs). On average the SN-PTC method resulted in the most repeatable results and the GN-PTC in the least repeatable results in terms of ftip and ERB (see Total in Table 3 and Table 4). However, some frequency specific differences were also observed. In general, the SN-PTC resulted in the smallest MAD values across the methods for either ftip or ERB at most signal frequencies, with the only considerably larger MAD for ERB at 1000 Hz, as compared to the GN-PTC method (Table 3 and Table 4). The addition of the AM probe to the gated-noise condition seemed to stabilize the subjects' performance at 500 Hz and 4000 Hz, which was reflected by smaller MAD values for both ftip and ERB, as compared to the GN-PTC condition. At 1000 Hz the addition of the AM probe had a detrimental effect on the repeatability of results, especially when the ERB was considered. However, at 2000 Hz effect of the AM probe on the MAD was not consistent for ftip and ERB. A within-subject analysis (fixed factors: fast-PTC method and fsignal) did not show a significant effect of the method on MAD ERB (F2,19.9 = 3.38, p = .05) and MAD ftip (F2,18.3 = 1.94, p = .17), which was most probably caused by the limited number of subjects. There were significant effects of fsignal on MAD ERB and MAD ftip (F3,27.7 = 6.27, p < .005, F3,25.5 = 3.08, p < .05, respectively). In general, larger MAD values were observed for higher signal frequencies than for lower frequencies. The interactions were not significant.
Table 3.
Mean absolute difference (MAD) between the frequencies at the tip (ftip) obtained for the first run and the second run calculated separately for each fast-PTC method and for each signal frequency as well as for data collapsed across signal frequencies (Total).
| Signal frequency | MAD for ftip (Hz) | ||
|---|---|---|---|
| SN-PTC | GN-PTC | GN-AM-PTC | |
| 500 Hz | 19 | 47 | 38 |
| 1000 Hz | 46 | 48 | 50 |
| 2000 Hz | 64 | 93 | 60 |
| 4000 Hz | 35 | 111 | 89 |
|
| |||
| Total (SD) | 41 (47) | 78 (68) | 62 (40) |
Table 4.
Mean absolute difference (MAD) between the equivalent rectangular bandwidth (ERB) obtained for the first run and the second run calculated separately for each fast-PTC method and for each signal frequency as well as for data collapsed across signal frequencies (Total).
| Signal frequency | MAD for ERB (Hz) | ||
|---|---|---|---|
| SN-PTC | GN-PTC | GN-AM-PTC | |
| 500 Hz | 14 | 26 | 13 |
| 1000 Hz | 36 | 25 | 42 |
| 2000 Hz | 50 | 65 | 74 |
| 4000 Hz | 40 | 140 | 59 |
|
| |||
| Total (SD) | 35 (25) | 68 (81) | 50 (36) |
To establish whether performance changed between run 1 and run 2 in a consistent direction or in a frequency dependent manner, within-subject ANOVA (fixed factors: run and fsignal) were performed separately for data obtained with any of the three methods. There was a significant effect of run on ERB only for the GN-PTC method, (F1,9.4 = 9.05, p < 0.02). Even though the interaction between run and fsignal did not reach the significance level (F3,14 = 3.10, p =.06), plausibly due to the small sample, mean data shown in Table 2 suggest that ERBs for GN-PTCs at 2000 and 4000 Hz were the only ones considerably different between the two runs. The tendency for GN-PTCs to get narrower over time within the recording session is plausibly due to training effects as demonstrated by a decrease in data scatter (Table 2). This suggests that the GN-PTC task could have been more difficult. A similar trend was not observed for the other two methods, suggesting that the subjects' performance for the SN-PTC and GN-AM-PTC methods was stable over the recording session even though only a minimal amount of training was provided. Thus, differences in ERBs observed between the methods were exaggerated due to inclusion only of data from run 1 in the previous analyses. Clearly GN-PTC run 2 ERBs were in good agreement with ERBs for either run 1 or 2 for SN-PTC and GN-AM-PTC methods (Table 2). The mean frequency shift at the tip was not consistently different between the runs for either method (data not shown).
Effect of signal frequency on PTC features
In this section the effect of the signal frequency on PTC parameters is considered. For brevity only SN-PTCs (run 1) are presented here. Similar trends were observed for GN-PTCs and GN-AM-PTCs.
Figure 5 summarizes the dependence between the sharpness of tuning expressed as QERB (ftip /ERB) and fsignal for the SN-PTCs as well as for previously-reported results using the simultaneous masked notched-noise method (Glasberg & Moore, 1990; Oxenham & Shera, 2003). The mean QERB are in good agreement with the notched-noise data at fsignal ≤ 2000 Hz. At 4000 Hz, SN-PTC suggests sharper tuning than predicted by previous studies (Glasberg & Moore, 1990; Oxenham & Shera, 2003). The fast-PTC QERB seems to depend on fsignal in a roughly linear way (for fsignal ≥ 1000 Hz). These changes correspond to an increase in average ERB with increasing fsignal at a rate of 0.73 oct/oct (Fig. 3), similar to the trend observed in animal data for auditory nerve fiber tuning curves (Temchin et al, 2008). In a within-subject ANOVA the fsignal had a significant effect on QERB (F3,21 = 14.54, p < .001), and subsequent paired comparisons showed that QERB at 4000 Hz was significantly larger from QERB at any other frequency. The same trends were observed for Q10 (ftip / width 10 dB above level at the tip), (see Table 5).
Fig. 5.
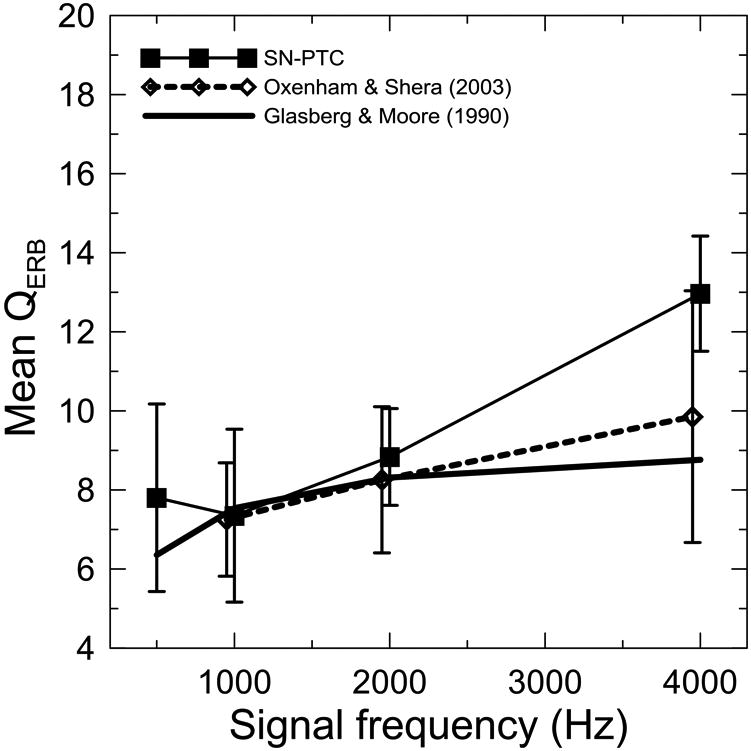
Mean QERB for SN-PTCs obtained in run 1 (squares). The QERBs of auditory filters derived with the simultaneous masked notched-noise paradigm are shown for comparison: the thick solid line corresponds to Glasberg and Moore's predictions (1990) and the dashed line with diamonds was replotted from Fig. 7 (signal level of 10 dB SL) of Oxenham and Shera (2003). Data points are offset slightly for clarity.
Table 5.
Mean QERB, Q10, low-frequency (LF) side slopes and high-frequency (HF) side slopes for SN-PTCs (run 1).
| Signal frequency | Mean (SD) | |||
|---|---|---|---|---|
| QERB | Q10 | LF slope (dB/oct) |
HF slope (dB/oct) |
|
| 500 Hz | 7.8 (2.4) | 4.1 (1.3) | −42 (5) | 79 (15) |
| 1000 Hz | 7.3 (2.2) | 4.4 (0.9) | −55 (3) | 96 (15) |
| 2000 Hz | 8.8 (1.2) | 4.9 (0.8) | −40 (5) | 101 (25) |
| 4000 Hz | 13.0 (1.5) | 7.1 (0.7) | −46 (8) | 158 (34) |
The slopes of the low-frequency (LF) and high-frequency (HF) sides of the PTCs were calculated for masker center frequencies from 0.7ftip to 0.95ftip and from 1.05ftip to 1.4ftip, respectively (Table 5). The absolute values of LF slope were considered in the statistical analysis. Within-subject ANOVA (fixed factors: LF vs. HF side, fsignal) showed significant side (F1,7 = 197.58, p < .001) and signal frequency effects (F3,21 = 16.35, p < .001) with significant interaction (F3,56 = 15.86, p < .001). In paired comparisons, significant differences between slopes were observed for any pair of comparisons (p < .01), but not between 2000 Hz and both 500 Hz (p = .08) and 1000 Hz (p = .33). The LF slope did not vary systematically with fsignal, while the HF slope increased with increasing fsignal and was always steeper than the LF slope (Table 5). These findings are consistent with an asymmetrical shape of the tuning curve (steeper HF than LF slopes) and an increase in asymmetry with increasing fsignal (increase in HF slope with increasing fsignal).
IV. Discussion
The aim of this study was to examine different approaches to measure fast PTCs. The main findings are as follows. The SN-PTC method resulted in sharper curves than the GN-PTC with the difference between the two methods increasing with increasing signal frequency (Fig. 3); however, the difference was exaggerated by possible effects of training on GN-PTC which were negligible for the SN-PTC method (Table 2). Amplitude modulating the probe in the GN-PTC paradigm significantly narrowed the curves, most prominently at higher fsignal's (Fig. 3). To estimate the shift at the tip frequency (e.g., for cochlear dead region diagnostics) the swept-noise (SN) and gated-noise (GD) methods may be used interchangeably. There was a tendency for SN-PTC to exhibit smaller data scatter (see Table 2 and Fig. 4) and better test-retest repeatability (Table 3 and Table 4) than GN-PTC. Whereas the AM probe had inconsistent effects on test-retest repeatability (Table 3 and Table 4), it considerably diminished training effects (Table 2), suggesting that the AM probe makes the task easier in the gated-noise fast-PTC paradigm.
Smoothing raw fast-PTC data
The fast-PTC paradigm results in “jagged” curves that need to undergo a preliminary analysis (smoothing) before parameterizing. Initially, Sęk et al. (2005) proposed to smooth the raw PTC with a two-point running average of successive reversal points and then to approximate the tip of the curve with two straight lines fitted to the low- and high-frequency sides of the smoothed curve. However, this method resulted in unreliable estimates of the frequency at the tip in approximately 15% of our fast-PTCs, in line with the observations of Malicka et al. (2009). Following the recommendations of Sęk et al (2007), we applied a polynomial fit, but with a higher order to approximate the PTC width. However, for reliable estimation of ERB a different order of polynomial had to be chosen separately for PTCs collected at different signal frequencies. The LOESS strategy, with smoothing parameter set at .25, resulted in smoothed curves that still closely followed the original data. Our fast-PTCs consisted of 61 (SD = 27) reversal points on average, whereas curves with substantially fewer points would plausibly require increasing α and the opposite would be true for more densely sampled tuning curves.
Equivalent Rectangular Bandwidth
The effects of masker sweep direction on the sharpness of tuning (Q10) have been reported by Malicka et al. (2009) as insignificant, which suggests that curves were simply shifted horizontally depending on the masker sweep direction. However, it must be pointed out that a relatively small sample size was used in that study, which could have prevented them from detecting significant effects. We believe that even if masker sweep direction could have affected the ERB values presented here, the effect was most probably similar across fast-PTC methods (as observed in case of shift at the ftip), thus it should not have compromised between-methods comparisons.
Temporal effects can have a substantial influence on the estimation of frequency selectivity, so that PTCs measured with a gated-masker were less sharply tuned compared to continuous-masker PTCs (e.g., Bacon & Moore, 1986; Bacon & Viemeister, 1985). A similar trend was observed in this study, where GN-PTCs were significantly broader at high signal frequencies than SN-PTCs (Fig. 3, circles and squares). However, this difference was exaggerated by the fact that only curves from the first run were considered in the statistical analysis. While ERBs did not change systematically with repeated runs for the SN-PTC method, the curves obtained during the second run were significantly narrower compared to the first run for the GN-PTC method (Table 2). Differences between SN-PTCs and GN-PTCs diminished when run 2 data were considered (Table 2); we conclude that gating the noise had a minor influence on estimates of frequency selectivity, but it made the task more difficult possibly due to confusion between the synchronously pulsed probe and noise.
Amplitude modulating the probe in the gated-noise condition was expected to minimize the effect of beat detection (Malicka et al, 2009), which should result in more consistent and broader PTC (Kluk & Moore, 2004). We did not observe any consistent differences in the PTC shapes when using an AM probe in the gated-noise condition. However, GN-AM-PTCs were significantly narrower than GN-PTCs, particularly at higher fsignal's (Fig. 3, triangles and circles). Absence of the expected AM probe effects could be caused by our use of relatively wide maskers, which are known to reduce beat detection as well (Kluk & Moore, 2004). The difference in tuning was caused by greater susceptibility of GN-PTC method to training effects, because the run 2 curves had widths comparable to GN-AM-PTC (Table 2). Accordingly, amplitude modulating the probe does not affect the PTC width (Markessis et al, 2009), but it makes the task easier when combined with a gated-noise masker. This conclusion is also supported by the substantially lower rejection rate of PTCs in the GN-AM-PTCs condition as compared to GN-PTCs.
Frequency at the PTC tip
For all fast-PTC methods the tip of the PTC was usually shifted away from the signal frequency in the direction of the masker sweep, which could be the result of a subject's responses lagging behind the change in percept (Sęk et al, 2005). In our experiments only an upward masker sweep direction was used (i.e., masker center frequency changed from low to high frequencies). The direction (in 80 - 88% of cases the ftip > fsignal) as well as magnitude of the shift at ftip (Fig. 4) was similar across the methods and consistent with published data (Malicka et al, 2009; Sęk et al, 2005; Sęk et al, 2007).
Optimizing fast-PTC recordings
The SN-PTC and GN-AM-PTC methods resulted in similar estimates of tuning curve features (Fig. 3 and Fig. 4) and were not susceptible to training, thus either method can be used for time-efficient assessment of frequency selectivity. However, the SN-PTC method resulted in a considerably higher rejection rate than GN-AM-PTC method (see Results), which could be a result of an excessively rapid sweep rate of the noise in the former condition (recall, that noise frequency changed here on a logarithmic scale, whereas in the GN methods it changed on a linear scale). The change of masker center frequency over time was chosen based on data available for the GN-PTC condition (Malicka et al, 2009, 2010) and SN-PTC masker duration was matched accordingly, implying that we possibly did not use optimal testing conditions for the latter method.
Comparison with notched-noise auditory filters
There is a very good agreement for frequencies up to 2000 Hz between QERBs derived from fast-PTCs and auditory filters measured with the notched-noise technique (Glasberg & Moore, 1990; Oxenham & Shera, 2003), (Fig. 5). The discrepancy at higher signal frequencies between the two sets of notched-noise data has been explained by differences in measurement techniques (fixed-noise with mid-level probe approach vs. fixed low-level probe approach, see Oxenham & Shera, 2003). It seems to be more appropriate to relate the fast-PTC data to Oxenham and Shera's (2003) results rather than to Glasberg and Moore's (1990) predictions. The former were acquired at the same probe levels (10 dB SL) as our fast-PTCs and with a similar approach (fixed-probe) where the masker level was adjusted until masked threshold was reached. A good agreement between fast-PTCs and fixed-probe notched-noise QERBs suggests that off-frequency listening, i.e., combining auditory information from multiple cochlear sites to improve signal detection (e.g., Johnson-Davies & Patterson, 1979; Moore, 2004; Moore et al, 1984) had a negligible influence on the width of tuning curves. Small discrepancies at 4000 Hz could result from use of only one masker sweep direction in fast-PTC measurements, differences in measurement techniques, or from individual differences in the sharpness of tuning. It remains unclear how sweep direction or general differences between measurement paradigms would lead to disagreements only at 4000 Hz but not at the remaining signal frequencies. Similarly, our data are in good agreement with Q10s of PTCs recorded with either traditional or fast methods at corresponding masker bandwidths for 1000 and 2000 Hz, but at 4000 Hz our subjects appear to have narrower curves (Kluk & Moore, 2004; Malicka et al, 2009; Markessis et al, 2009). Thus, it is most plausible that the observed differences at 4000 Hz reflect individual differences in frequency selectivity. The active cochlear mechanisms contributing to sharpness of tuning are believed to be stronger at higher signal frequencies, thus small differences in cochlear function across subjects may be more noticeable for high than low frequencies (Hicks & Bacon, 1999).
Conclusions
The swept-noise fast-PTC paradigm provided high-resolution and repeatable PTCs. The gated-noise method resulted in equivalent estimates of frequency selectivity in the condition with an amplitude modulated signal which diminished training effects as compared to the gated-noise condition with a steady signal. Thus, both methods show promise for use in laboratory or clinical settings as a time-efficient measure of frequency selectivity where a single PTC could be obtained within 3-4 minutes. In future studies effects of the rate of masker frequency change need to be evaluated to further optimize the measurement conditions.
Acknowledgments
This work was supported by NIDCD grant DC006014 and Northwestern University. We thank Dr. Aleksander Sęk for providing the swept-noise fast-PTC software and for help with implementing the method in our laboratory. We thank Dr. Sumitrajit Dhar, Dr. Beverly Wright and Dr. Steven Zecker for fruitful discussions and Kathleen Dunckley for reading the manuscript. We are also grateful to Dr. Andrew Oxenham and Dr. Christopher Shera for sharing their data. Preliminary data from this study were presented at the 34th MidWinter Meeting of the Association for Research in Otolaryngology in Baltimore, Maryland, February 2011.
Abbreviations
- AM
amplitude modulation
- ERB
equivalent rectangular bandwidth
- GN
gated-noise
- PTC
psychophysical tuning curve
- SN
swept-noise
Footnotes
For any filter, the ERB corresponds to the bandwidth of the rectangular filter that has the same center frequency and passes the same total power.
LOESS smoothing was utilized instead of a two-point running average (e.g., Sęk et al, 2005), because the former strategy resulted in more regular curves than the latter one without compromising the overall shape.
Declaration of interest: The authors report no declaration of interest.
References
- Bacon SP, Moore BCJ. Temporal effects in masking and their influence on psychophysical tuning curves. J Acoust Soc Am. 1986;80:1638–1645. doi: 10.1121/1.394328. [DOI] [PubMed] [Google Scholar]
- Bacon SP, Repovsch-Duffey JL, Liu L. Effects of signal delay on auditory filter shapes derived from psychophysical tuning curves and notched-noise data obtained in simultaneous masking. J Acoust Soc Am. 2002;112:227–237. doi: 10.1121/1.1485972. [DOI] [PubMed] [Google Scholar]
- Bacon SP, Viemeister NF. Simultaneous masking by gated and continuous sinusoidal maskers. J Acoust Soc Am. 1985;78:1220–1230. doi: 10.1121/1.392890. [DOI] [PubMed] [Google Scholar]
- Badri R, Siegel JH, Wright BA. Auditory filter shapes and high-frequency hearing in adults who have impaired speech in noise performance despite clinically normal audiograms. J Acoust Soc Am. 2011;129:852–863. doi: 10.1121/1.3523476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cleveland WS. Robust locally weighted regression and smoothing scatterplots. J Am Stat Assoc. 1979;74:829–836. [Google Scholar]
- Cleveland WS. The elements of graphing data: Rev edition. Murray Hill, N.J.: AT&T Bell Laboratories; 1994. [Google Scholar]
- Florentine M, Buus S, Scharf B, Zwicker E. Frequency selectivity in normally-hearing and hearing-impaired observers. J Speech Hear Res. 1980;23:646–669. doi: 10.1044/jshr.2303.646. [DOI] [PubMed] [Google Scholar]
- Gaudrain E, Grimault N, Healy EW, Bera JC. Effect of spectral smearing on the perceptual segregation of vowel sequences. Hear Res. 2007;231:32–41. doi: 10.1016/j.heares.2007.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasberg BR, Moore BCJ. Auditory filter shapes in subjects with unilateral and bilateral cochlear impairments. J Acoust Soc Am. 1986;79:1020–1033. doi: 10.1121/1.393374. [DOI] [PubMed] [Google Scholar]
- Glasberg BR, Moore BCJ. Derivation of auditory filter shapes from notched-noise data. Hear Res. 1990;47:103–138. doi: 10.1016/0378-5955(90)90170-t. [DOI] [PubMed] [Google Scholar]
- Grimault N, Gaudrain E. The consequences of cochlear damages on auditory scene analysis. Curr Top Acoust Res. 2006;4:17–24. [Google Scholar]
- Haggard MP, Lindblad AC, Foster JR. Psychoacoustical and audiometric prediction of auditory disability for different frequency responses at listener-adjusted presentation levels. Audiology. 1986;25:277–298. doi: 10.3109/00206098609078393. [DOI] [PubMed] [Google Scholar]
- Hicks ML, Bacon SP. Psychophysical measures of auditory nonlinearities as a function of frequency in individuals with normal hearing. J Acoust Soc Am. 1999;105:326–338. doi: 10.1121/1.424526. [DOI] [PubMed] [Google Scholar]
- Jacoby WG. Loess: a nonparametric, graphical tool for depicting relationships between variables. Elect Stud. 2000;19:577–613. [Google Scholar]
- Johnson-Davies D, Patterson RD. Psychophysical tuning curves - restricting the listening band to the signal region. J Acoust Soc Am. 1979;65:765–770. [Google Scholar]
- Kishon-Rabin L, Segal O, Algom D. Associations and dissociations between psychoacoustic abilities and speech perception in adolescents with severe-to-profound hearing loss. J Speech Lang Hear Res. 2009;52:956–972. doi: 10.1044/1092-4388(2008/07-0072). [DOI] [PubMed] [Google Scholar]
- Kluk K, Moore BCJ. Factors affecting psychophysical tuning curves for normally hearing subjects. Hear Res. 2004;194:118–134. doi: 10.1016/j.heares.2004.04.012. [DOI] [PubMed] [Google Scholar]
- Kluk K, Moore BCJ. Factors affecting psychophysical tuning curves for hearing-impaired subjects with high-frequency dead regions. Hear Res. 2005;200:115–131. doi: 10.1016/j.heares.2004.09.003. [DOI] [PubMed] [Google Scholar]
- Kluk K, Moore BCJ. Detecting dead regions using psychophysical tuning curves: a comparison of simultaneous and forward masking. Int J Audiol. 2006;45:463–476. doi: 10.1080/14992020600753189. [DOI] [PubMed] [Google Scholar]
- Lutman ME, Gatehouse S, Worthington AG. Frequency resolution as a function of hearing threshold, level and age. J Acoust Soc Am. 1991;89:320–328. doi: 10.1121/1.400513. [DOI] [PubMed] [Google Scholar]
- Lutman ME, Wood EJ. A simple clinical measure of frequency resolution. Br J Audiol. 1985;19:1–8. doi: 10.3109/03005368509078956. [DOI] [PubMed] [Google Scholar]
- Malicka AN, Munro KJ, Baker RJ. Fast method for psychophysical tuning curve measurement in school-age children. Int J Audiol. 2009;48:546–553. doi: 10.1080/14992020902845899. [DOI] [PubMed] [Google Scholar]
- Malicka AN, Munro KJ, Baker RJ. Diagnosing cochlear dead regions in children. Ear Hear. 2010;31:238–246. doi: 10.1097/AUD.0b013e3181c34ccb. [DOI] [PubMed] [Google Scholar]
- Markessis E, Poncelet L, Colin C, Coppens A, Hoonhorst I, Kadhim H, Deltenre P. Frequency tuning curves derived from auditory steady state evoked potentials: a proof-of-concept study. Ear Hear. 2009;30:43–53. doi: 10.1097/AUD.0b013e31818fbb7a. [DOI] [PubMed] [Google Scholar]
- Moore BCJ. Perceptual consequences of cochlear hearing loss and their implications for the design of hearing aids. Ear Hear. 1996;17:133–161. doi: 10.1097/00003446-199604000-00007. [DOI] [PubMed] [Google Scholar]
- Moore BCJ. Dead regions in the cochlea: diagnosis, perceptual consequences, and implications for the fitting of hearing aids. Trends Amplif. 2001;5:1–34. doi: 10.1177/108471380100500102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore BCJ. An introduction to the psychology of hearing 5th edition. London: Elsevier Academic Press; 2004. [Google Scholar]
- Moore BCJ. Cochlear hearing loss physiological psychological and technical issues 2nd edition. Chichester, UK: John Wiley; 2007. [Google Scholar]
- Moore BCJ, Glasberg BR, Roberts B. Refining the measurement of psychophysical tuning curves. J Acoust Soc Am. 1984;76:1057–1066. doi: 10.1121/1.391425. [DOI] [PubMed] [Google Scholar]
- Moore BCJ, Poon PW, Bacon SP, Glasberg B. The temporal course of masking and the auditory filter shape. J Acoust Soc Am. 1987;81:1873–1880. doi: 10.1121/1.394751. [DOI] [PubMed] [Google Scholar]
- Moore BCJ, Vickers DA, Plack CJ, Oxenham AJ. Inter-relationship between different psychoacoustic measures assumed to be related to the cochlear active mechanism. J Acoust Soc Am. 1999;106:2761–2778. doi: 10.1121/1.428133. [DOI] [PubMed] [Google Scholar]
- Nakaichi T, Watanuki K, Sakamoto S. A simplified measurement method of auditory filters for hearing-impaired listeners. Acoust Sci Technol. 2003;24:365–375. [Google Scholar]
- Oxenham AJ, Shera CA. Estimates of human cochlear tuning at low levels using forward and simultaneous masking. J Assoc Res Otolaryngol. 2003;4:541–554. doi: 10.1007/s10162-002-3058-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson JD, Baer T, Moore BCJ. Using transposition to improve consonant discrimination and detection for listeners with severe high-frequency hearing loss. Int J Audiol. 2007;46:293–308. doi: 10.1080/14992020601188591. [DOI] [PubMed] [Google Scholar]
- Sęk A, Alcantara J, Moore BCJ, Kluk K, Wicher A. Development of a fast method for determining psychophysical tuning curves. Int J Audiol. 2005;44:408–420. doi: 10.1080/14992020500060800. [DOI] [PubMed] [Google Scholar]
- Sęk A, Moore BCJ. Implementation of a fast method for measuring psychophysical tuning curves. Int J Audiol. 2011;50:237–242. doi: 10.3109/14992027.2010.550636. [DOI] [PubMed] [Google Scholar]
- Sęk A, Wicher A, Drgas S. A fast method for the determination of psychophysical tuning curves: further refining. Arch Acoust. 2007;32:707–728. [Google Scholar]
- Stone MA, Glasberg BR, Moore BCJ. Simplified measurement of auditory filter shapes using the notched-noise method. Br J Audiol. 1992;26:329–334. doi: 10.3109/03005369209076655. [DOI] [PubMed] [Google Scholar]
- Summers V, Molis MR, Musch H, Walden BE, Surr RK, Cord MT. Identifying dead regions in the cochlea: psychophysical tuning curves and tone detection in threshold-equalizing noise. Ear Hear. 2003;24:133–142. doi: 10.1097/01.AUD.0000058148.27540.D9. [DOI] [PubMed] [Google Scholar]
- Temchin AN, Rich NC, Ruggero MA. Threshold tuning curves of chinchilla auditory-nerve fibers. I. Dependence on characteristic frequency and relation to the magnitudes of cochlear vibrations. J Neurophysiol. 2008;100:2889–2898. doi: 10.1152/jn.90637.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wegel RL, Lane CE. The auditory masking of one pure tone by another and its probable relation to the dynamics of the inner ear. Phys Rev. 1924;23:266–285. [Google Scholar]
- Wright BA, Dai H. Detection of unexpected tones in gated and continuous maskers. J Acoust Soc Am. 1994;95:939–948. doi: 10.1121/1.410011. [DOI] [PubMed] [Google Scholar]
- Zwicker E. On a psychoacoustical equivalent of tunning curves. In: Zwicker, Terhardt, editors. Facts and models in hearing. Berlin: Springer-Verlag; 1974. pp. 132–140. [Google Scholar]
- Zwicker E, Schorn K. Psychoacoustical tuning curves in audiology. Audiology. 1978;17:120–140. doi: 10.3109/00206097809080039. [DOI] [PubMed] [Google Scholar]


