Kinematics of cardiac growth: In vivo characterization of growth tensors and strains

Abstract

Progressive growth and remodeling of the left ventricle are part of the natural history of chronic heart failure and strong clinical indicators for survival. Accompanied by changes in cardiac form and function, they manifest themselves in alterations of cardiac strains, fiber stretches, and muscle volume. Recent attempts to shed light on the mechanistic origin of heart failure utilize continuum theories of growth to predict the maladaptation of the heart in response to pressure or volume overload. However, despite a general consensus on the representation of growth through a second order tensor, the precise format of this growth tensor remains unknown. Here we show that infarct-induced cardiac dilation is associated with a chronic longitudinal growth, accompanied by a chronic thinning of the ventricular wall. In controlled in vivo experiments throughout a period of seven weeks, we found that the lateral left ventricular wall adjacent to the infarct grows longitudinally by more than 10%, thins by more than 25%, lengthens in fiber direction by more than 5%, and decreases its volume by more than 15%. Our results illustrate how a local loss of blood supply induces chronic alterations in structure and function in adjacent regions of the ventricular wall. We anticipate our findings to be the starting point for a series of in vivo studies to calibrate and validate constitutive models for cardiac growth. Ultimately, these models could be useful to guide the design of novel therapies, which allow us to control the progression of heart failure.

1. INTRODUCTION

Heart disease is the leading cause of death and disability both in the industrialized nations and in the developing world, accounting for 40% of all human mortality. More than 25 million people worldwide suffer from heart failure, a chronic condition in which pumping efficiency is gradually reduced as the heart muscle becomes progressively weaker [46]. The single most common cause of heart failure is ischemic heart disease with an episode of acute myocardial infarction. Despite intensive research, there is no medical therapy at present to stop or reverse the advancement of heart failure. The dilation of the left ventricle, the change in ventricular shape, and the decrease in ejection fraction are clinical indicators of disease progression and strong predictors of survival [32]. Effective therapies for heart failure seek to attenuate these indicators and reverse the growth and remodeling process. Currrent research in biomaterials focuses on three classes of therapies with the common goal to provide structural support to the ventricular wall: the injection of living cells into the damaged myocardium [54], the implantation of in vitro engineered active cardiac tissue patches [4, 34], and the use of synthetic passive patches [13] or passive support devices [10] to reduce ventricular wall strains.

Continuum mechanics models in combination with new imaging techniques and modern simulation tools are now being recognized to have a great potential in predicting and improving these treatment strategies [5, 31, 53]. The first continuum approach to characterize growth in soft biological tissues was introduced two decades ago [44]. It is based on the multiplicative decomposition of the deformation gradient into an elastic and a growth part [49]. Key to this theory is the identification of the underlying second order growth tensor and its evolution in response to changes in mechanical loading [21, 36]. In the context of cardiac growth, isotropic [28, 48], transversely isotropic [42, 49], and general anisotropic [18, 19, 23] growth tensors have been proposed, to characterize ideopathic and infarct-induced growth [3, 27]. The identification of growth tensors for different types of tissue has been recognized as one of the most important challenges in growth and remodeling and remains an active area of research [1].

For more than three decades, the use of implanted radiopaque markers has provided considerable insight into the complex dynamics of the healthy and diseased ventricular myocardium [16]. One of the major breakthroughs enabled by the transmural marker technique [52] was to precisely quantify how individual strain components change from the epicardium, the outer wall, to the endocardium, the inner wall [35]. Marker techniques have been used successfully to identify acute changes in strain profiles, for example initiated by varying afterload [50] or by ventricular pacing [11]. However, the true strength of this technique lies in its permanent nature, which allows us to precisely quantify chronic changes, for example in response to mitral regurgitation [6] or myocardial infarction [9, 56]. Here, we utilize the transmural marker technique to characterize growth tensors and strains in the lateral left ventricular wall in response to myocardial infarction. In combination with fiber directions identified from tissue histology [15], this allows us to quantify fiber strains throughout the cardiac cycle [2, 51], and characterize chronic fiber lengthening, which is believed to be one of the major microstructural mechanisms for cardiac dilation in heart failure [12, 19]. Our main objective is to demonstrate how continuum growth models for cardiac growth [18, 23, 28] could potentially be calibrated and validated using the transmural marker technique.

2. MATERIALS AND METHODS

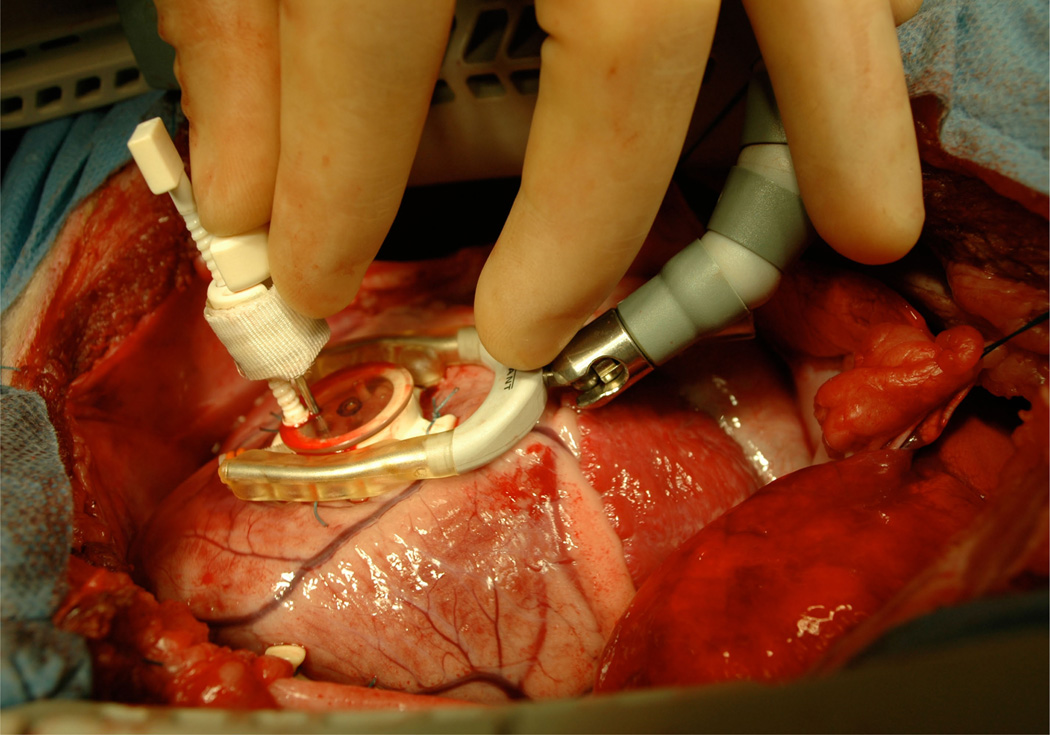
This study is approved by the Stanford Medical Center Laboratory Research Animal Review Committee and conducted along Stanford University policy. We premedicate eleven adult male dorsett-hybrid sheep with ketamine for venous and arterial catheter placement. Then, we induce anastesia with thiopental sodium, and maintain it with inhalational isoflurane and supplemental oxygen. We perform a left thoracotomy and measure the left ventricular wall thickness of the midlateral equatorial region with epicardial echocardiography. In this region, we implant three transmural columns of four bead sets each, using a depth-adjustable bead insertion trocar [52]. To guide the trocar, we suture a planar plexiglas template with three holes, spaced 10 mm apart, to the epicardial surface, see Figure 1. First, we insert three 0.7 mm diameter beads in each column, evenly spaced between the endo- and epicardial surfaces. Then, we sew a fourth 1.7 mm diameter bead onto the epicardial surface above each of the three columns [7], see Figure 2. Last, we pass polypropylene sutures around one or two obtuse marginal branches of the left circumflex coronary artery, where they are loosely snared [33]. Finally, we close the chest and recover the sheep.

Figure 1.

Three transmural columns of four bead sets each are implanted across the lateral wall using a depth-adjustable bead insertion trocar. To guide the trocar, a planar plexiglas template with three holes, spaced 10 mm apart, is sutured to the epicardial surface. First, three 0.7 mm diameter beads are inserted in each column, evenly spaced between the endo- and epicardial surfaces. Then, a fourth 1.7 mm diameter bead is sewn onto the epicardial surface above each column.

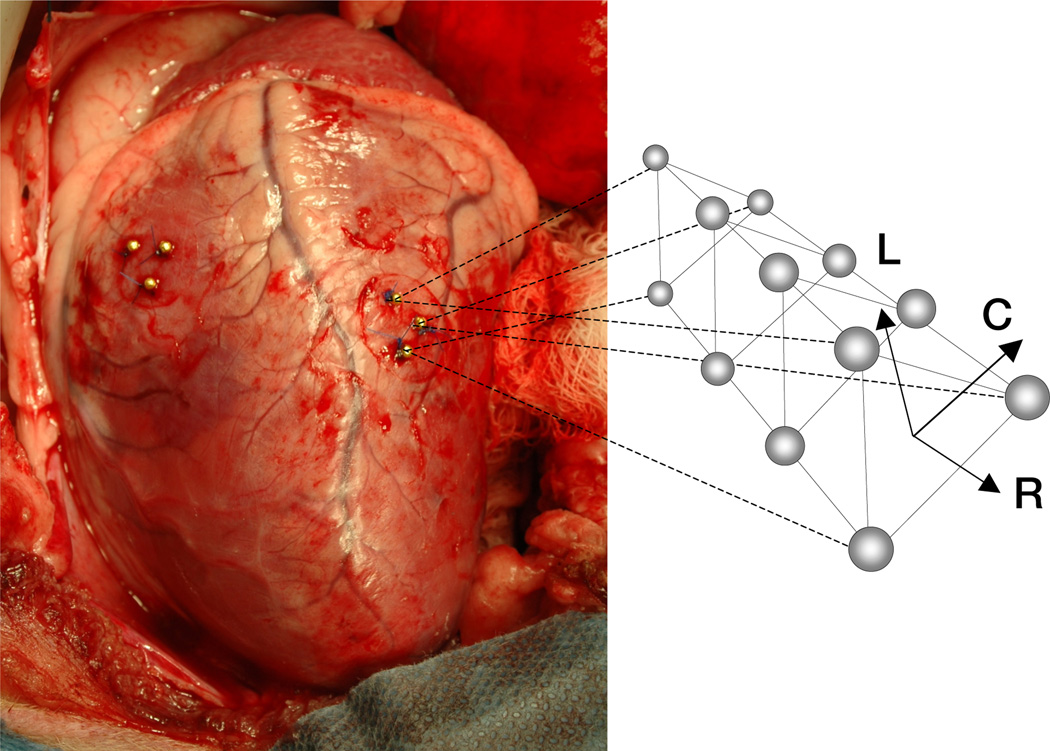
Figure 2.

Three transmural columns of four bead sets each are implanted across the lateral wall. We define a local Cartesian coordinate system {e_c, e_l, e_r} aligned with the local circumferential C, longitudinal L, and radial R directions. The radial axis e_r is oriented normal to the plane spanned by the three epicardial beads. The circumferential axis e_c wraps around the heart with a mathematically positive orientation, normal to the vector connecting the apex of the heart with the origin of the coordinate system, and normal to the radial axis e_r. The longitudinal axis e_l = e_r × e_c points from apex to base, normal to the radial and circumferential axes.

One week postoperatively, we take the sheep to the cardiac catheterization laboratory, where we sedate it with ketamine, intubate it, and ventilate it mechanically. We maintain general anasthesia with inhalational isoflurane. With the heart in normal sinus rhythm, and ventilation arrested at end expiration, we record image sequences of the twelve beads using biplane videofluoroscopy at a sampling frequency of 60 Hz. With the animal in the right lateral decubitus position, we simultaneously record aortic pressure, left ventricular pressure, and electrocardiogram voltage signals. Immediately thereafter, we premedicate the animal with lidocaine, bretylium, and magnesium, and tighten the coronary artery snares to occlude the selected vessel. After verifying the occlusion angiographically [9], we stabilize and recover the animal.

Eight weeks postoperatively, each animal returns to the cardiac catheterization laboratory to record hemodynamic data and bead coordinates as described above. Using a semi-automated digitization software [38], we extract the three-dimensional coordinates x(X, t) of the four by three beads from the acquired biplane images at an accuracy of 0.1±0.3 mm [14].

3. THEORY AND CALCUATION

3.1. Cardiac Coordinates

To create a functional representation of the strain field across the lateral wall, we define a local Cartesian coordinate system {e_c, e_l, e_r} aligned with the local circumferential, radial, and longitudinal directions, see Figure 2. We place its origin into the geometric center of the three epicardial beads. The radial axis e_r is oriented normal to the plane spanned by these beads, with a positive outward direction. The circumferential axis e_c wraps around the heart with a mathematically positive orientation, normal to the vector connecting the apex of the heart with the origin of the coordinate system, and normal to the radial axis e_r. The longitudinal axis e_l points from apex to base, normal to the radial and circumferential axes, e_l = e_r × e_c.

3.2. Temporal Interpolation

To create an average spatio-temporal strain representation across the lateral left ventricular wall, we map all eleven experimental data sets into four time intervals between End Diastole, ED, defined as the time point before the pressure begins to increase, End Isovolumic Contraction, EIC, defined as one time point after maximum dLVP /dt, End Systole, ES, defined as one time point before minimum dLVP /dt, and End Isovolumic Relaxation, EIR, defined as the beginning of filling when the pressure stops to increase [51]. These four time intervals are further subdivided into five segments from ED to EIC, eleven segments from EIC to ES, six segments from ES to EIR, and fifteen segments from EIR to ED, respectively, based on different average interval lengths. To create temporally aligned data sets of hemodynamic and kinematic data, we apply an averaging method previously described [40, 41]: At the four characteristic time points of ED, EIC, ES, and EIR, we perform an exact averaging of the experimentally acquired left ventricular pressures LVP(t) and the raw data points x(X, t) of all eleven animals. At the remaining four, ten, five, and fourteen points, we perform a time-aligned averaging based on a linear temporal interpolation between the experimentally acquired data sets within the respective interval. As a result, we can now represent the cardiac cycle through t_n discrete time points n = 1, …, 37, i.e., four exactly averaged and 33 time-aligned and averaged [43, 51]. Using these time-aligned data sets, we perform the strain calculations described in the following section.

3.3. Spatial Interpolation

We assume that, within the space enclosed by each bead set, the current placement φ(X, t) of each material point X at each time t can be approximated by a time-dependent mapping c_I (t) of the spatial interpolation N_I (X) in the reference configuration,

$$\mathit{\phi }(\mathit{X},t)={\displaystyle {\sum }_{I=1}^{n_{\text{apx}}}}{\mathit{c}}_I(t)N_I(\mathit{X})$$ (1)

where I = 1, …, n_apx is the order of the approximation [51]. In particular, at each of the J = 1, …, n_pnt experimentally measured data points this implies that

$${\mathit{x}}_J(t)={\displaystyle {\sum }_{I=1}^{n_{\text{apx}}}}{\mathit{c}}_I(t)N_I({\mathit{X}}_J)$$ (2)

where x = [x_c, x_l, x_r]^t are the measured data points, c = [c_c, c_l, c_r]^t are the unknown coefficients at each discrete time point t associated with the circumferential, longitudinal, and radial directions, and N_I are the interpolation terms associated with the corresponding coordinates X of point J in the reference configuration. We choose a linear interpolation in the circumferential and longitudinal directions and a quadratic interpolation in the radial direction [24], such that N_I can be expressed through the following n_apx = 9 terms, $N_I={[X_c{X}_r^2,X_c{X}_r,X_c,X_l{X}_r^2,X_l{X}_r,X_l{X}_r^2,X_r,1]}^{\mathrm{t}}$. Since we acquire the coordinates of twelve data points while only applying an approximation with nine unknowns, i.e., n_pnt = 12 > n_apx = 9, the overall system for the unknown coefficients c_I

$$\mathbf{x}{(t)}_{[3\times 12]}=\mathbf{c}{(t)}_{[3\times 9]}·{\mathbf{N}}_{[9\times 12]}$$ (3)

is overdetermined. In the above matrix representation of equation (2), we have introduced the matrix notation for the measured coordinates of the data points x_[3×12] = [x₁, …, x₁₂], for the unknown coefficients c_[3×9] = [c₁, …, c₉], and for the interpolation matrix N_[9×12] = [N_I(X₁), …, N_I(X₁₂)]^t. We solve this system for the unknown coefficient matrix c(t) using the pseudo inverse of the interpolation matrix N [51].

$$\mathbf{c}{(t)}_{[3\times 9]}=\mathbf{x}{(t)}_{[3\times 12]}·{\mathbf{N}}_{[12\times 9]}^{\mathrm{t}}·{[{\mathbf{N}}_{[9\times 12]}·{\mathbf{N}}_{[12\times 9]}^{\mathrm{t}}]}^{-1}$$ (4)

With the coefficients c(t) known at each discrete time point t, we can evaluate the nonlinear deformation map $\mathit{\phi }(\mathit{X},t)={\displaystyle {\sum }_{I=1}^{n_{\text{apx}}}}{\mathit{c}}_I(t)N_I(\mathit{X})$ as introduced in equation (1).

3.4. Deformation gradients

With the help of equation (1), the deformation gradient F = ∇φ takes the following functional representation,

$$\mathit{F}(\mathit{X},t)={\displaystyle {\sum }_{I=1}^{n_{\text{apx}}}}{\mathit{c}}_I(t)\otimes \mathbf{\nabla }{N}_I(\mathit{X})$$ (5)

where ∇(∘) = [∂_c(∘), ∂_l(∘), ∂_r(∘)]^t denotes the spatial gradient with respect to the local cardiac coordinate system. Its determinant

$$J(\mathit{X},t)=\text{det }(\mathit{F}(\mathit{X},t))$$ (6)

characterizes the local volume change between the reference and the current configuration. To characterize changes in muscle fiber length, we calculate the local fiber stretch

$${\lambda }_{\text{FF}}(\mathit{X},t)={[\mathit{f}(\mathit{X})·{\mathit{F}}^{\mathrm{t}}(\mathit{X},t)·\mathit{F}(\mathit{X},t)·\mathit{f}(\mathit{X})]}^{1/2}$$ (7)

as a function of the deformation gradient F and the local fiber direction f = [cos α, sin α, 0]^t, which is parameterized in terms of the fiber angle α. According to the literature, we vary α transmurally as α = −22.5°, +10.0°, +55.0° at 20%, 50%, 80% depth [15]. To illustrate the difference between the elastic deformation gradient ${\mathit{F}}_{\mathrm{W}1}^{\mathrm{e}}$ at week 1 and ${\mathit{F}}_{\mathrm{W}8}^{\mathrm{e}}$ at week 8, we evaluate equations (5), (6), and (7) with the end diastolic state ED as reference configuration and the end systolic state ES as current configuration, report means and standard deviations for all eleven animals, and compare ${\mathit{F}}_{\mathrm{W}1}^{\mathrm{e}}\text{ and }{\mathit{F}}_{\mathrm{W}8}^{\mathrm{e}}$ using student’s paired t-test in Table 1. To illustrate chronic changes between week 1 and week 8, we evaluate the end-diastolic growth tensor ${\mathit{F}}_{\text{ED}}^{\mathrm{g}}$ and the end-systolic growth tensor ${\mathit{F}}_{\text{ES}}^{\mathrm{g}}$ with week 1 as reference configuration and week 8 as current configuration, report means and standard deviations for all eleven animals, and show p-values from two-tailed paired t-tests comparing week 8 with the identity tensor in Tables 2 and 3. We report values at 20%, 50%, and 80% depth. We consider comparisons with p < 0.05 as statistically significant and indicate them in grey in the corresponding tables.

Table 1.

Transmural elastic deformation gradients ${\mathit{F}}_{\mathrm{W}1}^{\mathrm{e}}\text{ and }{\mathit{F}}_{\mathrm{W}8}^{\mathrm{e}}$ at weeks 1 and 8 from ED to ES. Means and standard deviations are displayed for n=11 animals. P-values are from two-tailed paired t-tests comparing ${\mathit{F}}_{\mathrm{W}1}^{\mathrm{e}}\text{ with }{\mathit{F}}_{\mathrm{W}8}^{\mathrm{e}}$.

	epicardium - 20% depth			midwall - 50% depth			endocardium - 80% depth
	week 1	week 8	p	week 1	week 8	p	week 1	week 8	p
${\mathrm{F}}_{\text{CC}}^{\mathrm{e}}$	0.96±0.03	1.00±0.07	0.98	0.93±0.04	0.96±0.07	0.31	0.90±0.05	0.93±0.07	0.21
${\mathrm{F}}_{\text{CL}}^{\mathrm{e}}$	0.02±0.03	−0.03±0.07	0.08	0.03±0.03	−0.02±0.08	0.06	0.04±0.05	−0.01±0.08	0.04
${\mathrm{F}}_{\text{CR}}^{\mathrm{e}}$	0.06±0.16	0.15±0.13	0.09	0.08±0.05	0.10±0.09	0.56	0.10±0.06	0.06±0.10	0.27
${\mathrm{F}}_{\text{LC}}^{\mathrm{e}}$	−0.01±0.05	0.06±0.09	0.04	0.00±0.06	0.07±0.10	0.02	0.03±0.05	0.10±0.09	0.01
${\mathrm{F}}_{\text{LL}}^{\mathrm{e}}$	1.00±0.05	1.01±0.09	0.60	0.97±0.06	1.00±0.10	0.31	0.94±0.05	0.99±0.11	0.07
${\mathrm{F}}_{\text{LR}}^{\mathrm{e}}$	0.03±0.05	0.20±0.16	0.00	0.11±0.09	0.23±0.12	0.04	0.18±0.15	0.21±0.16	0.63
${\mathrm{F}}_{\text{RC}}^{\mathrm{e}}$	0.01±0.03	0.02±0.09	0.61	0.02±0.05	0.04±0.13	0.51	0.03±0.04	0.06±0.10	0.28
${\mathrm{F}}_{\text{RL}}^{\mathrm{e}}$	0.00±0.02	−0.00±0.04	0.75	−0.00±0.04	−0.00±0.06	0.84	−0.01±0.07	−0.00±0.06	0.61
${\mathrm{F}}_{\text{RR}}^{\mathrm{e}}$	1.04±0.05	1.08±0.15	0.42	1.10±0.05	1.07±0.10	0.40	1.16±0.09	1.07±0.12	0.03
Je	0.99±0.04	1.03±0.07	0.16	0.99±0.05	1.02±0.04	0.01	0.98±0.04	0.99±0.07	0.60
${\lambda }_{\text{FF}}^{\mathrm{e}}$	0.96±0.03	0.96±0.07	0.88	0.94±0.04	0.98±0.08	0.17	0.97±0.03	1.03±0.06	0.01

Table 2.

Transmural end-diastolic growth tensor ${\mathit{F}}_{\text{ED}}^{\mathrm{g}}$ from ED week 1 to ED week 8. Means and standard deviations are displayed for n=11 animals. P-values are from two-tailed paired t-tests comparing ED at week 8 with ED at week 1, i.e., with the identity tensor.

	epi		mid		endo
	20% depth	p	50% depth	p	80% depth	p
${\mathrm{F}}_{\text{CC}}^{\mathrm{g}}$	1.00±0.12	0.96	1.03±0.14	0.46	1.02±0.10	0.44
${\mathrm{F}}_{\text{CL}}^{\mathrm{g}}$	0.04±0.14	0.42	0.01±0.10	0.77	0.01±0.09	0.61
${\mathrm{F}}_{\text{CR}}^{\mathrm{g}}$	−0.07±0.29	0.46	−0.03±0.16	0.61	0.05±0.14	0.29
${\mathrm{F}}_{\text{LC}}^{\mathrm{g}}$	−0.02±0.17	0.75	−0.04±0.13	0.33	−0.04±0.11	0.24
${\mathrm{F}}_{\text{LL}}^{\mathrm{g}}$	1.10±0.15	0.06	1.10±0.13	0.03	1.11±0.11	0.01
${\mathrm{F}}_{\text{LR}}^{\mathrm{g}}$	0.02±0.16	0.71	0.10±0.20	0.11	0.18±0.34	0.12
${\mathrm{F}}_{\text{RC}}^{\mathrm{g}}$	−0.01±0.09	0.64	−0.03±0.17	0.54	−0.05±0.19	0.41
${\mathrm{F}}_{\text{RL}}^{\mathrm{g}}$	0.00±0.05	0.86	−0.00±0.09	0.96	−0.01±0.11	0.67
${\mathrm{F}}_{\text{RR}}^{\mathrm{g}}$	0.68±0.15	0.00	0.73±0.15	0.00	0.77±0.22	0.01
Jg	0.74±0.19	0.00	0.82±0.19	0.01	0.89±0.21	0.10
${\lambda }_{\text{FF}}^{\mathrm{g}}$	1.03±0.12	0.49	1.04±0.16	0.36	1.08±0.11	0.04

Table 3.

Transmural end-systolic growth tensor ${\mathit{F}}_{\text{ES}}^{\mathrm{g}}$ from ES week 1 to ES week 8. Means and standard deviations are displayed for n=11 animals. P-values are from two-tailed paired t-tests comparing ES at week 8 with ES at week 1, i.e., with the identity tensor.

	epi		mid		endo
	20% depth	p	50% depth	p	80% depth	p
${\mathrm{F}}_{\text{CC}}^{\mathrm{g}}$	1.00±0.16	0.96	1.06±0.17	0.27	1.07±0.13	0.13
${\mathrm{F}}_{\text{CL}}^{\mathrm{g}}$	−0.01±0.16	0.80	−0.04±0.12	0.25	−0.06±0.10	0.07
${\mathrm{F}}_{\text{CR}}^{\mathrm{g}}$	−0.03±0.21	0.63	−0.02±0.09	0.54	0.03±0.13	0.52
${\mathrm{F}}_{\text{LC}}^{\mathrm{g}}$	0.04±0.21	0.55	0.02±0.18	0.73	0.02±0.13	0.56
${\mathrm{F}}_{\text{LL}}^{\mathrm{g}}$	1.11±0.18	0.07	1.13±0.18	0.04	1.18±0.16	0.00
${\mathrm{F}}_{\text{LR}}^{\mathrm{g}}$	0.10±0.11	0.02	0.12±0.13	0.01	0.13±0.27	0.15
${\mathrm{F}}_{\text{RC}}^{\mathrm{g}}$	−0.00±0.07	0.91	−0.01±0.15	0.85	−0.02±0.21	0.76
${\mathrm{F}}_{\text{RL}}^{\mathrm{g}}$	0.00±0.03	0.99	0.00±0.06	0.91	0.00±0.10	0.92
${\mathrm{F}}_{\text{RR}}^{\mathrm{g}}$	0.70±0.19	0.00	0.72±0.19	0.00	0.75±0.22	0.00
Jg	0.76±0.22	0.01	0.86±0.22	0.06	0.92±0.21	0.22
${\lambda }_{\text{FF}}^{\mathrm{g}}$	1.02±0.14	0.59	1.08±0.17	0.13	1.15±0.13	0.00

3.5. Strains

Using the deformation gradient F defined in the previous section, we can introduce the Green-Lagrange strain tensor in the cardiac coordinate system.

$$\mathit{E}(\mathit{X},t)=\frac{1}{2}[{\mathit{F}}^{\mathrm{t}}·\mathit{F}-\mathit{I}]$$ (8)

To characterize the local fiber strains E_FF(X, t), we project E onto the local fiber direction f (X),

$${\mathrm{E}}_{\text{FF}}(\mathit{X},t)=\mathit{f}(\mathit{X})·\mathit{E}(\mathit{X},t)·\mathit{f}(\mathit{X})$$ (9)

such that ${\mathrm{E}}_{\text{FF}}=1/2[{{\lambda }_{\text{FF}}}^2-1]$. To demonstrate the difference between the elastic strains ${\mathit{E}}_{\mathrm{W}1}^{\mathrm{e}}$ at week 1 and ${\mathit{E}}_{\mathrm{W}8}^{\mathrm{e}}$ at week 8, we evaluate equations (8) and (9) with the end diastolic state ED as reference configuration and the end systolic state ES as current configuration, report means and standard deviations for all eleven animals, and compare ${\mathit{E}}_{\mathrm{W}1}^{\mathrm{e}}\text{ and }{\mathit{E}}_{\mathrm{W}8}^{\mathrm{e}}$ using student’s paired t-test in Table 4. To illustrate chronic changes between week 1 and week 8, we evaluate the end-diastolic growth strains ${\mathit{E}}_{\text{ED}}^{\mathrm{g}}$ and the end-systolic growth strains ${\mathit{E}}_{\text{ES}}^{\mathrm{g}}$ with week 1 as reference configuration and week 8 as current configuration, report means and standard deviations for all eleven animals, and show p-values from two-tailed paired t-tests comparing growth strains at week 8 with the ungrown state at week 1 in Tables 2 and 3. We report discrete values at 20%, 50%, and 80% depth. We consider comparisons with p < 0.05 as statistically significant and indicate them in grey in the corresponding tables. To illustrate the temporal variation of the elastic cardiac strains ${\mathit{E}}_{\mathrm{W}1}^{\mathrm{e}}\text{ and }{\mathit{E}}_{\mathrm{W}8}^{\mathrm{e}}$, we evaluate equation (8) in the midwall, i.e., at 50% depth throughout an entire cardiac cycle t, and report means and standard deviations for all eleven animals in Figure 4. To illustrate the spatio-temporal variation of the elastic cardiac strains ${\mathit{E}}_{\mathrm{W}1}^{\mathrm{e}}\text{ and }{\mathit{E}}_{\mathrm{W}8}^{\mathrm{e}}$, we evaluate equation (8) for varying depths, i.e., along the radial direction X = [0, 0, X_r]^t, and report the average strains for all eleven animals throughout the three consecutive heart beats t in Figure 5.

Table 4.

Transmural elastic strains ${\mathit{E}}_{\mathrm{W}1}^{\mathrm{e}}\text{ and }{\mathit{E}}_{\mathrm{W}8}^{\mathrm{e}}$ at weeks 1 and 8 from ED to ES. Means and standard deviations are displayed for n=11 animals. P-values are from two-tailed paired t-tests comparing ${\mathit{E}}_{\mathrm{W}1}^{\mathrm{e}}\text{ with }{\mathit{E}}_{\mathrm{W}8}^{\mathrm{e}}$.

	epicardium - 20% depth			midwall - 50% depth			endocardium - 80% depth
	week 1	week 8	p	week 1	week 8	p	week 1	week 8	p
${\mathrm{E}}_{\text{CC}}^{\mathrm{e}}$	−0.04±0.02	−0.03±0.06	0.69	−0.06±0.03	−0.02±0.08	0.19	−0.09±0.05	−0.05±0.07	0.10
${\mathrm{E}}_{\text{LL}}^{\mathrm{e}}$	0.00±0.05	0.01±0.09	0.44	−0.03±0.05	0.01±0.09	0.19	−0.05±0.04	0.00±0.10	0.03
${\mathrm{E}}_{\text{RR}}^{\mathrm{e}}$	0.05±0.05	0.15±0.16	0.07	0.12±0.06	0.12±0.10	0.94	0.21±0.12	0.12±0.14	0.10
${\mathrm{E}}_{\text{CL}}^{\mathrm{e}}$	0.01±0.02	0.02±0.05	0.58	0.02±0.03	0.03±0.05	0.47	0.03±0.02	0.04±0.05	0.43
${\mathrm{E}}_{\text{LR}}^{\mathrm{e}}$	0.02±0.03	0.10±0.08	0.08	0.05±0.05	0.11±0.07	0.21	0.08±0.08	0.10±0.08	0.65
${\mathrm{E}}_{\text{CR}}^{\mathrm{e}}$	0.03±0.03	0.10±0.10	0.00	0.05±0.03	0.08±0.07	0.04	0.06±0.03	0.07±0.06	0.40
${\mathrm{E}}_{\text{FF}}^{\mathrm{e}}$	−0.04±0.03	−0.04±0.06	0.83	−0.06±0.03	−0.01±0.08	0.16	−0.03±0.03	0.03±0.06	0.01

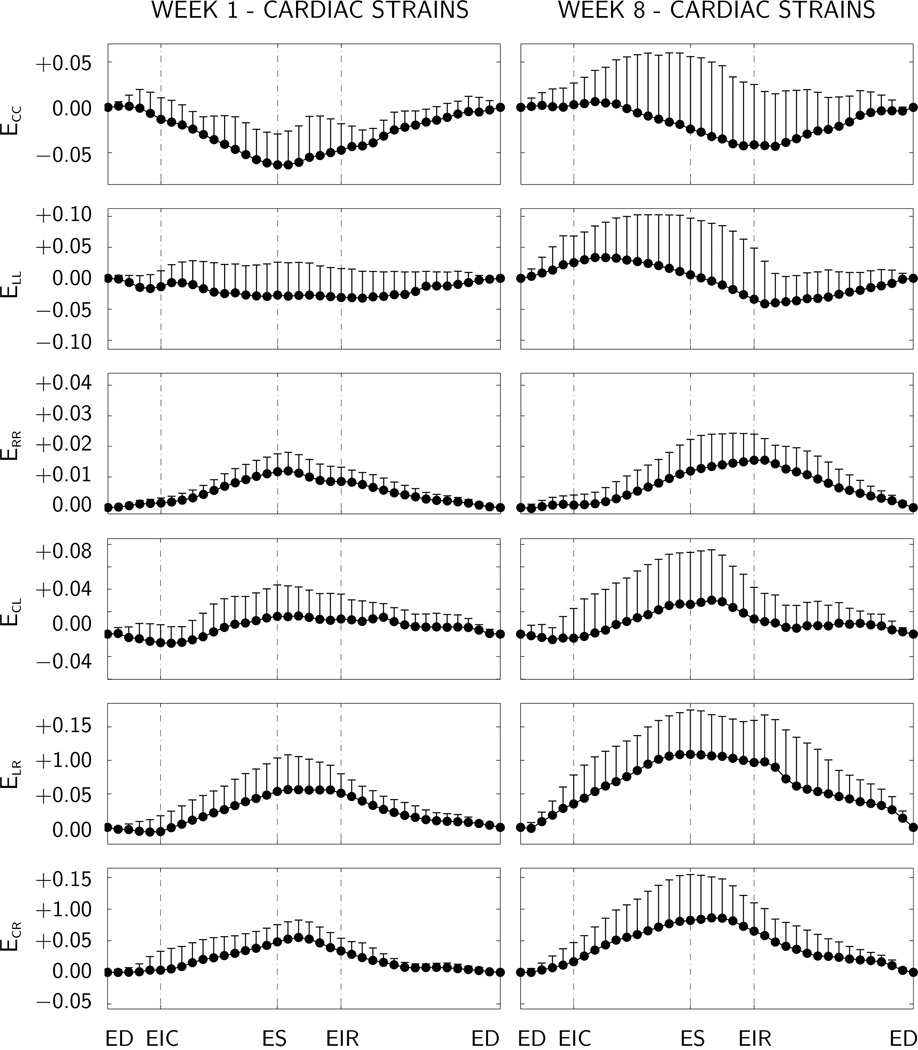
Figure 4.

Temporal evolution of elastic strains ${\mathit{E}}_{\mathrm{W}1}^{\mathrm{e}}\text{ and }{\mathit{E}}_{\mathrm{W}8}^{\mathrm{e}}$ at weeks 1 and 8, displayed at 50% depth of the lateral left ventricular wall. Maximum circumferential contraction E_CC is −6.34±3.73% at week 1 and −4.31±5.79% at week 8, maximum wall thickening E_RR is 11.96±6.09% at week 1 and 15.48±7.05% at week 8. Means and standard deviations of time-aligned components of the Green Lagrange strains are displayed for n=11 animals. C circumferential, R radial, and L longitudinal direction. ED end diastole, EIR end isovolumetric relaxation, ES end systole, and EIC end isovolumetric contraction.

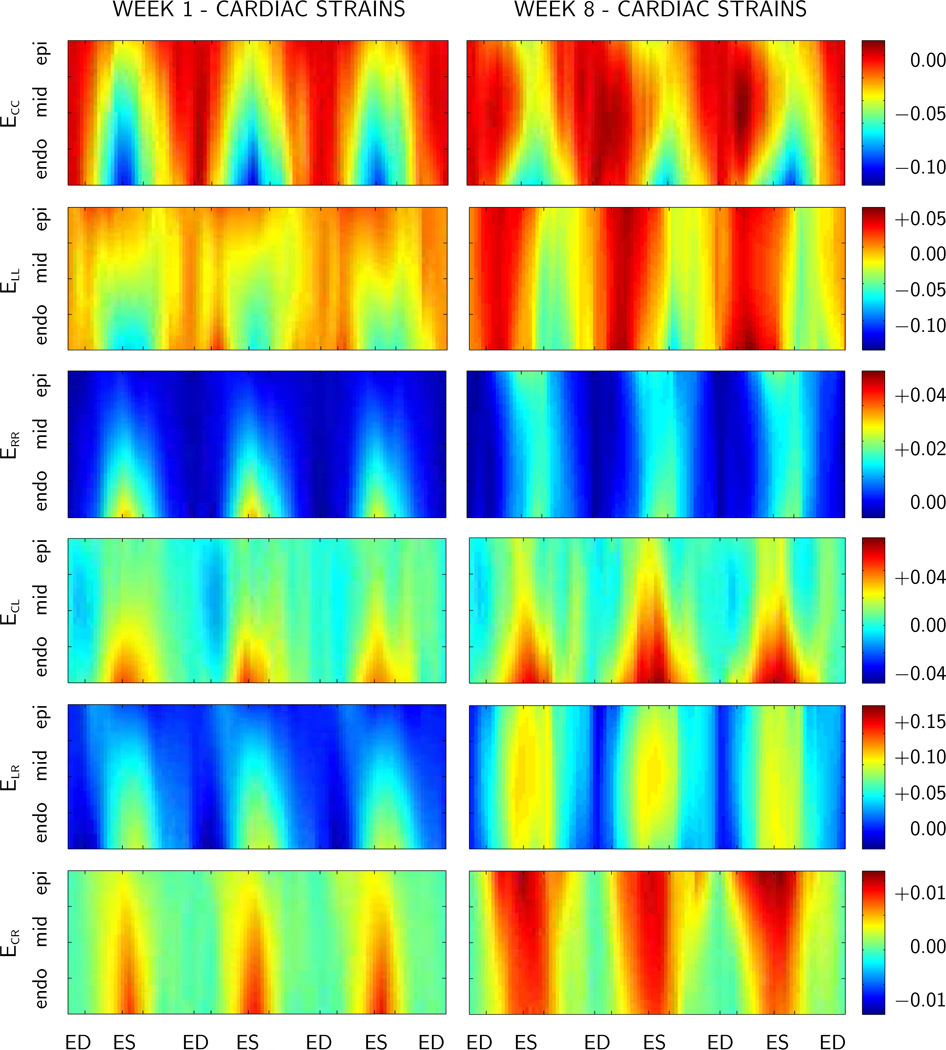
Figure 5.

Spatio-temporal evolution of elastic strains ${\mathit{E}}_{\mathrm{W}1}^{\mathrm{e}}\text{ and }{\mathit{E}}_{\mathrm{W}8}^{\mathrm{e}}$ in the lateral left ventricular wall at weeks 1 and 8, time-aligned and averaged over n=11 animals. Components of the Green Lagrange strains are displayed across the ventricular wall for three consecutive heartbeats. C circumferential, R radial, and L longitudinal direction. ED end diastole, EIR end isovolumetric relaxation, ES end systole, and EIC end isovolumetric contraction.

4. RESULTS

4.1. Hemodynamics

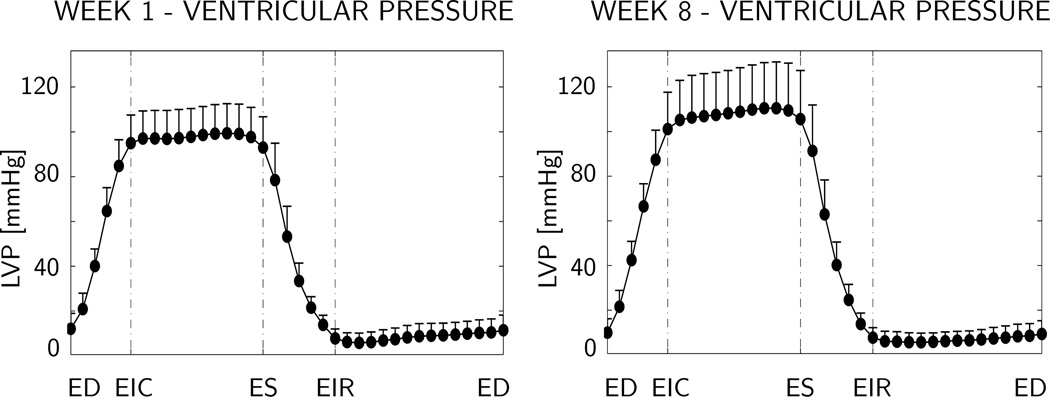
Figure 3 shows the temporal evolution of the time-aligned average left ventricular pressure LVP over the cardiac cycle, displayed at week 1, i.e., before myocardial infarction, left, and at week 8, i.e., seven weeks after myocardial infarction, right. Maximum left ventricular pressure is 99 ± 13 mmHg at week 1, and 110 ± 21 mmHg at week 8.

Figure 3.

Temporal evolution of left ventricular pressure at week 1 before infarction, left, and at week 8, seven weeks after infarction, right. Maximum left ventricular pressure is 99 ± 13 mmHg at week 1, and 110 ± 21 mmHg at week 8. Means and standard deviations of time-aligned pressure are displayed for n=11 animals. LVP left ventricular pressure, LVV left ventricular volume, ED end diastole, EIR end isovolumetric relaxation, ES end systole, and EIC end isovolumetric contraction.

4.2. Deformation gradients

Table 1 displays the elastic deformation gradients ${\mathit{F}}_{\mathrm{W}1}^{\mathrm{e}}\text{ and }{\mathit{F}}_{\mathrm{W}8}^{\mathrm{e}}$ calculated with the end diastolic state ED as reference configuration and the end systolic state ES as current configuration. The first column of each section displays the components of ${\mathit{F}}_{\mathrm{W}1}^{\mathrm{e}}$ at week 1, prior to myocardial infarction. The second column displays the components of ${\mathit{F}}_{\mathrm{W}8}^{\mathrm{e}}$ at week 8, seven weeks after myocardial infarction. The third column shows the results of student’s paired t-test between both columns. From week 1 to week 8, we observe a significant decrease in the radial component ${\mathrm{F}}_{\text{RR}}^{\mathrm{e}}$ from 1.16 ± 0.09 to 1.07 ± 0.12 at 80% depth and in the shear component ${\mathrm{F}}_{\text{CL}}^{\mathrm{e}}$ from 0.04 ± 0.05 to −0.01 ± 0.08 at 80% depth. In addition, we see a significant increase in the shear components ${\mathrm{F}}_{\text{LR}}^{\mathrm{e}}$ from 0.03 ± 0.05 to 0.20 ± 0.16 at 20% depth, ${\mathrm{F}}_{\text{LC}}^{\mathrm{e}}$ from 0.00 ± 0.06 to 0.07 ± 0.10 and ${\mathrm{F}}_{\text{LR}}^{\mathrm{e}}$ from 0.11 ± 0.09 to 0.23 ± 0.12 at 50% depth, and ${\mathrm{F}}_{\text{LC}}^{\mathrm{e}}$ from 0.03 ± 0.05 to 0.10 ± 0.09 at 80% depth. The elastic volume change J_e from ES to ED does not change significantly between weeks 1 and 8 at 20% and 80%, but increases slightly from 0.99 ± 0.05 to 1.02 ± 0.04 at 50% depth. Similarly, the elastic fiber stretch ${\lambda }_{\text{FF}}^{\mathrm{e}}$ from ES to ED does not differ significantly between weeks 1 and 8 at 20% and 50% depth, but changes from contractile 0.97 ± 0.03 to tensile 1.03 ± 0.06 at 80% depth.

Table 2 displays the end-diastolic growth tensor ${\mathit{F}}_{\text{ED}}^{\mathrm{g}}$ calculated with the end diastolic state ED at week 1 as reference configuration and ED at week 8 as current configuration. The first column of each section displays the values of the nine components of the growth tensor. The second column shows the p-values from two-tailed paired t-tests comparing ED at week 8 with ED at week 1, i.e., with the identity tensor. We observe a significant increase in the longitudinal component ${\mathrm{F}}_{\text{LL}}^{\mathrm{g}}$ of +0.10 ± 0.13 at 50% depth and of +0.11 ± 0.11 at 80% depth. This change is accompanied by a decrease in the radial component ${\mathrm{F}}_{\text{RR}}^{\mathrm{g}}$ of −0.32 ± 0.15 at 20% depth, of −0.27 ± 0.15 at 50% depth, and of −0.23 ± 0.22 at 80% depth. Overall, these changes result in a significant chronic decrease in volume J^g of −0.26 ± 0.19 at 20% depth and of −0.18±0.19 at 50% depth, while the volume change J^g of −0.11 ± 0.21 at 80% depth remains statistically non-significant. When projected onto the local fiber direction, we observe a significant chronic fiber stretch ${\lambda }_{\text{FF}}^{\mathrm{g}}$ of 1.08 ± 0.11 at 80% depth, while the fiber stretch ${\lambda }_{\text{FF}}^{\mathrm{g}}$ of 1.03 ± 0.12 at 20% depth and of 1.04 ± 0.16 at 50% depth remain statistically non-significant.

Table 3 displays the end-systolic growth tensor ${\mathit{F}}_{\text{ES}}^{\mathrm{g}}$ calculated with the end diastolic state ES at week 1 as reference configuration and ES at week 8 as current configuration. The first column of each section displays the values of the nine components of the growth tensor. The second column shows the p-values from two-tailed paired t-tests comparing ES at week 8 with ES at week 1, i.e., with the identity tensor. Similar to the end-diastolic growth tensor, we see a significant increase in the longitudinal component ${\mathrm{F}}_{\text{LL}}^{\mathrm{g}}$ of +0.13 ± 0.18 at 50% depth and of +0.18 ± 0.16 at 80% depth. Again, we observe a significant decrease in the radial component ${\mathrm{F}}_{\text{RR}}^{\mathrm{g}}$ of −0.30 ± 0.19 at 20% depth, of −0.28 ± 0.19 at 50% depth, and of −0.25 ± 0.22 at 80% depth. We also see a significant increase in the shear component ${\mathrm{F}}_{\text{LR}}^{\mathrm{g}}$ of +0.10 ± 0.11 at 20% depth and of +0.12 ± 0.13 at 50% depth. The chronic decrease in volume J^g at ES is less pronounced than at ED, and is significant only at 20% depth with −0.24±0.22. On the contrary, the chronic fiber stretch ${\lambda }_{\text{FF}}^{\mathrm{g}}$ at ES is more pronounced than at ED with values of of 1.02 ± 0.14 at 20% depth, of 1.08 ± 0.17 at 50% depth, and of 1.15 ± 0.13 at 80% depth, respectively.

4.3. Strains

Table 4 displays the transmural elastic strains ${\mathit{E}}_{\mathrm{W}1}^{\mathrm{e}}\text{ and }{\mathit{E}}_{\mathrm{W}8}^{\mathrm{e}}$ from ED to ES at weeks 1 and 8. The first column of each section displays the strain components ${\mathit{E}}_{\mathrm{W}1}^{\mathrm{e}}$ at week 1, prior to myocardial infarction. The second column displays the strain components ${\mathit{E}}_{\mathrm{W}8}^{\mathrm{e}}$ at week 8, seven weeks after myocardial infarction. The third column shows the results of student’s paired t-test between both columns. Only three strain components display a statistically significant difference when compared at weeks 1 and 8. The radial strain ${\mathrm{E}}_{\text{RR}}^{\mathrm{e}}$ decreases from −0.05 ± 0.04 to 0.00 ± 0.10 at 80% depth, and the shear strain ${\mathrm{E}}_{\text{CR}}^{\mathrm{e}}$ increases from 0.03 ± 0.03 to 0.10 ± 0.10 at 20% depth and from 0.05 ± 0.03 to 0.08 ± 0.07 at 50% depth. The corresponding fiber strain ${\mathrm{E}}_{\text{FF}}^{\mathrm{e}}$ increase significantly from −0.03 ± 0.03 to 0.03 ± 0.06 at 80% depth, while changes in fiber strains at 20% and 50% depth remain statistically non-significant.

Table 5 summarizes the end-diastolic growth strains ${\mathit{E}}_{\text{ED}}^{\mathrm{g}}$ calculated with the end diastolic state ED at week 1 as reference configuration and ED at week 8 as current configuration. The first column of each section displays the values of the six Green-Lagrange strain components. The second column shows the p-values from two-tailed paired t-tests comparing ED at week 8 with ED at week 1, i.e., with zero. Remarkably, we only observe significant changes in the longitudinal and radial growth strains. Those changes are, however, statistically significance across the entire wall. The longitudinal growth strain ${\mathrm{E}}_{\text{LL}}^{\mathrm{g}}$ increases by +0.12 ± 0.17 at 20% depth, by +0.12 ± 0.15 at 50% depth and by +0.13 ± 0.12 at 80% depth. At the same time, the radial growth strain ${\mathrm{E}}_{\text{RR}}^{\mathrm{g}}$ decreases by −0.21 ± 0.12 at 20% depth, by −0.19 ± 0.09 at 50% depth and by −0.10 ± 0.15 at 80% depth. Along the fiber direction, we observe a significant chronic lengthening ${\mathrm{E}}_{\text{FF}}^{\mathrm{g}}$ of +0.09 ± 0.12 at 80% depth, while fiber lengthening of +0.03 ± 0.13 at 20% depth and of +0.06 ± 0.18 at 50% depth remains statistically non-significant.

Table 5.

Transmural end-diastolic growth strains ${\mathit{E}}_{\text{ED}}^{\mathrm{g}}$ from ED week 1 to ED week 8. Means and standard deviations are displayed for n=11 animals. P-values are from two-tailed paired t-tests comparing ED at week 8 with ED at week 1, i.e., with zero.

	epi		mid		endo
	20% depth	p	50% depth	p	80% depth	p
${\mathrm{E}}_{\text{CC}}^{\mathrm{g}}$	0.03±0.15	0.56	0.06±0.18	0.27	0.05±0.13	0.20
${\mathrm{E}}_{\text{LL}}^{\mathrm{g}}$	0.12±0.17	0.04	0.12±0.15	0.03	0.13±0.12	0.00
${\mathrm{E}}_{\text{RR}}^{\mathrm{g}}$	−0.21±0.12	0.00	−0.19±0.09	0.00	−0.10±0.15	0.05
${\mathrm{E}}_{\text{CL}}^{\mathrm{g}}$	0.01±0.15	0.79	−0.01±0.09	0.63	−0.01±0.06	0.46
${\mathrm{E}}_{\text{LR}}^{\mathrm{g}}$	0.00±0.08	0.86	0.06±0.11	0.10	0.11±0.19	0.10
${\mathrm{E}}_{\text{CR}}^{\mathrm{g}}$	−0.04±0.17	0.51	−0.03±0.11	0.39	0.00±0.10	0.88
${\mathrm{E}}_{\text{FF}}^{\mathrm{g}}$	0.03±0.13	0.42	0.06±0.18	0.31	0.09±0.12	0.03

Table 6 completes the strain characterization with the end-systolic growth strains ${\mathit{E}}_{\text{ES}}^{\mathrm{g}}$ calculated with the end systolic state ES at week 1 as reference configuration and ES at week 8 as current configuration. The first column of each section displays the values of the six Green-Lagrange strain components. The second column shows the p-values from two-tailed paired t-tests comparing ES at week 8 with ES at week 1, i.e., with zero. Similar to the end-diastolic comparison, we observe significant changes in the longitudinal and radial growth strains across the entire cardiac wall. The longitudinal growth strain ${\mathrm{E}}_{\text{LL}}^{\mathrm{g}}$ increases by +0.14 ± 0.20 at 20% depth, by +0.16 ± 0.20 at 50% depth and by +0.21 ± 0.18 at 80% depth. At the same time, the radial growth strain ${\mathrm{E}}_{\text{RR}}^{\mathrm{g}}$ decreases by −0.21 ± 0.12 at 20% depth, by −0.20 ± 0.10 at 50% depth and by −0.15 ± 0.14 at 80% depth. In contrast to end diastole, at end systole, we also observe a significant increase in the shear strains ${\mathrm{E}}_{\text{LR}}^{\mathrm{g}}$ of +0.04 ± 0.06 at 20% depth and of +0.07 ± 0.08 at 50% depth. Again, chronic fiber lengthening ${\mathrm{E}}_{\text{FF}}^{\mathrm{g}}$ is only significant with +0.16 ± 0.15 at 80% depth, while is statistically non-significant with +0.03 ± 0.15 at 20% depth and with +0.10 ± 0.21 at 50% depth.

Table 6.

Transmural end-systolic growth strains ${\mathit{E}}_{\text{ES}}^{\mathrm{g}}$ from ES week 1 to ES week 8. Means and standard deviations are displayed for n=11 animals. P-values are from two-tailed paired t-tests comparing ES at week 8 with ES at week 1, i.e., with zero.

	epi		mid		endo
	20% depth	p	50% depth	p	80% depth	p
${\mathrm{E}}_{\text{CC}}^{\mathrm{g}}$	0.03±0.19	0.58	0.10±0.22	0.16	0.11±0.17	0.07
${\mathrm{E}}_{\text{LL}}^{\mathrm{g}}$	0.14±0.20	0.04	0.16±0.20	0.03	0.21±0.18	0.00
${\mathrm{E}}_{\text{RR}}^{\mathrm{g}}$	−0.21±0.12	0.00	−0.20±0.10	0.00	−0.15±0.14	0.01
${\mathrm{E}}_{\text{CL}}^{\mathrm{g}}$	0.02±0.13	0.56	0.00±0.10	0.95	−0.01±0.09	0.60
${\mathrm{E}}_{\text{LR}}^{\mathrm{g}}$	0.04±0.06	0.03	0.07±0.08	0.02	0.09±0.17	0.12
${\mathrm{E}}_{\text{CR}}^{\mathrm{g}}$	−0.02±0.14	0.68	−0.01±0.07	0.49	0.01±0.09	0.73
${\mathrm{E}}_{\text{FF}}^{\mathrm{g}}$	0.03±0.15	0.49	0.10±0.21	0.14	0.16±0.15	0.00

4.4. Temporal Strain Evolution

Figure 4 displays the temporal evolution of the time-aligned average elastic strains ${\mathit{E}}_{\mathrm{W}1}^{\mathrm{e}}\text{ and }{\mathit{E}}_{\mathrm{W}8}^{\mathrm{e}}$ at the lateral left ventricular midwall, i.e., at 50% depth, calculated with the end diastolic state ED as reference configuration. Baseline strains ${\mathit{E}}_{\mathrm{W}1}^{\mathrm{e}}$ at week 1, prior to myocardial infarction are shown on the left. Strains ${\mathit{E}}_{\mathrm{W}8}^{\mathrm{e}}$ at week 8, seven weeks after myocardial infarction, are shown on the right. Maximum circumferential contraction E_CC is −6.34±3.73% at week 1 and −4.31±5.79% at week 8. Maximum wall thickening E_RR is 11.96±6.09% at week 1 and 15.48±7.05% at week 8. While extreme values occur at end systole at week 1, prior to myocardial infarction, extreme values seem to shift in time towards end isovolumetric relaxation at week 8, seven weeks after myocardial infarction.

4.5. Spatio-Temporal Strain Evolution

Figure 5 depicts the spatio-temporal evolution of the time-aligned average elastic strains ${\mathit{E}}_{\mathrm{W}1}^{\mathrm{e}}\text{ and }{\mathit{E}}_{\mathrm{W}8}^{\mathrm{e}}$ across the lateral left ventricular wall, where red indicates positive, i.e., tensile strains, and blue indicates negative, i.e., compressive strains. Baseline strains ${\mathit{E}}_{\mathrm{W}1}^{\mathrm{e}}$ at week 1, prior to myocardial infarction are shown on the left. Strains ${\mathit{E}}_{\mathrm{W}8}^{\mathrm{e}}$ at week 8, seven weeks after myocardial infarction, are shown on the right. Overall, Figure 5 indicates that in the baseline state, strains display a significant transmural heterogeneity. Circumferential and longitudinal strains E_CC and E_LL are smaller the inner wall than in the outer wall, indicating a larger endocardial contractility. Radial strains E_RR are larger in the inner than in the outer wall, indicating a more pronounced endocardial wall thickening. After myocardial infarction, however, these transmural strain gradients vanish, and the wall responds almost homogeneously across the thickness.

5. DISCUSSION

We have introduced a method to characterize growth of cardiac muscle tissue in the beating heart during a chronic eight-week long study using radiopaque markers and videofluroscopy. Marker methods are unique in that, unlike other imaging technologies such as computer tomography or magnetic resonance imaging [17], they allow us to follow specific anatomic landmarks over long periods of time [52]. The use of four-by-three ventricular bead sets enables a precise characterization of cardiac strains in a specific region of the heart, and identify their transmural variations throughout the cardiac cycle [51]. Here, we have used this technology to quantify infart-induced growth in the form of second order growth tenors ${\mathit{F}}_{\text{ED}}^{\mathrm{g}}\text{ and }{\mathit{F}}_{\text{ES}}^{\mathrm{g}}$ relevant to the biomechanics community [18, 28], and growth strains ${\mathit{E}}_{\text{ED}}^{\mathrm{g}}\text{ and }{\mathit{E}}_{\text{ES}}^{\mathrm{g}}$ more intuitive to the clinical community [10, 45]. Both metrics indicate a significant chronic lengthening in the longitudinal direction with average diastolic and systolic growth strains of ${\mathrm{E}}_{\text{LL}}^{\mathrm{g}}=0.12\text{ and }{\mathrm{E}}_{\text{LL}}^{\mathrm{g}}=0.17$, in comparison to a sham study with implanted markers but no infarct, for which ${\mathrm{E}}_{\text{LL}}^{\mathrm{g}}=0.01\text{ and }{\mathrm{E}}_{\text{LL}}^{\mathrm{g}}=-0.03$, respectively [7]. This is accompanied by a chronic shortening in the radial direction with average diastolic and systolic growth strains of ${\mathrm{E}}_{\text{RR}}^{\mathrm{g}}=-0.17\text{ and }{\mathrm{E}}_{\text{RR}}^{\mathrm{g}}=-0.19$, in comparison to the sham study with ${\mathrm{E}}_{\text{RR}}^{\mathrm{g}}=-0.08\text{ and }{\mathrm{E}}_{\text{RR}}^{\mathrm{g}}=-0.03$, respectively [7]. In a comparable three-week long chronic infarct study in pigs, the diastolic growth strains at a similar location were found to ${\mathrm{E}}_{\text{LL}}^{\mathrm{g}}=0.11$, slightly lower than in our study, ${\mathrm{E}}_{\text{CC}}^{\mathrm{g}}=0.24$, significantly larger than in our study, and ${\mathrm{E}}_{\text{RR}}^{\mathrm{g}}=0.05$, positive rather than negative as in our study [56]. When projected onto the histologically identified averaged fiber orientations [15], we observe an average chronic diastolic and systolic fiber lengthening of ${\mathrm{E}}_{\text{FF}}^{\mathrm{g}}=0.06\text{ and }{\mathrm{E}}_{\text{FF}}^{\mathrm{g}}=0.10$. This is in good qualitative agreement with the chronic pig study, in which average diastolic fiber lengthening was approximately ${\mathrm{E}}_{\text{FF}}^{\mathrm{g}}=0.17$ [56]. The corresponding sham study, however, reported an average chronic diastolic and systolic fiber shortening of ${\mathrm{E}}_{\text{FF}}^{\mathrm{g}}=-0.07\text{ and }{\mathrm{E}}_{\text{FF}}^{\mathrm{g}}=-0.08$, respectively [8]. To our surprise, these kinematic changes are accompanied by a significant decrease in myocardial volume with an average diastolic and systolic volume decrease of J^g =0.82 and J^g =0.85, respectively. The observed average diastolic and systolic chronic fiber stretches of ${\lambda }_{\text{FF}}^{\mathrm{g}}=1.05\text{ and }{\lambda }_{\text{FF}}^{\mathrm{g}}=1.08$ are intuitive, but slightly smaller than expected. They indicate that microstructural changes other than plain myocyte elongation, for example myofiber slippage, shear, rearrangement, and reorientation, may play an equally significant role in the remodeling process [39].

For the sake of completeness, we would like to point out that our elastic baseline strains ${\mathit{E}}_{\mathrm{W}1}^{\mathrm{e}}$ at week 1 are in excellent qualitative and quantitative agreement with previously reported values [7, 8, 51]. In addition, our elastic strains ${\mathit{E}}_{\mathrm{W}8}^{\mathrm{e}}$ at week 8 agree nicely with the values reported in a chronic infarct study [9].

5.1. Limitations

To our knowledge, this is the first study to experimentally characterize growth tensors in the lateral left ventricular wall. While the quantification of these second order tensors is essential to calibrate and validate continuum theories of growth, it is important to keep in mind that we have derived our growth tensors ${\mathit{F}}_{\text{ED}}^{\mathrm{g}}\text{ and }{\mathit{F}}_{\text{ES}}^{\mathrm{g}}$ from a continuous bijective mapping φ, assuming that the growth process is inherently compatible [1]. Enforcing compatibility may induce additional constraints, and it may be possible that the components of growth tensors associated with incompatible growth theories [18, 44] take significantly larger values. However, these effects, which are essentially correlated to the presence of residual stresses [37], are virtually impossible to isolate in vivo, and we assume that our characterization of growth represents a reasonable first approximation.

An inherent limitation of proposed marker technique is that it is invasive in nature and therefore not applicable to humans, for which methods like tagged magnetic resonance imaging are more appropriate, however, unfortunately also less accurate [17]. An advantage of animal models over studying disease in humans is obviously that it allows us to precisely define the beginning of the growth process. Ovine hearts are of the same size and beat at the same frequency as human hearts, and thus represent a good model system. Nevertheless, we have to be careful when extrapolating our findings to cardiac growth in humans. Another potential limitation might be that the implantation of myocardial markers and transmural beads is an invasive procedure associated with local left ventricular wall trauma, which could potentially lead to chronic changes in the ventricular wall. To quantify these potential artifacts, we compare our results to sham operations with plain marker implantation, but without myocardial infarction [7, 9, 25]. Although one sham study found slight alterations in the elastic cardiac strains between weeks one and eight, from a statistical point of view, these changes remained non-significant [7]. The only statistically significant change was a change in radial strains ${\mathrm{E}}_{\text{RR}}^{\mathrm{e}}$ in the epicardial wall, which increased from 0.08 ± 0.08 at week 1 to 0.19 ± 0.07 at week 8. However, several other studies have demonstrated that marker and bead implantation may unfavorably impact hemodynamics, whereas the impact on absolute strain values was rather minor, and general trends remained unchanged [9, 25].

It could be viewed as a limitation that we have used generic fiber orientation maps generated by tissue histology averaged over five animals [15] to calculate the local fiber stretches ${\lambda }_{\text{FF}}^{\mathrm{e}}\text{ and }{\lambda }_{\text{FF}}^{\mathrm{g}}$ and fiber strains ${\mathrm{E}}_{\text{FF}}^{\mathrm{e}}\text{ and }{\mathrm{E}}_{\text{FF}}^{\mathrm{g}}$. It would, of course, be more appropriate to utilize subject-specific fiber orientations f when projecting deformation and strain tensors onto local fiber directions. A similar study with seven sheep reported subject-specific variations of fiber angles of ±8, ±9, and ±10 degrees in the epicardium, midwall, and endocardium, respectively [8]. We thus assume that our generic fiber orientations represent a sufficiently accurate approximation of the fiber orientation in the healthy ovine heart. However, this does not imply that the fiber orientations could have changed in response to an infarct-induced reorientation of the principal stress and strain axes [29, 30].

Time-aligned averaging [40, 41] could be viewed as a limitation of the present study. We would like to reiterate that it has only been used to create Figures 3, 4, and 5, while Tables 1 to 6 are based on an exact data averaging at ED and ES. Time-aligned averaging allows us to create an illustrative visualization of averaged spatio-temporal phenomena in the ventricular wall [51]. Although maybe less relevant for the clinical community, we believe that spatio-temporal representations provides valuable insight into essential mechanisms of force generation. These might be critical for the continuum mechanics community to calibrate and validate the passive and active components of constitutive models for cardiac tissue [20, 22, 47].

Lastly, here, as a proof of concept, we have only demonstrated the derivation of growth tensors in the lateral-equatorial left ventricular wall. As part of this animal experiment, however, bead sets have been implanted in both the lateral-equatorial and the anterior-basal wall [10]. This allows us to compare growth in regions close to and away from the infarct [9]. Although not reported here, we have evaluated both data sets, and found the growth tensors and growth-induced strains to display similar trends in both regions.

5.2. Engineering Relevance

Throughout the past two decades the theoretical and computational prediction of growth and remodeling of living tissues has been an active area of continuously growing research interest [44]. However, the acceptance of growth theories crucially hinges on a sound experimental calibration, validation, and verification in chronic long-term studies [1]. Here, we have presented our first attempt to characterize chronic cardiac growth in response to myocardial infarction. We have elaborated two different interpretations of growth, i.e., during end diastole and end systole, which naturally lend themselves to two alternative multiplicative decompositions of the deformation gradient, $\mathit{F}={\mathit{F}}_{\mathrm{W}8}^{\mathrm{e}}·{\mathit{F}}_{\text{ED}}^{\mathrm{g}}\text{ and }\mathit{F}={\mathit{F}}_{\text{ES}}^{\mathrm{g}}·{\mathit{F}}_{\mathrm{W}1}^{\mathrm{e}}$. In our special case of compatible growth, both formulations are inherently identical, with the former representing the classical interpretation of growth [44]. This representation is in line with the theoretical characterization of cardiac growth [49] and its recently proposed computational realizations [18, 28, 42]. Our study thus provides critical guidelines for cardiac growth tensors in infact-induced remodeling, suggesting that they should reflect growth in the longitudinal direction ${\mathrm{F}}_{\text{LL}}^{\mathrm{g}}>1$ and shrinkage in the radial direction ${\mathrm{F}}_{\text{RR}}^{\mathrm{g}}<1$, associated with increased shearing in the ${\mathrm{F}}_{\text{LR}}^{\mathrm{g}}>0$ direction. According to our study, infarct-induced growth seems to be associated with a significant decrease in ventricular volume J^g < 1 and chronic muscle fiber lengthening ${\lambda }_{\text{FF}}^{\mathrm{g}}>1$, at least in regions of the lateral left ventricular wall.

5.3. Clinical Significance

Left ventricular wall strains are believed to be important indicators for ventricular remodeling [32]. Altered wall strains can result in the production of cytokines and reactive oxygen species stimulating cardiomyocyte apoptosis and extracellular matrix disruption which, in turn, might trigger global left ventricular dilation and remodeling [39]. This study therefore aims at characterizing infarct-induced changes in myocardial kinematics throughout the cardiac cycle to quantify acute and chronic temporal and transmural variations of cardiac strains, fiber stretches, and myocardial volumes in the beating heart. In contrast to most existing marker studies, which report strains only between discrete time points of the cardiac cycle [7, 24, 26, 35, 56], we use a novel time-aligned averaging technique [40], to reconstruct strain profiles throughout the entire wall, throughout the entire cardiac cycle, averaged over all eleven animals [51]. To illustrate infarct-induced alterations, we visualize the individual strain profiles side by side, before and after myocardial infarction. In particular, these strain profiles reveal a severe loss of transmural strain heterogeneity in circumferential, longitudinal, and radial strains E_CC, E_LL, and E_RR. The identification of deviations from baseline strains is clinically important to guide the optimal timing of clinical interventions, e.g., in asymptomatic severe mitral regurgitation [6] or in progressive heart failure [18].

Recent studies seek to identify mechanotransduction pathways during the growth and remodeling process [12]. It has been suggested that cardiac dilation is primarily associated with the serial deposition of sarcomeres within the individual cardiac muscle cells, which, in turn, grow along their long axis [19, 39]. Our study provides an in vivo quantification of fiber growth with an average chronic diastolic and systolic fiber stretch of ${\lambda }_{\text{FF}}^{\mathrm{g}}=1.05\text{ and }{\lambda }_{\text{FF}}^{\mathrm{g}}=1.08$. Chronic fiber lengthening is not homogeneous across the wall; it is largest in the endocardium with values of ${\lambda }_{\text{FF}}^{\mathrm{g}}=1.08\text{ and }{\lambda }_{\text{FF}}^{\mathrm{g}}=1.15$, respectively. Although the trends are qualitatively similar, these values are smaller than reported values of approximately ${\lambda }_{\text{FF}}^{\mathrm{g}}=1.50$ found in rodent hearts subject to chronic volume overload [55]. These differences could be attributed to our short time window of seven weeks post infarction, which is obviously too short for the heart to develop severe end-stage heart failure.

6. CONCLUSIONS

In summary, this study presents a methodology to characterize kinematic changes during infarct-induced cardiac growth. Seven weeks after myocardial infarction, in a lateral-equatorial region adjacent to the infarct, we observe significant chronic lengthening of more than 10% in the longitudinal direction, accompanied by chronic shortening of more than 25% in the radial direction, while the circumferential direction remains virtually unaffected. These changes are accompanied by a local volume reduction of more than 15%. Alterations are not uniform across the wall; longitudinal lengthening is larger in the endocardium, while radial shortening is larger in the epicardium. We believe that this work provides valuable insight into kinematic changes of the left ventricular wall, which are believed to be a strong indicator for progressive heart failure. The side-by-side comparison of local deformation gradients, growth tensors, fiber stretches, volumes, normal strains and shear strains before and after infarct-induced growth and remodeling provides a unique data base to judge strain alterations in response to cardiac disease, to calibrate and validate material models and computational tools to simulate the heart, and to engineer synthetic or living biomaterials with similar structure and function.