Abstract
A central problem in evolutionary theory concerns the mechanisms by which adaptations requiring multiple mutations emerge in natural populations. We develop a series of expressions that clarify the scaling of the time to establishment of complex adaptations with population size, mutation rate, magnitude of the selective disadvantage of intermediate-state alleles, and the complexity of the adaptation. In general, even in the face of deleterious intermediate steps, the time to establishment is minimized in populations with very large size. Under a broad range of conditions, the time to establishment also scales by no more than the square of the mutation rate, regardless of the number of sites contributing to the adaptive change, demonstrating that the emergence of complex adaptations is only weakly constrained by the independent acquisition of mutations at the underlying sites. Mutator alleles with deleterious side effects have only moderate effects on the rate of adaptation in large populations but can cause a quantum decrease in the time to establishment of some adaptive alleles in small populations, although probably not at a high enough rate to offset the increased deleterious mutation load. Transient hypermutability, whereby a subset of gamete-producing cells mutate at an elevated rate in a nonheritable manner, may also elevate the rate of adaptation, although the effect is modest and appears to result from a simple increase in the rate of transitions between intermediate states rather than from the saltational production of doublet mutations. Taken together, these results illustrate the plausibility of the relatively rapid emergence of specific complex adaptations by conventional population genetic mechanisms and provide insight into the relative incidences of various paths of allelic adaptation in organisms with different population genetic features.
Keywords: adaptation, adaptive evolution, evolutionary rate, genome evolution, molecular evolution, mutation rate, mutator, fixation time, transient hypermutability
Introduction
Understanding the mechanistic origins of complex adaptations (here defined as character alterations requiring more than one novel mutation to yield a functional advantage) remains a central challenge for evolutionary biology (Hartl and Taubes 1998; Orr 2002; DePristo et al. 2005; Dean and Thornton 2007). Some have even questioned whether conventional mutational mechanisms and current principles of population genetics are capable of explaining the emergence of complex adaptations on reasonable evolutionary time scales (e.g., Behe and Snoke 2004; Pigliucci 2008). Because mutations are rare events, the origin of complex adaptations is often expected to occur at very low rates in small populations, owing to the long cumulative time span necessary for the independent arrival and sequential fixation of multiple mutations. In contrast, whereas large populations provide more individual targets for mutational origin, should the intermediate steps toward a complex adaptation be disadvantageous, the increased efficiency of selection against intermediate mutants in large populations might inhibit adaptational advance.
A number of factors may facilitate the rate of emergence of complex adaptations in ways that defy these simple expectations. First, despite the short persistence times of deleterious intermediate-stage mutations in large populations, the steady input of new mutations results in the maintenance of a small stable reservoir of intermediate alleles poised to take the next step(s) in the path toward adaptation (Gillespie 1984). Likewise, even though nearly all neutral intermediate-step alleles are destined to be lost by drift, their accumulation by mutation pressure can provide a growing resource for secondary adaptive mutations. Second, owing to the reduced efficiency of natural selection, populations with small effective sizes are vulnerable to the accumulation of mutations with mild effects on the efficiency of DNA replication and repair loci (Lynch 2008). The predicted increase in the per capita mutation rate is consistent with the known gradient in the per-generation mutation rate from prokaryotes to multicellular eukaryotes (Lynch 2007) and could offset the decline in the number of individual mutational targets in species with relatively small population sizes. Third, because the principle of selection–mutation balance extends to the loci that define the mutation rate, even large populations will always contain a pool of individuals with mutation rates elevated above the population norm. Although maladapted at the individual level, this small segment of the population might be a major source of evolutionary novelties.
In the following sections, we attempt to incorporate the above-mentioned issues into a more comprehensive framework for understanding the population genetic environments in which complex adaptations are most likely to emerge by alternative routes. A series of analytical approximations, supported by computer simulations, demonstrate the existence of many plausible pathways by which complex adaptations can emerge much more rapidly than expected when mutations at independent sites are assumed to proceed to fixation in a sequential manner. Our results also reveal several scaling properties for the time to establishment of complex adaptations with respect to population size, mutation rate, and degree of adaptive complexity, providing the seeds for a general theory for the contexts in which adaptive evolution is most likely to proceed in organisms residing at different positions along these fundamental population genetic axes.
Background
The focus throughout will be on diploid sexual populations, with segregation of chromosomes occurring each generation, but complete linkage between the sites at the locus under consideration. For a variety of aspects of selection, mutation, and random genetic drift, stochastic computer simulations are used to estimate the mean time to establishment of a novel adaptation (defined as the first time at which all alleles in the population are of the adaptive type, starting with a population devoid of such an allele). A Wright–Fisher type of population structure is assumed such that random mating occurs in discrete generations, with the expected frequencies of gametes arising after each generation of selection and mutation being evaluated deterministically with sets of transition equations and then random genetic drift being imposed by multinomial sampling of the population at the expected set of genotypic frequencies. In most cases, it has been possible to obtain analytical approximations to provide mechanistic explanations for the results.
The initial focus will be on the simplest case in which the adaptation is a function of changes at two sites at a particular locus, with the fitness of genotypes at the locus being defined by the two alternative states at each site. These sites may represent a wide variety of molecular contexts: codons for two potentially interacting amino acids within a single protein-coding gene, two latent splice sites for a novel intron, a regulatory site and its associated coding region, or two entirely different interacting linked loci. Both sites will be assumed to be initially fixed in an ancestral state whose genotypic fitness is scaled to equal 1.0. The fitnesses of alternative genotypes involving the two sites will then be assumed to be additively determined such that alleles with single mutations at either site have a reduction in fitness equal to s1 ≥ 0, whereas alleles with mutations at both sites have an increment in fitness equal to s2 > 0. Under this scheme, denoting derived mutations with uppercase letters, the fitnesses of (unordered) genotypes Ab/ab and aB/ab are 1 − s1, of Ab/Ab, aB/aB, and Ab/aB are of Ab/AB and aB/AB are of ab/AB is and of AB/AB is
Throughout, we assume mutation rates (u) and effective population sizes (N) that are well within the limits of existing biological observations (Lynch 2007). Because the mutations arising at any particular locus are specific to two individual sites, the rates of production of alternative allelic states are expected to be very low, typically <10 − 6 per site per generation, and the back-mutation rate is assumed to equal zero.
Results
Constant Mutation Rate
Prior to evaluating the consequences of background variation in the mutation rate, we
consider the classical case in which the mutation rate is assumed to be invariant among
individuals. For the special situation in which the intermediate state at the adaptive
locus is neutral (), some fairly simple analytical approximations for the time
to origin and complete fixation of the adaptive allele (hereafter, the time to
establishment or  ) are attainable. Several aspects of this behavior have been
described by previous authors for different ranges of population size (e.g., Gillespie 1984; Stephan 1996; Christiansen et al. 1998;
Higgs 1998; Innan and Stephan 2001; Carter and Wagner
2002; Komarova et al. 2003; Iwasa et al. 2004, 2005; Weinreich and Chao 2005; Durrett and Schmidt 2008; Weissman et al. 2009), but the following appears to provide a
unifying approach to the problem.
) are attainable. Several aspects of this behavior have been
described by previous authors for different ranges of population size (e.g., Gillespie 1984; Stephan 1996; Christiansen et al. 1998;
Higgs 1998; Innan and Stephan 2001; Carter and Wagner
2002; Komarova et al. 2003; Iwasa et al. 2004, 2005; Weinreich and Chao 2005; Durrett and Schmidt 2008; Weissman et al. 2009), but the following appears to provide a
unifying approach to the problem.
First, as noted by prior authors, if the population is sufficiently small in size, the
evolutionary dynamics will proceed as a two-step process, with a first-step mutant almost
always becoming fixed prior to the arrival of any second-step mutation. In the initial
stages, 4Nu first-step mutations arise per generation
(because either A or B mutations can arise in the 2N gametes), each with
fixation probability so the mean arrival time of the first first-step mutation
destined to fix is 2u generations. Because the average time to fixation
of a neutral allele is 4N generations under the Wright–Fisher
model, and the rate of origin of second-step mutations is ≤ 2Nu per
generation (because there are no more than 2N first-step mutations in the
population), there is a negligible chance of a second-step mutation arising prior to
fixation of a first-step mutation if
(4N)(2Nu)≪1 or equivalently
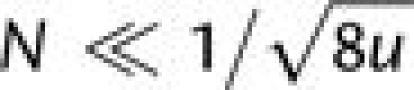 Letting
Letting
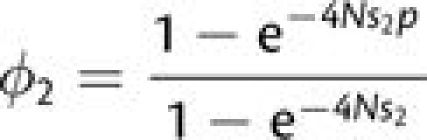 |
(1) |
denote the probability of fixation of a beneficial (second-step) mutation initiating at frequency p (Kimura 1962), then for mutations that fix sequentially, the rate of appearance of the first double mutant destined to fix is the reciprocal of the sum of the average arrival times of the two mutations,
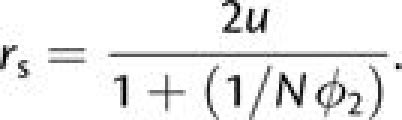 |
(2a) |
The initial frequency of the mutant allele is equal to 1/(2N), in which case the probability of fixation can be approximated by 2s2 provided 4Ns2 ≫ 1. The mean time to complete establishment of the double mutant is then
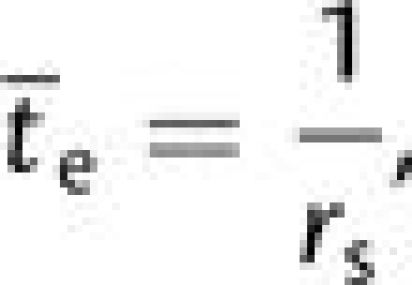 |
(2b) |
ignoring the time for the second mutation to fix, which is negligible compared with the arrival times of mutations when N is small.
Second, for 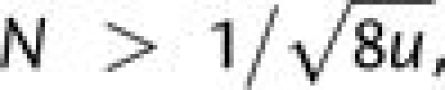 there is a significant chance
that a beneficial second-step mutation will arise on a descendant of a first-step mutation
prior to fixation of the latter. Although all but a tiny fraction (1/2N)
of first-step mutations are destined to be lost by drift, such a process can occasionally
rescue such mutants, propelling them to fixation by positive selection. This type of
pathway, in which a beneficial second-step mutation goes to fixation prior to the
population ever achieving a pure first-step state, has been called stochastic tunneling by
Komarova et al. (2003) and Iwasa et al. (2004) in the context of cancer
development, and a similar phenomenon has been described in the context of duplicate-gene
evolution (Lynch et al. 2001; Lynch 2005). The rate of tunneling with a neutral
intermediate has been worked out by Komarova et al.
(2003) and Iwasa et al. (2004) in an
application of the Moran model, where allele frequency changes occur by a random
birth–death process involving single individuals in each unit of time. With some
modifications, their results are readily extended to the current case. After accounting
for diploidy and the 2-fold reduction in the rate of drift with the Wright–Fisher
model, the rate of appearance of the first double mutant destined to fixation by tunneling
becomes
there is a significant chance
that a beneficial second-step mutation will arise on a descendant of a first-step mutation
prior to fixation of the latter. Although all but a tiny fraction (1/2N)
of first-step mutations are destined to be lost by drift, such a process can occasionally
rescue such mutants, propelling them to fixation by positive selection. This type of
pathway, in which a beneficial second-step mutation goes to fixation prior to the
population ever achieving a pure first-step state, has been called stochastic tunneling by
Komarova et al. (2003) and Iwasa et al. (2004) in the context of cancer
development, and a similar phenomenon has been described in the context of duplicate-gene
evolution (Lynch et al. 2001; Lynch 2005). The rate of tunneling with a neutral
intermediate has been worked out by Komarova et al.
(2003) and Iwasa et al. (2004) in an
application of the Moran model, where allele frequency changes occur by a random
birth–death process involving single individuals in each unit of time. With some
modifications, their results are readily extended to the current case. After accounting
for diploidy and the 2-fold reduction in the rate of drift with the Wright–Fisher
model, the rate of appearance of the first double mutant destined to fixation by tunneling
becomes
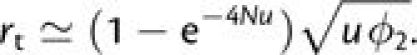 |
(3a) |
Two modifications appear in equation (3a) relative to previous derivations: 1) In prior applications, the leading term in this expression has been 4Nu rather than (1 − e−4Nu), and this has constrained the generality of tunneling theory to situations in which 4Nu < 1 because the probability that a given generational cohort can ultimately fix in a population cannot exceed 1.0 (Weissman et al. 2009). This limitation is dealt with by the leading term in equation (3a), which is well approximated by 4Nu when 4Nu ≪ 1, but asymptotically approaches one as 4Nu → ∞. 2) In prior applications, the initial frequency of a mutant allele has been assumed to equal 1/(2N) (as noted above), but in sufficiently large populations (2Nu > 1), more than one mutant allele appears per generation, so a more appropriate estimate of the probability of fixation of a secondary mutation is obtained by solving equation (1) with p = [1 + (2N − 1)u]/(2N) (one mutation has definitely arisen, but a fraction u of all other members of a cohort will also have accumulated mutations at the same time).
Accounting for both the sequential and the tunneling paths and including the final time
required for the fixation of a beneficial allele 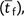 the mean number of generations until the establishment of the double
mutant generalizes to
the mean number of generations until the establishment of the double
mutant generalizes to
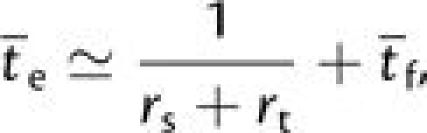 |
(3b) |
where the final fixation time can be obtained by a deterministic approximation (derived from equation 5.3.13 in Crow and Kimura 1970), with the beneficial allele increasing from frequency [1 + (2N − 1)u]/(2N) to 1 − (1/2N),
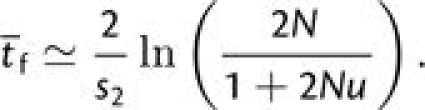 |
(3c) |
As the fixation time is relatively fast, this final term is of negligible importance when the arrival times of mutations are limiting (4Nu < 1).
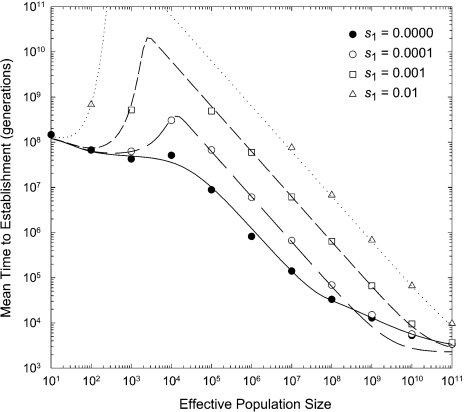
Despite its approximate nature, equation (3b) yields predictions that are in close agreement with simulated data over the
full range of population sizes (fig. 1). With
neutral intermediates, the time to establishment of the double mutant declines
monotonically with population size, although there are three approximate domains of
scaling behavior. 1) At small population sizes  establishment of the double mutant almost always proceeds by
sequential fixation, with a slight reduction in
establishment of the double mutant almost always proceeds by
sequential fixation, with a slight reduction in  as population size increases and selection is more effective at
promoting the second-step mutation. 2) At intermediate population sizes, tunneling becomes
an increasingly large contributor to the establishment process, with
as population size increases and selection is more effective at
promoting the second-step mutation. 2) At intermediate population sizes, tunneling becomes
an increasingly large contributor to the establishment process, with  scaling inversely with N in accordance with equation (3a) provided N ≪
1/4u. 3) At very large population sizes, multiple adaptive mutations
arise each generation and the time to establishment of the adaptive mutation is limited
only by the essentially deterministic expansion of the aggregate pool to frequency
1.0.
scaling inversely with N in accordance with equation (3a) provided N ≪
1/4u. 3) At very large population sizes, multiple adaptive mutations
arise each generation and the time to establishment of the adaptive mutation is limited
only by the essentially deterministic expansion of the aggregate pool to frequency
1.0.
FIG. 1.
Mean number of generations until establishment of a double mutant as a function of
the effective population size, with the intermediate states having a selective
disadvantage of s1. Data points are based on 50–300
independent simulations with a constant mutation rate of u =
10−8 per site involved in the adaptation. The double mutant is
assumed to have a selective advantage of s2 = 0.02.
Simulations were not run for conditions in which the time to establishment was on the
order of 109 generations or greater. The continuous lines give the
analytical approximations described in the text. (The slight underestimates of the
time to establishment at very large N and very small
s1 relative to the simulation results is simply a
consequence of the simulations having been initiated under states in which first-step
mutations are initially absent, whereas the theory assumes an equilibrium frequency at
the outset. It can be shown that the time to attain a fraction x of
the equilibrium frequency of the deleterious first-step mutation is ∼ −[ln(1
− x)]/(s1 −
u) generations. With very small s1 and
large N, the time to reach the initial equilibrium state makes a
nonnegligible contribution to  [with s1 = 0.0001, as in the
lowest curve, it takes about 2,000 generations for the frequency of first-step alleles
to approximate the equilibrium, and this accounts for the discrepancy in the
figure]).
[with s1 = 0.0001, as in the
lowest curve, it takes about 2,000 generations for the frequency of first-step alleles
to approximate the equilibrium, and this accounts for the discrepancy in the
figure]).
We now turn to the situation in which first-step alleles are disadvantageous. For populations sufficiently small that fixation proceeds only in a sequential manner, the rate of appearance of double mutants destined to fix is
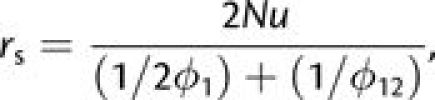 |
(4a) |
where ϕ1, the probability of fixation of a newly arisen (deleterious) first-step mutation, is obtained by substituting −s1 for s2 in equation (1) and ϕ12 is obtained by applying (s1 + s2) in place of s2. Both fixation probabilities are evaluated with initial frequency p = 1/(2N). At population sizes large enough to prevent fixation of first-step mutations (N ≫ 1/4s1), the latter are expected to rapidly approach the low frequency maintained under selection–mutation balance (2u/s1 in this case), providing a launching pad for beneficial second-step alleles. Following the logic leading to the development of equation (3a), earlier results of Komarova et al. (2003) and Iwasa et al. (2004, 2005) can then be modified to obtain an analytical approximation for the rate of tunneling,
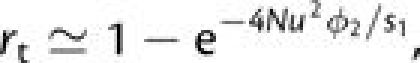 |
(4b) |
where ϕ2 is evaluated with
p = 1/(2N). The structure of this equation can
be understood as follows. In each generation, there are an expected
4Nu/s1 copies of the first-step mutation
segregating in the population, a fraction u of which are converted to
second-step mutations, which fix with probability ϕ2. As
above, use of the exponential approximation accounts for the fact that no more than one
tunneling event can occur per cohort, although with which will be satisfied in all but enormous populations,
the preceding expression is adequately approximated by
rt 4Nu2ϕ2/s1.
Provided , ϕ2 is close enough to
2s2 that rt further simplifies
to
4Nu2ϕ2/s1.
Provided , ϕ2 is close enough to
2s2 that rt further simplifies
to  8Nu2s2/s1.
8Nu2s2/s1.
The predicted mean time to establishment with deleterious intermediates, which is given
by equation (3b) using equations (4a, b) and (3c) to define
rs, rt, and
 , respectively, fits the
simulated data quite closely throughout the entire range of population sizes and selection
coefficients (fig. 1). Again, it can be seen that
there are three predominant domains of behavior with respect to population size. 1) At
small population sizes, establishment of the double mutant almost always proceeds by
sequential fixation, but after a slight decline in
, respectively, fits the
simulated data quite closely throughout the entire range of population sizes and selection
coefficients (fig. 1). Again, it can be seen that
there are three predominant domains of behavior with respect to population size. 1) At
small population sizes, establishment of the double mutant almost always proceeds by
sequential fixation, but after a slight decline in  with initial increases in population size, there is an increase in
with initial increases in population size, there is an increase in
 . This increase, which is
quite dramatic when first-step mutations are highly deleterious, arises in populations
that are large enough that there is a very low probability of fixing a deleterious
first-step mutation but small enough that the rate of tunneling is also very low. 2) For
population sizes in excess of 4/s1, there is essentially no
chance of establishment by sequential fixation, and the process of adaptive evolution is
governed entirely by tunneling, the rate of which scales nearly linearly with population
size. 3) At enormous population sizes, there is again a slowdown in the decrease in
. This increase, which is
quite dramatic when first-step mutations are highly deleterious, arises in populations
that are large enough that there is a very low probability of fixing a deleterious
first-step mutation but small enough that the rate of tunneling is also very low. 2) For
population sizes in excess of 4/s1, there is essentially no
chance of establishment by sequential fixation, and the process of adaptive evolution is
governed entirely by tunneling, the rate of which scales nearly linearly with population
size. 3) At enormous population sizes, there is again a slowdown in the decrease in
 with increasing
N due to the saturating effect of multiple tunneling mutations being
produced per generation and the added constraint on the time to fixation of such
mutations.
with increasing
N due to the saturating effect of multiple tunneling mutations being
produced per generation and the added constraint on the time to fixation of such
mutations.
Mutator Alleles
All the preceding results (and indeed, almost all prior applications of population genetic theory) assume that all members of the population have identical mutation rates. However, a substantial number of loci produce proteins with roles involved in DNA replication and repair, and like all other genes, they are subject to mutation. As a consequence, variation in the mutation rate must exist among individuals, the most extreme examples being manifest in the numerous human genetic disorders caused by mutations at DNA repair loci (including Fanconi anemia, xeroderma pigmentosum, Bloom's syndrome, Werner syndrome, and Lynch syndrome). This raises the possibility that a small (maladapted) fraction of the population may be a primary source of mutations with long-term adaptive advantages.
To gain a qualitative understanding of this matter, we evaluate the situation in which a single diallelic locus governs the mutation rate. Letting M and m designate alternative alleles at the mutator locus, the per-locus mutation rates for genotypes mm, Mm, and MM are, respectively, denoted as u0, u1, and u2, where the subscript represents the number of mutator alleles in the genotype. Under this scheme, the gametic fractions of mutator (M) alleles produced by mm, Mm, and MM genotypes are u0, , and 1.0, respectively. Back mutations (M → m) are assumed to occur at a negligible rate because whereas there are multiple ways to deactivate an allele, restoration requires a very specific back mutation. To convert the per-locus mutation rates relevant to the inactivation of m alleles to per-site rates at the adaptive locus, u0, u1, and u2 are multiplied by a factor k, here generally assumed to equal 0.01. The definition of a mutator allele used here is general, in that it applies to any allelic variant that magnifies the mutation rate, no matter how small.
Mutator alleles are expected to confer a selective disadvantage (resulting, e.g., from elevated rates of somatic mutation and/or the associated load of linked deleterious germline mutations; Dawson 1999; Johnson 1999; Lynch 2008) such that the fitnesses of the mm, Mm, and MM genotypes are 1, and , respectively, where sM is the selective disadvantage of a mutator homozygote and hM is a measure of dominance of the mutator allele (0.5 implying additivity). The overall fitness of an individual is then the product of the fitnesses at the mutator and adaptive loci.
If the frequencies of the mutator alleles are set to their expectations
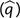 in the absence of selection
on the adaptive locus, this sets up an immediate discontinuity in the mutation rate with
respect to population size. For situations in which the heterozygous disadvantage of the
mutator allele is smaller than the power of random genetic drift, 1/(2N),
selection is incapable of preventing fixation of the mutator allele. With the initial
frequency of the M allele being 1.0, all the preceding expressions can then be used to
estimate
in the absence of selection
on the adaptive locus, this sets up an immediate discontinuity in the mutation rate with
respect to population size. For situations in which the heterozygous disadvantage of the
mutator allele is smaller than the power of random genetic drift, 1/(2N),
selection is incapable of preventing fixation of the mutator allele. With the initial
frequency of the M allele being 1.0, all the preceding expressions can then be used to
estimate  after substituting
for u. In contrast, when the power of
drift is weaker than the selective disadvantage, the mutator allele will be maintained at
a low frequency by selection–mutation balance, the expected value of which is
obtained by solving equation (6) in Lynch (2008).
The approximate effective population size at which this transition in behavior occurs is
Nc
after substituting
for u. In contrast, when the power of
drift is weaker than the selective disadvantage, the mutator allele will be maintained at
a low frequency by selection–mutation balance, the expected value of which is
obtained by solving equation (6) in Lynch (2008).
The approximate effective population size at which this transition in behavior occurs is
Nc 1/(4hMsM),
assuming , which is generally likely to be the case.
1/(4hMsM),
assuming , which is generally likely to be the case.
For situations in which the M/m polymorphism is maintained, the estimation of
 must take into account the
relative probabilities of mutations arising at the adaptive locus on different
mutation-rate backgrounds, as outlined in the Appendix. Again, the derived analytical
approximations, equations (A1a–c), yield results
that are in close accordance with those obtained by stochastic simulations for the full
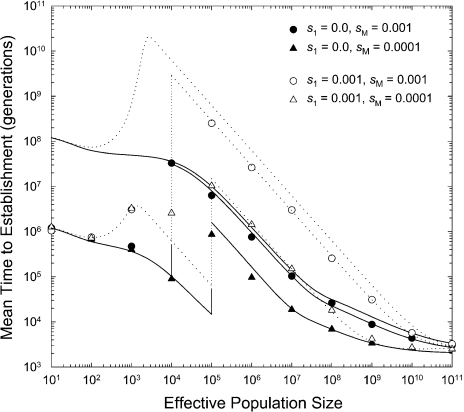
range of population sizes (fig. 2). Several notable
points can be gained from these observations.
must take into account the
relative probabilities of mutations arising at the adaptive locus on different
mutation-rate backgrounds, as outlined in the Appendix. Again, the derived analytical
approximations, equations (A1a–c), yield results
that are in close accordance with those obtained by stochastic simulations for the full
range of population sizes (fig. 2). Several notable
points can be gained from these observations.
FIG. 2.
Mean number of generations until establishment of an advantageous double mutant as a function of the effective population size in populations containing mutator alleles. The lines unaccompanied by data points give the theoretical expectations for situations in which there is a constant mutation rate per site at the adaptive locus, (from fig. 1). The lines accompanied by data points are the theoretical expectations for situations in which the mutation rate can evolve, obtained using equations (5a–c) and (3b), with the data points derived from computer simulations. The genotypic mutation rates are equal to and per locus for the mm, Mm, and MM genotypes, respectively, and in all cases, , , and . Solid points and lines: the intermediate (first-step) mutation at the adaptive locus is neutral (); open points and dotted lines: the first-step mutation has a 0.1% selective disadvantage (). The lower left sets of lines give the expectations under the assumptions that the mutator allele has fixed. The vertical lines denote the critical threshold population size , above which the mutator allele is expected to be maintained at selection–mutation balance in the early phase of the adaptive process.
First, as noted above, there is an abrupt transition in the behavior of the establishment
time at population sizes near with the same scaling with population size above and below
this point, but a stepwise reduction in the establishment time below the critical
population size necessary for preventing fixation of the mutator allele. Second, for
population sizes larger than Nc, mutator alleles must have
very minor heterozygous effects if they are to enhance the overall rate of adaptive
evolution. With the mutation rates applied in figure
2, mutator alleles with and (i.e., a 0.1% reduction in fitness in heterozygotes) have
an equilibrium frequency of 0.001 and essentially no influence on
 relative to the case with a
constant background mutation rate. Third, for mutators with very weak heterozygous fitness
effects, there can be a substantial decline in
relative to the case with a
constant background mutation rate. Third, for mutators with very weak heterozygous fitness
effects, there can be a substantial decline in  at intermediate population sizes, where because the establishment
time is otherwise quite long, numerous opportunities exist for successful tunneling
events. Fourth, at very large population sizes, the effects of mutator alleles become
asymptotically negligible due to the fact that double mutants arise frequently even in
nonmutator backgrounds. Taken together, all these factors imply an overall dampening of
the influence of population size on the time to establishment of a complex adaptive allele
when the mutation rate is an evolvable feature.
at intermediate population sizes, where because the establishment
time is otherwise quite long, numerous opportunities exist for successful tunneling
events. Fourth, at very large population sizes, the effects of mutator alleles become
asymptotically negligible due to the fact that double mutants arise frequently even in
nonmutator backgrounds. Taken together, all these factors imply an overall dampening of
the influence of population size on the time to establishment of a complex adaptive allele
when the mutation rate is an evolvable feature.
Transient Hypermutability
A major limitation of mutator alleles is that they reduce the net selective advantage of the linked beneficial mutations that they produce (and hence the fixation probability of the latter) via the indirect consequences of the additional background rain of linked and unlinked deleterious mutations that they produce in both the germline and the soma. Both these complications were implicitly incorporated into the theory in the preceding sections. To produce scenarios that avoid these long-term costs, previous theoretical attempts to highlight the prospects of mutator alleles in adaptive evolution have assumed a high rate of reversion to nonmutators following the promotion of an adaptation (Taddei et al. 1997).
An alternative mechanism that can yield elevated mutation rates with no heritable long-term disadvantage is transient hypermutability, whereby a subset of germline replication events experience elevated levels of mutagenicity associated with an aberrant DNA polymerase/damage repair apparatus or reaction (Ninio 1991; Drake 2007). Stochastic variation associated with transcription or translation errors, erroneous protein folding, nucleotide pool imbalance, and/or metabolic limitations will inevitably generate intercellular variation in mutation rates, but unlike the situation with mutator alleles, the mutagenic conditions will not be heritable. Thus, transient hypermutability might provide a mechanism for a substantial elevation in the rates of origin of complex adaptations by concentrating the production of multiple mutations within single replication events (Drake et al. 2005; Drake 2007). Observations on elevated frequencies of doublet and triplet mutations relative to random expectations in reporter constructs in microbes and mice and in de novo human disease alleles have encouraged this view (Drake et al. 2005; Drake 2007; Wang et al. 2007; Chen et al. 2008, 2009), and the unexpectedly high clustering of mutations seen in some phylogenetic analyses (Bazykin et al. 2004; Davis et al. 2009; Donmez et al. 2009) might also be a consequence of such effects.
Although there may be a near continuum of cell-specific mutation rates within an individual organism (or population of cells), the data are also compatible with a distinct subset of up to 3% of replication events experiencing an up to 200-fold inflation in the mutation rate. Thus, to evaluate the degree to which transient mutation magnifies the rate of origin of complex adaptations, we assume a population in which a random fraction (fm) of replicons mutates x times faster than the baseline rate. The expressions for the time to establishment of an adaptive mutation then need to modified in two ways. First, with a baseline mutation rate of u, the expected mutation rate becomes or for x ≫ 1. All the preceding expressions for rates and times to fixation then apply after multiplying each mutation rate by (1 + fmx). Second, the existence of hypermutable cells introduces a new pathway for the production of adaptations—the immediate appearance of an adaptive allele by simultaneous mutations at multiple sites within a single gamete (Appendix). However, even with a substantial increase in the baseline mutation rate in a subset of cells, the probability of the instantaneous production of a double mutant is still a very low probability event, raising the question as to whether this mode of production actually elevates the rate of production of evolutionary adaptations.
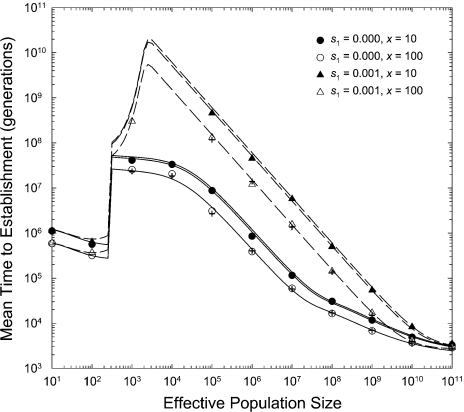
Both the simulation and the theoretical results indicate that the mean time to establishment of a complex adaptation scales with population size in essentially the same way in the presence and absence of transient hypermutability (fig. 3). In small populations, transient hypermutability has very small effects because there are still insufficient numbers of mutational targets to avoid the usual path of sequential fixation, whereas at larger population sizes, the rate of tunneling proceeds in the same way as described above after accounting for the increased mutation rate. As essentially the same theoretical results are obtained by ignoring the path of double mutation (Appendix), it appears that transient hypermutability primarily influences the rate of adaptation by simply magnifying the mutation rate and elevating the rate of passage of secondary mutations through the tunneling pathway, rather than by the simultaneous production of double mutants.
FIG. 3.
Mean number of generations until establishment of an advantageous double mutant as a function of the effective population size in the presence of transient hypermutability. In all cases, the genotypic mutation rates are equal to and per locus for the mm, Mm, and MM genotypes, respectively, and and Results for and x = 1000 are given by crosshairs for comparison with those for and x = 100, with both cases implying The lines give the theoretical expectations; for each set of s1, the top line gives the results assuming no transient hypermutability (). For parameters leading to mean times to establishment substantially in excess of 108 generations, simulation results could not be readily obtained, but it is apparent that the theoretical expressions work well through all domains of analysis.
The latter point can be seen in the following way. From the preceding expressions, the rate of tunneling is a function of , whereas the rate of production of double mutants is a function of . Thus, if transient hypermutability primarily influences the rate of establishment of adaptations by elevating the rate of origin of nonsynchronous mutations, the mean time to establishment should be independent of fm and x so long as their product remains constant. The results in figure 3 demonstrate that this is the case. For both and , the mean time to establishment behaves as though the mutation rate is doubled (in both cases, ), with no need to account for the concentrated incidence of double mutants in the small subset of transient mutators.
Increasing Complexity
Having established the basic behavior of the two-site model, we now consider the
situation with larger numbers of sites. Although such complexity introduces numerous
higher order effects that thwart the development of a general analytical treatment, some
results for limiting conditions are readily obtained. Consider first the situation in
which changes at d sites are essential to the novel adaptation, with all
alleles carrying changes at fewer than d sites being neutral. In the
first step toward adaptation, there are d sites at which changes may
occur, whereas there are d − 1 second-step sites, and so on.
Therefore, confining our attention to the situation in which the mutation rate is a
constant u per site, for populations that are sufficiently small that the
only route to adaptation involves sequential fixation, which requires
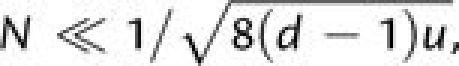
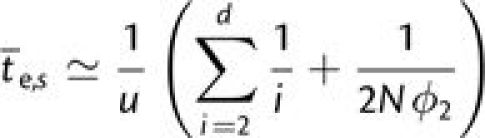 |
(5a) |
(Gokhale et al. 2009). Although increasing the
number of steps involved in adaptation increases the mean time to establishment, the
effect is fairly weak at small population sizes because of the elevated number of paths
toward the final adaptation. For d = 2, 3, 4, 5, and 10, the
summation in the preceding expression is 0.50, 0.83, 1.08, 1.28, and 1.93, respectively,
implying a less than 4-fold increase in  over this 5-fold range of complexity.
over this 5-fold range of complexity.
The limiting behavior as N → ∞ can also be inferred for
neutral intermediates by treating the population deterministically and noting that
fixation of the d-step mutation will occur before fixation has occurred
at any intermediate step. The expected frequency of d-step alleles at
time t is  (ut)d for
ut ≪ 1 and taking
1/(4Ns2) to be the frequency at which the
probability of fixation is essentially 1.0,
(ut)d for
ut ≪ 1 and taking
1/(4Ns2) to be the frequency at which the
probability of fixation is essentially 1.0,
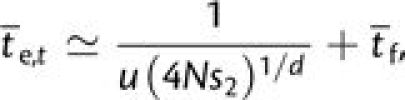 |
(5b) |
where the latter term again accounts for the time to fixation.
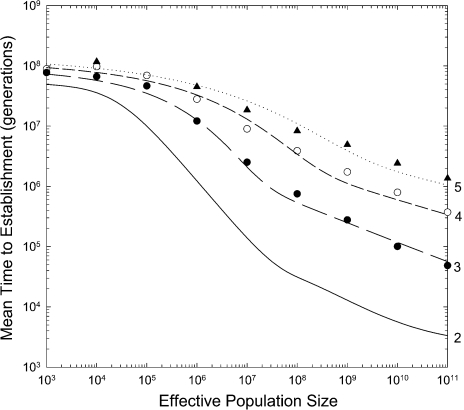
These expressions point to two striking aspects of the rate of origin of complex
adaptations via neutral intermediates. First, regardless of the complexity of the
adaptation, the time to establishment is inversely proportional to the rate at which
mutations arise at single sites, not the low probability of multiple independent mutations
(ud). Second, with increasing
d, the response of  to population size becomes progressively flatter (fig. 4).
to population size becomes progressively flatter (fig. 4).
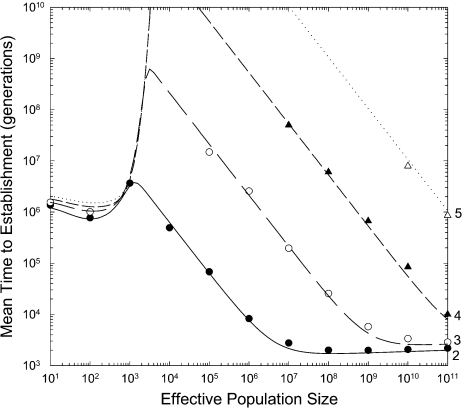
FIG. 4.
Mean number of generations until establishment for complex adaptive alleles involving d = 2, 3, 4, and 5 sites (denoted in the right margin) for the case in which the intermediate states are neutral. The lower solid line gives the theoretical results for d = 2. A constant mutation rate of per site is assumed, and the adaptive allele is assumed to have a selective advantage of The data are based on simulations of 25–100 replicates, and the curved lines are the approximate fits described in the text.
Using a branching process approach, Durrett et al. (2008) concluded that the time to
establishment scales inversely with , but as can be seen in figure 4, the domain of this scaling is extremely restrictive for biologically
realistic parameters, as for any particular d, the scaling first
increases and then decreases with increasing N, and for
d > 3 is never as steep as 1/N, becoming
progressively flatter with increasing d. Although we have been unable to
obtain a direct analytical approximation for the full behavior of this multidimensional
diffusion process, the following ad hoc expression appears to provide a reasonable
first-order approximation of the transition of  from low to high N,
from low to high N,
 |
(5c) |
where
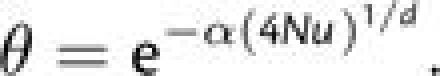 |
(5d) |
The most unsatisfactory aspect of this expression is the lack of an explicit definition
of α, which governs the rate of decline of
 with increasing
N, but for the parameters utilized in figure 4, α
with increasing
N, but for the parameters utilized in figure 4, α  6.0, 3.0, and 2.2 for d = 3, 4, and 5,
respectively. Schweinsberg (2008) provides a
detailed evaluation of the purely neutral model, yielding approximate scalings for
first-arrival times for various ranges of N, although the approximation
domains become diminishingly small with increasing d, for example, with
nine domains of behavior with respect to N recognized when
d = 3.
6.0, 3.0, and 2.2 for d = 3, 4, and 5,
respectively. Schweinsberg (2008) provides a
detailed evaluation of the purely neutral model, yielding approximate scalings for
first-arrival times for various ranges of N, although the approximation
domains become diminishingly small with increasing d, for example, with
nine domains of behavior with respect to N recognized when
d = 3.
The scaling of the time to establishment with the number of sites is substantially
altered when the intermediate states are deleterious, where
 increases dramatically with
increasing d at moderate to large population sizes (fig. 5). Such behavior results from the fact that when the power of
drift is weak relative to the strength of selection against deleterious intermediate-step
alleles, the frequencies of the latter hover near the selection–mutation balance
expectation. In this situation, each newly arisen first-step allele is eliminated quite
rapidly either by drift or by selection (the expected half-life being no more than
1/s1 generations; Garcia-Dorado et al. 2003). In order for tunneling to yield an adaptive allele
in this short period of time, a descendant of a first-step allele must accumulate an
additional d − 1 mutations, the probability of which becomes
diminishingly small with larger d. In contrast, at the smallest
population sizes, there is only a small increase in
increases dramatically with
increasing d at moderate to large population sizes (fig. 5). Such behavior results from the fact that when the power of
drift is weak relative to the strength of selection against deleterious intermediate-step
alleles, the frequencies of the latter hover near the selection–mutation balance
expectation. In this situation, each newly arisen first-step allele is eliminated quite
rapidly either by drift or by selection (the expected half-life being no more than
1/s1 generations; Garcia-Dorado et al. 2003). In order for tunneling to yield an adaptive allele
in this short period of time, a descendant of a first-step allele must accumulate an
additional d − 1 mutations, the probability of which becomes
diminishingly small with larger d. In contrast, at the smallest
population sizes, there is only a small increase in  with increasing complexity because deleterious intermediate-state
alleles are capable of drifting to fixation in an effectively neutral manner, thereby
providing a progressive stepwise path to the final adaptive state.
with increasing complexity because deleterious intermediate-state
alleles are capable of drifting to fixation in an effectively neutral manner, thereby
providing a progressive stepwise path to the final adaptive state.
FIG. 5.
Mean number of generations until establishment for complex adaptive alleles involving d = 2, 3, 4, and 5 sites (denoted in the right margin) for the case in which the intermediate states are deleterious ( for all intermediate-state alleles) relative to the starting state. Because of the very extended times to establishment in this case, the mutation rate employed in simulations was quite high (); mutator alleles and transient hypermutability are ignored. The adaptive allele is assumed to have a selective advantage of and each data point is based on simulations of 25–100 replicates. The smooth lines are derived from the analytical approximations described in the text.
For the special situation in which all intermediate-state alleles are equally deleterious (fig. 5), a good analytical approximation to the time to establishment can be obtained as follows. Sequential fixation follows the path in which 1) the first deleterious mutation, which can occur at d sites, drifts to fixation; 2) the next d − 2 mutations drift to fixation in a neutral manner because they are selectively equivalent to the first-step allele; and 3) the final mutation is fixed by positive selection. The mean time to sequential fixation is then
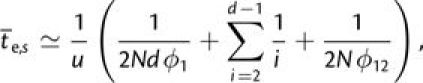 |
(6a) |
and the rate of sequential fixation is the reciprocal of
 . Fixation via tunneling
requires that, prior to being eliminated by selection, a deleterious first-step mutant
allele procures all the downstream mutations necessary for progression to fixation by
positive selection. Letting the mean time that a deleterious first-step mutation remains
segregating prior to elimination by selection be ∼1/s1
generations, and assuming that each such mutation is generally present in just a single
copy most of the time, the rate of tunneling is
. Fixation via tunneling
requires that, prior to being eliminated by selection, a deleterious first-step mutant
allele procures all the downstream mutations necessary for progression to fixation by
positive selection. Letting the mean time that a deleterious first-step mutation remains
segregating prior to elimination by selection be ∼1/s1
generations, and assuming that each such mutation is generally present in just a single
copy most of the time, the rate of tunneling is
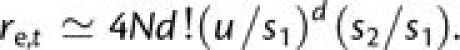 |
(6b) |
Finally, under the assumption that final-step beneficial mutations generally arise as single copies in any generation, the final fixation time is
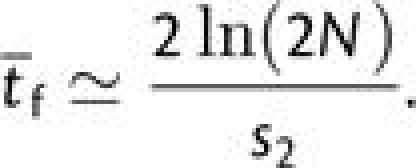 |
(6c) |
When these expressions are applied to equation (3b), they are in excellent agreement with simulation data for nearly the full range of population sizes.
The Effect of Recombination
Although recombination has been ignored in the previous analyses, so long as the mutations underlying the adaptations under consideration reside within gene-sized stretches of DNA, the following arguments suggest that recombination will usually either have negligible effects or accelerate the rate of adaptation. First, recombination will have no impact at population sizes where adaptation proceeds entirely by sequential fixation, simply because multiple polymorphic sites are never present simultaneously. Second, in populations of moderate size, recombination between alternative intermediate-state alleles can be a major source of origin of adaptive alleles, although too high a recombination rate will impede the maintenance of an adaptive allele when it is at low frequency. Third, at very large population sizes, where evolution proceeds in a nearly deterministic fashion, multisite mutants are created so frequently that recombination between intermediate-state alleles becomes a negligible source of origin of the final adaptive allele, although the progression of such alleles to fixation will be inhibited if the recombination rate exceeds the selective advantage.
Weinreich and Chao (2005) demonstrated that recombinational breakdown of adaptive alleles will be of negligible significance if adaptive mutants destined to fixation are able to attain a sufficiently high frequency for selection to operate in an effectively deterministic fashion prior to a recombination event. This requires a recombination rate between sites smaller than , which for 0.01, and 0.1 is 0.00018, 0.0030, and 0.097, respectively. High-density genetic maps indicate that the recombination rate per site ranges from / nucleotide site in microbial eukaryotes with small genomes to in the bloated genomes of animals and land plants (Lynch 2007). To an order of magnitude, genes in the former group are ∼103 bp in length, whereas those in multicellular organisms range from ∼103 to ∼106 bp (including introns). Considering a full range of potential distances between adaptive sites within genes and a minimum of ∼10, this implies recombination rates between selected sites <0.001 in essentially all situations, ranging down to for closely spaced sites in multicellular species. These observations suggest that at the within-gene level recombination will generally be a very weak force opposing the establishment of complex adaptive alleles.
Discussion
The preceding results illustrate that the mean times to establishment of complex adaptations often exhibit a simple scaling with basic population genetic parameters. As variables such as N and u vary by orders of magnitude across phylogenetic lineages in predictable ways (Lynch 2007), this opens the possibility of developing a general framework for understanding the likelihood of alternative paths to adaptive evolution in lineages varying with respect to population genetic parameters.
Considering first the situation in which the mutation rate is assumed to be immune to
evolutionary change and the intermediate states are neutral, the mean time to establishment
of the adaptive allele ( ) monotonically declines with increasing population size, with the
steepness of this decline becoming more relaxed when larger numbers of sites are involved in
the adaptation, scaling with N − 1/d at very large
N (fig. 4). If the intermediate
states are deleterious,
) monotonically declines with increasing population size, with the
steepness of this decline becoming more relaxed when larger numbers of sites are involved in
the adaptation, scaling with N − 1/d at very large
N (fig. 4). If the intermediate
states are deleterious,  is maximized at an intermediate population size, where both the rates
of sequential fixation and tunneling are low (figs. 1
and 5), and the log of
is maximized at an intermediate population size, where both the rates
of sequential fixation and tunneling are low (figs. 1
and 5), and the log of
 increases linearly with
increasing complexity at moderate N and at accelerating rate at very large
N (due to the diminishingly low probability of a multisite mutant arising
in a deleterious lineage otherwise destined to rapid purging).
increases linearly with
increasing complexity at moderate N and at accelerating rate at very large
N (due to the diminishingly low probability of a multisite mutant arising
in a deleterious lineage otherwise destined to rapid purging).
In general, the mean time to establishment of a novel adaptive allele scales inversely with
the 0.5–2.0 power of the mutation rate regardless of the level of complexity of the
adaptation, provided there are not multiple deleterious states (in which case
 scales with
1/u to depending on the population size). Thus, with increasing
numbers of sites necessary for an adaptation, the increase in
scales with
1/u to depending on the population size). Thus, with increasing
numbers of sites necessary for an adaptation, the increase in
 is often relatively modest. A
primary reason for this behavior is that a multistage route to adaptation increases the
number of paths to the final adaptive state by magnifying the numbers of possible mutations
in the early stages of the process. At large d, this increase in the number
of possible paths comes close to compensating for the increase in the number of steps
required to reach the final adaptive state. Remarkably, as can be seen from equation (5b) in very large populations with neutral
intermediates, as d → ∞, the time to establishment converges on
the reciprocal of the per-site mutation rate, becoming independent of the number of
mutations required for the adaptation.
is often relatively modest. A
primary reason for this behavior is that a multistage route to adaptation increases the
number of paths to the final adaptive state by magnifying the numbers of possible mutations
in the early stages of the process. At large d, this increase in the number
of possible paths comes close to compensating for the increase in the number of steps
required to reach the final adaptive state. Remarkably, as can be seen from equation (5b) in very large populations with neutral
intermediates, as d → ∞, the time to establishment converges on
the reciprocal of the per-site mutation rate, becoming independent of the number of
mutations required for the adaptation.
This scaling of  with population size will be
altered when mutator alleles are allowed to enter the population, for under the assumption
that the latter have mild deleterious effects, such alleles will only rise to high
frequencies in small populations. Thus, allowing for genetic variation in the mutation rate,
even with neutral intermediates,
with population size will be
altered when mutator alleles are allowed to enter the population, for under the assumption
that the latter have mild deleterious effects, such alleles will only rise to high
frequencies in small populations. Thus, allowing for genetic variation in the mutation rate,
even with neutral intermediates,  may be maximized at an intermediate population size (fig. 2), although
the gradient in change of
may be maximized at an intermediate population size (fig. 2), although
the gradient in change of  with population size will become progressively relaxed when mutator
alleles have milder effects on fitness and can even rise to moderate frequencies in
intermediate-sized populations. Transient hypermutability, a purely physiological effect in
a subset of cells that has no heritable component, appears to increase the rate of
adaptation only to the extent that it magnifies the average population-level mutation rate,
without altering the scaling with population size noted above.
with population size will become progressively relaxed when mutator
alleles have milder effects on fitness and can even rise to moderate frequencies in
intermediate-sized populations. Transient hypermutability, a purely physiological effect in
a subset of cells that has no heritable component, appears to increase the rate of
adaptation only to the extent that it magnifies the average population-level mutation rate,
without altering the scaling with population size noted above.
Overall, our results suggest that segregating mutator alleles and transient hypermutability are unlikely to make major contributions to the origins of adaptations in natural populations unless the former have much milder associative deleterious effects or the latter have much higher incidences or magnifying effects than assumed in the preceding analyses. Although fixed mutator alleles theoretically have an especially high likelihood of spawning adaptive alleles in small populations, one could argue that the latter situation is unlikely to be biologically sustainable, as any population that is capable of fixing alleles with mildly deleterious effects will typically be on a path to extinction (Lynch et al. 1995).
Noting that realistic population sizes, mutation rates, and selection coefficients have been applied throughout, these results suggest that quite complex alleles, with multiple neutral or deleterious intermediate states, can readily emerge in populations on time scales of 103–108 generations. Thus, for microbes with generation lengths of hours to days and very large population sizes, the mean time to establishment can easily be on the order of a few weeks to several months depending on the complexity of the final allelic state. Even multicellular species, with effective population sizes in the vicinity of 106 (Lynch 2007), are capable of establishing fairly complex adaptations on time scales of a few tens of millions of generations, the exact time span depending on the magnitude of the selective (dis)advantages of the intermediate and end states.
For several reasons, these conclusions should be viewed as quite conservative. First, in
the case of neutral intermediates, it has been assumed throughout that the base population
is completely devoid of site-specific mutational variants that might contribute to the final
adaptation, although first-step alleles were incorporated into the theory for the case of
deleterious intermediates. Owing to the recurrent input of mutations, such variants can be
expected to be present in most settings. Second, the adaptations that we have envisioned
have been assumed to be products of mutations at specific nucleotide sites. If multiple
combinations of sites can be deployed for construction of the novel adaptation (e.g.,
multiple pairs of amino acid–encoding sites for a protein adaptation), the mutation
rates to various states would have to be magnified accordingly (by simply multiplying the
mutation rates at each stage by the number of relevant sites). Finally, although the results
presented herein have focused on the mean time to establishment of an adaptive allele, for
any specific set of conditions, the distribution of establishment times is typically very
broad, approaching negative exponential, with high probabilities of establishment at times
far below the mean (e.g., Durrett et al. 2009), and
the standard deviation of te among replicate runs being
approximately equal to  .
.
A highly informative aspect of the preceding results is what they reveal about the
potential mechanisms for the origin and establishment of novel adaptations in populations
experiencing different intensities of random genetic drift and mutation. Consider the
situation in which populations are large enough that tunneling is the primary mode of
establishment of a complex adaptation. As just two examples, note that for any set of
specific fitness effects of the intermediate- and final-state alleles: 1) for a two-step
model with neutral intermediates, the rate of tunneling is proportional to
(eq. 3a); and
2) for situations in which there are d deleterious intermediate states, the
rate of tunneling is proportional to Nud (eqs.
4b and 6b). As a first-order approximation, Nu averages
∼0.001 in vertebrates and land plants, ∼0.01 in smaller eukaryotes, and approaches
0.1 in some prokaryotes (Lynch 2007). For these
same groups, for base substitution mutations,
u 10−8, and , respectively (Lynch
2007). Thus, for two-step adaptations involving neutral intermediates, the rate of
establishment of an adaptive allele scales 1:3:10 for vertebrates, small eukaryotes, and
prokaryotes, whereas the scaling is approximately 1:1:1 for a two-step adaptation involving
a deleterious intermediate. For situations in which there are two deleterious intermediate
states, the scaling is 100:10:1, and with four deleterious intermediate states, it is
10,000:100:1.
10−8, and , respectively (Lynch
2007). Thus, for two-step adaptations involving neutral intermediates, the rate of
establishment of an adaptive allele scales 1:3:10 for vertebrates, small eukaryotes, and
prokaryotes, whereas the scaling is approximately 1:1:1 for a two-step adaptation involving
a deleterious intermediate. For situations in which there are two deleterious intermediate
states, the scaling is 100:10:1, and with four deleterious intermediate states, it is
10,000:100:1.
Ultimately, the paths most frequently taken in the origins of evolutionary novelties will also depend on the rates at which neutral versus deleterious intermediate mutations arise. However, assuming that the distributions of selection coefficients for de novo mutations are not radically different among organisms, the preceding observations strongly suggest that the paths to adaptation may deviate strongly among organisms from different domains of life. Relative to multicellular eukaryotes, prokaryotes are expected to acquire adaptive alleles by paths involving neutral intermediates several times more rapidly than eukaryotes on a per-generation basis. In contrast, when there are multiple deleterious intermediate steps, multicellular species have much greater expected rates of acquisition of adaptive alleles on a per-generation basis. Of course, because the generation lengths of multicellular species can easily be 103–105 times greater than those for microbes, on an absolute time scale, rates of microbial adaptation may be comparable to or even greater than those for multicellular species even when intermediate allelic states are deleterious. However, the message to be gained from the preceding results is that the elevated power of both random genetic drift and mutation may enable the acquisition of complex adaptations in multicellular species at rates that are not greatly different from those achievable in enormous microbial populations.
Acknowledgments
We are very grateful to J. Thornton and other University of Oregon colleagues, as well as to J. Schweinsberg, for very helpful comments. This work was supported by the National Institutes of Health grant R01 GM036827 and National Science Foundation (NSF) grant EF-0827411 to M.L. and by an undergraduate NSF Research Experience for Undergraduates mathematics fellowship (DMS-0851852) to A.A.
Appendix
Mutator Alleles
Because mutator alleles have an intrinsic selective disadvantage, when the first-step
mutation confers no selective advantage (which is the case in all situations evaluated
here), the path of sequential fixation will almost always begin on a gamete containing a
nonmutator allele. The rate of origin of the first first-step mutation to fix will then
be  u0 is the average background mutation
rate for a m allele. Conditional on fixation of the first-step mutation, the rate of
fixation of the second-step mutation is then
u0 is the average background mutation
rate for a m allele. Conditional on fixation of the first-step mutation, the rate of
fixation of the second-step mutation is then 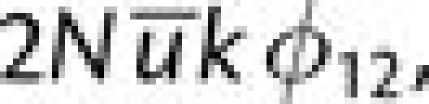 where
where 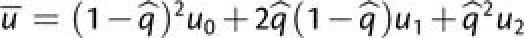 is the average background mutation rate experienced by the
first-step mutation, assuming that the polymorphism at the background mutator locus
remains at approximate selection–mutation equilibrium after the descendants of the
first-step mutation drift to fixation. The rate of sequential fixation is
then
is the average background mutation rate experienced by the
first-step mutation, assuming that the polymorphism at the background mutator locus
remains at approximate selection–mutation equilibrium after the descendants of the
first-step mutation drift to fixation. The rate of sequential fixation is
then
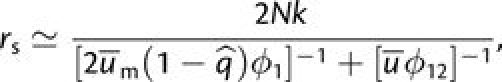 |
(A1a) |
with ϕ. in both cases being evaluated with p = 1/(2N).
The rate of tunneling must allow for the fact that first-step mutations arise linked to
the m and M alleles at the mutator locus at the rates 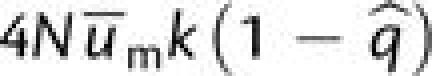 and
and 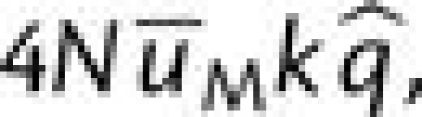 respectively. In the first case, assuming a neutral intermediate,
tunneling then proceeds at rate
respectively. In the first case, assuming a neutral intermediate,
tunneling then proceeds at rate  in the second case, it proceeds at the approximate rate
in the second case, it proceeds at the approximate rate
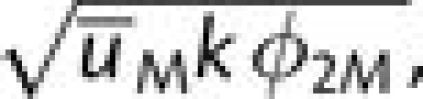 with the selective
advantage of the adaptive mutation being discounted by the selective disadvantage of the
linked mutator allele, that is, as s2 −
sM. The total rate of tunneling with neutral intermediates
is then approximated by an expansion of equation (3a),
with the selective
advantage of the adaptive mutation being discounted by the selective disadvantage of the
linked mutator allele, that is, as s2 −
sM. The total rate of tunneling with neutral intermediates
is then approximated by an expansion of equation (3a),
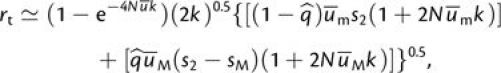 |
(A1b) |
As in the case of equation (3a), this expression attempts to correct for the constraints on the fixation probabilities of simultaneously segregating mutations, in this case weighting the probabilities for each mutation type according to the allele at the linked mutator locus. When first-step alleles are deleterious, expansion of equation (4b) leads to
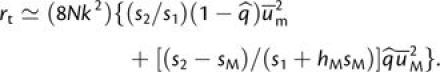 |
(A1c) |
No attempt is made to correct for the parallel origins of tunneling mutations here
because of their rarity (resulting from the fact that first-step mutations are kept at
low frequency by selection), and the fixation probabilities are evaluated with
p = 1/(2N). The mean time to establishment is
again approximated by substituting rs,
rt, and 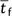 into equation (3b).
into equation (3b).
Transient Hypermutability
In the context of the material covered above, a fully general expression for the rate of establishment of double mutants by hypermutable cells is
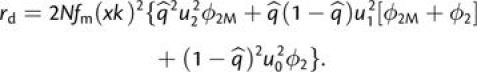 |
(A2a) |
Incorporating this third path toward adaptation into equation (3b),
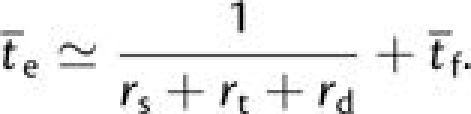 |
(A2b) |
References
- Bazykin GA, Kondrashov FA, Ogurtsov AY, Sunyaev S, Kondrashov AS. Positive selection at sites of multiple amino acid replacements since rat-mouse divergence. Nature. 2004;429:558–562. doi: 10.1038/nature02601. [DOI] [PubMed] [Google Scholar]
- Behe MJ, Snoke DW. Simulating evolution by gene duplication of protein features that require multiple amino acid residues. Protein Sci. 2004;13:2651–2664. doi: 10.1110/ps.04802904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter AJR, Wagner GP. Evolution of functionally conserved enhancers can be accelerated in large populations: a population-genetic model. Proc R Soc Lond B, Biol Sci. 2002;269:953–960. doi: 10.1098/rspb.2002.1968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen JM, Férec C, Cooper DN. Closely spaced multiple mutations as potential signatures of transient hypermutability in human genes. Hum Mutat. 2009;30:1435–1448. doi: 10.1002/humu.21088. [DOI] [PubMed] [Google Scholar]
- Chen Z, Feng J, Buzin CH, Sommer SS. Epidemiology of doublet/multiplet mutations in lung cancers: evidence that a subset arises by chronocoordinate events. PLoS One. 2008;3(11):e3714. doi: 10.1371/journal.pone.0003714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christiansen FB, Otto SP, Bergman A, Feldman MW. Waiting with and without recombination: the time to production of a double mutant. Theor Popul Biol. 1998;53:199–215. doi: 10.1006/tpbi.1997.1358. [DOI] [PubMed] [Google Scholar]
- Crow JF, Kimura M. An introduction to population genetic theory. New York: Harper and Row Publishers; 1970. [Google Scholar]
- Davis BH, Poon AF, Whitlock MC. Compensatory mutations are repeatable and clustered within proteins. Proc Biol Sci. 2009;276:1823–1827. doi: 10.1098/rspb.2008.1846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawson KJ. The dynamics of infinitesimally rare alleles, applied to the evolution of mutation rates and the expression of deleterious mutations. Theor Popul Biol. 1999;55:1–22. doi: 10.1006/tpbi.1998.1375. [DOI] [PubMed] [Google Scholar]
- Dean AM, Thornton JW. Mechanistic approaches to the study of evolution: the functional synthesis. Nat Rev Genet. 2007;8:675–688. doi: 10.1038/nrg2160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DePristo MA, Weinreich DM, Hartl DL. Missense meanderings in sequence space: a biophysical view of protein evolution. Nat Rev Genet. 2005;6:678–687. doi: 10.1038/nrg1672. [DOI] [PubMed] [Google Scholar]
- Donmez N, Bazykin GA, Brudno M, Kondrashov AS. Polymorphism due to multiple amino acid substitutions at a codon site within Ciona savignyi. Genetics. 2009;181:685–690. doi: 10.1534/genetics.108.097535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drake JW. Too many mutants with multiple mutations. Crit Rev Biochem Mol Biol. 2007;42:247–258. doi: 10.1080/10409230701495631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drake JW, Bebenek A, Kissling GE, Peddada S. Clusters of mutations from transient hypermutability. Proc Natl Acad Sci U S A. 2005;102:12849–12854. doi: 10.1073/pnas.0503009102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durrett R, Schmidt D. Waiting for two mutations: with applications to regulatory sequence evolution and the limits of Darwinian evolution. Genetics. 2008;180:1501–1509. doi: 10.1534/genetics.107.082610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durrett R, Schmidt D, Schweinsberg J. A waiting time problem arising from the study of multi-stage carcinogenesis. Ann Appl Probab. 2009;19:676–718. [Google Scholar]
- Garcia-Dorado A, Caballero A, Crow JF. On the persistence and pervasiveness of a new mutation. Evolution. 2003;57:2644–2646. doi: 10.1111/j.0014-3820.2003.tb01507.x. [DOI] [PubMed] [Google Scholar]
- Gillespie JH. Molecular evolution over the mutational landscape. Evolution. 1984;38:1116–1129. doi: 10.1111/j.1558-5646.1984.tb00380.x. [DOI] [PubMed] [Google Scholar]
- Gokhale CS, Iwasa Y, Nowak MA, Traulsen A. The pace of evolution across fitness valleys. J Theor Biol. 2009;259:613–620. doi: 10.1016/j.jtbi.2009.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartl DL, Taubes CH. Towards a theory of evolutionary adaptation. Genetica. 1998;102–103:525–533. [PubMed] [Google Scholar]
- Higgs PG. Compensatory neutral mutations and the evolution of RNA. Genetica. 1998;102–103:91–101. [PubMed] [Google Scholar]
- Innan H, Stephan W. Selection intensity against deleterious mutations in RNA secondary structures and rate of compensatory nucleotide substitutions. Genetics. 2001;159:389–399. doi: 10.1093/genetics/159.1.389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iwasa Y, Michor F, Komarova NL, Nowak MA. Population genetics of tumor suppressor genes. J Theor Biol. 2005;233:15–23. doi: 10.1016/j.jtbi.2004.09.001. [DOI] [PubMed] [Google Scholar]
- Iwasa Y, Michor F, Nowak MA. Stochastic tunnels in evolutionary dynamics. Genetics. 2004;166:1571–1579. doi: 10.1534/genetics.166.3.1571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson T. Beneficial mutations, hitchhiking and the evolution of mutation rates in sexual populations. Genetics. 1999;151:1621–1631. doi: 10.1093/genetics/151.4.1621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M. On the probability of fixation of mutant genes in populations. Genetics. 1962;47:713–719. doi: 10.1093/genetics/47.6.713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komarova NL, Sengupta A, Nowak MA. Mutation-selection networks of cancer initiation: tumor suppressor genes and chromosomal instability. J Theor Biol. 2003;223:433–450. doi: 10.1016/s0022-5193(03)00120-6. [DOI] [PubMed] [Google Scholar]
- Lynch M. Simple evolutionary pathways to complex proteins. Protein Sci. 2005;14:2217–2225. doi: 10.1110/ps.041171805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M. The origins of genome architecture. Sunderland (MA): Sinauer Associates Inc; 2007. [Google Scholar]
- Lynch M. The cellular, developmental and population-genetic determinants of mutation-rate evolution. Genetics. 2008;180:933–943. doi: 10.1534/genetics.108.090456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Conery J, Bürger R. Mutation accumulation and the extinction of small populations. Am Nat. 1995;146:489–518. [Google Scholar]
- Lynch M, O'Hely M, Walsh B, Force A. The probability of fixation of a newly arisen gene duplicate. Genetics. 2001;159:1789–1804. doi: 10.1093/genetics/159.4.1789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ninio J. Transient mutators: a semiquantitative analysis of the influence of translation and transcription errors on mutation rates. Genetics. 1991;129:957–962. doi: 10.1093/genetics/129.3.957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr HA. The population genetics of adaptation: the adaptation of DNA sequences. Evolution. 2002;56:1317–1330. doi: 10.1111/j.0014-3820.2002.tb01446.x. [DOI] [PubMed] [Google Scholar]
- Pigliucci M. The proper role of population genetics in modern evolutionary theory. Biol Theory. 2008;3:316–324. [Google Scholar]
- Schweinsberg J. The waiting time for m mutations. Electron J Probab. 2008;13:1442–1478. [Google Scholar]
- Stephan W. The rate of compensatory evolution. Genetics. 1996;144:419–426. doi: 10.1093/genetics/144.1.419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taddei F, Radman M, Maynard-Smith J, Toupance B, Gouyon PH, Godelle B. Role of mutator alleles in adaptive evolution. Nature. 1997;387:700–702. doi: 10.1038/42696. [DOI] [PubMed] [Google Scholar]
- Wang J, Gonzalez KD, Scaringe WA, Tsai K, Liu N, Gu D, Li W, Hill KA, Sommer SS. Evidence for mutation showers. Proc Natl Acad Sci U S A. 2007;104:8403–8408. doi: 10.1073/pnas.0610902104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinreich DM, Chao L. Rapid evolutionary escape by large populations from local fitness peaks is likely in nature. Evolution. 2005;59:1175–1182. [PubMed] [Google Scholar]
- Weissman DB, Desai MM, Fisher DS, Feldman MW. The rate at which asexual populations cross fitness valleys. Theor Popul Biol. 2009;75:286–300. doi: 10.1016/j.tpb.2009.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]