Abstract
The intrinsic property of liquids is a vital indicator of formulation performance and stability. Therefore, investigation of the interfacial phenomenon of surface tension is a routine procedure in the development of products in a wide variety of areas including foods, pharmaceuticals, cosmetics, and painting technologies. We hypothesize that studies related to the maximum pull on a rod can be extrapolated to disk geometry and applied to measure surface tension using a texture analyzer. A glass disk probe was attached to the arm of a texture analyzer and pulled from the liquid surface. The maximum force of detachment was used to calculate surface tension extrapolating from the theory of maximum pull on a rod. The surface tension of water, ethanol, and a hydroalcoholic solution was measured and compared with literature values to validate this hypothesis. The calculated values of surface tension for the liquids studied were within 5% of the reported values. Probe diameter appears to have an important role on surface tension accuracy compared with literature values. Slight discrepancies can be attributed to temperature control and leveling of liquid surface, although still in accordance with the reported values of surface tension measured using different methods. This study presents a simple, precise, and quick method to determine the surface tension of liquids from the maximum pull on a disk. Further studies are warranted to determine the optimum glass disk probe diameter for better accuracy.
KEY WORDS: interfacial phenomena, pull on a disk, surface tension, texture analyzer
INTRODUCTION
Interfacial phenomena are important aspects in the formulation development process of liquids in the pharmaceutical, cosmetics, consumer product, painting, and food industries. Particularly, this physicochemical property is critical in the pharmaceutical formulation development of microemulsions, suppositories, topical and transdermal delivery systems, eye drops, and nasal aerosols (1). Surface tension properties can be affected by the addition of ingredients to a liquid; moreover, the presence of surface-active agents in formulations aid in the stability of suspensions, emulsions, and foams (2). Of particular importance to the development of inhalable pharmaceutical product is that the surface tension of liquids has been shown to influence the aerosolization performance of nebulizers (3–5). Numerous methods exist to determine liquid surface tensions, which can be either dependent or independent of contact angle (6,7). Considering their widely established use and acceptance, the DuNoüy ring and the capillary rise methods are the most noteworthy techniques applied to the evaluation of surface tension.
Several different probe geometries, including rings, cones, and rods, have been used for the pull technique to measure surface tension from the menisci at a free liquid surface (8–10). To date, there have been limited publications on the pull on a disk method after this technique was deemed not to offer applicable solutions for measuring surface tension (7). According to Nietz and Lambert, disk geometry “presents complex problems” due to the exponential increase in force as a function of probe diameter. Ultimately, it was determined that the linear relationship found for rings reasoned probe ring geometry to be the most suitable method for the measurement of surface tension. However, as an alternative approach, Padday et al. (11) previously determined the physical aspects governing the maximum pull on a rod. They found that the maximum force used to suspend the liquid underneath the rod, expressed as volume, is a characteristic property of the system that can be numerically correlated to the probe radius in order to determine surface tension.
In order to determine the suspension force of a liquid rapidly, the inclusion of a force measurement apparatus is therefore essential in the evaluation of surface tension. Traditionally, analytical balances are the predominant apparatus used to measure force exerted by raising the liquid above a general level (12). The DuNoüy method requires a microbalance to measure the detachment force of the liquid surface from a platinum–iridium ring. The texture analyzer is a force measurement instrument with a high force sensitivity and measurement range, although not capable of measuring the very small detachment force for a ring probe. The texture analyzer has in recent years become a standard for force measurement applications and has been widely used as a research tool in the pharmaceutical as well as the food industries (13–16). With measurement time, arm speed, and displacement distance as parameters that can be finely controlled, this versatile equipment offers the tools needed to investigate a variety of formulation aspects including material hardness, adhesiveness, stickiness, swelling, and penetration properties (17–19).
The relative larger diameter of disks, as compared with rods and rings, is capable of suspending a greater volume of liquid underneath the probe, therefore requiring a greater maximum force to be measured. This increased detachment force measured is sufficient to fall within the measurement range of the texture analyzer. Previous work has not focused on disk geometry due to the reasons described above. In this study, we hypothesize that the work performed by Padday et al. on the theory of maximum pull on a rod can be extrapolated to the application of disks as the probe geometry, considering their similarities in shape. Their large differences in dimensions, however, may alter the dynamics of static interfacial phenomenon measurement by modifying the magnitude of maximum detachment force. The objective of this study was to explore the feasibility of using a glass disk probe in conjunction with a texture analyzer instrument to develop an accurate, precise, and reproducible analytical method for the determination of the surface tension of liquids. The novelty of this work is in exploring the disk geometry capable of suspending a significant volume of liquid underneath its leveled surface, making the force measurement fall within the range of measurement of the texture analyzer. Therefore, it eliminates the need of an extremely sensitive instrument to measure force, like the analytical microbalances commonly used to measure surface tension. Given its versatile and widespread application in a variety of laboratory settings, expanding the capabilities of this instrument would greatly benefit the fast screening of formulations for diversified industries.
EXPERIMENTAL
Materials
A texture analyzer from Texture Technologies, model TA.XTPlus (Scarsdale, NY, USA) was used for all experiments in this study. A PYREX® 150 × 75-mm crystallizing dish (product no. 3140-150) (Lowell, MA USA) was used as the liquid reservoir, and Alconox® Powdered Precision Cleaner (White Plains, NY, USA) was used as the cleaning agent. The ethanol used was procured from Fisher Science Education (Hanover Park, IL, USA), and deionized water was obtained from a central reverse osmosis/demineralizer system commonly found in research laboratories. Duco® Cement from ITW Performance Polymers, Devcon (Danvers, MA, USA) was used to assemble the probes.
Two commissioned machine-made aluminum probes were made at the University of Texas at Austin Department of Chemistry and Biochemistry machine shop. For each probe, an aluminum rod of radius 3.2 mm with thread on both ends was screwed perpendicularly into the probe housing of the texture analyzer on one end and to a circular aluminum plate of radius 3.12 cm on the other. Two handmade borosilicate glass disks were made by the University of Texas at Austin Chemistry Glass Shop; the glass disks were adhered to the bottom of the aluminum plates with Duco® Cement (Fig. 1). The small and large probes consisted of a radius of XS = 2.53860 ± 0.00402 cm and XL = 2.97375 ± 0.00403 cm, and a width of WS = 6.571 ± 0.0547 mm and WL = 6.684 ± 0.060 mm, respectively, using a caliper and average of eight points about the circumference.
Fig. 1.
Schematic diagram of the texture analyzer used to measure the surface tension of liquid. Details of the probe appear in the zoomed-in area. X and W represent the radius and width of the glass disk probe, respectively
METHODS
Preparation
Prior to testing, probes and the liquid container were cleaned with a concentrated detergent (Alconox®), rinsed with deionized water, sprayed with ethanol, and allowed to air dry, followed by a thorough drying with compressed air. Additionally, an internal height calibration was performed on the texture analyzer as reference prior to each series of tests, as well as weight calibration check.
Procedure
Surface tension was measured by attaching the probe to the texture analyzer arm and lowering the probe until the bottom surface of the glass probe contacted the surface of a test liquid contained in a reservoir (Fig. 1). At the start of the test, the probe was raised from the surface of the liquid at a constant speed to a specific height, while the texture analyzer registered force as a function of time or distance. The maximum force represents the force of detachment of the probe from the surface of the liquid, which was used to calculate the surface tension, as will be explained later. The settings on the texture analyzer were shown in Table I.
Table I.
Settings on Texture Analyzer for the Measurement of Surface Tension of Liquids from the Maximum Pull on a Disk
| Parameters | Value |
|---|---|
| Texture analyzer protocol | Adhesive test |
| Speed of descent | 0.5 mm/s |
| Trigger force | 0.20 mN |
| Contact time | 5 s |
| Return distance | 10 mm |
| Return speed | 0.05 mm/s |
| Data acquisition | 5 points per second |
In this protocol, the probe was set to descend at a set speed until a trigger force is reached; this subsequently initiated the pre-programmed ascending movement to the return distance. The small trigger force of 0.20 mN was intentionally set to prevent the creation of disturbances on the liquid surface from any descending movement. Therefore, contact time with the liquid was maintained for a set time before the probe started its ascent.
Calculation of Surface Tension
Padday et al. (11) have thoroughly investigated the surface tension measurement of liquids from the maximum pull on a rod. Our study on the calculation of surface tension from the maximum pull on a disk is derived from their work. The rationale for using specific equations developed by Padday and coworkers is described below.
By raising a probe from the free surface of a liquid, the maximum force, Fmax, observed before meniscus breakaway, is the result of hydrostatic pressure and surface tension contributions:
 |
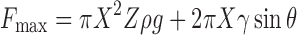1 |
where X is the probe radius, Z is the distance above the free surface of a liquid, ρ and γ are respectively the density and surface tension differences between the liquid and the surrounding fluid, g is the gravitational acceleration, and θ is the angle between the vertical longitudinal axis and the meniscus angle at the junction of the disk. Therefore, the determination of surface tension is based on the following relationship:
 |
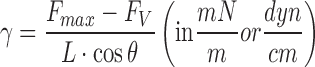2 |
where FV is the force related to the hydrostatic pressure created by the volume of liquid lifted by the probe, L is the probe perimeter, and θ is the contact angle. The commonly used DuNoüy ring is made of platinum, a material that presents zero contact angle with water, similar to glass (20,21).
In their work, Padday et al. express the maximum force as volume, V, according to the following equation:
 |
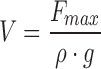3 |
By introducing a meniscus coefficient, k,
 |
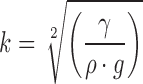4 |
The relationship between volume, probe radius, and meniscus coefficient is established as
 |
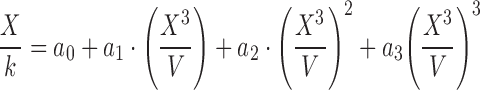5 |
According to the mathematical analysis made by Padday et al., at different domains of X3/V, different coefficients, an, of Eq. 5 are defined. In general, the greater the probe radius, the less degree of the polynomial equation above is necessary to determine surface tension. In their work, Padday and coworkers present an extensive table of coefficients focusing on the lower range of X3/V to fit values from the maximum pull on a rod. A rod of small radius and capable of suspending a low volume of liquid from the surface justifies the focus of this work on the low range of X3/V. Since the ratio X3/V is largely determined by the probe radius and considering that our probe is significantly larger than a rod, in this study, we calculate the surface tension of liquids using the coefficients related to the upper range of X3/V as determined by the envelope construction technique used by Padday and coworkers. The studied equations are presented in Table II.
Table II.
Relation of 
as a Function of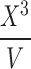 
for the Calculation of Surface Tension of Liquids from the Maximum Pull on Rods with Different Diameters (11)
| Equation | Range of X 3/V | Formula |
|---|---|---|
| A | 0.50–0.60 |
|
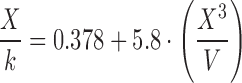
| B | 0.60–0.80 |
|
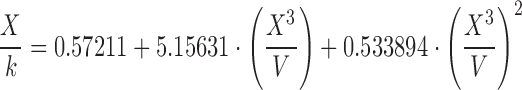
| C | 0.80–1.00 |
|
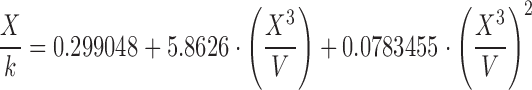
| D | 1.00–1.20 |
|
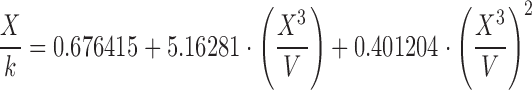
| E | 1.20–1.40 |
|
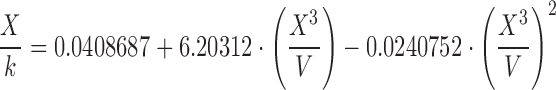
| F | 1.40–1.60 |
|
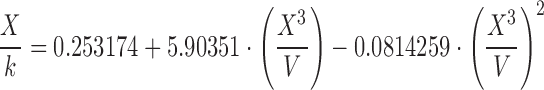
| G | 1.60–1.85 |
|
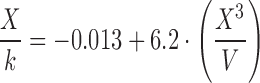
More recently, Christian and coworkers have synthesized all 18 polynomial expressions developed by Padday et al. into one cumbersome formula (Eq. 6, presented below) regardless of the range of X3/V.
 |
6 |
In this work, we also analyze whether Eq. 6 is capable of accurately measuring surface tension from the maximum pull on a disk.
Validation Design
To validate this test, surface tensions of 300 mL of distilled water, ethanol (EtOH), or 10% (w/w) ethanol in distilled water (10% EtOH/H2O), were analyzed for each of the two probes (n = 5). These three liquids were chosen to cover a broad range of surface tension according to their literature values (approximately 22–72 mN/m). The liquid temperature was registered prior to each test. To compare with literature values, accuracy was measured according to Eq. 7.
 |
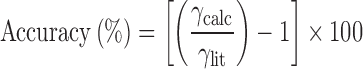7 |
where γcalc and γlit are the calculated and literature values of the surface tension of liquids, respectively.
Statistical Analysis
The data are presented as the average±standard deviation and the samples analyzed for statistical differences using t test for significance when p < 0.05.
RESULTS AND DISCUSSION
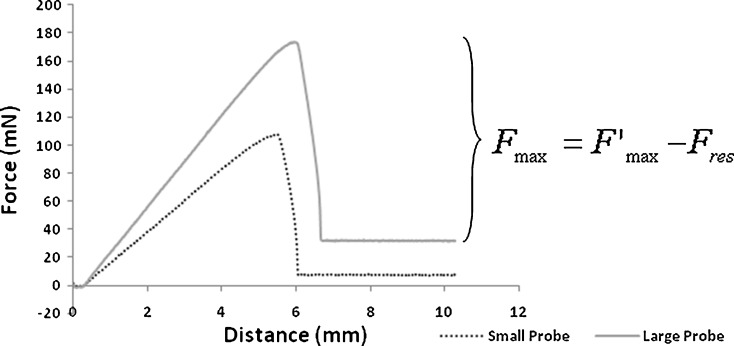
Force increases as a function of time when considering the distance moved by the texture analyzer arm at a constant speed. A typical graph of the measurement of surface tension of liquids using this method is shown in Fig. 2.
Fig. 2.
Typical graph from the maximum pull on a disk using the present method for small and large probes
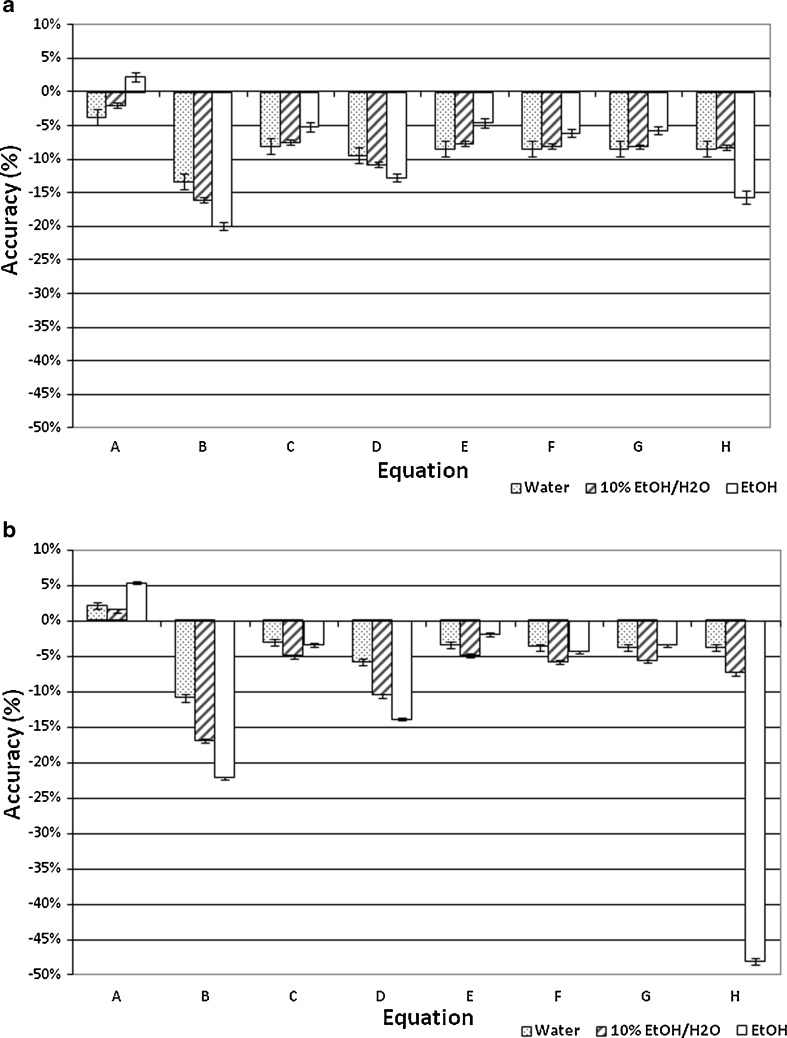
The peak (Fmax) represents the force of probe detachment from the surface of the liquid. Fmax values measured for water, 10% (w/w) ethanol in water, and ethanol and their respective calculated X3/V are shown in Table III. Considering the radius of the probes and the maximum force, most of the values of X3/V for the liquids evaluated in this study do not fall within the ranges provided in the work by Padday and coworkers, namely, 0.01–1.85. Interestingly, both probe sizes presented very precise results, with coefficients of variation smaller than 1%, indicating the high reproducibility of this method. Nevertheless, Fmax (and consequently X3/V) was more precise for the large probe diameter. Based on the study of maximum pull on a rod, we empirically use the equations related to the upper range of X3/V (Table II) to calculate the surface tension values of the referred liquids and compare with the literature values (22). We also fit the results of X3/V to Eq. 6 as previously described. The accuracy results are presented in Fig. 3 for small- and large-diameter probes.
Table III.
Values of Measured F max for Three Different Liquids and their Respective Calculated X 3/V at 25°C, Unless Specified
| Liquid | F max (mN) | X 3/V | ||
|---|---|---|---|---|
| X S | X L | X S | X L | |
| Water | 101.44 ± 0.65a (0.64%) | 142.57 ± 0.36 (0.25%) | 1.577 ± 0.010a (0.64%) | 1.804 ± 0.005 (0.25%) |
| 10% (w/w) ethanol in water | 81.79 ± 0.16 (0.20%) | 113.71 ± 0.16 (0.14%) | 1.923 ± 0.004 (0.20%) | 2.223 ± 0.003 (0.14%) |
| Ethanol | 50.25 ± 0.17 (0.33%) | 69.78 ± 0.08 (0.11%) | 2.506 ± 0.008 (0.33%) | 2.901 ± 0.003 (0.11%) |
Results are expressed as mean±standard deviation (coefficient of variation) for five replicates
aThe liquid temperature during measurement was 24°C
Fig. 3.
Accuracy in the measurement of surface tension of three different liquids based on extrapolation on the theory of maximum pull on a rod to the application of disks as probe geometries. Results are expressed as the mean±standard deviation (n = 5). Equations A–G are shown in Table II; Eq. H is presented as Eq. 6 in the section “Calculation of Surface Tension.” a Small probe (X S). b Large probe (X L)
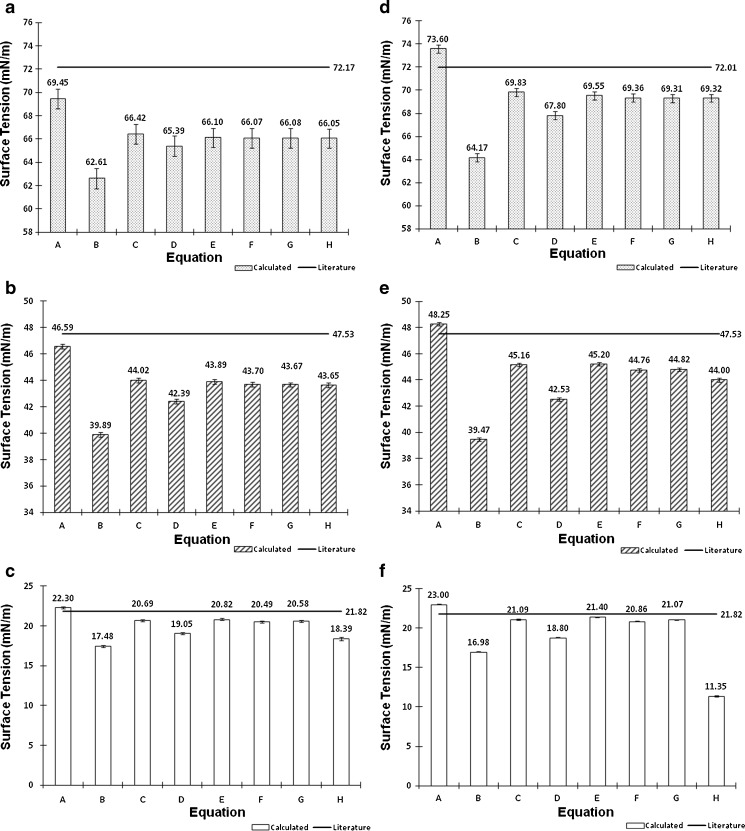
The surface tension of water, ethanol, and the hydroalcoholic solution calculated using Eqs. A–G in Table II and Eq. 6 overall presented underestimated values compared with literature data. Regardless of probe size, similar patterns were observed for equation groups B/D and C/E/F/G in Table II. Besides more precise results, the large-diameter probe also presented more accurate values than the small probe. This may indicate that accuracy and precision may be dependent on an optimum probe diameter. Figure 4 helps elucidate this trend. Considering the differences in the accuracy of surface tension according to the probes investigated (radius of approximately 2.5 and 3.0 cm), we believe that increasing the probe radius to about 3.5–4.0 cm may provide even more accurate results. Further studies are warranted to verify this relationship, but it is noteworthy to highlight that with increased radius, a wider container is necessary to maintain the infinite interface configuration later discussed, consequently requiring a greater sample volume. Nevertheless, using the large probe and Eq. E in Table II, for instance, provided results with accuracy within <5% from literature values for water (69.55 ± 0.34 mN/m), 10% (w/w) ethanol in water (45.20 ± 0.13 mN/m), and ethanol (21.40 ± 0.05 mN/m). Interestingly, Eqs. C, E, F, and G in Table II, which provided similar better accuracy results to the large probe, are either first- or second-order polynomial forms of X3/V. This indicates that not necessarily an exponential function models the increase in force as a function of disk diameter, as previously described by Nietz and Lambert (7). Finally, Eq. 6 appears to be unfeasible to calculate surface tension from maximum pull on a disk since it is equally accurate compared with Eqs. C, E, F, and G in Table II when X3/V is below 2.0, but largely deviates from the literature values when this parameter increases.
Fig. 4.
Comparison with literature values of the surface tension of water (dotted), 10% ethanol in water (diagonal), and ethanol (empty columns) based on extrapolation on the theory of maximum pull on a rod to the application of disks as probe geometries. Results are expressed as the mean±standard deviation (n = 5). Equations A–G are shown in Table II; Eq. H is presented as Eq. 6 in the section “Calculation of Surface Tension.” a–c Small probe (X S). d–f Large probe (X L). Measurements were performed at 25°C (except graph A, 24°C)
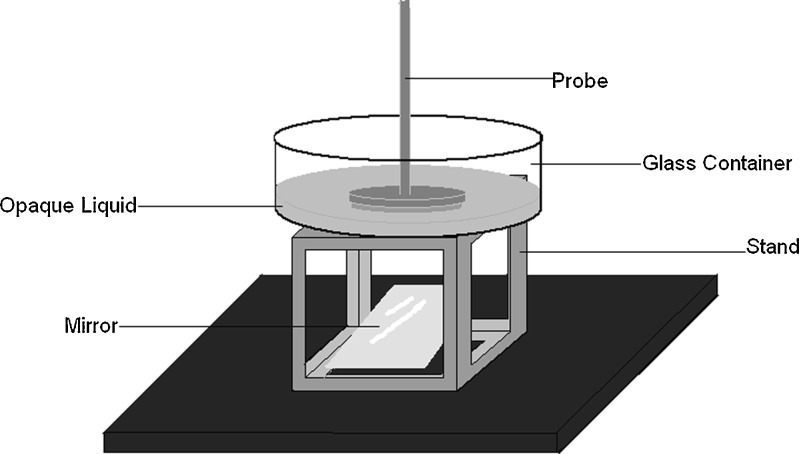
Any slight discrepancy between the calculated values of surface tension measured by the large probe (e.g., using Eq. E in Table II) and the literature values may be explained by a number of factors that could be considered limitations of this method. Most importantly, the probe and liquid surfaces must be in full and close contact throughout the measurement. To ensure this, the probe and container surfaces were thoroughly cleaned prior to experiments with an abrasive detergent and adequately dried to remove any dust, followed by careful handling to avoid particle settling. Additionally, our in-house-constructed glass probe is prone to present a non-ideal edge roughness as well as microchips and microcracks despite careful handling and storage. A glass probe produced and stored under strict specifications in terms of edge roughness, radius measurement, and storage container may potentially provide even more accurate results. Moreover, considering the large surface area of the probes, any tilt in probe position in relation to the surface of the liquid must be avoided. In this study, leveling was performed by placing a level instrument on the texture analyzer platform and adjusting the legs of the equipment. Lastly, the operator must certify that any bubble underneath the probe is removed prior to starting the test. This has been performed in this study purely based on visual observation. In the case of a high volume of sample being analyzed (e.g., 300 mL, as initially tested), the operator can easily identify the presence of bubbles by looking upward at the liquid–probe contact point from a low eye position. In the case of opaque liquids (e.g., suspensions, emulsions) and low-volume samples, the configuration in Fig. 5 with a mirror positioned underneath the sample container is very useful. Frequently, a series of upward and downward movements with the texture analyzer arm is necessary until no bubbles are impeding the direct contact between the glass probe and the liquid surface. A container equipped with ultrasonication capability is an alternative option to help remove bubbles, both dissolved in the liquid and generated by the contact of the probe with the surface of the liquid.
Fig. 5.
Setup for the measurement of surface tension of opaque liquids, such as suspensions and emulsions, and/or low-volume samples for better visualization of the presence of bubbles between the liquid surface and the glass disk probe. The stand is a cube-shaped structure with open walls in all faces. Therefore, the movement of the texture analyzer arm should be controlled to avoid breaking the glass container
Furthermore, temperature highly influences the surface tension of liquids and should be strictly controlled. In our proof-of-concept experiments, the liquid temperature was registered using an ordinary alcohol lab thermometer. Alternatively, a thermal cabinet adequately adapted to enclose the container (and possibly the texture analyzer arm) could provide improved temperature control. Furthermore, there must be sufficient distance between the probe and container walls to eliminate cross-interference in the measurement of surface tension of liquids (infinite interface) (23,24). For this reason, and considering probe diameter, a wide circular container was used in our study, necessitating a sample volume of a few hundred milliliters. Further studies to determine the minimum sample volume for this setup have also been performed. Using 50 mL, the surface tension of water analyzed at 24°C was calculated using Eq. E (in Table II) of this method and was found to be 69.79 ± 0.24 mN/m. This is not statistically different from the measurement made with 300 mL of water. With smaller sample volumes, a stricter temperature control is even more important because heat transfer to the liquid mass turns the sample more prone to temperature variation. Lastly, any difficulty in measuring the surface tension of surfactant solutions due to the rise of liquid against the glass probe wall may be circumvented via careful control of the ascending arm speed of the texture analyzer. This would allow adequate time for the liquid to drain down as the peak force is approached.
Remarkably, uncertainty in the absolute values of surface tension of liquids using different methods has been widely described. For instance, the surface tension of water at 25°C has been reported between 71.82 and 73.0 mN/m (25,26). Therefore, our method presents an acceptable accuracy. Particularly, the method presents excellent precision, with coefficients of variation below 0.5% for the large probe (1.4% for the small probe). During our studies, though, we observed that more precise measurements were obtained at the end of a series of analysis. Studies on the dehydration of glass surfaces indicate an increase in contact angle as a function of water drying time (27). These findings may indicate that the glass probe needs to be in contact with aqueous solutions for a certain period of time prior to the analysis of surface tension.
CONCLUSION
A glass probe disk with a radius of approximately 3 cm attached to the arm of a texture analyzer can be used to measure the detachment force from a liquid surface. This maximum force can be extrapolated to equations previously developed to calculate surface tension from the maximum pull on a rod. Using this method, the calculated absolute values of the surface tension of selected liquids are within 5% from the literature values. With this setup, sample volumes as low as 50 mL can be analyzed. Using a texture analyzer to determine surface tension provides an additional feature for this versatile equipment already used in a multitude of testing procedures and therefore widely available in such research laboratories. This experiment provides a precise, simple, and quick method to determine the surface tension of liquids from the maximum pull on a disk. Further studies are warranted to ensure the optimal probe diameter to improve accuracy in the values of surface tension compared with the literature.
REFERENCES
- 1.Fathi-Azarbayjani A, Jouyban A, Chan SY. Impact of surface tension in pharmaceutical sciences. J Pharm Pharm Sci. 2009;12(2):218–228. doi: 10.18433/j32p40. [DOI] [PubMed] [Google Scholar]
- 2.Bummer PM. Interfacial phenomena. In: Hendrickson R, editor. Remington: the science and practice of pharmacy. 21. Baltimore: Lippincott Williams & Wilkins; 2005. pp. 280–292. [Google Scholar]
- 3.Ghazanfari T, Elhissi AMA, Ding Z, Taylor KMG. The influence of fluid physicochemical properties on vibrating-mesh nebulization. Int J Pharm. 2007;339(1–2):103–111. doi: 10.1016/j.ijpharm.2007.02.035. [DOI] [PubMed] [Google Scholar]
- 4.McCallion ONM, Taylor KMG, Thomas M, Taylor AJ. The influence of surface tension on aerosols produced by medical nebulisers. Int J Pharm. 1996;129(1–2):123–136. doi: 10.1016/0378-5173(95)04279-2. [DOI] [Google Scholar]
- 5.McCallion ONM, Taylor KMG, Thomas M, Taylor AJ. Nebulization of fluids of different physicochemical properties with air-jet and ultrasonic nebulizers. Pharm Res. 1995;12(11):1682–1688. doi: 10.1023/A:1016205520044. [DOI] [PubMed] [Google Scholar]
- 6.Minko T. Interfacial phenomena. In: Sinko PJ, editor. Martin’s physical pharmacy and pharmaceutical sciences. 5. Baltimore: Lippincott Williams & Wilkins; 2006. pp. 437–467. [Google Scholar]
- 7.Nietz AH, Lambert RH. Effect of some factors on the ring method for determining surface tension. J Phys Chem. 1929;33(10):1460–1467. doi: 10.1021/j150304a003. [DOI] [Google Scholar]
- 8.Ugarcic Z, Vohra DK, Atteya E, Hartland S. Measurement of surface tension using a vertical cone. J Chem Soc-Faraday Trans I. 1981;77:49–61. doi: 10.1039/f19817700049. [DOI] [Google Scholar]
- 9.Freud BB, Freud HZ. A theory of the ring method for the determination of surface tension. J Am Chem Soc. 1930;52(5):1772–1782. doi: 10.1021/ja01368a005. [DOI] [PubMed] [Google Scholar]
- 10.Harkins WD, Jordan HF. A method for the determination of surface and interfacial tension from the maximum pull on a ring. J Am Chem Soc. 1930;52(5):1751–1772. doi: 10.1021/ja01368a004. [DOI] [Google Scholar]
- 11.Padday JF, Pitt AR, Pashley RM. Menisci at a free liquid surface—surface tension from maximum pull on a rod. J Chem Soc-Faraday Trans I. 1975;71:1919–1931. doi: 10.1039/f19757101919. [DOI] [Google Scholar]
- 12.Christian SD, Slagle AR, Tucker EE, Scamehorn JF. Inverted vertical pull surface tension method. Langmuir. 1998;14(11):3126–3128. doi: 10.1021/la971384i. [DOI] [Google Scholar]
- 13.Schulz M, Fussnegger B, Bodmeier R. Drug release and adhesive properties of crospovidone-containing matrix patches based on polyisobutene and acrylic adhesives. Eur J Pharm Sci. 2010;41(5):675–684. doi: 10.1016/j.ejps.2010.09.011. [DOI] [PubMed] [Google Scholar]
- 14.Majzoobi M, Ostovan R, Farahnaky A. Effects of hydroxypropyl cellulose on the quality of wheat flour spaghetti. J Texture Stud. 2011;42(1):20–30. doi: 10.1111/j.1745-4603.2010.00264.x. [DOI] [Google Scholar]
- 15.Bansal K, Rawat MK, Jain A, Rajput A, Chaturvedi TP, Singh S. Development of satranidazole mucoadhesive gel for the treatment of periodontitis. AAPS PharmSciTech. 2009;10(3):716–723. doi: 10.1208/s12249-009-9260-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Mei XH, Etzler FM, Wang Z. Use of texture analysis to study hydrophilic solvent effects on the mechanical properties of hard gelatin capsules. Int J Pharm. 2006;324(2):128–135. doi: 10.1016/j.ijpharm.2006.06.017. [DOI] [PubMed] [Google Scholar]
- 17.Lu S, Chen JJ, Chen YK, Li CY, Lai P, Chen HH. Water mobility, rheological and textural properties of rice starch gel. J Cereal Sci. 2011;53(1):31–36. doi: 10.1016/j.jcs.2010.08.006. [DOI] [Google Scholar]
- 18.Tukaram BN, Rajagopalan IV, Shartchandra PSI. The effects of lactose, microcrystalline cellulose and dicalcium phosphate on swelling and erosion of compressed HPMC matrix tablets: texture analyzer. Iranian J Pharm Res. 2010;9(4):349–358. [PMC free article] [PubMed] [Google Scholar]
- 19.Li CB, Shi PL, Xu C, Xu XL, Zhou GH. Tracing processes of rigor mortis and subsequent resolution of chicken breast muscle using a texture analyzer. J Food Eng. 2010;100(3):388–391. doi: 10.1016/j.jfoodeng.2009.10.040. [DOI] [Google Scholar]
- 20.Bernardin JD, Mudawar I, Walsh CB, Franses EI. Contact angle temperature dependence for water droplets on practical aluminum surfaces. Int J Heat Mass Transfer. 1997;40(5):1017–1033. doi: 10.1016/0017-9310(96)00184-6. [DOI] [Google Scholar]
- 21.Richards TW, Carver EK. A critical study of the capillary rise method of determining surface tension, with data for water, benzene, toluene, chloroform, carbon tetrachloride, ether and dimethyl aniline. J Am Chem Soc. 1921;43(4):827–847. doi: 10.1021/ja01437a012. [DOI] [Google Scholar]
- 22.Surface tension of aqueous mixtures. In: Lide DR, editor. CRC handbook of chemistry and physics, 90th edition (Internet version 2010). Boca Raton, FL: CRC Press; 2010. p. 6–131.
- 23.Furlong DN, Hartland S. Wall effects in measurement of surface tension using a vertical cylinder. 1. Theory. J Chem Soc-Faraday Trans I. 1980;76:457–466. doi: 10.1039/f19807600457. [DOI] [Google Scholar]
- 24.Furlong DN, Hartland S. Wall effects in measurement of surface tension using a vertical cylinder. 2. Experimental. J Chem Soc-Faraday Trans I. 1980;76:467–472. doi: 10.1039/f19807600467. [DOI] [Google Scholar]
- 25.Pallas NR, Pethica BA. The surface tension of water. Colloids Surf. 1983;6(3):221–227. doi: 10.1016/0166-6622(83)80014-6. [DOI] [Google Scholar]
- 26.Gaonkar AG, Neuman RD. The uncertainty in absolute values of surface tension of water. Colloids Surf. 1987;27(1–3):1–14. [Google Scholar]
- 27.Englander T, Wiegel D, Naji L, Arnold K. Dehydration of glass surfaces studied by contact angle measurements. J Colloid Interface Sci. 1996;179(2):635–636. doi: 10.1006/jcis.1996.0260. [DOI] [Google Scholar]