Non-exponential T₂^* decay in White Matter

Abstract

Visualizing myelin in human brain may help the study of diseases such as multiple sclerosis. Previous studies based on T₁ and T₂ relaxation contrast have suggested the presence of a distinct water pool that may report directly on local myelin content. Recent work indicates that T₂^* contrast may offer particular advantages over T₁ and T₂ contrast, especially at high field. However, the complex mechanism underlying T₂^* relaxation may render interpretation difficult.

To address this issue, T₂^* relaxation behavior in human brain was studied at 3 and 7 tesla. Multiple gradient echoes covering most of the decay curve were analyzed for deviations from mono-exponential behavior. The data confirm the previous finding of a distinct rapidly relaxing signal component (T₂^* ~ 6 ms), tentatively attributed to myelin water. However, in extension to previous findings, this rapidly relaxing component displayed a substantial resonance frequency shift, reaching 36 Hz in the corpus callosum at 7 T. The component’s fractional amplitude and frequency shift appeared to depend on both field strength and fiber orientation, consistent with a mechanism originating from magnetic susceptibility effects. The findings suggest that T₂^* contrast at high field may be uniquely sensitive to tissue myelin content, and that proper interpretation will require modeling of susceptibility-induced resonance frequency shifts.

Introduction

Loss of axonal myelin in human brain white matter (WM) may lead to impaired brain function. Such loss may result from normal aging as well as a number of neurological diseases, most notably multiple sclerosis (MS). For this reason, the measurement of local myelin content has been a longstanding goal of MRI technique development. Most of the current techniques aim at measuring the relative concentration of myelin water based on its characteristic relaxation properties. The term “myelin water” is used here as a loosely defined entity which includes all water that is in close vicinity to myelin. It is often assumed that the myelin water may be physically restricted to the spaces between myelin sheets surrounding axons, and may experience accelerated relaxation due to reduced mobility.

Several methods have been proposed to distinguish myelin water from other water signals, based on various contrast mechanisms. Magnetization transfer (MT) effects (1) can be exploited to selectively saturate water in contact with macromolecules or myelin (e.g. (2)). Subtraction of MT-saturated images from unsaturated images may thus provide an estimate of myelin water content. T₂ relaxation measurements can be used to identify fast and slow T₂ components (3,4), with the fast component interpreted as myelin water. Simultaneous T₁ and T₂ information maybe obtained with the DESPOT1 and DESPOT2 techniques (5)(driven equilibrium single pulse observation of T₁ and T₂). Inclusion of T₁ information may improve the reliability of the estimated fast T₂ fraction and, under some conditions, allow estimation of exchange rates between the differentially relaxing putative compartments or “pools”. More quantitative methods, based on MT measurements at a range of saturation frequencies and T₁ measurements, and analyzed with a two-pool model of magnetization (6), have been proposed as well. These methods allow estimation of the size of the rapidly decaying proton fraction and its exchange rate (7–9), resulting in a measure of a bound proton pool, generally assumed to be representative of larger molecules, such as those forming myelin. However, a comparison between quantitative MT and T₂ data in MS patients showed little correlation between the myelin water fractions derived with these methods (10), indicating that the underlying contrast mechanisms are still poorly understood.

Although promising, current myelin water measurement methods generally suffer from long measurement time, poor signal to noise ratio (SNR), and limited specificity to myelin water. Some of the methods furthermore lack the ability to provide reproducible quantitative numbers. The hope is therefore that further improvements in MRI measurement of myelin water will arise from novel methods.

One very recent and particularly promising technique to measure myelin associated water is the use of T₂^* contrast (11,12). Similar to the T₁ or T₂ based methods, the premise is that the myelin associated water has a distinctly reduced T₂^*, and that the exchange between the free and myelin water pools is slow enough to observe multi-exponential T₂^* decay as function of echo time (TE) for myelin containing tissue.

Potential advantages of using T₂^* contrast over alternative methods are its rather strong (relative to other contrasts) amplification at high field strength and the fact that the relatively simple gradient echo (GRE) pulse sequence can be used. Moreover, GRE pulse sequences have low RF power deposition. This is important, because RF power deposition increases quadratically with field strength, and thus may limit the field strength at which T₁ and T₂ measurements are practical. The goal of this study therefore was to investigate whether T₂^* decay at 7 T can be used to detect and further characterize myelin water. For this purpose, multi-echo GRE data were acquired in a number of normal volunteers at 7 T. For comparison, similar data were acquired at 3 T as well in a smaller group of subjects. It should be pointed out that it is not proven here that the short component is indeed a myelin water fraction; although this seems plausible, there maybe other sources of susceptibility associated with myelin that could produce similar results.

Methods

Seven healthy volunteers (3 female, 4 male, ages 33–54, average age 41) were studied at 7 T, one of whom was scanned twice. Four volunteers (1 female, ages 24–45, average 36 years) were scanned at 3 T, three of which also participated in the 7 T study. Both scanners were General Electric (GE, Milwaukee, Wisconsin) systems, equipped with standard clinical gradients (maximum amplitude 40 mT/m, slew rate 150 T/m/s). For the 7 T study, a Nova Medical (Wilmington, Massachusetts) birdcage transmit coil was used in combination with a 32 channel receive coil, for the 3 T study the GE body coil was used for transmission and a 16 channel Nova Medical coil for reception. All studies were performed under an Internal Review Board approved human protocol.

The pulse sequence was an in-house developed multi GRE acquisition for mapping the T₂^* decay. A train of echoes was produced by alternating the acquisition gradient, similar to an echo planar imaging (EPI) acquisition, but omitting the phase encoding blips between echo acquisitions. Only the positive gradient lobes were used to avoid misalignment between positive and negative echoes due to local off resonance effects, and the negative gradient lobes were maximized for minimum inter echo spacing (13). The acquisition time of the first echo was minimized by using a short (1.6 ms) RF excitation pulse and combining the slice rephrasing, phase encoding and acquisition dephasing gradients. A single 2 mm slice was measured per scan, with an in plane resolution of 256×96 voxels and a field of view of 240×180 mm. The repetition time was 70 ms, and the flip angle (as estimated at the center of the slice) was 30 degrees. The single slice acquisition was repeated 50 times for a total scan time was 336 s. The repetitions were selectively averaged (see below) for improved SNR and stability. The shortest echo time (TE) was 2.7 ms, the longest one 45.0 ms, for a total of 19 echoes spaced at 2.35 ms. The tenth echo was programmed to be used a navigator; for this purpose, the phase encoding was rewound before the echo and re-applied immediately after. This navigator was intended to help improve the stability, but not used in the final analysis. Two slices were scanned in separate experiments, in a close to axial orientation parallel to the AC/PC line (anterior and posterior commissure). One slice was positioned a few millimeters above AC/PC to capture a section of the corpus callosum, and a second slice was acquired at a position approximately 25 mm higher to capture white matter outside the major fiber bundles.

The images from individual receiver channels were combined using a sensitivity encoding (SENSE)(14) type calculation without external reference (15) based on the first echo of the first repetition. For each repetition and each voxel, the signal across echo times was fitted to a single-exponential decay using a Levenberg-Marquardt non-linear least squares algorithm. The results were averaged over repetitions after excluding outliers. The outliers were determined by analyzing the fluctuation over the repetitions of the fitted amplitudes. These amplitudes were averaged over the repetitions. Susequently, the difference of the amplitudes with this average was calculated and normalized by its standard deviation (SD), and then summed over all voxels. The repetitions for which the summed deviation from average was more than twice the SD were excluded from further analysis.

Subsequent analysis was geared towards investigating the potential presence of multi-exponential relaxation, as previously found at 3 T (11,12), by looking at the deviation from single exponential relaxation. To determine this deviation, the averaged fit results were compared with the averaged echo signals, resulting in average difference maps for each TE measured. These maps were then further analyzed in selected regions of interest (ROIs). Using the average R₂^* map as a guide, ROIs were selected in posterior part (the splenium) of the corpus callosum (SCC), in the posterior internal capsule (PIC) and in the white matter surrounding the posterior part of the CC, not associated with any major fiber bundle. In the following the last of these is referred to as general white matter (GWM).

After region selection, ROI averaged signals were used to derive quantitative estimates of a potential fast relaxing component. For this purpose, a single exponential, slow relaxation component was estimated by performing a single exponential fit to ROI-averaged data after exclusion of data from the first two TEs for the 7 T data and exclusion of the first four echoes for the 3 T data. This exclusion was designed to select the slow component in the data. The difference with this fit was used to study the deviation from single exponential decay resulting from a putative fast component.

The choice of the ROIs was informed by comparison of the R₂^* maps with diffusion derived fiber orientation and anisotropy maps acquired in a previous, unrelated study. Two of the subjects in the current study had also participated in that diffusion study and a closely corresponding slice position and orientation could be selected in one of these two volunteers to allow identification of several structures in the R₂^* data using the diffusion maps as a guide. The fiber orientation in the three selected ROIs (SCC, PIC and GWM) was predominantly perpendicular to the main magnetic field, parallel to it and mixed, respectively. Susceptibility effects in structured tissue, like parallel fiber bundles, are dependent on the angle of the structure with respect to the main magnetic field (16,17). As a result, the T₂^* decay may show a deviation from single exponential behavior that is orientation dependent.

Further analysis revealed that a three-component model, as suggested in (18) may produce a better fit to the data, provided that a variable offset frequency is allowed for the components. This analysis is analogous to the model proposed previously for the separation of grey matter, cerebrospinal fluid (CSF) and intravascular signals (19), and that for the separation of tissue water and CSF (20). In white matter, compartment-specific resonance frequency shifts may occur due to the magnetic susceptibility effects of the distribution of myelin-associated lipids and iron (21). If one assumes that there is one dominant component and two components of relatively small amplitude, then only the frequency difference between the two smaller components and the dominant term is relevant when considering magnitude data. The phase of the total signal will be set by the dominant component, and this phase is removed by taking the magnitude of the signal. The resulting model is:

$$S(t)=\left|\right|A_1{e}^{-{tR}_{2,1}^{\ast }-i2\pi f_{1}t}+A_2{e}^{-{tR}_{2,2}^{\ast }}+A_3{e}^{-{tR}_{2,3}^{\ast }-i2\pi f_{3}t}\left|\right|$$ [1]

where S is the magnitude signal as function of time, ||•|| indicates the magnitude operator, and A_i is the amplitude, f_i the off-resonance frequency (in Hz) and $R_{2,i}^{\ast }$ the relaxation rate of component i. The model has eight free parameters (f₂ is zero and therefore not included in the model, as this component is assumed to be on resonance). All components start in-phase at t=0. The first (fast) component is tentatively assigned to myelin water, the second component represents the dominant, larger signal of the on-resonance tissue water, the third and longer component represents mobile water in CSF and extracellular spaces.

As the fitting of such a model to data acquired in a relatively short range of echo times is inherently an ill-conditioned problem, a simple (and slow) fitting procedure was followed in which in successive iterations every component in the model was optimized by minimizing the quadratic sum of the residue of the fit for a given range of its parameters. The search was limited to positive values for the amplitude and relaxation rates. After each iteration, the range was reduced by a factor of two to refine the search if an optimum was found within the given range; otherwise the range was increased by a factor two. The initial search range was 70–130% of the initial guess for each parameter. The optimization was halted when further reduction of the residue was no longer significant. This fitting procedure was only applied to the 7 T ROI averaged signal in the SCC and GWM areas, as the PIC data did not give reproducible results.

On the 3 T data the fitting of the three components did not result in reproducible results, so those data were fitted with a comparable two-component model:

$$S(t)=\left|\right|A_1{e}^{-{tR}_{2,1}^{\ast }-i2\pi f_{1}t}+A_2{e}^{-{tR}_{2,2}^{\ast }}\left|\right|$$ [2]

leaving out the third, slow component, reducing the number of parameters to five.

Results

The SNR in the coil-combined images for the first echo (TE 2.7 ms) was 30–90 at 3 T and 70–180 at 7 T(before averaging). The large range at each field is attributed to the highly inhomogeneous B₁ profile of the receive coil arrays. The temporal stability, expressed as mean divided by the SD of the fitted amplitude over time, was 20–60 for both field strengths before the rejection of deviating repetitions (see Methods). After this rejection, the stability was 50–90 for the 3 T scans and 60–150 for the 7 T scans. In the majority of studies, the fraction of rejected repetitions was below 20%.

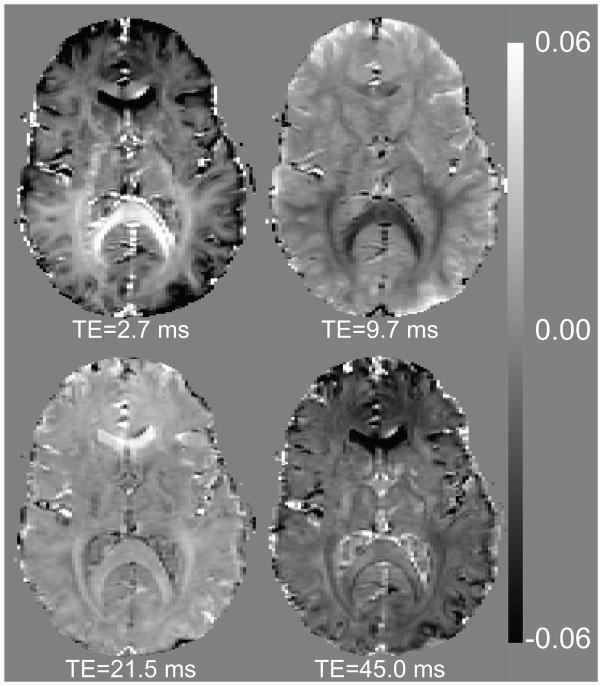
Figure 1 shows an example of the average difference maps (the difference between data and the mono-exponential fit) at selected echo times, calculated from 46 repetitions. Substantial difference signal is observed at the shortest echo time (TE=2.7 ms), which is most pronounced in the myelin-rich SCC. Interestingly, substantial difference signal remains visible at longer echo times, both in grey and white matter regions. Even at TE=45 ms, significant deviation from the single-exponential fit is observed. This observed contrast evolution with echo time appears inconsistent with the difference of a previously suggested multi-exponential decay (12) and a mono-exponential fit (see Appendix 1).

Figure 1.

The difference between a mono-exponential model and the T₂^*-weighted data at four selected echo times, as fraction of the fitted amplitude for echo time zero. The echo times are indicated below each image. The images show that the deviation from exponential behavior is not limited to the contribution of a fast component, and notably different in contrast for different anatomical structures.

Results of the ROI-based T₂^* decay analysis are shown in Figs. 2 and 3. Fig. 2 shows an example of ROI selection; ROI-and subject-averaged differences between the data and the mono-exponential fit for the 7 T data are shown in Fig. 3. The error bars in the plot, derived from the SD over the subjects, show that the shape of the decay curves is very reproducible. Across ROIs, substantial differences in amplitude and shape are observed. An illustration of the field dependence of the non-exponential T₂^* decay is shown in Fig. 4, showing the subject averaged differences with a mono-exponential fit for the SCC ROI data at 3 T. The error bars reflect the standard error or the averages. The shape is notably different than the residue for the 7 T data, plotted in the same figure for comparison (it is the same curve as in Fig 3b). The 3 T curve is expanded in time compared to the 7 T curve and lower in amplitude.

Figure 2.

ROIs selection based on R₂^* maps using diffusion data to identify the structures of interest. The diffusion data were processed to show fractional anisotropy (FA) and a color-coded predominant fiber orientation with green for left-right, red for anterior-posterior and blue for the superior-inferior direction. The three ROIs represent the posterior corpus callosum (CC, red) with predominantly left-right fibers, the posterior internal capsule (PIC, brown) with mostly up-down fibers and a mixed WM area (GWM) in green containing fibers of various orientations and therefore has a lower FA. The scale for the R₂^* images is in Hz.

Figure 3.

a) An example of the decay curve, averaged over a ROI in the splenium of the corpus callosum (SCC), and the corresponding mono-exponential fit for one subject.

b) Plots of the subject-averaged differences between the ROI averaged T₂^* weighted data and a mono-exponential fits. The curves show the mean over 8 studies at 7 T with error bars indicating the standard error of the mean for the three ROIs (see Figure 2 for locations).

Figure 4.

Plot of the subject averaged difference between the splenium of the corpus callosum (SCC) ROI data and a mono-exponential fit for 3 T. The error bars reflect the standard error of the mean. The 7 T data is repeated from Fig 3b for comparison.

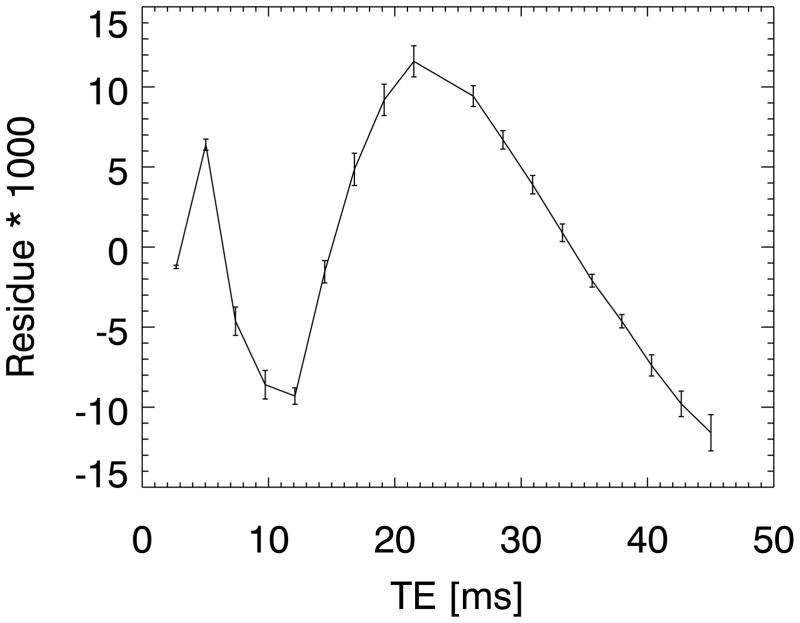
The deviation from single exponential decay appears not to be consistent with a multi-compartment model without frequency offsets, as discussed Appendix 1. A model including a frequency offset for the two smaller components (Eq.1) however fits the data very well, as shown in Fig. 5. The adjusted coefficient of determination (R²) improved from 1–1.8·10⁻⁴ for the model without frequency offsets to 1–1.6·10⁻⁶ for the model with the offsets. The average of the fit parameters for the 7 T and 3 T data is presented in Table 1. As demonstrated by the SD of the fit parameters, the 7 T results are reproducible over subjects. However the results of the fit of the three-compartment model to the 3 T data were not reproducible between subjects and therefore only the results of fit with the two-compartment model (Eq. 2) are shown.

Figure 5.

Results of a 3-compartment model fit (Eq. 1) for the same data as in Fig. 3 (SCC ROI), a) data with the fitted model, b) the residue, scaled up 1000 times.

Table 1.

The average and SD (over subjects) of multi compartment model parameters (Eq. 1 for 7 T and Eq. 2 for 3 T) fitted to the SCC ROI averaged signal decays for two field strengths; the corresponding GWM data for 7 T are also shown.

B0 [T]	ROI		A1	$R_{2,1}^{\ast }[\text{Hz}]$	f1 [Hz]	A2	$R_{2,2}^{\ast }[\text{Hz}]$	A3	$R_{2,3}^{\ast }[\text{Hz}]$	f3 [Hz]
7	SCC	av	0.130	159	35.8	0.776	36.5	0.094	22.8	7.0
		sd	0.020	12	2.9	0.018	1.0	0.011	6.4	0.7
7	GWM	av	0.077	169	31.8	0.809	36.0	0.114	10.8	5.9
		sd	0.009	11	3.3	0.008	1.4	0.011	2.01	0.7
3	SCC	av	0.054	92	19.4	0.946	21.2
		sd	0.019	10	2.6	0.019	0.7

The triple-exponential model could not be fitted reliably to the data on a voxel by voxel basis. In order to create a map of the fast component, the model was modified by fixing the relaxation and frequency parameters to the values determined in the fit to the SCC ROI averaged data. This reduced the fitting problem to a three parameter linear least squares optimization to find the amplitudes of the three components. The resulting map of the amplitude of the fast component is shown in Fig. 6, together with the difference between the data at TE 2.7 ms and a mono-exponential model, fitted excluding the first two echoes. For comparison, the map of the fast component reflects the amplitude of this component at the same 2.7 ms TE, not directly the fitted amplitude parameter in the exponential model (which would be the amplitude at TE0 ms).

Figure 6.

Image showing the relative amplitude of the fast component of a triple-exponential fit on the right and the difference between the data and a mono-exponential fit at TE 2.7 ms on the left. The triple-exponential model was fitted with the relaxation and frequency parameters fixed to the values found for the CC ROI averaged signal, the image is scaled to reflect the amplitude of the fast component at TE 2.7 ms.

Discussion

In the experiments described above, extensive signal averaging was performed to investigate a previously reported multicomponent T₂^* relaxation in white matter of human brain (12). Using 40 to 50 averages the SNR was sufficient to accurately observe small (< 8%) deviations from single exponential decay in various areas of WM on a single voxel level. The most pronounced deviations were found at the shortest TE (2.7 ms). The deviations varied across WM and were different between major fiber bundles such as the corona radiata and optic radiation. The highest amplitude of deviation was found in the posterior part of the SCC. This appears inconsistent with the findings of Hwang et al. in (12), who concluded that the fast component is almost uniform throughout the WM. Also, our values for the deviation at TE=2.7 ms are lower than those reported for the fast component in (12), in particular for the 3 TSCC data: 5.4% found in this study versus 13% reported in (12). The discrepancy with results reported by Hwang et al. (11,12) may be party due to the differences in processing. In the current study, only the deviation from a mono-exponential model was considered, without further filtering or processing. Hwang et al. used a non-linear spatial filter that tends to eliminate contrast in areas that do not have sharp edges and they used a triple exponential model to fit their data. The high degree of interdependence of the exponential functions (their non-orthogonallity) makes it hard to assign accurate amplitudes to the three decay functions in such a model.

The three-compartment model with offset frequencies appears to explain the data better than a model without these, as shown in Appendix 1. It should be noted that fitting a model with eight parameters to a decay of 18 echoes, with a limited range of TEs, is an inherently ill-conditioned problem. Fitting the model to single voxel data did not produce stable and meaningful results, therefore only the ROI averaged signals in the SCC and the GWM were analyzed with this model. For the same reason the results of the 3 T fit were not very reliable. Comparing the 3 T and 7 T results in Fig. 4 it appears short component is decaying slower at 3 T, which is reflected in both the decay rate and offset frequency of the fitted results in Table 1. The susceptibility induced frequency offset and decay scale with field strength, confirming a susceptibility related source for the observed component reported in Table 1. Note that the susceptibility induced frequency differences can contribute to both a higher decay rate and an observable offset frequency, depending on the homogeneity of the frequency distribution in the compartment in question. That the amplitude of the short component appears lower at 3 T compared to 7 T may have several reasons: lower SNR, differences in T₁ saturation and differences the separation between the short and main components in the decay. The T₁ tends to go up with field strength, which means the 7 T had relatively more T₁ saturation than the 3 T experiments. This may be relevant if the main component of the GRE (T₂^*) decay is saturated more than the short component, due to a shorter T₁ in the short one, resulting in a relative enhancement of the short component. At 3 T, all the T₁’s are shorter, resulting in less saturation and less enhancement, hence a lower relative signal amplitude for the short component at 3 T. The difference in separation from the main component is related to the influence of the T₂ on the GRE decay. The T₂ does not change much with field strength, while the susceptibility induced dephasing scales linear with field. As a consequence, the T₂^* of the main signal component is limited by the T₂ at 3 T, resulting in a less than linear scaling of the decay constants with field strength (see R_2,2^* in Table 1). This results in less separation between the short and main components, which in turn, together with the lower SNR, makes the fitting of multiple components less reliable and could cause an underestimation of the relative amplitude of the short component at 3 T.

To investigate the possibility that microscopic magnetic susceptibility variations indeed could underlie the observed relaxation behavior, we simulated the signal decay of spins surrounding a cylindrical susceptibility perturber. The results suggest that the signal decay can be distinctly different from mono-exponential behavior, as illustrated in Appendix 2. Not enough detail is known about the exact distribution of susceptibility sources in brain tissue to create an accurate and realistic model, but this simulation shows it is at least plausible that the T₂^* decay is partly shaped by the susceptibility variations on a microscopic scale..

The dependence of amplitude of the short component on fiber orientation with respect to the B₀ field and the resulting strong contrast within the WM also support a susceptibility-related source, the effects being the strongest in highly oriented fibers perpendicular to the main field (SCC), small in oriented fibers parallel with the field (PIC) and in between for a more mixed source (GWM). The GWM ROI contains a mix of fibers types and orientations, which may explain the results shown in Table 1. The fibers oriented parallel with the magnetic field and those with a more random structure would not contribute to the fast component, while bundles with an orientation predominantly perpendicular to the field may show a frequency effect similar to the SCC, or perhaps a somewhat smaller effect if the local fibers have a different structure. Averaging these various orientations together could result in the observed lower amplitude and frequency for the short component in the GWM ROI. The susceptibility induced field changes in and around elongated structures in general have a sin²θ dependence for their orientation with respect to the main magnetic field (17), which can easily be derived from the two-fold rotation symmetry, meaning the largest difference in orientation effects will be found between parallel and perpendicular fibers. While it cannot be proven to be the sole source of the observed signal decay behavior, it appears likely that the microscopic susceptibility distribution is responsible for most, if not all, of the observed deviations from mono-exponential decay. It may be possible to exploit these effects and use T₂^* based measurements to study the microscopic structure of brain tissue. T₂^* data are easier to acquire and could provide a higher spatial resolution than alternative MR contrasts.

One obvious feature in the residue images (see Fig. 1) is a region in the anterior part of the brain that shows a smaller effect and generally a negative deviation from exponential decay for the shorter echo time. This negative deviation is likely related to macroscopic susceptibility effects, which are strongest in orbito-frontal areas. Comparison with B_o field maps (not shown) indeed confirmed that the areas of poor B_o homogeneity correspond to the darker areas for the short and long echo times in Fig. 1, and the brighter ones for the intermediate echo times. A calculation based on the 2 D phase map did show that shimming could explain a large part of the observed effects. The amplitude map of the fast component of the triple-exponential fit (Fig. 6) appears less sensitive to this problem, which may be explained by the fact that the poor (macroscopic) shimming primarily changes the slower component in the signal and not the amplitude of the fast one. Fitting a mono-exponential function as done for Fig. 1 will result in a lower T₂^* in areas of poor shimming, bringing the fit closer to the fast component and reducing the difference signal. Macroscopic susceptibility effects can also give rise to a more quadratic exponential decay (17), which would influence mostly the later echoes. The triple-exponential model can account for that effect in the third component, while the mono-exponential fit would be adversely affected, contributing to the differences between Fig. 1 and 6. A double exponential model with a linear and quadratic term in the second (and dominant) exponent resulted in a similar residue after fitting as the presented triple exponential model. Based on these data, it can not be determined which of these models is the best to explain the deviation from exponential decay in the later echo times.

Fiber structure differences in the anterior and posterior parts of the CC may explain some of the differences in deviation from exponential decay. Interestingly, the contrast in the deviation map (as in Fig. 1) bears resemblance to the contrast observed in a bSSFP asymmetry study (22), including the difference between posterior and anterior CC and orientation dependence. The frequency shifts observed in that study (20–25 Hz in the perpendicular CC fibers) appear somewhat higher than expected based the frequency of the fast component in the 3 compartment fit of the 7 T data (36 Hz), assuming that the frequency shifts scale with field strength. The deviation maps from Fig. 1 also resemble the maps of the fast relaxation water fraction in a cross-relaxation (MT) study ((9), Fig 2), suggesting again that both methods are sensitive to the local fiber density.

A 3D multi echo experiment on a fixed section of brain tissue containing the CC, WM and some grey matter showed an only very small deviation from mono-exponential T₂^* decay in all tissue types (less than 0.6%, data not presented here). In contrast, a previous T₂ study (23) found a preservation of a fast T₂ component after fixation. The short component reported there at 20 ms may be too close to the main component in the T₂^* decay to be observable as a separate fraction in T₂^* data.

A limitation of the implementation presented here is the use of a single slice acquisition mode with a long total scan time due to the number of repetitions. This method was chosen to maximize the achievable resolution, SNR and stability of the scans. Single image acquisitions were occasionally degraded by small motion artifacts. Using a large number of repetitions and rejecting the outliers from the average resulted in high quality data where the small deviations from exponential decay could reliably be detected and analyzed. Some form of 3D acquisition with motion correction (navigators etc.) is likely of more practical value. This would also improve the available phase information to possibly allow for a correction of the macroscopic susceptibility effects (shimming).

Conclusion

Multi-gradient echo data obtained at 7 T suggest non-exponential T₂^* decay in white matter fiber bundles. Multi-component fitting of the decay characteristics confirm earlier indications of the presence of a short component whose amplitude and resonance frequency appeared to depend on fiber orientation relative to B₀. This phenomenon may be exploited to investigate the local myelin structure and will need to be taken into account when estimating tissue myelin content from T₂^* data.

Appendix 1. Multi-exponential model without frequency offsets

Fig. A1 shows the residual after fitting a triple-exponential model without frequency offsets to the 7 T CC ROI averaged and normalized data. The residuals are averaged over the 8 subjects and the standard error of the average is indicated with the error bars. Although the differences are small (+/−1%), they are highly significant, showing the model does not properly fit the data. The model fit including the offset frequencies reduces the residue to noise, as shown in Fig. 4b. The improvement in the fitting is reflected in the adjusted R² value: 1–1.8·10⁻⁴ versus 1–1.6·10⁻⁶. The R² values are close to 1, because the signal is dominated by the intermediate (main) component, which is fitted well by both models.

Figure A1.

The residue of a ROI averaged decay curve (from the splenium of the corpus callosum) fitted with a triple-exponential model without frequency offsets.

Appendix 2. Simulated decay functions in the presence of susceptibility induced inhomogeneities

To illustrate that the presence of susceptibility-induced inhomogeneities can result in a non-exponential T₂^* decay, the field around a cylinder of higher susceptibility was calculated and the resulting signal evolution as a function of echo time was simulated. Note this is not intended to be an accurate model of human brain tissue, merely an illustration of a mechanism that could contribute to a non-exponential decay. Therefore the simulation is of unrealistic simplicity and lacks for example T₂ and diffusion effects.

A uniform spin density was assumed outside of the cylinder, and zero inside. The phase was calculated as product of the field strength and echo time, after which the decay curve was calculated as the complex sum over all points outside of the cylinder. The FOV (‘voxel size’) of the simulation was 9 times the diameter of the cylinder. The field was calculated using a k-space filtering technique (24), assuming the cylinder axis to be perpendicular to the main magnetic field. A plot of the resulting decay is shown in Fig. A2a. Anon-exponential, sinc-like behavior can be readily appreciated. In a similar fashion, the decay in the presence of a closely packed set of hollow cylinders, filling the entire FOV, was calculated. The size of each cylinder was again 1/9^th of the FOV. The result is shown in Fig. A2b. Again a non-exponential decay is observed, albeit with a rather different temporal evolution than the signal in Fig. A2a.

Figure A2.

Simulations of the dephasing effects of the susceptibility-induced field inhomogeneity around a) one solid cylinder and b) in and around a bundle of hollow cylinders, all perpendicular to the main field.