Age-specific profiles of tissue-level composition and mechanical properties in murine cortical bone

Abstract

There is growing evidence that bone composition and tissue-level mechanical properties are significant determinants of skeletal integrity. In the current study, Raman spectroscopy and nanoindentation testing were co-localized to analyze tissue-level compositional and mechanical properties in skeletally mature young (4 or 5 months) and old (19 months) murine femora at similar spatial scales. Standard multivariate linear regression analysis revealed age-dependent patterns in the relationships between mechanical and compositional properties at the tissue scale. However, changes in bone material properties with age are often complex and nonlinear, and can be missed with linear regression and correlation-based methods. A retrospective data mining approach was implemented using non-linear multidimensional visualization and classification to identify spectroscopic and nanoindentation metrics that best discriminated bone specimens of different age-classes. The ability to classify the specimens into the correct age group increased by using combinations of Raman and nanoindentation variables (86–96% accuracy) as compared to using individual measures (59–79% accuracy). Metrics that best classified 4 or 5 month and 19 month specimens (2-age classes) were mineral to matrix ratio, crystallinity, modulus and plasticity index. Metrics that best distinguished between 4, 5 and 19 month specimens (3-age classes) were mineral to matrix ratio, crystallinity, modulus, hardness, cross-linking, carbonate to phosphate ratio, creep displacement and creep viscosity. These findings attest to the complexity of mechanisms underlying bone tissue properties and draw attention to the importance of considering non-linear interactions between tissue-level composition and mechanics that may work together to influence material properties with age. The results demonstrate that a few non-linearly combined compositional and mechanical metrics provide better discriminatory information than a single metric or a single technique.

1. Introduction

The strength and fracture resistance of bone are primarily dependent on its mass, architecture, and material properties. Bone mineral density (BMD) measured using dual-energy X-ray absorptiometry (DXA) remains the gold standard for diagnosis of osteoporosis. While BMD is negatively correlated with fracture, it inadequately predicts increase in fracture risk and explains only a limited proportion of the anti-fracture efficacy observed with anti-resorptive therapies [1]. The heterogeneous and hierarchical nature of bone makes it unlikely for a single measurement to fully characterize its structural integrity or accurately predict fracture risk. Hence, studies are increasingly focused on understanding the contributions of architecture, composition, material properties and remodeling dynamics to the maintenance of bone strength [2–5].

At the tissue level, contributions from collagen and mineral components to bone quality and strength are not yet fully understood. Quantification of molecular structure and material properties at the tissue level would also assist in understanding the composite nature of bone and its effect on whole bone strength [6]. Factors such as aging and disease decrease bone mass, reorganize architecture and compromise tissue and structural-level properties. While compositional changes with age may precede fracture, the relationship between tissue composition and material behavior at different ages is not fully characterized [7–9]. Combining different methods for characterizing material properties may provide a better understanding of how age-related material changes relate to whole bone and tissue-level mechanics. For instance, co-localization of compositional and mechanical property measurements allows for correlations at the same spatial scale, minimizing variance due to spatial heterogeneity of bone tissue.

One would expect that material properties in a biological system may be associated in a non-linear fashion and hence, more information can be gained by observing a set of metrics as a group, rather than averaging their individual effects. Probing the complex relationships between composition and mechanics at the tissue level could provide us with a better understanding of how aging and disease affect bone function at different hierarchical levels. However, a common assumption in studies investigating bone material properties is linearity. Univariate strategies make an assumption that variables are independent and exclude potentially informative interactions that might exist with other variables. For example, composition and nanomechanical properties have either been examined independently [10, 11] or by assuming linear relationships [12–14].

The combination of Raman spectroscopy and nanoindentation testing has been employed by Donnelly et al. to investigate tissue-level material properties at defined spatial positions [14]. Raman spectroscopy provides important compositional measures of the mineral and matrix components, such as amount of mineralization, crystallinity, degree of carbonate substitution in the mineral, collagen content and cross-linking at micron-scale spatial resolution. Nanoindentation testing provides local (1–2 µm scale) information on the hardness, elastic modulus and viscoelastic behavior of the tissue. By co-localizing Raman microspectroscopy and nanoindentation testing, Donnelly et al. studied the effects of tissue age on compositional and nanomechanical properties in femora of immature rats [14] while the present work on mouse bone investigates the effects of specimen age over a larger fraction of the life span. While Donnelly and co-workers used linear approximations for the relationships between compositional and mechanical properties, the variables appear to follow vary non-linearly with age.

As most biological systems, including bone, are inherently non-linear, analyzing changes in properties with age to obtain a quantitative understanding of the underlying biological mechanisms is a complex problem. Many methods such as machine learning and high-dimensional data visualization can be applied to combined data sets of different properties to study non-linear behavior. Machine learning involves applying a statistical modeling algorithm to a data set. The chosen model attempts to learn the underlying concept rather than fit a provided model. Applications to microarray analysis [15], mass spectrometry [16] and optical spectroscopy [17] for biomarker discovery are examples of where machine learning has made contributions. On the other hand, popular dimension reduction methods such as linear principal component analysis and linear discriminant analysis find linear combinations of variables that best predict a class type. However, they do not account for the inherent underlying nonlinear structure associated with most biomedical data and the new representation that is generated is often difficult to interpret. Also, commonly used analytic methods exclude the possibility of epistasis, i.e., interactions between variables that do not display any main effects [18].

In the current study, Raman microspectroscopy and nanoindentation were used to measure compositional and mechanical properties at the same spatial location and with similar depth in femora of mice from three age groups. Regression analysis was used across age groups and within age groups to determine correlations between Raman and nanoindentation metrics as well as the effects of age group on those associations. Further, the age-dependent non-linear interdependence between compositional and mechanical properties in murine femora was examined using a retrospective data mining approach. Spectroscopic and nanoindentation metrics that best discriminated bone specimens of different age-classes were identified using two machine learning algorithms – RadViz for non-linear multidimensional visualization, and VizRank for classification and visual projection scoring. The added value of combining compositional and mechanical properties in discriminating between specimens of different age groups was also investigated.

2. Material and Methods

2.1. Data sets

Mechanical and compositional measurements from the right femora of 4, 5, and 19 month old male C57Bl/6 mice (protocol approved by University of Michigan Committee on Use and Care of Animals) were used in this study. Four month old mice are nearing skeletally maturity but still growing, 5 month old mice have a fully developed skeleton, and 19 month old mice have compromised structural integrity [19–21]. The 5 and 19 month age groups included both non-exercised mice and mice subjected to an exercise program (running on a treadmill, 12 m/min, 5 degree incline, 30 minutes/day) for the 21 days prior to euthanasia. There were 8 femora from four month old mice (all non-exercised), 13 from five month old mice (6 non-exercised and 7 exercised), and 12 from nineteen month old mice (6 non-exercised and 6 exercised). Specimens were first analyzed by Raman microspectroscopy, a nondestructive technique, and then by nanoindentation. Between analyses, femora were kept frozen in Ca buffer (−20 °C).

2.2 Sample preparation

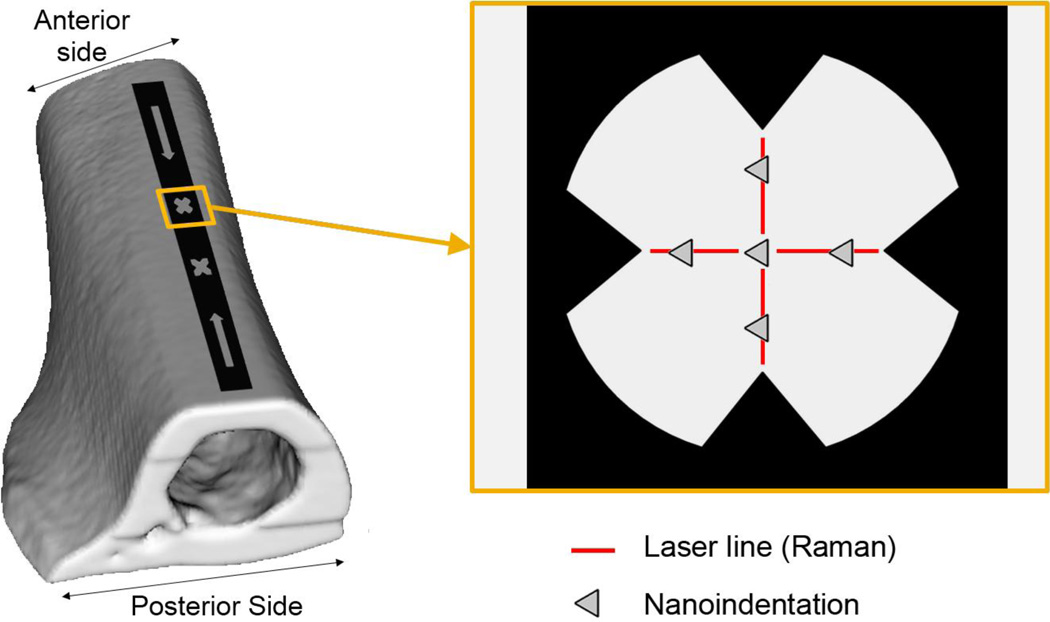
Femora were prepared for co-localized analysis by Raman microspectroscopy and nanoindentation by creating a flat smooth surface and stamping a marker system onto that surface [22]. An approximately 10 mm longitudinal section, starting near the proximal end of the trochanter and running distally, was removed from the mid-diaphysis of the femora using a low-speed sectioning saw (South Bay Technology, San Clemente, CA). A custom designed specimen holder was used with a polishing wheel, rigid and soft polishing cloths, a 3 µm diamond suspension and a 0.05 µm alumina suspension (Buehler, Inc., Lake Bluff, IL) to create a flat surface on the anterior side. In total, a depth of approximately 20–30 µm was removed from the anterior surface of each bone. After polishing, bones were ultrasonically cleaned for 20 seconds in Calcium buffered saline and stamped with a marker by micro-contact printing. The stamp was created using a micro-fabricated polydimethylsiloxane (PDMS) master and custom designed lithographic ink (The Flint Group, Plymouth, MI). A thin layer of ink was manually rolled onto the surface of the PDMS master and then stamped precisely on the flat, smooth surface of the bones by using a custom built, three dimensional micrometer stamping stage. The stamp pattern had two regions of interest, each with a diameter of 60 µm (Figure 1). Only one region of interest was used in each sample, but two regions were included in the stamp in case one of the regions covered an area of bone that had micro-cavities from vascularization. To avoid disparity in length scales between measured properties, this marker served as a guide for co-localizing Raman and nanoindentation measurements (Figure 1).

Fig 1.

Marker used to co-localize Raman microspectroscopy and nanoindentation. A marker was stamped on to the flat, smooth surface of the anterior side of femoral sections. The marker was used as a guide to ensure Raman spectra (4 lines) and nanoindentation measurements (5 indents) were taken at the same location.

2.3. Raman spectroscopy

Samples were thawed to room temperature immediately before use, and remained in calcium buffer throughout the analysis. Four Raman spectra were collected within the ink marker of each sample as shown in Figure 1. At each location, a line-focused 785 nm laser (Invictus, Kaiser Optical Systems, Inc., Ann Arbor, MI) was focused on the specimens through a NIR-optimized 60X, 1.0NA water immersion objective (Fluor series, Nikon USA, Melville, NY). The approximate length of the laser line was 10–20 µm with a depth of field of 2–3 µm. Raman scatter was collected with 60s integration time through the objective and focused into an axial-transmissive spectrograph (HoloSpec f/1.8I, Kaiser Optical Systems Inc., Ann Arbor, MI) equipped with a 25 µm slit, providing a maximum spectral resolution of 3–4 cm⁻¹. Polarization scramblers (Thor Labs, Newton, NJ) were used at the laser exit and at the spectrometer entrance slit to remove orientation effects from the spectra. After the spectra were collected, the samples were kept wet, covered with gauze soaked in Ca buffer and refrozen (−20 °C).

Spectral processing was performed with locally written scripts on Matlab (Math Works, Natick, MA) and GRAMS/AI (Thermo Fisher Scientific, Waltham, MA). All Raman spectra were corrected for spectrograph image curvature, dark-current subtraction and white-light correction (flat-fielding). The spectra were normalized to the height of phosphate (959 cm⁻¹) and band areas were determined for select Raman peaks representing bone mineral (phosphate, 959 cm⁻¹; carbonate, 1071 cm⁻¹) and bone matrix (hydroxyproline, 851 and 875 cm⁻¹; proline, 917 cm⁻¹; amide I, 1660 and 1690 cm⁻¹) components. Four Raman metrics - carbonate to phosphate ratio (1071/959) representing degree of carbonate substitution in the mineral, mineral to matrix ratio (MMR, 959/(851+875+917)) describing the amount of mineralization, crystallinity (inverse of 959 peak width at half maximum) representing mineral crystal size and perfection, and cross-linking ratio (1660/1690) quantifying collagen cross-linking were calculated.

2.4. Nanoindentation

After Raman spectra were collected, samples were subjected to nanoindentation using a Nanoindenter II equipped with a diamond Berkovich indenting tip and a lock-in amplifier for continuous stiffness measurements (MTS Nano Instruments, Oak Ridge, TN). Five indents were made within the marker as shown in Figure 1. The loading profile at each location consisted of two indenting procedures. The first part of the profile consisted of a loading segment to a depth of 2000 nm, in which the ratio of current loading rate to current load was maintained at 0.05 sec⁻¹ to produce an approximately constant strain rate [23]. This indentation depth was matched to the depth of field from the Raman analysis. While the volume of tissue probed by Raman and nanoindentation might be different, it is assumed that material properties will remain uniform within these micro-volumes which only differ by the order of 1 µm³. After the indentation depth was reached, a constant-load hold period of 100 seconds was used to prevent viscoelastic behavior from contributing to the unloading behavior [24]. The samples were then unloaded to 10% of the maximum load and held at constant load for 50 seconds to allow for thermal drift correction and viscoelastic recovery of the sample. Finally, samples were completely unloaded and kept unloaded for 10 seconds. This indentation procedure was also performed on a single-crystal aluminum standard to confirm that measurements were consistent from day to day. The second part of the indentation procedure consisted of a step load of 60 mN followed by a 100 second constant-load hold period and a complete unloading to record creep behavior in the hold period after the step loading. As the step load of 60 mN was greater than the load required to reach a depth of 2000 nm in the first segment of the indenting procedure, the step loading caused new plastic and elastic deformation in each sample.

A Matlab (Mathworks, Natick, MA) program was written to analyze data collected by nanoindentation. For each indentation profile, the first loading/unloading segment was used to calculate modulus and contact hardness by the Oliver-Pharr method [25], using an assumed Poisson ratio of 0.3 for bone [26]. Calculation of contact hardness by the Oliver-Pharr method assumes that the contact area between the sample and the indenter tip at maximum load is equivalent to the area of the residual indent after unloading. However, the assumption made in the Oliver-Pharr method is violated due to the significant elastic recovery upon unloading in bone. Therefore, a correction was applied to account for elastic recovery and transform contact hardness to true hardness [27]. The first loading/unloading segment was also used to calculate plasticity index, the ratio of plastic work during loading and unloading to the total work to reach peak indentation depth [28]. The amount of plastic work is equivalent to the total work minus the work accounted for by elastic recovery of the sample during unloading. Therefore, larger values of plasticity index indicate less elastic recovery and a greater percentage of plastic deformation to elastic deformation.

The creep behavior following step loading was modeled for a conical indenter using a combined Maxwell-Voigt model for viscoelasticity and viscoplasticity [29]. The model included a spring and damper in parallel to model viscoelasticity in series with a spring to model viscoplasticity. In the time frame of 100 seconds, there was always linear displacement with time at the end of the hold period, making the Maxwell-Voigt model an appropriate choice. The values for modulus and viscosity were calculated by fitting the model with load, displacement and time data from the hold period. Even though creep displacement varied between samples (ranging from 300–1600 nm), the model fit creep behavior well (R² > 0.999) for all samples. Load-displacement and stiffness-displacement (by continuous stiffness measurements) profiles were analyzed to find improper surface contact or micro-failures during indentation. After eliminating 14 problematic indentations, the remaining indentations were averaged in each sample. Although the assumption of sample isotropy is violated for the mechanical calculations, the error in the calculations is similar between bones and much less than the variance in calculated properties between bones.

2.5. Statistical analysis

Statistical analyses were performed using SPSS (version 16). For all statistical tests, p < 0.05 was considered significant and p < 0.1 was considered marginally significant. The effects of age and exercise on the means of Raman and nanoindentation metrics were evaluated by two-way analyses of variance (ANOVA) with Bonferroni and Holm-Sidak post-hoc tests. Because there was no significant or marginally significant effect of exercise on the means of any metric, exercised groups were not separated from non-exercised groups in the presentation of means in order to improve clarity. However, exercise was still included as a potential factor in model selection for linear regressions.

Linear regressions were conducted using Raman metrics as covariates and nanoindentation metrics as dependent variables. A natural log transformation was applied to creep metrics (displacement, modulus parallel, viscosity parallel and viscosity series) that did not follow a normal distribution. Raman metrics were centered so that interactions between the metrics could be analyzed without creating a covariance problem. Several different regression models were considered. First, each covariate was linearly regressed alone with each dependent variable, across all age groups. Next multivariate linear regressions were conducted using all Raman covariates and step-wise selection with the criteria p < 0.1 to include a covariate in the model and p > 0.11 to remove a covariate. Age group was also available for step-wise selection into the model as well as the interaction between age and Raman covariates. There was a consistent significant effect of the 19 month age group as main or interactive effect, indicating that the relations in this group were significantly different than the 4 and 5 month age groups. Therefore, the multivariate analysis was repeated separately on 19 month old bones and on 4 and 5 month old bones. In all the models, there were no significant contributions from interactive terms. The contributions of covariates included in the model were judged by their partial correlation with the dependent variable and the corresponding p-value. Multicovariance was not a problem in any model, as judged by variance inflation factor and condition index. Models fits were not driven by influential points as judged by the Cook’s Distance and the difference in fits (DFFIT).

2.6. Data mining

To probe relationships between composition and mechanics at the tissue level, machine learning algorithms, RadViz and VizRank, were used to better understand the interaction between multiple variables. The nonlinear multidimensional radial visualization algorithm, RadViz, maps n data dimensions (variables) onto two dimensional circular space [30]. The advantage of this algorithm lies in its use of original, untransformed set of features without any feature reduction. This is in contrast to multidimensional scaling techniques which do not preserve the original feature information and are harder to interpret. The usefulness of radial visualization depends on the selection and ordering of variables around the circle circumference because these determine the quality of the multidimensional projection. The visualization ranking algorithm, VizRank, provides a heuristic search technique to guide the ordering of variables and evaluating the resulting radial projections by their ability to discriminate between classes. The classification quality (score) is the predictive accuracy of k-nearest neighbor (k-NN) classifier on the radially projected data set as estimated through 10-fold cross validation, with k is set to sqrt(N), where N is the number of specimen points [31]. VizRank automatically ranks the projections according to their score. Projections providing perfect class separation receive a 100 and less informative projections receive correspondingly lower scores. In this study, we used only the single best-ranked projection for classification. A more detailed description of the data mining algorithms is provided in Appendix 1.

2.7. Implementation

RadViz and VizRank algorithms were implemented within Orange (http://www.ailab.si/orange), an open-source data mining suite with a user-friendly graphic interface [32]. First, non-linear projection and classification were performed with nanoindentation metrics as the dependent class, and Raman metrics, age and exercise (control/exercise) groups as independent variables. All data were grouped under two age classes - 4 and 5 months representing skeletally mature young and 19 month representing skeletally mature old mice. The dependent variables were binned into two classes (high and low) using an equal-frequency discretization method, because the classification algorithm requires a discrete dependent class. This method divides the continuous attribute in intervals containing approximately the same number of instances with adjacent values. VizRank algorithm was restricted to combinations of up to four variables. As the direction of dependencies between compositional and mechanical variables is not clear, non-linear projection and classification were also performed with Raman metrics as the dependent class, and nanoindentation metrics, age (4 or 5 months/19 months) and exercise (control/exercise) groups as independent variables. It is possible that there might not always be a linear or non-linear dependence or association between bone compositional and mechanical metrics at the tissue level. Hence, multidimensional projection and classification were used to identify predictive Raman and nanoindentation variables that best discriminated bone specimens of different age-classes. Different data sub-sets were considered for age-based classification: with only Raman variables, with only nanoindentation variables, and with combined Raman and nanoindentation variables. Classification was performed with 2-age classes (4 or 5 months and 19 months) and 3-age classes (4, 5 and 19 months).

2.8. Classifier comparison

To compare VizRank’s accuracy to that of other machine learning approaches and to exclude possible overfitting, we trained and classified upon the same data sets (2-age classes and 3-age classes) using support vector machines (SVM) with a linear kernel, a k-nearest neighbor learner (kNN, where k equal to square root of number of data instances in learning set), a naive Bayesian classifier and a C4.5 decision tree within Orange. A bootstrap resampling technique was used with the sampling repeated 100 times, as this technique provides a less variable estimate than cross-validation despite its computational cost [33]. The classification performance was obtained using the 0.632 bootstrap estimator that combines both the bootstrap sampling error rate and the re-substitution error rate [34]. The area under the receiver operating curve (AUC) was also calculated as a performance measure. A classifier is considered better if it has a larger AUC compared to a different classifier.

3. Results

3.1. Univariate statistics

Raman spectroscopic and nanoindentation variables from the data set are presented in table 1. The material properties of 4 month old specimens were not significantly different from that of 5 month old specimens, except for a marginal increase in collagen cross-linking ratio and a marginal decrease in hardness at 4 months (p < 0.1). Therefore, these two age groups were combined and considered as a single age group (skeletally mature young specimens). Mineral to matrix ratio (MMR), carbonate to phosphate ratio and crystallinity were significantly greater in the 19 month (skeletally mature old) specimens compared to that in the skeletally mature young specimens. Crosslinking ratio and nanoindentation measurements were not significantly different between the two age groups. Exercise had no significant effect on any metric.

Table 1.

Compositional and mechanical metrics determined by Raman spectroscopy and nanoindentation testing in each age group

	Age
Variable	4 or 5 months (n=21)	19 months (n=12)
MMR	7.327 ± 0.996	10.18 ± 1.28*
Carbonate/Phosphate	0.267 ± 0.018	0.284 ± 0.029*
Crystallinity	0.0534 ± 0.0004	0.0544 ± 0.0005*
Cross-linking	2.08 ± 0.36	1.92 ± 0.22
Modulus (GPa)	7.55 ± 1.97	8.11 ± 2.30
Hardness (GPa)	1.22 ± 0.41	1.40 ± 0.45
Plasticity index	0.77 ± 0.03	0.76 ± 0.03
Creep displacement (nm)	833 ± 336	823 ± 360
Creep modulus parallel (GPa)	884 ± 782	992 ± 740
Creep viscosity parallel(GPa-s)	11200 ± 8826	12175 ± 8280
Creep viscosity series (GPa-s)	15179 ± 15166	15508 ± 17900

^*p≤0.05

3.2. Linear correlation between tissue composition and mechanical properties

In linear regressions of single Raman metrics with mechanical properties across all age groups, plasticity index was significantly and positively correlated to carbonate to phosphate ratio (R²=0.22). Similarly, plasticity index was significantly correlated to MMR (R²=0.19). Modulus was significantly, positively correlated with crystallinity (R²=0.14), but no other mechanical properties. In contrast, modulus (R²=0.13), hardness (R²=0.35) and creep viscosity series (R²=0.23) were significantly, negatively correlated with cross-linking ratio, whereas creep modulus parallel (R²=0.10) and creep viscosity parallel (R²=0.11) were marginally negatively correlated with cross-linking ratio. Plasticity index (R²=0.26) and creep displacement (R²=0.21) were also significantly but positively correlated with cross-linking ratio.

In multivariate linear regressions, the effect of covariates in the 4 or 5 month age groups was different than in the 19 month age group (table 2). In the 4 or 5 month age group, MMR significantly and positively contributed to modulus, creep modulus parallel and creep viscosity parallel, while cross-linking ratio had a significant negative contribution to those properties. In the models of creep displacement and creep viscosity series, there was a marginal contribution of exercise. Cross-linking ratio was the only Raman metric that significantly correlated to hardness (negative effect), creep displacement (positive effect) and creep viscosity series (negative effect). Carbonate to phosphate ratio significantly and positively contributed to plasticity index.

Table 2.

Partial correlations relating tissue level composition and mechanical properties in skeletally mature young (4 or 5 months) and old (19 months) age groups

	Age (months)	Carbonate/ Phosphate	MMR	Cross- linking	Group Effect	p	Adjusted R2
Modulus	4 or 5 19	N.S. N.S.	0.538 N.S.	−0.650 N.S.		<0.05 N.S.	0.426
Hardness	4 or 5 19	N.S. N.S.	N.S. −0.883	−0.598 N.S.		<0.05 <0.05	0.324 0.757
Plasticity Index	4 or 5 19	0.768 N.S.	N.S. 0.914	N.S. N.S.		<0.05 <0.05	0.632 0.818
Creep Displaceme nt (ln)	4 or 5 19	N.S. N.S.	N.S. N.S.	0.606 N.S.	E=0.429Δ	<0.05 N.S.	0.328
Creep modulus parallel (ln)	4 or 5 19	N.S. N.S.	0.653 N.S.	−0.609 N.S.		<0.05 N.S.	0.462
Creep viscosity parallel(ln)	4 or 5 19	N.S. N.S.	0.656 N.S.	−0.590 N.S.		<0.05 N.S.	0.453
Creep viscosity series (ln)	4 or 5 19	N.S. N.S.	N.S. −0.531Δ	−0.613 N.S.	E=− 0.439Δ	<0.05 <0.1	0.339 0.211

^Δindicates significance of partial correlation 0.05 < p < 0.10. All other partial correlations significant at p < 0.05.

N.S. indicates no significant model existed with covariates.

^(ln)indicates that the natural log of dependent variable was used in the regression (to satisfy normality assumption)

E = Effect of exercise

Crystallinity was excluded from the table because it did not significantly contribute to any model.

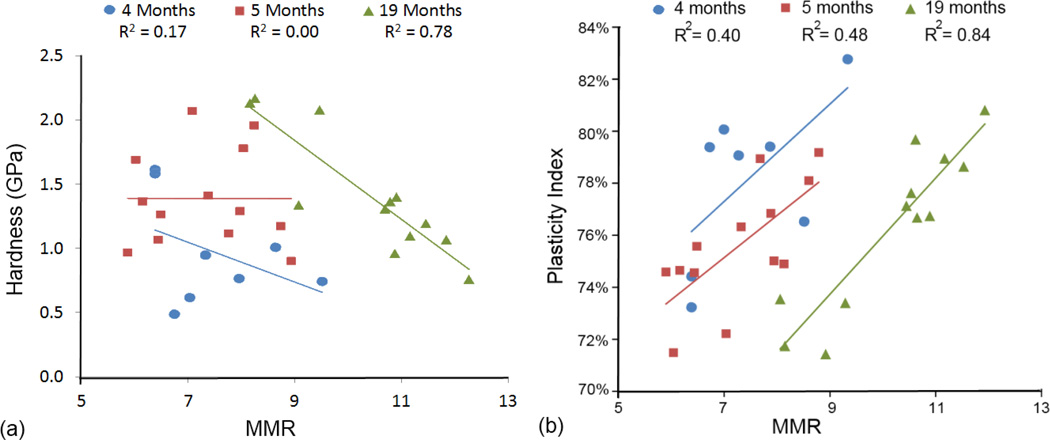
In 19 month old bones, MMR was the only covariate that significantly or marginally contributed (p < 0.1) to mechanical properties. MMR was positively correlated with plasticity index and negatively associated with hardness and creep viscosity series. The adjusted R² values denote the proportion of the variance in each of the mechanical properties that is explained by the examined compositional properties. For the 4 or 5 month age group, Raman variables explained 32% to 63% of the variance in all measured nanoindentation variables. For the 19 month age group, R² values increased to 76% and 82% for hardness and plasticity index, respectively. Regression models for other nanoindentation variables were not significant in this age group. The relationship between MMR vs. hardness and plasticity index in the three age groups were further investigated. Increasing MMR had no significant effect on hardness in either 4 or 5 month old femora, but significantly reduced hardness in 19 month femora (Figure 2a). In all age groups, plasticity index significantly increased with MMR, but with similar slopes (Figure 2b).

Fig 2.

(a) Relationship between MMR and hardness. MMR had no significant correlation with hardness in 4 and 5 month old femora, but had a significant negative relationship with hardness in 19 month old femora. (b) Relationship between MMR and plasticity index. Plasticity index significantly increased with MMR in all age groups and with slopes that were not significantly different.

3.3. Nanoindentation measures as the dependent metric

The best non-linear RadViz projections for the data set with dependent nanoindentation metrics containing only 4 or 5 month and only 19 month old specimens are outlined in table 3a. Independent variables consisted of a combination of continuous Raman and discrete exercise metrics. Classification accuracy greater than 80% was observed for plasticity index, creep modulus parallel and creep viscosity parallel in the 4 or 5 month age group and for hardness in the 19 month age group. Modulus, hardness, creep displacement and creep viscosity series in the 4 or 5 month age group and plasticity index in the 19 month age group were classified with greater than 70% accuracy. The highest classification accuracy was observed for plasticity index (86%) for the 4 or 5 month age group and for hardness (87%) in the 19 month age group. In 4 or 5 month old skeletally mature specimens, Raman compositional metrics were better associated with viscoelastic properties (plasticity index, creep metrics), whereas in 19 month old specimens, they related better to the measure of hardness (resistance to plastic deformation).

Table 3.

a Nanoindentation vs. Raman metrics for skeletally mature young (4 or 5 months) and old (19 months) age groups
Dependent class (Discretized)	Age (months)	Classification Accuracy	Independent variables used in the top projection
Modulus	4 or 5 19	79% 56%	MMR, Crosslinking, C/P, Crystallinity MMR, Crystallinity, Crosslinking, C/P
Hardness	4 or 5 19	72% 87%	MMR, Crosslinking, Exercise MMR, Crystallinity, Crosslinking, Exercise
Plasticity index	4 or 5 19	86% 75%	C/P, Crosslinking, MMR, Exercise Crystallinity, MMR, C/P, Exercise
Creep displacement	4 or 5 19	76% 65%	Crosslinking, MMR, Exercise Crosslinking, MMR, Exercise
Creep modulus parallel	4 or 5 19	84% 65%	MMR, Crystallinity, Crosslinking, Exercise Crosslinking, MMR, Exercise
Creep viscosity parallel	4 or 5 19	84% 65%	MMR, Crystallinity, Crosslinking, Exercise Crosslinking, MMR, Exercise
Creep viscosity series	4 or 5 19	75% 65%	MMR, Crystallinity, Crosslinking, Exercise Crosslinking, MMR, Exercise

b Raman vs. nanoindentation metrics for skeletally mature young (4 or 5 months) and old (19 months) age groups
Dependent class (Discretized)	Age (months)	Classification Accuracy	Independent variables used in the top projection
Carbonate/Phosphate	4 or 5 19	86% 76%	Creep modulus parallel, Hardness, Modulus, Creep viscosity parallel Hardness, Modulus Creep viscosity parallel, Creep modulus parallel
Crystallinity	4 or 5 19	69% 74%	Creep displacement, Hardness, Creep viscosity parallel, Modulus Creep modulus parallel, Plasticity index, Hardness, Exercise
MMR	4 or 5 19	88% 83%	Modulus, Hardness, Creep viscosity parallel, Creep viscosity series Hardness, Modulus, Plasticity index, Creep viscosity series
Crosslinking	4 or 5 19	78% 90%	Modulus, Creep viscosity series, Plasticity index, Creep modulus parallel Creep modulus parallel, Creep displacement, Hardness, Exercise

3.4. Raman spectroscopy measures as the dependent metric

Changes in bone composition might either be a cause for or consequence of changes in bone mechanical properties. Hence, non-linear multidimensional classifications were also assessed with dependent Raman and independent nanoindentation metrics. Table 3b outlines the best non-linear multidimensional classifications for the data set with dependent Raman metrics containing only 4 or 5 month and 19 month age groups. In both age groups, all Raman metrics were classified with almost 70% accuracy or greater. In the 4 or 5 month age group, MMR featured the highest classification accuracy (88%) with creep viscosity series, creep viscosity parallel, hardness and modulus as the relevant independent variables. In the 19 month age group, the highest classification accuracy was observed for cross-linking (90%) with creep modulus parallel, creep displacement, hardness and exercise as the relevant independent variables. These results also confirm that aging results in altered patterns of observed associations between compositional and mechanical properties. In 4 or 5 month age group, nanoindentation metrics were better associated with mineralization, whereas in 19 month age group, they related better to collagen crosslinking.

3.5. Multivariate discrimination of age classes

The best ranked non-linear multidimensional classifications for the data sets with only Raman variables, with only nanoindentation variables, and with combined Raman and nanoindentation variables for 2-age and 3-age classification are shown in figures 3, 4 and 5. When all measurements were taken from either only Raman (figure 3) or only nanoindentation experiments (figure 4), classification accuracy ranged from 59% to 79%. Using only Raman variables, the 2-age class and 3-age class data sets were classified with 79% and 59% accuracy respectively. Using only nanoindentation variables, the 2-age class and 3-age class data sets were classified with 63% and 62% accuracy respectively.

Fig 3.

Classification using only Raman variables for (a) 2 age groups and (b) 3 age groups. Classification scores computed by VizRank are 79% and 59% respectively. The points are scaled up by a factor of 1.2 to 1.4.

Fig 4.

Classification using only nanoindentation variables for (a) 2 age groups and (b) 3 age groups. Classification scores computed by VizRank are 63% and 62% respectively. The points are scaled up by a factor of 1.2 to 1.4.

Fig 5.

Classification using both Raman and nanoindentation variables for (a) 2 age groups and (b) 3 age groups. Classification scores computed by VizRank are 96% and 86% respectively. The points are scaled up by a factor of 1.2 to 1.4.

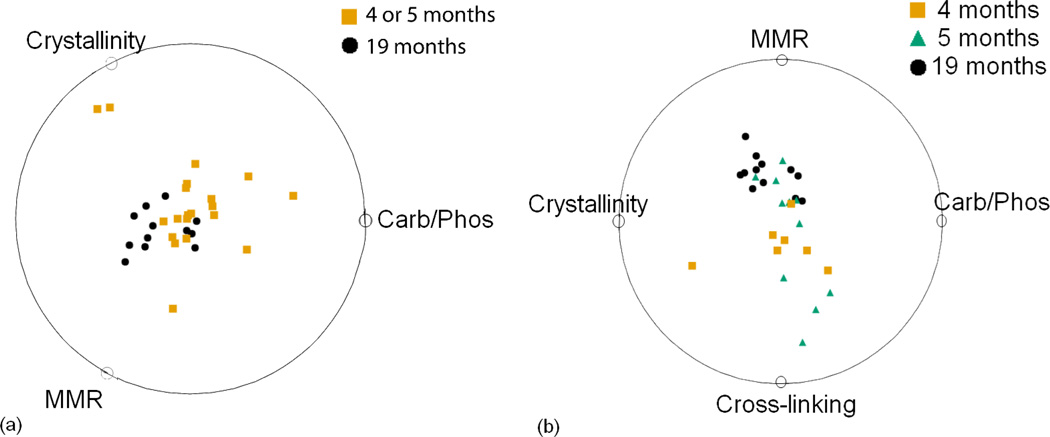
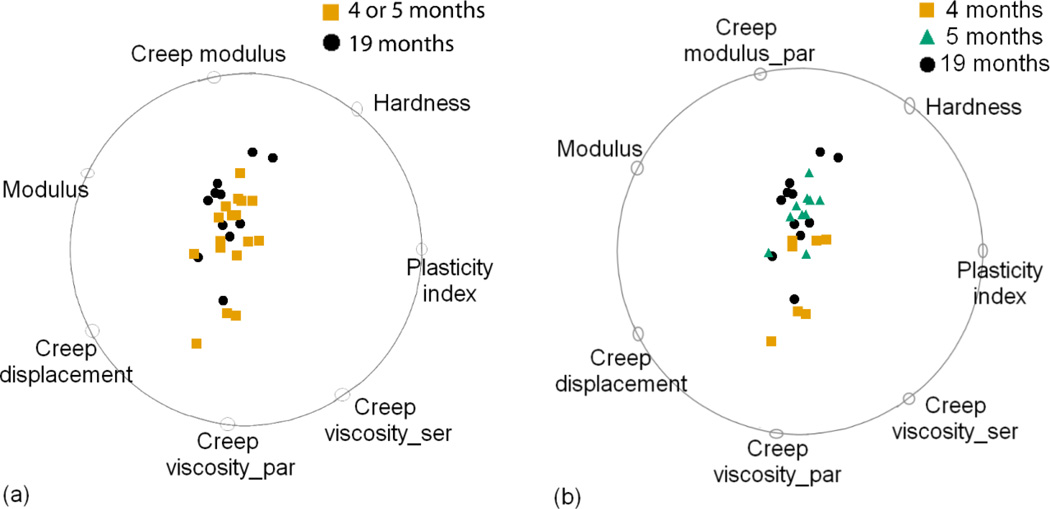
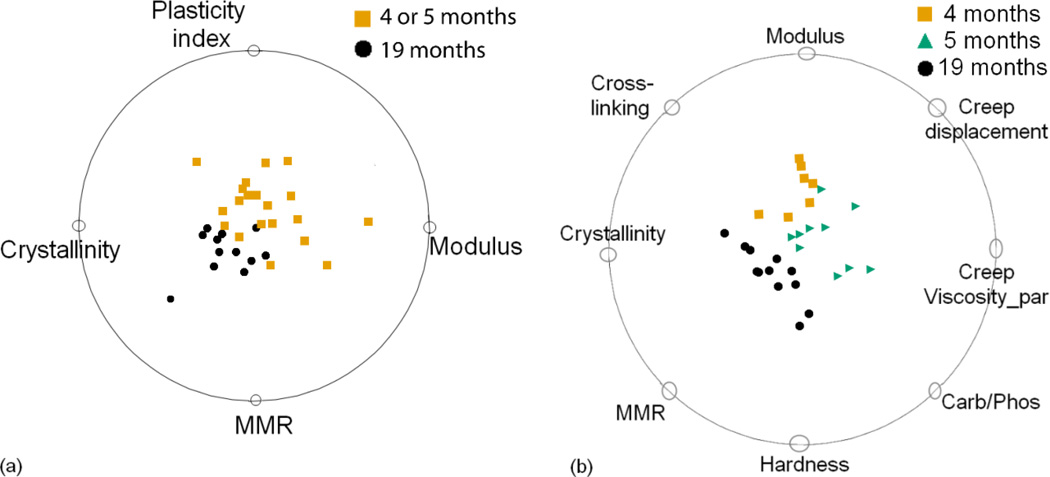
Figure 5a shows that a combination of Raman and nanoindentation variables were identified that distinguish the two age classes with greater than 90% accuracy. In this data set, MMR, crystallinity, plasticity index and modulus contained the most discriminative information. Interestingly, only MMR and crystallinity had significant main effects in the univariate analysis. The increase in classification accuracy on integrating Raman and nanoindentation metrics reinforces the importance of considering non-linear interactions among tissue-level composition and mechanics that may work together to influence bone material properties with age. Traditional statistical methods are not well suited for this task and will overlook variable interactions if not properly investigated. In the 3-age class data set (figure 5b), the best multidimensional classification used a combination of eight Raman and nanoindentation variables to classify the three age groups with 86% accuracy.

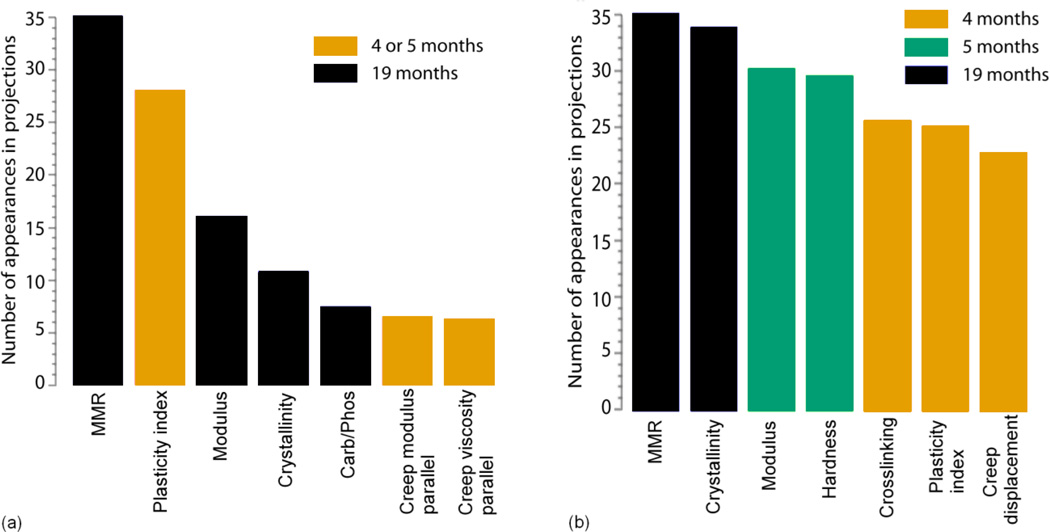
The performance of VizRank and four other standard machine learning classifiers in labeling blinded data are reported in terms of average classification accuracies and AUC values in table 4. In terms of classification accuracy, VizRank performed comparably to SVM, kNN and decision trees in both the 2-age class and 3-age class data sets. The area under ROC curve (AUC) values also confirmed that VizRank performed comparably to other classification algorithms and was stable and robust. Only the performance of the naive Bayesian classifier was poor relative to other algorithms. Figure 6 shows histograms of the seven variables most often used in top-rated RadViz visualizations of the data sets with 2-age classes and 3-age classes respectively. It is valuable to know if a particular variable appears in several top ranked classifications and not just the best ranked one. The class association of the variables was computed by examining the role of a variable taking into account its interaction with other variables in the data set [35]. Ultimately, these top-ranked variables defining the best ranked projections hold the most information for class discrimination.

Table 4.

Bootstrap estimated classification accuracy and area under ROC (AUC) of VizRank compared to four standard machine learning algorithms

	Classification Accuracy (%)		Area under ROC (AUC)
	2 age classes	3 age classes	2 age classes	3 age classes
VizRank	89.5 ± 11.5	73.0 ± 14.3	0.94 ± 0.12	0.85 ± 0.12
SVM	87.6 ± 19.8	76.2 ± 18.9	0.91 ± 0.21	0.92 ± 0.13
kNN	85.7 ± 11.9	77.5 ± 13.1	0.90 ± 0.13	0.87 ± 0.11
Naive Bayes	84.6 ± 11.8	62.9 ± 14.1	0.87 ± 0.11	0.77 ± 0.12
Decision trees	87.2 ± 8.2	72.6 ± 13.3	0.87 ± 0.09	0.83 ± 0.11

Fig 6.

A histogram of the seven Raman and nanoindentation variables most often used in the top 100 nonlinear multidimensional classifications of the data set (a) with 2 age groups and (b) with 3 age groups. The y-axis score shows the number of appearances of a variable in 100 best ranked projections. The colors of the bars indicate the class that has the highest average association for that variable. The order in which features appear in the histogram reflects their importance.

MMR and plasticity index were the two most important variables present in the almost 30% of the top-rated classifications with the role of separating skeletally mature young (4 or 5 months) and skeletally mature old (19 months) specimens (Figure 6a). Seven out of eight variables discriminating between 4 month vs. 5 month vs. 19 month age groups in the best ranked projection each appeared in a quarter of all top ranking projections (Figure 6b). MMR, crystallinity, modulus and hardness were present in almost 30% of the top-rated classifications and the other variables - crosslinking, plasticity index and creep displacement, appeared in almost 25% of the top 100 classifications. Figure 6b portrays the complexity in interpreting short term, age-related changes in bone quality.

4. Discussion

Standard multivariate linear regression analysis revealed an age-dependent pattern in the relationships between mechanical and compositional properties at the tissue-level. Mineral to matrix ratio correlated negatively with hardness and creep viscosity series in 19 month old bones, but positively with modulus, creep modulus parallel and creep viscosity parallel in 4 or 5 month old bones. The reason that mineralization was negatively associated with mechanical properties in 19 month old but not 4 or 5 month old bones could be due to significantly higher mineralization in the 19 month old specimens.

Cross-linking ratio was negatively correlated with modulus, hardness, creep modulus parallel, creep viscosity parallel and creep viscosity series in 4 or 5 month old bones but showed no significant correlation with any mechanical property in 19 month old bones. These relations between mechanical properties and cross-linking ratio within skeletally mature young mice may have been driven by the marginal decrease in cross-linking ratio in 5 month old femora compared to 4 month old femora. These results suggest that in bones nearing skeletal maturity, mineralization makes the tissue stiffer and less viscoelastic while cross-linking maturity has the opposite effect on those properties and also decreases hardness and resistance to viscoplastic creep.

Cross-linking ratio is conventionally thought to increase with tissue maturity, as immature cross-links become mature cross-links and thereby improve mechanical properties [36]. Therefore, at first inspection, our data showing negative correlations between many mechanical properties and cross-linking (Table 2) may appear to contradict conventional thought. However, this presumption is most often based on observations from newly formed bone or bone that has been perturbed by chemical treatment, genetic disruption, or enzymatic and dietary interventions. In unperturbed adult bone, there has been no demonstrated positive association between maturation of enzymatic cross-linking and mechanical properties [37–41]. On the contrary, increased cross-linking ratio has been associated with osteoporotic fractures and spontaneous fractures in premenopausal women with normal bone mass [42, 43]. It could also be possible that an increase in the cross-linking ratio reflected a reduction in reducible cross-links without changing the number of non-reducible cross-links [44]. Further, not all changes to collagen cross-linking are described by the spectroscopic cross-linking ratio [36]. While this ratio has been associated with specific enzymatic cross-links, it is still possible that other changes to collagen, such as altered collagen organization or the formation of non-enzymatic cross-links, could affect the cross-linking ratio. These changes have also been associated with significantly compromised mechanical properties in bone [37, 39, 40].

While cross-linking ratio was also correlated with mechanical properties in 4 or 5 month old bones, only MMR was significantly or marginally correlated with any mechanical property in 19 month old bones. While increased mineralization can improve the strength and stiffness of poorly mineralized immature bone [45], further increases in mineralization or crystal size could make bone brittle and weak [7]. The relation between mineralization and hardness, which represents the bone’s resistance to plastic deformation at its surface, particularly demonstrates the possibility of a threshold before mineralization negatively impacts hardness (Figure 2a). For values of MMR below 10, there is no correlation with hardness, but for MMR values above 10 which only occur in 19 month old bones, there is a significant negative correlation with hardness.

Plasticity index was the exception to the disparity between 4 or 5 month and 19 month old bones in compositional-mechanical correlations, and was positively correlated with mineralization across all age groups and all degrees of mineralization (Figure 2b). However, the reason that mineralization was associated with plasticity index may be different in skeletally mature young and old bones. In 4 or 5 month old bones, mineralization was also significantly associated with increased elastic modulus and viscoelastic modulus (Table 2), which could increase plasticity index by decreasing the elastic and viscoelastic storage of work. Alternatively, the association between mineralization and plasticity index in 4 or 5 month old bones may have been dependent on carbonate substitution, which is highly correlated with mineralization and could increase plasticity index by making the bone crystals more amorphous and less tough [7]. In 19 month old bones, mineralization was associated with decreased resistance to viscoplastic creep, which would increase plasticity index by increasing the amount of permanent plastic deformation during the hold period at maximum load.

Non-linear classification analyses were performed with either Raman or nanoindentation metrics as dependent variables. It was again observed that the associations between compositional and mechanical metrics were different for each age class. This suggests that changes in compositional characteristics may be responsible for alterations in mechanical properties and vice versa. Not only are composition and mechanical properties important for defining tissue-level function, but also the associations among them. Further, it is possible that there might be unmeasured changes in other factors that influence composition and mechanical properties individually at the tissue-scale. Such factors could be non-enzymatic cross-linking, collagen organization, disruption of non-collagenous proteins, or accumulation of microdamage, all of which may depend on the age of the tissue [37–40, 46–49].

Raman and nanoindentation metrics were combined to assess whether simultaneous analysis of multiple metrics produced more accurate classification than any single metric. The visual nonlinear multidimensional classifications confirmed that it is unlikely for a single variable (compositional or mechanical) or a single analytical technique (Raman or nanoindentation) to provide complete information about bone material properties and their transformation through various stages of aging. Interestingly, the combination of Raman and nanoindentation variables in a non-additive fashion provided the best classification performance in both 2-age and 3-age classes. Different combinations of variables were selected depending on the classification problem. The variables containing the most discriminative information for the 2-age class data set were MMR and plasticity index, each appearing in greater than 25% of top 100 projections. MMR, crystallinity, modulus, hardness, cross-linking and plasticity index appeared in 25% or greater of top 100 projections in the 3-age class data set. While MMR and crystallinity distinguished specimens from the 19-month old group, the 4-month old (nearing skeletal maturity) and 5-month old (skeletally mature) specimens exhibited similar tissue-level properties as measured by nanoindentation. This is in agreement with an earlier finding in C57BL/6 mice that material properties appeared to reach peak values at 4 months and did not increase significantly past 4 months, in contrast to cross-sectional femur geometry which continued to increase up to 5 months [21]. As the difference between the two age groups is small, suitable classification required information from more variables in the projection.

Although none of the mechanical properties showed a discernible main independent effect, their inclusion in the classification schemes shows that they may influence bone material properties by acting synergistically or antagonistically. The inclusion of exercise marginally improved the classification performance, although it was not included in the top ranking variables. It should be noted that exercise was only a marginal contributor in the multivariate linear model (table 2) and did not exhibit a significant main effect. Hence, it is likely that interactions between variables were taken into account even when there were no significant main effects individually.

Knowledge of such sets of metrics may serve as a guide to probe into the biological mechanisms underlying the maintenance of tissue-level material properties in bone. Sorting out the nature of interactions in multi-dimensional space to infer biological relevance remains an interpretative challenge. Nonetheless, our classification results have their own biologic plausibility. In newly formed bone, mechanical competence is established by a rapid increase in mineralization and cross-link formation [50]. As bones near skeletal maturity (4 months), mechanical properties are also improved [21]. After skeletal maturity (5 months), tissue-level mechanical competence may be fully realized and increasing mineralization or cross-linking may not impart any further benefit [19]. However, as growth proceeds (19 months), some threshold might be reached at which further increases in mineralization and possibly cross-linking will have detrimental effects on mechanical competence [19].

The advantages of multidimensional approaches arise from the recognition that many important composition-mechanics relationships are non-linear. By not assuming independence or linearity of variables, interactions or associations between variables are taken into account when the variables are ranked by importance. Thus, not only the main effects in a data set but also the variables with weak to small effects that mainly contribute by interactions can be detected. Further, the visualizations directly use the original variables, unlike multidimensional scaling or partial least squares approaches that use their computed combinations [51, 52]. Different machine learning techniques can be applied at different steps, depending on the goal and preferences of the researcher. For instance, instead of radial multidimensional visualization, other methods that take variable interactions into account can be used. Classification techniques other than k-NN can also be substituted. The classifier performance can be further improved through preprocessing by data transformation. For instance, logarithmic transformation and normalization methods can be used to stabilize variance in the data set and thereby, improve classification accuracy.

The advantages of using a non-linear multidimensional technique come at a price, as this approach is not suitable for modeling the interactions or non-linear relationships between variables. However, techniques such as information theory based approaches, Bayesian model selection and pathway analyses are available to analyze the functional form of the underlying relationships. The analyses performed in this study were limited to three ages at which compositional and mechanical properties were measured. A within-study cross-validation design was employed due to the nature of the data set, although an internal validation method called bootstrapping was used to avoid inflated estimates of classification accuracy. We do not expect that a satisfactory non-linear model that can predict age-related changes in bone function can be developed, as it would not fully explain the age-related changes in bone material properties. However, we demonstrate that by integrating composition and mechanical information, discriminatory accuracy was increased from 59–79% to 86–96%.

The study of structure-function relationships in bone will benefit from adding additional age groups and measurements of mechanical, structural, chemical, morphological, biological and other properties across multiple scales using multiple techniques and performing external validations. Despite the limitations outlined above, the results suggest that it may be possible to derive sets of metrics that explain aging effects on the material properties of bone, given a large enough data set. Unlike regression based methods, machine learning approaches will also allow more input variables (or features) than samples. The methodology of variable selection incorporating established biological information can be applied to studies involving any measurable distinction in bone quality due to aging, disease or other factors. Indeed, the recent study of Zebaze et al. reinforces the need to use a set of measures rather than a single measure to develop a better understanding of bone quality and mechanics [53]. In reporting a weak correlation between tissue mineral density and elastic modulus in human cortical bone, the authors caution against the popular practice of using only mineral density as a surrogate for elastic modulus.

In summary, this study demonstrates that the mechanical consequence of compositional changes in bone may depend on the age and initial compositional state of the bone. The mechanical correlations with cross-linking were particularly strong in skeletally mature young bones. However, in skeletally mature old bones, mineralization was the dominant predictor of mechanical competence and was negatively correlated with mechanical properties. These results highlight the potential utility of using bone compositional measurements in diagnosing skeletal fragility, but also show the difficulty in making assumptions about the linearity of the effects of compositional changes in bone. So, a novel approach using the statistical combination of Raman spectroscopic and nanoindentation measures was adopted to analyze the age-dependent nonlinear interdependence between compositional and mechanical properties. Our results demonstrate that a few non-linearly combined compositional and mechanical variables provide better discriminatory information than single variables. Classification was better for the 2-age class data set than for the 3-age class data set, because the 4-month and 5-month old specimens exhibited similar material properties. We believe that this approach, while hypothesis generating and needing further validation and inclusion of multi-scale and multi-technology measures, can provide insight into factors affecting the quality of bone. Such combined measures would be more likely to offer better sensitivities and specificities than individual markers and single out critical features that are relevant for diagnostic purposes.

Research Highlights.

• Mechanical consequence of compositional changes in bone may depend on the age and initial compositional state of the bone; difficult to assume linearity of the effects of compositional changes

• Data mining to assess non-linear interdependence between compositional and mechanical properties in murine femora as a function of age

• Unlikely for a single measure (Raman or nanoindentation) to sufficiently classify how aging manifests itself at the tissue-level; non-linear combined measures offer better sensitivity and specificity

Appendix 1

A.1. Multidimensional visualization

A variety of visualization algorithms are available for multidimensional data exploration [54]. Geometric projection techniques such as scatter plot matrices and parallel coordinates are often used to find informative projections of multidimensional data. The parallel coordinates technique maps n data dimensions onto two dimensional space by drawing n equally spaced axes, each corresponding to a data dimension [55]. Each data element is displayed as a line passing through the dimensions or axes. For large data sets, this leads to visual clutter and overlap of data points limiting the interpretability of the graphical model. Further, the order of the axes impacts how data patterns are understood. For instance, relationships between adjacent dimensions are easier to understand than between non-adjacent dimensions. These limitations can be minimized by arranging the axes on a circle on a two dimensional plane [56]. For n dimensional visualization, n lines, each associated with a dimension, emanate radially from the center of a circle and terminate at its circumference with equal angles between the axes. Each multidimensional data element is represented as a point inside the circle whose location is determined by its values for each dimension. This radial coordinate technique is well suited for visualization of a multidimensional data set in a compact form and offers intuitive interpretation of complex relationships among various dimensions or features.

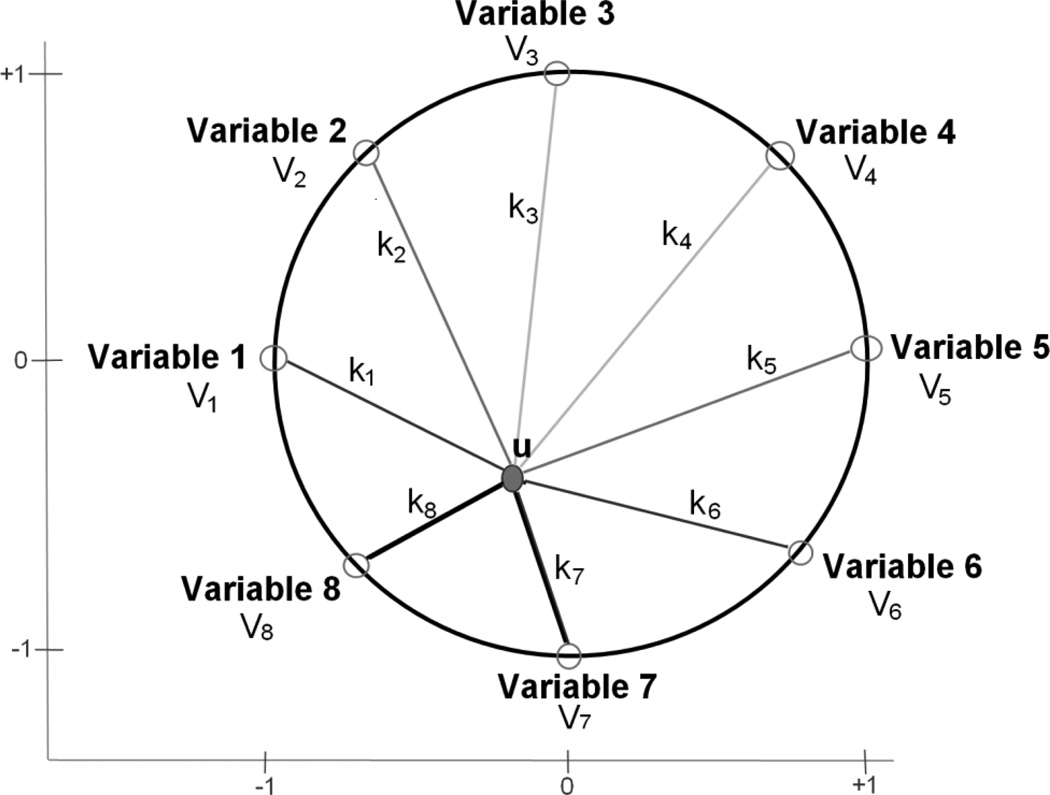
We briefly summarize the RadViz algorithm which is explained in greater detail elsewhere [57]. The data set consists of data values, x_ij, where i denotes the specimen number, and j denotes the variable number. The data for each variable j are standardized to the interval between 0 and 1 over all specimens, as follows:

$${\overline{x}}_{\mathit{\text{ij}}}=\left(x_{\mathit{\text{ij}}}-{\text{min}}_j\right)/\left({\text{max}}_j-{\text{min}}_j\right)$$ (1)

To project multidimensional data onto a two dimensional plane, the variables describing specimen characteristics are equally spaced around the perimeter of a circle, as shown by points V_j in figure a. The normalized data value, x̄_ij, corresponding to each variable j for a specimen i is considered to be the influence parameter, k_ij. The sum of all influence parameters corresponding to variables V_j acting on a specimen i as given by:

$$k_i={\displaystyle \sum _{j=1}^n}{k}_{\mathit{\text{ij}}}={\displaystyle \sum _{j=1}^n}{\overline{x}}_{\mathit{\text{ij}}}$$ (2)

Fig a.

RadViz representation of the positioning of a specimen point, u, based on the influence, k_j, of each its eight variables, V_j, where j = 1 to 8.

Each specimen i is then mapped onto a single point, u_i, inside the circle at which all its variable influences are balanced. This can mathematically be represented as:

$${\displaystyle \sum _{j=1}^n}(\left({\mathbf{V}}_j-{\mathbf{u}}_i\right)·k_{\mathit{\text{ij}}})=0$$ (3)

The position, u_i = (u₁, u₂), for each specimen i inside the circle is then given by:

$${\mathbf{u}}_i=({\displaystyle \sum _{j=1}^n}\left({\mathbf{V}}_j·k_i\right))/k_i$$ (4)

Equation 3 has the same functional form as that of Hooke’s law of elasticity. A physical metaphor for this algorithm would be multiple springs connecting a specimen point inside the circle to its variables (loads) on the circle perimeter. The spring equation relates the spring force to the displacement of the spring (equivalent to |V_j| − |u_i|) by a spring constant (equivalent to k_ij). For the case of a single spring connecting specimen point u to variable V₁ in figure a, the spring force is the product of spring stiffness and spring displacement, given by:

$$f_1=k_1·d_1$$ (5)

By balancing all such spring forces acting on a specimen, the equilibrium position of the specimen point, u_i, can be located. In the RadViz illustration in figure a, the spring constant, i.e., stiffness, is higher for variables 7 and 8 (black springs) and lower for the other variables (grey springs). Hence, the specimen point is positioned closer to variables 7 and 8 than the others. If all springs had equal stiffness values, then the specimen point would be placed close to the center. Thus, RadViz produces an intuitive display of the multidimensional data and preserves the correlation between variables in the original multidimensional data set. The specimen points visualized by RadViz are described uniquely by their x-y position and could carry class labels, if any. RadViz also makes it easy to spot clusters and outliers in the data set. For larger data sets where specimen points could potentially overlap, PolyViz, a polygon visualization method, can be used [58].

A.2. Variable selection and classification

For a given set of n variables, m variables can be selected in C(n, m) unique ways and the selected subset of m variables can be ordered around the circle in (m−1)!/2 unique projections. For instance, each specimen in this data set is described by eleven variables which include four Raman and seven nanoindentation measures. When we evaluate possible RadViz projections that show 6 of total 11 variables, the 6 variables can be chosen in C(11, 6) different ways. Each selection of 6 variables can then be ordered around the circle in 5!/2 different ways. Hence, a total of 27720 (462 selections * 60 orderings) unique RadViz projections are possible in this case. To find useful and informative projections of class-labeled data involving 6 variables, these 27720 RadViz projections have to be evaluated and scored by their ability to discriminate between classes. The classification quality (score) is the predictive accuracy of k-nearest neighbor (k-NN) classifier on the RadViz data set.

The VizRank algorithm employs a feature selection method, ReliefF, to choose optimal subsets of original variables which will still contain information necessary for the classification task, while reducing the computational burden imposed by too many variables [31]. ReliefF employs a statistical approach to estimate the importance of variables (discrete or continuous) based on their ability to distinguish between similar examples belonging to different classes and without assuming independence of variables [59]. Hence, ReliefF provides a statistical measure of variable quality and identifies top ranked variables in the data set that predict class primarily through dependencies or interactions with other variables.