Non-Homogeneous Stereological Properties of the Rat Hippocampus from High-Resolution 3D Serial Reconstruction of Thin Histological Sections

Abstract

Integrating hippocampal anatomy from neuronal dendrites to whole-system may help elucidate its relation to function. Towards this aim, we digitally traced the cytoarchitectonic boundaries of the dentate gyrus (DG) and areas CA3/CA1 throughout their entire longitudinal extent from high-resolution images of thin cryostatic sections of adult rat brain. The 3D computational reconstruction identified all isotropic 16 µm voxels with appropriate sub-regions and layers (http://krasnow1.gmu.edu/cn3/hippocampus3d). Overall, DG, CA3, and CA1 occupied comparable volumes (15.3, 12.2, and 18.8 mm³, respectively), but displayed substantial rostro-caudal volumetric gradients: CA1 made up more than half of the posterior hippocampus while CA3 and DG were more prominent in the anterior regions. The CA3/CA1 ratio increased from ~0.4 to ~1 septo-temporally, due to a specific change in stratum radiatum volume. Next we virtually embedded 1.8 million neuronal morphologies stochastically resampled from 244 digital reconstructions, emulating the dense packing of granular and pyramidal layers, and appropriately orienting the principal dendritic axes relative to local curvature. The resulting neuropil occupancy reproduced recent electron microscopy data measured in a restricted location. Extension of this analysis across each layer and sub-region over the whole hippocampus revealed highly non-homogeneous dendritic density. In CA1, dendritic occupancy was >60% higher temporally than septally (0.46 vs. 0.28, s.e.m. ~0.05). CA3 values varied both across subfields (from 0.35 in CA3b/CA3c to 0.50 in CA3a) and layers (0.48, 0.34, and 0.27 in oriens, radiatum, and lacunosum-moleculare, respectively). Dendritic occupancy was substantially lower in DG, especially in the supra-pyramidal blade (0.18). The computed probability of dendro-dendritic collision significantly correlated with expression of the membrane repulsion signal DSCAM. These heterogeneous stereological properties reflect and complement the non-uniform molecular composition, circuit connectivity, and computational function of the hippocampus across its transverse, longitudinal, and laminar organization.

INTRODUCTION

The hippocampus plays a prominent role in spatial navigation and episodic memory processes (Scoville and Milner, 1957; O'Keefe and Nadel, 1978; Morris et al., 1982; Squire and Zola-Morgan, 1991; Eichenbaum and Cohen, 2001). The main hippocampal areas, dentate gyrus (DG) and Cornu Ammonis (CA3 and CA1), have distinct anatomy (Lorente de No, 1934; Amaral et al., 1990) and functions (Vazdarjanova and Guzowski, 2004; Treves, 2004; Kunec et al., 2005; Leutgeb et al., 2007). Neurons from DG, CA3, and CA1 display different molecular, morphological, and physiological properties (Ishizuka et al., 1995; Granger et al., 1996; Cannon et al., 1999; Newrzella et al., 2007; Datson et al., 2009). A growing literature suggests that the genetic makeup and cognitive involvement of the hippocampus may be highly heterogeneous even within these areas (Moser and Moser, 1998; Fanselow and Dong, 2010). Specifically, recent biochemical analyses demonstrated clear septo-temporal gradients in each hippocampal area (Leonardo et al., 2006; Thompson et al., 2008; Dong et al., 2009; Greene et al., 2009), paralleling behavioral and electrophysiological differentiation (Bannerman et al., 1999; Kesner, 2007; Hunsaker and Kesner, 2008; Hunsaker et al., 2008; Royer et al., 2010). Neuronal morphology and numerical density also vary septo-temporally in DG, CA3, and CA1 principal cells (Claiborne et al., 1990; Rihn and Claiborne, 1990; Turner et al., 1995; Pyapali et al., 1998; Ahmad et al., 2002; Daisu et al., 2009; Jinno and Kosaka, 2009).

Such evidence suggests that regional volumes and dendritic occupancy may also follow similar heterogeneous patterns. These stereological properties constrain network connectivity (Ropireddy and Ascoli, 2011) and therefore are relevant to the structure-function relationship. The dense packing of somata in the principal cell layers and of neuropil elsewhere implies a tight association between volume distributions and dendritic occupancy (Chklovskii et al., 2002). Hippocampal lamination confines distinct axonal projections to specific cytoarchitectonic layers (Forster et al., 2006), as recently reviewed (van Strien et al., 2009). Briefly, entorhinal stellate cells project through the perforant pathway to the middle and distal third of granule cell dendrites in the dentate molecular layer. The perforant pathway also projects to the distal dendrites of CA3 pyramidal neurons in the lacunosum-moleculare layer. The granule cells project to the CA3 pyramidal neurons through mossy fibers and the CA3 pyramidal neurons project to the CA3 and CA1 neurons through recurrent and Schaffer collaterals respectively (Witter and Amaral, 2004). The recurrent collaterals synapse on the CA3 dendrites on the basal and apical dendrites in the oriens and radiatum layers, respectively. The Schaffer collaterals synapse on the CA1 apical and, to a lesser extent, basal dendrites.

Volumetric measurements are conventionally estimated from histological sections by randomly sampling from particular regions of interest (Schmitz and Hof, 2005), such as individual areas and/or layers (Boss et al., 1987; West, 1990; Tinsley et al., 2001; Geinisman et al., 2004; Akdogan et al., 2008) or the complete hippocampus (Schmitt et al., 2004). Dendritic occupancy can be measured by dense electron microscopy reconstruction (Chklovskii et al., 2010), but the labor intensity and restricted coverage field of this high-resolution technique have so far limited data collection to a contained CA1 mid-radiatum location (Mishchenko et al., 2010). These limitations and the statistical nature of unbiased stereolology have practically prevented a complete analysis across the entire hippocampus of the subregional and laminar differences in volume distributions and dendritic occupancy. To the best of our knowledge, regional volumes have been estimated only once before by layer segmentation over the entire longitudinal extent of the rat hippocampus (West et al., 1978). However, this earlier study did not attempt a full three-dimensional (3D) reconstruction, which is necessary to extract measurements along directions other than parallel and perpendicular to the slicing plane.

Here we describe the creation of a cellular-level 3D hippocampal model by serial tracing of high resolution thin histological sections of rat brain and dense digital embedding of reconstructed neuronal morphologies. We quantified the volumetric distributions and dendritic occupancy across the layers and subregions of the hippocampus relative to canonical brain coordinates and hippocampal axes. Our finding of highly heterogeneous stereological properties may offer novel insight into the functional organization of the hippocampus.

MATERIALS AND METHODS

Experimental Procedure and Raw Image Acquisition

Four male Long-Evans hooded rats (22 day old, 226–237 g; Harlan, Indianapolis, IN) were housed in metal wire-hanging cages at 22–24 °C on a 12 h light/dark cycle (lights on at 0700 h) with access to ad libitum food and water. Animal care was in accordance with George Mason University and National Institute of Health Guide for the Care and Use of Laboratory Animals guidelines. Animals were sacrificed by decapitation with a guillotine when 45 days old. The brains were quickly removed, frozen in powdered dry ice, and stored in air-tight ziplock plastic bags at −80 °C until sectioning. Brains were sectioned coronally at 16 µm on an IEC Minotome Microtome cryostat at −18 °C in three different directions. Two brains were sectioned dorso-ventrally, one ventro-dorsally, and one latero-medially. For each brain, the coronal sections encompassing the entire extent of the hippocampus were mounted on gelatin-subbed glass slides, thionin-stained with a standard protocol (Wouterlood, 1993), and cover-slipped. Of the four datasets, those sectioned dorso-ventrally displayed the least tissue distortion in the hippocampal region and were selected for digital tracing and 3D reconstruction of the cytoarchitectonic boundaries (Fig. 1). The hippocampal region had a rostro-caudal span of 4.35 mm, corresponding to 272 slices. A total of 290 sections (including 12 and 6 extra ones on the rostral and caudal ends, respectively) were imaged on an EPSON 3200 dpi scanner and contrast enhanced with the Matlab routine ‘imcontrast’.

Figure 1. Cytoarchitectonic segmentation of hippocampal regions and layers in the coronal plane.

A) At the most rostral level, the dorsal hippocampus (septal pole) appears first (enlarged in a1). B) Moving from rostral to caudal, the ventral hippocampus (temporal pole) appears next. C) At the most caudal level, the dorsal and ventral regions merge into the posterior hippocampus. In all panels, different shades of blue (CA3/CA1) and red (DG) denote the layers: hilus, granule cell (GC), molecular (ML), pyramidal (PC), radiatum (RAD), lacunosum-moleculare (LM), and oriens (OR). Scale bars in panels A, a1, and B are 4.0, 0.50 and 3.0 mm, respectively. The insets (adapted from Swanson, 2003, with permission from Elsevier) indicate the rostro-caudal position of each coronal plane.

To evaluate shrinkage and distortion in the sectioning plane, we acquired whole mount pictures of the block face prior to slicing for the 10 middle sections of the acquired series (slices 140–150) using a Kodak digital camera at 300 dpi resolution (Fig. 2A). Planar shrinkage was estimated under isotropic assumption as the ratio of the area difference between the block face (A_B) and the histological Nissl (A_N) images to the area of the block face image (Fig. 2A). The resulting mean value was 7.0% (s.e.m. 0.8%, N=10). The 10 histological Nissl images were then scaled to correct for their individual planar shrinkages and manually overlayed onto corresponding block face pictures to maximize visual overlap. Distortion was defined as the ratio of the area difference between the block face image and the overlap area image (A_O) to the area of the block face image (Fig. 2A). The resulting mean was 1.5% (s.e.m. 0.1%), which we consider reassuringly modest. All measures described below were corrected for the same average planar shrinkage of 7%. Shrinkage was not estimated in Z because the nominal sectioning value (16 µm) was used as interslice distance in all subsequent analyses.

Figure 2. Experimental set-up and digital representation.

A) Planar shrinkage and distortion are computed from the surface areas of the block face (A_B) image, Nissl scan image (A_N), and the overlap between block face and scaled Nissl scan images (A_O). B) Representative tracing of a cytoarchitectonic area. The granule cell layer (top row) is traced with a set of points (magnified on the right) representing the boundary contour as a closed polygon, which is further processed by triangulation and filling (bottom row).

For comparison, we used an ex-vivo magnetic resonance microscopy (µMRI) dataset of an excised rat brain (Lester et al., 2002). The µMRI image stack consisted of 50 consecutive coronal images, kindly provided by Dr. David S. Lester (U.S. Food and Drug Administration, Rockville, MD, USA) with a pixel size of 47 µm and and inter-image distance of 94 µm.

Data Digitization: 3D Hippocampus Model Reconstruction

For digital tracing, image stacks were loaded into Reconstruct (Fiala, 2005; http://synapses.clm.utexas.edu/tools/reconstruct/reconstruct.stm) with appropriate pixel/µm conversion factor (4.28). Images were manually registered by mid-line guided alignment (Cohen et al., 1998). Identification of seven cytoarchitectonic layers was validated with two independent rat atlases (Paxinos and Watson, 1986; Swanson, 2003): hilus, granule cell layer (GC), and molecular layer (ML) in Dentate Gyrus (DG); and oriens (OR), pyramidal cell (PC), radiatum (RAD), and lacunosum-moleculare (LM) layers in Cornu Ammonis (CA3 and CA1). In one dataset, we traced inner and outer boundaries of all seven layers through the entire rostro-caudal extent of the left hippocampus. Sections with insufficient image quality (totaling 42) were interpolated based on adjacent slices. In a second dataset, we also traced inner and outer boundaries of all seven layers, but only within the middle third of the hippocampal rostro-caudal extent. The CA3 lucidum and CA3/CA1 alveus were not traced. Subicular layers were also traced but not analyzed because of their less clear identification. In the µMRI dataset, due to lower contrast compared to Nissl, only the cellular (PC, GC) and outer (OR, ML) layers of the dorsal hippocampus could be reliably traced.

Serial tracing of each section produced sets of pixels representing layer boundaries as closed polygons (Fig. 2B). All pixels inside each individual contour, corresponding to inner spatial locations of the respective cytoarchitectonic regions, were identified by triangulation (Fig. 2B) using circular linked lists (Kernighan and Ritchie, 1998). This ‘filling’ algorithm, written in C++ (Ropireddy et al., 2008), is applicable to both convex and concave polygons and was extended further to obtain 3D voxels from neighboring slices, analogous to the marching cube approach (Lorensen and Cline, 1987).

The hippocampus outer contours (lacunosum-moleculare and oriens in CA3/CA1, molecular and hilus in DG) in each traced section were used to refine the manual registration. First, several zones were manually identified along the rostro-caudal progression based on discontinuous geometrical changes of these boundaries (Fig. 1). For example, ventral hippocampus starts at approximately one-third rostro-caudal extent (anterior-posterior position −4.16 mm in Paxinos and Watson, 1986). The dorsal and ventral hippocampus regions merge just after the rostro-caudal midpoint (anterior-posterior position −4.80 mm in Paxinos and Watson, 1986), marking the beginning of the posterior hippocampus. The registration of sections within each zone was then separately fine-tuned by iteratively applying a three-point average to the centroid location of the hippocampus outer contours until each zone reached geometric convexity or concavity. Translating every section according to the resulting centroid coordinates ensured smooth 3D zone boundaries. Finally, the separate zones were manually adjusted to achieve satisfactory inter-zone registration. The final longitudinal centroid series was taken to define the septo-temporal axis.

Surface/Volume Representation and Analysis

The digital architecture resulting from the above process can be rendered by a set of surfaces encompassing the outer boundaries of the hippocampus as well as its inner cytoarchitectonic divisions. Alternatively, the same data can be represented as sets of locations spanning each of the regional volumes. Surface rendering is particularly amenable to two-dimensional display and three-dimensional virtual reality exploration (Fig. 3). Volumetric representation enables the direct implementation of stereological analyses as well as a complementary visualization style. The triangulation algorithm described above can fill space with pixels of arbitrary size. In order to maintain 3D isotropy (cubic voxels), the resolution was set to the nominal cryostatic section thickness of 16 µm, resulting in over 10 million discrete locations.

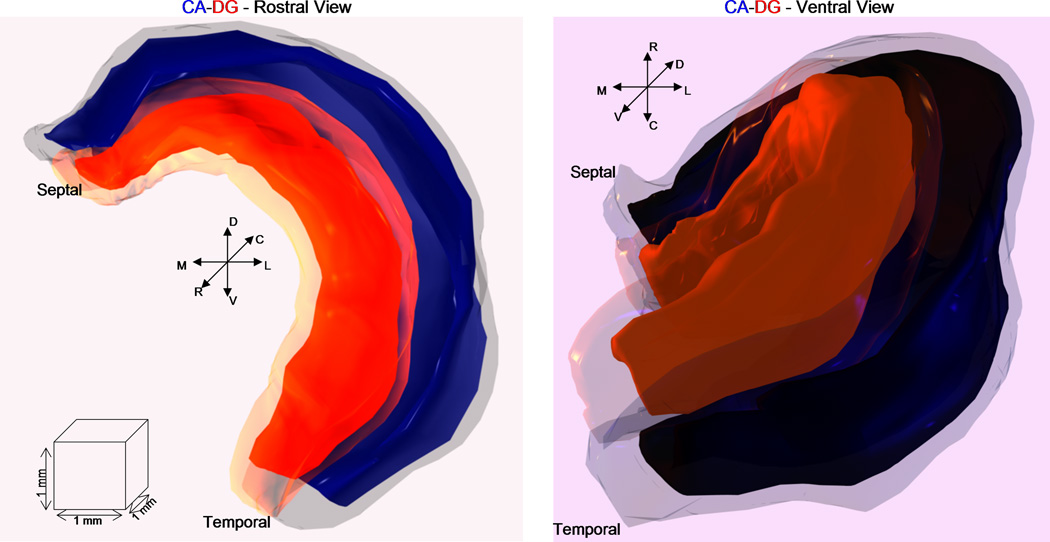
Figure 3. Hippocampus 3D renderings.

Rostral (left) and ventral (right) views of the 3D hippocampal reconstruction with CA and DG rendered in blue and red, respectively. For each region, two surfaces are shown: the outer ones (lighter shades) correspond to the overall boundaries, whereas the internal ones (darker shades) represent the principal cell layers.

In the volumetric representation, the three dimensions of each voxel location correspond to Cartesian axes perpendicular to the canonical brain planes (coronal, sagittal, and horizontal), respectively rostro-causal, dorso-ventral, and medio-lateral. Additionally, each voxel was mapped onto a complementary coordinate system relative to the hippocampus reference frame, i.e. denoting septo-temporal, transverse, and depth (layer) positions. The septo-temporal coordinate was taken as the distance from the septal end along the longitudinal series of centroids defined by the tracings after registration. To define the transverse and depth coordinates, we first generated 60 virtual transverse planes at uniform distances along the septo-temporal axis. In particular, for every such position, we selected all voxels perpendicular to the longitudinal direction. In each of these equidistant reference planes, the voxels corresponding to the principal cell layers (granular in DG and pyramidal in CA) displayed the classic double ‘C’ shape of hippocampal cross-sections. In every generated plane, the transverse position was defined as the distance along these layer centroids from the suprapyramidal tip in DG and from the CA3c end in CA. Depth was defined as the distance on each of these planes along the line perpendicular to the transverse position from the first voxel toward the hilus in DG and toward the oriens in CA. The mapping of all voxels in the hippocampus to these septo-temporal, transverse, and depth coordinates was completed by assigning to each voxel the coordinates of its projection to the nearest of the 60 reference transverse planes.

Based on this six-dimensional dual reference system, we further catalogued all voxels with common labels. In particular, each voxel was assigned bregma position and lambda or inter-aural distance corresponding to the stereotaxic coordinates of the closest locations in reference atlases (Paxinos and Watson, 1986; Swanson, 2003). Moreover, voxel layer identities were tagged along the transverse axis as belonging in DG to either the infra- (‘I’) or supra-pyramidal (‘S’) blades and in CA to CA3c (near the hilus), CA3b, CA3a, CA2, CA1c, CA1b, and CA1a (near the subiculum). As a result of this processing, each voxel is stored with 3 Cartesian coordinates, 3 hippocampal coordinates, 2 stereotaxic coordinates, and a tag denoting one of 9 subregions and 7 layers. Using such a database, the volume of each identified cytoarchitectonic subregion and/or layer can be measured along any of the common brain or hippocampus anatomical coordinates by simple voxel count. The three hippocampal coordinates in this voxel database were computed based on the 60-reference transverse planes described above. The reference atlases were referred to for mapping the two stereotaxic coordinates by comparing the coronal sections in the atlases to the closest traced sections in the 3D model. Paxinos & Watson, (2006) discuss the variability in the stereotaxic coordinates between different ages and strains, mentioning (page × of the introduction) that the atlas can successfully be used with male or female rats of different strains, with weight ranging from 250 to 350 g. The weight range of the Long-Evans rats used in this study falls within ~5% from the lower bound.

Three-Dimensional Embedding of Neuronal Reconstructions

To augment and integrate the 3D hippocampus model with cellular-level information, we populated it with a realistic number of digital reconstructions of neuronal morphologies with appropriate spatial distributions. Previous efforts in the dentate gyrus were limited to surface representations not amenable to stereological analysis (Scorcioni et al., 2002). The following subsections describe the methodology to (i) empirically estimate the numerical density of neurons and assess its gradients in our experimental data; (ii) map the location of suitable dendritic reconstructions in voxel coordinates, and stochastically sample neurons with proper orientations in the 3D hippocampus model; and (iii) analyze dendritic spatial occupancy, overlap, and direction.

(i) Neuron Density Estimates and Gradients

Realistic embedding of neurons in the 3D model requires determining the number of cells to distribute. Although the hippocampal principal cell layers are typically assumed to be largely filled with somata, the exact neuron number cannot be derived from the granular and pyramidal layer volumes without knowledge of the somatic diameter, shape, and packing density. The neuron number reported in the literature for the rat hippocampus depends greatly on the animal strain and age (Hosseini-Sharifabad and Nyengaard, 2007; Boss et al., 1987; West, 1990; West et al., 1991). Here we use the available data for the appropriate strain (Long-Evans) and age group, i.e. 1.2 million granule, 225,000 CA3 pyramidal, and 390,000 pyramidal neurons (Rapp and Gallagher, 1996).

Recent reports have also demonstrated clear gradients in numerical density along the mouse hippocampus (Jinno and Kosaka, 2009), with considerably higher dorsal than ventral values (e.g. 3-fold for CA1 principal neurons). Previous research in different rat strains and ages yielded inconclusively conflicting results, from complete lack of dorso-ventral differences (West et al. 1991), to significant dorso-ventral differences in CA1 but not CA3 (Daisu et al. 2009). Since no spatial gradient data were reported for young adult Long-Evans, we performed an unbiased cell count from the dorsal and ventral principal layers of CA3, CA1 and DG directly in our tissue. We used the optical fractionator probe (Schmitz and Hof, 2005) using MicroBrightField StereoInvestigator (mbfbioscience.com) on an Olympus BX51 microscope equipped with an achromatic 100× oil immersion lens with a numerical aperture of 1.25.

We found a significant numerical density gradient in CA1, with a 1.27 dorsal/ventral ratio, but no statistical dorso-ventral differences in DG and CA3. Thus, we embedded granule cells and CA3 pyramidal cells uniformly in their respective principal layers, and using a linear dorso-ventral gradient in CA1 corresponding to the observed numerical density ratio. To produce the correct density, one granule cell was allocated in each of the DG granular layer 890,000 voxels, and a second granule cell was added in 25% of those locations. In CA3, a pyramidal cell was allocated in a random 37% sample of the 730,000 principal layer voxels. In CA1, the fraction of the 540,000 pyramidal layer voxels selected for cell embedding decreased from 71% dorsally to 45% ventrally.

(ii) Sources, Stochastic Sampling, and 3D Orientation of Digitized Dendritic Arbors

The digital reconstructions of 244 dendritic morphologies of hippocampus principal neurons were downloaded from NeuroMorpho.Org (Ascoli et al., 2007). These were all and the only DG granule and CA pyramidal cells available from young adult rats in control conditions with complete 3D dendritic arbors at the time of this work. NeuroMorpho.Org adopts a rigorous protocol of quality control and editing to correct the most common morphological errors and data inequalities (Ascoli et al., 2007). While not all reconstructions can be assumed to be of equal quality, all these morphologies were carefully inspected and judged to be suitable for the present analysis. In specifying the anatomical location of these reconstructions, the original references reported either stereotaxic bregma/lambda coordinates (typically for preparations from brain slices) or the septo-temporal and transverse positions (for preparations from excised hippocampus). This common usage could be directly mapped onto our reference framework by selecting a range of voxels corresponding to the reported locations. Such mapping was used as described below to stochastically resample the neurons during the embedding process. When no detailed positional information was documented, which was the case for 53 reconstructions, cell bodies were assumed to be located anywhere within the principal layer of their respective field.

In DG, 81 granule cells were selected from the Claiborne and Turner archives of NeuroMorpho.Org. The Claiborne cells (Carnevale et al., 1997; Rihn and Claiborne, 1990) were located within the middle third of the septo-temporal axis and 39 of these cells had additional information on the depth and position in the supra-pyramidal blade. In CA3, the 54 pyramidal cells came from five archives: 20 from Amaral, 8 from Barrionuevo, 4 from Claiborne, 6 from Jaffe (Jaffe and Carnevale, 1999), and 16 from Turner. Forty-eight of these reconstructions specified the subfield (CA3c, CA3b or CA3a). The Amaral data included comprehensive details of the transverse and depth positions in the middle third of the septo-temporal axis (Ishizuka et al., 1995). The Barrionuevo neurons (Henze et al., 1996) were from CA3b only. The Claiborne pyramidal cells came from CA3c in the middle septo-temporal third. Turner had reconstructions from each of the 3 CA3 subfields and reported individual septo-temporal and transverse positions (Turner et al., 1995). In CA1, 109 pyramidal cells were identified from eight archives: Amaral (23), Ascoli (2), Claiborne (7), Gulyas (18), Spruston (3), and Turner (56). The Amaral and Claiborne CA1 neurons were all situated in the middle septo-temporal third. Amaral also relayed comprehensive positional information, specifying the subfield (CA1c, CA1b or CA1a) and transverse/depth locations in the middle septo-temporal third. No additional anatomical data were reported for neurons from the Ascoli (Brown et al., 2005) and Spruston (Golding et al., 2005) archives. The Gulyas (Megias et al., 2001) and Turner neurons (Pyapali and Turner, 1994; Pyapali and Turner, 1996; Pyapali et al., 1998) indicated the stereotaxic coordinates from in vivo cell labeling.

These digital neuromorphological reconstructions were embedded in the 3D hippocampal model through a probabilistic approach. For every voxel, we define the Available Neuronal Count (ANC) as the number of reconstructions with positional information consistent with that location. The positional information of every neuron i correspond to a definite number of voxels V_i: neurons with more precise localization match a stricter selection of voxels (lower V_i). To choose a particular reconstruction for embedding in a given voxel, each of the ANC neurons available at that location is assigned a relative sampling probability reciprocal to the number of voxels it matches. In this way, neurons with more precise localization are favored relative to neurons that can be sampled in a larger number of locations. The Available Neuronal Density Index (ANDI) for a given voxel is the sum of these relative sampling probabilities over all ANC neurons:

$$\mathit{\text{ANDI}}={\displaystyle \sum _{i=1}^{\mathit{\text{ANC}}}}(1/V_i).$$

Spatial maps were plotted using the R package ggplot2 (http://had.co.nz/ggplot2).

The pyramidal and granule cell reconstructions were oriented such that the principal axis of their dendritic arborization was perpendicular to the cellular layer and the secondary axis lay on the septo-temporal plane (Scorcioni et al., 2002; Ropireddy et al., 2008). To account for the natural variability observed in this general alignment (Claiborne et al., 1990; Ishizuka et al., 1995), the axes were stochastically tilted between 0 and 5 degrees around a random 0–360 degree rotation. The principal and secondary axes were computed relative to the soma by single value decomposition of the digital reconstructions using standard numerical recipes (Press, 1988). The dendritic tree lengths were scaled up or down so as to terminate at the respective boundaries (ML/LM for granule and pyramidal apical, and OR for basal trees). This scaling is required given that the embedded neuronal reconstructions came from different animals. Both granule and pyramidal cells are known to systematically reach, but not cross, the hippocampal fissure (Claiborne et al., 1990; Ishizuka et al., 1995). Dendritic length was scaled uniformly in 3D without changing the branch diameter. Virtual Reality Modeling Language files (Ames et al., 1997) were generated with the freeware viewer view3dscene (http://view3dscene.sourceforge.net).

(iii) Dendritic Spatial Occupancy, Overlap, and Direction Analyses

Dendritic spatial occupancy is the volumetric fraction of a given region/layer that is occupied by dendrites. This parameter is usually measured from electron micrographs limited to an extremely narrow field of view. Embedding the reconstruction in the 3D model according to the correct densities, gradients, and orientations (Rapp and Gallagher, 1996; Jinno and Kosaka, 2009) allows computing dendritic occupancy across the entire septo-temporal and transverse extent of the hippocampus. Our protocol parceled the hippocampus into “cell-boxes” corresponding to the average dimension of dendritic arbors. The pyramidal cell-box spanned 1/14 of the longitudinal extent and approximately corresponded transversally to subregions CA3c, CA3b, CA3a, CA2, CA1c, CA1b, and CA1a (Fig. 1a1). The granule cell-box spanned 1/26 of the longitudinal extent and compartmentalized the DG into Infra/Tip, Infra/Crest, Crest, Supra/Crest, and Supra/Tip sub-regions (Fig. 1a1). The probability of spatial collision among dendrites is proportional to the square dendritic occupancy. In order to relate this measure to molecular mechanisms of dendro-dendritic avoidance, we analyzed sagittal images of Down syndrome cell adhesion molecule (DSCAM) gene expression from the Allen Brain Atlas (Ng et al., 2009; mouse.brain-map.org). After segmenting the seven CA and five DG sub-regions, average relative intensity values were extracted with the ImageJ ‘image processing’ plug-in (rsb.info.nih.gov/ij).

The direction of dendritic segments was analyzed relative to the normal to the tissue curvature (along the primary axis of the arbors). Since 3D angular deviations do not add linearly, they first need to be transformed to compute common statistics. To this aim, we adopted from the field of material science the nematic order parameter (de Gennes and Prost, 1993), defined as S=0.5×(3×cos²θ – 1), where θ is the angle between a dendritic segment and the reference axis. The average and standard deviations of these values weighed by segment length over a given region and layer are then converted back to angular deviations. Note that the random isotropic solid angle, with no preferred orientation, is 55° rather than 45°.

Computational Details and Availability of 3D Model Data

All algorithms described above were developed in the C/C++ programming language under Fedora Core 8 Linux environment and executed on an eight-node cluster of Intel 3.0 GHz dual-Pentium IV processors. We are making the 3D hippocampus data freely available for download from http://krasnow1.gmu.edu/cn3/hippocampus3d. The distributed files include the raw high resolution coronal Nissl images in the whole rostro-caudal extent, the hippocampus segmentation (manual XML tracing) compatible with the Reconstruct tool (http://synapses.clm.utexas.edu/tools/reconstruct/reconstruct.stm), the entire voxel database with documentation explaining the brain-based and hippocampus-based coordinate systems, and the virtual reality (VRML) surfaces of the CA and DG cytoarchitectonic layers.

RESULTS

The reconstructed 3D hippocampus model (Fig. 3) spanned approximately 5 mm in the rostro-caudal axis and 7 mm both medio-laterally and dorso-ventrally. Along its internal coordinates, the maximum length was approximately 6 mm longitudinally, 6 mm transversally from CA3c to the CA1/subiculum border, and 4 mm transversally from the infrapyramidal to the suprapyramidal DG blade tips. As commonly observed in histological preparations, virtual sectioning of the model in any of the three canonical brain planes (coronal, horizontal or sagittal) or along the main hippocampal directions (longitudinal or transverse) resulted in a characteristic double-C shape through most of the slices.

Volumetric Differences in CA and DG

The total hippocampal volume of 46.3 mm³ consisted, for almost exactly one third, of DG (15.3 mm³) and two thirds of CA (31.0 mm³), consistent with previous findings (West et al., 1978). The volumetric distribution along the longitudinal progression from septal to temporal ends revealed striking differences between DG and CA (Fig. 4A). The posterior division (defined as the region without separate dorsal and ventral components in the coronal section) contained half of the CA volume (15.9 mm³), but only one third of the volume of DG (5.9 mm³). The dorsal volume was similar to the posterior in the DG, and was twice the value of the ventral volume in both DG and CA.

Figure 4. Regional and layer volumes.

A) Relative contributions of the dorsal, ventral (jointly forming anterior), and posterior regions to the overall hippocampus volume in CA and DG. B) Volumes of the “outer” (OR+PC) and “inner” (RAD+LM) layers in anterior and posterior CA3 and CA1. The inner/outer volumetric ratio grows transversally from the CA3c to the CA1a subregions (inset). C) Molecular and non-molecular (GC+hilus) layer volumes in DG infra- and supra-pyramidal blades.

Within CA, the anterior and posterior divisions also differed substantially in the balance between CA3 and CA1 as well as the relative layer composition (Fig. 4B). CA1 was three times as large as CA3 in the posterior division, while the difference was much more marginal in the anterior hippocampus. The “inner” layers (radiatum and lacunosum-moleculare) were twice the size of the “outer” layers (oriens and pyramidale) in CA1. Conversely, these two components were essentially equivalent in CA3, and the outer layers were actually dominant in posterior CA3. In fact, the ratio between inner and outer layers (corresponding to apical and basal arbors, respectively) increased transversally from CA3c to CA1a (Fig. 4B inset). In contrast to CA, the transverse distribution of DG volumes between infra- and supra-pyramidal blades as well as the relative layer contribution (molecular vs. granular and hilus) were essentially identical in the anterior and posterior divisions. The supra-pyramidal blade was larger than the infra-pyramidal one, and the molecular layer was similarly dominant relative to the non-molecular layers (Fig. 4C). As a consequence, the supra-pyramidal molecular volume was as prominent as the total size of the infra-pyramidal DG (~5.9 mm³).

Next we sought to evaluate the effective magnitude of the observed septo-temporal differences between CA and DG relative to inter-animal variability and other limits of methodological reliability. To this aim, we compared our volumetric measures against 3 distinct data sets (see Methods): the reconstruction from a second brain following the same histological procedure and Nissl staining protocol (Nissl#2); a reconstruction from an independent preparation imaged by ex-vivo MRI and digitally traced with the same technique (µMRI); and previously published measures from a different (Wistar) rat strain (West et al., 1978). Each of the reconstruction data sets only covered either part or layer aggregates of the hippocampus. In all three cases, the corresponding portions were analyzed in our data (Table 1). The first partial data set, providing a comparison between animals (Nissl#1 vs. Nissl#2), included all seven layers but only within the middle-third of the hippocampus. The second partial data set, adding a differentiation between imaging techniques (Nissl vs. µMRI), only consisted of CA and DG cellular and outer layer segmentations in the dorsal hippocampus. The third partial data set, further adding variation between strains (Long-Evans vs. Wistar), reported the combined volumes of CA deep (OR+PC) and superficial (RAD+LM) layers and of DG molecular (ML) and non-molecular (GC+HILUS) layers sampled throughout the hippocampus (West et al., 1978).

Table 1. Volumetric comparison across preparations, imaging modalities, and strains.

Individual layer volumes of the complete Long-Evans rat hippocampus reconstruction (Nissl#1) are compared with a second partial reconstruction (Nissl#2), ex-vivo magnetic resonance imaging (µMRI), and published literature data (Wistar).

Data Set	(Nissl#1 Vs Nissl#2)1 (Δ%) (mm3)	(Nissl Vs µMRI)2 (Δ%) (mm3)	(Long-Evans Vs Wistar)3 (Δ%) (mm3)
Layer
OR	3.12 − 3.02 (−3.20%)	2.10 − 2.01 (−4.29%)	11.75 − 10.84 (7.75%)
PC	2.60 − 2.46 (−5.39%)	1.70 − 1.69(−0.59%)
RAD	8.17 − 7.53 (−7.84%)	–	19.26 − 19.60 (−1.77%)
LM	0.74 − 0.69 (−6.76%)	–
ML	2.16 − 2.06 (−4.63%)	4.05 − 4.12 (1.73%)	9.02 − 8.99 (0.34%)
GC	0.81 − 0.76 (−6.18%)	1.75 − 1.67 (−4.58%)	6.30 − 4.81 (23.6%)
HILUS	0.46 − 0.46 (0.00%)	–
Total	18.06 − 16.98 (−5.98%)	9.60 − 9.49 (−1.15%)	46.33 − 44.24 (4.51%)

The volume comparison between the two Nissl data sets revealed their overall consistency with maximum relative difference across all regions and layers of <8% (Table 1). Much of the volumetric discrepancy in every layer was accounted for by an overall ~6% disparity in total volume. The comparison with the µMRI data set showed even greater similarity between all corresponding segmentations (as well as between overall volumes), suggesting that the imaging modality affects the selection of visible structures but does not add substantial variability relative to inter-subject diversity. The between-strain comparison based on earlier data (West et al., 1978) exposed a larger difference in the combined volumes of the dentate gyrus granule layer and hilus, which in our Long-Evans sample was considerably larger than previously reported for Wistar rats. Given the relatively small size of these structures, however, the absolute volumetric difference was still marginal compared to the effects displayed in Fig. 4. The rest of the dentate gyrus (molecular layer) had nearly identical volumes in the two samples, and the total hippocampal volume differed by less than 5%. The total volume in our complete reconstruction closely matched (within 5%) the measurements from multiple structural MRI studies of the rat hippocampus (Wolf et al., 2002a; Wolf et al., 2002b; Kalisch et al., 2006; Lee et al., 2009). Interestingly, compared to our data, the volumetric measurements of the total hippocampus obtained from stereological sampling of histological data are under-estimated by at least 15% (Ahmad et al., 2002; Schmitt et al., 2004), though the pyramidal layer volumes are in close agreement (Ahmad et al., 2002; Akdogan et al., 2008).

Uniform Ratios Between Non-Principal and Principal Layers in CA and DG

The hippocampus is laminated into cytoarchitectonic layers with distinct structures, histochemistry, and function (Witter and Amaral, 2004; Forster et al., 2006). While the pyramidal and granular layers are densely packed with cell bodies, the vast majority of neuronal membrane and synapses are distributed on dendrites and axons in the other layers. Thus, quantifying the volumetric ratios between principal and non-principal layers across the hippocampus may shed light on circuit organization. Taking advantage of our 3D digital reconstruction, we analyzed layer volumes along multiple directions (Fig. 5D inset) beyond the original (rostro-caudal) slicing orientation. In particular, we followed the canonical brain orientations (rostro-caudal, dorso-ventral, and medio-lateral) and the hippocampal axes (septo-temporal and transverse).

Figure 5. Spatial distribution of layer volumes.

A) CA layer volumes in the coronal plane as a function of the rostro-caudal position binned at 16 µm. Shaded bands denote the 95% confidence intervals. The overlaid scatter points show the ratio between OR and PC volumes multiplied by a factor of 10 (denoted by *) to match the scale of the ordinate axis. B) Volumetric ratios between every CA layer and the pyramidal layer averaged across each of the five examined orientations (N~40 sections, mean ± SD). The grand average and mean coefficients of variation are shown for each layer ratio. C) DG layer volumes in the transverse plane as a function of the position along the dentate “C-shape” binned at 16 µm. The overlaid scatter points show the ratio between OR and PC volumes multiplied by a factor of 100 (denoted by **) to match the scale of the ordinate axis. D) Volumetric ratios between every DG layers and the granular layer averaged across each of the five examined orientations.

Advancing from rostral to caudal, only the dorsal hippocampus was present in the first third of the coronal planes, then the ventral portion appeared, and the two merged together into the posterior hippocampus at approximately half way (2.4 out of 4.6 mm). The majority of the volume for all CA layers, except LM, was distributed in the medial portions of the hippocampus, peaking around the anterior/posterior cusp position (Fig. 5A). The dominant RAD layer occupied a volume approximately equal to the sum of all other layers at each rostro-caudal position. The LM layer did not appear until 1 mm into the rostral pole, contributed the smallest volume, and peaked in the posterior hippocampus. Although each layer clearly differed in terms of total volume, their ratio appeared to remain constant along the rostro-caudal axis. For example, the OR:PC ratio stayed close to the mean of 0.95 (Fig. 5A) with no significant changes from the anterior to posterior ends (R² ~0.08, p> 0.05).

This observation generalized to all non-principal to principal layer ratios, and in each of the 5 examined orientations (Figure 5B). In particular, the ratio between OR and PC narrowly hugged the unity value in every orientation, with coefficients of variation (CV=σ/μ) generally smaller than 0.1. The same situation occurred for the RAD:PC and LM:PC ratios, although with higher and lower average values. In all cases, ANOVA statistics confirmed the constancy of these values (p>0.05 for each of the 3 groups of ratios).

A similar analysis is illustrated for the DG layers along the transverse axis (Fig. 5C). The volumes of all layers remained fairly constant in the infrapyramidal blade, and progressively decreased in the suprapyramidal blade. Except for a narrow peak of the dominant ML in the crest, the ratio between the molecular and granular layer was uniform both along this (R² ~0.13, p>0.05) and all other orientations (Fig. 5D), and the same held for the hilus:GC ratio. Similarly to CA, the coefficients of variation were remarkably small, and the means were the same in each direction (ANOVA p>0.05 for both groups of ratios). These results indicate a uniform and constant distribution of the examined volumetric ratios throughout the whole hippocampal extent. Such a finding raises the possibility of developmental control during the structural maturation of the hippocampus to maintain a tight volumetric balance between non-principal and principal cell layers in both CA and DG.

Non-Uniform Ratios Between CA3 and CA1 in Rostro-Caudal and Septo-Temporal Axes

The above results indicate that CA volumes vary from anterior to posterior as well as between dorsal and ventral hippocampus (Fig. 4 and 5). The functional differences between CA3 and CA1 (e.g. Vazdarjanova and Guzowski, 2004; Leutgeb et al., 2007) raise the question of whether their volumetric ratio changes across the hippocampus. To address this issue, we analyzed the volume distributions of these two areas in all five orientations.

The total volume of both CA3 and CA1 followed similar bell-shape distributions along the rostro-caudal axis (Fig. 6A). However, CA3 peaked just rostrally to the anterior-posterior division, whereas CA1 peaked caudally. Moreover, the caudal (but not the rostral) CA3 distribution tail tapered to zero volume, while exactly the opposite trend was observed in CA1. As a result, the CA3 volume dominates in the rostral and CA1 dominates in the caudal pole. The continuous transition between these two extremes is evidenced by linear fit of the volumetric ratio between CA3 and CA1 (R = −0.96, p<10⁻⁴). Interestingly, the CA3 and CA1 volume distributions followed an opposite trend along the longitidinal hippocampal axis (Fig. 6B). The CA1 volume dominates at the septal pole, but is comparable to the CA3 volume at the temporal pole. The increasing trend of CA3/CA1 ratio is quantified by a significantly positive linear regression (R=0.73, p<10⁻⁴). In contrast to the rostro-caudal and septo-temporal axes, the CA3/CA1 ratio displayed no statistically significant variation along the other canonical directions (R² ~0.0004 and ~0.2 in the dorso-ventral and medio-lateral axes, respectively, p>0.05 for both). For DG, none of the examined orientations revealed any significant change in the volumetric ratio between the infra- and supra-pyramidal blades (not shown).

Figure 6. Spatial distribution of CA3/CA1 area volumes.

A) CA3 and CA1 volumes in the coronal plane as a function of the rostro-caudal position binned at 16 µm. Shaded bands denote the 95% confidence intervals. Overlaid scatter points and corresponding regression line show the CA3/CA1 volume ratio. B) CA3 and CA1 volumes in the transverse plane as a function of the septo-temporal position binned at 16 µm. C) CA3/CA1 volume ratios in the coronal plane for each CA layer with corresponding linear regression fits. D) CA3/CA1 volume ratios in the transverse plane for each CA layer with corresponding linear regression fits.

An interesting question arises from the decreasing and increasing CA3/CA1 ratios in the rostro-caudal and septo-temporal axes. Do all CA layers contribute equally to the uneven distribution of the CA3 and CA1 volumes in these two orientations? In order to answer this question we analyzed the CA3/CA1 volumetric ratios for each individual layer. In the rostro-caudal axis (Fig. 6C), all CA layers demonstrated a significantly decreasing CA3/CA1 ratio (R<−0.88, p<10⁻⁴), except lacunosum-moleculare (R² ~0.08, p>0.05). In the septo-temporal axis, in contrast, the CA3/CA1 ratio only increased in radiatum (R >0.77, p<10⁻⁴), and not in the other three layers (R² <0.02, p>0.05). Such a layer-specific non-uniform distribution of the CA3 and CA1 volumes may reflect differential neuropil densities, with potential implications for network connectivity. We thus turn to the analysis of neuronal occupancy.

Mapping and Embedding of Neuronal Morphologies

In order to integrate relevant neuronal morphologies within this whole-hippocampus reconstruction, we repeatedly embedded all the available digital tracings of hippocampal neurons into our 3D framework based on the positional information reported in the original publications. A total of 244 hippocampal cells (163 in CA, 81 in DG) from different animals of various ages, rat strains, and sexes, were downloaded from sixteen different archives of NeuroMorpho.Org (Ascoli et al., 2007). The stochastic sampling is described by two complementary spatial maps (Fig. 7). The Available Neuronal Count (ANC) indicates the number of reconstructed neurons available at each location. The Available Neuronal Density Index (ANDI), in contrast, expresses the precision of the localization of neuronal data at a given position. A small ANDI value reflects information dilution, in the sense that neurons sampled at that location could also be sampled in many other locations.

Figure 7. Availability map of digital reconstructions of hippocampus neuronal morphology.

Spatial distribution of the Available Neuronal Count (ANC) for CA pyramidal cells (panel A) and DG granule cells (panel B). The intensity of each pixel represents the number of morphological reconstructions available for sampling at the given position. Spatial distribution of the Available Neuronal Density Index (ANDI) for CA (panel C) and DG (panel D) principal neurons. Pixel intensity represents the number of available morphological reconstructions in that position, each divided by their potential spatial range (positional uncertainty).

The ANC map revealed a net majority of reconstructed pyramidal neurons in CA1, especially relative to CA3a and CA2 (Fig. 7A). A similar but less dramatic imbalance was apparent in DG, where more granule cells have been reconstructed in the supra- than in the infra-pyramidal blade (Fig. 7B). Both maps also revealed a clear abundance of data in the middle third of the hippocampus compared to the septal and temporal poles. Except for a few CA2 locations, at least 12 different neurons could be sampled in each position. In contrast, the highest ANDI values were narrowly localized within a few positions in the septal third of both the pyramidal (Fig. 7C) and granule cell maps (Fig. 7D). This reflects the greater precision with which neuronal location was reported in a small number of studies from the dorsal hippocampus. The DG also displayed higher ANDI values in the supra-pyramidal middle third of the map.

Examples of digital tracings of neuronal morphologies embedded in the 3D hippocampal reconstructions are displayed for illustration (Fig. 8). For optimal visualization, only ~200 dendritic arbors are sparsely embedded within a 400 µm rostro-caudal span (Fig. 8A). In the model, as in the real hippocampus, pyramidal cells are densely packed and cannot be individually distinguished if visualized all together. The average dendritic arbor spread of granule cells in the septo-temporal and transverse axes computed after embedding was 351±39 µm and 171±16 µm, respectively. These values fall within ±10% of those measured experimentally (Claiborne et al., 1990). Similarly, in the model the dendritic arbors of CA3b pyramidal cells had septo-temporal and transverse spreads of 310±102 µm and 333±59 µm, respectively, not significantly deviating from the values reported in the literature (Henze et al., 1996). For comparison, we also embedded an axonal arbor of a CA2 pyramidal cell filled in vivo, which invades nearly half of the hippocampal volume (Fig. 8B).

Figure 8. Digital neuronal embedding.

A) CA pyramidal (yellow) and DG granule cell (green) dendrites from NeuroMorpho.Org embedded in the 3D hippocampal model (magnified view in the inset). For this visualization, approximately only 200 neurons were embedded within a 400 µm rostro-caudal span. The DG and CA principal cell layers are opaque red and blue, respectively, and the outer boundaries are transparent. B) Axonal arbor of a single CA2 pyramidal cell (yellow: axon; green: dendrite) from the NeuroMorpho.Org Ascoli/Tamamaki archive embedded in the 3D model.

Dendritic Occupancy Differences in CA and DG

The hippocampal neuropil is one of the most densely packed among all cortical circuits (Stepanyants et al., 2002; Escobar et al., 2008). Of particular theoretical importance are the proportions of neuropil volume occupied by wire (axons and dendrites) and other constituents (boutons, spines, glia, extra-cellular matrix, and vasculature). Previous work addressing this issue characterized the wiring fraction in a restricted region of CA1 radiatum layer (Chklovskii et al., 2002). In light of the non-uniform volumetric distributions across layers, sub-regions, and longitudinal poles (Figs. 4, 5, 6), as well as varying packing densities of CA1 pyramidal cells (Jinno and Kosaka, 2009), it is essential to assess whether the wiring fraction might change through the septo-temporal extent of the hippocampus.

In order to validate our framework, we first computed the dendritic occupancy in the mid-radiatum layer of CA1 at the central septo-temporal level corresponding to the only available dense electron microscopy (EM) measurements (Mishchenko et al., 2010). The value obtained in our model (0.38±0.01, mean±SD from 10 embeddings) fell within the rounding approximation of the EM measure (0.4). Thus, we extended the measurement of dendritic occupancy over the entire extent of the hippocampus (Fig. 9). Dendritic occupancy in CA1 displayed a discontinuous pattern along the longitudinal axis of the hippocampus (Fig. 9A). In particular, the values remained constant within the dorsal half as well as within the ventral half, but were substantially different between the two, increasing more than 50% at the septo-temporal midpoint, from 0.29±0.02 to 0.46±0.01 (p<0.01). This same pattern was also preserved across the transverse extent, i.e. individually within CA1a, b, and c (not shown). In contrast, the CA3 dendritic occupancy was uniform throughout the length of the hippocampus (0.44±0.07 septal, 0.37±0.07 temporal, p>0.1). As a consequence, the CA3/CA1 dendritic occupancy ratio was nearly opposite in the septal and temporal divisions (Fig. 9A inset).

Figure 9. Dendritic occupancy in CA3, CA1, and DG.

(A) Distribution along the longitudinal axis of CA1 and CA3 dendritic occupancy weight-averaged by volume across layers and transverse sub-regions. The CA1, but not CA3, values (and corresponding linear fits) show separate septal and temporal components. Inset: average CA1 and CA3 dendritic occupancy (N=7, mean±SD) in the septal and temporal halves. B) Distribution along the longitudinal axis of DG dendritic occupancy in the infra- and supra-pyramidal blades. Inset: average DG dendritic occupancies (N=13, mean±SD) in the septal and temporal divisions.

Dendritic occupancy in DG was uniform throughout the septo-temporal axis both in the infra- and supra-pyramidal blades (Fig. 9B), with values consistently higher (by >20%) in the infra-pyramidal blade (Fig. 9B inset). The observed trends in dendritic occupancy approximately reflected volume distributions in DG (Fig. 4C) and in the CA3/CA1 ratio (Fig. 6B). Strikingly, however, the nearly constant, but substantially different, septal and temporal dendritic occupancies in CA1 resulted from a balance between the numerical density gradient of CA1 pyramidal cells and the longitudinal volumetric changes in the dominant radiatum layer (Figs. 5A and 6D).

We also compared dendritic occupancies across sub-regions and layers after weight-averaging by volume across the septo-temporal axis (Table 2). Among sub-regions, only CA3a stood out with values (>35%) higher compared to the other CA3 sub-regions, whereas dendritic occupancies were uniform across the transverse extent in CA1. The oriens and radiatum layers displayed a pronounced difference between overall CA3 and CA1 dendritic occupancy. Specifically, OR had (>40%) higher CA3 dendritic occupancy than RAD. In contrast, RAD had (>20%) higher CA1 dendritic occupancy than OR. These different values in OR and RAD between CA3 and CA1 reflect complementary differences in basal and apical dendritic length between CA3 and CA1 pyramidal neurons (Ishizuka et al., 1995) as well as volume differences between OR and RAD in CA3 and CA1 (Fig. 6). In DG, the distal ML had (>30%) higher dendritic occupancy compared to proximal and medial ML, in agreement with the differential dendritic density of infra- and supra-pyramidal granule cells in the inner, medial and outer ML (Claiborne et al., 1990; Rihn and Claiborne, 1990). Recently, Jinno (2011) showed topographic differences in adult neurogenesis between the DG infra- and supra-pyramidal blades using endogenous markers. Specifically, the numerical densities of doublecortin-expressing cells were significantly higher in the supra- than in the infra-pyramidal blade of the dorsal DG. The complementary volumetric differences we found between the infra- and supra-pyramidal blade volumes (see Figure 4) could compensate for greater adult neurogenesis in the supra-pyramidal blade. In particular, the significantly higher dendritic occupancy in the infra- than in the supra-pyramidal blade (see our Figure 9B inset) could relate directly to the experimental findings (Jinno, 2011).

Table 2. Dendritic occupancy by layer and sub-region, weight-averaged by volume across the septo-temporal extent.

	OR	RAD	LM	Depth
CA3c	0.44 (± 0.09)	0.31 (± 0.07)	-	0.37 (± 0.06)
CA3b	0.48 (± 0.10)	0.33 (± 0.08)	0.22 (± 0.05)	0.34 (± 0.07)
CA3a	0.66 (± 0.14)	0.41 (± 0.10)	0.39 (± 0.06)	0.50 (± 0.07)
CA3	0.48 (± 0.12)	0.34 (± 0.09)	0.27 (± 0.07)	0.40 (± 0.06)

	OR	RAD	LM	Depth
CA1c	0.35 (± 0.08)	0.43 (± 0.10)	0.34 (± 0.06)	0.37 (± 0.09)
CA1b	0.32 (± 0.07)	0.35 (± 0.11)	0.39 (± 0.08)	0.35 (± 0.10)
CA1a	0.36 (± 0.08)	0.42 (± 0.09)	0.38 (± 0.11)	0.40 (± 0.09)
CA1	0.33 (± 0.07)	0.40 (± 0.11)	0.35 (± 0.09)	0.37 (± 0.09)

	Proximal ML	Medial ML	Distal ML	ML
Infra Tip	0.20 (± 0.07)	0.22 (± 0.05)	0.39 (± 0.12)	0.27 (± 0.05)
Infra Crest	0.17 (± 0.03)	0.21 (± 0.05)	0.35 (± 0.12)	0.24 (± 0.05)
Supra Crest	0.16 (± 0.03)	0.21 (± 0.06)	0.23 (± 0.06)	0.20 (± 0.03)
Supra Tip	0.14 (± 0.03)	0.19 (± 0.03)	0.24 (± 0.08)	0.19 (± 0.04)
DG	0.17 (± 0.03)	0.21 (± 0.02)	0.30 (± 0.08)	0.23 (± 0.04)

Correlation of Square Dendritic Occupancy with DSCAM Expression

The dense packing of neurons places an important constraint on dendritic growth (Parrish et al., 2007). In order to efficiently occupy space, neurons employ different signaling mechanisms (Sestan et al., 1999; Cove et al., 2006). In particular, the Down syndrome cell-adhesion molecule (DSCAM) is involved in dendro-dendritic avoidance (Matthews et al., 2007; Schmucker, 2007; Fuerst et al., 2008; Millard and Zipursky, 2008). The “tiling effect” observed in the retina (Cook and Chalupa, 2000) and in invertebrate systems requires a mechanism of neuronal self-recognition, which may involve a large number of DSCAM splice variants. However, dense packing may simply result from dendrites seeking a spatial domain not yet occupied by other branches, independent of whether belonging to the same or other neurons. For this basic process, multiple DSCAM variants are not necessary. Accordingly, DSCAM expression in the hippocampus should be highest in the regions with maximal dendritic occupancy. In particular, the probability of dendro-dendritic collision (and thus, under this hypothesis, DSCAM expression) is proportional to the square dendritic occupancy. The non-uniform dendritic occupancy across hippocampal sub-regions and layers (Fig. 9 and Table 2) implies an even greater non-homogeneity in square dendritic occupancy, which we hypothesized to correlate with DSCAM expression.

Relative DSCAM gene expression in the hippocampus was quantified from sagittal DSCAM in situ hybridization images of the Allen Brain Atlas (mouse.brain-map.org, Ng et al., 2009). Corresponding square dendritic occupancy values were computed in our framework by averaging the values from the voxels of all the virtual sagittal sections that matched the atlas location and were visually consistent with the cytoarchitectonic shape. Dendritic occupancy was computed in all layers, but the results were translated to the corresponding somatic location to reflect gene expression. In agreement with the hypothesis, we found a high correlation between square dendritic occupancy and DSCAM expression (CA: r=0.97, p<0.003; DG: r=0.88, p<0.05). In particular, CA3 has higher expression than CA1 (and higher square occupancy), and even at the subfield level, CA3a and CA1b have the highest and lowest values, respectively, of both DSCAM values and (square) occupancy (Fig. 10A). Although with a narrower range of expression values, the same phenomenon was observed in DG (Fig. 10B). The DSCAM gene expression obtained from the in-situ hybridization images are from the mouse hippocampus. However, a recent report (Shen et al., 2011) showed that the highly curved regions of CA3 and CA2 have higher DSCAM expression compared to other regions in control rats (Figure 2 in Shen et al., 2011). This study suggests that the rat hippocampus DSCAM expression is similar to that of the mouse.

Figure 10. Correlation of square dendritic occupancy with DSCAM expression across hippocampal sub-regions.

(A) DSCAM expression in the mouse hippocampus obtained from Allen Brain Atlas in the dorsal hippocampus with CA3/CA1 and DG sub-regions labeled. (B) Regression analysis of square dendritic occupancy against normalized DSCAM expression for the CA3/CA1 sub-regions. Values are averaged over the five identifiable sections (in dorsal hippocampus) and corresponding locations and orientations in the 3D model. Horizontal and vertical bars represent standard errors of the means. (C) Regression analysis of square dendritic occupancy against normalized DSCAM expression for DG sub-regions.

Dendritic Orientation Anisotropy in CA and DG Layers

Lastly, we analyzed dendritic directionality across the hippocampal sub-regions and layers. If dendrites were oriented randomly in space, the average orientation of any small dendritic stretch relative to an arbitrary fixed direction (e.g. the “Y” axis) would be 55° (this value would be 45° in two dimensions). Thus, it is convenient to express dendritic directionality in terms of angular deviation (Δ θ) from this isotropic angle (θ=55°, Δθ = 0). As a reference, we selected the main axis longitudinally and transversally perpendicular to the somatic layer (i.e., parallel to the pyramidal apical trunk). Thus, dendritic branches perfectly aligned with this axis would have angular deviation of −55°. The opposite case of extreme anisotropy, corresponding to branches running perpendicular to this axis, would have angular deviation of 35° (Table 3, inset illustration). First we validated our angular deviation values with the only available EM based measurements, in CA1 mid-radiatum at mid-septotemporal levels (Mishchenko et al., 2008). The weight-averaged angular deviations of CA1 dendrites in this particular region were −10.4°±1.4° from all CA1 sub-regions (N=10 simulations, mean ± SD) and −11.7°±1.5° from CA1b, consistent with the EM-based approximate value of −11.7° corresponding to a nematic order parameter of 0.3 (Mishchenko et al., 2008; and D.B. Chklovskii’s personal communication, 2009).

Table 3. Dendritic orientation anisotropy by regions and layers.

Directionality of dendrites is reported as angular deviation (Δ θ) from the isotropic angle (55°) relative to the axis perpendicular to the somatic layer based on ten independent embeddings. Statistical analysis was performed by Bonferroni-corrected one-way ANOVA against the CA3-LM and CA1-LM values, with single and double asterisks denoting p<0.03 and p<0.001, respectively. The schematic inset illustrates the extreme cases of complete anisotropy parallel (left) or perpendicular (right) to the reference axis, and complete random orientation (middle), in terms of the dendrite angular deviation (Δθ) from and angle of incidence (θ) with the reference axis.

	OR (Δ θ ± SD, N=10)	RAD (Δ θ ± SD, N=10)	LM (Δ θ ± SD, N=10)
CA3	−10.2° ± 4.90° **	−10.2° ± 5.50° **	−0.9° ± 3.20°
CA1	−8.1° ± 3.98° **	−12.8° ± 4.42° ***	1.7° ± 4.64°
DG-ML	−15.9 ± 3.98° ***

In both CA3 and CA1, the dendrites in OR and RAD (corresponding to basal and apical trees, respectively) were significantly anisotropic, with an average orientation that tended to parallel the main apical axis, as denoted by the negative values in Table 3. In CA1, the deviation in RAD was 50% larger than that in OR. Conversely, in CA3 the OR and RAD values were identical and intermediate between those measured in CA1. In contrast, the dendrites in LM (corresponding to the distal apical tuft) were oriented isotropically, with no significant deviation from random directionality. Comparatively, the DG ML (corresponding to granule cell dendrites) displayed the most anisotropic pattern (again parallel to the main axis), with angular deviation 50% larger than the average OR and RAD values (Table 3). These observations are in agreement with the anisotropic tissue architecture in hippocampal layers studied from high-resolution diffusion tensor imaging and tractography of isolated rat hippocampus (Shepherd et al., 2006). The functional significance of the differences in dendritic anisotropy across layers might relate to the laminar or local organization of the inputs. For example, the distal dendrites of CA1 pyramidal neurons, which have isotropic dendritic orientation within the LM layer, receive more synapses from inhibitory interneurons and fewer from long-range excitatory fibers (Megias et al., 2001). Comparatively, the proximal dendrites in OR and RAD layers have higher proportion of excitatory inputs and lower proportions of local inhibitory contacts. Their anisotropy reflects the tendency to orient perpendicular to the incoming laminar excitatory pathways.

DISCUSSION

Due to the tight packing of the principal cell layers and the laminar organization of interneurons, fibers, and neuropil, volumetric distributions can place considerable constraints on hippocampal function. Many pathological conditions and animal models are characterized by changes in hippocampus volumes (Wolf et al., 2002a; Lee et al., 2009). Numerous studies have been carried out to estimate hippocampal layer volumes by unbiased stereology (Schmitz and Hof, 2005; Boss et al., 1987; Tinsley et al., 2001; Ahmad et al., 2002; Akdogan et al., 2008; West et al., 1991; Slomianka and West, 2005). However, the precision of absolute volume estimations of these design based stereology techniques is typically impossible to assess (Glaser, 2005). We followed the alternative strategy, pioneered in earlier seminal work (West et al., 1978), to trace the histological boundaries comprehensively across the entire hippocampus. This approach avoids the statistical error of random stereological sampling, but is too labor-intensive to quantify inter-subjects variability. Our overall volumetric analyses agree with these published results, as well as with ex-vivo micro-MRI measures, both ours and previously reported (Wolf et al., 2002a; Wolf et al., 2002b; Kalisch et al., 2006; Lee et al., 2009), that minimize tissue distortion at the expense of image resolution.

These earlier seminal attempts, however, lacked the technology and computational power for creating a comprehensive 3D model to enable re-analysis in any virtual sectioning orientation and integration with digital reconstructions of neuronal morphology. Our complete 3D reconstruction allows layer volume analysis in any arbitrary plane, including along the canonical brain axes (rostro-caudal, dorso-ventral, and medio-lateral), and the natural hippocampal directions (septo-temporal and transverse). Such flexibility provides a more extended opportunity to explore the relation between systems level structure and functional differentiation among hippocampal sub-regions (e.g. supra/infra-pyramidal DG, CA3c/CA3a, dorsal/posterior/ventral, etc.). Embedding digitally traced neuronal arbors within a high-resolution 3D reconstruction of the rat hippocampus required pooling morphological tracings from rats of different strains and ages. Previous analysis of these neuronal reconstructions (Scorcioni et al., 2004) showed that these factors do not significantly alter the statistics of any morphometric parameters relevant to the results presented here.

Because of tight somatic packing, the principal layer volume directly affects the absolute numbers of principal cells (Boss et al., 1987; Amaral et al., 1990; Braitenberg and Schultz, 1998). Neuronal density in turn influences dendritic occupancy in non-principal layers (Stepanyants et al., 2002; Chklovskii et al., 2002). We found that the non-principal to principal layer volumetric ratios were uniform in both CA and DG in all examined directions. In contrast, we observed a reverse relationship in the CA3/CA1 volume ratio between the rostro-caudal and septo-temporal axes. Optimal spatial partition between somatic packing and neuropil implies efficient wiring (Chklovskii et al., 2002; Buzsaki et al., 2004). Theoretical estimates on wiring optimization suggested an ideal value of 0.4 for dendritic occupancy (Chklovskii et al., 2002). This prediction was in fact confirmed empirically in the only available dense EM reconstruction (Mishchenko et al., 2010), in CA1 mid-radiatum at mid-septotemporal level. Unfortunately, however, dendritic occupancy can only be examined by EM in a very narrow region. Our study reproduced the observed value within the accuracy of the experimental measure in the corresponding location, but allowed extending a thorough analysis across the whole hippocampus.

Notwithstanding the quasi-optimal value of 0.4 in the CA1 RAD layer, dendritic occupancy displayed considerable regional differences both in CA and DG. While uniform in CA3, dendritic occupancy in CA1 was lower septally than temporally by 60%. In DG, dendritic occupancy did not change septo-temporally, but remained 20% higher in the infra- than the supra-pyramidal blade. There was also extensive variation in dendritic occupancy among layers in all three regions, with numerous significant deviations from the theoretical 0.4 prediction. Specifically, CA3 OR had the highest dendritic occupancy, close to 0.5. On the opposite end, DG ML had the lowest values, ranging from only 0.17 to 0.30 from the proximal to distal thirds. This might appear surprising in light of the very high numerical densities in the granule cell layer (Jinno and Kosaka, 2009). Nevertheless, these results are consistent with earlier experimental estimates showing that the distal third ML sub-layer contains 30% of the granule cell dendrites (Amaral et al., 1990; Claiborne et al., 1990; Rihn and Claiborne, 1990; Rahimi and Claiborne, 2007).

In estimating dendritic occupancy, we did not volumetrically embed interneurons. In an earlier study, we have demonstrated the embedding of CA3b interneurons to compute the potential synaspes between their axons and the CA3 pyramidal dendrites (Ropireddy & Ascoli, 2011). Similar to the neuronal availability maps for principal neurons (Figure 7), we mapped the available interneuron data from NeuroMorpho.Org to our framework (not shown). Unfortunately, the available interneuron data were insufficient to robustly estimate their occupancy ratios. Moreover, there is no information on interneurons in the dentate molecular layer and in different CA1 layers (the same applies to glia and axons). We intend to extend this study when the data become available. Based on EM neuropil reconstruction of the CA1 radiatum layer (Mishchenko et al., 2010), we do not expect the interneuron absence to drastically impact dendritic occupancy. Specifically, only two interneuron dendrites out of a total of 37 dendrites passed within a neuropil volume of 167 µm³ (Mishchenko et al., 2010).

The non-homogeneous dendritic occupancy in both CA and DG has implications with respect to the volume available to axons and other components (e.g. interneurons, glia, blood vessels etc.). Differences among layers could reflect distinct patterns of intrinsic and extrinsic connectivity (Witter and Amaral, 2004; Amaral and Lavenex, 2006). Previous research has shown the non-homogeneous axonal collateral distributions of the CA3 neurons originating from different sub-regions (Ishizuka et al., 1990; Li et al., 1994; Wittner et al., 2007; Ropireddy et al., 2011). CA3 pyramidal neurons located near the hilus have a more widespread projection to the medial-distal CA1 regions through Schaffer collaterals and more locally within the CA3c,b sub-regions through recurrent collaterals. Medial-distal CA3 pyramidal neurons near the CA2 border have recurrent collaterals distributed across the entire CA3 transverse axis and proximal to the CA1 regions. This topographical and laminar organization of the axonal projections is reflected in different dendritic occupancy across CA3 sub-regions and layers (see Results and Figs. 6, 9). Particularly, the higher dendritic occupancy in the CA3 OR layer could mean that the recurrent collaterals have higher synapse density compared to the CA3 pyramidal dendrites in the RAD layer. The significantly higher dendritic occupancy in the CA1 temporal division than the septal reflects the different pattern of CA3-to-CA1 connectivity in the dorsal vs. ventral divisions (Amaral and Lavenex, 2006; Ropireddy et al., 2011).

The low dendritic occupancy in the DG ML might also be related to adult neurogenesis of granule cells (Kaplan and Hinds, 1977; Kuhn et al., 1996; Kempermann et al., 1998). Greater spatial availability might facilitate the growth of new granule cells and their functional incorporation into the dentate neuronal network (Gould et al., 1999). The significant correlation we demonstrated between square dendritic occupancy and relative DSCAM expression levels suggests that the spatial density of dendrites might be regulated by molecular recognition. The documented roles of DSCAM in dendritic self-avoidance in drosophila (Matthews et al., 2007; Millard and Zipursky, 2008) and in mosaic spacing in the mouse retina (Fuerst et al., 2008; Yamagata and Sanes, 2008) are consistent with the maintenance of proper dendritic field organization. DSCAM-mediated dendro-dendritic repulsion could minimize the occurrence of double occupancy of the same spatial domain by two dendrites in the more densely packed hippocampal regions (Barlow et al., 2002). This mechanism does not require alternative splicing to give rise to multiple protein isoforms, which occurs in drosophila but not in mammals (Schmucker, 2007; Agarwala et al., 2000).

An ideal approach to create a reference 3D template is to warp different brains into one using multiple landmarks (Toga and Mazziotta, 2002). This process has been successfully carried out in smaller, more transparent, and more genetically tractable invertebrates (Rein et al., 2002; Brandt et al., 2005; Kurylas et al., 2008; Rybak et al., 2010). Applying this approach to rodent brains would require automated segmentation. Once future methodologies are designed to create a reference 3D rodent brain system, the computational framework introduced here for mapping and digitally packing dendritic arbors can be employed to relate single neurons to systems neuroanatomy. This approach can also be used to extract potential synaptic connectivity patterns at systems level based on spatial overlap of dendritic and axonal arbors (Stepanyants and Chklovskii, 2005; Jefferis et al., 2007; Stepanyants et al., 2008; Chiang et al., 2011; Ropireddy and Ascoli, 2011). Analysis of potential connections between different neuron types throughout the hippocampus requires suitable digital reconstructions of axonal morphologies completely filled in vivo (Ropireddy et al., 2011).

Structure is quintessential for understanding the neural basis for brain function. The influence of dendritic morphology on neuronal electrophysiology has been extensively investigated over the past decades (Krichmar et al., 2002; Poirazi et al., 2003; Komendantov and Ascoli, 2009). Dendritic morphology has also been modeled to compare branching patterns across neuron types, developmental stages, animal species, and experimental conditions (Ascoli et al., 2001; Van Pelt et al., 2001; Ascoli, 2002). Most such studies, however, examine the three-dimensional geometry of neuronal arbors without fully considering the surrounding brain system. Extending these examinations beyond individual neurons and onto systems level requires bridging the microscopic and macroscopic scales. The present work constitutes a first step towards a cellular-resolution whole-hippocampus model. The open access distribution of the histological images, digital reconstructions, and computational framework (http://krasnow1.gmu.edu/cn3/hippocampus3d) is intended to foster further knowledge integration between single neurons and systems neuroanatomy. Other 3D models such as wholebraincatalog.org provide a sophisticated graphical user interface to visualize the neuronal embeddings and cytoarchitectonic boundaries. However, our focus on the hippocampus enables a far higher volumetric resolution compared to available whole-brain models. In relating structure and function, such a focused 3D framework could be advantageously linked to a neural network simulation for investigating either pathological conditions (Santhakumar et al., 2005) or the influence of adult neurogenesis on memory encoding (Aimone et al., 2009).

Highlights.

• →Novel integration of hippocampal anatomy from dendritic arbors to whole-system
• →Non-homogeneous volume and dendritic occupancy in DG, CA3/CA1 sub-regions and layers
• →CA3/CA1 volumetric ratio increased septo-temporally due to a specific change in s.r.
• →Probability of dendro-dendritic collision significantly correlated with DSCAM
• →Complements non-uniform molecular and functional properties of the hippocampus