Fosmid-based whole genome haplotyping of a HapMap trio child: evaluation of Single Individual Haplotyping techniques

Abstract

Determining the underlying haplotypes of individual human genomes is an essential, but currently difficult, step toward a complete understanding of genome function. Fosmid pool-based next-generation sequencing allows genome-wide generation of 40-kb haploid DNA segments, which can be phased into contiguous molecular haplotypes computationally by Single Individual Haplotyping (SIH). Many SIH algorithms have been proposed, but the accuracy of such methods has been difficult to assess due to the lack of real benchmark data. To address this problem, we generated whole genome fosmid sequence data from a HapMap trio child, NA12878, for which reliable haplotypes have already been produced. We assembled haplotypes using eight algorithms for SIH and carried out direct comparisons of their accuracy, completeness and efficiency. Our comparisons indicate that fosmid-based haplotyping can deliver highly accurate results even at low coverage and that our SIH algorithm, ReFHap, is able to efficiently produce high-quality haplotypes. We expanded the haplotypes for NA12878 by combining the current haplotypes with our fosmid-based haplotypes, producing near-to-complete new gold-standard haplotypes containing almost 98% of heterozygous SNPs. This improvement includes notable fractions of disease-related and GWA SNPs. Integrated with other molecular biological data sets, this phase information will advance the emerging field of diploid genomics.

INTRODUCTION

Human individuals are diploid, with each somatic cell containing two sets of chromosomes, one from each parent. However, current standard sequencing technologies provide mostly mixed-diploid readout, missing intrinsic information on the unique haploid structures of each individual chromosome. This limits the description, analysis and interpretation of individual genomes and their function. In view of abundant genome sequence variability within a diploid genome, it is essential to determine the specific combinations of variants for each of the two homologous chromosomes (haplotypes). Knowledge of phase may be key to understanding the relationships between genetic variation and gene function, phenotype, and medically relevant traits such as susceptibility to disease and individual response to drugs (1–4).

To be able to resolve the underlying haplotype sequences of individual genomes, both computational and experimental approaches have been developed. Computational approaches to haplotyping are preassumption based (5,6) and require genotypic data from entire populations or trios to predict the most likely haplotypes for an individual. In the case of population-based statistical phasing, phase can be determined at common SNP positions but not for rare and novel SNPs. Also, the quality of this phasing is lower than other methods, especially in regions with low linkage disequilibrium. Trio-based phasing (5,7) is generally accurate but unable to phase variants for which both parents are heterozygous (~20% of SNPs). Experimental techniques that attempt to physically separate entire (homologous) chromosomes, such as chromosome micro-dissection (8) or micro-fluidic separation (9) should provide accurate results, but are currently still very challenging. Thus, to date, no complete whole genome haplotypes have yet been resolved by such a method. A more feasible, alternative strategy is to perform shotgun sequencing of an entire genome and then attempt to assemble long, contiguous haplotypes using the heterozygous variant positions within overlapping sequenced fragments. Fragments must be long enough to span at least two heterozygous loci, providing evidence for co-occurrence of alleles on the same chromosome. This approach was taken to assemble the genome of J. Craig Venter, using Sanger sequencing of mate-paired reads (10). However, Sanger sequencing is cost-intensive and in this case only allowed the reconstruction of partial haplotypes with an N50 length close to 300 kb. Specifically, in the context of this article, N50 is defined as the phased block length such that blocks of equal or longer lengths cover half the bases of the total phased portion of the genome. Next-generation sequencing (NGS) technologies provide a cost-effective way to assemble diploid genomes (11,12) but such technologies fail to directly deliver the information required, mainly because reads are too short to cover more than one heterozygous position (13). To provide sequence fragments long enough to assemble large segments of homologous chromosomes, we developed a fosmid pool-based approach to whole genome haplotype analysis (14). This technique yields haploid DNA segments significantly larger than any other standard shotgun sequencing technology (40 kb fosmids) and when used in conjunction with NGS provides a scalable shotgun sequencing technique for individual whole-genome haplotyping [E.-K. Suk et al., 2008, Personal Genomes, abstract, (15,16)]. Fragments of this size are likely to span several heterozygous variants and can be tiled into large contiguous haplotypes based on identical alleles within regions of overlap. A schematic overview of this method as outlined in detail by Suk et al. (16) is provided in Figure 1. Fosmid-based haplotyping was used to achieve N50 block lengths of about 300 kb (15), similar to the Venter genome (10) and we were able to achieve blocks of almost 1 Mb covering 99% of SNPs in the genome of a European individual (16). Although these are not complete chromosomal haplotypes, they are long enough to be used for many practical applications.

Figure 1.

Fosmid pool-based NGS approach to haplotype-resolve whole genomes (16). (A) Diploid genomic DNA of an individual is used to generate approximately 1.5 Mio fosmid clones, and (B) partitioned into pools of 15 000 fosmids, each covering about 15% of the genome in 40-kb haploid DNA segments. (C) Fosmid pools are sequenced using NGS. Here only three pools are shown as an example. (D) Fosmids are mapped to the genome and positions of heterozygous variants detected. (E) Single Individual Haplotyping is used to separate fragments into the two underlying haplotypes based on allelic identity at overlapping positions. With low coverage fosmid data, the presence of fosmids on only one haplotype can be used to inform the phase, given accurate SNP calling data. (F) Long contiguous haplotype blocks are generated, covering the entire genome.

The computational problem of reconstructing haplotypes from fragments generated by sequencing is known as Single Individual Haplotyping (SIH), and has been studied from the theoretical perspective for more than 10 years (17,18). In brief, for each chromosome, the two alleles of each heterozygous variant are encoded as 0 and 1 and fragments mapping to that chromosome (fosmids in this case) are aligned as rows of a matrix M with as many columns as heterozygous variants. Any algorithm aiming to solve this problem has two major tasks: (i) Split the fragments (rows of M) into two disjoint sets such that, if two fragments were extracted from the same chromosome copy, they should belong to the same set. (ii) group all allele calls belonging to the same chromosome copy to reconstruct the final haplotypes. The outcome of this technique when using real sequencing data is a set of haplotype blocks, where each block contains variants that can be linked together by one or more fragments. The number and composition of blocks depends solely on the information from the fragment matrix and can even be calculated before solving SIH (19,20). Simulations indicate that longer fragment lengths are able to link more variants with the same coverage (21). If fragments could be sequenced without errors, the solution for SIH within each block would be straightforward. Overlapping fragments would be assigned to the same group if they are equal and to different groups if they differ, and subsequently haplotypes could be assembled by simple consensus. However, sequencing errors and uncalled variants make the problem computationally difficult (22), giving rise to a wide variety of problem formulations and algorithms (19,21,23,24). Most of these algorithms aim to find haplotypes that minimize the number of allele calls that have to be corrected in the input matrix to make it consistent (which give rise to the metric Minimum number of Entries to Correct, MEC). For this reason, SIH can also be seen as an error correction problem (20). Currently, due to lack of real sequence data for testing, most comparisons between algorithms have been carried out on simulated fragments (21,23) with MEC generally being used to assess quality of the haplotypes under the assumption that lower MEC implies better quality (19,20). Real data currently exists for the Venter genome (10), a Gujarati individual (15) and a European genome (16) but for all of these a validated haplotype to assess the accuracy of the resulting haplotypes is not available and therefore quality assessment was done indirectly by comparing output haplotypes with HapMap haplotypes of the population of Utah residents with ancestry from northern and western Europe (CEU) (25).

In this work we generated whole genome fosmid sequence data for NA12878, a HapMap trio child from the CEU population, providing molecular contiguity over 40 kb haploid DNA segments. Confident trio-based phasing of about 80% of the SNPs for which NA12878 is heterozygous, has been provided as part of the 1000 Genomes Project. Using this trio-based haplotype as a gold-standard we can directly assess both the validity of our fosmid pool-based NGS approach to haplotype-resolve whole genomes and the accuracy of SIH algorithms for assembly using real (molecular) sequence data. Specifically, we implemented and compared eight published SIH algorithms, including our own algorithm ReFHap (21). We provide, for the first time, solid evidence that fosmid pool-based whole genome haplotyping can deliver highly accurate results even at low fosmid coverages. We examine current quality metrics and propose alternative ones to compare different algorithms for SIH. Particularly we find that minimizing MEC does not guarantee finding the true haplotypes and that lower MEC solutions do not imply better quality haplotypes. This justifies the use of efficient heuristic algorithms such as ReFHap to assemble confident haplotypes, and indeed we find that ReFHap delivers the highest quality haplotypes of all algorithms compared in a computationally efficient manner. We provide publicly available implementations of several alternative fast heuristics for SIH, including ReFHap under GPL license (see Web Resources). Finally, we have expanded the haplotypes for NA12878 to almost the full set of SNPs detected by the 1000 Genomes Project by combining haplotypes assembled by fosmid pool-based NGS with the haplotypes obtained by trio phasing. These near-to-complete haplotypes define a new gold-standard, which can be used for further advances in experimental and computational methods.

MATERIALS AND METHODS

Generation of fosmid pool-based NGS data for NA12878

We have applied our fosmid pool-based NGS approach, which has previously been described in detail (16), to generate whole genome fosmid sequence data from NA12878 as the input for analyses. As indicated above, NA12878, a HapMap trio child, has undergone deep resequencing as part of the 1000 Genomes Project, and therefore provides a gold-standard as reference for analysis. Independent molecular haplotype-resolving NA12878 offers potential synergy with genetic variation studies in this context, particularly to assist validation and inform development of new approaches for using shotgun short-read data, especially within complex genomic regions. NA12878 is available as a lymphoblastoid cell line (GM12878), generated from the DNA of a female donor with Northern and Western European ancestry. To haplotype-resolve the genome of NA12878, about 1.44 million fosmids were generated using a modified version of our previously described protocol (14,16). Briefly, particular modifications included selection of two distinct sizes of haploid DNA inserts (33–38 kb and 38–45 kb), which were ligated to the pCC2FOS™ Vector (Epicentre Copy Control HTP Fosmid Library Production Kit) to facilitate subsequent DNA purification. Fosmids were pooled into working units of 15 000 cfu. For sequencing with the SOLiD system, barcoded sequencing libraries were prepared from 32 pools as per standard protocol, and up to 8 pools sequenced in a single flow cell. Raw reads have been deposited in the European Nucleotide Archive (ENA) with accession number ERP000819. After sequencing, SOLiD reads were aligned to the reference genome (Hg18) with Bioscope 1.2 (www.solidsoftwaretools.com) using default parameters and only reads mapping uniquely to the genome were retained. To detect fosmids we used a sliding window approach to locate suitable length regions above a coverage threshold, defined dynamically based on the total number of mapped bases. Fosmids were detected as un-gapped contigs ranging from 3 kb to 45 kb. We performed fosmid-specific allele calls for the heterozygous SNPs obtained by the 1000 Genomes Project using the SNVQ SNP caller (26). We finally detected events of co-occurrence of homologous fosmids by looking at heterozygous calls in individual fosmid pools; where such events were identified, fosmids were broken down and only their homozygous tails were retained to prevent chimeric fragments with switch errors.

Genotype and trio-based haplotypes for NA12878

We utilized the 1000 Genomes Project genotype information for NA12878, which includes 1 704 166 heterozygous SNPs. The trio-based haplotypes for NA12878 generated by the 1000 Genomes Project contained phase information for 1 411 836 heterozygous SNP positions.

ReFHap algorithm

In (21), we introduced a novel algorithm for SIH which we called ReFHap (Reliable and Fast Haplotyping). We presented an alternative problem formulation, aiming to find the partition of fragments that maximizes an objective function which resembles the real origin of the fragments. The input for SIH is a matrix M with m rows, one for each fragment, and n columns, one for each heterozygous variant. Each entry M_ij ∈ {0, 1, −} represents the allele call in the fragment i for the variant j. The character ‘–’ is used for variants not covered by each fragment. For two fragments in rows i₁ and i₂ of the matrix M, we define the score s(M, i₁, i₂) as in (17):

(1)

where the score s(a₁, a₂) of two allele calls is defined by:

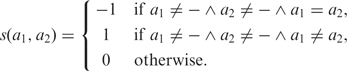(2)

This score works better in practice than the traditional hamming distance because it takes into account both matches and mismatches to separate fragments. While a highly positive score indicates that the two fragments are likely to be extracted from different chromosome copies, a highly negative score indicates that the two fragments are likely to be extracted from the same chromosome copy. Inconsistencies will produce scores close to zero which is the score for fragments that do not have overlapping allele calls. Now, if we define a partition of the fragments as a subset I of the rows of M, we can assign a score to I by adding the scores of every pair of rows i₁, i₂ for which i₁ ∈ I and i₂ ∉ I:

(3)

Finally, we formalize the Maximum Fragments Cut (MFC) problem as finding the partition I maximizing s(M, I). In (21) we shown that this formulation is NP-Complete and we introduced the following heuristic algorithm, which is based on the Max-CUT problem (27):

1. Build a graph G with fragments as vertices and edges connecting overlapping fragments. The weight of each edge is the score s(M, i₁, i₂)

2. Solve Max-CUT on this graph to find the subset I maximizing s(M, I)

3. Build haplotypes consistent with I by generalized consensus, assuming that all variants are heterozygous

To solve Max-CUT, we implemented a heuristic algorithm similar to the one used in HapCUT (19). We use a greedy algorithm to initialize a cut starting from a single edge and then we use common heuristics to improve the score of this cut. In contrast to HapCUT, we do not try random edges to start the cut but we sort edges from largest to smallest weight and then we start solutions from the first K edges, where K can be adjusted. The assumption is that edges with high scores are more likely to cross the cut.

For the last step, ReFHap assumes that all variants in M are heterozygous. Although the allele calls in M could be used to validate which SNPs are really heterozygous, often genotyping results are derived from different sources of information which are more reliable. In our testing data set, genotyping was performed by the 1000 Genomes Project (28) based on three large separate short-read sequencing experiments, so we can safely assume that the heterozygous calls are correct. Instead of calculating a separate consensus on the fragments that belong to I and on fragments that do not belong to I, which can lead to homozygous calls, we calculated a generalized consensus for a partition I as follows:

1. For each column j

   1. I_j,0 ← {i:(i ∈ I ∧ M[i, j] = 0)∨(i ∉ I ∧ M[i, j ] = 1)}
   2. I_j,1 ← {i:(i ∈ I ∧ M[i, j] = 1)∨(i ∉ I ∧ M[i, j ] = 0)}
   3. If |I_j,0| > |I_j,1| then h_j ← 0
   4. If |I_j,0| < |I_j,1| then h_j ← 1
   5. Otherwise, let h_j undefined

2. output h

The last step of the cycle in this algorithm is actually different from the one proposed in (21). This step determines what to do if the consensus assigns the same score to both alleles. The two possible options are (i) decide at random or (ii) leave the allele call undecided. The main advantage of the first option is that the output haplotypes are complete within blocks whereas the second option leaves gaps. However, we find that in practice, even at low coverage, this situation occurs for only a small number of variants, and moreover it is better for the quality of the haplotype to highlight difficult variants by leaving them undecided rather than generating a random phase which will be incorrect half of the time. We discuss in detail this compromise between completeness and accuracy in the ‘Results’ section.

MEC algorithms for SIH

Most of the algorithms that have been proposed to solve SIH try to find the haplotype for which the number of entries to correct (MEC) in the input matrix is minimized. Since this problem formulation has been shown to be NP-Complete and difficult to approximate (22), all proposed exact algorithms have an exponential dependency on at least one parameter. For example, the runtime of the dynamic programming approach proposed by (24) is exponential in the maximum number of allele calls for a fragment. Whereas this is a feasible approach for short reads that are not likely to span more than a few variants, it is not suitable for fosmids because they often span even more than 100 variants, making this approach computationally unfeasible. We will briefly discuss in this section eight different heuristic algorithms for the MEC problem formulation, which were previously reviewed by (23). The first published algorithm for SIH, called FastHare (17), sorts the fragments based on their first informative locus and then goes left to right assigning each fragment to the closest haplotype and recalculating consensus after each step. Due to its simplicity, FastHare is a very fast algorithm. The algorithms MLF (29), 2d-MEC (30) and DGS (used to assemble the Venter genome) (10) are variants of the same repetitive general procedure consisting of iterating until convergence the following two steps:

1. Calculate the haplotype H_i by consensus given a fixed partition I_i of the fragments

2. Calculate the partition I_i+1 of fragments by assigning each fragment to the closest between the haplotype H_i and its complement.

The differences among these algorithms lie mainly on the strategies used to create the initial partition I₁ and in the distance measures applied to decide if a fragment is close to H_i or to its complement. In MLF, since the partition is started at random, the whole procedure is repeated 100 times to enlarge the space of visited solutions.

The algorithm chosen to assemble the Gujarati haplotypes is called HapCUT (19). HapCUT also works by improving the answer haplotype iteratively but, instead of using partitions of the fragments set, it tries to find alleles that after flipping will reduce the MEC. The improvement step can be summarized in the following steps:

1. Build a graph G(M, H_i) with variants as vertices and weighted edges between variants linked by at least one fragment. The weight of an edge is the number of fragments inconsistent with H_i minus the number of fragments consistent with H_i.

2. Run a heuristic algorithm for Max-Cut on G to find a subset V_i of the variants for which if alleles are flipped in H_i, the MEC will be reduced. In practice, any cut with positive weight is enough to improve the current haplotype

3. Build H_i+1 by flipping the allele calls corresponding with variants in V_i

A randomized heuristic is applied for Max-CUT to increase the number of visited solutions. The complexity of the graph on which Max-CUT is solved makes this algorithm the slowest but also the best to find close to optimal MEC solutions.

Two more algorithms are mentioned in (23), a randomized one called SHRThree (31), and SpeedHap (32) which tries to build first a core solution with variants and fragments with full agreement and evidence of presence of the two alleles for each variant, and then includes the remaining fragments and variants by relaxing constraints. Among all these algorithms, HapCUT was the only one for which there was an implementation available to be applied to real data and to perform independent validation. We decided to implement all the other heuristic algorithms and made them available along with ReFHap as part of a single software package. We now release this package under GPL license in (http://www.molgen.mpg.de/~genetic-variation/SIH/data), so that our implementations can be evaluated, improved and used for further advances in haplotyping techniques.

Quality measures

Until now, there has not been a conclusive study ranking SIH algorithms in terms of quality. This is mainly due to the lack of real data but also to the lack of a standard quality measure allowing the comparison of different approaches. Most previous studies use the hamming distance between the answer haplotype and the closest of the real haplotypes as a measure of quality (23,29). However, this measure can over-penalize simple switch errors (20). Other studies compare MEC values mainly because that is the optimization objective in the MEC problem formulation, and because the MEC value of a solution can be calculated without requiring the real haplotype (24). Unfortunately, the correlation between MEC values and haplotype quality is not perfect, which makes this measure inaccurate for comparing similar solutions (see ‘Results’ section for details).

Another more effective strategy to assign a score to a completely assembled haplotype is to count the number of switch errors. In general, a switch error (SE) is an inconsistency between an assembled haplotype and the real haplotype between two contiguous variants. If either the real or the assembled haplotype include gaps, then switch errors are counted between pairs of variants for which there is no intervening variant that has allele calls in both the real and the assembled haplotype. This count needs to be divided by the total number of overlapping variants, and the normalized count is called the switch error rate. Switch error rate is a good measure to assess quality but it does not provide information on completeness of the haplotype. In an extreme case, a haplotype with just two allele calls well phased has a zero switch error rate.

An alternative measure, called adjusted N50 (AN50) was proposed by (20). This measure is calculated as follows:

1. Calculate span (in reference base pairs) from first to last phased variant for each block

2. Multiply each span by the proportion of phased alleles inside the block (to correct for uncalled alleles)

3. Sort blocks from largest to smallest adjusted span

4. Traverse the list counting the number of phased variants until this count is more than half of the total number of variants.

A similar measure of completeness called S50 can also be calculated by sorting the blocks by number of phased SNPs instead of adjusted span. Both measures penalize incomplete haplotypes, but do not provide information about quality.

To account for both completeness and quality, we propose the following two steps procedure to calculate an alternate measure that we called quality adjusted N50 (QAN50).

1. Break each haplotype block into the longest possible sub-blocks for which no switch error can be detected

2. Calculate AN50, as described above, for these sub-blocks.

This measure establishes a compromise between accuracy and completeness and also gives an idea on to which extent (in genomic bases) assembled haplotypes can be trusted. In the next sections we will show how different algorithms score in terms of AN50, switch errors and QA50.

RESULTS

Fosmid pool-based NGS input data and NA12878 haplotype assembly

Sequencing of 32 fosmid pools of NA12878 (see ‘Materials and Methods’ section for details) resulted in 941 793 498 mapped reads, equivalent to a median 10x genome coverage after duplicated reads had been removed. Over 81% of the genome was covered at least 2× or greater. Heterozygous SNPs positions from the 1000 Genomes Project data set for NA12878 (1 704 166 SNPs) were used to inform the positions where alleles were called within each fosmid, informing a total of 5 145 474 allele calls across all fosmids. For comparison, this average of 18.03 calls per fosmid is six times larger than the corresponding average number of calls in the Venter genome. Only fosmids which contain two or more SNPs are informative for phasing and our data set contained 285 341 phase-informative fosmids (hereafter termed fragments). From the input matrix for SIH, the total number of blocks containing variants that can be linked together by one or more fragments was 17 839, covering 2.04 Gb of the genome. Figure 2 shows the distribution of blocks per number of SNPs. Even though the fragment coverage is just 3.02 on average, long overlapping fragments allow the phasing of up to 1 582 652 (92.9% of the total) SNPs into blocks with an S50 of 215 SNPs. It is worth noting that this percentage of SNPs seems to be inconsistent with the percentage of the genome included in blocks (about 64%). The reason for this difference is the existence of large repetitive regions in the genome, such as the centromeres, in which it is very difficult to map reads and reliably call SNPs. The largest block contains 3921 SNPs and it is located in the MHC region, which is known to have higher variability than other regions in the genome. These blocks were used as the input for eight SIH algorithms (namely ReFHap, HapCUT, FastHare, DGS, MLF, 2d-MEC, SHRThree and SpeedHap). Input matrices and assembled haplotypes are available for download at (http://www.molgen.mpg.de/~genetic-variation/SIH/data).

Figure 2.

Distribution of blocks per different number of phased SNPs.

We verified that our coverage results were consistent with other similar studies. The N50 phased block length achieved for sequencing of the Gujarati individual (15) was 386 kb, mainly because they sequenced about 600 000 fosmids (25% more), but also because they considered 1.9 million predicted heterozygous variants (about 10% more), which produces a greater number of overlaps between fosmids. The N50 for Venter's genome (10) was about 350 kb after performing Sanger sequencing of 103 356 fragments covering 1.85 million predicted heterozygous variants. A large N50 value was achieved in this case by sequencing 1 kb ends of fragments larger than 100 kb, which allowed distant variants to be connected. We have been able to generate the most comprehensively haplotype-resolved individual genome, ‘Max Planck One’ (MPI) to date using our fosmid pool-based NGS approach, and have achieved an N50 phased block length of almost 1 Mb containing 99% of SNPs (16). This level of completeness required sequencing of 67 pools of 15 000 fosmids which resulted in 1.16 million phase informative fosmids, equivalent to 6.38× fosmid coverage of each haplotype.

Unfortunately, for all of these haplotyped genomes it is not feasible to make a direct assessment of quality. Validation for these haplotypes was performed by comparison to HapMap haplotypes assembled by statistical phasing, on regions known to have high linkage disequilibrium. Although comparisons with HapMap haplotypes provide some general sense of reliability, they are not informative enough to produce an accurate estimation of the switch error rate and to investigate potential causes of errors. When compared to haplotypes of 83 HapMap trio children from the CEU population, the percentage of concordance in the phasing of consecutive variants for NA12878, MP1 and the Gujarati individual is consistent with the demographic origin of the samples (Supplementary Figure S1). In the following sections we use the trio-phased haplotype for NA12878 as a reference to make a direct assessment of quality of our whole genome haplotype assembly and compare different algorithms for SIH.

Overall quality assessment

A comparison between all heuristic algorithms for SIH across four different measures is shown in Figure 3, A–D: (A) AN50, (B) switch error rate, (C) QAN50 (described above) and (D) runtime for our dataset. Using ReFHap, 91.7% of SNPs were phased and the QAN50 block size was 117.8 kb. ReFHap had the lowest switch error rate (1.69%) and the highest QAN50 of the eight SIH algorithms. DGS and FastHare phase about the same number of SNPs as ReFHap but with slightly larger switch error rates (1.82 and 1.74%, respectively). HapCUT, for which we ran 10 iterations, phased slightly more SNPs than any other algorithm, phasing 1068 (0.06% of input SNPs) more SNPs than ReFHap. HapCUT also covered the largest fraction of the genome after adding up the lengths of the blocks for which no switch error can be detected and adjusting for unphased SNPs (1.82 Gb). ReFHap, FastHare and DGS were close with 1.8 Gb (1.79 Gb for DGS). However, as expected, HapCUT also had significantly longer running time than the other methods (Figure 3D). While ReFHap, DGS and FastHare were all able to phase full chromosomes within a few seconds, HapCUT can take hours for a single iteration. This happens because the runtime for the first three methods mainly depends on the number of overlapping fragments in one block, while for HapCUT it depends on the maximum number of SNPs connected in one block. Fosmids are able to connect large numbers of SNPs at low coverage, so algorithms such as ReFHap require significantly less computational resources. Chromosome 6 is an extreme case with HapCUT taking more than 10 h to complete one single iteration compared to 3.29 s for ReFHap; this is mainly due to the large blocks of connected SNPs within the MHC region. As fosmid coverage and number of heterozygous variants analyzed increases, the number of connected components also increases, making the instances more difficult to solve for HapCUT.

Figure 3.

Comparison of algorithms for SIH on NA12878 whole genome fosmid sequence data. (A) Adjusted N50 which takes into consideration block length and number of phased SNPs but not quality; (B) Switch error rate, calculated using comparison with gold-standard trio haplotypes; (C) Quality adjusted N50 which combined measures of completeness and quality; (D) Runtimes of each algorithm on this data set (log scale); (E) QAN50 for ReFHap, DGS, FastHare and HapCUT on subsets of the data built by varying the number of fosmid pools considered; (F) QAN50 for ReFHap, DGS, FastHare and HapCUT for different heterozygosity rates obtained by varying the percentages of SNPs considered.

We investigated the correlation between switch error rate and different properties of the blocks such as size, span, number of fragments, average fragment length and coverage. We did not find positive or negative correlation of switch errors with any of the analyzed characteristics. As we show with the MEC analysis performed in the next section, switch errors are directly correlated with the allele calling error rate. The distribution of switch error rates and correlation coefficients for each characteristic of the input are included in the Supplementary Figure S2.

Given the lack of correlation between coverage and switch error rate, we might wrongly infer that it is not worth increasing the number of fragments sequenced to improve the quality of the haplotypes. In practice, however, increasing the number of variants and fragments will generally change the number and composition of the blocks, affecting the overall quality. To determine how different input sizes change the quality of the haplotypes and to assess how different algorithms are affected by the input size, we ran the pipeline on subsets of the fragments (8, 16 and 24 fosmid pools), and on subsets of the SNPs (25, 50 and 75%) and we calculated the QAN50 of haplotypes assembled by ReFHap, DGS, FastHare and HapCUT. We found that the results of the comparison with the whole dataset were consistent across the different datasets. Figure 3E shows that the QAN50 grows linearly with the number of fosmids, being zero for eight pools because less than half of the total SNPs are phased, and growing up to 111 395 bp, which is the maximum value achieved by ReFHap for the whole data set. Taking subsets on the total number of SNPs is a way to simulate variation in the heterozygosity rate of the individual. Low heterozygosity rates reduce the number of variants linked in blocks and reduce the size of the blocks which affects the QAN50. As the heterozygosity rate increases, the length of the blocks also increases but also more switch errors can be detected. Figure 3F shows that the QAN50 grows with the number of SNPs, up to 75% of the data set. After this point, the effect of switch errors equates and even becomes more important than the increase in block length reducing the final QAN50. HapCUT seems to be more affected by this effect than the other algorithms.

MEC as a measure of quality

Previous studies compare algorithms based on the minimum number of entries to correct to make the input matrix consistent with the assembled haplotypes (MEC) (19,24). If the complete real haplotypes were available, it would be easy to align each fragment to the closest haplotype and to identify exactly the allele calls to be corrected. Unfortunately our gold-standard is not complete, and hence it can not be determined if allele calls in variants uncalled by the gold-standard should be corrected or not. To overcome this issue we ran SIH using only the alleles calls from the subset of SNPs that are present in the trio-phased gold-standard. Since in this case the gold-standard haplotype is complete, we were able to calculate the real MEC. It is interesting to note that the MEC percentage of the gold-standard, which was 2.89%, is the exact allele calling error rate for this experiment.

We can also use the real MEC values of each block to make direct comparisons with MEC values of assembled haplotypes and check if optimizing MEC increases quality. We compared the MEC of the gold-standard with the MEC of HapCUT haplotypes, taking into account that HapCUT is the algorithm achieving the lowest MEC values. We found that the MEC values of the gold-standard are consistently higher across all blocks than those of the HapCUT haplotypes (see Figure 4). This means that solutions with optimal, or close to optimal, MEC values are likely to fix less erroneous calls than actually need to be corrected and, in general, are not guaranteed to have better quality. To confirm this statement, we calculated correlation coefficients between MEC percentages and switch error rates for both the gold-standard and HapCUT. We found a high correlation (Pearson Correlation=0.84) between the MEC percentage of the gold-standard and the switch error rate. However, we found that the correlation of the HapCUT MEC percentage with the switch error rate decreased to just 0.11. This means that predicted MEC values are skewed and hence are not good predictors of the switch error rate. Finally, we divided the set of blocks into bins of allele calling error rates to look for another determinant of switch errors. Surprisingly we found consistent negative correlation (−0.5, −0.4) between HapCUT MEC values and switch error rates, which means that solutions with lower MEC values are more likely to increase the number of switch errors.

Figure 4.

Comparison of MEC values predicted by HapCUT with real MEC values. The dark grey bars show the increase of MEC percentage for the gold-standard as the switch error rate increases. However, MEC percentages predicted by HapCUT (light grey bars) do not increase as they should because HapCUT tries to find the solution minimizing MEC. The number of blocks analyzed for each bin (medium grey bars) is shown in the right Y axis.

Construction of a new gold-standard haplotype

The current gold-standard haplotypes only contain phase information for ~80% of SNP positions due to the fact that trio phasing cannot resolve SNPs that are heterozygous in both parents and the child. Fosmid pool-based phasing is theoretically able to resolve the phase of all SNPs. Therefore we decided to create a new gold-standard for NA12878 combining all SNPs from both methods. We assembled these new gold-standard haplotypes by combining both data sets and correcting the switch errors as follows. We initially selected one of the trio haplotypes as the template and then, for the fosmid-based haplotypes, we built blocks of maximal length within which no switch error is detected (the same blocks built to calculate QAN50). Inside each of these blocks, we augmented the template by filling uncalled variants with calls of the assembled haplotype consistent with the template. Between blocks, by definition, we know that a switch error occurred in one of the variants. To correct this error, we ranked called variants by consensus value and selected the variant with lowest consensus as the position i where it is most likely that the switch error was produced. We filled the uncalled variants in the template before i with the haplotype selected for the left-hand block and then we filled the uncalled variants after i with the haplotype selected for the right-hand block.

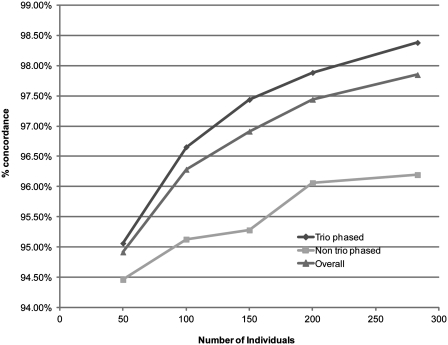
A priori there is no reason to think that the accuracy of fosmid-based haplotyping would decrease in SNPs not phased by the trio, and hence this procedure should correct a large percentage of switch errors in the assembled solutions. However, to assess the accuracy of phasing for the SNPs not verified by the parental genotypes, we compared our results with haplotypes assembled with statistical phasing. We downloaded the latest genotype calls released by the 1000 Genomes Project for a collection of 288 individuals with European ancestry (EUR). This collection groups samples from the following populations: Utah residents (CEPH) with Northern and Western European ancestry (CEU), Toscani in Italia (TSI), British from England and Scotland (GBR), Finnish from Finland (FIN) and Iberian populations in Spain (IBS). We used FastPHASE (6) to predict the most likely haplotypes for 21 878 SNPs in chromosome 22 of NA12878, which has 22 801 SNPs in total (the remaining 923 SNPs were not present in the 1000 Genomes Project genotypes). We also predicted haplotypes based on subsets of the reference population of size 50, 100, 150 and 200 to test how the concordance with the new gold-standard haplotypes changes as the number of individuals in the sample increases. We calculated separately the concordance for adjacent SNPs phased with the parental information (16 346) and SNPs phased with fosmid-based NGS (5255), which add up to the 21 601 SNPs shared between the statistical and the new gold-standard haplotypes. Figure 5 shows that the concordance is lower for the adjacent SNPs phased with fosmid-based NGS, but it is still larger than 95% after 100 or more individuals are included. The concordance always grows with the number of individuals which means that, as the quality of the haplotypes derived with statistical phasing improves, the concordance with the new gold-standard haplotypes increases. Even if the differences between the new gold-standard haplotype and the haplotypes predicted by FastPHASE in adjacent SNPs phased with fosmids sequencing (207) were all due to errors in the new gold-standard, the overall switch error rate would be <1%.

Figure 5.

Comparison of the new gold-standard haplotype (“Overall”) with haplotypes predicted by statistical phasing using different numbers of individuals in the reference panel. The concordance was calculated separately for pairs of adjacent SNPs phased using parental genotypes (trio phased) and pairs phased using fosmid-based haplotyping (non-trio phased).

We were able to phase an additional 257 245 SNPs that were not resolved in the trio phased haplotypes to achieve a new total of 1 669 081 phased SNPs. The haplotypes combining parental information with fosmid-based haplotyping resolve the phase of 97.9% of SNPs in NA12878 (compared to 82.8% previously) producing almost complete SNP haplotypes in this individual. The corrected haplotypes are available for download (http://www.molgen.mpg.de/~genetic-variation/SIH/data). These new haplotypes increase the phase information within various important functional units or disease-related regions (see Supplementary Table). For example an additional 96 849 SNPs are phased within genes, including 816 SNPs that cause non-synonymous mutations or splice site mutations. In particular 847 of the newly phased SNPs produce an amino acid exchange in proteins, 108 of which are predicted to be damaging by PolyPhen-2 (33) and 184 are predicted to be damaging by SIFT (56 predictions overlap). The new gold-standard also contains the phase of an additional 263 GWA SNPs across the genome, a useful addition as it has been shown that haplotype information increases the power of genome-wide association studies (GWAS) (34). An additional 11 395 phased SNPs were contained within genes annotated by the Genome Association Database (GAD), with single genes containing hundreds of newly phased SNPs (Table 1). Some specific examples of GAD genes containing many additional phased SNPs and including at least one GWA SNP are shown in Figure 6. These examples are associated with various cancers (AGT1A genes and CDH1), drug sensitivity (UGT1A9), and hypertension and osteoporosis (COL1A2).

Table 1.

Comparison of numbers of phased SNPs in functional units or disease-related regions between trio gold-standard and new gold-standard haplotypes

	Trio gold- standard	New gold- standard	Additional SNPS phased	Increase (%)
Total SNPs phased	1 411 836	1 669 081	257 245	18.2
Genes	506 276	603 125	96 849	19.1
Missense, nonsense, splice variants	4650	5466	816	17.5
GWA SNPs	1323	1568	245	18.5
GAD disease genes	63 085	74 480	11 395	18.1
ENCODE regions	13 140	16 207	3 067	23.3

Figure 6.

Examples of GAD genes containing many additional phased SNPs. Fosmid-based phasing allows resolution of the phase of significant numbers of additional SNPs which may be particularly useful within disease-associated genes and SNPs detected in genome-wide association studies (GWA SNPs). Here, we show three examples of disease-relevant genes that contain many additional phased SNPs: UGT1A genes associated with various cancers; CDH1 which plays a role in drug sensitivity and COL1A2 associated with hypertension and osteoporosis. Tracks are taken from the UCSC Genome Browser. SNPs resolved by trio phasing are shown in the top track with SNPs resolved using fosmid-based phasing shown below. SNPs from the GWAS Catalog are shown as green bars in a separate track and those GWA SNPs that are resolved by fosmid-based phasing are indicated by pink arrows. Annotation from the Gene Association Database (GAD) and OMIM are shown in the lower tracks.

DISCUSSION

Haplotyping has been identified as one of the most difficult steps toward full genome completion (13) and therefore the development of an accurate and scalable technique for direct haplotyping of diploid samples is of great interest for researchers in both theoretical and applied genetics and genomics (4). Fosmid pool-based haplotyping, utilizing NGS, is a scalable and cost-effective method for the assembly of whole genomes into large contiguous haplotypes and in this study we have undertaken comprehensive assessment of quality for this method. We confirm for the first time that this method allows assembly of highly accurate haplotypes, and we also show that this accuracy is correlated with the allele calling error rate. Hence, improvements in quality and analysis of NGS reads will also increase the accuracy of fosmid pool-based haplotyping. We believe that this makes fosmid pool-based haplotyping a valuable approach for a wide variety of applications of human genome haplotyping such as cancer genome sequencing, and it can even be applied for sequencing of other types of organisms. The SIH problem is at the core of the bioinformatics analysis needed for any haplotyping technique based on shotgun sequencing. Although this problem has been studied for a long time, novel experimental approaches, such as fosmid pool-based haplotyping, provide the real data needed to find new directions for improvement. We have compared a wide variety of algorithms for SIH, specifically assessing accuracy, completeness and runtime for eight different algorithms using real sequence data from fosmid pools. Utilizing the genome of an individual for which there already exists a gold-standard haplotype has allowed us to comprehensively assess the quality of different methods. For this quality assessment, we have proposed a new metric which takes into consideration both the completeness and accuracy of the haplotypes which we call quality adjusted N50 (QAN50). We find that according to both switch error rate and QAN50, ReFHap yields the best compromise between completeness, accuracy and computational resources. We also show that the MEC-based problem formulation used in most of the recently proposed algorithms for SIH can lead to suboptimal haplotypes, even if the MEC problem is solved optimally. This finding justifies the use of heuristic methods not only because of their better efficiency, but also because they yield higher accuracy, and leaves an open door for novel bioinformatics solutions to SIH.

Despite the accuracy of the current gold-standard haplotypes, the phase of almost 20% of the SNPs remained unresolved by trio phasing. Here, utilizing our fosmid-based phasing data in conjunction with the trio haplotypes, we provide a nearly complete new gold-standard haplotype for NA12878, covering 97.9% of heterozygous SNPs that have been genotyped in this widely studied HapMap individual. This has generated phase information for almost all potentially disease predisposing SNPs allowing them to be analyzed now in their molecular context, an indispensable prerequisite to explore their potential functional implications and pathophysiology. Furthermore, we were able to include a notable fraction of GWA SNPs into phase context, an important step to be able to track the underlying causative variants. This phase information is particularly useful in NA12878 given that this individual (in the form of a stable lymphoblastoid cell line) has been extensively analyzed in a variety of projects, such as the ENCODE project (35) and the 1000 Genomes Project (28). As data accumulates for this individual on gene expression, histone modifications, transcription factor binding sites and other such functional assays (36), avenues for examining the effect of phase at a functional level are opened. Our molecular phase data from NA12878 can be integrated with data from all other omics levels to develop a more coherent picture of ‘phase-sensitive’ functional genomics (37). These improved haplotypes will be of use to the scientific community when analyzing functional genomic data for NA12878, allowing new insights into the importance of phase.

ACCESSION NUMBER

European Nucleotide Archive: ERP000819.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online: Supplementary Table 1 and Supplementary Figures 1 and 2.

FUNDING

The German Federal Ministry of Science and Education (BMBF), through the NGFN-2 program and the NGFN-Plus program grants (201GR0414, 01GS0863 to M.R.H.); European Research Council Young Investigator grant (241426 to K.V.); Vlaams Instituut voor Biotechnologie; Katholieke Universiteit Leuven; Fonds Wetenschappelijk Onderzoek Vlaanderen; and the European Molecular Biology Organization through the Odysseus program and the YIP program. Funding for open access charge: Max Planck Institute for Molecular Genetics.

Conflict of interest statement. None declared.