¹³¹I-Tositumomab Radioimmunotherapy: Initial Tumor Dose–Response Results Using 3-Dimensional Dosimetry Including Radiobiologic Modeling

Abstract

For optimal treatment planning in radionuclide therapy, robust tumor dose–response correlations must be established. Here, fully 3-dimensional (3D) dosimetry was performed coupling SPECT/CT at multiple time points with Monte Carlo–based voxel-by-voxel dosimetry to examine such correlations.

Methods

Twenty patients undergoing ¹³¹I-tositumomab for the treatment of refractory B-cell lymphoma volunteered for the study. Sixty tumors were imaged. Activity quantification and dosimetry were performed using previously developed 3D algorithms for SPECT reconstruction and absorbed dose estimation. Tumors were outlined on CT at multiple time points to obtain absorbed dose distributions in the presence of tumor deformation and regression. Equivalent uniform dose (EUD) was calculated to assess the biologic effects of the nonuniform absorbed dose, including the cold antibody effect. Response for correlation analysis was determined on the basis of the percentage reduction in the product of the largest perpendicular tumor diameters on CT at 2 mo. Overall response classification (as complete response, partial response, stable disease, or progressive disease) used for prediction analysis was based on criteria that included findings on PET.

Results

Of the evaluated tumor-absorbed dose summary measures (mean absorbed dose, EUD, and other measures from dose-volume histogram analysis), a statistically significant correlation with response was seen only with EUD (r = 0.36 and P = 0.006 at the individual tumor level; r = 0.46 and P = 0.048 at the patient level). The median value of mean absorbed dose for stable disease, partial response, and complete response patients was 196, 346, and 342 cGy, respectively, whereas the median value of EUD for each of these categories was 170, 363, and 406 cGy, respectively. At a threshold of 200 cGy, both mean absorbed dose and EUD had a positive predictive value for responders (partial response + complete response) of 0.875 (14/16) and a negative predictive value of 1.0 (3/3).

Conclusion

Improved dose–response correlations were demonstrated when EUD incorporating the cold antibody effect was used instead of the conventionally used mean tumor-absorbed dose. This work demonstrates the importance of 3D calculation and radiobiologic modeling when estimating absorbed dose for correlation with outcome.

There has been recent interest in developing dosimetry-based patient-specific treatment planning to optimize therapy with internal emitters as is routine in external-beam therapy. Because of the inherent heterogeneity of radiopharmaceutical distribution in tumor and normal organs, the preferred methodology for absorbed dose estimation is imaging-based 3-dimensional (3D) calculation (1). The recent advances in hybrid imaging and computational power have made such calculations possible in a research environment and a realistic clinical goal for the future.

At present, the common approach for ¹³¹I anti-CD20 radioimmunotherapy of lymphoma is to deliver 65–75 cGy to the whole body based on estimates from a tracer study. Although this conservative approach has produced promising results (2,3), there is much room for improving efficacy by tailoring the treatment on a patient-by-patient basis to deliver the therapeutic absorbed dose to the tumor while avoiding critical organ toxicity. Apart from treatment planning, tumor-absorbed dose estimates from a tracer study can potentially be used for improved clinical management by timely initiation of alternative treatment.

To make advances toward tumor dosimetry–based radionuclide therapy, robust tumor dose–response correlations must be established. Studies on tumor dosimetry in radioimmunotherapy of lymphoma are limited and have not established strong dose–response correlations for either of the 2 Food and Drug Administration–approved radiopharmaceuticals, ⁹⁰Y-ibritumomab or ¹³¹I-tositumomab (4–7). In these past studies, the mean absorbed dose to the tumor was the only dose measure that was calculated, except in the study by Sgouros et al., in which correlations were also investigated with minimum absorbed dose, maximum absorbed dose, and a uniformity index. Although the equivalent uniform dose (EUD) model has been proposed for assessing the biologic effect of a nonuniform tumor-absorbed dose distribution (8), it has not been used in past studies evaluating dose–response correlations. Past tumor dosimetry studies have also relied on planar imaging methods or methods combining SPECT at a single time point with planar imaging at multiple time points to determine pharmacokinetics. The superiority of SPECT over planar methods for activity quantification is well established.

Here, we present tumor dosimetry results from a fully 3D approach coupling hybrid SPECT/CT at multiple time points with Monte Carlo radiation transport–based voxel-by-voxel absorbed dose calculation. Past radioimmunotherapy studies have shown dramatic regression of malignant lymphomas within days of the therapeutic administration (9–11). In the present study, the anatomic CT information from multiple time points allowed us to incorporate tumor regression and deformation into the calculation to estimate spatial absorbed dose distributions at the voxel level. In addition, EUD was calculated to assess the biologic effects of the nonuniform absorbed dose, including the effects of the cold antibody administered with the ¹³¹I-labeled antibody and the effects of cell proliferation (12). Tumor dose–response correlations were investigated using mean absorbed dose and EUD as well as other measures from dose-volume histogram analysis.

MATERIALS AND METHODS

Patients

Patients were recruited from those scheduled for ¹³¹I-tositumomab therapy of relapsed or refractory (previously treated with chemotherapy) B-cell lymphoma at the University of Michigan. The treatment protocol, which includes administration of 450 mg of the unlabeled antibody (tositumomab) before both the diagnostic (tracer) and the therapeutic administration of ¹³¹I-tositumomab has been described (2). From planar γ-camera measurements after tracer administration (185 MBq), the amount of radioactivity necessary to deliver 65–75 cGy to the whole body is determined for each patient and is administered 8 d after the tracer. For the present research study, this protocol was unchanged, but the patients gave their separate informed consent for the SPECT/CT examination, which was not part of the treatment protocol. This imaging examination received separate approval by the University of Michigan Internal Review Board. Data are presented here for 20 patients (13 men and 7 women; age range, 33–81 y; median age, 53 y). Eighteen of the volunteers had follicular lymphoma, and 2 had marginal zone lymphoma. The administered therapy activity ranged from 2.15 to 5.68 GBq (58–153 mCi).

SPECT/CT and Tumor Definition

The imaging protocol on the Symbia TruePoint SPECT/CT scanner (Siemens) has been described (11). The SPECT camera field of view was 39 cm in the axial direction. Hence, only part of the body was imaged, focusing on the region with the largest tumors. In most patients, multiple (up to 7) tumors were included in the field of view. Patients were imaged 3 times after the tracer had been administered (days 0, 2, and 6) and 3 times after the therapy had been administered (days 2, 5, and 7–9). At each time point, the tumor volumes of interest were defined on CT, plane by plane, by a nuclear medicine specialist with radiology CT training. These volumes of interest were used for activity quantification and dosimetry and also provided information on initial tumor shrinkage, which was used to determine radiosensitivity and cold protein sensitivity parameters for the EUD calculation.

Activity Quantification

For SPECT reconstruction and quantification, software previously developed at the University of Michigan was used. Posttherapy SPECT projection data were corrected for dead time using a paralyzable model (13). Projection data were reconstructed with 35 iterations (6 subsets) of 3D ordered-subsets expectation maximization including triple-window–based scatter correction, CT-based attenuation correction, and compensation for depth-dependent detector response (14,15).

It was necessary to use a counting rate–dependent calibration factor to convert reconstructed counts to activity. The need was due to the observed shift in the ¹³¹I energy spectra at high counting rates, which was attributed to pulse pile-up effects (13). The calibration experiment using a phantom of known activity was performed at 3 different counting rates (21, 9, and 2 kcps) as the activity decayed over 1 mo. The validity of the corrections for high-counting-rate imaging is evident from the robust correlations (r > 0.9) reported previously between tracer and therapy residence times for a subset of the present patients (16). To account for partial-volume effects, recovery coefficients were determined from phantom measurements. The measured recovery coefficients ranged from 99% to 58% for spheres ranging from 100 to 4 mL. Activity in tumor voxels was corrected for partial-volume effects by applying CT-volume–dependent recovery coefficients uniformly to all voxels within a tumor.

After activity quantification, rest-of-body time–activity data were fitted by a monoexponential function, and tumor-time–activity data were fitted by a biexponential, to model the uptake and clearance phases. Tumor time–activity fitting was performed via maximum likelihood within a mixed model incorporating tumor-level random effects (17).

Patient-Specific 3D Tumor Dosimetry

Dosimetry was performed using a version of the Dose Planning Method Monte Carlo program (adapted for internal emitter therapy (18)) in conjunction with MATLAB (MathWorks)-based routines. Key features were voxel-by-voxel absorbed dose calculation coupled to deformable image registration, which relates tumor voxels that are changing from one time point to the next due to deformation or regression. At each time point, SPECT activity maps and CT-based density maps were input to the Dose Planning Method program. The SPECT maps were sampled to provide antibody uptake sites (in 3 dimensions), after which ¹³¹I decay and radiation transport were simulated to determine 3D self-dose-rate and rest-of-body dose-rate maps (in units of mGy/MBq-s originating in tumor and rest of body, respectively) at each of the 6 imaging points. The first tracer scan (at which tumor volumes were almost always largest) was used as the reference scan. After cropping all maps to the size of the largest tumor, maps for the other 5 time points were deformed and registered to the reference tumor shape and size. First, the tumor centers of masses were aligned. Each voxel was then mapped into the reference scan by conserving its fractional distance along a radius from the tumor center to the tumor edge (uniform radial deformation). Interpolation and extrapolation were applied as appropriate to complete the deformed maps, and total absorbed dose rates were preserved. The registered tumor self-dose-rate maps were then multiplied by the total tumor activity as a function of time (taken from the fitted tumor time–activity mentioned in the previous section) and integrated (over time) to obtain the self-component of the tumor-absorbed dose distribution (in mGy). Similarly, the rest-of-body component of the tumor-absorbed dose distribution was obtained. Here we are assuming that the registered absorbed dose-rate maps are piecewise constant over the times between scans, which permits analytic integration of the time–activity fits over each of the numeric steps in the integration. (Note that we choose to account for the variations in voxel-by-voxel time–activity in the manner described here because voxel-level fitting can be significantly noisier than the tumor-level fitting of the present approach, especially with deforming tumors.) Finally, the self- and rest-of-body components of the absorbed dose distribution were added to obtain the total 3D distribution for the tumor, which represents the total delivered absorbed dose from the tracer and therapy administrations.

The EUD is defined as the spatially-uniform biologically effective absorbed dose that would result in a level of cell inactivation equivalent to that of the nonuniform biologically effective absorbed dose (8). Our EUD model was described previously (12) and is summarized here. The model is based on tracking the surviving fraction of clonogenic subunits (voxels, v) over time, S(v,t). The minimum of the surviving fraction averaged over the subunits, <S(v, t_min)>_V, can be defined as the desired therapeutic endpoint and is related to EUD as

$$\text{EUD}=-\frac{1}{a}ln[<S(v,t_{min}){>}_V],$$ Eq. 1

where S(v, t) = exp{(−α · BED(v, t)} and α is the linear sensitivity coefficient of the linear-quadratic dose–response model. The spatial and time-varying biologically effective dose (BED) for each voxel was calculated as the sum of relevant quantities affecting therapeutic outcome, in this case the absorbed dose effect, the cell proliferation effect, and the cold antibody effect,

$$\text{BED}(v,t)=\text{D}(v,t)·\text{RE}(v,t)-(1/\alpha )·{\lambda }_{\text{t}}·t+(1/\alpha )·{\lambda }_{\text{p}}·\text{P}(v,t),$$ Eq. 2

where D(v,t) is the 3D cumulative absorbed dose delivered over time, RE(v,t) is the relative effectiveness, λ_t is the proliferation coefficient, λ_p is the cold protein sensitivity coefficient, and P(v,t) is the cumulative distribution of cold protein residence time per unit mass. Parameters α and λ_p were determined based on model fits to initial changes in tumor volumes measured on SPECT/CT following both tracer and therapy. Average parameters for patients showing cold effect were obtained separately from those for patients not showing cold effect. For the present patients, average parameters used in the biologically effective dose calculation were α = 0.22 Gy⁻¹, λ_p = 0, for no cold effect and α = 0.41 Gy⁻¹, λ_p = 0.10 g_T/mg_p-h, with cold effect. For the proliferation effect, the effective cell-doubling time was set to be 150 d, representing approximately 12 mo to recurrence (2). Details of the calculation of RE(v,t) and P(v,t) from the decay-corrected activity distribution were given by Amro et al. (12).

Response

As part of the clinical protocol, patients were followed up with diagnostic CT or PET/CT at around 2 mo. In the present study, response was determined on the basis of these data because most nonresponders or partial responders go on to have alternative treatment after the initial follow-up. Tumors initially imaged on SPECT/CT were evaluated on the follow-up CT by the same specialist who defined the tumors for dosimetry. Unlike on the initial images, where volumes were defined for dosimetry, here perpendicular diameters were defined as this measure is routinely used in lymphoma response criteria. For each tumor, the longest diameter was defined on a transverse slice and a second, perpendicular, measurement was made on the same slice. At the tumor level, response was calculated by the percentage change in the product of perpendicular diameters at 2 mo, compared with that product for the baseline scan, which was the first SPECT/CT scan immediately after the tracer administration. At the patient level, response was calculated by the percentage change in the sum of the product of diameters for all tumors, compared with baseline. In addition, an overall response classification as progressive disease, stable disease, partial response, or complete response was made for each patient by evaluating all lesions based on the revised response criteria for malignant lymphoma (19). These criteria incorporate findings from PET/CT (when available).

Statistical Analysis

Pearson correlations were computed along with P values corresponding to a test for whether the correlation was significantly different from zero (P < 0.05 was considered statistically significant). These were computed using log(dose) as correlates of response. All analyses presented are exploratory in nature, and thus no multiplicity adjustments were made to P values. Correlation was assessed both at the tumor level and at the patient level. When evaluating correlation at the patient level, we calculated the mean value of each absorbed dose summary measure across all tumors within a subject. Positive or negative predictive values were calculated as simple proportions of subjects with absorbed dose values above or below a threshold that were responders or nonresponders. For this analysis, complete and partial responders were lumped together as responders.

RESULTS

SPECT/CT

Typical SPECT/CT images are shown in Figure 1. The initial tumor volumes and shrinkage during SPECT/CT are summarized in Table 1 (values for individual tumors are listed in Table 1 of the supplemental material [available online only at http://jnm.snmjournals.org]). For most tumors, significant shrinkage was measured on CT within days of the therapy administration and in some cases within days after the tracer administration.

FIGURE 1.

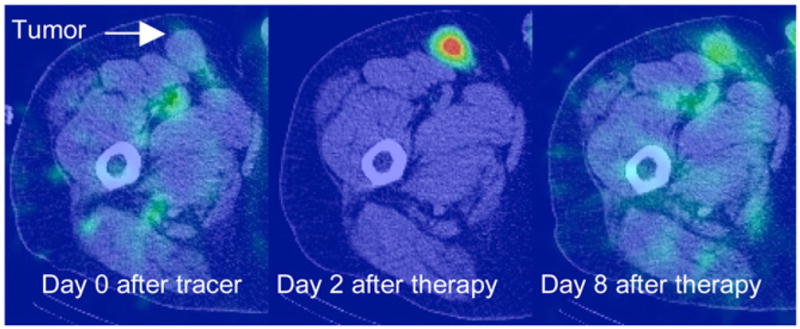
SPECT/CT images showing uptake in an inguinal tumor at day 0 after tracer, day 2 after therapy, and day 8 after therapy.

TABLE 1.

Summary of Tumor Dosimetry Results and Response

Parameter	Sample size	Median	Range
Initial tumor volume (mL)	60	34	2 to 423
Volume decrease during tracer SPECT/CT* (%)	60	12	−10 to 49
Volume decrease during therapy SPECT/CT† (%)	60	30	2 to 76
Decrease in product of diameters at 2 mo‡ (%)	60	72	−45 to 100
Average dose (cGy)	57	341	102 to 711
EUD (cGy)	57	391	113 to 764
Maximum dose (cGy)	57	508	162 to 1,404
D99 (cGy)	57	203	35 to 373
D80 (cGy)	57	269	58 to 466

^*Difference in volumes defined on first and last posttracer scans (6 d).

^†Difference in volumes defined on first and last posttherapy scans (~6 d).

^‡Difference in product of largest perpendicular diameters at 2 mo compared with the first posttracer imaging time point.

Results for individual tumors are given in the supplemental material.

Tumor Dosimetry

Nineteen subjects (with 57 tumors) had datasets complete enough for dosimetric evaluation, whereas 1 patient who developed human-antimouse antibodies had too few SPECT counts for dosimetry. Typical tumor dose-volume histograms are shown in the supplemental material demonstrating the nonuniformity of the absorbed dose distribution. Tumor dosimetry results (total delivered from the tracer and therapy) are summarized in Table 1, with values for individual tumors listed in the supplemental material. The maximum absorbed dose refers to the maximum value to any voxel within the tumor volume of interest. Minimum absorbed dose is not listed; instead, we have defined the measure D99 (or D80) as the absorbed dose received or exceeded by 99% (or 80%) of the tumor volume. These measures are more reliable than the minimum absorbed dose, which is based on the value at a single voxel and is highly susceptible to registration error and reconstruction artifacts at tumor boundaries.

The EUD is higher than the mean absorbed dose when the cold antibody effect is higher than the nonuniformity effect plus the cell proliferation effect. For comparison, we also calculated the EUD without the cold antibody effect. EUD (without cold) ranged from 77 to 550 cGy, with a median of 298 cGy. In the present study, the loss of effectiveness due to nonuniformity was not severe (ratio of EUD without cold to mean absorbed dose ranged from 0.72 to 0.94 with a median of 0.87) because tumor-absorbed dose values were relatively low. The loss of effectiveness increases as the mean absorbed dose increases (8).

Response

The response at 2 mo is summarized in Table 1. Response for individual tumors and patient response classifications are given in Supplemental Table 1. Complete responses were observed in 10 patients, partial responses in 4 patients, and stable disease in 6 patients. No patients met the criteria for progressive disease at 2 mo. PET data were available for 14 of 20 patients. At the time of this report, 6 mo of follow-up data were available for 18 of 20 patients. Of these, 7 of 9 patients who did not achieve a complete response had undergone alternative treatment (salvage chemotherapy or external-beam therapy). In 8 of 9 of the remaining patients, the 2-mo complete response classification was confirmed by the 6-mo imaging data. The one exception was patient 5, who relapsed at 6 mo.

Correlation Analysis Using Initial Shrinkage During SPECT/CT

We evaluated the relationship between the percentage reduction in tumor volume measured on SPECT/CT during therapy and each of the absorbed dose parameters of Table 1 (mean, maximum, D99, D80, and EUD). A statistically significant correlation was seen with D99 (r = 0.318; P = 0.016), D80 (r = 0.299; P = 0.024), and EUD (r = 0.473; P = 0.0002). When EUD was calculated without the cold effect term, the correlation was less robust (r = 0.292; P = 0.028).

Correlation Analysis Using Response at 2 Months

At the individual-tumor level, dose–response correlations were evaluated between the percentage reduction in the product of perpendicular diameters at 2 mo and the various absorbed dose measures of Table 1. The results are given in Table 2, and only the correlation with EUD was statistically significant (r = 0.357; P = 0.006). The tumor level dose response data are plotted in Figure 2 for both mean absorbed dose and EUD with a logarithmic fit. For EUD calculated without the cold effect term, the correlation was not statistically significant (r = 0.229; P = 0.087).

TABLE 2.

Pearson Correlations Between Various Dose Measures and Response at 2 Months Determined by Percentage Reduction in Product of Longest Diameters (Tumor Level) or Sum of Product of Diameters (Patient Level)

Parameter	Tumor level		Patient level
	rp	P	rp	P
Mean tumor dose	0.189	0.159	0.226	0.352
Maximum tumor dose	0.033	0.809	0.086	0.726
D99	0.164	0.222	0.193	0.429
D80	0.200	0.136	0.223	0.359
EUD	0.357	0.006	0.459	0.048

FIGURE 2.

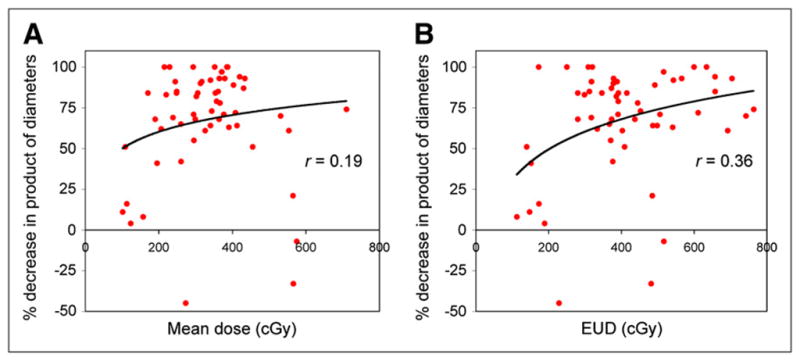
Response at 2 mo plotted against mean tumor-absorbed dose (A) and EUD (B), at tumor level (n = 57).

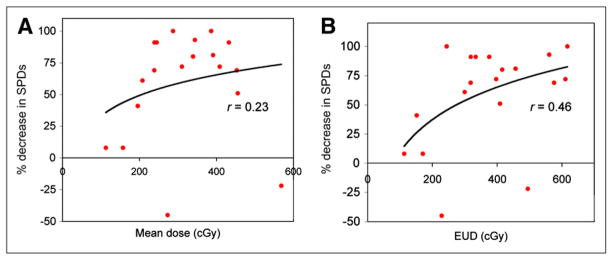
At the patient level, absorbed dose values were averaged over the multiple tumors for each patient, and the correlation with patient level response (based on sum of the product of diameters) was examined (Table 2). A statistically significant dose–response correlation was observed only with EUD (r = 0.459; P = 0.048). The patient-level dose–response data are plotted in Figure 3 for both mean absorbed dose and EUD with a logarithmic fit. For EUD calculated without the cold effect term, the correlation was not statistically significant (r = 0.274; P = 0.256).

FIGURE 3.

Response at 2 mo (based on sum of products (SPDs) of perpendicular tumor diameters) plotted against mean tumor-absorbed dose (A) and EUD (B), at patient level (n = 19). Dose values were averaged over multiple tumors of each patient.

Apart from the above dose–response evaluations, relationships were also examined between response at 2 mo and initial tumor volume and between response at 2 mo and early tumor shrinkage (measured during SPECT/CT). A statistically significant negative correlation was observed between the percentage reduction in the product of the diameters at 2 mo and the initial tumor volume (r = −0.33; P = 0.01), indicating that smaller tumors responded better. (This correlation did not translate to a statistically significant correlation between mean tumor-absorbed dose and initial tumor volume.) There was a high correlation between the percentage reduction in the product of the diameters at 2 mo and percentage reduction in tumor volume measured during posttherapy SPECT/CT (r = 0.55; P < 0.0001), showing that early shrinkage is a good indicator of response on follow-up CT.

Prediction Analysis

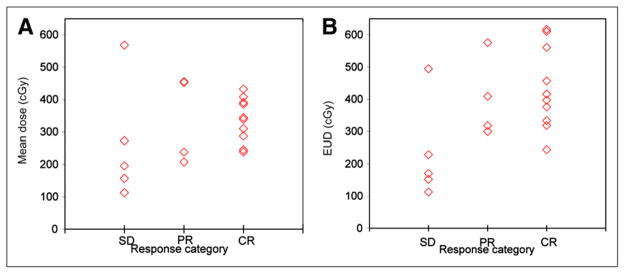
At the patient level, mean tumor-absorbed dose and EUD were plotted as a function of the overall response classification (Fig. 4). The median value of mean absorbed dose for patients with stable disease, partial response, and complete response was 196, 346, and 342 cGy, respectively. The median value of EUD for patients with stable disease, partial response, and complete response was 170, 363, and 406 cGy, respectively. To summarize the relationship between absorbed dose and overall response classification, positive and negative predictive values were computed. Based on Figure 4, a value of 200 cGy was chosen as a good value for separating responders (those achieving a partial response or complete response) from nonresponders. At this threshold, the positive and negative predictive values were 0.875 (14/16) and 1.0 (3/3), respectively, for both mean absorbed dose and EUD. Although choosing a threshold and estimating predictive values based on the same data can lead to optimistic bias, these results are nonetheless promising.

FIGURE 4.

Mean tumor-absorbed dose (A) and EUD (B) as function of patient response as assessed by Cheson et al. (19).

DISCUSSION

A fully 3D dosimetry calculation using SPECT/CT at multiple time points was performed to obtain absorbed dose distributions in the presence of tumor deformation and regression. Most past studies have relied on a constant tumor mass or volume when estimating the absorbed dose. The significant tumor regression measured within days of administration of the tracer (up to 49%) and therapy (up to 76%) in the present study demonstrates the need to consider regression when estimating absorbed dose. Because the amount of tracer administered was only 185 MBq, it can be inferred that the tumor shrinkage during administration was in response to the cold antibody. In a randomized study with ¹³¹I tositumomab and unlabeled tositumomab, the unlabeled antibody has been shown to have some therapeutic effect, but the effect was greatly enhanced by the addition of labeled antibody (20).

The mean tumor-absorbed dose values of the present study (102–711 cGy, with a median of 341 cGy) are consistent with those reported previously for ¹³¹I radioimmunotherapy of non-Hodgkin lymphoma (5,6). The mean tumor-absorbed dose did not have a statistically significant correlation with response, as is also consistent with previous reports (5–7). As recognized previously, evaluating correlations is more difficult for radioimmunotherapy than for other radiopharmaceuticals because of the intrinsic therapeutic efficacy of the unlabeled antibody (21,22). Limited clinical studies with other radiopharmaceuticals have demonstrated a statistically significant correlation between mean tumor-absorbed dose and response in radiopeptide therapy of neuroendocrine tumors with ⁹⁰Y-somatostatin analogs (23) and ¹³¹I-metaiodobenzylguanidine therapy of neuroblastoma (24). In these 2 studies, there was no confounding effect due to cold antibody, and significantly higher tumor-absorbed doses were delivered by administering higher activities.

The relevance of radiobiologic modeling in absorbed dose estimation has been well recognized (8,21), but to our knowledge this is the first time that EUD was used for patient dose–response evaluation in radionuclide therapy. The present EUD not only assessed the biologic effects of the nonuniform absorbed dose but also incorporated both the cold antibody and cell proliferation effects. Of the various absorbed dose measures considered here, a statistically significant correlation with response at 2 mo was demonstrated only with EUD. In the present work, correlations with dose-volume histogram summary measures such as D99 and D80 were also examined because it has been postulated that underdosing a part of the tumor results in treatment failure (8).

Although correlations were improved by using EUD, there was considerable scatter in the dose–response data and overlap in dose values for patients with stable disease, partial response, and complete response. One possible reason for the scatter and overlap is inaccuracies in methods used to quantify activity and estimate absorbed dose. To improve estimates, we used state-of-the-art hybrid imaging and in-house–developed algorithms for SPECT reconstruction and Monte Carlo–based dosimetry. However, inaccuracies can remain because of uncertainty in tumor volume determination, misregistration, limited imaging time points, assumption of uniform radial deformation when correlating changing tumor voxels, and approximations made when correcting for SPECT resolution effects. Even with 3D detector response compensation, partial-volume effects are a significant source of SPECT quantification error (15). In the present work, CT-volume–based recovery coefficients were applied to recover total target activity, but this does not correct for resolution effects at the voxel level. The finite SPECT resolution will tend to reduce any nonuniformities in the calculated tumor-absorbed dose distribution; however, the impact of this on EUD will be small in the present study because nonuniformity effects are more pronounced when the mean absorbed dose is high (8). It is difficult to estimate the overall error in tumor dosimetry due to the various inaccuracies, but we can expect the errors to be larger for smaller tumors. For example, quantification errors in ¹³¹I phantom studies with reconstruction methods similar to those used here were 4%, 11%, and 24% for target volumes of 60, 16, and 7 mL, respectively (25). In the present study, although tumors as small as 2 mL were analyzed, most were much larger (range, 2–423 mL; median, 34 mL). As more patients are enrolled in this ongoing study, we will investigate whether excluding smaller tumors from the analysis improves dose–response correlations.

Another possible reason for the scatter is that the study combined patients whose disease is diverse. When examining the dose–response plots of Figure 3, it is apparent that the 2 data points with negative response (tumor growth) at 2 mo are outliers. The correlation with response for both mean absorbed dose and EUD can be considerably improved if these 2 data points are excluded from the analysis. Although cell proliferation was included in the EUD model, an average value was used for the proliferation coefficient since data were not available to determine patient-specific values. If more information on disease status can be obtained for each patient, it may be beneficial to separate patients into subgroups when evaluating correlations. We also plan to use regression models to simultaneously evaluate the effect of multiple factors on response. For example, we can assess the correlation of absorbed dose with response while accounting for patient level differences in tumor burden (e.g., number of tumors and size). A model-based predictor may do much better at predicting response than the univariate analyses presented here.

Although promising, patient-level dose–response correlations and predictive values were estimated from data on only 19 patients and will need to be confirmed using more patients. Previously, we reported the strong correlation (r > 0.9) between tracer-predicted and therapy-delivered tumor-absorbed dose values for a subset of patients in the present study (16). If the dose–response correlations demonstrated in the present report hold or improve as more patients are enrolled in this ongoing study, the combined results will have important implications for tumor dosimetry–based treatment planning and also for improved clinical management.

CONCLUSION

Improved tumor dose–response correlations were demonstrated in ¹³¹I-tositumomab radioimmunotherapy patients when EUD incorporating the cold antibody effect was used instead of the conventionally used mean tumor-absorbed dose. This work demonstrates the importance of 3D calculation and radiobiologic modeling when estimating absorbed dose for correlation with outcome.