Genome-Wide Networks of Amino Acid Covariances Are Common among Viruses

Abstract

Coordinated variation among positions in amino acid sequence alignments can reveal genetic dependencies at noncontiguous positions, but methods to assess these interactions are incompletely developed. Previously, we found genome-wide networks of covarying residue positions in the hepatitis C virus genome (R. Aurora, M. J. Donlin, N. A. Cannon, and J. E. Tavis, J. Clin. Invest. 119:225–236, 2009). Here, we asked whether such networks are present in a diverse set of viruses and, if so, what they may imply about viral biology. Viral sequences were obtained for 16 viruses in 13 species from 9 families. The entire viral coding potential for each virus was aligned, all possible amino acid covariances were identified using the observed-minus-expected-squared algorithm at a false-discovery rate of ≤1%, and networks of covariances were assessed using standard methods. Covariances that spanned the viral coding potential were common in all viruses. In all cases, the covariances formed a single network that contained essentially all of the covariances. The hepatitis C virus networks had hub-and-spoke topologies, but all other networks had random topologies with an unusually large number of highly connected nodes. These results indicate that genome-wide networks of genetic associations and the coordinated evolution they imply are very common in viral genomes, that the networks rarely have the hub-and-spoke topology that dominates other biological networks, and that network topologies can vary substantially even within a given viral group. Five examples with hepatitis B virus and poliovirus are presented to illustrate how covariance network analysis can lead to inferences about viral biology.

INTRODUCTION

Viral genomes are usually small, and as a group, they are structurally very diverse. This places significant constraints on viral genetic coding patterns and leads to the variety of gene expression strategies and replication mechanisms that are summarized by Baltimore's seminal viral classification system (4). These constraints affect the selection pressures on viral genomes, often in ways not normally encountered by the genomes of cellular organisms. Although the effects of complex selective processes, such as epistasis and pleiotropy, on viral intragenomic interactions are partially understood in theoretical terms (24, 33, 37), observation of their effects on a genome-wide scale has proven difficult.

The multiple-sequence alignments that underlie most genetic analyses assume that each position in an alignment is independent of all others, and hence, the alignments are blind to intragenomic dependencies. Such dependencies are clearly of major biological importance, because folding of proteins and RNAs brings distant residues into close proximity, so there is more information in sequence sets than standard analytical methods reveal. One method to find long-distance genetic interactions is to identify covariances among a collection of related sequences. Covariance is present when the identity of a residue at one position in a sequence is at least partially dependent upon the identity of the residue at another position. Covariance has been widely used to evaluate RNA structure (27, 34, 36, 46, 69, 73) and less extensively to probe intraprotein interactions (26, 42, 53). We and others recently applied it to the full amino acid coding potential of the hepatitis C virus (HCV) genome (3, 11, 41). This genome-wide approach identifies covariances resulting from all possible causes, including selective pressures, such as interresidue contacts within a protein, allostery, interprotein interactions, genetic epistasis, and chance associations due to bottlenecks in the viral lineages.

HCV is a small enveloped hepatotropic flavivirus with an ∼9,600-nucleotide (nt) positive-polarity single-stranded RNA genome that causes hepatitis, cirrhosis, and liver cancer (43). HCV has 6 genotypes whose sequences differ from each other by >28% and multiple subtypes per genotype. Individual isolates of a given viral subtype differ from each other by ∼5 to 8% (68). Two independent genome-wide covariance analyses of HCV's complete coding potential revealed that about 10% of HCV's amino acid positions covary with one or more other positions, that covariances occur both within and between viral proteins, and that the covariances linked together into a single genome-wide hub-and-spoke network of interactions (3, 11). In these networks, the “nodes” are the covarying amino acid positions and the “edges” are the covariances between the positions. The hub-and-spoke network topology indicates that most nodes covary with only a few other nodes, but a few “hub” nodes covary with very many nodes (51).

To help evaluate the pressures that led to the development of the HCV covariance networks, we mapped all 273 genotype HCV intraprotein covarying pairs within the available crystal structures for the viral NS2, NS3, NS5A, and NS5B proteins (3). The vast majority of the pairs (255/273) were found on solvent-accessible surfaces of the proteins, and the residues in only one pair were close enough (≤7.5 Å between the closest atoms) to directly bind to each other. This indicates that the intraprotein covariant pairs were due to either long-range functional interactions (allostery or epistasis) or chance associations. Campo et al. (11) employed a different covariance algorithm with HCV 1b sequences and found a network of covariances extending throughout the viral genome, similar to the networks we identified. They explicitly addressed the evolutionary implications of the networks and concluded that the network formed by coordinate evolution of multiple residue positions (11). Overall, the observations that the large majority of the covarying positions are on the surfaces of the proteins and that they usually involve residues on different proteins support the hypothesis that they often represent compensatory adaptations within multiprotein complexes or other forms of genetic epistasis.

Our HCV covariance network analyses (3) were conducted using viral sequences from patients in the Virahep-C study (15, 21) for whom the outcome of alpha-interferon-based antiviral therapy was known. The covariance networks formed by sequences from responders to therapy differed from those formed by the nonresponder sequences both in their in connection patterns and in network characteristics, such as the density of the connections among the covariant positions. Similar conclusions were reached by Lara et al. (41) using the pre- and posttherapy Virahep-C HCV sequences that we generated (12). Lara et al. developed two Bayesian network models that could distinguish primary nonresponse to therapy from partial response or relapse with >85% accuracy (41). These associations of covariance network patterns with a medically relevant phenotype imply that patterns in the covariance networks could be used as biomarkers for complex phenotypes if methods to recognize the network configuration present in a given viral sequence can be developed.

Here, we extended these covariance analyses to ask (i) whether amino acid covariance networks are present in diverse viral families using primary field isolates whenever possible and (ii) if networks are present, what they may imply about viral biology.

MATERIALS AND METHODS

Sequence acquisition and curation.

Sequences for all viruses examined were obtained from the NIAID Virus Pathogen Resource Database and Analysis Resource (http://www.viprbrc.org). Sequences from naturally occurring isolates were used whenever possible by eliminating strains identified as laboratory adapted or vaccine derived in the GenBank record. If a subset of the total number of acceptable sequences was used, the sequences were randomly selected. All sequences were confirmed to be independent either by reciprocal BLASTP analysis or by importing the alignment into ToPali and using the summary information function (47).

All sequences in these analyses must be colinear to maintain a consistent numbering system, so infrequent insertions were manually deleted. The first open reading frame (ORF) in the hepatitis E virus (HEV) sequences contains a polyproline stretch of ∼52 amino acids (57, 58) that failed to align and hence was removed from the covariance analyses. The first 240 residues of the Crimean-Congo hemorrhagic fever virus (CCHV) M segment contains a stretch of variable, mucin-like repeats that failed to align (19), so this repetitive sequence was removed. All alignments were analyzed in ToPali, and neighbor-joining phylogenetic trees were generated (F84/WAG+G with 30 bootstrap runs). The accession numbers for all sequences are listed in Table S1 in the supplemental material, and the phylogenetic trees are shown in Fig. S1q to ag in the supplemental material.

Sequence alignments and covariance identification.

Alignments for use in the covariance algorithm were generated using MUSCLE and exported in msf format (23). Covariant positions in the sequence alignments were identified by applying the observed-minus-expected-squared (OMES) approach to all possible pairs of amino acid positions using our previously described methods (3). To identify the covarying pairs, we calculated for every possible pair of columns i and j a score S using observed and expected pairs:

$$S=\frac{{\displaystyle \sum _1^L{\left(N_{\text{obs}}-N_{\exp }\right)}^2}}{N_{\text{valid}}}$$

where L is the number of observed pairs and N_obs is the number of occurrences for a pair of residues. The expected number for the pair is given by the following equation:

$$N_{\exp }=\frac{C_{\text{xi}}{C}_{\text{yj}}}{N_{\text{valid}}}$$

where N_valid is the number of sequences in the alignment that are nongap residues, C_xi is the observed number of residues x at position i, and C_yj is the observed number of residues y at position j. The expected number of column pairs calculated in this manner provides a null model for comparisons of the observed pairs.

To determine the cutoff score for S to be used for each alignment, the number of covarying pairs was plotted over a range of scores. This curve was compared to a similar curve generated from alignments of sequences in which the residues at positions of variance were shuffled, and the score cutoff at which the number of covarying pairs in the shuffled alignment was ≤1% of the number of covarying pairs in the unshuffled alignment was used to define the covariances. All covariances are listed in Table S2 in the supplemental material.

Network analysis.

Networks were generated from the covariance lists as previously described (3). The covariance scores were converted to a simple interaction file (SIF) format at the chosen OMES score cutoff using a Python script. Network views were generated using Cytoscape (67), and basic topological parameters were determined using the Cytoscape plug-in Network Analyzer (2).

Structural mapping and evaluation of selective pressures.

Positions of covariance were plotted using the PyMol Molecular Graphics System version 1.3 on the dengue virus (DV) env (Protein Data Bank [PDB] 1TG8), NS3 helicase (PDB 2BMF), and NS5 (PDB 2P3L) proteins; the poliovirus type 1 (PV1) capsid (PDB 1HXS), 3C protease (PDB 1L1N), and 3D RNA polymerase (PDB 1RA6) proteins; and the reverse transcriptase domain molecular model (17) of the hepatitis B virus polymerase. Selective pressures on codons in selected viral genomes were evaluated using the single-likelihood ancestor-counting method (56) with the HKY85 nucleotide substitution bias model as implemented at the DataMonkey website (http://www.datamonkey.org).

RESULTS

Standardization of the covariance definition.

To establish a consistent definition of covariance applicable to the wide range of viruses in Table 1, we identified the number of covariances that would occur by chance in a given alignment of sequences and then used this pattern to define the covariance score cutoff at which the number of chance covariances was ≤1% of the total number of covariances in the alignment.

Table 1.

Viruses employed

Virus species	Abbreviation	Genotype	Family	Genus	Genome structurea	No. of genome segments	No. of sequences	Genome size (bp)	Coding capacity (aa)b	Avg pairwise identity (%)
Hepatitis C virus	HCV	1a	Flaviviridae	Hepacivirus	ssRNA, + polarity	1	300	9,033	3,011	94.9
		1b					300	9,030	3,010	94.2
GB virus C	GBV-C		Flaviviridae	Unassigned	ssRNA, + polarity	1	27	9,392	2,842	96.6
Dengue virus	DV	2	Flaviviridae	Flavivirus	ssRNA, + polarity	1	100	10,173	3,391	98.2
West Nile virus	WNV		Flaviviridae	Flavivirus	ssRNA, + polarity	1	64	11,000	3,448	98.9
Hepatitis A virus	HAV		Picornaviridae	Hepativirus	ssRNA, + polarity	1	33	7,478	2,228	98.2
Poliovirus	PV	1	Picornaviridae	Enterovirus	ssRNA, + polarity	1	63	7,441	2,209	97.7
Hepatitis E virus	HEV	3	Hepeviridae	Hepevirus	ssRNA, + polarity	1	41	7,176	2,432c	97.8
Crimean-Congo hemorrhagic fever virus	CCHV		Bunyaviridae	Nairovirus	ssRNA, + polarity	3	24	19,146	5,871d	94.8
Rabies virus	RV	1	Rhabdoviridae	Lyssavirus	ssRNA, − polarity	1	26	11,932	3,600	95.8
Hepatitis delta virus	HDV	1	Unassigned	Deltavirus	ssRNA, − polarity	1	75	1,680	195e	85.1
Influenza virus	IV-A	A	Orthomyxoviridae	Influenzavirus A	ssRNA, − polarity	8	32	13,400	4,555	99.1
Parvovirus B19	B19	2	Parvoviridae	Erythrovirus	ssDNA, mixed polarity	1	20	5,594	1,452	98.0
Hepatitis B virus	HBV	B	Hepadnaviridae	Orthohepadnavirus	Partially double-stranded DNA	1	100	3,221	1,609	97.3
		C					100	3,215	1,609	95.9
		D					100	3,182	1,587	97.1

^ass, single stranded; +, positive; −, negative.

^baa, amino acids.

^cCoding sequences for CDS1 were edited to remove the repetitive region.

^dCoding sequences for the M segment were edited to remove the highly variable first 240 aa.

^eSmall form of the HDV delta antigen.

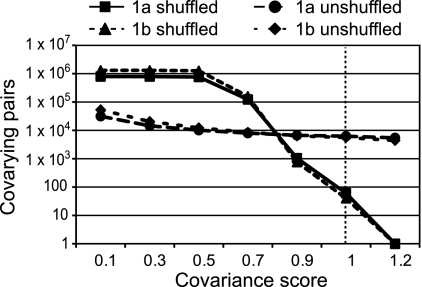
To establish the number of random covariances expected in an alignment of a given set of sequences, we extracted the amino acids at the variable positions in the alignment, shuffled the order of the extracted residues, and reinserted them into their source sequence at positions of variance. The shuffled sequences were forced into a colinear alignment with the original alignment, covariance scores were calculated for all possible amino acid pairs, and the numbers of covarying pairs at increasing score cutoff values were plotted. Figure 1 shows these plots for alignments of 300 HCV subtype 1a and 1b sequences and their shuffled controls. Shuffling the variable positions would be predicted to disrupt high-scoring, biologically relevant covariances and to increase the number of low-scoring pairs that occurred by chance. As predicted, very many covariances were detected in the shuffled alignments at low scores, and the number of covarying pairs dropped rapidly within the score cutoff range of 0.7 to 0.9. Many fewer covariances were found in alignments of natural sequences at low cutoff scores, but there were many more high-scoring pairs than in the shuffled alignments. At a covariance score of 1.0, the number of covarying pairs in the alignments of HCV 1a and 1b shuffled sequences was ≤1% of the number of covariances for the corresponding unshuffled alignments, yielding a false-discovery rate of ≤1%. This procedure was used to define the covariances in all subsequent alignments, and in all cases, a score cutoff of approximately 1.0 was used.

Fig 1.

Effect of increasing the covariance cutoff score on the number of covariances for alignments of natural and scrambled HCV sequences.

HCV covariance networks.

The presence of networks among the covariances in alignments of the 300 randomly selected HCV 1a and 1b sequences was assessed using Cytoscape, as we had previously done for the Virahep-C HCV sequences (3). About 10% of the residue positions in the new alignments covaried with one or more other positions, with high average covariance scores for the 1a network (S = 4.9 compared to a cutoff value of 1.0) and moderate average scores for 1b (S = 2.3) (Table 2). Phylogenetic analysis revealed no deep splits in the tree structure for these sequences that would be expected to skew the covariance calculations (Fig. 2A; see Fig. S1q in the supplemental material).

Table 2.

Covariance network characteristics for all viruses examined

Virus network	Genotype	No. of residue positions (nodes)	No. of covarying pairs (edges)	Avg covariance score	Avg connectivity	Density	Heterogeneity	Centralization	Avg clustering coefficient	Characteristic path length	Power law coefficient	Topology
Hepatitis C virusa	1a	251	6,226	4.9	49.6	0.21	0.94	0.37	0.64	2.2	0.40	Hub and spoke
	1b	328	5,589	2.3	34.1	0.10	0.96	0.36	0.46	2.3	0.59	Hub and spoke
GB virus C		82	1,011	1.9	24.6	0.30	0.71	0.33	0.65	2.1	NAb	Random
Dengue virus	2	56	427	4.0	15.2	0.27	0.58	0.27	0.75	2.2	NA	Random
West Nile virus		26	115	2.9	8.8	0.35	0.59	0.44	0.76	1.8	NA	Random
Hepatitis A virus		37	335	3.0	18.1	0.50	0.44	0.32	0.84	1.6	NA	Random
Poliovirus	1	99	1,736	2.6	35.1	0.36	0.43	0.34	0.77	1.8	NA	Random
Hepatitis E virusc	3	50	208	2.0	8.3	0.17	0.88	0.29	0.53	2.5	NA	Random
Crimean-Congo hemorrhagic fever virusd		432	16,595	1.5	76.8	0.18	0.62	0.29	0.66	2.1	NA	Random
Rabies virus	1	166	2,541	1.7	30.6	0.19	0.73	0.32	0.62	2.4	NA	Random
Hepatitis delta virus	1	37	128	1.6	7.0	0.19	0.61	0.27	0.39	2.2	NA	Random
Influenza virus	A	50	671	2.6	26.1	0.55	0.43	0.28	0.81	1.4	NA	Random
Parvovirus B19	2	45	485	1.5	21.4	0.49	0.45	0.37	0.83	1.6	NA	Random
Hepatitis B virus	B	78	1,303	2.5	33.4	0.43	0.57	0.35	0.81	1.7	NA	Random
	C	104	1,616	4.7	31.1	0.30	0.65	0.31	0.70	2.1	NA	Random
	D	89	1,255	2.3	28.2	0.32	0.49	0.32	0.74	1.9	NA	Random

^aNetworks were formed from 300 sequences for each subtype.

^bNA, not applicable because the correlation coefficient for the power law calculation was below 0.5.

^cCoding sequences for CDS1 were edited to remove the repetitive region.

^dCoding sequences for the M segment were edited to remove the highly variable first 240 aa.

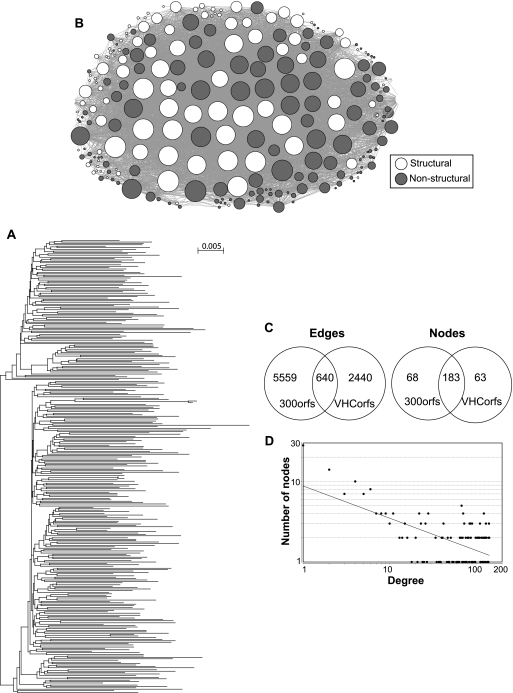
Fig 2.

Covariance network for the set of 300 hepatitis C virus 1a sequences. (A) Phylogenetic tree for the HCV 1a sequences. (B) Network graph. The circles represent the amino acid positions (nodes), and the lines (edges) between the nodes represent covariances. The sizes of the nodes are proportional to the number of edges they contact. (C) Comparison of the numbers of edges and nodes in the original HCV covariance networks generated from 47 HCV subtype 1a sequences (VHCorfs) and in the new networks generated from 300 1a sequences (300orfs). (D) Degree distribution plot fitted to the power law for the network in panel B.

The covariance sets each formed a single network that contained >99% of the covariances (Fig. 2B; see Fig. S1a in the supplemental material). The network extended throughout the viral coding region, with similar numbers of covarying positions in the structural and nonstructural genes. The networks had relatively low density, relatively high heterogeneity, and short characteristic path lengths (Table 2; definitions of the metrics are in references 14 and 20). The majority of the nodes (covarying positions) in these networks overlapped with the nodes in the previously described Virahep-C networks, but the overlap in the edges (covarying pairs) was smaller (Fig. 2C). This was expected, because the larger number of sequences increased the detection power for covariances, whereas the number of covarying positions remained relatively constant because the number of positions at which variance (and hence potential covariance) exists is limited. The degree (number of edges per node) distribution plot for the HCV subtype 1a and 1b networks followed the inverse-power law (Fig. 2D; see Fig. S1a in the supplemental material), where the probability that any node has k edges is given by the following equation: P(k) = −γ log(k) (1, 5). The γ value was 0.40 for subtype 1a and 0.59 for 1b (Table 2), indicating that both networks had hub-and-spoke topologies in which there were no discrete subdomains.

We also asked if a genotype 1 level HCV network could be identified by combining the 300 HCV subtype 1a and 300 1b sequences into a single alignment. The deep phylogenetic split in the alignment led the OMES algorithm to identify all subtype-specific differences as covariances, resulting in >90,000 covarying pairs. Therefore, the OMES method is inappropriate for sequence sets with deep phylogenetic divisions. Consequently, subsequent analyses employed sequences selected from the lowest possible taxonomic division of the respective viral groups, and the phylogenetic trees were inspected to ensure that they lacked deep divisions. This led to pairwise identities among the various viral groups that were comparable to the pairwise identities in HCV subtypes 1a and 1b, where the OMES algorithm previously performed acceptably (Table 1).

Effect of sequence number on the covariance networks.

Our previous network analyses for HCV employed 16, 32, or 47 Virahep-C sequences each for subtypes 1a and 1b (reference 3 and unpublished data). To determine how this small number of sequences may have affected the networks, we compared parameters for networks generated with increasing numbers of HCV 1a sequences.

Overall, the network formed from 300 HCV 1a sequences was very similar to the networks formed from 16, 32, 47, or 100 randomly selected sequences as measured by key network metrics, including formation of a single network, density, heterogeneity, centralization, average clustering coefficient, characteristic path length, γ value, and topology (Table 3). These characteristics were also shared by the network formed from an alignment of 300 non-Virahep-C subtype 1b sequences (Table 2). Therefore, the basic network characteristics were identified from rather small sequence sets, and the major effect of increasing the number of sequences from 16 to 300 was to obtain greater sensitivity in identifying covariances, with a concomitant increase in the average connectivity and density. Consequently, for the remaining analyses, we employed 100 randomly selected sequences if more than 100 were available or all sequences if fewer than 100 were available. The caveats to this approach are that the sequences must be representative of the viral genomes in circulation (which is unknown in most cases) and that greater confidence should be placed in metrics for networks derived from larger data sets.

Table 3.

Network characteristics for HCV subtype 1a alignments of various sizes

Alignment sizea	No. of residue positions (nodes)	No. of covarying pairs (edges)	Avg covariance score	Avg connectivity	Density	Heterogeneity	Centralization	Avg clustering coefficient	Characteristic path length	Power law coefficient	Topology
16	109	712	1.4	13.1	0.12	1.05	0.30	0.46	2.5	0.56	Hub and spoke
32	152	1,206	1.8	15.9	0.11	1.15	0.30	0.41	2.9	0.67	Hub and spoke
47	171	1,416	1.7	16.6	0.10	1.11	0.27	0.38	2.7	0.70	Hub and spoke
100	195	3,199	3.0	32.8	0.17	1.01	0.39	0.59	2.2	0.42	Hub and spoke
300	251	6,226	4.9	49.6	0.21	0.94	0.37	0.64	2.2	0.40	Hub and spoke

^aNumber of sequences.

Evaluation of the possibility that the networks may be computational artifacts.

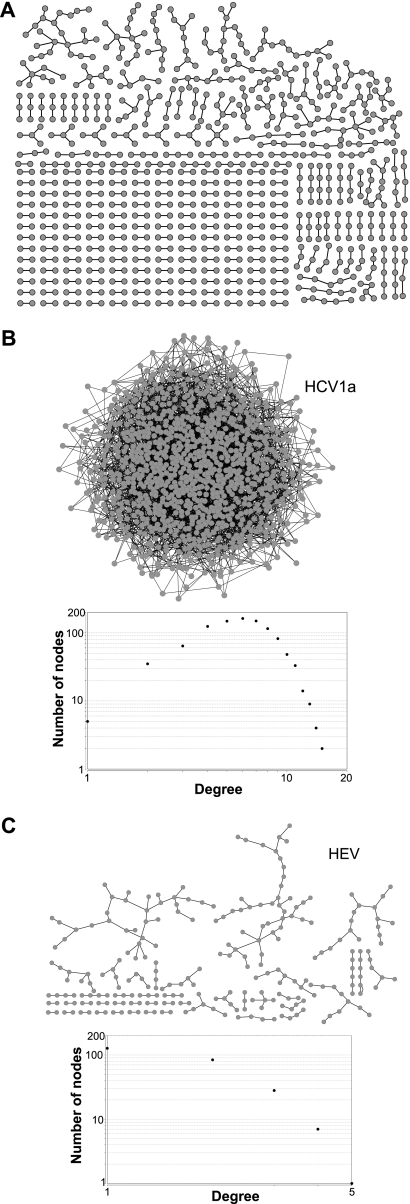
The possibility that the covariance networks may have been artifacts of our computational approach was evaluated in two ways. First, we graphed the 807 nodes and 543 edges in the shuffled control alignment of 300 HCV 1a sequences at a covariance cutoff value of 0.9 (Fig. 3A). The largest network formed by these irrelevant covariances contained only 22 nodes. Furthermore, the overall density of this set of irrelevant networks was 0.001, and their average connectivity was 1.3, compared to a density of 0.21 and average connectivity of 49.6 for the intact network formed from the natural sequences. Similar results were obtained when biologically irrelevant covariances from alignments of randomized sequences for other viruses were graphed (data not shown). Second, we generated 3,199 random associations among the 994 variable positions in the HCV 1a alignments of 100 sequences to mimic the number of covariances in an alignment of 100 HCV 1a sequences. These pairings created an intact network that looked superficially like the natural networks (Fig. 3B), but the network metrics revealed it to be fundamentally different. The degree plot formed a smooth arc rather than a descending line, and it had many more nodes (994 versus 195) and much lower connectivity (6.4 versus 32.8), density (0.006 versus 0.17), centralization (0.009 versus 0.39), and average clustering coefficient (0.007 versus 0.59) than the natural network. We also created 208 random associations of residues among the variable positions in the HEV alignment to mimic the number of covariances in the HEV network (Fig. 3C) (see below). This random covariance set failed to form a network. Therefore, formation of a single network containing the vast majority of the covariances in the viral genomes as observed for all viruses examined here was not an artifact of chance.

Fig 3.

Randomly associating residue positions does not generate networks similar to the viral covariance networks. (A) Networks generated from covariances in a control hepatitis C virus alignment of 300 sequences in which residues at positions of variance were scrambled. (B) Network and degree distribution plot generated from 3,199 randomly linked positions to mimic the number of edges in the alignment of 100 HCV 1a sequences. (C) Network and degree distribution plot generated from 208 randomly linked positions to mimic the number of edges in the alignment of 41 HEV sequences.

Levels of information revealed by covariance analyses.

This example with HCV shows the three levels of increasing complexity in covariance network analyses. The first level addresses the pairwise interactions (covariances), including their number and strength (S value). For HCV, about 10% of the positions covaried with relatively high S values that are indicative of relatively strong genetic linkages (typically, an S value of 2 to 5 compared to a cutoff of 1.0 for a ≤1% false-discovery rate). The second level of complexity is the network connectivity, characterized by whether the covariances link together into a network, the number of independent networks formed, and the density of the network connections. For HCV, this is characterized by the presence of a single network with a modest density. The highest level of complexity is network topology, which describes patterns among the connections within a network and is most easily discerned from the degree distribution plot. For HCV, the topology was nonhierarchical hub and spoke, implying that residues found at the most highly connected nodes have a very strong influence on the identities of residues at the less connected nodes. Although hub-and-spoke networks strongly predominate in biology (6, 51), other topologies, such as linear, star shaped, and random, are possible. Each of these topologies has its own implications about how the components of the network interact.

Covariances in other flaviviruses.

We expanded our assessment of viral covariance networks to three other members of the family Flaviviridae. GB virus C (GBV-C) is a parenterally transmitted lymphotropic virus that is moderately related to HCV (60). Dengue virus (DV) and West Nile virus (WNV) (28) are insect-vectored flaviviruses distantly related to HCV. Full-genome sequences (GBV-C, n = 27; DV type 2 [DV2], n = 100; and WNV, n = 64) were downloaded and confirmed to be independent. The amino acid sequences for each sequence set were aligned, covariances were identified at a false-discovery rate of ≤1%, and the presence of networks among the covariances was evaluated as described above.

The number of covarying positions in the alignments for these three viruses ranged from 26 (0.75% of the positions) in WNV to 82 (2.9% of the positions) in GBV-C (Table 2). This was primarily due to differences in the average pairwise identity in the alignments, with an R² value of 0.93 for the inverse linear relationship between the number of nodes and percent identity. The average covariance scores for GBV-C, DV2, and WNV were 1.9, 4.0, and 2.9, respectively, due in part to the increasing sensitivity associated with larger sequence sets.

We mapped the covarying pairs for DV2 onto all available protein crystal structures for the virus. Ten covariant positions were within the env structure, eight were in the NS3 helicase structure, and two were in the NS5 structure. All of these positions covaried with other positions in the same protein and also with positions in other proteins. Similar to what we previously reported for HCV subtypes 1a and 1b (3), all of these covariant positions were on solvent-accessible surfaces of the proteins, and none of the residues in intraprotein pairs were close enough to bind directly to each other.

Like HCV, each of the other flavivirus covariance sets formed a single genome-wide network containing essentially all of the covariances, with many positions from both the structural and nonstructural genes (see Fig. S1f to h in the supplemental material). All three of these networks were denser than the HCV networks (Table 2). Unlike the HCV networks, the degree distribution plot of these networks revealed a large proportion of highly connected nodes. Consequently, these plots did not follow the power law, and the networks were less heterogeneous than the HCV networks (Table 2; see Fig. S1f to h in the supplemental material). This indicates that the networks formed by GBV-C, DV2, and WNV had random topologies in which there were no discernible patterns among the node connections rather than the hub-and-spoke topology of the HCV networks.

Therefore, genome-wide covariance networks are widespread in the Flaviviridae, with the size of the network being affected by the average genetic distance among the viral sequences. However, network topology was not conserved among the flaviviruses.

Covariances in other single-stranded positive-polarity RNA viruses.

Networks were evaluated in four additional single-stranded positive-polarity RNA viruses, three with unsegmented genomes (hepatitis A virus [HAV], PV1, and HEV), and one with a tripartite segmented genome (CCHV) (Table 1). HAV (30) is a picornavirus for which we were able to analyze 33 independent genomes. PV1 (54, 59) is a picornavirus for which 63 full-ORF sequences were identified. Unlike those of the other viruses, all of the PV1 sequences were descended from the vaccine strains rather than primary field isolates. HEV (25) is a hepevirus for which 41 genomes could be analyzed, and CCHV is a bunyavirus (62) for which 24 independent genomes could be assessed.

Thirty-seven residue positions that covaried with one or more other positions were identified for HAV (1.75% of the positions), 99 covariant positions were found for PV1 (4.5% of the positions), 50 covariant positions were found for HEV (2.1% of the positions), and 432 positions covaried in CCHV (7.4% of the positions) (Table 2). The mean covariance scores for PV1, HAV, and HEV were moderate (S = 2.6, 3.0, and 2.0, respectively), but they were weak for CCHV (S = 1.5). Again, the percentage of the genome that was covariant was inversely proportional to the mean pairwise identity in the alignments, and the modest average covariance scores for HAV, HEV, and CCHV were partially due to the relatively small number of sequences available.

The 51 positions forming 254 covariances within the VP1, VP2, VP3, VP4, 3C, and 3D proteins of PV1 were mapped onto the available crystal structures. All of these positions covaried with positions both in the same protein and in other proteins. Similar to what we found for HCV (3) and DV2, all of these covariant positions were on solvent-accessible surfaces of the proteins. Thirty-five of 254 covariances (13.8%) of the residues in intraprotein pairs were close enough to potentially bind directly to each other (≤16 Å between α-carbon atoms). The availability of the full PV1 capsid structure (29) allowed us to evaluate the higher-order organization of covariant residues in the VP1 to -4 proteins. There were 217 covariances between 29 residues within or between the capsid proteins, for which we could evaluate 1,953 possible intra- or intercapsomere interactions. Twenty-three of the 29 covariant positions, representing 25 out of 217 covariances (11.5%), were close enough to possibly touch their covariant partner in at least one of their potential intracapsid interactions. Nine of these covariances were between different capsid proteins. Eighteen of them were between residues within the same capsomere, five crossed the 3-fold axis of symmetry, and two crossed the 5-fold axis of symmetry. These 25 covariances formed five subnetworks, four of which overlapped the receptor binding site on the capsid (7).

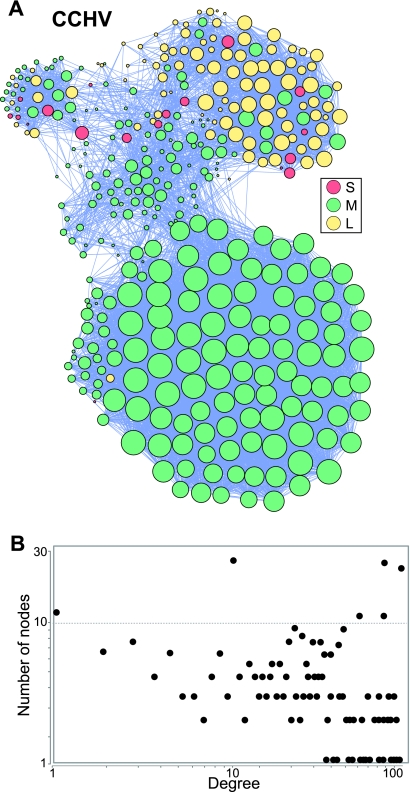
The covariances for HAV, PV1, HEV, and CCHV each formed a single network that contained all or nearly all of the covariant positions and included residues from both the structural and nonstructural regions of the genomes (Fig. 4; see Fig. S1i to k in the supplemental material). The HAV and PV1 networks were relatively dense, but the HEV and CCHV networks had low densities (Table 2). All four degree distribution plots failed to follow the power law due to a large number of highly connected nodes, leading to random network topologies. The CCHV network had clear subnetworks that were largely coincident with the genomic segments (Fig. 4). Therefore, all positive-polarity single-stranded RNA viruses examined had extensive networks of intragenomic genetic dependencies extending through their structural and nonstructural genes.

Fig 4.

Covariance network for the Crimean-Congo hemorrhagic fever virus. (A) Network graph. The node color indicates the viral genomic segment, and the node sizes are proportional to the number of edges contacting each node. (B) Degree distribution plot for the network.

Covariances in single-stranded negative-polarity RNA viruses.

Three negative-polarity single-stranded RNA viruses were examined next, two unsegmented (rabies virus [RV] and hepatitis delta virus [HDV]) and one segmented (influenza A virus [IV-A]) (Table 1). RV is a rhabdovirus (18, 45) for which we were able to examine 26 genomes from independent field isolates, and HDV (71) is an unassigned viroid-like satellite virus for which 75 genotype 1 genomes could be assessed. IV-A is an orthomyxovirus (74) that shows substantial time-dependent genetic variation, as variants are replaced on an annual basis. Preliminary analyses of the available IV-A sequences revealed deep phylogenetic splits, the latest of which corresponded to sequences collected before 2005, and covariance analyses using the entire data set revealed patterns dominated by the time-dependent phylogenetic divides. Consequently, we restricted our analysis to 32 sequences from samples collected at geographically diverse sites between 2005 and 2009 plus 1 sample collected in 2003 that clustered with the later sequences.

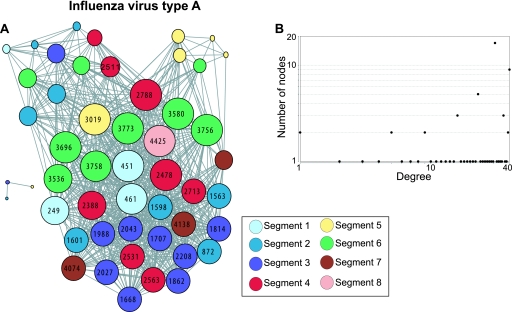
The RV alignments had 166 covariant positions (6.2% of the coding positions); 37 covariant positions were found for HDV (19% of the positions), and 50 were found for IV-A (1.1% of the positions). The mean covariance scores were moderate for IV-A and weak for RV and HDV (S = 2.6, 1.7, and 1.6, respectively) (Table 2). As before, an inverse relationship was observed between the average pairwise identity in the alignments and the proportion of the viral positions that were covariant. Again, each of the covariance sets formed a single genome-wide network that contained essentially all of the covariant positions (Fig. 5; see Fig. S1l to m in the supplemental material). As with the other viruses, the networks contained many positions from both the structural and nonstructural genes (HDV encodes a single protein that functions both in RNA replication and as a virion component). The IV-A networks had a high density, whereas the RV and HDV networks had relatively low densities (Table 2). The degree distribution plots for these three networks did not follow the power law. The low number of nodes in the HDV network made unambiguous characterization of its topology difficult, but it appeared to be random. The RV and IV-A networks both had random topologies, and the IV-A network had weakly defined subnetworks (Table 2 and Fig. 5; see Fig. S1l in the supplemental material).

Fig 5.

Covariance network for influenza virus A. (A) Network graph. The sizes of the nodes are proportional to the number of edges that they contact. The nodes are color coded by segment, and the node numbers indicate the position in the concatenated gene alignments. See Table S2 in the supplemental material for a key to the numbering of the various genes. (B) Degree distribution plot.

Therefore, covariance networks in negative-polarity virus genomes resembled the networks in most of the positive-polarity RNA viruses in that each network was genome-wide, included essentially all covariances in a single network, and had a random topology. The subnetworks in the IV-A network were less distinct than the subnetworks formed by the other segmented virus we examined (CCHV), and they were not coincident with the viral genetic segments. Therefore, although segmentation of a viral genome may influence the intragenomic genetic associations reflected in the networks, it is not necessarily a dominant factor.

Covariances in a single-stranded mixed-polarity DNA virus.

Parvovirus B19 (65) has a small single-stranded DNA genome in which the plus- or minus-polarity strand can be packaged into virions (Table 1). We identified 20 independent sequences for which covariance analyses could be conducted. The 485 covariances between 45 nodes in these alignments had a low average covariance score of 1.5 and formed a single network comprised of 3.1% of the 1,452 viral amino acids. The network contained many covarying residues from both the structural and nonstructural genes, and it had a high density (Table 2; see Fig. S1n in the supplemental material). The degree distribution plot did not follow the power law, again due to a large proportion of highly connected nodes leading to a random network topology. Overall, the network parameters for the B19 network were similar to the parameters observed for the majority of the RNA viruses we examined, including average connectivity, density heterogeneity, clustering coefficient, characteristic path length, and topology (Table 2).

This indicates that covariance networks can exist in DNA viruses if they have sufficient genetic diversity, and hence, genome-wide amino acid covariance networks are not solely a property of RNA viruses.

Covariances in a partially double-stranded DNA virus.

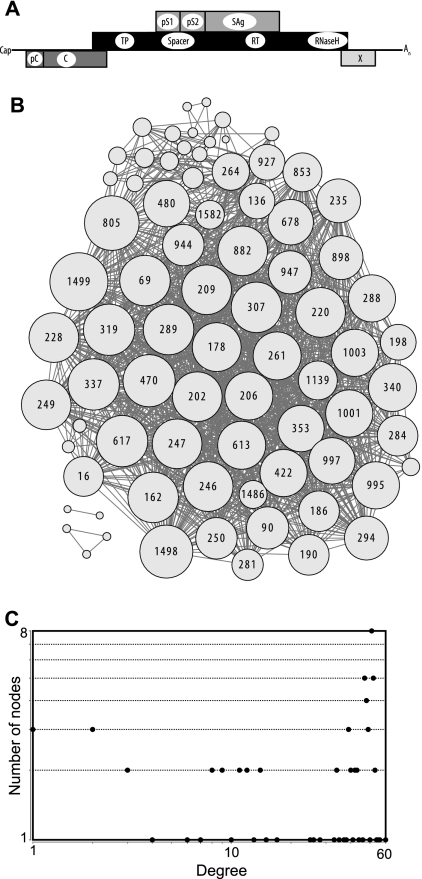
Finally, we examined hepatitis B virus (HBV) (63) because it is a partially double-stranded DNA virus with adequate genetic diversity (38, 39). Furthermore, over half of its genome encodes two proteins simultaneously in overlapping frames (Fig. 6A), and this unusual genetic organization may have impacted its intragenomic genetic interactions.

Fig 6.

Covariance network for hepatitis B virus genotype B. (A) HBV genetic organization in its linear RNA phase. Cap, mRNA cap; pC, pre-C coding region that, together with the C sequences, encodes the HBeAg. C, core gene; TP, terminal protein domain of the polymerase gene; Spacer, spacer domain of the polymerase; RT, reverse transcriptase domain of the polymerase; RNaseH, RNase H domain of the polymerase; pS1, the pre-S1 domain of the largest of the three carboxy-coterminal surface proteins; pS2, the pre-S2 domain of surface proteins; SAg, the smallest surface protein (HBsAg); X, X gene; A_n, polyadenyl tail. The X and pre-C regions overlap in the circular DNA phase. (B) Network graph. The sizes of the nodes are proportional to the number of edges they contact, and the node numbers indicate the positions in the concatenated gene alignments (see Table S2 in the supplemental material). (C) Degree distribution plot.

One hundred independent sequences each were obtained for HBV genotypes B, C, and D (Table 1); amino acid sequences were extracted from their overlapping genomic positions; and the sequences were aligned. Covariances within the alignments were identified at a ≤1% false-discovery rate, pseudocovariances stemming from variation at a single nucleotide affecting overlapping codons were manually eliminated, and the presence of covariance networks was assessed as usual.

About 5% of the HBV amino acid positions covaried with one or more other positions at moderate to high average covariance scores (S = 2.3 to 4.7) (Table 2), consistent with the inverse relationship between mean pairwise identity in the sequences and the proportion of covarying positions in the viral coding capacity observed with the other viruses. Approximately half of the HBV covariances were intergenic (Table 4). The large majority (83 to 92%) of the covariances involved the viral polymerase, which accounts for about half of the viral coding potential. Covariances were overrepresented in the spacer domain of the polymerase and in the pre-S1 region of the largest surface protein (Table 4), but these overrepresentations disappeared when the number of covariances was normalized to either the sum of Shannon's entropy or the number of variant positions for each genetic region (data not shown). This indicates that the location of the covarying positions was affected by the pattern of amino acid variation in the genome. The exception to this pattern was that covariances were markedly underrepresented in the core (capsid) gene even after normalizing to entropy (especially for genotypes B and C [Table 4]), implying that the core has fewer genetic associations than the other genes.

Table 4.

Distribution of covariances in the HBV genome

Parameter	Value for genotypea:
	B	C	D
Intergenic	43	49	60
Involving Pb	92	89	83
Involving spacer region of P	44	58	42
Involving SAgsc	36	41	37
Involving pre-S1 region of the SAgs	19	23	11
Involving Cd	0.20	0.30	7.0

^aPercentage of total covariances in the indicated genotype.

^bP, polymerase.

^cSAgs are the viral large, medium, and small surface antigen proteins.

^dC, core (capsid).

Each of the three HBV covariance sets formed a single network with high density that contained essentially all the covariances (Fig. 6B; see Fig. S1o to p in the supplemental material). The degree distribution plots for these networks failed to fit the power law (Fig. 6C), again due to a large number of highly connected nodes, leading to a random topology (Table 2). As with the other DNA virus we examined (B19), the HBV network metrics were comparable to the metrics for the majority of RNA viruses. This reinforces the concept that genome-wide covariance networks are a common feature of viral genomes, regardless of their physical structure.

Evaluation of selection and random association in formation of the networks.

Intact, genome-wide covariance networks were found in all 16 viruses examined. Two basic processes could have produced these networks: coordinate selection of functionally compatible residue sets and/or bottlenecks that randomly associated pairs of residues at variable positions in a parental viral population. We evaluated the possible roles for these processes in two ways.

First, generating the covariance networks through a bottleneck would result in deep splits in the phylogenetic trees consistent with ancestry from a few subpopulations of the virus. The phylogenetic trees reveal no evidence for such splits, although shallow or internal splits were common, as would be expected among a collection of independent viral isolates (Fig. 2A; see Fig. S1q to ag in the supplemental material). Mapping the identities of the most highly connected nodes and highest-scoring covariant pairs onto the phylogenetic trees for HEV and HDV also failed to support a simple bottleneck model. In both cases, segregation of the node/edge identity could be seen with internal splits in the tree, but the segregation patterns were not uniform among the covariance and node sets for a given virus. The number of concordant covariance patterns in the trees implied that if bottlenecking had generated the covariances, then the effective population size of the bottleneck must have been ∼3 to 6. Therefore, we tested the effect of generating covariances from 100 HCV 1a sequences derived from an effective population size of four with the assumption of equal fitness for each variant. Just as we observed when we tried to generate networks by combining the subtype 1a and 1b sequences, the deep divisions in the phylogenetic tree in these test sets led to >40,000 covariances rather than the 3,199 seen with the natural HCV sequences. These covariances were not graphed as a network because they would saturate the connections between the variant positions. Similar results were obtained when we modeled a bottleneck for HEV. These covariances formed a network that was larger than the natural network (3,702 covariances between 123 positions compared to 208 covariances and 50 positions) and was much denser than the natural network (average connectivity, 60.5 versus 8.3). Furthermore, the degree plot for the bottleneck network revealed a single sharp peak centered on 60 connections rather than the random scattering found for the natural network. Therefore, we were unable to mimic natural covariance networks by modeling a simple bottleneck. This indicates that if the bulk of the covariances resulted from unselected random association through a bottleneck, then mutation must have subsequently obscured >90% of them.

Second, generation of random covariances by bottleneck events would randomly distribute the covariances among the variable positions in the ancestral viral sequence pool. However, as shown in Fig. 3, generation of networks from random associations of residues at the variable positions in alignments of HCV and HEV sequences either failed to generate a network or produced a network that did not resemble the covariance network formed by natural sequences.

Third, Campo et al. examined amino acid covariance in 114 HCV 1b sequences and independently found that the covariant positions formed an extensive genome-wide hub-and-spoke network (11). These researchers explicitly examined the role selective pressures may have played in the origin of the network. They made three observations: (i) positive selection dominated network positions with low connectivity, (ii) negative selection dominated in the highly connected core region of the network, and (iii) ∼90% of the neutrally selected positions in the network had direct connections to positively and/or negatively selected sites. They concluded that the HCV network arose by coordinated selection among the variable sites. To determine if these observations may apply to the viruses examined here, we assessed selection at network positions for HCV 1a, HCV 1b, DV2, WNV, PV1, HEV, HDV, and HBV genotype B. An average of 31% of the network positions for these viruses had dN/dS ratios (normalized ratios of nonsynonymous to synonymous evolutionary changes) consistent with the residues being under selective pressures. Negative selection (dN/dS < 1) strongly predominated in the viral genomes as a whole, but seven of the eight genomes had codons with evidence of positive selection (dN/dS > 1). In all seven of these viruses, positively selected codons were heavily overrepresented and negatively selected positions were underrepresented in the networks compared to the genome as a whole (P < 0.001 for each virus). For example, the networks contain less than 10% of the residues in each genome, but 71/77 positively selected codons in HCV 1a and 7/9 in HBV genotype B were in the networks. Therefore, many of the residues in the networks are under selective pressures, and these pressures differ from those on the genome as a whole.

These analyses imply that selection was a major force in the evolution of the networks and that founder events during the evolution of HCV were not the primary cause of their development. However, they do not exclude a role for associations generated through bottlenecks during viral evolution. As these processes are not mutually exclusive, it is likely that both contributed to some extent to the covariances reported here.

DISCUSSION

We and others previously identified genome-wide networks of covarying amino acids in HCV (3, 11). These networks were interpreted to indicate that the viral genome evolved as a coordinated unit and to imply the existence of many previously unknown intra- and interprotein genetic dependencies. Here, we asked whether similar covariance networks exist in other viral genomes, and if so, what the patterns among the covariances may imply about the viruses' biology. Four observations resulted from this work.

(i) Genome-wide covariance networks exist in all viruses examined.

Amino acid covariances were found in each of the 16 viral genomes we examined from 13 species and nine viral families, and in every case, the vast majority of the covariances formed a single genome-wide network of genetic associations. These viruses included RNA and DNA viruses with a variety of genomic segmentation patterns, genetic organizations, mean pairwise identities, replication patterns, and transmission mechanisms (Table 1). Control experiments with irrelevant covariances revealed that formation of a single network containing most of the covariances was not an artifact of chance (compare Fig. 2A and 3). Furthermore, the natural networks could not be reproduced through modeling experiments that mimicked a genetic bottleneck. In contrast, we and others (11) found extensive evidence for selective pressures acting on network positions. Therefore, the genome-wide covariance networks are not computational artifacts, and it is likely that selection played a major role in their evolution. The presence of such networks in all viruses we examined indicates that the basic implications of the covariance networks apply widely to viral genomes. These implications include the presence of selective pressures acting coordinately on multiple regions of the genome, coordinate evolution of at least parts of the genome, and widespread genetic dependencies between structural and enzymatic/regulatory proteins.

(ii) Viral amino acid covariance networks usually have a random topology rather than the hub-and-spoke topology found in almost all other biological networks.

The very large majority of biological networks have a hub-and-spoke topology (6, 51). The key implications of this topology are that the network grew by addition of new nodes to the older nodes (accretion) (6, 10), that the most highly connected nodes (hubs) are the most ancient interactions in the network, and that the hubs exert a disproportionately strong influence on the network. This implies that formation of amino acid covariances at most positions in the networks was influenced by preexisting genetic dependencies at the hub positions. It also indicates that the identities of residues at the hub positions disproportionately affect permissible genetic variation at a large number of other positions. Thus, genetic variation at a given site in the network, for example, in an immunological epitope, would be particularly sensitive to the identity of the hub residue with which it is most strongly associated. This also implies that the viral genomes with this topology must rarely undergo molecular recombination, because recombination between two independent genomes would tend to mix network configurations and disrupt the accretion process that underlies the development of a hub-and-spoke topology. HCV has a hub-and-spoke network, and it has a low rate of molecular recombination (49) consistent with this topology. However, low rates of molecular recombination can occur in viruses with a random network topology (i.e., WNV [55]), and viruses with high recombination rates can also have random network topologies (i.e., the parvoviruses [66]). Therefore, differences in recombination rates are not the sole reason why the HCV network has a hub-and-spoke topology whereas the other viral networks do not.

In contrast, the key implications of a random network topology are that the covariances did not develop by accretion and that despite the large number of highly connected nodes, none of them exert disproportionately large influences on the identities of residues at other sites in the network. Random networks could reflect a collection of compensatory variations within a single highly integrated functional unit or they could result from the constraint of a set of functionally independent compensatory adaptations on a restricted number of sites. The strong correlation between the mean pairwise identity in the sequence sets and the percentage of the genome found in the networks (R² = 0.88 for all viruses examined here) argues for a constraint model, as does the correlation between the distribution of covariant positions in the HBV genome and the distribution patterns of its variable positions. However, the existing data are insufficient to resolve these models, and the causes for the random topology are not necessarily the same for all viruses. For example, it is plausible that the HDV network is random because it occurs within a single protein, whereas for HBV, it is plausible that the random network resulted from the overlapping nature of its genes constraining the locations where compensatory amino acid substitutions could occur.

(iii) Network topologies can vary within a given viral group.

Covariance patterns were examined in four species in the family Flaviviridae (HCV, GBV-C, DV, and WNV), in two species within the Picornaviridae (PV1 and HAV), and in multiple representatives within two viral species (two HCV subtypes and three HBV genotypes). This allowed a preliminary assessment of covariance patterns among viruses at different taxonomic levels of a viral group. Both HCV subtypes had hub-and-spoke topologies, and all three HBV genotypes had random topologies. Although not enough examples were examined for generalizations, this implies that subdivisions of a given viral species may usually share a network topology. Both picornaviruses had random network topologies, but the network topologies were not the same among the flaviviruses. The HCV networks were hub-and-spoke, whereas the networks for the other flaviviruses were random. Therefore, viruses with similar genomic structures and genomic replication patterns do not necessarily have the same organization of their intragenomic genetic associations.

(iv) Covariance network analysis can provide inferences regarding viral biology.

The viral covariance patterns contain substantial information that is not accessible by other methods. Five inferences that can be drawn from the HBV and PV1 covariance patterns are presented as examples of the utility of genome-wide covariance analyses.

The first inference is that the HBV core protein must be unusually structurally flexible to accommodate substantial sequence variance without needing intra- or interprotein covariant compensations. This inference is consistent with four other observations. First, core dimers form both T=3 capsids and T=4 capsids, and the dimers pack in slightly different conformations in each capsid isoform (9, 16, 22, 75). Second, the pre-S1 region of the large viral surface glycoprotein contacts the capsid at the tips of spikes formed by the core in multiple partially redundant interactions (64), and the spikes are flexible. This structural plasticity may help to insulate the spikes from allosteric changes in the rest of the molecule. Third, the capsid particle appears to alter conformation late during reverse transcription to trigger envelopment (61). Fourth, core gene sequences encode both the core protein and most of the HBV e antigen (HBeAg). HBeAg is a secreted folding variant of the core protein that functions as an immunomodulator (72). The need for one primary amino acid sequence to support two folding/assembly patterns may have helped limit the development of covariances. This prediction can be tested by using biophysical methods to compare the molecular dynamics of the core protein in its unassembled dimer form and in the capsid compared to the capsid proteins of other viruses.

The second inference involves the spacer domain of the HBV polymerase, for which no molecular function is known. The polymerase (Fig. 6A) is a reverse transcriptase in which the spacer appears to simply link the terminal protein domain to the catalytically active reverse transcriptase and RNase H domains (13, 52, 70). The large number of covariances in the spacer domain (Table 4), many of which are high scoring, implies that it is under coordinate selective pressure with much of the rest of the genome. This implies that the spacer domain has a function, even if it may only be to accommodate conformational flexibility in the polymerase's interactions with other molecules.

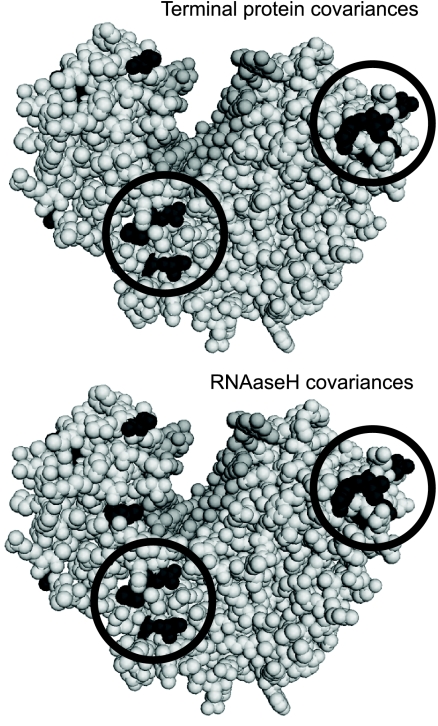
The third inference is the prediction of interdomain coordination sites in the HBV polymerase. No structural information is available for the polymerase, but partially validated molecular models exist for the reverse transcriptase domain based on the HIV reverse transcriptase (17, 40). To determine if covariances may provide guidance about the orientation and/or interaction of the polymerase's domains, we plotted the locations of residues in the reverse transcriptase domain that covaried with residues in the terminal protein or RNase H domain. The only clusters of positions that covaried with the terminal protein that were common to all three genotypes were at the tip of the “finger” region of the reverse transcriptase domain and at the interface between the “palm” and “thumb” regions (Fig. 7 and data not shown). The same two regions also contained the only clusters of covariances with the RNase H domain that were common to all three genotypes. Therefore, these two regions of the reverse transcriptase domain appear to play an important role(s) in the overall coordination of the structure and/or function of the polymerase. We speculate that they may be sites of compensatory adaptations to support the conformational flexibility needed as the enzyme shifts from protein priming (where the terminal protein occupies the reverse transcriptase active site) to DNA elongation (where nucleic acids are in the active site) and/or that they may be sites of direct contact between the domains. The latter speculation is the most plausible reason for the reverse transcrptase-RNase H interdomain interface being at the tips of the fingers, because the RNase H active site must be 50 to 60 Å from the DNA polymerase active site (44), and binding of the RNase H domain at this site could provide the appropriate distance. The polymerase has resisted crystallographic analyses, but this prediction could be tested through hydrodynamic analyses or cross-linking/mass spectrometry studies of polymerases carrying mutations in the putative interdomain interface.

Fig 7.

Regions of the HBV reverse transcriptase domain that covary with both the terminal protein and RNase H domains. Residues in the HBV polymerase reverse transcriptase domain model that covary with terminal protein (top) or RNase H (bottom) domain residues for HBV genotype D are in black. Regions of the model in which covariance is found for all three genotypes with both the terminal protein and RNase H domains are circled. The “thumb” region of the model is at the upper left, and the “finger” region is at the upper right. The darker gray is DNA modeled into the active-site groove.

The fourth inference involves the interaction of PV1 with its cellular receptor. Four of the five subnetworks formed by covariant positions of capsid residues close enough for local contact had residues within the receptor binding site (7). The largest of these subnetworks included VP1 residues 32, 221, and 215 and VP2 residues 140, 141, 169, and 173 along the capsid's 3-fold axis. The clustering of closely spaced covariant positions within the receptor binding sites implies that these variations may provide structural compensation to maintain the function of the receptor binding site (second-site compensatory adaptations have been reported for the PV capsid [50]). This prediction can be tested by creating sets of disfavored residue pairs at network positions and then creating secondary mutations that restore compatible amino acid combinations. The prediction is that receptor binding and viral infectivity would be impaired by the disfavored amino acid permutations and that second-site restoration of compatible sets of residues at the network positions would restore receptor binding and infectivity.

The final inference relates to HBV's low evolutionary rate (relative to HIV), which has been ascribed to the constraining effects of the extensive overlap of HBV's genes and cis-acting genetic elements (48, 76). The very dense, genome-wide nature of the HBV covariance network indicates that by constraining evolution of the overlapping elements, the overlaps also constrain evolution at distant sites that covary with positions in the overlaps. Therefore, one role of the networks is to help visualize the effects that pleiotropy has on epistatic amino acid interactions. Consequently, the long-distance genetic constraints revealed by the covariance networks may help illustrate why molecular-clock models for RNA virus evolution often appear to give inaccurately short divergence times between viral lineages (8, 31, 32, 35). Such long-distance interactions also have implications for vaccine design in cases where sets of epitopes with clear genetic interdependencies can be identified. Including multiple variations of the target epitopes that encompass the network-compatible configurations in a vaccine may reduce the rate of vaccine escape by limiting second-site adaptive options available to the virus.

Concluding comment.

The networks presented here illustrate that variable positions in sequence alignments carry substantial biological information when they are considered in their native context. A few examples of how to access this information using covariance network analyses are presented, but much remains to be done before this and similar approaches reach their potential.