Automated Discovery and Quantification of Image-Based Complex Phenotypes: A Twin Study of Drusen Phenotypes in Age-Related Macular Degeneration

Computational discovery of genetically determined features can reveal quantifiable AMD phenotypes that are genetically determined in a rapid and unbiased fashion that is suitable for large datasets and that should lead to determination of the genes responsible for this phenotypic variation.

Abstract

Purpose.

Determining the relationships between phenotype and genotype of many disorders can improve clinical diagnoses, identify disease mechanisms, and enhance therapy. Most genetic disorders result from interaction of many genes that obscure the discovery of such relationships. The hypothesis for this study was that image analysis has the potential to enable formalized discovery of new visible phenotypes. It was tested in twins affected with age-related macular degeneration (AMD).

Methods.

Fundus images from 43 monozygotic (MZ) and 32 dizygotic (DZ) twin pairs with AMD were examined. First, soft and hard drusen were segmented. Then newly defined phenotypes were identified by using drusen distribution statistics that significantly separate MZ from DZ twins. The ACE model was used to identify the contributions of additive genetic (A), common environmental (C), and nonshared environmental (E) effects on drusen distribution phenotypes.

Results.

Four drusen distribution characteristics significantly separated MZ from DZ twin pairs. One encoded the quantity, and the remaining three encoded the spatial distribution of drusen, achieving a zygosity prediction accuracy of 76%, 74%, 68%, and 68%. Three of the four phenotypes had a 55% to 77% genetic effect in an AE model, and the fourth phenotype showed a nonshared environmental effect (E model).

Conclusions.

Computational discovery of genetically determined features can reveal quantifiable AMD phenotypes that are genetically determined without explicitly linking them to specific genes. In addition, it can identify phenotypes that appear to result predominantly from environmental exposure. The approach is rapid and unbiased, suitable for large datasets, and can be used to reveal unknown phenotype–genotype relationships.

Since the time of Mendel, identification of a genotype has primarily relied on the identification of visible phenotypes as biomarkers for genetic variation. Phenotype definitions can range from biometrics such as eye color and height, which are straightforward to measure, to more complex phenotypes that rely on recognition of similarities between subtle qualitative or quantitative clinical characteristics. Phenotypic definitions can include measurement of multiple characteristics, such as physical features, laboratory values, and imaging results.^1–4

Recognition of complex phenotypes, although occasionally achieved by meticulous study of large datasets, formal manual schemes to describe (retinal) morphology, or statistical analysis such as that used in AREDS, more often has relied on an individual or collaborating clinicians recognizing a phenotype after prolonged, intensive study and contemplation. Specifically with regard to AMD, the description of endophenotypes such as drusen size, drusen area, and pigment clumping, began as qualitative hypotheses to be later confirmed by statistical associations. Image analysis has the potential for a formalized and unbiased discovery of new phenotypes through analysis of high-dimensional feature matrices obtained from the images of a tissue.⁵ Such an approach is especially helpful when a phenotype can be defined by the patterns or distributional relationships among lesions within the tissue.⁶ Recent advances in our understanding of specific genetic risk factors associated with age-related macular degeneration (AMD) coupled with the complex fundus appearances seen in this disease offer an ideal substrate to test this approach.

AMD is the most common cause of visual loss in the United States and Europe and is a growing public health problem.⁷ Currently, almost 7.2 million Americans, or 6.5% of the U.S. population 40 years of age and older, are estimated to have AMD, and it is the cause of blindness in 54% of all legally blind Americans.⁸ AMD is a major societal problem in terms of disability and health care costs.^9,10The prevalence of AMD is expected to double over the next 25 years.¹¹

A growing number of genes and genetic loci have been shown to contribute to the development of the AMD phenotype (see http://www.hugenavigator.net/HuGENavigator/geneProspector.do?query=age+related+macular), although only three of these account for large population-attributable risk in the United States: complement factor H (CFH), ARMS2/HTRA1 and complement component 2/factor 3 (CC2-CF3). Based on the population-attributable risk of their study samples, it has been estimated by various investigators that 40% to 75% or more of genetic variance from AMD can be explained by common variation at the five most common single nuclear polymorphisms (SNPs).^12,13 The genotypic landscape of AMD remains complex and undiscovered, with novel data added regularly.

AMD patients exhibit diverse and complex fundus appearances. The clinical hallmark of AMD is the drusen deposit, although deposition of other clinically invisible accumulations, such as basal laminar and basal linear deposits, may be more specific.^14–16 In fundus photographs, drusen appear as yellow or white, round or confluent deposits between the basement membrane of the retinal pigmented epithelium (RPE) and the elastic portion of Bruch's membrane.¹⁷ Cross-sectional, longitudinal, and interventional studies, including the Age-Related Eye Disease Study (AREDS), have evaluated the role of drusen and other factors and shown that AMD visual outcome is related to clinically visible characteristics.^18–22 These characteristics include the presence of large drusen (>125 μm), the presence of multiple intermediate drusen (>63 and <125 μm), the presence of RPE pigmentary abnormalities (hyperpigmentation), and contralateral disease severity.^17,19,21 In addition, AMD shares, with other forms of macular degeneration, the development of RPE atrophy and an increased incidence of choroidal neovascularization (CNV).²³ An important obstacle to the recognition of AMD phenotype–genotype relationships is that after the development of CNV (exudative AMD), exudation and atrophy can obscure the presence and relationship of drusen and other AMD-related lesions.

Many investigators regard the appearance and/or enlargement of drusen as a stochastic process in which an increasing number or size of drusen are associated with increased progression of disease. In this view, drusen, and other AMD lesions are randomly distributed over the macula (central fundus) in a pattern that is independent of genotype, but may over time increase or, in rare instances, decrease in area. The risk of incident complication of CNV has been associated with a threshold drusen size and number,²⁴ but not with their distribution. In 2001, Hageman et al.¹⁷ concluded that phenotypic variation, especially the amount of RPE pigmentation and size and extent of drusen, is associated with AMD severity, but is not related to genotype, based on the data available to them.²⁵ Exceptions to the assumption that a larger drusen burden parallels progression are common. For instance, a rare form of AMD known to be associated with a mutation in fibulin-6 (hemicentin-1), an RPE basement membrane component, presents with small, central drusen and small, parafoveal regions of geographic atrophy that progressively enlarge to involve the fovea.²⁶ Seddon et al.²⁷ showed a heritable contribution to early, intermediate, and advanced AMD, including drusen area, which has a hereditability of up to 0.71. Hammond et al.²⁸ evaluated early maculopathy, using twin data, and came to similar conclusions. Peripheral retinal drusen and reticular pigment changes have been shown to be related to CFH genotypes.²⁹

In this study, we hypothesized that there are heritable drusen distribution phenotypes for AMD, that they are associated with genotypic variation, and that these phenotypes can be discovered and quantified by using automated image analysis of fundus (retinal) color images. Because of the topographic complexity of AMD abnormalities, we believe that sub- or endophenotypes of nonexudative AMD may provide the necessary complexity and information content to establish genotypic relationships.

Methods for segmentation of drusen in fundus photographs—that is, for partitioning the image into two sets of pixels, one for the drusen and one for the nondrusen background—have been described, but have always required some human input and were thus never fully automated and unbiased. Recent methods have been based on mathematical morphology,³⁰ histogram-based adaptive local thresholding,³¹ background removal and histogram-based thresholding,³² and pixel classification.³³ In our experience, it has been difficult to efficiently and automatically detect all drusen using single detector approaches, given the large range of drusen size (from discrete, hard drusen to large confluent so-called soft drusen), shape (described as punctiform, confluent, or fused), and contrast (from indistinct to distinct).^19,34 Thus, we developed two wavelet-based lesion detectors to recognize hard and soft drusen separately in retinal color images, which we showed to be superior to other approaches.³⁵

After detection and segmentation of drusen, their number, size, and distribution can be numerically characterized as features. A mathematical definition of “feature” provides a repeatable, quantifiable description and thus an accurate and objective representation of the patients' clinical appearance, although this may not correspond to the clinicians' or geneticists' implicit concept of a phenotypic characteristic. Thus defined, features will in some cases directly correspond to clinically visible lesions or relationships between lesions (Table 1). If these features are shown to be under genetic influence, they can reveal novel or confirmatory, quantitative, objective phenotype–genotype relationships.

Table 1.

Visual Features Evaluated in This Study

No.	Description	Detector	Color	Texture	Shape	Quantity	Spatial	P
1	Wavelet analysis of the lesions53	Shape (sens)	✓	✓	✓			0.221
2	Wavelet analysis of the lesions53	Shape (spec)	✓	✓	✓			0.310
3	Wavelet analysis of the entire field of view (FOV)53	None	✓	✓	✓			0.940
4	Wavelet analysis of the 1st 1/4 of the FOV, from nasal to temporal53	None	✓	✓	✓			0.956
5	Wavelet analysis of the 2nd 1/4 of the FOV, from nasal to temporal53	None	✓	✓	✓			0.968
6	Wavelet analysis of the 3rd 1/4 of the FOV, from nasal to temporal53	None	✓	✓	✓			0.587
7	Wavelet analysis of the 4th 1/4 of the FOV, from nasal to temporal53	None	✓	✓	✓			0.215
8	Average color of the lesions in the RGB space54	Shape (sens)	✓					0.266
9	Average hue of the lesions54	Shape (sens)	✓					0.860
10	Average color of the lesions in the RGB space54	Shape (spec)	✓					0.576
11	Average hue of the lesions54	Shape (spec)	✓					0.576
12	Average number of neighbors in the triangulated lesions graph55	Shape (sens)				✓	✓	0.751
13	Average distance between neighbors in this graph55	Shape (sens)				✓	✓	0.422
14	Distribution of the distances to the centroid of the lesions56	Shape (sens)					✓	0.403
15	Average number of neighbors in the triangulated lesion graph55	Shape (spec)				✓	✓	0.422
16	Average distance between neighbors in this graph55	Shape (spec)				✓	✓	0.793
17	Distribution of the distances to the centroid of the lesions56	Shape (spec)					✓	0.181
18	Histogram of the lesions along the x-axis, from nasal to temporal56	Shape (sens)					✓	0.187
19	Histogram of the lesions along the x-axis, from nasal to temporal56	Shape (spec)					✓	0.998
20	Average elongation of the lesions57	Shape (sens)			✓			0.793
21	Average elongation of the lesions57	Shape (spec)			✓			0.246
22	Wavelet analysis of the lesions53	Texture	✓	✓	✓			0.908
23	Area covered by the lesions22	Texture				✓		7.58 × 10−5
24	Distribution of the distances to the centroid of the lesions56	Texture					✓	0.377
25	Coefficient of dispersion58	Shape (spec)					✓	0.609
26	Coefficient of aggregation58	Shape (spec)					✓	0.152
27	Mean crowding vector59	Shape (spec)					✓	0.928
28	Mean crowding regression59	Shape (spec)					✓	0.451
29	Coefficient of dispersion58	Texture					✓	0.783
30	Coefficient of aggregation58	Texture					✓	0.152
31	Directional correlogram60	Texture					✓	0.084
32	Anisotropy index (extracted from the directional correlogram)60	Texture					✓	0.266
33	Fractal dimension (extracted from the directional correlogram)60	Texture					✓	0.368
34	Fractal dimension (extracted from the wavelet analysis)61	Texture		✓	✓			0.901
35	Edge histogram62	Texture		✓	✓			0.227
36	Number of lesions22	Shape (spec)				✓		0.326
37	Moran's 1 of the drusen distribution (spatial autocorrelation)48	Texture					✓	0.040
38	Geary's c of the drusen distribution (spatial autocorrelation)47	Texture					✓	0.012
39	Standard deviational ellipse57	Shape (spec)					✓	0.318
40	Standard deviational ellipse57	Texture					✓	0.215
41	Semivariogram of the drusen distribution46	Texture				✓	✓	2.67 × 10−4

Shape (sens) and shape (spec) stand for the shape-based detector, with a high sensitivity or high specificity detection setting, respectively. Texture refers only to the texture based detector.

In this preliminary study, we selected fundus photographs from a unique genetic population, a cohort of identical (monozygotic; MZ) and fraternal (dizygotic; DZ) twins, in which one or both were affected by AMD.²⁷ Targeting a population of twins that manifest AMD allows us to use powerful classic twin modeling methods to select gene-associated features that have not been shown or been suspected of being linked to an AMD phenotype and to efficiently define disease features rather than nondisease or wild-type variations.

The purpose of this study is to test our hypotheses that heritable macular drusen distribution phenotypes exist for AMD, that they are associated with genotypic variation, and that these phenotypes can be discovered and quantified using automated image analysis of fundus (retinal) color images.

Methods

Subjects

The study population was derived from the National Academy of Sciences–National Research Council World War II Veteran Twin Registry as described elsewhere,^36,37 which includes 15,924 white male twin pairs born between 1917 and 1927 who served in the U.S. armed forces. From this registry, a subset of 840 twins were enrolled in the U.S. Twin Eye Study, including 340 twin pairs (n = 680) in which one or both twins reported having AMD, 51 twin pairs (n = 102) in which neither twin reported having AMD, and 58 singletons (Seddon JM, et al. IOVS 1997;38:ARVO Abstract 3172).²⁷ All 840 twins in this subset were photographed, and the macular photographs were graded according to the Clinical Age-Related Maculopathy grading System (CARMS)³⁶ and the Wisconsin grading system.³⁸

This preliminary or proof-of-concept study is based on the initial set of twins who were identified and digitized. Digitization was performed in alphabetical order, and this data set represents approximately half of the NAS-NRC WWII Veteran Twin Registry twin data set that was included in prior AMD studies.²⁷ Entry criteria included twin pairs, for which at least one eye had adequate complexity of AMD (nonexudative AMD) and for which photographs of adequate quality for analysis were available. One hundred sixty-two twins of 81 twin pairs were graded, and the image quality was assessed. Of these, 148 subjects (representing 74 twin pairs) met the entry criteria of CARMS grade 3 in the worse eye (extensive intermediate or large drusen, with or without RPE abnormalities) and were of adequate image quality for human grading.

Fundus images were originally acquired with a 30° (FF4; Carl Zeiss, Dublin, CA) or 60° (Canon, Tokyo, Japan) fundus camera, with the field centered near the fovea, and recorded on color film (Ektachrome 100; Kodak, Rochester, NY). The film images were shared with us by the U.S. Twin Study of AMD (courtesy of author JMS) and digitized at Iowa by a high-throughput digitization device that used a CCD detector, at a resolution of 1953 × 1301 at 16 bits per pixel per color channel. Both eyes of each twin and both twins in a pair were imaged with the same camera, and a 30° field of view was evaluated (where available). Most images were of a 30° field of view; if they were not, they were cropped to 30° before image analysis.

Study Design and Definition of Terminology

We set out to test our hypothesis in two steps: first, by determining the drusen distribution features (potential phenotypes) that are capable of differentiating MZ from DZ twins to a statistically significant threshold and then by evaluating the heritability of these potential drusen distribution features using an ACE model.^27,39 In this preliminary study, we tested these hypothesis-driven relationships without explicitly associating each feature to one or more specific AMD-associated genes.

We mathematically defined and calculated a drusen distribution feature as a number that expresses how close all drusen in an image fit a certain distribution type. For example, a clustered drusen distribution feature would have a larger value if the drusen in the image were clustered together and a smaller value if the drusen were more evenly dispersed across the image. We then calculated the incongruence between twin pairs for each of the drusen distribution features. A larger incongruence for a given twin pair and for a specific drusen distribution feature means that the two individuals' fundus images differed more in this feature, and a smaller incongruence means that they were more similar when measured according to this feature. If we observed a larger average incongruence for a specific drusen distribution feature in DZ than MZ twin pairs, we judged that this feature was more likely to be under genetic control, because MZ twins share almost their entire genetic material, whereas DZ twin pairs on average share only half.

For details of how we performed automated drusen detection, calculated drusen distributional features and drusen higher order statistics, measured image incongruence measures between images, and calculated intertwin incongruence for a feature, see Appendix sections A–D.

Outcome Parameters and Data Analysis

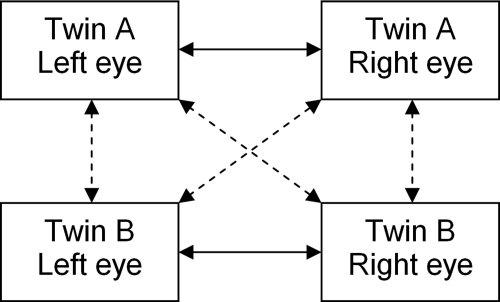
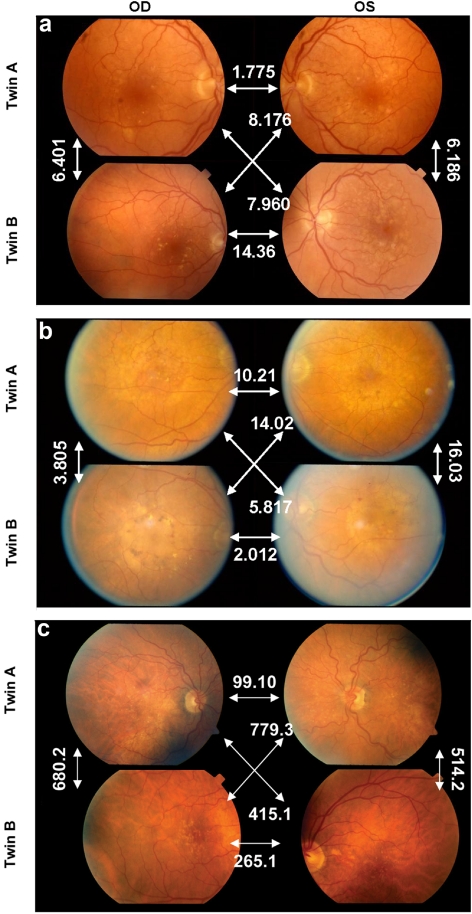
If a drusen feature is controlled genetically, we expect intertwin (i.e., twin A to twin B) image incongruencies and intratwin (i.e., right eye compared to mirror image of left eye of individual) image incongruencies (definitions illustrated in Figs. 1, 2) to be similar in MZ twin pairs. Except for epigenetic or somatic variation, both eyes of an individual should have the same nuclear DNA. Therefore, the incongruency (i.e., image distance) between two persons is not expected to be smaller than the differences between the eyes of each of these persons. For DZ twin pairs, this expectation is not necessarily the case. One would expect the intertwin image incongruencies (between the two individuals in a twin pair) to be larger than the intratwin image incongruencies (between the eyes of a single individual), as the twins within any pair are on average more genetically heterogeneous (farther apart). As a consequence, on average, if a feature or group of features, f, is controlled genetically, the intertwin incongruence or distance, D_f, as defined in Appendix D, in a given twin pair is approximately equal to the distance between MZ twin pairs and smaller than the distance between DZ twins. The larger the average intertwin incongruence D_f for feature(s) f, therefore, the greater the possibility that f is not completely controlled genetically and is under partial or complete (shared or nonshared) environmental or epigenetic control. Because few phenotypes are 100% genetically determined, we do not expect that drusen features would show a perfect separation between all MZ and DZ twin pairs. However, we do expect to find a significant difference in the distribution of the incongruencies between MZ twin pairs and that of the incongruencies between DZ twin pairs. To measure the statistical significance of the difference, if any, between these two distributions, we used the two-sample Kolmogorov-Smirnov test (K-S test).⁴⁰ The K-S test was applied to the incongruency distributions derived from a single drusen feature. Since we also computed the total incongruencies for two features, we used a 2-D generalization of the K-S test to measure the significance if any of the differences on those combinations of features.⁴¹ The results were presented in terms of P value, and a significance level of 95% was used to analyze the results. Let m₁ = 42, the number of MZ twins, and m₂ = 32, the number of DZ twins in the dataset, and let M be the normalized number of samples:

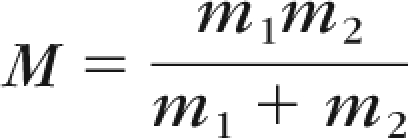The condition for the P to be meaningful is M ≥ 4, for the 1-D K-S test, and M approximately equal to or greater than 20, for the 2-D K-S test^40,42; in our dataset, M = 18.16. For this study, only 1- and 2-D values or vectors were compared.

Figure 1.

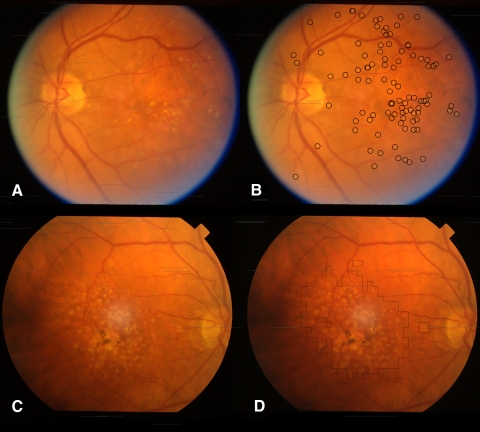
Examples of automated soft and hard drusen detection. (A) Left eye of a twin with predominantly hard drusen. (B) Circles outline hard drusen candidates that were above a predefined probability threshold, as detected by our shape-based hard drusen detector applied to image (A). (C) Right eye of twin with predominantly soft drusen, as well as some pigmentation centrally. (D) Outlined region indicates a soft drusen-containing area that was over a predefined probability threshold, as detected by our soft drusen texture–based detector applied to (C). The region in (D), although primarily consisting of soft drusen, also includes a small area of pigmentation adjacent to confluent soft drusen that is ignored by the segmentation method.

Figure 2.

Definition of incongruencies between twins. The incongruency between twin A and twin B is the ratio of the average intertwin incongruency (dashed arrows) and the average intratwin incongruency (solid arrows).

Structural Equation Modeling of ACE Contributions

Using standard structural equation modeling techniques on data for twins reared together, additive genetic effects (A), shared environmental effects (C), and nonshared environmental effects (E) can be differentiated.^27,39 In brief, this technique assumes that additive genetic effects (A) result from multiple genes, whose influences are additively combined. Shared environmental effects (C) are environmental factors shared by siblings reared in the same family or circumstances. Nonshared environmental effects (E) are environmental effects unique to an individual, or their epigenetic variation, making the twins less similar. Assuming that both MZ and DZ twins share similar contributions of familial environmental effects on the phenotype (the so-called equal-environments assumption), any greater similarity between MZ twin pairs than between DZ twin pairs should be the result of genetic influences.⁴³ The genetic models were estimated by full-information maximum likelihood estimation, with the program OpenMX.⁴⁴ OpenMX arrives at estimates of the A, C, and E components through an iterative process, during which it identifies those values of the components that best reproduce the observed variance–covariance matrices for the MZ and DZ twins, considering the theoretical model of how the different components affect twin resemblance. The full ACE model is statistically compared to the more restricted AE, CE, and E models, where the value of one component—or, in the E model, two components—had been fixed at 0. By comparing the fit statistics of the full model with the more restricted ones, the impact on a phenotypic measure of a specific component can be estimated. For example, if the A component is removed from the model and the resulting, more restricted, CE model is found to have a statistically significant reduction of model fit compared with the full ACE model, it suggests that the A component is statistically significant, and it is necessary to include it in the model. The Akaike Information Criterion (AIC)⁴⁵ was used as an indicator of model fit. Lower AIC values for a model compared with another model indicate that the first model mentioned has a better fit and should be preferred.

Results

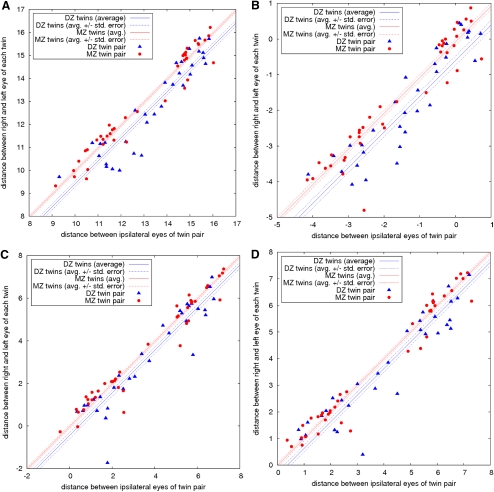
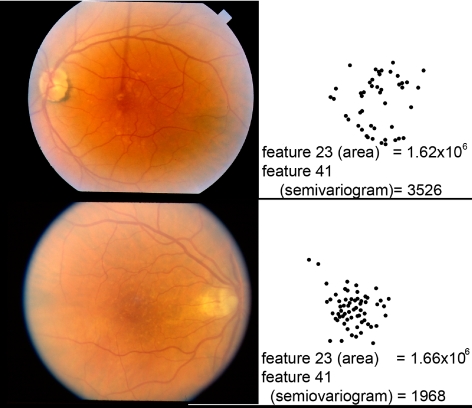
All features could be successfully measured from all images. The resulting 1-D Kolmogorov-Smirnov analysis P values are given in Table 1. Most features did not have intertwin incongruencies that were significantly different between the MZ and DZ twins. The exceptions were features 23 (P = 0.0000758, area covered by lesions), 41 (P = 0.000267, semivariogram of drusen distribution),⁴⁶ 38 (P = 0.0124, Geary's spatial autocorrelation of drusen distribution),⁴⁷ and 37 (P = 0.0403, Moran's spatial autocorrelation of drusen distribution).⁴⁸ Feature 23 (area covered by lesions) is related to the quantity of drusen, whereas 41 (semivariogram of drusen distribution), 38 (Geary's spatial autocorrelation of drusen distribution), and 37 (Moran's spatial autocorrelation of drusen distribution) are related to the spatial distribution. Scatterplots illustrating the discrimination ability of these four features are shown in Figure 3.

Figure 3.

Average intratwin incongruencies as a function of the average intertwin incongruencies. The incongruencies are computed with respect to the four most discriminant visual features: (a) the area covered by drusen, feature 23; (b) the semivariogram of the drusen distribution, feature 41; (c) the Geary's c of the drusen distribution, feature 38; and (d) the Moran's I of the drusen distribution, feature 37. The incongruencies are displayed on a logarithmic scale.

For combinations of two features, 120 feature pairs had an uncorrected P < 0.05, including feature pairs 23 and 41 (P = 0.000328), 23 and 37 (P = 0.000531) and 23 and 38 (P = 0.000678). Scatterplots (Fig. 4) illustrate the ability of these pairs of features to discriminate the MZ from the DZ twin pairs. As explained in the methods section, selected MZ twin pairs did not follow the expected intertwin incongruence and demonstrated high intertwin distances (Fig. 5).

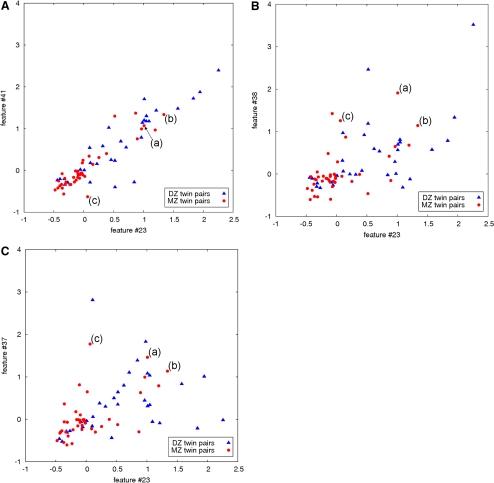
Figure 4.

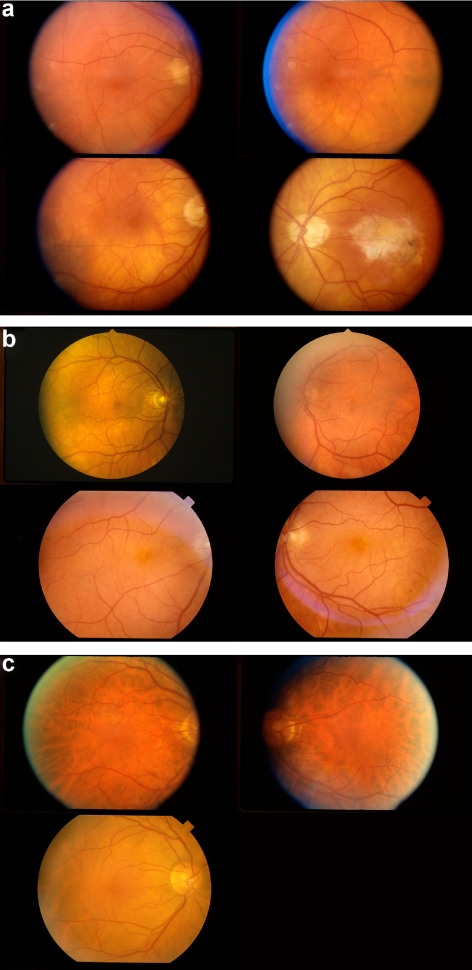
Intertwin incongruencies, shown on a logarithmic scale, for three discriminant pairs of visual features: (a) visual features 23 and 41; (b) visual features 23 and 38; and (c) visual features 23 and 37. Feature 23 is the area covered by drusen, 41 is the semivariogram of the drusen distribution, 38 is the Geary's c of the drusen distribution, and 37 is the Moran's I of the drusen distribution. Because phenotypes are not under complete genetic control, a perfect separation between all MZ twin pairs and DZ twin pairs is not expected in examining these feature pairs. For example, MZ twin pairs (a), (b), and (c) (outliers) were misclassified as DZ by all three feature pairs The corresponding fundus images for these twin pairs are shown in Figure 5.

Figure 5.

Because AMD fundus phenotypes are never under 100% genetic control, there was no perfect separation between all MZ twin pairs and DZ twin pairs, as exemplified by the fundus image feature pairs of the twins shown in Figure 4. (a–c) Fundus images for both individuals in three sets of MZ twin pair outliers (indicated with the corresponding letters in Figure 4) that were misclassified as DZ.

Features 23 (area covered by lesions), 41 (semivariogram of drusen distribution), 38 (Geary's spatial autocorrelation of drusen distribution), and 37 (Moran's spatial autocorrelation of drusen distribution) exhibited an MZ versus a DZ twin pair classification accuracy of 75.7%, 74.3%, 67.6%, and 67.6%, respectively. We observed nonsignificant clustering of incongruencies for DZ twin pairs, meaning that the tail of the distribution did not monotonously decrease, but rather had a few peaks.

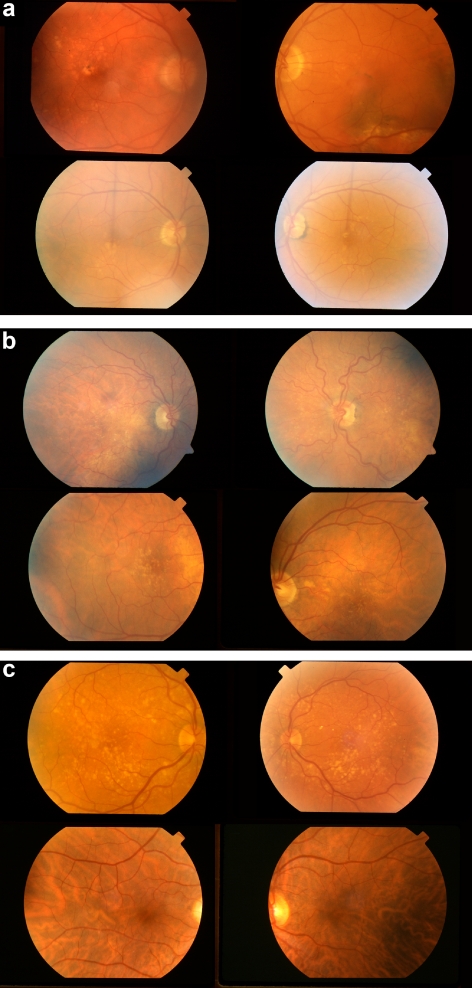
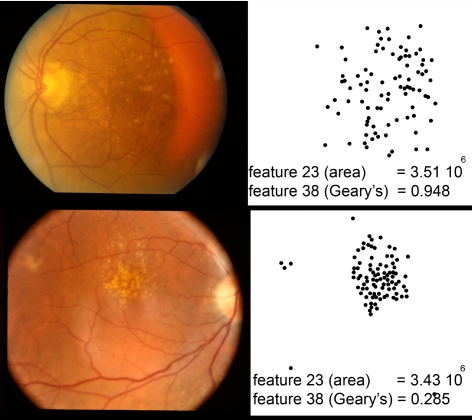
To illustrate the correspondence between the most discriminant drusen features and their human visual appearance, examples of twin pairs with indicated intereye and intertwin incongruencies are displayed in Figure 6, for feature 23, and in Figure 7, for feature 38. Feature 38 (Geary's autocorrelation) measures the spatial autocorrelation, with emphasis on the local autocorrelation at a scale adapted to the drusen (the resolution of the soft drusen detector), as opposed to feature 37 (Moran's autocorrelation) (Fig. 8). Feature 41 (semivariogram of drusen distribution) is a generalization of Geary's spatial autocorrelation of drusen distribution, where the scale varies continuously (Fig. 9). A positive autocorrelation means that neighboring areas have similar values. Applied to the spatial distribution of drusen probability, a positive autocorrelation discerns the presence of large lesions such as soft drusen, and a negative autocorrelation distinguishes the presence of small lesions such as hard drusen.

Figure 6.

(a–c) White arrows: typical interimage incongruencies for three twin pairs with feature 23, representing the area covered by drusen, and the intertwin incongruency for feature 23 between the individuals in each twin pair. (a) MZ twin pair with similar feature 23 (drusen area) values for all four eyes, and an intertwin incongruency of 0.977; (b) DZ twin pair had a larger feature 23 for both eyes of individual A than for individual B, but contralateral eyes for each individual had similar values and an intertwin incongruency of 1.68; (c) DZ twin pair with drusen in both eyes of individual A but not in those of individual B and an intertwin incongruency of 6.26 with respect to this feature.

Figure 7.

(a–c) White arrows: typical interimage incongruencies in three twin pairs for feature 38, representing the spatial autocorrelation of the lesion distribution (Geary's c) and the intertwin incongruency for feature 38 between the individuals in each twin pair. (a) MZ twin pair with similar donutlike distribution of drusen in all four eyes, with an intertwin incongruency of 0.890. (b) MZ twin pair with spread out drusen in individual A, but homogenous drusen perifoveally in individual B and an intertwin incongruency of 1.62. (c) DZ twin pair with spread out drusen in individual A but clustered in individual B in both eyes and an intertwin incongruency of 11.7 with respect to feature 38. The area covered by drusen (feature 23) was approximately identical in each image in (a) and (b).

Figure 8.

Feature 38, the Geary's c statistic of drusen distribution, in two images from two individuals in different twin sets, with similar values for feature 23, total area of drusen, but highly different values for feature 38, Geary's c statistic. Left: fundus images, right: drusen detected on the same scale.

Figure 9.

Feature 41, a semivariogram of the drusen distribution, in two images from two individuals from different twin sets, with similar values for feature 23 (total area of drusen), but highly different values for feature 41 (semivariogram). Left: fundus images; right: drusen detected on the same scale.

Each of the features identified as significant was analyzed using structural equation modeling (ACE) to assess the relative contributions of genetic and environmental contributions. For three of the four features evaluated, the AE model (lacking any shared environmental effect) was found to be the best fit. In the remaining case, the E model (to which only nonshared environmental factors contribute) was the best fit for the observed data. Specifically, features 23 (area covered by lesions), 41 (semivariogram of drusen distribution), and 37 (Moran's spatial autocorrelation of drusen distribution) had 55%, 77%, and 25% genetic contribution, respectively, with the remainder from nonshared environmental contribution. The best fit model for feature 38 (Geary's spatial autocorrelation of drusen distribution) was solely based on nonshared environmental components.

Discussion

The results of this preliminary or proof-of-concept study show that heritable, but previously unrecognized, drusen distribution phenotypes exist in AMD, that these are associated predominantly with genotypic variation, and that these phenotypes can be discovered and quantified using automated image analysis of fundus color images. Image analysis of digitized fundus images of AMD patients has the potential to identify heritable features that differentiate MZ from DZ twins, indicating that specific differences in drusen quantity and distribution are largely determined by genetic factors. We have recently demonstrated the use of this approach in identifying heritable optic nerve head shape components.⁴⁹

The results also allow initial conclusions to be made about the mapping between AMD genotype and drusen phenotype. Although color and texture features are relevant to the detection of drusen, these features were not significant in separating MZ from DZ twin pairs, within the limits of a three-color channel camera–scanner combination. As a consequence, the observed differences in drusen color and texture among subjects were not found to be affected by genotype within this dataset. We have not yet explored the shape parameters thoroughly enough to comment on whether drusen shape variations among subjects are likely to be affected by genotype. A more advanced study of drusen shape would be needed, to answer the question of shape determination.

Quantity and spatial distribution features of drusen are evidently highly relevant in separating the MZ from the DZ twin pairs. Indeed, we have shown that intertwin incongruencies, based on drusen quantity (feature 23, area covered by lesions), and drusen spatial distribution (feature 41, semivariogram of drusen distribution; 38, Geary's spatial autocorrelation of drusen distribution; 37, Moran's spatial autocorrelation of drusen distribution), are significantly different for MZ and DZ twin pairs. ACE structural equation modeling showed that there is a substantial genetic component (55%–77%) to the variation in these features. The lack of any substantial shared environmental effect of these features is not surprising, in that AMD is a disease associated with advanced age. Twins spend perhaps the first 18 years of life together, but the AMD twin pairs have lived much more than half of their lives apart.

As expected, some MZ twin pairs had relatively large intertwin incongruencies and were therefore misclassified as DZ. Three examples of such MZ twin pairs with large intertwin incongruencies are shown in Figure 5. The most likely explanation is that these fundus phenotypes are not 100% under genetic control; partial shared or nonshared environmental exposure plays a role, and such an effect is not unlikely for a phenotype that typically manifests with advanced age. Other potential explanations are epigenetic effects or that the genes contributing to a particular drusen feature may not be identical, because of the somatic mutations.⁵⁰ In other words, a perfect separation between MZ twin pairs and DZ twin pairs, according to the drusen phenotypes discovered in this study, is unlikely.

Three weaknesses of this study are related to the inherent limitations of the twin population. First, the twin pairs do not represent all stages of AMD, but rather are biased toward the moderate to severe forms of nonexudative AMD. We incorporated this potential bias when we restricted the inclusion to those with CARMS grade 3. This bias may lower the statistical power of detecting some features of a phenotype, as the number of available twin pairs is reduced. The alternative scenario of including nonexudative AMD subjects with less severe disease (CARMS grade 2) would potentially include subjects who had incompletely expressed phenotypes (i.e., a few drusen or minimal pigment change) that may dilute feature detection. We judged that the inclusion of minimally or mildly affected AMD subjects may increase the statistical variability of a stage-expressed feature or detract from the statistical signal by including subjects with incompletely expressed phenotypes.

Second, this twin population contains exclusively males, as most of the soldiers in World War II were male. Thus, any sex-specific skew in phenotype or AMD-associated allele frequencies may bias our results. No sex-specific differences in genotypes have been detected in AMD to date. Third, we did not include genetic data in this study. One approach to further explore the genetic basis of drusen distribution would be to determine whether known AMD-associated genes or genome-wide single-nucleotide polymorphisms (GW SNPs) preferentially segregate in image-analysis–based phenotypic features.

Obviously, this preliminary study is unable to provide insights into the genes that have a role in the drusen distribution phenotypes that we have found. One approach to further explore the genetic basis of drusen distribution would be to perform a genome-wide association scan on the full twin dataset. Such a study may have sufficient power to identify the genes that have even modest influence on the drusen distribution phenotypes. Potentially, the detectors that measure drusen phenotypes will also be useful for evaluation of larger nontwin populations of nonexudative AMD, such as the subjects in the AREDS. We propose that phenotype discovery from images using image analysis, quantification of higher order statistics and use of a distance metric has the potential to reveal phenotypic differences in other, extraocular organs. In addition, this approach can also be applied to images of other modalities such as fundus optical coherence tomography and fundus autofluorescence. Finally, it may in the future allow the role of genetic contribution to phenotype in unrelated individuals to be evaluated.

In summary, new, previously unrecognized, quantifiable drusen distributional phenotypes were identified in fundus photographs of twins with AMD. Most of the variation in these phenotypes was found to be genetic. We expect that our approach of automated discovery and quantification of phenotypes with higher order statistics of images will also be useful in other biological and medical fields in which visible phenotypes are complex, and the genotypic associations are also complex. The results of this preliminary study further support efforts to search for the genes that control drusen distributional phenotypes, using an array of gene discovery approaches.

Appendix A

Automated Drusen Detection

Most images contained large (soft) and small (hard) drusen that were detected and segmented using two automated algorithms: shape- and texture-based. They were based on a wavelet transform to increase the signal-to-noise ratio and allow multiscale analysis. The shape-based detector was a slightly modified version of a previously published microaneurysm detector, used in the wavelet domain.³⁵ The shape-based detector was designed to detect hard drusen and small, distinct, soft drusen. A texture-based detector was newly developed for this study and models the distribution of the wavelet transform coefficients in several frequency subbands, after preprocessing (described more completely in Appendix B).³⁵

Appendix B

Texture-Based Drusen Detector

The texture-based drusen detector consists of an optimal sequence of image processing and machine learning steps: (1) Images are denoised with a small circular median filter, (2) the green and the red channels of images are decomposed on three levels, on the cubic B-spline wavelet basis, (3) the average and standard deviation of the absolute value of the wavelet coefficients are extracted in each subband of the wavelet transform of image patches of 64 × 64 pixels, and (4) the extracted feature vectors are classified by a support vector machine. The novelty of the proposed texture-based detector comes from the selection of the processing sequence and parameters: They are automatically selected by grammatical evolution among several tunable processing steps.⁵¹ In particular, it turned out that none of the eye fundus background normalization techniques known in the art improved the classification accuracy.

Most soft drusen and confluent hard drusen are segmented by this texture-based detector. Both detectors were trained on a set of 100 previously annotated images of patients with AMD containing soft and hard drusen, obtained from the de-identified cohort of the Iowa AMD Registry. Thus, none of the test images was ever used for algorithm training. The output of both texture- and shape-based detectors produce an output of lesion probability maps that give the likelihood that each pixel is part of a soft or hard drusen (Niemeijer M, et al. IOVS 2005; 46:ARVO E-Abstract 3468).⁵² In the shape-based detection probability maps, pixels above a given probability threshold were clustered to isolate individual drusen; only the drusen center points were stored. Because a center point is ambiguous for noncircular soft drusen, a center point for these lesions was not included in computing the algorithm. Instead the output was retained within the probability map. Figure 1 shows examples of the outlines of the high-probability areas. The shape-based automated drusen detector was compared with a human expert standard (obtained by three experts) in a totally independent 12-image dataset: A 74% agreement score was achieved at the pixel level compared with the scores of the experts.

Appendix C

Drusen Distributional Features and Calculation of Drusen Higher Order Statistics

Next, the detected and segmented drusen were automatically quantified individually and as a group on the following characteristics: color, texture, shape, quantity, and spatial distribution. As we did not want to bias the study in terms of these specific candidate drusen features, we extensively reviewed the digital image processing and quantitative biology literature, to find candidate features. This resulted in the list of 41 features that are listed in Table 1. When each feature required specification of additional shape or scale parameters, these were specified before analysis of any twin-pair images and were not adjusted based on the results, to avoid selection bias and over-fitting.

Appendix D

Image Incongruence between Images, D_f: Intertwin Incongruence for a Feature

For any pair of images, the incongruence was represented mathematically by the arithmetic difference between the value of convolution of each feature (filter) with each image. For every twin pair, we defined the distance between twin A and twin B as the ratio of the average intertwin image distances (sum along the dashed arrows or [AL,BL+AR,BR+AL,BR+AR, BL]/4; Fig. 2) and the average intratwin distances (average along the solid arrows or [AL,AR+BL,BR]/2; Fig. 2).

If a feature analysis consisted of a vector or a maximum of two values in this study (e.g., the average intensity in the red, green, and blue color channels), then the image incongruence was the Euclidian distance between these two vectors. Let d_f (I, J) denote the image incongruence between the two images I and J, with respect to a given feature f. Intertwin incongruence between twins A and B was then defined as follows: D_f (A, B), the ratio between the average intertwin image incongruence (I belonged to twin A and J to twin B), as well as the average intratwin image incongruence (I and J belong to the same twin). Let A_R and A_L (or B_R and B_L) denote the fundus image of the left and of the right eye of twin A (or twin B). D_f (A, B) is then expressed as follows (see Fig. 2):

For twin pairs in which one twin had had only one eye photographed, the numerator's sum consists of two terms and the denominator's sum consists of a single term.